Область определения функции
Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.
В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.
Понятие и обозначение области определения функции
Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой. На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.
По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:
Определение 1Числовая функция с областью определения D – это соответствие значений переменной x некоторому числу y, которое находится в зависимых отношениях с x.
Используя это определение, охарактеризуем нужное нам понятие более четко:
Определение 2Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.
Теперь рассмотрим, как правильно обозначать ее на письме. Ранее мы договорились, что для записи самих функций будем использовать маленькие латинские буквы, например, g, f и др. Чтобы указать на наличие функциональной зависимости, используется запись вида y=f(x). Таким образом, функция f представляет собой некоторое правило, согласно которому каждому значению переменной x можно поставить в соответствие значение другой переменной y, которая находится в зависимых отношениях от x.
Возьмем для примера функцию y=x2. Можно записать ее как f(x)=x2. Это функция возведения в квадрат, которая ставит в соответствие каждому значению переменной x=x0 некоторое значение y=x02. Так, если мы возьмем число 3, то функция поставит ему в соответствие 9, поскольку 32=9.
Чтобы обозначить область определения некоторой функции f, используется запись D(f). Однако нужно помнить, что у некоторых функций есть собственные обозначения, например, у тригонометрических. Поэтому в учебниках иногда встречаются записи вида D(sin) или D(arcsin). Их следует понимать как области определения синуса и арксинуса соответственно. Допустима и запись вида D(f), где f – функция синуса или арксинуса.
Если мы хотим записать, что функция f определена на множестве значений x, то используем формулировку D(f)=X. Так, для того же арксинуса запись будет выглядеть как D(arcsin)= [−1, 1] (подробнее об области определения арксинуса мы расскажем далее.)
Как найти области определения для основных элементарных функций
Прочитав определения выше, легко понять, что понятие области определения очень важно для любой функции. Это ее неотъемлемая часть, которую задают вместе с самой функцией. То есть когда мы вводим какую-либо функцию, то мы сразу указываем и область ее определения. Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y=x2 и т.д., а их области определения указываются в качестве основных свойств.
Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y=x2 и т.д., а их области определения указываются в качестве основных свойств.
В этом пункте мы расскажем, какие области определения имеют основные элементарные функции.
Область определения постоянной функции
Определение 3Вспомним формулу, которой задается постоянная функция: y=C, или f(x)=C. Переменная C может быть любым действительным числом.
Смысл функции в том, что каждому значению аргумента будет соответствовать значение, равное C, следовательно, областью определения данной функции будет множество всех действительных чисел. Обозначим его R.
Пример 2Так, если у нас есть функция y=−3 (или в другой записи f(x)=−3), то (D(f)= (−∞, +∞) или D(f)=R).
Если же мы возьмем функцию y=73, то для нее, как и для любой постоянной функции, область определения будет равна R.
Область определения функции с корнем
С помощью знака корня, или радикала, мы можем задать функцию извлечения квадратного корня y=x, либо в обобщенном виде функцию корня степени N, которую можно записать в виде формулы y=xn. В этих случаях n может быть любым натуральным числом, которое больше 1.
В этих случаях n может быть любым натуральным числом, которое больше 1.
Область определения таких функций будет зависеть от того, является ли показатель четным или нечетным числом.
Определение 4- Возьмем сначала случай, когда n – четное число, т.е. n=2·m, где m∈N. Тогда областью определения станет множество всех неотрицательных действительных чисел: D2·m=[0; +∞).
- Если же n представляет из себя нечетное число, которое больше 1, т.е. n=2·m+1, то областью определения будет множество всех действительных чисел: D2·m+1=(-∞; +∞).
Таким образом, область определения функций с корнем y=x, y=x4, y=x6 – это числовое множество [0, +∞), а функций y=x3, y=x5, y=x7 – множество (−∞, +∞).
Область определения степенной функции
Запись степенной функции выглядит как y=xa или f(x)=xa, где x является переменной, которая лежит в основании степени, и a представляет из себя определенное число в ее показателе. Мы берем область определения степенной функции в зависимости от значения ее показателя.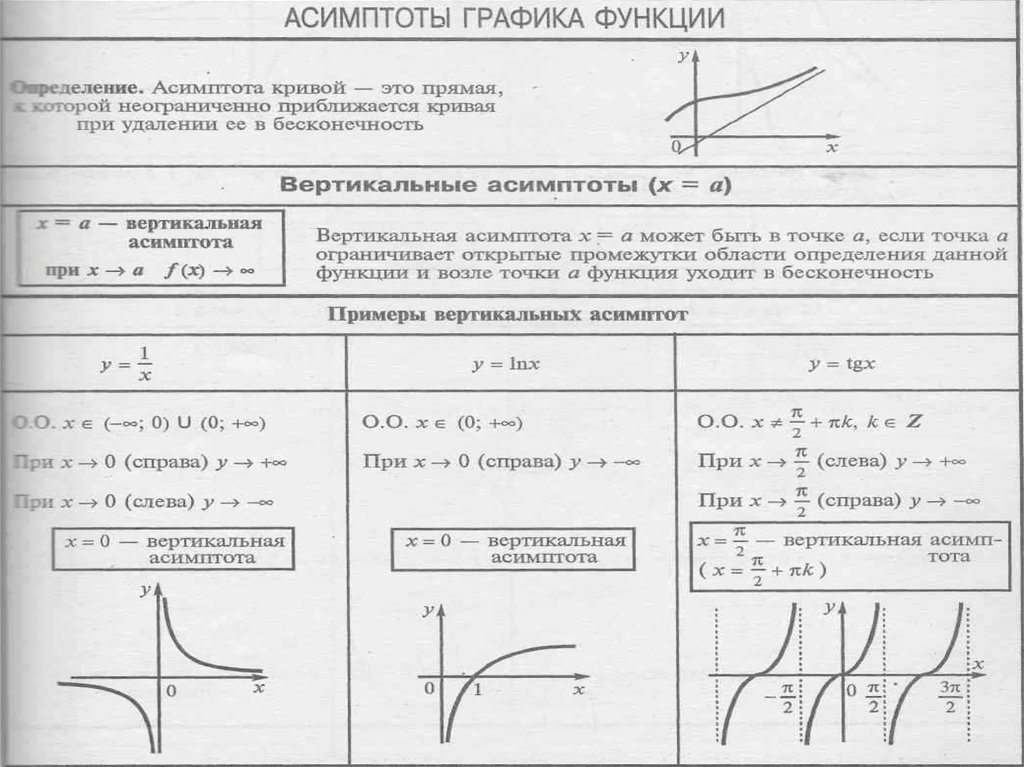
Перечислим возможные варианты.
Определение 5- Допустим, что a будет положительным целым числом. Тогда областью определения степенной функции будет множество действительных чисел (−∞, +∞).
- Если a является нецелым положительным числом, то D(f)= [0, +∞).
- В случае, когда a относится к целым отрицательным числам, областью определения такой функции становится множество (−∞, 0)∪(0, +∞).
- В остальных случаях, т.е. когда a будет отрицательным нецелым числом, область определения будет числовым промежутком (0, +∞).
- Если a имеет нулевое значение, то такая степенная функция будет определена для всех действительных x, кроме нулевого. Это связано с неопределенностью 00. Мы знаем, что любое число, кроме 1, при возведении в нулевую степень будет равно 1, тогда при a=0 у нас получится функция y=x0=1, область определения которой (−∞, 0) ∪ (0, +∞).
Поясним нашу мысль несколькими примерами.
Пример 4Для функций y=x5, y=x12 область определения представляет собой множество всех действительных чисел R, поскольку показатели степени являются целыми положительными числами.
Для степенных функций y=x63, y=xπ, y=x74, y=x23 будут определены на интервале [0, +∞), поскольку показатели являются положительными, но не целыми числами.
Пример 63. Для функции y=x−5 с целыми отрицательными показателями областью определения будет множество (−∞, 0)∪(0, +∞).
Пример 74. Для степенных функций y=x-19, y=x-3e, y=x-98, y=x-311 область определения будет представлять из себя открытый числовой луч (0, +∞), т.к. их показателями являются нецелые отрицательные числа.
Область определения показательной функции
Определение 6Такую функцию принято записывать как y=ax, причем переменная будет располагаться в показателе функции. Основанием степени здесь является число a, которое больше 0 и не равно 1.
Область определения такой функции есть множество всех действительных чисел, т.е. R.
Пример 8Например, если у нас есть показательные функции y=14x, y=ex, y=13x, y=15x, то они будут определены на промежутке от минус бесконечности до плюс бесконечности.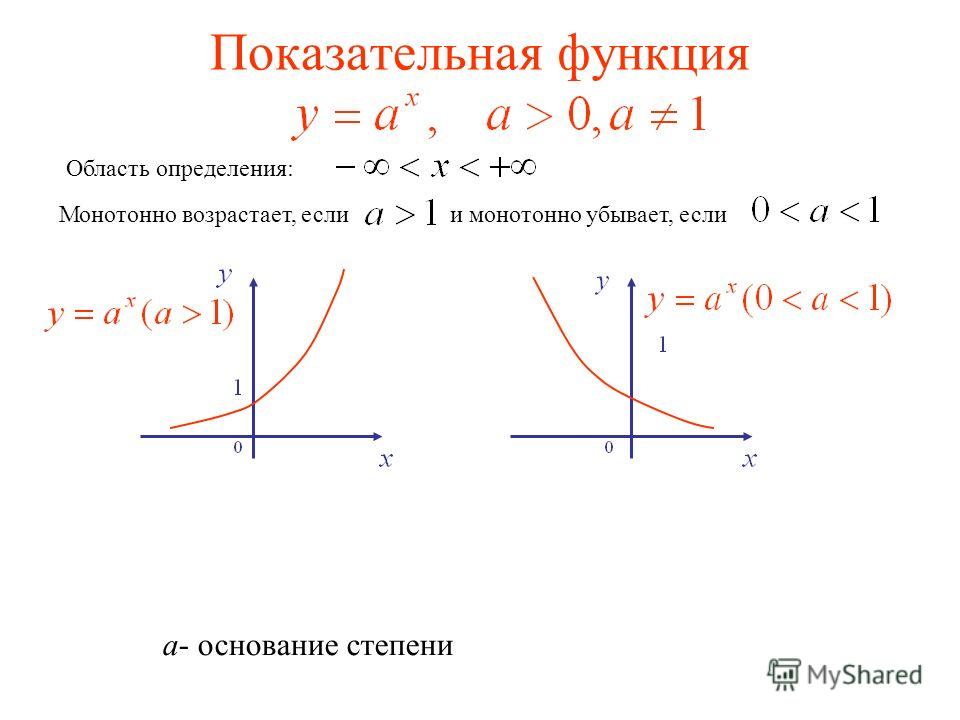
Область определения логарифмической функции
Определение 7Функция логарифма задается как y=logax , где a – основание, большее 0 и не равное 1. Она определена на множестве всех положительных действительных чисел. Это можно записать как
Так, для логарифмических функций y=log23x, y=log3x, y=log7x, y=lnx областью определения будет множество (0, +∞).
Область определения тригонометрических функций
Чтобы узнать, на каком промежутке будут определены тригонометрические функции, нужно вспомнить, как именно они задаются и как называются.
Определение 8- Формула y=sin x обозначает функцию синуса (sin). Она будет определена на множестве всех действительных чисел. Можно записать, что D(sin)=R.
- Формула y=cos x означает функцию косинуса (cos). Она также будет определена на множестве всех действительных чисел, т.е. D(cos)=R.

- Формула y=tg x означает функцию тангенса (tg), а y=ctg x– котангенса. Областью определения тангенса будет множество всех действительных чисел, за исключением π2+π·k, k∈Z.
Областью определения котангенса будет также множество R, за исключением π·k, k∈Z.
Иными словами, если мы знаем, что x является аргументом функций тангенса и котангенса, то нужно помнить, что данные функции определены при x∈R, x≠π2+π·k, k∈Z и x∈R, x≠π·k, k∈Z.
Область определения тригонометрических функций
К обратным тригонометрическим относятся функции арксинуса, арккосинуса, арктангенса и арккотангенса.
Определение 9- Формула y=arcsin x обозначает функцию арксинуса. Обычно она рассматривается на отрезке [−1, 1]] и обозначается arcsin. Промежуток [−1, 1] и будет нужной нам областью определения данной функции. Можно записать, что D(arcsin)=[−1, 1].
- Формула y=arccos x выражает функцию арккосинуса (обозначается arccos). Она рассматривается на том же отрезке, что и арксинус.
 Следовательно, областью определения данной функции является [−1, 1], т.е. D(arccos)=[−1, 1].
Следовательно, областью определения данной функции является [−1, 1], т.е. D(arccos)=[−1, 1]. - Функции y=arctg x и y=arcctg x означают арктангенс и арккотангенс. Они рассматриваются на множестве всех действительных чисел, значит, областью их определения является R. Можем записать, что D(arctg)=R и D(arcctg)=R.
Области определения основных функций в табличном виде
Чтобы запомнить или легко найти нужные нам области, правила вычисления которых мы объяснили выше, представим всю информацию в табличном виде. Не лишним будет оформить ее на отдельном листе и держать под рукой, так же, как и таблицу простых чисел, квадратов и др. Она очень пригодится при работе с функциями, пока вы не выучите ее содержимое наизусть.
| Области определения функций | |
| Функиця | Ее область определения |
| Постоянная y=C | R |
| Корень y=xn | [0; +∞), если n — четное |
| Степенная y=xa | -∞; +∞, если a>0, a∈Z 0; +∞, если a∈R, a≠Z -∞; 0∪0, +∞, если a=0 |
| Показательная y=ax | R |
| Логарифмическая y=logax | 0; +∞ |
Тригонометрические y=sin xy=cos xy=tg xy=ctg x |
RRx∈R, x≠π2+π·k, k∈Zx∈R, x≠π·k, k∈Z |
Обратные тригонометрические y=arcsin xy=arccos xy=arctg xy=arcctg x |
-1; 1-1; 1RR |
Подводя итоги статьи, следует отметить, что в рамках школьного курса изучаются не только основные элементарные функции, но и их различные сочетания. Задачи такого типа встречаются очень часто. Области определения таких комбинированных функций указываются далеко не всегда. Авторы задач подразумевают, что в таких случаях областью определения функции можно считать множество таких значений аргумента, при которых она будет иметь смысл. Это позволяет нам приблизиться к ответу на вопрос, как именно вычисляется область определения функции в подобных случаях.
Задачи такого типа встречаются очень часто. Области определения таких комбинированных функций указываются далеко не всегда. Авторы задач подразумевают, что в таких случаях областью определения функции можно считать множество таких значений аргумента, при которых она будет иметь смысл. Это позволяет нам приблизиться к ответу на вопрос, как именно вычисляется область определения функции в подобных случаях.
Область определения функции
Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.
В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.
Понятие и обозначение области определения функции
Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой.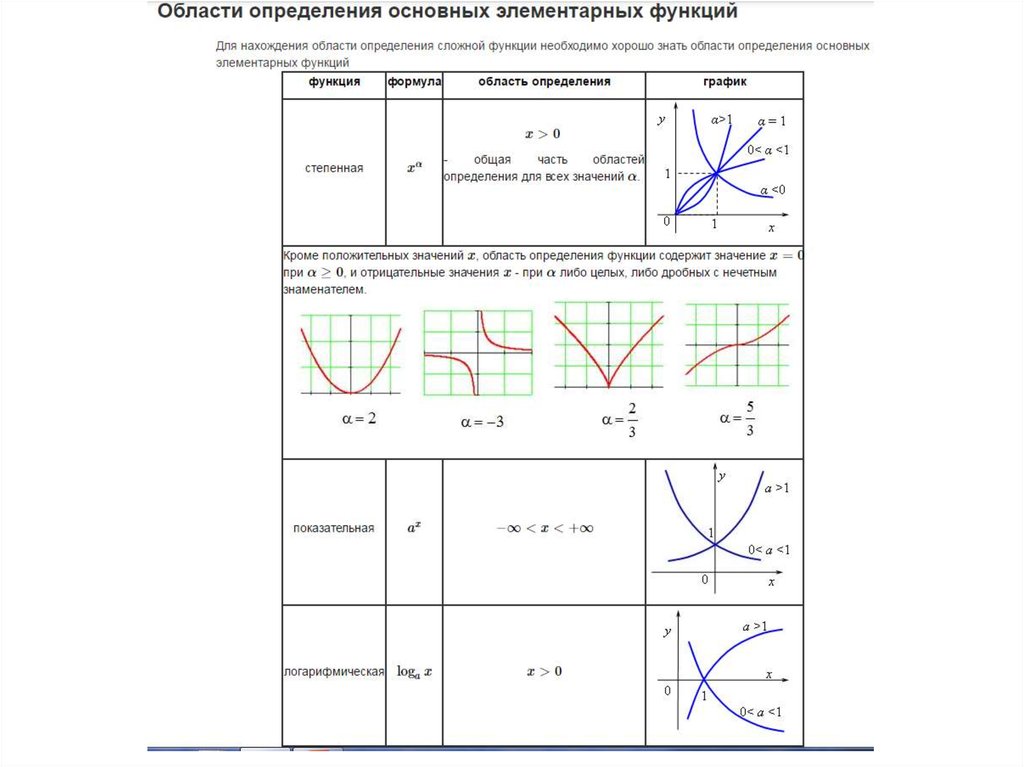 На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.
На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.
По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:
Определение 1Числовая функция с областью определения D – это соответствие значений переменной x некоторому числу y, которое находится в зависимых отношениях с x.
Используя это определение, охарактеризуем нужное нам понятие более четко:
Определение 2Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.
Теперь рассмотрим, как правильно обозначать ее на письме. Ранее мы договорились, что для записи самих функций будем использовать маленькие латинские буквы, например, g, f и др. Чтобы указать на наличие функциональной зависимости, используется запись вида y=f(x). Таким образом, функция f представляет собой некоторое правило, согласно которому каждому значению переменной x можно поставить в соответствие значение другой переменной y, которая находится в зависимых отношениях от x.
Возьмем для примера функцию y=x2. Можно записать ее как f(x)=x2. Это функция возведения в квадрат, которая ставит в соответствие каждому значению переменной x=x0 некоторое значение y=x02. Так, если мы возьмем число 3, то функция поставит ему в соответствие 9, поскольку 32=9.
Чтобы обозначить область определения некоторой функции f, используется запись D(f). Однако нужно помнить, что у некоторых функций есть собственные обозначения, например, у тригонометрических. Поэтому в учебниках иногда встречаются записи вида D(sin) или D(arcsin). Их следует понимать как области определения синуса и арксинуса соответственно. Допустима и запись вида D(f), где f – функция синуса или арксинуса.
Если мы хотим записать, что функция f определена на множестве значений x, то используем формулировку D(f)=X. Так, для того же арксинуса запись будет выглядеть как D(arcsin)= [−1, 1] (подробнее об области определения арксинуса мы расскажем далее. )
)
Как найти области определения для основных элементарных функций
Прочитав определения выше, легко понять, что понятие области определения очень важно для любой функции. Это ее неотъемлемая часть, которую задают вместе с самой функцией. То есть когда мы вводим какую-либо функцию, то мы сразу указываем и область ее определения. Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y=x2 и т.д., а их области определения указываются в качестве основных свойств.
В этом пункте мы расскажем, какие области определения имеют основные элементарные функции.
Область определения постоянной функции
Определение 3Вспомним формулу, которой задается постоянная функция: y=C, или f(x)=C. Переменная C может быть любым действительным числом.
Смысл функции в том, что каждому значению аргумента будет соответствовать значение, равное C, следовательно, областью определения данной функции будет множество всех действительных чисел. Обозначим его R.
Обозначим его R.
Так, если у нас есть функция y=−3 (или в другой записи f(x)=−3), то (D(f)= (−∞, +∞) или D(f)=R).
Если же мы возьмем функцию y=73, то для нее, как и для любой постоянной функции, область определения будет равна R.
Область определения функции с корнем
С помощью знака корня, или радикала, мы можем задать функцию извлечения квадратного корня y=x, либо в обобщенном виде функцию корня степени N, которую можно записать в виде формулы y=xn. В этих случаях n может быть любым натуральным числом, которое больше 1.
Область определения таких функций будет зависеть от того, является ли показатель четным или нечетным числом.
Определение 4- Возьмем сначала случай, когда n – четное число, т.е. n=2·m, где m∈N. Тогда областью определения станет множество всех неотрицательных действительных чисел: D2·m=[0; +∞).
- Если же n представляет из себя нечетное число, которое больше 1, т.е. n=2·m+1, то областью определения будет множество всех действительных чисел: D2·m+1=(-∞; +∞).

Таким образом, область определения функций с корнем y=x, y=x4, y=x6 – это числовое множество [0, +∞), а функций y=x3, y=x5, y=x7 – множество (−∞, +∞).
Область определения степенной функции
Запись степенной функции выглядит как y=xa или f(x)=xa, где x является переменной, которая лежит в основании степени, и a представляет из себя определенное число в ее показателе. Мы берем область определения степенной функции в зависимости от значения ее показателя.
Перечислим возможные варианты.
Определение 5- Допустим, что a будет положительным целым числом. Тогда областью определения степенной функции будет множество действительных чисел (−∞, +∞).
- Если a является нецелым положительным числом, то D(f)= [0, +∞).
- В случае, когда a относится к целым отрицательным числам, областью определения такой функции становится множество (−∞, 0)∪(0, +∞).
- В остальных случаях, т.е. когда a будет отрицательным нецелым числом, область определения будет числовым промежутком (0, +∞).

- Если a имеет нулевое значение, то такая степенная функция будет определена для всех действительных x, кроме нулевого. Это связано с неопределенностью 00. Мы знаем, что любое число, кроме 1, при возведении в нулевую степень будет равно 1, тогда при a=0 у нас получится функция y=x0=1, область определения которой (−∞, 0) ∪ (0, +∞).
Поясним нашу мысль несколькими примерами.
Пример 4Для функций y=x5, y=x12 область определения представляет собой множество всех действительных чисел R, поскольку показатели степени являются целыми положительными числами.
Пример 5Для степенных функций y=x63, y=xπ, y=x74, y=x23 будут определены на интервале [0, +∞), поскольку показатели являются положительными, но не целыми числами.
Пример 63. Для функции y=x−5 с целыми отрицательными показателями областью определения будет множество (−∞, 0)∪(0, +∞).
Пример 74. Для степенных функций y=x-19, y=x-3e, y=x-98, y=x-311 область определения будет представлять из себя открытый числовой луч (0, +∞), т. к. их показателями являются нецелые отрицательные числа.
к. их показателями являются нецелые отрицательные числа.
Область определения показательной функции
Определение 6Такую функцию принято записывать как y=ax, причем переменная будет располагаться в показателе функции. Основанием степени здесь является число a, которое больше 0 и не равно 1.
Область определения такой функции есть множество всех действительных чисел, т.е. R.
Пример 8Например, если у нас есть показательные функции y=14x, y=ex, y=13x, y=15x, то они будут определены на промежутке от минус бесконечности до плюс бесконечности.
Область определения логарифмической функции
Определение 7Функция логарифма задается как y=logax , где a – основание, большее 0 и не равное 1. Она определена на множестве всех положительных действительных чисел. Это можно записать как D(loga)=(0, +∞), например, D(ln)=(0, +∞) и D(lg)=(0, +∞).
Пример 9Так, для логарифмических функций y=log23x, y=log3x, y=log7x, y=lnx областью определения будет множество (0, +∞).
Область определения тригонометрических функций
Чтобы узнать, на каком промежутке будут определены тригонометрические функции, нужно вспомнить, как именно они задаются и как называются.
Определение 8- Формула y=sin x обозначает функцию синуса (sin). Она будет определена на множестве всех действительных чисел. Можно записать, что D(sin)=R.
- Формула y=cos x означает функцию косинуса (cos). Она также будет определена на множестве всех действительных чисел, т.е. D(cos)=R.
- Формула y=tg x означает функцию тангенса (tg), а y=ctg x– котангенса. Областью определения тангенса будет множество всех действительных чисел, за исключением π2+π·k, k∈Z.
Областью определения котангенса будет также множество R, за исключением π·k, k∈Z.
Иными словами, если мы знаем, что x является аргументом функций тангенса и котангенса, то нужно помнить, что данные функции определены при x∈R, x≠π2+π·k, k∈Z и x∈R, x≠π·k, k∈Z.
Область определения тригонометрических функций
К обратным тригонометрическим относятся функции арксинуса, арккосинуса, арктангенса и арккотангенса.
Определение 9- Формула y=arcsin x обозначает функцию арксинуса. Обычно она рассматривается на отрезке [−1, 1]] и обозначается arcsin. Промежуток [−1, 1] и будет нужной нам областью определения данной функции. Можно записать, что D(arcsin)=[−1, 1].
- Формула y=arccos x выражает функцию арккосинуса (обозначается arccos). Она рассматривается на том же отрезке, что и арксинус. Следовательно, областью определения данной функции является [−1, 1], т.е. D(arccos)=[−1, 1].
- Функции y=arctg x и y=arcctg x означают арктангенс и арккотангенс. Они рассматриваются на множестве всех действительных чисел, значит, областью их определения является R. Можем записать, что D(arctg)=R и D(arcctg)=R.
Области определения основных функций в табличном виде
Чтобы запомнить или легко найти нужные нам области, правила вычисления которых мы объяснили выше, представим всю информацию в табличном виде. Не лишним будет оформить ее на отдельном листе и держать под рукой, так же, как и таблицу простых чисел, квадратов и др. Она очень пригодится при работе с функциями, пока вы не выучите ее содержимое наизусть.
Не лишним будет оформить ее на отдельном листе и держать под рукой, так же, как и таблицу простых чисел, квадратов и др. Она очень пригодится при работе с функциями, пока вы не выучите ее содержимое наизусть.
| Области определения функций | |
| Функиця | Ее область определения |
| Постоянная y=C | R |
| Корень y=xn | [0; +∞), если n — четное |
| Степенная y=xa | -∞; +∞, если a>0, a∈Z |
| Показательная y=ax | R |
| Логарифмическая y=logax | 0; +∞ |
Тригонометрические y=sin xy=cos xy=tg xy=ctg x |
RRx∈R, x≠π2+π·k, k∈Zx∈R, x≠π·k, k∈Z |
Обратные тригонометрические y=arcsin xy=arccos xy=arctg xy=arcctg x |
-1; 1-1; 1RR |
Подводя итоги статьи, следует отметить, что в рамках школьного курса изучаются не только основные элементарные функции, но и их различные сочетания. Задачи такого типа встречаются очень часто. Области определения таких комбинированных функций указываются далеко не всегда. Авторы задач подразумевают, что в таких случаях областью определения функции можно считать множество таких значений аргумента, при которых она будет иметь смысл. Это позволяет нам приблизиться к ответу на вопрос, как именно вычисляется область определения функции в подобных случаях.
Задачи такого типа встречаются очень часто. Области определения таких комбинированных функций указываются далеко не всегда. Авторы задач подразумевают, что в таких случаях областью определения функции можно считать множество таких значений аргумента, при которых она будет иметь смысл. Это позволяет нам приблизиться к ответу на вопрос, как именно вычисляется область определения функции в подобных случаях.
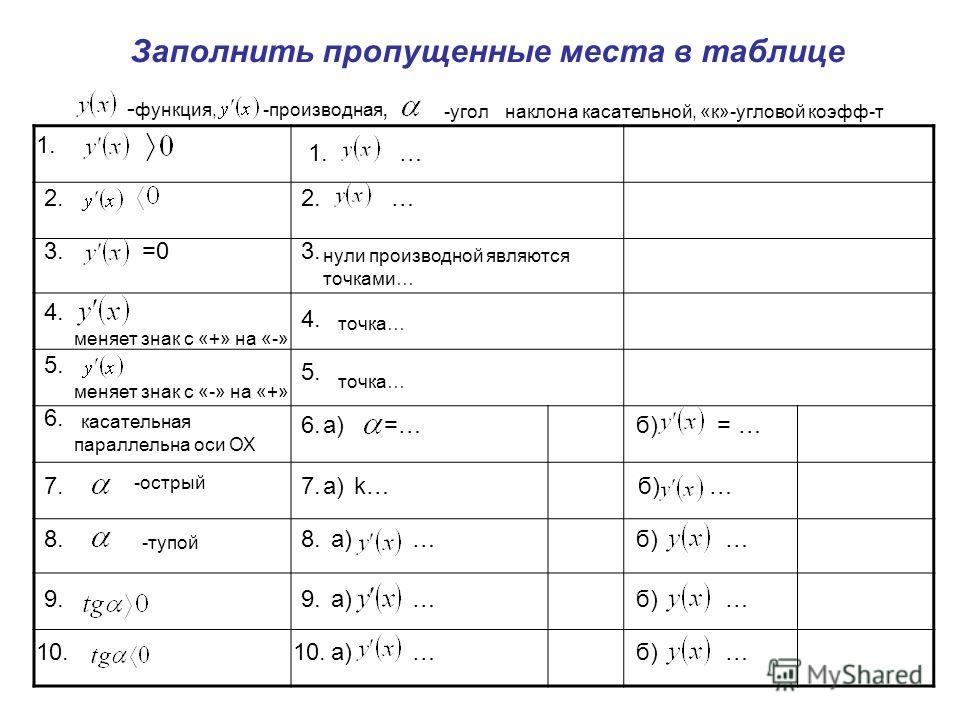
H63: Использование атрибута области для связывания ячеек заголовков и ячеек данных в таблицах данных
Важную информацию об использовании этих информативных методов и о том, как они соотносятся с нормативными критериями успеха WCAG 2.0, см. в разделе «Понимание методов для критериев успеха WCAG». В разделе «Применимость» объясняется область применения метода, и наличие методов для конкретной технологии не означает, что эту технологию можно использовать во всех ситуациях для создания контента, соответствующего WCAG 2.0.
Цель этого метода — связать ячейки заголовков с ячейками данных в сложных таблицах с помощью область атрибут. Атрибут
Атрибут scope может использоваться для уточнения
область действия любой ячейки, используемой в качестве заголовка. Область определяет, является ли ячейка
заголовок для строки, столбца или группы строк или столбцов. Значения строк , col , rowgroup и colgroup идентифицируют их
возможные области применения соответственно.
Для простых таблиц данных, в которых заголовок не находится в первой строке или столбце, например в примере 1 можно использовать эту технику. Основываясь на сегодняшней поддержке программы чтения с экрана, ее использование предлагается в двух ситуациях, относящихся к простым таблицам:
ячейки данных, помеченные
td, которые также функционируют как заголовок строки или столбца заголовокячейки заголовка, размеченные
tdвместоth. Иногда авторы
используйте это, чтобы избежать характеристик дисплея, связанных с
Иногда авторы
используйте это, чтобы избежать характеристик дисплея, связанных с -м-м, а также не выбирайте использование CSS для управления отображением для-го-го.
Примечание 1: Для простых таблиц, заголовки которых находятся в первой строке или столбце, достаточно просто использовать элементы TH без области видимости.
Примечание 2: Для сложных таблиц используйте идентификаторы и заголовки, как в h53: Использование атрибутов id и заголовков для связывания ячеек данных с ячейками заголовков в таблицы данных .
Примечание 3: Некоторым пользователям может быть проще работать с несколькими простыми таблицами, чем с одной более сложной таблицей. Авторы могут подумать, могут ли они преобразовать сложные таблицы в одну или несколько простых таблиц.
В следующем примере столбец № 1 содержит порядковые номера строк в таблице. а второй столбец содержит значение ключа для строки. Клетки во втором
столбец может затем использовать
а второй столбец содержит значение ключа для строки. Клетки во втором
столбец может затем использовать область = "строка" . Ячейки в первой строке тоже
помечены td и использовать область = "кол" .
Пример кода:
<граница таблицы="1">Контактная информация <тд> Имя Телефон# Факс# Город 1. Джоэл Гарнер 412-212-5421 412-212-5400 Питтсбург 2. Клайв Ллойд 410-306-1420 410-306-5400 Балтимор 3. Гордон Гринидж <тд>281-564-6720 <тд>281-511-6600Хьюстон
Ресурсы предназначены только для информационных целей, одобрение не подразумевается.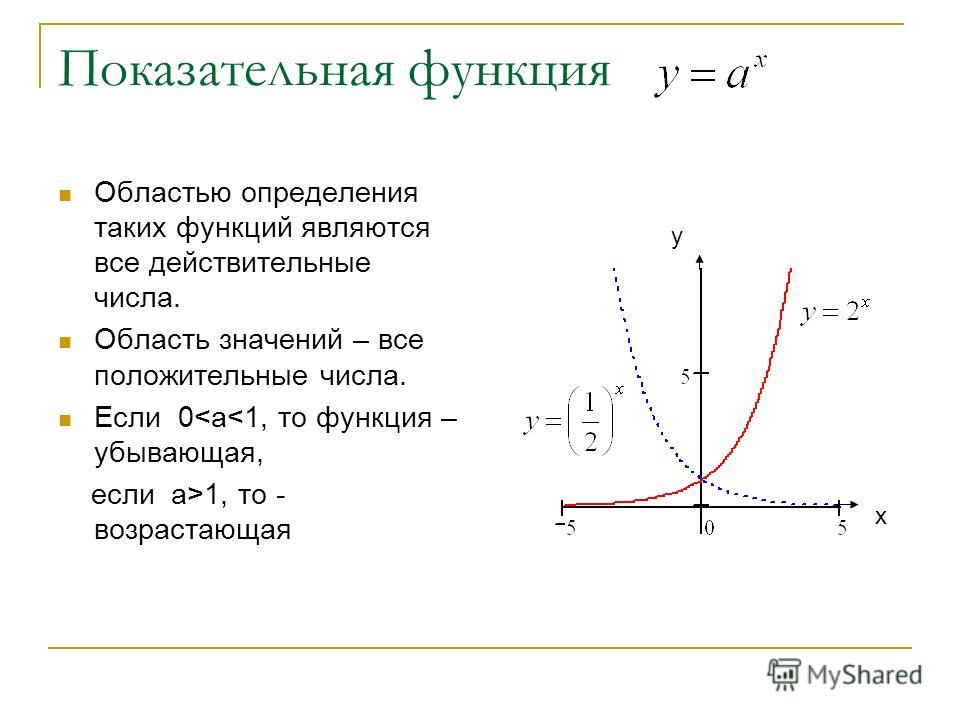
Ячейки таблицы HTML 4.01: атрибут области
HTML 4.01 Ячейки таблицы: элементы TH и TD
Вспомогательные технологии столы для чтения
Процедура
Для каждой таблицы данных:
Проверить, что все
-еэлементов имеютобластьатрибут.Проверить, что все элементы
td, которые действуют как заголовки для других элементов иметь атрибутScope.Убедитесь, что все атрибуты области
, строка,col,rowgroupилиcolgroup.
Ожидаемые результаты
Если это достаточный метод для критерия успеха, то неудача этой процедуры тестирования не обязательно означает, что критерий успеха не был удовлетворен каким-либо другим способом, а только то, что этот метод не был успешно реализован и не может использоваться для утверждения соответствия.
Атрибут области HTML th
❮ Тег HTML
Пример
Укажите, что две ячейки заголовка являются заголовками для столбцы:
| Месяц | Экономия | |
|---|---|---|
| 1 | Январь | 100 долларов США |
| 2 | Февраль | 80 долларов США |
Попробуйте сами »
2
Определение и использование
Атрибут Scope указывает, является ли ячейка заголовка заголовком для столбца, строки или группы столбцов или строк.
Примечание: Атрибут scope не имеет визуального эффекта в обычных веб-браузерах, но может быть
используется программами чтения с экрана.
Поддержка браузера
| Атрибут | |||||
|---|---|---|---|---|---|
| прицел | Да | Да | Да | Да | Да |
Синтаксис
Значения атрибутов
| Значение | Описание |
|---|---|
| цвет | Указывает, что ячейка является заголовком для столбца |
| ряд | Указывает, что ячейка является заголовком для строки |
| колгруппа | Указывает, что ячейка является заголовком для группы столбцов |
| группа строк | Указывает, что ячейка является заголовком для группы строк |
❮ Тег HTML
ВЫБОР ЦВЕТА
Лучшие учебники
Учебник по HTMLУчебник по CSS
Учебник по JavaScript
Учебник How To
Учебник по SQL
Учебник по Python
Учебник по W3.
 CSS
CSS Учебник по Bootstrap
Учебник по PHP
Учебник по Java
Учебник по C++
Учебник по jQuery
903 Справочник 903
903
Справочник по HTML
Справочник по CSS
Справочник по JavaScript
Справочник по SQL
Справочник по Python
Справочник по W3.CSS
Справочник по Bootstrap
Справочник по PHP
Цвета HTML
Справочник по Java
Справочник по Angular
Справочник по jQuery
Основные примеры
Примеры HTMLПримеры CSS
Примеры JavaScript
Примеры How To Примеры
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры PHP
Примеры Java
Примеры XML
Примеры jQuery
| О
W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения.
Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания.


 Следовательно, областью определения данной функции является [−1, 1], т.е. D(arccos)=[−1, 1].
Следовательно, областью определения данной функции является [−1, 1], т.е. D(arccos)=[−1, 1].

 Иногда авторы
используйте это, чтобы избежать характеристик дисплея, связанных с
Иногда авторы
используйте это, чтобы избежать характеристик дисплея, связанных с