Логарифмическая функция. Смотр знаний
Цель:
- повторить свойства логарифмической функции.
- проверить усвоение темы на обязательном уровне.
- применять свойства при решении уравнений, неравенств.
- воспитывать интерес к предмету.
Оборудование: мультимедийный проектор, экран, 2 компьютера с установленной программой “Математика 5–11”
Ход урока
1. Организационный момент
Учитель: Французский писатель Анатоль Франс заметил: “Что учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом”.
Последуем совету писателя: будем “поглощать” знания с большим желанием, ведь они скоро вам понадобятся.
Цель урока: систематизировать знания по теме “Логарифмическая функция” Приложение 1 (Слайд 1)
На уроке рассматриваются пять вопросов:
А) Логарифмическая функция. 
Б) Логарифмические тождества.
В) Область определения логарифмической функции.
Г) Логарифмические уравнения.
Д) Логарифмические неравенства. (слайды 2, 3)
2. Усвоение знаний
Вопрос 1: “Существование логарифмической функции”.
Еще Аристотель говорил, что определение того или иного понятия, еще не доказывает его существования. Итак, докажем, что логарифмическая функция существует.
Ученик 1 (слайд 4)
Рассмотрим показательную функцию у = ах, где а ≠ 1, а > 0
Пусть а >1, у = ах непрерывна и возрастает на (– ∞; + ∞). По теореме об обратной функции на промежутке (0; + ∞) определена обратная функция по отношению к показательной, причем она непрерывна и возрастает.
Пусть 0 < а < 1, у = ах непрерывна и убывает на (-∞; + ∞), поэтому на участке (0; + ∞) определена обратная к ней функция.
Эта обратная функция – логарифмическая.
Функция у = logax называется логарифмической, где а ≠ 1, а >0, х >0
Вопросы для обсуждения (задают учащиеся):
- имеет ли функция экстремумы
- принимает ли функция наибольшее значение в некоторой точке ХО
- является ли функция четной, нечетной
- в какой точке функция пересекает ось ОХ
- пересекает ли функция ось ОУ
Вопрос 2:
“Логарифмические тождества”
| Слово логарифм происходит от греческого Его математические труды направлены на упрощение и упорядочение арифметики, алгебры и тригонометрии. Какими же основными тождествами мы пользуемся для вычисления? |
В 1614 году Непер издал труд “Описание удивительной таблицы логарифмов”, в котором не только дал определение логарифма, описал его свойства, но и предложил таблицы логарифмов синусов, косинусов и тангенсов. Также Непер открыл логарифмическую кривую. Позднее им была изобретена логарифмическая линейка, которой пользовались до 70-х годов ХХ
в.Ученик 2:
Логарифмом числа в по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число в
- Формулу
, где а ≠ 1, а >0, в >0
называют основным логарифмическим тождеством.
- Основные свойства логарифмов (слайд 6)
– логарифм произведения равен сумме логарифмов
– логарифм частного равен разности логарифмов
– логарифм степени равен произведению показателя степени на логарифм основания этой степени
- Десятичный логарифм
Вопросы для обсуждения: (задают учащиеся)
- найти значение log232, log216
- найти число log5 x = 2, log7 x = -2
- вычислить; lg
3 вопрос:
“Область определения логарифмической функции”
Ученик 3 (слайд 7)
- Область определения логарифмической функции множество всех положительных чисел
Д(
logа) = R+
- Область значений логарифмической функции множество всех действительных чисел
E
(logа) = R
- Логарифмическая функция у = logax возрастает при а >1
- Логарифмическая функция у = logax убывает при 0 < а < 1
Используя свойства логарифмической функции можно не только вычислять значения логарифма, но и сравнивать
Например:
а) log35 < log37
б) log0,25 > log0,27
Также, находить область определения выражения
Например:
|
Решением данного неравенства есть множество точек (-∞; –4) v (4; + ∞)
Вопросы для обсуждения: (задают учащиеся):
- как сравнить выражения log232 и 1
4 вопрос:
“Логарифмические уравнения”
Ученик 4 (
Простейшее логарифмическое уравнение имеет вид logа х = в
Логарифмическая функция возрастает или убывает на промежутке (0; + ∞) и принимает на этом промежутке все действительные значения.
По теореме о корне, для любого в данное уравнение имеет и притом только одно решение.
Теорема: Уравнение вида logа f(х) = logа g(х) равносильно уравнению вида f(х) = g(х) при ограничении
f(х) > 0
g(х) > 0
|
Пример: |
(2х – 4) = –2 2х = 8 х = 4 |
ОДЗ: | 2х – 4 > 0 |
Ответ: х = 4
Вопросы для обсуждения (задают ученики):
- всегда нужно находить область определения функции, когда решаем логарифмическое уравнение?
5 вопрос: “Логарифмические неравенства”
Ученик 5 (слайд 9)
- Простейшие логарифмические неравенства имеют вид:
|
|
Неравенство вида logа f(х) > logа g(х) равносильно неравенству вида f(х) > g(х) при ограничении
f(х) > 0
g(х) > 0
и также используют такие правила:
– если а > 1, то знак неравенства сохраняем
– если 0 < а < 1, то знак неравенства меняем на противоположный.
Пример: Решить неравенство
| log4 | х > log4 (3х – 4) х > 3х – 4 х – 3х > – 4 – 2 х > – 4 х < – 4 : (– 2) х < 2 |
ОДЗ:
х > 0
3х – 4 > 0
х > 0
3х > 4
х > 0
х > 4 : 3
Ответ:
3. Физкультминутка
Мы с вами комплексно повторили знания по теме “Логарифмическая функция”.
На следующем этапе урока нам предстоит работать всем сосредоточенно. Внимательны были? Мы рассмотрели логарифмическую функцию у = logax , если а >1 то функция возрастает. Покажем это.(учитель плавно показывает как функция возрастает).Если 0<а<1 функция убывает, покажем это. Теперь усложним работу, я называю функцию, а вы показываете функция возрастает или убывает.
(у = log3x, , у = log5x)
4. Проверка знаний
Проверку знаний проведем в виде зачета. Одни ученики у нас выступают в роли преподавателей, другие ученики – абитуриенты.
Ваша задача: успешно сдать зачет по теме “Логарифмическая функция”.
Рассматриваются пять вопросов:
А) Логарифмическая функция.
Б) Логарифмические тождества.
В) Область определения логарифмической функции.
Г) Логарифмические уравнения.
Д) Логарифмические неравенства.
Преподаватели, могут оказывать помощь своим
абитуриентам, но для этого нужно будет отдать жетон.
Жетонов у каждого абитуриента 3, вопросов 5, так что абитуриенты надейтесь только на свои силы. Результаты сдачи зачета преподаватели будут заносить в контрольный лист. Приложение 2
Зачет начинается. Преподаватели приготовьте свои экзаменационные билеты.
Абитуриентам, я желаю удачи, преподавателям хороших результатов, по своим темам.
Начало и конец зачета начинаем звонком (колокольчик).
5. Зачетные задания
“Логарифмическая функция”
Работа за компьютером. Программа “Математика. 5–11”
Вопросы:
- Построить график функции у = log3х и график симметричный относительно у = х.
- Принимает ли логарифмическая функция наибольшее значение в некоторой точке.
- Построить график функции у = 5х и график симметричный относительно
у = х.
- Имеет ли логарифмическая функция экстремумы
- Построить график функции и график симметричный относительно у = х.
- Является ли логарифмическая функция четной, нечетной
- Построить график функции у = х и график симметричный относительно у = х.
- В какой точке логарифмическая функция пересекает ось ОХ.
- Пересекает ли логарифмическая функция ось ОУ.
“Логарифмические тождества”
Применяя формулы выполнить задания: Приложение 3
“Область определения логарифмической функции”
- Приведите пример логарифмической функции, которая возрастает на всей области определения.
- Приведите пример логарифмической функции, которая убывает на всей области определения.
- Найти область определения выражений
а) logπ(10 – 2x)
б) log5(9 – x2)
в) log0,3(x2 – 16)
г) log3(x – 4)
- Сравнить числа
а) log2 5,2 и log2 3,6
б) log0,2 6 и log0,2 8
в) log0,3 √2 и log0,3 0,3
г) log5 3 и 1
д) log π 2,9 и 1
- Найти область определения выражений
а) log√2(x2— 2x – 3)
б)
в)
“Логарифмические уравнения”
Решить уравнения:
- log3(x – 2) = 2;
- log3(2 x – 4) = log3(x + 7)
- (5 +2 ч) = 1;
- log π (х2 + 2х + 3) = log π 6
- log2(x – 4) = 3;
- log3(x – 5) = 0
- log2(3 – x) = 0;
- log8(x 2 – 1) = 1
“Логарифмические неравенства”
Решить неравенства:
- log4 х > log4 (3х – 4)
- (2х – 5) < –2
- log0,2 (1 – х) >1; log3 (16 – 2х) < log3 4х
- lоg2х < lg(х + 1)
- log2 (8 – 6х) < log2 2х; log5 (2х + 3) < log5 (х – 1)
- > l
- (2х – 5) > х
6.
Итог урока
П.Л.Чебышев говорил: “Сближение теории с практикой дает самые благотворные результаты”
Мы с вами сегодня на уроке убедились в справедливости этих слов. (слайд 10)
Преподаватели выставляют зачет в контрольные листы абитуриентов. Готовятся к выступлению, характеризуют свою тему, справились абитуриенты с заданиями или нет, пользовались ли подсказкой. Тема, на которую было допущено больше всего ошибок, выносится на доработку на следующие уроки.
7. Домашнее задание
(слайд 11)
1-я группа
Работа с учебником М.И. Башмаков, с. 194 (модуль перехода)
Вопрос: Как связать между собой степени и логарифмы с разными основаниями?
№ 55 стр. 225. Решить логарифмические уравнения
2-я группа
1.Найдите промежуток, которому принадлежит корень уравнения loga(1 – х) = 4
1) (62; 64)
2) (79; 81)
3) (–81; –79)
4) (–12; –10)
2.
Найдите сумму корней уравнения lg(4х – 3) = 2 lgx
1) –2
2) 4
3) –4
4) 2
3. Подпишите графики Приложение 4
Домен и диапазон экспоненциальных и логарифмических функций
Напомним, что домен функции представляет собой набор входных или Икс -значения, для которых определена функция, а диапазон это набор всех выходных или у -значения, которые принимает функция.
Простая экспоненциальная функция, например
ф
(
Икс
)
«=»
2
Икс
имеет своей областью всю реальную линию. Но его диапазон только положительный вещественные числа,
у
>
0
:
ф
(
Икс
)
никогда не принимает отрицательное значение. Кроме того, он никогда не достигает
0
, хотя асимптотически приближается к
Икс
идет к
−
∞
.
Если мы заменим Икс с − Икс чтобы получить уравнение г ( Икс ) «=» 2 − Икс , график отражается вокруг у -axis, но домен и диапазон не меняются:
Если мы поставим перед собой знак минус, чтобы получить уравнение час ( Икс ) «=» − 2 Икс , график отражается вокруг Икс -ось. У нас все еще есть целая действительная линия в качестве нашего домена, но диапазон теперь состоит из отрицательных чисел, у < 0 .
Теперь рассмотрим функцию
ф
(
Икс
)
«=»
(
−
2
)
Икс
. Когда
Икс
«=»
1
2
,
у
должно быть комплексным числом, так что все усложняется.
Для этого урока нам потребуется, чтобы наши базисы были положительными на данный момент, чтобы мы могли оставаться в реальном мире.
В общем случае график основной экспоненциальной функции у «=» а Икс капли от ∞ к 0 когда 0 < а < 1 как Икс варьируется от − ∞ к ∞ и поднимается из 0 к ∞ когда а > 1 .
Экспоненциальная функция
у
«=»
а
Икс
, можно сдвинуть
к
единицы по вертикали и
час
единицы по горизонтали с уравнением
у
«=»
а
(
Икс
+
час
)
+
к
. Тогда область определения функции остается неизменной, а диапазон становится
{
у
е
ℝ
|
у
>
час
}
.
Пример 1:
Найдите область определения и диапазон функции у «=» 3 Икс + 2 .
График функции на координатной плоскости.
График не что иное, как график у «=» 3 Икс переведено 2 единицы влево.
Функция определена для всех действительных чисел. Итак, областью определения функции является множество действительных чисел.
Как Икс как правило ∞ , значение функции также стремится к ∞ и в качестве Икс как правило − ∞ , функция приближается к Икс -ось, но никогда не касается ее.
Следовательно, диапазон функции представляет собой набор действительных положительных чисел или
{
Икс
е
ℝ
|
Икс
>
0
}
.
Пример 2:
Найдите область определения и диапазон функции у «=» ( 1 4 ) 2 Икс .
График функции на координатной плоскости.
График не что иное, как график у «=» ( 1 4 ) Икс сжатый в разы 2 .
Функция определена для всех действительных чисел. Итак, областью определения функции является множество действительных чисел.
Как Икс как правило ∞ , значение функции стремится к нулю, а график приближается Икс -ось, но никогда не касается ее.
Как Икс как правило − ∞ , функция также стремится к ∞ .
Следовательно, диапазон функции представляет собой набор действительных положительных чисел или
{
у
е
ℝ
|
у
>
0
}
.
Обратная экспоненциальная функция является логарифмической функцией.
Просто логарифмическая функция у «=» бревно 2 Икс где Икс > 0 эквивалентна функции Икс «=» 2 у . То есть, у «=» бревно 2 Икс является обратной функцией у «=» 2 Икс .
Функция у «=» бревно 2 Икс имеет область определения множества положительных действительных чисел и диапазон множества действительных чисел.
Помните, что, поскольку логарифмическая функция является обратной экспоненциальной функции, областью определения логарифмической функции является диапазон экспоненциальной функции, и наоборот.
В общем случае функция
у
«=»
бревно
б
Икс
где
б
,
Икс
>
0
и
б
≠
1
является непрерывной и однозначной функцией.
Обратите внимание, что логарифмическая функция не определен для отрицательных чисел или для нуля. График функции приближается к
у
-ось как
Икс
как правило
∞
, но никогда не касается его.
Следовательно, область определения логарифмической функции у «=» бревно б Икс — множество положительных действительных чисел, а диапазон — множество действительных чисел.
Функция возникает из − ∞ к ∞ как Икс увеличивается, если б > 1 и падает с ∞ к − ∞ как Икс увеличивается, если 0 < б < 1 .
Логарифмическая функция,
у
«=»
бревно
б
Икс
, можно сдвинуть
к
единицы по вертикали и
час
единицы по горизонтали с уравнением
у
«=»
бревно
б
(
Икс
+
час
)
+
к
.
Тогда область определения функции становится
{
Икс
е
ℝ
|
Икс
>
−
час
}
. Однако ассортимент остается прежним.
Пример 3:
Найдите область определения и диапазон функции у «=» бревно ( Икс ) − 3 .
Начертите функцию на координатной плоскости. Помните, что если основание не показано, то под основанием понимается 10 .
График не что иное, как график у «=» бревно ( Икс ) переведено 3 единиц вниз.
Функция определена только для положительных действительных чисел. Итак, область определения функции — это множество положительных действительных чисел или
{
Икс
е
ℝ
|
Икс
>
0
}
.
Функция принимает все действительные значения из − ∞ к ∞ .
Таким образом, диапазон функции представляет собой множество действительных чисел.
Пример 4:
Найдите область определения и диапазон функции у «=» бревно 3 ( Икс − 2 ) + 4 .
График функции на координатной плоскости.
График не что иное, как график у «=» бревно 3 ( Икс ) переведено 2 единицы вправо и 4 единиц вверх.
Как
Икс
как правило
2
, функция приближается к прямой
Икс
«=»
2
но никогда не прикасается к нему. Как
Икс
как правило
∞
значение функции также стремится к
∞
.
То есть функция определена для действительных чисел, больших, чем
2
. Итак, область определения функции — это множество положительных действительных чисел или
{
Икс
е
ℝ
|
Икс
>
2
}
.
Функция принимает все действительные значения из − ∞ к ∞ .
Таким образом, диапазон функции представляет собой множество действительных чисел.
Логарифмические функции — формула, домен, диапазон, график
Логарифмическая функция является важным средством математических вычислений. Логарифмы были открыты в 16 веке шотландским математиком, ученым и астрономом Джоном Нейпиром. Он имеет множество применений в астрономических и научных расчетах, связанных с огромными числами. Логарифмические функции тесно связаны с экспоненциальными функциями и рассматриваются как обратные экспоненциальной функции.
Показательная функция a x = N преобразуется в логарифмическую функцию log a N = x.
Логарифм любого числа N, если его интерпретировать как экспоненциальную форму, представляет собой показатель степени, до которой следует возвести основание логарифма, чтобы получить число N. Здесь мы будем стремиться узнать больше о логарифмических функциях, типах логарифмов, график логарифмической функции и свойства логарифмов.
| 1. | Что такое логарифмические функции? |
| 2. | Домен и диапазон функций журнала |
| 3. | Логарифмический график |
| 4. | Графики логарифмических функций |
| 5. | Свойства логарифмических функций |
| 6. | Производная и интеграл логарифмических функций |
| 7. | Часто задаваемые вопросы о логарифмических функциях |
Что такое логарифмические функции?
Основная логарифмическая функция имеет вид f(x) = log a x (r) y = log a x, где a > 0.
Это обратная экспоненциальная функция a y = х. Логарифмические функции включают натуральный логарифм (ln) или десятичный логарифм (log). Вот несколько примеров логарифмических функций:
- f(x) = ln (x — 2)
- г(х) = log 2 (х + 5) — 2
- h(x) = 2 log x и т. д.
Некоторые значения нецелого порядка можно легко вычислить с помощью логарифмических функций. Найти значение x в экспоненциальных выражениях 2 x = 8, 2 x = 16 легко, но найти значение x в 2 x = 10 сложно. Здесь мы можем использовать логарифмические функции для преобразования 2 x = 10 в логарифмическую форму как log 2 10 = x, а затем найдите значение x. Логарифм подсчитывает количество вхождений основания в повторяющихся кратных числах. Формула преобразования показательной функции в логарифмическую выглядит следующим образом.
Показательная функция вида a x = N может быть преобразована в логарифмическую функцию log a N = x.
Логарифмы обычно рассчитываются по основанию 10, а логарифмическое значение любого числа можно найти с помощью таблицы логарифмов Нейпира. Логарифмы можно вычислять для положительных целых чисел, дробей, десятичных дробей, но нельзя вычислять для отрицательных значений.
Домен и диапазон функций журнала
Рассмотрим базовую (родительскую) десятичную логарифмическую функцию f(x) = log x (или y = log x). Мы знаем, что log x определяется только тогда, когда x > 0 (попробуйте найти log 0, log (-1), log (-2) и т. д. с помощью калькулятора. Вы получите ошибку). Таким образом, областью определения является множество всех положительных действительных чисел. Теперь мы рассмотрим некоторые значения y (выходные данные) функции для разных значений x (входные данные).
- Когда x = 1, y = log 1 = 0
- Когда x = 2, y = log 2 = 0,3010
- Когда x = 0,2, y = -0,6990
- Когда x = 0,01, y = -2 и т. д.
Мы видим, что y может быть как положительным, так и отрицательным действительным числом (или) также может быть нулевым.
Таким образом, y может принимать значение любого действительного числа. Следовательно, диапазоном логарифмической функции является множество всех действительных чисел. Таким образом:
- Область определения логарифмической функции y = log x равна x > 0 (или) (0, ∞).
- Диапазон любой логарифмической функции — это набор всех действительных чисел (R)
Пример: Найдите область определения и диапазон логарифмической функции f(x) = 2 log (2x — 4) + 5.
Решение:
0 и найти х.
2x — 4 > 0
2x > 4
x > 2
Таким образом, область определения = (2, ∞).
Как мы видели ранее, диапазон любой логарифмической функции равен R. Таким образом, диапазон f(x) равен R.
Логарифмический график
Мы уже видели, что область определения основной логарифмической функции y = log a x — это множество положительных действительных чисел, а диапазон — множество всех действительных чисел.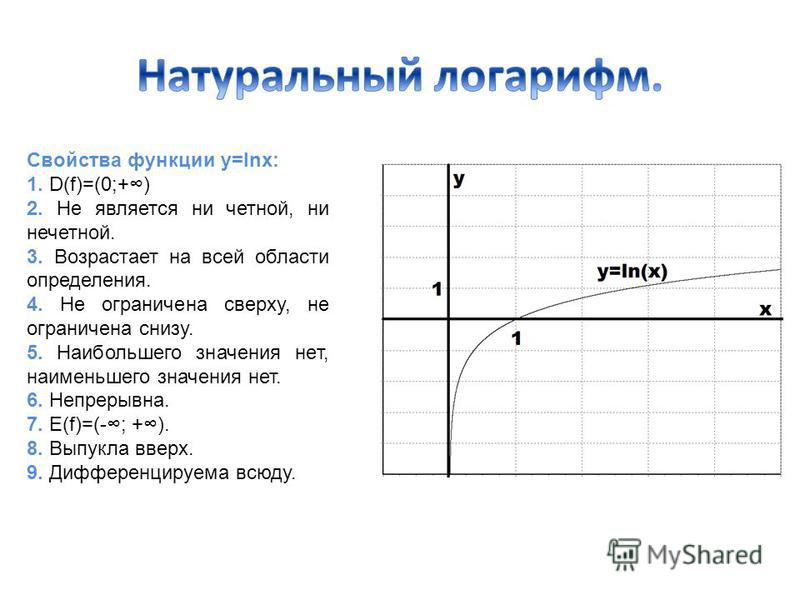
Мы знаем, что экспоненциальная и логарифмическая функции обратны друг другу и, следовательно, их графики симметричны относительно прямой y = x. Также обратите внимание, что y = 0, когда x = 0, поскольку y = log a 1 = 0 для любого «a». Таким образом, все такие функции имеют x-пересечение (1, 0). Логарифмическая функция не имеет точки пересечения с осью Y, поскольку журнал a 0 не определен. Суммируя все это, графики экспоненциальных функций и логарифмический график выглядят так, как показано ниже.
Свойства логарифмического графика
- а > 0 и а ≠ 1
- Логарифмический график увеличивается, когда a > 1, и уменьшается, когда 0 < a < 1.
- Домен получается заданием аргумента функции больше 0.
- Диапазон представляет собой набор всех действительных чисел.
Графики логарифмических функций
Прежде чем рисовать график логарифмической функции, просто подумайте, какую кривую вы получите в ответ: возрастающую или убывающую.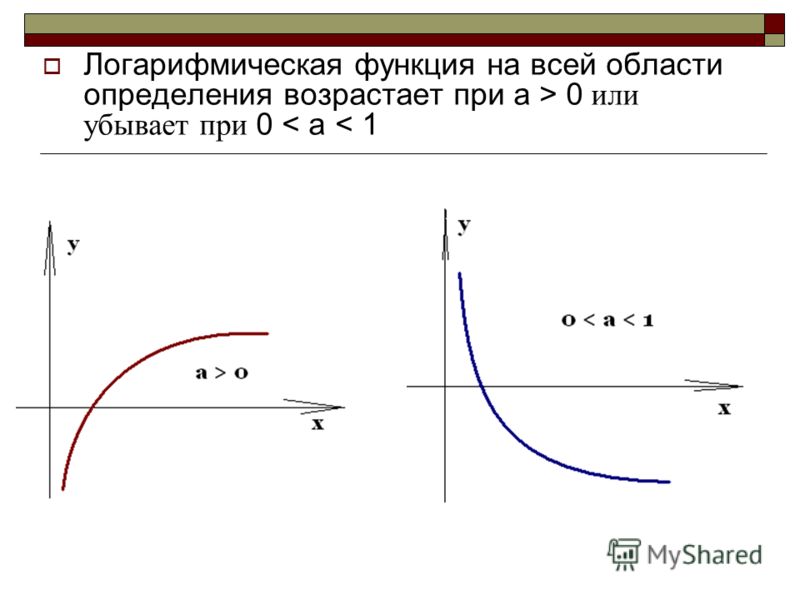
Если основание > 1, то кривая возрастает; а если 0 < основание < 1, то кривая убывающая. Вот шаги для построения графика логарифмических функций :
- Найдите домен и диапазон.
- Найдите вертикальную асимптоту, установив аргумент равным 0. Обратите внимание, что логарифмическая функция не имеет горизонтальной асимптоты.
- Подставьте некоторое значение x, которое сделает аргумент равным 1, и используйте свойство log a 1 = 0. Это дает нам точку пересечения x.
- Подставьте некоторое значение x, которое сделает аргумент равным основанию, и используйте свойство log a a = 1. Это даст нам точку на графике.
- Соедините две точки (из последних двух шагов) и продлите кривую с обеих сторон относительно вертикальной асимптоты.
Пример: Постройте график логарифмической функции f(x) = 2 log 3 (x + 1).
Решение:
Здесь основание равно 3 > 1.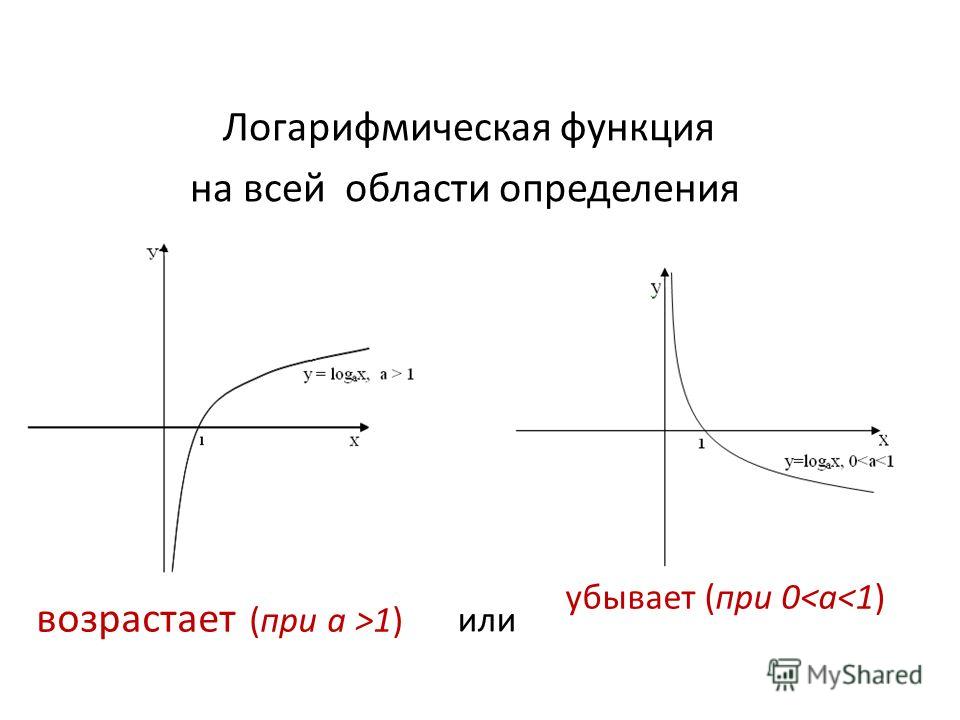
Таким образом, кривая будет возрастать.
Для домена: x + 1 > 0 ⇒ x > -1. Итак, домен = (-1, ∞).
Диапазон = R.
Вертикальная асимптота x = -1.
- При x = 0, y = 2 log 3 (0 + 1) = 2 log 3 1 = 2 (0) = 0
- При x = 2, y = 2 log 3 (2 + 1) = 2 log 3 3 = 2 (1) = 2
Если мы хотим большей ясности, мы можем сформировать таблицу значений с некоторыми случайными значениями x и подставить каждое из них в заданную функцию для вычисления значений y. Таким образом, мы получаем больше точек на графике, и это помогает получить идеальную форму графика.
Таким образом, (0, 0) и (2, 2) — две точки на кривой. Таким образом, график логарифмической функции выглядит следующим образом.
Свойства логарифмических функций
Свойства логарифмической функции полезны при работе со сложными функциями журнала. Все общие арифметические операции с числами преобразуются в другой набор операций с логарифмами.
Произведение двух чисел, взятое внутри логарифмических функций, равно сумме логарифмических значений двух функций. Точно так же операции деления преобразуются в разность логарифмов двух чисел. Перечислим важные свойства логарифмических функций в следующих пунктах.
- журнал аб = журнал а + журнал б
- loga/b = log a — log b
- log b a = (log c a)/(log c b) (изменение базового правила)
- логи х = х логарифм
- журнал a 1 = 0
- журнал а а = 1
Производная и интеграл логарифмических функций
Вывод логарифмической функции дает наклон касательной к кривой, представляющей логарифмическую функцию. Формула производной десятичной и натуральной логарифмической функций выглядит следующим образом.
- Производная от ln x равна 1/x. т. е. d/dx. ln х = 1/х.
- Производная logₐ x равна 1/(x ln a). т. е. d/dx (logₐ x) = 1/(x ln a).
Интегральные формулы логарифмических функций следующие:
- Интеграл от ln x равен ∫ ln x dx = x (ln x — 1) + C.
- Интеграл от log x равен ∫ log x dx = x (log x — 1) + C.
Связанные темы:
- Экспоненты
- Экспонентные правила
- Свойства логарифмов
- Логи в расчетах
Часто задаваемые вопросы о логарифмических функциях
Как решать логарифмические функции?
Логарифмическую функцию можно решить с помощью логарифмических формул. Произведение функций внутри логарифмов равно (log ab = log a + log b) сумме двух логарифмических функций. Деление двух логарифмических функций (loga/b = log a — log b) заменено на разность логарифмических функций. Логарифмические функции также можно решить, придав им экспоненциальную форму.
Как построить график логарифмических функций?
График логарифмической функции y = log x можно получить, найдя ее область определения, область значений, асимптоты и некоторые точки на кривой.
Чтобы найти некоторые точки на кривой, мы можем использовать следующие свойства:
- log 1 = 0
- журнал 10 = 1
Что такое асимптоты логарифмической функции?
Вот асимптоты логарифмической функции f(x) = a log (x — b) + c:
- Вертикальная асимптота x = b.
- Горизонтальная асимптота отсутствует.
Как связаны экспоненциальные и логарифмические функции?
Показательная функция вида a x = N может быть преобразована в логарифмическую функцию log a N = x. Здесь экспоненциальная функция 2 x = 10 преобразуется в логарифмическую форму как log 2 10 = x, чтобы найти значение x. Логарифм подсчитывает количество вхождений основания в повторяющихся кратных числах.
В чем разница между натуральным логарифмом и десятичным логарифмом?
Логарифмические функции можно разделить на два типа в зависимости от основания логарифмов. У нас есть натуральные логарифмы и десятичные логарифмы.
Натуральные логарифмы — это логарифмы по основанию «е», а десятичные логарифмы — это логарифмы по основанию 10. Дальнейшие логарифмы можно вычислять по любому основанию, но часто они рассчитываются по основанию «е» или «10». Натуральные логарифмы записываются как log e x (или) ln x, а десятичные логарифмы записываются как log 10 x (или) log x. Чтобы получить значение x из натуральных логарифмов, оно равно степени, в которую нужно возвести e, чтобы получить x.
- е = 2,718
- log e N = 2,303 × log 10 N
- log 10 N = 0,4343 × log e N
Значение e = 2,718281828459, но его часто записывают кратко как e = 2,718. Также приведенные выше формулы помогают при взаимном преобразовании натуральных логарифмов и десятичных логарифмов.
Как дифференцировать логарифмические функции?
Дифференцирование логарифмической функции приводит к обратной функции. Дифференциация ln x равна 1/x.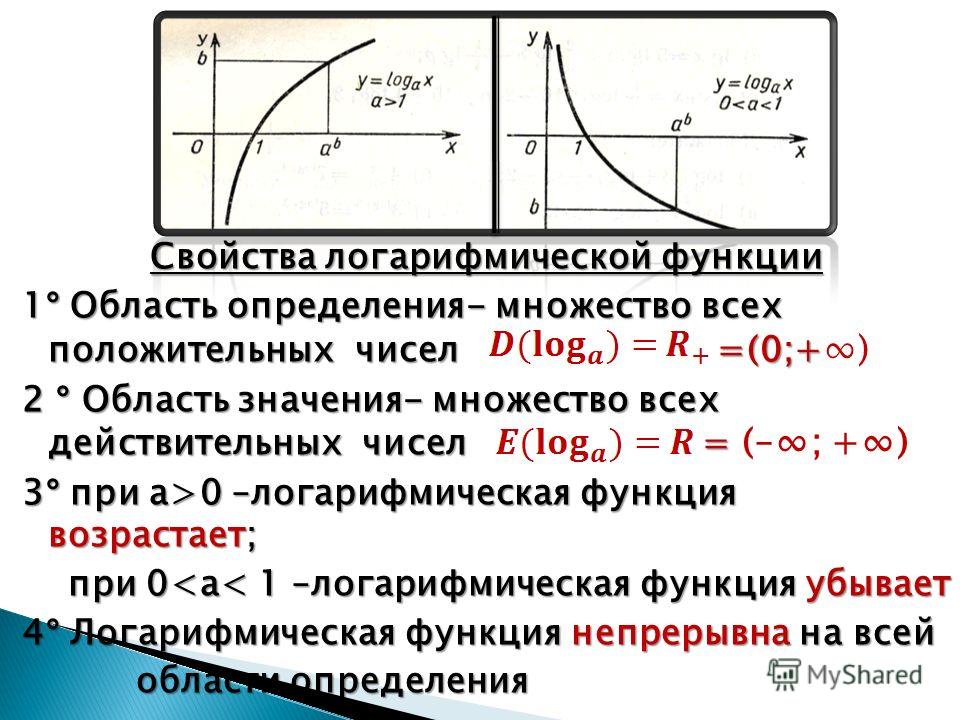
(d/dx .ln x = 1//x). Кроме того, первообразная 1/x возвращает функцию ln.
Что такое диапазон логарифмических функций?
Диапазон логарифмической функции принимает все значения, включая положительные и отрицательные действительные числа. Таким образом, диапазон логарифмической функции находится в диапазоне от отрицательной бесконечности до положительной бесконечности.
Что такое область логарифмических функций?
Логарифмы можно вычислять для положительных целых чисел, дробей, десятичных дробей, но нельзя вычислять для отрицательных значений. Следовательно, областью определения логарифмической функции является множество всех положительных действительных чисел.
Что такое формула логарифмических функций?
Следующие формулы полезны для работы и решения логарифмических функций.
- журнал аб = журнал а + журнал б
- loga/b = log a — log b
- log b a = (log a)/(log b)
- логи х = х логарифм
Для чего используются логарифмические функции?
Логарифмические функции имеют множество приложений в физике, технике, астрономии.