Sin 2 arccos x: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значение
cos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74 Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Mathway | Популярные задачи

1Trovare la Derivata — d/dxнатуральный логарифм x
2Вычислим интегралинтеграл натурального логарифма x по x
3Trovare la Derivata — d/dxe^x
4Вычислим интегралинтеграл e^(2x) по x
5Trovare la Derivata — d/dx1/x
6Trovare la Derivata — d/dxx^2
7Trovare la Derivata — d/dx1/(x^2)
8Trovare la Derivata — d/dxsin(x)^2
9Trovare la Derivata — d/dxsec(x)
10Вычислим интегралинтеграл e^x по x
11Вычислим интегралинтеграл x^2 по x
12Вычислим интегралинтеграл квадратного корня из x по x
13Trovare la Derivata — d/dxcos(x)^2
14Вычислим интегралинтеграл 1/x по x
15Вычислим интегралинтеграл sin(x)^2 по x
16Trovare la Derivata — d/dxx^3
17Trovare la Derivata — d/dxsec(x)^2
18Вычислим интегралинтеграл cos(x)^2 по x
19Вычислим интегралинтеграл sec(x)^2 по x
20Trovare la Derivata — d/dxe^(x^2)
21Вычислим интегралинтеграл в пределах от 0 до 1 кубический корень из 1+7x по x
22Trovare la Derivata — d/dxsin(2x)
23Trovare la Derivata — d/dxtan(x)^2
24Вычислим интегралинтеграл 1/(x^2) по x
25Trovare la Derivata — d/dx2^x
26Графикнатуральный логарифм a
27Trovare la Derivata — d/dxcos(2x)
28Trovare la Derivata — d/dxxe^x
29Вычислим интегралинтеграл 2x по x
30Trovare la Derivata — d/dx( натуральный логарифм от x)^2
31Trovare la Derivata — d/dxнатуральный логарифм (x)^2
32Trovare la Derivata — d/dx3x^2
33Вычислим интегралинтеграл xe^(2x) по x
34Trovare la Derivata — d/dx2e^x
35Trovare la Derivata — d/dxнатуральный логарифм 2x
36Trovare la Derivata — d/dx-sin(x)
37Trovare la Derivata — d/dx4x^2-x+5
38Trovare la Derivata — d/dxy=16 корень четвертой степени из 4x^4+4
39Trovare la Derivata — d/dx2x^2
40Вычислим интегралинтеграл e^(3x) по x
41Вычислим интегралинтеграл cos(2x) по x
42Trovare la Derivata — d/dx1/( квадратный корень из x)
43Вычислим интегралинтеграл e^(x^2) по x
44Вычислитьe^infinity
45Trovare la Derivata — d/dxx/2
46Trovare la Derivata — d/dx-cos(x)
47Trovare la Derivata — d/dxsin(3x)
48Trovare la Derivata — d/dx1/(x^3)
49Вычислим интегралинтеграл tan(x)^2 по x
50Вычислим интегралинтеграл 1 по x
51Trovare la Derivata — d/dxx^x
52Trovare la Derivata — d/dxx натуральный логарифм от x
53Trovare la Derivata — d/dxx^4
54Оценить пределпредел (3x-5)/(x-3), если x стремится к 3
55Вычислим интегралинтеграл x^2 натуральный логарифм x по x
56Trovare la Derivata — d/dxf(x) = square root of x
57Trovare la Derivata — d/dxx^2sin(x)
58Вычислим интегралинтеграл sin(2x) по x
59Trovare la Derivata — d/dx3e^x
60Вычислим интегралинтеграл xe^x по x
61Trovare la Derivata — d/dxy=x^2
62Trovare la Derivata — d/dxквадратный корень из x^2+1
63Trovare la Derivata — d/dxsin(x^2)
64Вычислим интегралинтеграл e^(-2x) по x
65Вычислим интегралинтеграл натурального логарифма квадратного корня из x по x
66Trovare la Derivata — d/dxe^2
67Trovare la Derivata — d/dxx^2+1
68Вычислим интегралинтеграл sin(x) по x
69Trovare la Derivata — d/dxarcsin(x)
70Оценить пределпредел (sin(x))/x, если x стремится к 0
71Вычислим интегралинтеграл e^(-x) по x
72Trovare la Derivata — d/dxx^5
73Trovare la Derivata — d/dx2/x
74Trovare la Derivata — d/dxнатуральный логарифм 3x
75Trovare la Derivata — d/dxx^(1/2)
76Trovare la Derivata — d/d@VARf(x) = square root of x
77Trovare la Derivata — d/dxcos(x^2)
78Trovare la Derivata — d/dx1/(x^5)
79Trovare la Derivata — d/dxкубический корень из x^2
80Вычислим интегралинтеграл cos(x) по x
81Вычислим интегралинтеграл e^(-x^2) по x
82Trovare la Derivata — d/d@VARf(x)=x^3
83Вычислим интегралинтеграл 4x^2+7 в пределах от 0 до 10 по x
84Вычислим интегралинтеграл ( натуральный логарифм x)^2 по x
85Trovare la Derivata — d/dxлогарифм x
86Trovare la Derivata — d/dxarctan(x)
87Trovare la Derivata — d/dxнатуральный логарифм 5x
88Trovare la Derivata — d/dx5e^x
89Trovare la Derivata — d/dxcos(3x)
90Вычислим интегралинтеграл x^3 по x
91Вычислим интегралинтеграл x^2e^x по x
92Trovare la Derivata — d/dx16 корень четвертой степени из 4x^4+4
93Trovare la Derivata — d/dxx/(e^x)
94Оценить пределпредел arctan(e^x), если x стремится к 3
95Вычислим интегралинтеграл (e^x-e^(-x))/(e^x+e^(-x)) по x
96Trovare la Derivata — d/dx3^x
97Вычислим интегралинтеграл xe^(x^2) по x
98Trovare la Derivata — d/dx2sin(x)
99Вычислитьsec(0)^2
100Trovare la Derivata — d/dxнатуральный логарифм x^2

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1
1 Найти производную — d/dx бревно натуральное х
2 Оценить интеграл интеграл натурального логарифма x относительно x
3 Найти производную — d/dx
21 Оценить интеграл интеграл от 0 до 1 кубического корня из 1+7x относительно x
22 Найти производную — d/dx грех(2x)
23 Найти производную — d/dx
41 Оценить интеграл интеграл от cos(2x) относительно x
42 Найти производную — d/dx 1/(корень квадратный из х)
43 Оценка интеграла 9бесконечность
45 Найти производную — d/dx х/2
46 Найти производную — d/dx -cos(x)
47 Найти производную — d/dx грех(3x)
68 Оценить интеграл интеграл от sin(x) по x
69 Найти производную — d/dx угловой синус(х)
70 Оценить предел ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85 Найти производную — d/dx лог х
86 Найти производную — d/dx арктан(х)
87 Найти производную — d/dx бревно натуральное 5х92

Упрощение обратных тригонометрических функций

Как упростить выражения, включая обратные тригонометрические функции для 12 класса по математике.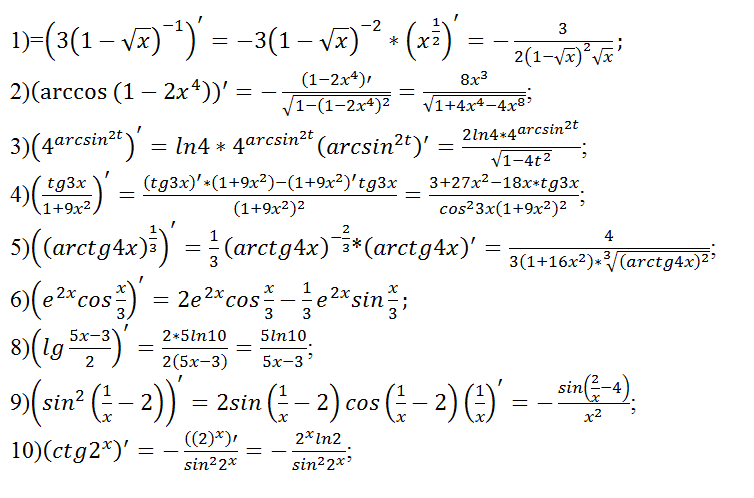 Также включены вопросы с подробными решениями.

    Вопрос 1

    Упростите выражения:
    а) sin(arcsin(x)) и arcsin(sin(x))
    b) cos(arccos(x)) и arccos(cos(x))
    c) tan(arctan(x)) и arctan(tan(x))
    Раствор
    а) sin и arcsin обратны друг другу, поэтому свойства обратных функций можно использовать для записи
    sin(arcsin(x)) = x , для -1 ≤ x ≤ 1
    arcsin(sin(x)) = x, для x ∈ [-π/2, π/2]
    ПРИМЕЧАНИЕ. Если x в arcsin(sin(x)) не находится в интервале [-π/2 , π/2], найдите θ в интервале [-π/2 , π/2] такое, что sin(x) = sin(θ), а затем упростить arcsin(sin(x)) = θ
    б) cos и arccos являются обратными друг другу, и поэтому свойства обратных функций могут быть использованы для записи
    cos(arccos(x)) = x , для -1 ≤ x ≤ 1
    arccos(cos(x)) = x, для x ∈ [0, π]
    ПРИМЕЧАНИЕ. Если x в arccos(cos(x)) не находится в интервале [0/2 , π], найдите θ в интервале [0 , π] такое, что cos(x) = cos(θ), а затем упростите arccos(cos(x)) = θ
    c) tan и arctan являются обратными друг другу, и поэтому свойства обратных функций могут быть использованы для записи
    тангенс (арктангенс (х)) = х
    arctan(tan(x)) = x, для x ∈ (-π/2, π/2)
    ПРИМЕЧАНИЕ. Если x в arctan(tan(x)) не находится в интервале (-π/2 , π/2), найдите θ в интервале (-π/2 , π/2) такое, что tan(x) = tan(θ), а затем упростить arctan(tan(x)) = θ

    Вопрос 2

    Выразите следующее в виде алгебраических выражений:
    sin(arccos(x)) и tan(arccos(x))
    Раствор
    Пусть A = arccos(x). Следовательно
    cos(A) = cos(arccos(x)) = x
    Используйте прямоугольный треугольник с углом A таким, что cos(A) = x (или x / 1), найдите второй катет и вычислите sin(A) и tan(A)

    .


    sin(arccos(x)) = sin(A) = √(1 — x 2 ) / 1 = √(1 — x 2 )     для x ∈ [-1, 1]
    тангенс(arccos(x)) = тангенс(A) = √(1 — x 2 ) / x     для x ∈ [-1 , 0) ∪ (0 , 1]

    Вопрос 3

    Выразите следующее в виде алгебраических выражений:
    cos(arcsin(x)) и tan(arcsin(x))
    Раствор
    Пусть A = arcsin(x). Следовательно
    грех (А) = грех (угловой грех (х)) = х
    Используйте прямоугольный треугольник с углом A таким, что sin(A) = x (или x / 1), найдите второй катет и вычислите cos(A) и tan(A)

    .


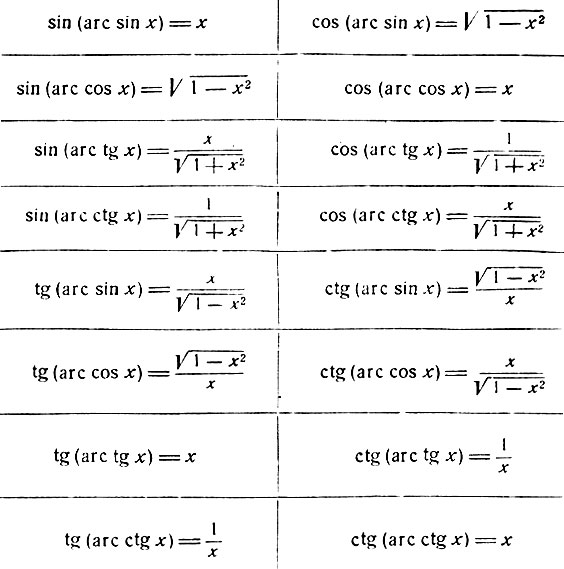
    cos(arcsin(x)) = cos(A) = √(1 — x 2 ) / 1 = √(1 — x 2 )     для x ∈ [-1, 1]
    tan(arcsin(x)) = tan(A) = x / √(1 — x 2 )     для x ∈ (-1, 1)

    Вопрос 4

    Выразите следующее в виде алгебраических выражений:
    sin(arctan(x)) и cos(arctan(x))
    Раствор
    Пусть A = arctan(x). Следовательно
    тангенс (А) = тангенс (арктангенс (х)) = х
    Используйте прямоугольный треугольник с углом A таким, что tan(A) = x (или x / 1), найдите гипотенузу и вычислите sin(A) и cos(A)

    .


    sin(arctan(x)) = sin(A) = x / √(1 + x 2 )
    cos(arctan(x)) = cos(A) = 1 / √(1 + x 2 )

    Вопрос 5

    Упростите следующие выражения:
    а) arccos(0) , arcsin(-1) , arctan(-1)
    b) sin(arcsin(-1/2)) , arccos(cos(π/2)) , arccos(cos(-π/2))
    c) cos(arcsin(-1/2)) , arcsin(sin(π/3)) , arcsin(tan(3π/4))
    d) arccos(tan(7π/4)) , arcsin(sin(13π/3)) , arctan(tan(-17π/4)) , arcsin(sin(9π/5))
    Раствор
    а) Используйте определение.
    arccos(0) = π/2, поскольку cos(π/2) = 0, а π/2 находится в пределах диапазона arccos, который равен [0 , π]
    arcsin(-1) = -π/2, потому что sin(-π/2) = -1 и -π/2 находится в пределах диапазона arcsin, который равен [-π/2 , π/2]
    arctan(-1) = -π/4, потому что tan(-π/4) = -1 и -π/4 находится в пределах диапазона arctan, который равен (-π/2 , π/2)
    b) Упростите внутренние функции, а затем внешние функции, используя определения.
    sin(arcsin(-1/2)) = sin(-π/6) = -1/2
    arccos(cos(π/2)) = arccos(0) = π/2
    arccos(cos(-π/2)) = arccos(0) = π/2
    c) Упростите внутренние функции, а затем внешние функции, используя определения.
    cos(arcsin(-1/2)) = cos(-π/6) = √3/2
    arcsin(sin(π/3)) = arcsin(√3/2) = π/3
    arcsin(tan(3π/4)) = arcsin(-1) = -π/2
    d) Упростите внутренние функции, а затем внешние функции, используя определения.
    arccos(tan(7π/4)) = arccos(-1) = π
    arcsin(sin(13π/3)) = arcsin(sin(4π + π/3)) = arcsin(sin(π/3)) = π/3
    arctan(tan(- 17π/4)) = arctan(tan(- 4π-π/4)) = arctan(tan(- π/4)) = — π/4
    arcsin(sin(9π/5)) = arcsin(sin(2π — π/5)) = arcsin(sin(- π/5)) = — π/5

    Вопрос 6

    Пусть A = arcsin(2/3) и B = arccos(-1/2). Найдите точное значение sin(A + B).
    Решение
    Используйте отступ sin(A + B) = sin(A)cos(B) + cos(A)sin(B), чтобы расширить данное выражение.
    sin(A + B) = sin(arcsin(2/3))cos(arccos(-1/2)) + cos(arcsin(2/3))sin(arccos(-1/2))
    Используйте приведенные выше отступы, чтобы упростить каждый член в приведенном выше выражении.
    грех (угловой грех (2/3)) = 2/3 (мы использовали sin(arcsin(x)) = x))
    cos(arccos(-1/2)) = -1/2 (мы использовали cos(arccos(x)) = x))
    cos(arcsin(2/3)) = √(1 — (2/3) 2 ) = √5/3 (мы использовали cos(arcsin(x)) = √(1 — x 2 ))
    sin(arccos(-1/2)) = √(1 — (- 1/2) 2 ) = √3/2 (мы использовали sin(arccos(x)) = √(1 — x 2 )) Подставить и рассчитать.
    sin(A + B) = (2/3)(-1/2)+(√5/3)(√3/2) = -1/3 + √(15)/6

    Вопрос 7

    Запишите Y = sin(2 arcsin(x)) как алгебраическое выражение.
    Раствор
    Пусть A = arcsin(x). Следовательно, Y можно записать как
    Y = sin (2 А)
    Используйте тождество sin(2 A) = 2 sin(A) cos(A), чтобы переписать Y следующим образом:
    Y = 2 sin (A) cos(A) = 2 sin(arcsin(x)) cos(arcsin(x))
    Используйте тождества sin(arcsin(x)) = x и cos(arcsin(x)) = √(1-x 2 ), чтобы переписать Y следующим образом:
    Y = 2 х √(1 — х 2 )

    Вопрос 8

    Найдите точное значение Y = sin(2 arctan(3/4)).

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *