Шлях до математики: кроки успіху: Функція
- Якщо є дріб, то його знаменник не дорівнює 0
- Якщо є корінь парного степеня, то його підкореневий вираз повинен бути більше або дорівнювати 0
- Якщо є логарифм, то його підлогарифмічний вираз повинен бути більше 0
- за парністю
- Парні: якщо f(-x)=f(x). Графік парної функції симетричний відносно осі Оу
- Непарні: якщо f(-x)= -f(x). Графік непарної функції симетричний відносно початку координат
- Ні парні ні непарні: не виконуються попередні умови
- за монотоністю
- Зростаючі: якщо більшому значенню аргументу відповідає більше значення функції (з x
- Спадні: якщо більшому значенню аргументу відповідає менше значення функції (з x1<x2 слідує f(x1)>f(x2))
- Зростаючі: якщо більшому значенню аргументу відповідає більше значення функції (з x
- періодичні з періодом Т: f(x-T)=f(x)=f(x+T)
- Обчисліть значення функції y= у точці х0=4.

ВідповідьА Б В Г Д -1 -2 2 3 0,5 Б.
Щоб обчислити значення функції в точці, потрібно в функцію замість невідомої підставити її значення. Маємо y(4)==-2 (так як =9). - Яку властивість із наведених має функція у=2х-9?
ВідповідьА Б В Г Д є парною є непарною є періодичною є спадною є зростаючою Д.
Оскільки коефіцієнт при х дорівнює 2>0, то функція є зростаючою. - 2019. Яку властивість із наведених має функція ?
ВідповідьА Б В Г Д набуває лише невід’ємних значень спадає на всій області визначення парна періодична має дві точки екстремуму А.

Значення кореня квадратного не може бути від’ємним, тому функція набуває лише невід’ємних значень. - Функція y=f(x) є спадною на проміжку (-∞;+∞). Укажіть правильну нерівність.
ВідповідьА Б В Г Д f(1)>f(-1) f(1)<f(8) f(1)>f(0) f(-1)<f(0) f(1)>f(10) Д.
Оскільки функція є спадною, то за означенням спадної функції маємо: при x1<x2 f(x1)>f(x2), тобто шукаємо, де знак між функціями протилежний знаку між аргументами.
А) 1>-1 і f(1)>f(-1), знак співпадає.
Б) 1<8 і f(1)<f(8), знак співпадає.
В) 1>0 і f(1)>f(0), знак співпадає.
Г) -1<0 і f(-1)<f(0), знак співпадає.
Д) 1<10 і f(1)>f(10), знаки протилежні. - Знайдіть область визначення функції y=2-.
ВідповідьА Б В Г Д (-∞;+∞) (-∞;0)U(0;+∞) (-∞;0)U(;+∞) (-∞;)∪(;+∞) (0;) Б.

Оскільки маємо дріб, то його знаменник не дорівнює 0, тобто x≠0. Тому областю визначення функції є всі числа, крім 0, який розриває проміжок (-∞;+∞) на 2 частини. Отже x∈(-∞;0)U(0;+∞) - Знайдіть область визначення функції y=.
ВідповідьА Б В Г Д (-∞;0)U(1;+∞) (-∞;-1) U(-1;+∞) (-∞;1)U(1;+∞) (-∞;0) U(0;1) U(1;+∞) (-∞;+∞) В.
Оскільки маємо дріб, то його знаменник не дорівнює 0, тобто x-1≠0, звідки x≠1. Тому областю визначення функції є всі числа, крім 1, яка розриває проміжок (-∞;+∞) на 2 частини. Отже x∈(-∞;1)U(1;+∞). - Укажіть область визначення функції y=.
ВідповідьА Б В Г Д (-∞;+∞) (-∞;5)U(5;+∞) (-∞;4)U(4;+∞) (-∞;) U (;+∞) (4;5) А.

Оскільки маємо дріб, то його знаменник не дорівнює 0, тобто 5≠0. Оскільки ця умова виконується завжди, то ніяких обмежень на область визначення функції нема. Отже областю визначення функції є всі числа, тобто x∈(-∞;+∞). - Знайдіть область визначення функції y=.
ВідповідьА Б В Г Д (-∞;2)U(2;+∞) (-∞;-1)U(2;+∞) (-∞;-2) U(-2;+∞) (-∞;-1) U(-1;2) U(2;+∞) (-∞;+∞) А.
Оскільки маємо дріб, то його знаменник не дорівнює 0, тобто x-2≠0, звідки x≠2. Тому областю визначення функції є всі числа, крім 2, яка розриває проміжок (-∞;+∞) на 2 частини. Отже x∈(-∞;2)U(2;+∞). - Знайдіть область визначення функції y=.
ВідповідьА Б В Г Д [3;+∞) (-∞;3) (-∞;-3] [-3;+∞) (-∞;3] Д.

Оскільки маємо корінь парного степеня, то підкореневий вираз повинен бути невід’ємним. Отже, 3-x≥0, звідки x≤3. Отже областю визначення функції є x∈(-∞;3]. - Знайдіть область визначення функції y=.
ВідповідьА Б В Г Д [-2;0)U(0;+∞) [-2;+∞) (-2;0)U(0;+∞) (-∞;-2] x≠1 А.
Оскільки маємо корінь парного степеня, то підкореневий вираз повинен бути невід’ємним. Отже, x+2≥0, звідки x≥-2. Крім того, маємо дріб, отже його знаменник не повинен дорівнювати 0. Маємо 2x-1≠0, звідки 2x≠1=20. Таким чином, x≠0. Отже маємо, що x≥-2 і x≠0, тому областю визначення функції є x∈[-2;0)U(0;+∞). - Укажіть область значень функції y=-6.
ВідповідьА Б В Г Д [9;+∞) [0;+∞) [3;+∞) [-3;+∞) (-∞;+∞) Г.

Для знаходження області значень функції знайдемо область значень х2 і поступово приведемо до значення функції, виконуючи однакові дії з лівою та правою частиною нерівності. Маємо:
х2≥0
х2+9≥0+9
х2+9≥9
≥3
-6≥3-6
-6≥-3
Отже, областю значень функції є y∈[-3;+∞). - 2020. Укажіть область значень функції у=2cosx+3.
ВідповідьА Б В Г Д [0;3] [-5;5] [1;5] [3;5] (-∞;+∞) В.
Оскільки -1≤cosx≤1, то -2≤2cosx≤2, звідки -2+3≤2cosx+3≤2+3. Отже, областю значень функції є y∈[1;5]. - Укажіть область значень функції f(x)=(sinx+cosx)2.
ВідповідьА Б В Г Д [1;2] [0;2] [-;] [0;1] інша відповідь Б.

Спростимо функцію. Маємо f(x)=(sinx+cosx)2= sin2x+2sinxcosx+cos2x= sin2x+cos2x+2sinxcosx=1+sin2x.
Оскільки -1≤sin2x≤1, то 1-1≤1+sin2x≤1+1, звідки 0≤1+sin2x≤2. Отже, областю значень функції є y∈[0;2]. - Парна функція y=f(x) визначена на проміжку (-∞;+∞). Які з наведених тверджень є правильними?
І. f(-10)= -f(10).
II. f(-6)=f(6).
ІІІ. Графік функції y=f(x) симетричний відносно осі у.
ВідповідьА Б В Г Д лише І лише ІІ лише І і ІІІ лише ІІ і ІІІ лише ІІІ Г.
Оскільки функція парна, то f(-х)=f(х). Тому перше твердження не є правильним, а друге правильне. Графік парної функції симетричний відносно осі у, отже третє твердження також правильне. - Укажіть парну функцію.
ВідповідьА Б В Г Д у=4x у=х y= y=tgx y=|x| Д.

Оскільки функція парна, то у(-х)=у(х). Перевіримо всі функції.
А) y(-x)=4-x=≠y(x). Отже, функція не підходить.
Б) у(-х)=-х≠y(x). Отже, функція не підходить.
В) Оскільки корінь парного степеня, то за ОДЗ x≥0. Оскільки парні функції мають симетричне ОДЗ, то ця функція не підходить.
Г) у(-х)=tg(-х)= -tgx≠y(x). Отже, функція не підходить.
Д) у(-х)=|-х|=|x|=y(x). Отже, ця функція підходить. - Укажіть непарну функцію.
ВідповідьА Б В Г Д у=х2-4 у=-х2 y=х3-1 y= y=x3-x Д.
Оскільки функція непарна, то у(-х)= -у(х). Перевіримо всі функції.
А) у(-х)=(-х)2-4=х2-4≠ -y(x). Отже, функція не підходить.
Б) у(-х)=-(-х)2=-х2≠ -y(x). Отже, функція не підходить. Отже, функція не підходить.
Отже, функція не підходить.
Г) Оскільки корінь парного степеня, то за ОДЗ x-2≥0, звідки x≥2. Оскільки непарні функції мають симетричне ОДЗ, то ця функція не підходить.
Д) у(-х)=(-x)3-(-x)= -x3+x= -(x3-x) = -y(x). Отже, ця функція підходить. - Укажіть з-поміж наведених функцію f(x), якщо для кожного х з області її визначення виконується рівність f(-x)=-f(x).
ВідповідьА Б В Г Д f(x)=х2 f(x)=3х f(x)=2х+5 f(x)=log3x f(x)= Д.
I спосіб. Оскільки записано означення непарної функції, то потрібно лише її знайти. Це функція f(x)=
ІІ спосіб. Перевіримо виконання умови f(-x)=-f(x) для всіх функцій.
А) f(-x)=(-х)2=х2=f(x). Отже, функція не підходить.
Б) f(-x)=(3)-х. Даний вираз не дорівнює ні f(x), ні -f(x). Отже, функція не підходить.
Отже, функція не підходить.
В) f(-x)= -2х+5. Даний вираз не дорівнює ні f(x), ні -f(x). Отже, функція не підходить.
Г) Так як х більше за 0 (область визначення логарифмічноїфункції), то ми не можемо підставляти протилежне йому значення. Отже, функція не підходить.
Д) f(-x)== -f(x). Отже, ця функція підходить. - Функція f(x) є парною, а g(x) — непарною. Обчисліть значення виразу 3f(-2)-g(1), якщо f(2)= -5, g(-1)=7.
ВідповідьА Б В Г Д -8 -22 22 8 1 А.
Оскільки f(x) парна, то f(-х)= f(х), оскільки g(x) непарна, то g(-х)= -g(х). Тоді 3f(-2)-g(1)=3f(2)+g(-1)=3⋅(-5)+7= -15+7= -8. - Укажіть найменший додатний період функції y=2ctg(3x).
ВідповідьА Б В Г Д 2π π В.

Оскільки для функції y=ctgx T=π, то для функції y=2ctg(3x) T= (період функції ділимо на коефіцієнт біля змінної х). - 2019. Укажіть нулі функції f(x)=2x2-5x-3.
ВідповідьА Б В Г Д -3; 0 -3; -3 ; 3 -1; 6 Г.
Нулями функції є ті значення аргумента, при яких значення функції дорівнює 0. Отже нулі функції — корені відповідного квадратного рівняння. Маємо:
2x2-5x-3=0
D=(-5)2-4⋅2⋅(-3)=25+24=49.
x1==3
x2=. - 2020. До кожного початку речення (1-3) доберіть його закінчення (А-Д) так, щоб утворилося правильне твердження.
ВідповідьФункція Властивість 1 Функція y=
2 Функція у=х+4
3 Функція у=х3А спадає на проміжку проміжок (-∞;+∞)
Б не визначена в точці х=1
В є парною
Г набуває додатного значення в точці х= -3
Д є непарною1-Б, 2-Г, 3-Д.

1) Так як при х=1 х-4=1-4=-3, а квадратного кореня з від’ємного числа не існує, то функція не визначена в точці х=1.
2) Так як при х=-3 х+4=-3+4=1, то функція набуває додатного значення в точці х= -3.
3) Так як у(-х)=(-х)3=-(х3)=-у(х), то функція є непарною. - 2019. Установіть відповідність між функцією (1-4) та її властивістю (А-Д).
ВідповідьФункція Властивість 1 y=x2
2 y=x3+1
3 у=3-х
4 у=sinxА спадає на всій області визначення
Б зростає на всій області визначення
В непарна
Г парна
Д областю значень функції є проміжок (0;+∞)1-Г, 2-Б, 3-А, 4-В.
1) Оскільки у=(-х)=(-x)2=x2=у(х), то це парна функція.
2) Дана функція є зростаючою на всій області визначення (чим більше значення х, тим більше значення x3+1).
3) Дана функція є спадною на всій області визначення (чим більше значення х, тим менше різниця 3 і х)
4) Оскільки у=(-х)=sin(-x)= -sinx= -у(х), то це непарна функція. - Установіть відповідність між твердженням (1-4) та функцією (А-Д), для якої це твердження є правильним.
ВідповідьТвердження Функція 1 графік функції не перетинає жодну з осей координат
2 областю значення функції є проміжок (0;+∞)
3 функція спадає на всій області визначення
4 на відрізку [-1,5;1,5] функція має два нуліА y= -x+2
Б y=x2-2
В y=
Г y=3x
Д y=cosx1-В, 2-Г, 3-А, 4-Б.
1) Серед запропонованих функцій є обернена пропорційність, графіком якого є гіпербола. Даних графік не перетинає жодну з осей координат. Маємо першу відповідь і з наступних перевірок виключаємо відповідь В.
2) А) область значень yєR. Б) область значень yє[-2;+∞). Г) область значень yє(0;+∞). Підходить. Маємо другу відповідь і з наступних перевірок виключаємо відповідь Г.
3) А) Оскільки коефіцієнт біля х від’ємний, то дана функція спадна. Підходить. Маємо третю відповідь і з наступних перевірок виключаємо відповідь А.
4) Б) Для знаходження нулів функції розв’язуємо рівняння x2-2=0, звідки x=±. Дані корені належать потрібному проміжку. Підходить. Маємо четверту відповідь. - Установіть відповідність між функціями, заданими формулами (1-4), та їхніми областями значень (А-Д).
ВідповідьФункція Область значень 1 y=log2х
2 y=2x
3 y=2
4 y=2-x2А [2;+∞)
Б [0;+∞)
В (-∞;2]
Г (0;+∞)
Д (-∞;+∞)1-Д, 2-Г, 3-Б, 4-В.
1) (-∞;+∞)
2) (0;+∞)
3) [0;+∞)
4) Оскільки областю значень y=x2 є проміжок [0;+∞), то областю значень y= -x2 є проміжок (-∞;0] і областю значень y= 2-x2 є проміжок (-∞;2] - Установіть відповідність між функціями, заданими формулами (1-4) та їхніми властивостями (А-Д).

ВідповідьФункція Властивість 1 y=x3
2 y=cosx
3 y=tgx
4 y=log0,2хА областю визначення функції є проміжок [0;+∞)
Б функція спадає на інтервалі (0;+∞)
В функція зростає на інтервалі (-∞;+∞)
Г парна функція
Д періодична функція з найменшим додатним періодом Т=π1-В, 2-Г, 3-Д, 4-Б.
1) Дана функція є зростаючою, тому маємо відповідь В.
2) Дана функція є парною, тому маємо відповідь Г.
3) Дана функція є періодичною з найменшим додатним періодом Т=π, тому маємо відповідь Д.
4) Дана функція спадає на інтервалі (0;+∞), тому маємо відповідь Б. - Установіть відповідність між функцією (1-4) та її властивістю (А-Д).
ВідповідьФункція Властивість 1 y=x2
2 y=x3+1
3 y=3-х
4 y=sinxА зростає на всій області визначення
Б спадає на всій області визначення
В є непарною
Г є парною
Д областю значень функції є проміжок (0;+∞)1-Г, 2-А, 3-Б, 4-В.

1) Дана функція є парною, тому маємо відповідь Г.
2) Дана функція є зростаючою, тому маємо відповідь А.
3) Дана функція є спадною (коефіцієнт біля х від’ємний), тому маємо відповідь Б.
4) Дана функція є непарною, тому маємо відповідь В. - Знайдіть область визначення функції y=. У відповіді запишіть найбільше ціле двоцифрове число, що належить області визначення цієї функції.
Відповідь
16.
Оскільки маємо корінь парного степеня, то підкореневий вираз більше або дорівнює 0. Маємо 50-3х≥0, звідки 3х≤50 і x≤16,(6). Тому у відповідь пишемо число 16. - Знайдіть область визначення функції y=. У відповіді запишіть найбільше ціле двоцифрове число, що належить області визначення цієї функції.
Відповідь
13.
Оскільки маємо корінь парного степеня, то підкореневий вираз більше або дорівнює 0; крім того, маємо знаменник, який не повинен дорівнювати 0. Отже, підкореневий вираз повинен бути більше 0. Маємо 56-4х>0, звідки 4х<56 і x<14. Тому у відповідь пишемо число 13.
Тому у відповідь пишемо число 13. - Знайдіть найбільше значення функції y=.
Відповідь
40,5.
Маємо додатний дріб, знаменник якого постійне число. Отже, найбільше значення буде при найбільшому значенні чисельника. Оскільки змінний вираз 2cosx віднімається від 1, то його найбільше значення буде при найменшому значення 2cosx. Найменше значення cosx дорнівнює -1. При ньому 1-2cosx=1-2(-1)=1+2=3. Тоді значення виразу маємо 34:2=81:2=40,5. - Знайдіть найменший додатний період функції f(x)=9-6cos(20πx+7).
Відповідь
0,1.
Оскільки для функції y=cosx T=2π, то для функції f(x)=9-6cos(20πx+7) T==0,1 (період функції ділимо на коефіцієнт біля змінної х). - Функцію y=x4+2x-3, визначену на множині всіх дійсних чисел, подайте у вигляді y=f(x)+g(x), де f(x) – парна функція, g(x) – непарна функція. У відповідь запишіть значення виразу f(-1)-4·g(3).
Відповідь
-26.
У парній функції при заміні х на -х не повинно нічого змінюватися. У функції у такими частинами є вираз x4-3, тому f(x)=x4-3 -парна функція і g(x)=2x — непарна функція. Маємо f(-1)-4·g(3)=(-1)4-3-4·2·3=1-3-24= -26.
У функції у такими частинами є вираз x4-3, тому f(x)=x4-3 -парна функція і g(x)=2x — непарна функція. Маємо f(-1)-4·g(3)=(-1)4-3-4·2·3=1-3-24= -26.
1. Для обчислення значення функції в точці хo потрібно це значення підставити у функцію замість х.
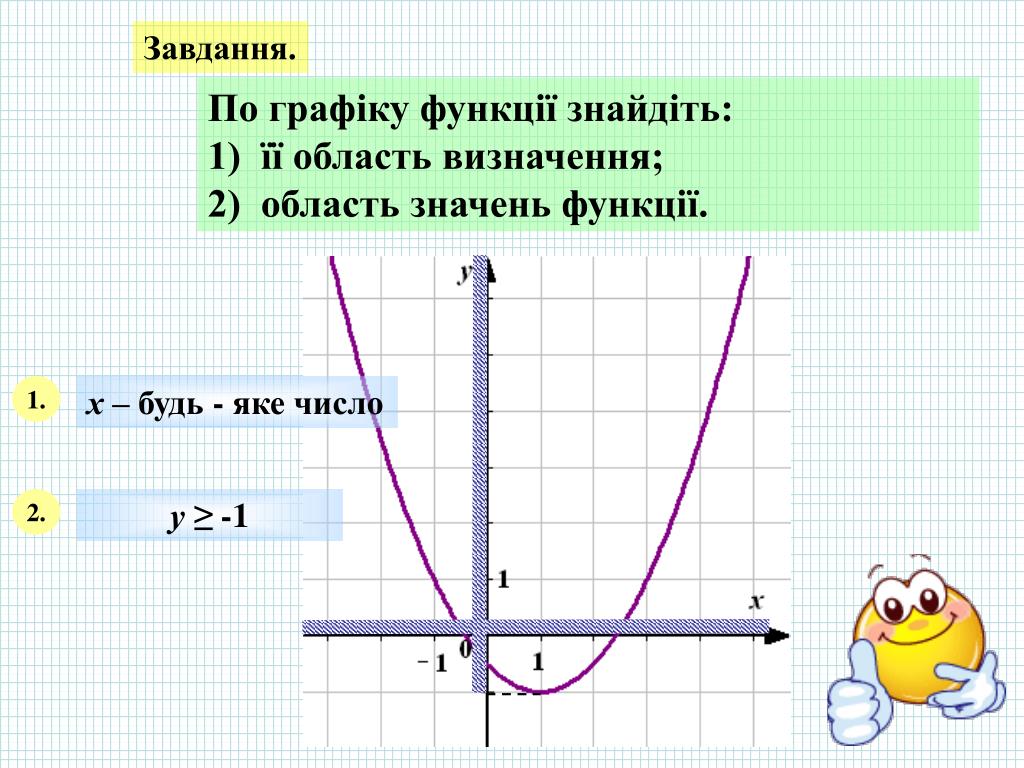
2. Область визначення функції: можливі значення, які може приймати змінна х. Тут можливі випадки:
3. Область значень функції: можливі значення. які може приймати у.
4. Функції розрізняють:
Знайдіть область значень нужно
Ответы
лаьтслчлвт 14.01.2021 22:08
Объяснение:
текст текст текст
ПОКАЗАТЬ ОТВЕТЫ
ТиматиТорнадо 15.12.2020 22:12
Если на множество задана функця,которое обозначает множество на другое множество ,то множество называется областью определения.
Область определения и область значения функций:Функция-это модель.Определим х
как множество значений независимой переменной(это значит любая).
ПОКАЗАТЬ ОТВЕТЫ
emdnick 15.12.2020 22:12
Область определения функции (ООФ) — D(y)
Обдасть хначений функции (ОЗФ) — E(y)
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
daxandra 06.04.2020 07:52
Решить квадратные неравенства Х²-6х+8 09х²-12+4 0-х²-2х-15 =0…
yra221111
11. 2-71x+22=0 найти целый корень уравнения…
2-71x+22=0 найти целый корень уравнения…
pampuzik 04.05.2020 00:47
Скільки первісних має одна функція?…
kristinka078 04.05.2020 00:47
Розвяжіть систему рівнянь 3х-7у=16, 7у+6х очень если правильно…
Оpiggyugrs 19.05.2019 10:00
Между числами 7 и 448 вставьте положительное число так, чтобы получилось три последовательных члена прогрессии….
Snihdsfg
10. 07.2019 07:10
07.2019 07:10
Найдите значение x при котором функция задана формулой y(x)=8-3x принимает значения y(x)=5 y(x)=11…
kvaisberg 25.08.2019 02:00
Как найти сторону равностороннего треугольника с периметром 8,1…
valentinalobanova 18.12.2020 10:48
В первой ёмкости на 3 л молока больше, чем во второй. Если из первой ёмкости перелить во вторую 10 л молока, то во второй ёмкости станет в 2 раза больше, чем останется в первой. Сколько…
барынмай
11. 04.2020 15:10
04.2020 15:10
Дана арифметическая прогрессия Вычислите а13, если a1=-20, d=1…
Python range() Функция
❮ Встроенные функции
Пример
Создайте последовательность чисел от 0 до 5 и напечатайте каждый элемент в sequence:
x = range(6)
for n in x:
print(n)
Попробуйте сами »
Определение и использование
Функция range() возвращает последовательность
числа, начиная с 0 по умолчанию и увеличиваясь на 1 (по умолчанию), и останавливается
перед указанным номером.
Синтаксис
диапазон (пуск, стоп, шаг )
Значения параметров
| Параметр | Описание |
|---|---|
| пуск | Дополнительно. Целое число, указывающее, с какой позиции начинать. По умолчанию 0 |
| стоп | Обязательно. Целое число, указывающее, в какой позиции остановиться (не
включены). Целое число, указывающее, в какой позиции остановиться (не
включены). |
| шаг | Дополнительно. Целое число, определяющее приращение. По умолчанию 1 |
Другие примеры
Пример
Создайте последовательность чисел от 3 до 5 и напечатайте каждый элемент в sequence:
x = range(3, 6)
for n in x:
print(n)
Попробуйте сами »
Пример
Создайте последовательность чисел от 3 до 19, но увеличивайте ее на 2 вместо 1:
x = диапазон (3, 20, 2)
для n в x:
print(n)
Попробуйте сами »
❮ Встроенные функции
NEW
Мы только что выпустили
Видео W3Schools
Узнать
COLOR PICKER
КОД ИГРЫ
Играть в игру
Top Tutorials
Учебное пособие по HTMLУчебное пособие по CSS
Учебное пособие по JavaScript
Учебное пособие
Учебное пособие по SQL
Учебное пособие по Python
Учебное пособие по W3.
 CSS
CSS Учебник по Bootstrap
Учебник по PHP
Учебник по Java
Учебник по C++
Учебник по jQuery
Лучшие ссылки
HTML ReferenceCSS Reference
JavaScript Reference
SQL Reference
Python Reference
W3.CSS Reference
Bootstrap Reference
PHP Reference
HTML Colors
Java Reference
Angular Reference
jQuery Reference
Top9 Examples
Примеры HTML
Примеры CSS
Примеры JavaScript
How To Примеры
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры PHP
Примеры Java
Примеры XML
Примеры jQuery
FORUM | О
W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения.
Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания. Используя W3Schools, вы соглашаетесь прочитать и принять наши условия использования,
куки-файлы и политика конфиденциальности.
Используя W3Schools, вы соглашаетесь прочитать и принять наши условия использования,
куки-файлы и политика конфиденциальности.
Copyright 1999-2022 Refsnes Data. Все права защищены.
W3Schools работает на основе W3.CSS.
Функция Python range() с примерами
Python range() Функция генерирует неизменяемую последовательность чисел , начиная с заданного начального целого числа и заканчивая конечным целым числом. range() — это встроенная функция, которая возвращает объект диапазона, состоящий из ряда целых чисел, которые мы можем выполнить с помощью цикла for .
В Python, используя цикл for с range() , мы можем повторить действие определенное количество раз. Например, давайте посмотрим, как использовать функцию range() из Python 3 для получения первых шести чисел.
Пример
# Генерация чисел от 0 до 6
для я в диапазоне (6):
print(i) Вывод
0 1 2 3 4 5Функция Python range()
Примечание : Как видно из вывода, мы получили шесть целых чисел, начиная с 0 до 5. Если вы заметили,
Если вы заметили, range() не включает 6 в свой результат, потому что он генерирует числа до конечного числа, но никогда не включает конечное число в свой результат .
range() работает по-разному в Python 3 и Python 2.
См. range() в Python 2
- последовательность чисел.
- В Python 3
xrange()переименован вrange()и исходная функцияrange()удалены. Мы обсудим это в следующем разделе статьи.
СОДЕРЖАНИЕ
- Как использовать диапазон () Функция в Python
- Синтаксис
- Параметры
- return
- Шаги на диапазон () Диаправляя
- Шаги на диапазон () Диаправляя
- Перебор списка с помощью функции range() и цикла for перевернуть список
- Уменьшение диапазона() с использованием шага
Синтаксис
Ниже приведен синтаксис функции range().
диапазон(начало, стоп[ шаг])
Требуется три аргумента. Из трех два являются необязательными. начинаются с и step — необязательные аргументы, а stop — обязательный аргумент.
Параметры
-
начало: (Нижний предел) Это начальная позиция последовательности. Значение по умолчанию равно 0 , если оно не указано. Например,диапазон(0, 10). Здесьstart=0иstop = 10 -
stop: (Верхний предел) генерирует числа до этого числа, т. е. целое число, указывающее, в какой позиции остановиться (верхний предел).range()никогда не включает номер остановки в результат -
шаг: укажите значение приращения. Каждое следующее число в последовательности генерируется путем добавления значения шага к предыдущему числу. Значение по умолчанию равно 1 , если оно не указано. Это не что иное, как разница между каждым числом в результате. Например, диапазон
Это не что иное, как разница между каждым числом в результате. Например, диапазон (0, 6, 1). Здесьшагов = 1.
Возвращаемое значение
Возвращает объект класса диапазон .
печать (тип (диапазон (10))) # Вывод
Действия по использованию функции range()
Функция range() генерирует последовательность целых чисел в соответствии с переданным аргументом. Следующие шаги показывают, как использовать функцию range() в Python.
- Передать начальное и конечное значения в range()
Например,
range(0, 6). Здесьstart=0иstop = 6. Он будет генерировать целые числа, начиная сстартчисло достоп -1. т. е.[0, 1, 2, 3, 4, 5] - Передать значение шага в range()
Шаг
(0, 6, 2). Здесь
Здесь шагов = 2. Результат:[0, 2, 4] - Используйте цикл for для доступа к каждому числу
Используйте цикл for для повторения и доступа к последовательности чисел, возвращаемой функцией
range().
range() Примеры
Теперь давайте рассмотрим все возможные сценарии. Ниже приведены три варианта range() .
range(stop) Когда вы передаете только один аргумент в range() , он сгенерирует последовательность целых чисел, начиная с 0 до stop -1 .
# Напечатать первые 10 чисел
# стоп = 10
для я в диапазоне (10):
напечатать (я, конец = '')
# Выход 0 1 2 3 4 5 6 7 8 9 Примечание :
- Здесь
начало = 0ишаг = 1в качестве значения по умолчанию. - Если вы установите
стопкак 0 или какое-либо отрицательное значение, тогда диапазон вернет пустую последовательность.
- Если вы хотите начать диапазон с 1, используйте
range(1, 10).
range(start, stop) Когда вы передаете два аргумента в range() , он будет генерировать целые числа, начиная с числа start до стоп -1 .
# Числа от 10 до 15
# начало = 10
# стоп = 16
для я в диапазоне (10, 16):
напечатать (я, конец = '')
# Вывод 10 11 12 13 14 15 Примечание
- Здесь шаг
= 1как значение по умолчанию. - Диапазон вернет пустую последовательность, если вы установите значение
stopменьше, чемstart.
range(start, stop, step) Когда вы передаете все три аргумента в range(), она возвращает последовательность чисел, начиная с начального номера, увеличиваясь на номер шага и останавливаясь перед номер остановки.
Здесь вы можете указать другое приращение, добавив параметр step .
# Числа от 10 до 15
# начало = 10
# стоп = 50
# шаг = 5
для i в диапазоне (10, 50, 5):
напечатать (я, конец = '')
# Вывод 10 15 20 25 30 35 40 45 Примечание :
- Здесь шаг
= 0как значение по умолчанию. - Python вызовет исключение
ValueError, если вы установите для шага
Что нужно помнить о функции range()
- Функция
range()работает только с целыми числами, поэтому все аргументы должны быть целыми числами. Вы не можете использовать числа с плавающей запятой или любой другой тип данных в качестве начального, конечного и шагового значения. См. генерацию диапазона чисел с плавающей запятой в Python - . Все три аргумента могут быть положительными или отрицательными.
- Значение шага
step=0, Python вызовет исключениеValueError.
Практическая задача : –
Используйте range() для создания последовательности чисел от 9 до 100, кратных 3.
# start = 9
# стоп = 100
# шаг = 3 (приращение)
для я в диапазоне (9, 100, 3):
печать (я)
См. : Упражнение Python for loop и range()
for loop with range()
Python for loop многократно выполняет блок кода или инструкцию фиксированное количество раз. Мы можем перебирать последовательность чисел, созданную функцией range(), используя цикл for.
Давайте посмотрим, как использовать цикл for с функцией range() для вывода нечетных чисел от 1 до 10. Используя этот пример, мы можем понять, как переменная итератора i получает значение, когда мы используем range( ) с циклом for.
для i в диапазоне (1, 10, 2):
print("Текущее значение i равно:", i) Вывод
Текущее значение i равно: 3 Текущее значение i: 5 Текущее значение i: 7 Текущее значение i: 9
Чтобы понять, что for i in range() означает, что в Python нам нужно сначала понять работу функции range() .
Функция range() использует генератор для получения чисел. Он не генерирует все числа сразу.
Как вы знаете, range() возвращает объект range . Объект диапазона использует один и тот же (небольшой) объем памяти, независимо от размера диапазона, который он представляет. Он сохраняет только начальные, конечные и ступенчатые значения и вычисляет отдельные элементы и поддиапазоны по мере необходимости.
Т. е. он генерирует следующее значение только тогда, когда его запрашивают для итерации цикла. В каждой итерации цикла он генерирует следующее значение и присваивает его переменной итератора i.
- Как видно из вывода, переменная
iне получает значения 1, 3, 5, 7 и 9 одновременно. - В первой итерации цикла значение
iявляется начальным номером диапазона. - Далее, в каждой последующей итерации цикла for значение
iувеличивается на значение шага. Значениеiопределяется по формулеi = i + шаг.
Таким образом, это означает, что range() выдает числа одно за другим по мере перехода цикла к следующей итерации. Это экономит много памяти, что делает range() быстрее и эффективнее.
Работа функции диапазона Python с циклом forПеребор списка с использованием
range() и для цикла Вы можете перебирать типы последовательностей Python, такие как список и строка, с помощью range() и цикл for.
При переборе списка только с помощью цикла вы можете получить доступ только к элементам. Когда вы перебираете список только с помощью цикла, вы можете получить доступ только к его элементам, но когда вы используете range() вместе с циклом, вы можете получить доступ к порядковому номеру каждого элемента.
Преимущество использования range() для итерации списка заключается в том, что он позволяет нам получить доступ к порядковому номеру каждого элемента. Используя порядковые номера, мы можем получить доступ, а также изменить элементы списка, если это необходимо.
Пример
Передайте количество элементов списка в range() с помощью функции len() . range() будет использовать его как аргумент stop .
list1 = ['Джесса', 'Эмма', 20, 30, 75,5]
# перебираем список с помощью range()
для i в диапазоне (len (list1)):
print(list1[i]) Вывод :
Джесса Эмма 20 30 75.5
Практическая задача
Распечатайте следующий числовой шаблон, используя Python range() и цикл.
1 2 2 3 3 3Показать решение
для числа в диапазоне (4):
для я в диапазоне (число):
печать (число, конец = "")
print() # новая строка после каждой строки для корректного отображения шаблона
Подробнее :
- Python для цикла и диапазона() Упражнение
Обратный диапазон
Вы можете отобразить последовательность чисел, созданную функцией range() , в порядке убывания или в обратном порядке.
Вы можете использовать следующие два способа, чтобы получить обратный диапазон чисел в Python.
- Использовать отрицательное значение шага
- Использовать функцию
reversed()
Использовать отрицательное значение шага
Использовать отрицательное значение шага в функции range() для создания последовательности чисел в обратном порядке . Например, range(5, -,1, -1) даст такие числа, как 5, 4, 3, 2 и 1.
Т. е., вы можете обратить цикл, установив аргумент шага диапазона ( ) до -1. Это вызовет цикл for повторяется в обратном порядке.
Давайте посмотрим, как зациклить обратную итерацию или обратную итерацию, чтобы отобразить диапазон чисел от 5 до 0.
# обратный диапазон с использованием отрицательного шага
# начало = 5
# стоп = -1
# шаг = -1
для i в диапазоне (5, -1, -1):
print(i) Вывод :
5 4 3 2 1 0
Использование функции reversed()
Используя встроенную в Python функцию reversed() , вы можете обратить любую последовательность, такую как список или диапазон.
- Передать
range()в качестве входных данных для функции reversed(). Она возвращаетrange_iterator, который обращается к последовательности чисел, предоставленнойrange(), в обратном порядке. - Затем повторите результат, предоставленный функцией
reversed(), используя цикл for.
Пример 2 : обратный диапазон, начиная с 20 до 10
для i в обратном порядке (диапазон (10, 21)):
напечатать (я, конец = '')
# Выход 19 18 17 16 15 14 13 12 11 10 Пример 3 : обратный диапазон, начиная с 20 до 10 с шагом 2
для i в обратном порядке (диапазон (10, 21, 2)):
напечатать (я, конец = '')
# Вывод 20 18 16 14 12 10 Примечание : reverse(range(n)) возвращает range_iterator , который обращается к последовательности чисел, предоставленной range() , в обратном порядке.
печать (тип (диапазон (0, 5))) # Вывод <класс 'диапазон'> печать (тип (обратный (диапазон (0, 5)))) # Вывод <класс 'range_iterator'>
Кроме того, если вам нужен список из него, вам нужно преобразовать вывод функции reversed() в список. Таким образом, вы можете получить обратный список диапазонов.
Используйте range() для обращения списка
Используйте range() для обращения списка путем передачи количества элементов списка в качестве начального аргумента и шага в качестве -1.
Давайте рассмотрим различные способы инвертирования списка чисел с помощью range()
list1 = [10, 20, 30, 40, 50]
# start = размер списка
# стоп = -1
# шаг = -1
# перевернуть список
для i в диапазоне (len (list1) - 1, -1, -1):
печать (список1 [я], конец = " ")
# Выход 50 40 30 20 10
Шаг диапазона Python
Шаг — это необязательный аргумент диапазона(). Это целое число, определяющее приращение между каждым числом в последовательности. т. е. указывает приращение.
т. е. указывает приращение.
Вы также можете определить его как разницу между каждым предыдущим и последующим числом в результирующей последовательности. Например, если шаг равен 2, то разница между каждым предыдущим и последующим числом составляет 2
Значение шага по умолчанию равно 1, если не указано явно.
Пример: увеличение с помощью шага
# шаг range() со значением по умолчанию
для я в диапазоне (10):
напечатать (я, конец = '')
# Выход 0 1 2 3 4 5 6 7 8 9
# Увеличение диапазона() с шагом = 2
# напечатать таблицу из 2, используя range()
для я в диапазоне (2, 22, 2):
напечатать (я, конец = '')
# Выход 2 4 6 8 10 12 14 16 18 20
Вы также можете выполнять множество операций, используя аргументы шага, такие как обращение последовательности, такой как список и строка.
Уменьшение диапазона() с использованием шага
Вы можете уменьшить range(), используя отрицательное значение шага .
Когда мы устанавливаем отрицательное значение шага, на каждой итерации число будет уменьшаться, пока не достигнет конечного числа.
# Уменьшить диапазон() с помощью шага
# старт = 30, стоп = 20
# шаг = -2
для i в диапазоне (30, 20, -2):
напечатать (я, конец = '')
# Выход 30 28 26 24 22
Примечание : Чтобы уменьшить range() , start должен быть больше, чем stop . Range() возвращает пустую последовательность, если start < stop .
для i в диапазоне (20, 30, -2):
print(i, end=' ') Кроме того, вы можете использовать шаг для генерации последовательности чисел, кратных n.
# Генерировать целые числа, умноженные на 7
для i в диапазоне (7, 77, 7):
напечатать (я, конец = '')
# Вывод 7 14 21 28 35 42 49 56 63 70 Кроме того, вы получите valueerror , если вы установите step = 0 .
для i в диапазоне (1, 5, 0):
напечатать (я, конец = '')
# Output ValueError: range() arg 3 не должен быть равен нулю
Также нельзя использовать десятичное значение с шагом . Если вы хотите использовать шаг с плавающей точкой/десятичной дробью в
Если вы хотите использовать шаг с плавающей точкой/десятичной дробью в range() , см. раздел Создание диапазона чисел с плавающей запятой.
Отрицательный диапазон() в Python
Вы можете использовать отрицательные целые числа в диапазоне().
В большинстве случаев мы используем отрицательное значение шага для обращения диапазона. Но помимо шага мы можем использовать отрицательные значения в двух других аргументах (начало и конец) функции range().
Пример: Отрицательный диапазон от -1 до -10
Давайте посмотрим на пример для печати диапазона чисел от отрицательного до положительного.
# отрицательный диапазон от -1 до -10
для i в диапазоне (-1, -11, -1):
напечатать (я, конец = ', ')
# Вывод -1, -2, -3, -4, -5, -6, -7, -8, -9, -10 Разбираемся в программе выше, устанавливаем –
-
start = -1(потому что мы хотели начать генерировать числа с -1) -
стоп = -11(Мы хотим прекратить генерировать числа, когда достигнем -11) -
Шаг = -1
Выполнение :
- В 1 -й итерации петли
I--1 - В 2 -й ирепеции для Loop,
I, потому что 2 -й иера 2 -й LoopI1210. Потому что 2 -й 2 -е. -1+(-1) = -2 , и этот процесс будет повторяться до конечного числа.
Потому что 2 -й 2 -е. -1+(-1) = -2 , и этот процесс будет повторяться до конечного числа.
Пример: Отрицательное обратное значение в диапазоне от -10 до -1
Вы также можете напечатать отрицательное обратное значение range() , используя положительное значение шаг целое число.
# отрицательный диапазон от -10 до -1
# начало = -10
# стоп = 0
# шаг = 1
для я в диапазоне (-10, 0):
напечатать (я, конец = ', ')
# Вывод -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, Комбинация отрицательных и положительных чисел
# stat = 2, стоп = -5, шаг = -1
для i в диапазоне (2, -5, -1):
распечатать (я, конец = ", ")
# Вывод 2, 1, 0, -1, -2, -3, -4, Преобразовать range() в список
Функция Python range() не возвращает список тип. Он возвращает неизменяемую последовательность целых чисел.
Мы можем преобразовать range() в список, используя конструктор list() .
- Передайте функцию
range()в качестве входных данных для конструктора списка. - Конструктор
list()автоматически создает список, заключая целые числа, возвращаемые функциейrange(), в квадратные скобки.
# создать список из диапазона()
образец_список = список (диапазон (2, 10, 2))
печать (тип (sample_list))
# Вывод <класс 'список'>
# показать список
печать (sample_list)
# Вывод [2, 4, 6, 8]
# итерировать список
для элемента в sample_list:
печать (элемент)
Доступ и изменение элемента списка с помощью range()
Кроме того, вы можете использовать range() для доступа и изменения списка элементов.
- Используя функцию
len(), вы можете получить количество элементов списка. - Затем используйте этот счетчик в качестве номера остановки в
range()и повторите циклstop-1раз.
- На каждой итерации вы получите порядковый номер текущего элемента списка.
# создать список из диапазона()
образец_список = список (диапазон (10, 100, 10))
# перебирать и изменять элемент списка, используя range()
# удвоить каждый номер списка
# start = 0, stop = размер списка, step = 1
для i в диапазоне (0, len (sample_list), 1):
список_образцов[i] = список_образцов[i] * 2
# отображаем обновленный список
печать (sample_list)
# Output [20, 40, 60, 80, 100, 120, 140, 160, 180] Инклюзивный диапазон
В этом разделе мы узнаем, как создать инклюзивный диапазон в Python. По умолчанию диапазон (n) является эксклюзивным, поэтому в результат не включается последнее число. Он создает последовательность чисел от start до stop -1 .
Например, range(5) даст [0, 1, 2, 3, 4] . Результат содержит числа от 0 до 5, но не пять.
Если вы заметили, результат содержит 5 элементов , что равно len(range(0, 5)) . Обратите внимание, индекс всегда начинается с 0, а не с 1.
Обратите внимание, индекс всегда начинается с 0, а не с 1.
Если вы хотите включить в результат конечное число, т.е. если вы хотите создать инклюзивный диапазон, то установите значение аргумента остановки как стоп+шаг .
Пример
# включая диапазон
начало = 1
стоп = 5
шаг = 1
# изменить остановку
стоп += шаг
для i в диапазоне (начало, стоп, шаг):
напечатать (я, конец = '')
# Выход 1 2 3 4 5
Пример 2: Даже включая диапазон()
шаг = 2
для i в диапазоне (2, 20 + шаг, шаг):
напечатать (я, конец = '')
# Вывод 2 4 6 8 10 12 14 16 18 20 range() против xrange() в Python 2 Сравнение range() и xrange() актуально, только если вы используете Python 2 и Python 3. Если вы не используете Python 2, вы можете пропустить это сравнение .
Функция range() работает по-разному в Python 3 и Python 2. Если ваше приложение работает как на Python 2, так и на Python 3, вы должны использовать
Если ваше приложение работает как на Python 2, так и на Python 3, вы должны использовать range() вместо xrange() для лучшей совместимости кода.
В Python 2 у нас есть range() и xrange() функции для создания последовательности чисел.
В Python 3 xrange() переименован в range() , а исходная функция range() была удалена.
Проще говоря, xrange() удалено из Python 3, и мы можем использовать только функцию range() для получения чисел в заданном диапазоне.
Использование range() и xrange()
- В Python 2,
range()возвращает объект списка(1, 500)создаст список Python из 499 целых чисел в памяти. Таким образом, он потребляет много памяти и увеличивает время выполнения. -
xrange(): Функцияxrange(1, 500)не генерирует все числа сразу. Он производит числа одно за другим по мере того, как цикл переходит к следующему числу. Таким образом, он потребляет меньше памяти и ресурсов.
Он производит числа одно за другим по мере того, как цикл переходит к следующему числу. Таким образом, он потребляет меньше памяти и ресурсов.
Пример
print 'Диапазон Python 2'
диапазон печати(10)
тип печати (диапазон (10))
распечатать 'Python 2 xrange'
для я в xrange (10):
напечатать я
тип печати (xrange (10)) Вывод
Python 2 range() [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] введите «список» Python 2 xrange() 0 1 2 3 4 5 6 7 8 9 введите 'xrange'
Объединение результатов двух range()
Допустим, вы хотите добавить range(5) + range(10,15) . И вам нужен объединенный диапазон, например [0, 1, 2, 3, 4, 10, 11, 12, 13, 14] .
Например, вы хотите сложить результат двух функций range() , чтобы получить другую последовательность чисел. Вы можете добавить/объединить результат нескольких функций range() , используя itertools. . chin()
chin()
из цепочки импорта itertools
# Объединение диапазонов
новый_диапазон = цепочка (диапазон (5), диапазон (5, 10))
для числа в новом_диапазоне:
печать (число, конец = '')
# Вывод 0 1 2 3 4 5 6 7 8 9 range() индексация и нарезка
Встроенная функция range() — это конструктор, который возвращает объект диапазона , к этому объекту диапазона также можно получить доступ по его порядковому номеру, используя индексирование и нарезку.
Доступ к атрибутам range()
Важно знать атрибуты range() , когда вы получаете их в качестве входных данных для своей функции, и вы хотите увидеть значение start , stop и шаг аргумент.
диапазон1 = диапазон (0, 10) # доступ к атрибутам range() печать(диапазон1.начало) # 0 печать(диапазон1.стоп) # 10 print(range1.step) # 1
Индексирование
range() поддерживает как положительные, так и отрицательные индексы. Пример ниже демонстрирует то же самое.
Пример ниже демонстрирует то же самое.
В случае range() значение индекса начинается с нуля до (стоп). Например, если вы хотите получить доступ к третьему числу, нам нужно использовать 2 в качестве порядкового номера.
диапазон1 = диапазон (0, 10) # первое число (начальный номер) в диапазоне печать (диапазон1 [0]) # доступ к 5-му номеру в диапазоне печать (диапазон1 [5]) # Выход 5 # доступ к последнему номеру печать (диапазон1[диапазон1.stop - 1]) # Выход 9
Отрицательная индексация
Доступ к номерам осуществляется справа налево при использовании отрицательной индексации.
# отрицательная индексация # доступ к последнему номеру печать (диапазон (10) [-1]) # Выход 9 # доступ к предпоследнему номеру печать (диапазон (10) [-2]) # Output 8
Slicing
Slicing a подразумевает доступ к части из range()
# slicing
для я в диапазоне (10) [3: 8]:
напечатать (я, конец = '')
# вывод 3 4 5 6 7 range() вместо символа или алфавита
Есть ли способ напечатать диапазон символов или алфавитов? Например вот так.
для символов в диапазоне ('a','z'):
print(char) Есть ли способ напечатать диапазон символов или алфавитов? Например вот так. Можно создать диапазон символов с помощью пользовательского генератора. Давайте посмотрим, как сгенерировать алфавит от «a» до «z», используя пользовательскую функцию range() .
Примечание : нам нужно использовать значение ASCII, а затем преобразовать значение ASCII в букву, используя Функция Chr() .
# диапазон от 'a' до 'z
def character_range (char1, char2):
для char в диапазоне (ord (char1), ord (char2) + 1):
выход (символ)
для буквы в character_range('a', 'z'):
печать (chr (буква), конец = ', ')
Выход
a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v , w, x, y, z,
Сводка
Я хочу услышать от вас. Что вы думаете об этом руководстве по Python range()? Дайте мне знать, оставив комментарий ниже.
Кроме того, попробуйте решить упражнение с циклом Python и викторину с циклом for.
Ниже приведен сводка всех операций, которые мы усвоили на этом уроке
| Операция | Описание |
|---|---|
Диапазон (Stop) | Generate. Последовательность из integers от Zero от Zero от Zero от Zero от Zero от Zero от Zero от Zero от Zero от Zero от Zero от Zero от Zero. |
диапазон(начало, стоп) | Генерация последовательности целых чисел от начала до конца-1 |
диапазон(начало, стоп, шаг) | Генерирует последовательность целых чисел, начиная с начального номера, увеличивая шаг и останавливаясь перед конечным номером. То есть каждое следующее число генерируется путем добавления значения шага к предыдущему числу. |
range(5, -1, -1) | Reverse range |
reversed(range(5)) | Reverse range using a reversed() function |
диапазон(-1, -11, -1) | Отрицательный диапазон от -1 до -10 |
список(диапазон(2, 10, 2)) | Преобразование диапазона() в список |
диапазон(начало, стоп+шаг, шаг) | Создание включающего диапазона |
диапазон(0, 10)[5] | Прямой доступ к пятому номеру диапазона () | диапазон(10)[3:8] | Разрезать диапазон для доступа к номерам от 3 до 8 |
range. | Get the start value of a range() |
range.stop | Get the stop value of a range() |
range .step | Получить значение шага range() |
Часто задаваемые вопросы
Начинается ли range() в Python с 0?
range() по умолчанию начинается с 0, а не с 1, если начальный аргумент не указан. Например, range(5) вернет 0, 1, 2, 3, 4.
Что возвращает range() в Python?
Функция range() возвращает объект класса range , который представляет собой не что иное, как серию целых чисел.
Является ли диапазон списком в Python?
№ range() не является списком и не возвращает тип списка.






 Отже, функція не підходить.
Отже, функція не підходить. Отже, функція не підходить.
Отже, функція не підходить.
 Тому у відповідь пишемо число 13.
Тому у відповідь пишемо число 13. У функції у такими частинами є вираз x4-3, тому f(x)=x4-3 -парна функція і g(x)=2x — непарна функція. Маємо f(-1)-4·g(3)=(-1)4-3-4·2·3=1-3-24= -26.
У функції у такими частинами є вираз x4-3, тому f(x)=x4-3 -парна функція і g(x)=2x — непарна функція. Маємо f(-1)-4·g(3)=(-1)4-3-4·2·3=1-3-24= -26.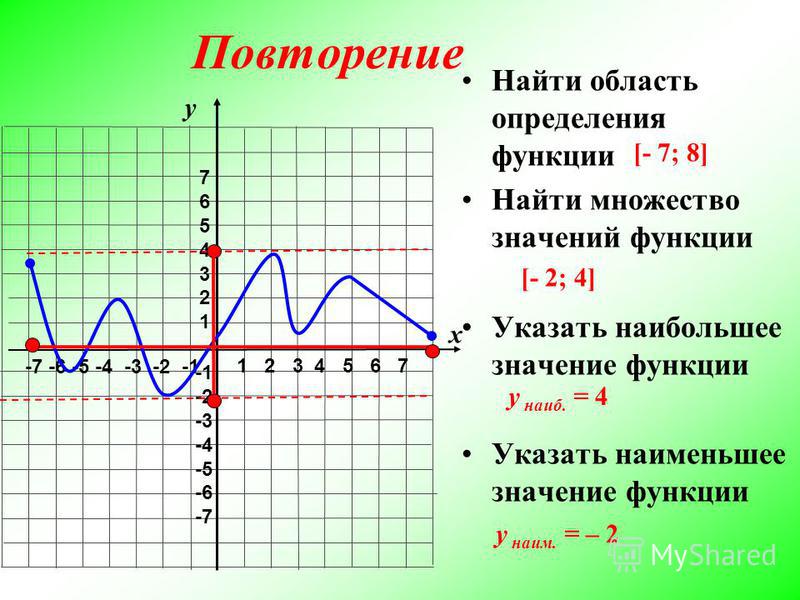 Это не что иное, как разница между каждым числом в результате. Например, диапазон
Это не что иное, как разница между каждым числом в результате. Например, диапазон  Здесь
Здесь 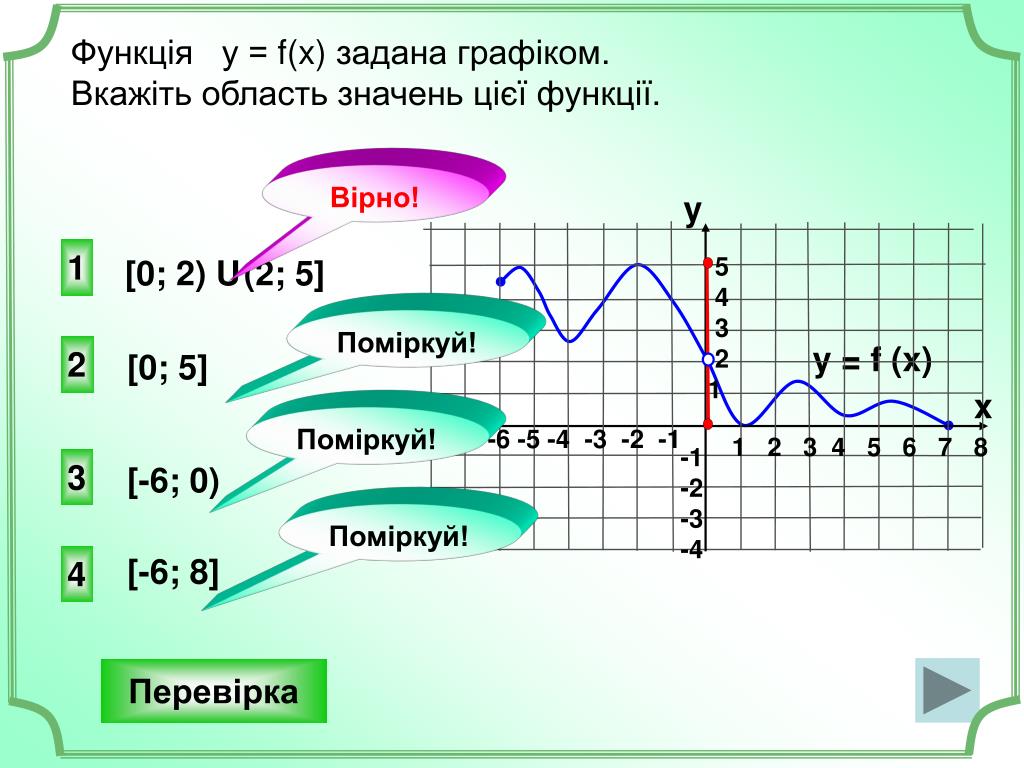

 Потому что 2 -й 2 -е. -1+(-1) = -2 , и этот процесс будет повторяться до конечного числа.
Потому что 2 -й 2 -е. -1+(-1) = -2 , и этот процесс будет повторяться до конечного числа.
 Он производит числа одно за другим по мере того, как цикл переходит к следующему числу. Таким образом, он потребляет меньше памяти и ресурсов.
Он производит числа одно за другим по мере того, как цикл переходит к следующему числу. Таким образом, он потребляет меньше памяти и ресурсов.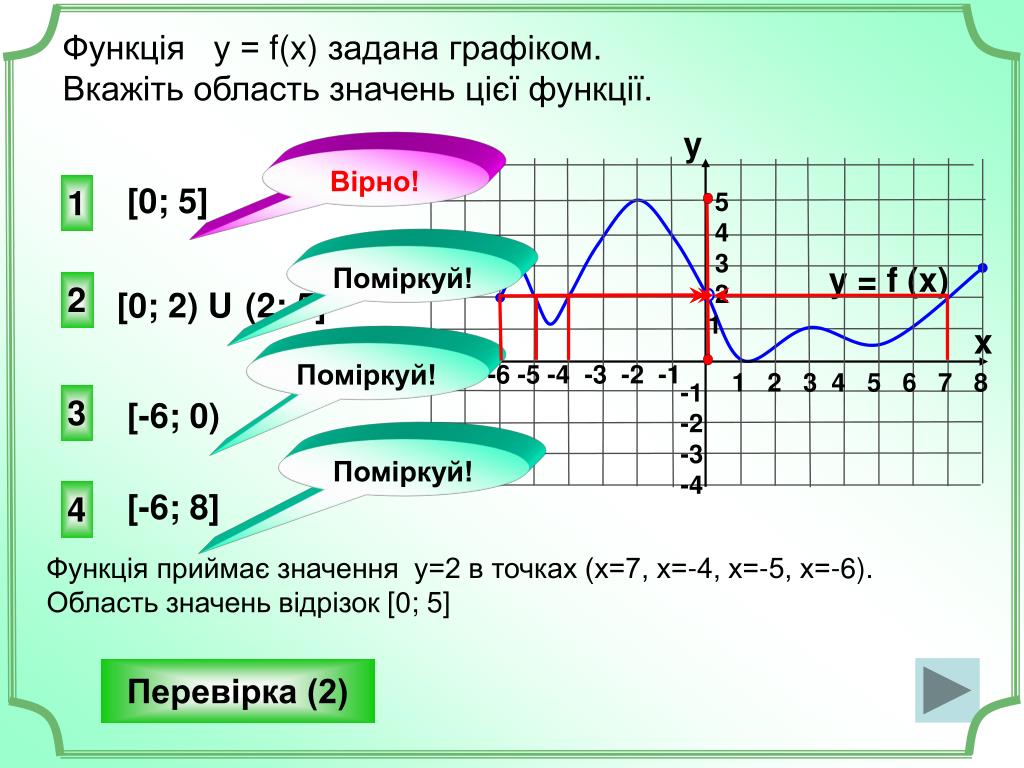 start
start