|
www.sites.google.com
Решить задачу помогут круги Эйлера.
Задача 1.
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.
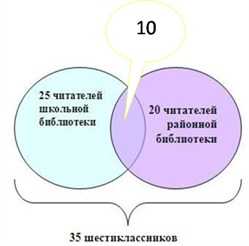
Сколько шестиклассников:
1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?
Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.
Решение.
1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)
3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)
4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)
5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).
Очевидно, что 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают.
При решении данной задачи мы использовали способ ее графического представления при помощи так называемых кругов Эйлера. Этот способ был предложен Леонардом Эйлером и широко используется при решении логических задач.
Леона́рд Э́йлер (4(15) апреля 1707, Базель, Швейцария – 7(18) сентября 1783, Санкт-Петербург, Российская империя) – швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Некоторые из его потомков до сих пор живут в России.
Рассмотрим еще один пример.
Задача 2.
Часть жителей нашего дома выписывают только газету «Комсомольская правда», часть – только газету «Известия», а часть – и ту, и другую газету. Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%?
Решение.
Здесь нет принципиального отличия от решения предыдущей. На готовом рисунке заменим данные: 25 на 85% и 20 на 75%. Учитывая, что все жители дома составляют 100%, заменяем 35 на 100% и получаем готовое решение: 85% + 75% – 100% = 60%.
Ответ: обе газеты выписывают 60% жителей.
Чем более сложная и запутанная логическая задача, связанная с множествами, тем более очевиден эффект от применения кругов Эйлера. Только после составления рисунка их решение становится достаточно очевидным.
Задача 3.
В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение.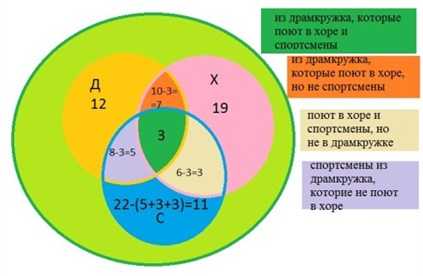
Пусть
Д – драмкружок,
Х – хор,
С – спорт.
Тогда
в круге Д – 27 ребят,
в круге Х – 32 человека,
в круге С – 22 ученика.
Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8 – 3 = 5 спортсменов, не поющих в хоре и 6 – 3 = 3, не посещающих драмкружок.
Легко видеть, что 5 + 3 + 3 = 11 спортсменов посещают хор или драмкружок,
22 – (5 + 3 + 3) = 11 занимаются только спортом;
70 – (11 + 12 + 19 + 7 + 3 + 3 + 5) = 10 – не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.
Ответ: 10 человек и 11 человек.
Задача 4.
В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Решение.
1 способ. Для решения опять воспользуемся кругами Эйлера. Пусть х человек 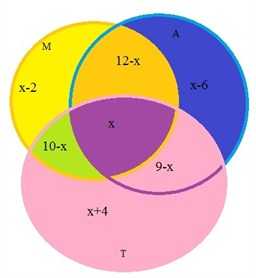 пользуется всеми тремя видами транспорта. Тогда пользуются
пользуется всеми тремя видами транспорта. Тогда пользуются
только метро и троллейбусом – (10 – х) человек,
только автобусом и троллейбусом – (9 – х) человек,
только метро и автобусом – (12 – х) человек.
Найдем, сколько человек пользуется одним только метро:
20 – (12 – х) – (10 – х) – х = х – 2.
Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.
2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х = 30, 27 + х = 30, х = 3. Здесь сложили количество учеников, которые пользуются хотя бы одним видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех учеников в классе.
Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.
Остались вопросы? Не знаете, как решить задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
» Решение задач с помощью КРУГОВ ЭЙЛЕРА»
Министерство образования, науки и молодежи Республики Крым Малая академия наук «Искатель»
Направление: математика
Решение задач с помощью кругов Эйлера
г. Красноперекопск– 2017
Работу выполнила:
Шумилина Мария Сергеевна,
ученица 7-Акласса муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная школа № 5» муниципального образования городской округ Красноперекопск
Научный руководитель:
Шеина Елена Николаевна, учитель математики муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная школа №5» муниципального образования городской округ Красноперекопск
СОДЕРЖАНИЕ:
ВВЕДЕНИЕ …………………………………………………………… 3
ГЛАВА 1. Немного из истории………………………………….5
ГЛАВА 2. Из теории множеств……………………………………….7
2.1. Понятие множества.……………………………………..8
2.2. Операции над множествами. …………………………..9
ГЛАВА 3. Решение задач с помощью кругов Эйлера ………………..10
ЗАКЛЮЧЕНИЕ…………………………………………………………..22
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ………………….23
ВВЕДЕНИЕ
Ничто так не способствует
формированию мыслительной культуры,
как решение логических задач. Математика-
не сухая и скучная наука, а полная
необычных и интересных открытий
Решать логические задачи очень увлекательно. Есть люди, для которых решение логической задачи — увлекательная, но несложная задача. Их мозг как луч прожектора сразу освещает все хитроумные построения, и к правильному ответу они приходят необычайно быстро. Замечательно, что при этом не могут объяснить, как пришли к решению.
Логические задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде, всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам.
Существует множество приемов, которые используются при решении текстовых логических задач. Очень часто решение помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению.
Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь.
Цель работы:
— познакомится с кругами Эйлера – Венна;
-научиться применять способ решения задач с помощью кругов Эйлера;
-составлять задачи практического содержания.
Глава 1. Немного из истории
Леонард Эйлер, крупнейший математик XVIII в., родился в Швейцарии в 1707г. В 1727 г. по приглашению Петербургской академии наук он приехал в Россию. В Петербурге Эйлер попал в круг выдающихся ученых: математиков, физиков, астрономов, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира. Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома. Среди его работ — первые учебники по дифференциальному и интегральному исчислению. В теории чисел Эйлер продолжил деятельность французского математика П. Ферма.
Эйлер много работает в области математического анализа. Ученый впервые разработал общее учение о логарифмической функции. В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку-топологию.
Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В -Р + Г = 2. Даже основные результаты научной деятельности Эйлера трудно перечислить. Здесь и геометрия кривых и поверхностей, и первое изложение вариационного исчисления с многочисленными новыми конкретными результатами. У него были труды по гидравлике, кораблестроению, артиллерии, геометрической оптике и даже по теории музыки. Он впервые дает аналитическое изложение механики вместо геометрического изложения Ньютона, строит механику твердого тела, а не только материальной точки или твердой пластины. Одно из самых замечательных достижений Эйлера связано с астрономией и небесной механикой. Он построил точную теорию движения Луны с учетом притяжения не только Земли, но и Солнца. Это пример решения очень трудной задачи.
Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал ученикам, которые проводили за него наиболее громоздкие вычисления.
С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения».
После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.
Глава 2. Из теории множеств
2.1. Понятие множества.
Одним из основных понятий, которые используются в математике, является понятие множества. Для него не дается определения. Можно пояснить, что множеством называют произвольную совокупность объектов, а сами объекты – элементами данного множества. Так, можно говорить о множестве учеников в классе (элементы – ученики ),множестве дней недели (элементы – дни недели ), множестве натуральных делителей числа 6 (элементы – числа 1, 2, 3, 6 ) и т. д.
В курсах алгебры и алгебры начало анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество M состоит из чисел 1; 2; 3, то его обозначают так: M = {1; 2; 3}. Тот факт, что число 2 входит в это множество
( является элементом данного множества M) записывается с помощью специального значка  следующим образом: 2
следующим образом: 2 M; а то что число 5 не входит в это множество ( не является элементом данного множества M ), записывается так: 5
M; а то что число 5 не входит в это множество ( не является элементом данного множества M ), записывается так: 5  M.
M.
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество. Например: множество простых делителей числа 1 – пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом  , множество всех натуральных чисел – буквой N, множество всех целых чисел – буквой Z, множество всех рациональных чисел – буквой Q, а множество всех действительных чисел буквой R. С помощью кругов Эйлера – Венна это можно изобразить так:
, множество всех натуральных чисел – буквой N, множество всех целых чисел – буквой Z, множество всех рациональных чисел – буквой Q, а множество всех действительных чисел буквой R. С помощью кругов Эйлера – Венна это можно изобразить так:
Рис.1
Если каждый элемент множества A является элементом множества B, то говорят, что множество A является подмножеством множества B.
Это записывают следующим образом: A  B.
B.
B
A
Рис.2
2.2. Операции над множествами.
Над множествами можно выполнять определенные действия: находить их пересечение, объединение. Дадим определение этих операций и проиллюстрируем их с помощью кругов.
Пересечением множеств A и B называют их общую часть, то есть множество C всех элементов, принадлежащих как множеству A, так и множеству B
Пересечение множеств обозначают знаком ∩ и записывают A ∩ B .
В
Рис.3
Объединением множеств A и B называют множество C, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств (A или B). Объединение множеств обозначают знаком  и записывают A
и записывают A  B
B
Глава3. Решение задач с помощью Кругов Эйлера
Задача № 1.
Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 — и значки, и марки.
Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием.
Решение.
В условии этой задачи не так легко разобраться. Если сложить 23 и 35, то получится больше 52. Это объясняется тем, что некоторых школьников мы здесь учли дважды, а именно тех, которые собирают и значки, и марки.
чтобы легче решать задачу, представим ее данные на следующей схеме
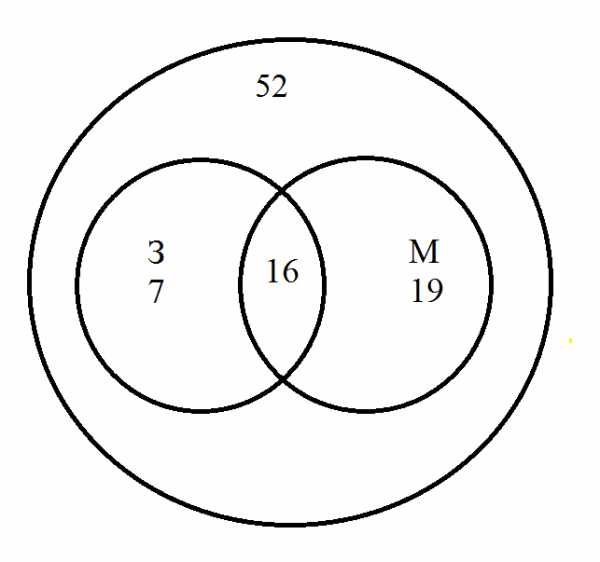 Рис.5
Рис.5
На этой схеме большой круг означает всех школьников, о которых идёт речь. Круг З изображает школьников, собирающих значки (всего их 23), а круг М — школьников, собирающих марки (всего их 35). В пересечении кругов З и М стоит число 16 — это те, кто собирает и значки, и марки. Значит, только значки собирает 23 — 16 = 7 человек, только марки собирает 35 — 16 = 19 человек. Всего марки и значкисобирает19 + 7 + 16 = 42 человека. Остаётся 52 — 42 = 10 человек, не увлечённых коллекционированием. Это число можно вписать в свободное поле круга. Ответ: 10 человек.
Задача 2.
В классе 15 мальчиков. Из них 10 человек занимается волейболом и 9 баскетболом. Сколько мальчиков занимается и тем, и другим?
Решение.
Изобразим условие с помощью кругов Эйлера . Этот рисунок подсказывает нам рассуждения. Разберём это рассуждение и впишем нужное число в каждую из образовавшихся на диаграмме частей .
Пусть всеми видами спорта занимаются х мальчиков. Тогда только волейболом занимаются (10-х) мальчиков, а только баскетболом (9-х) мальчиков. Составим уравнение: 10-х + х+ 9-х=15, откуда х=4
В
10-х Б
х 9-х
Рис.6
Ответ: 4 человека.
Задача № 3.
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Чучело», 11 человек – фильм «Выше неба», из них 6 смотрели и «Чучело», и «Выше неба». Сколько человек смотрели только фильм «Выше неба»?
Решение: Чертим два множества таким образом: 6 человек, которые смотрели фильмы «Чучело» и «Выше неба», помещаем в пересечение множеств.
15 – 6 = 9 – человек, которые смотрели только «Чучело».
11 – 6 = 5 – человек, которые смотрели только «Выше неба».
Получаем:
Рис.7
Ответ. 5 человек смотрели только «Выше неба».
Задача № 4.
В группе из 80 туристов, приехавших на экскурсию в Москву, 52 хотят посетить Большой театр, 30 — Художественный театр, 12 хотят посетить оба театра, остальные в театры ходить не хотят. Сколько человек не собирается идти в театр?
Решение.
Только большой театр посетят: 52-12=40 туристов;
только художественный театр посетят
30-12=18 туристов;
8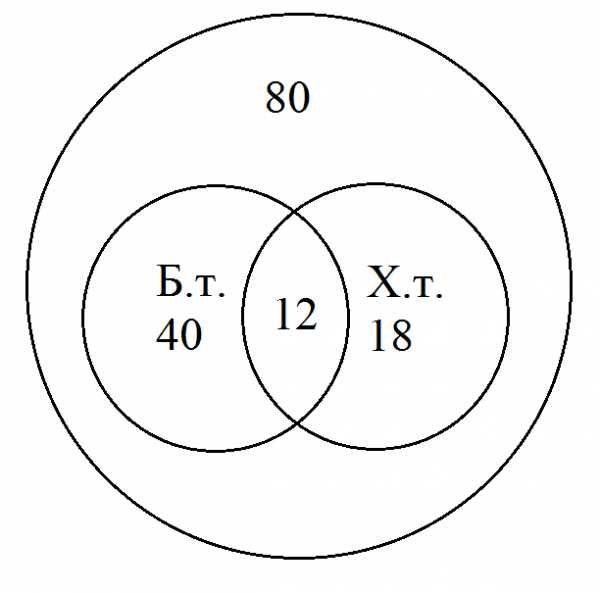 0-(40+18+12)=10 туристов не собираются идти в театр.
0-(40+18+12)=10 туристов не собираются идти в театр.
Рис.8
Ответ: 10 человек.
Задача № 5.
На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон?
Решение.
Учитывая условия задачи, чертеж будет таков:
Рис.9
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри.
Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон. Ответ. 8 книг прочитал Рон.
Задача№6.
В туристической группе из 100 человек 75 человек знают немецкий язык, 65 человек — английский язык, а 10 человек — не знают ни немецкого, ни английского языка. Сколько туристов знают два языка? Решение.
Изобразим условие задачи в виде кругов Эйлера.
Легко видеть, что 90 туристов (100-10) знают хотя бы один язык; Пусть х туристов знают и английский , и немецкий языки. Тогда (65-х) туристов знают только английскй, а (75-х) человек только немецкий. Получим уравнение 65-х+75-х+х=90, откуда х=50 – туристов знают оба языка. Ответ: 50 туристов.
Задача№7.
Сколько человек участвует в прогулке, если известно, что 16 из них взяли бутерброд с ветчиной, 24 — с колбасой, 15 — с сыром, 11 и с ветчиной, и с колбасой, 8 и с ветчиной, и с сыром, 12 и с колбасой, и с сыром, 6-бутерброды всех видов, а 5- взяли пирожки? Решение: Изобразим множества следующим образом: Рис.11
16+24+15-11-8-12+6=30(чел) — участвовали в прогулке и с собой брали бутерброды или 3+2+6+5+7+6+1=30(чел)
30+5=35(чел) — участвовали в прогулке
Ответ. 35 человек
Задача №8
В 5 классе нашей школы 22, в 6 классе – 16, в 7 классе – 23 ребят. Известно, что кружки по лыжам, шахматам и спортивным играм ходят 4 человека. Каждые две секции посещают 9 человек. Сколько человек ходит из каждого класса на секции? Сколько учеников не ходит ни на какой спортивный кружок?
Решение. Если на все три кружка ходят 4 ученика, а на каждые два – 9 человек, то две секции с 5 и 6 класса, с 6 и 7 класса, с 5 и 7 класса посещают по 5
человек.
Рис.12
Получаем 5+5+4=14 пятиклассников посещают кружки, 22-14=8 человек не ходят ни на какой кружков. Рассуждая также, из шестиклассников 16-14=2 ученика никуда не ходя, а из семиклассников – 23-14=9 человек.
Ответ: 14 учеников с каждого класса посещают кружки, не ходят ни на какой из 5-ого – 7, из 6-ого – 2, из 7-ого – 9 учеников.
Задача № 9.
Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Решение: Воспользуемся кругами Эйлера.
Рис.13
Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.
Задача № 10.
В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение. Д — драмкружок; Х — хор; С — спорт. В круге Д — 27 ребят, в круге Х — 32 человека, в круге С — 22 ученика. Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8-3=5
спортсменов, не поющих в хоре и 6-3=3, не посещающих драмкружок. Легко видеть, что 5+3+3=11 спортсменов посещают хор или драмкружок, 22-(5+3+3)=11 заняты только спортом; 70-(11+12+19+7+3+3+5)=10 — не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.

Рис.14 Ответ: 10 человек.
Задача№11. В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?
Решение.
Рис.15
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом —(12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30.
отсюда х = 3.
Ответ: 3 человека.
Задача № 12.
Из сотрудников фирмы 16 побывали во Франции,10-в Италии,6-в Англии; в Англии и Италии-5; в Англии и Франции -6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
Решение:
Нам известно, что во всех трех странах было 5 сотрудников. В Англии и Италии тоже 5, значит эти же сотрудники были и во Франции и поэтому в пересечении кругов А и И ставим 0. В Франции и Италии нам неизвестно поэтому пишем х-5 в пересечении кругов А и Ф. Т.к. в Англии было 6 человек, то 6-5-1=0 пишем 0,во Франции 16-х+5-6 и Италии 10-х+5-5 и всего в фирме 19 сотрудников, то остается составить и решить уравнение: 1+16-х+5-6+5+х-5+10-х+5-5=19, отсюда х=7, значит в Италии и Франции побывало 7-5=2 сотрудника фирмы.
Рис.16
Ответ: 2 сотрудника.
Задача № 13.
Ребят, которые хотят обмениваться различного рода журналами, собралось 10 человек. Среди них выписывают К — 6 человек, Т – 5 человек, Ю – 5 человек, К и Т – 3 человека, Т и Ю -2 человека, К и Ю – 3 человека., а один человек не выписывает ни одного журнала., но читает все эти журналы в библиотеке. Надо узнать, сколько человек выписывают все три журнала, сколько – два, а сколько – только один журнал.
Решение. Пусть большой круг, состоящий из 10 человек, – это множество всех ребят, обменивающихся журналами. Внутри большого круга нарисуем три меньших круга: К, Т, Ю, которые изображают ребят, подписавшихся на соответствующие журналы.. Известно, что один человек не выписывает ни одного журнала.
Пусть х ребят выписывают все три журнала, тогда (3-х)ребят выписывают только К и Т, (2-х) –только Т и Ю, (3-х)- только К и Ю. Значит, только журнал К выписывают 6-(3-х+х+3-х)=х человек, журнал Т 5-(3-х+х+2-х)=х, журнал Ю 5-(3-х+х+2-х)=х.
Рис .17
Составим уравнение: х+3-х+3-х+х+х+х+х+2-х=9, 8+х=9,х=1
Итак, 3 – это число ребят, подписавшихся только на один журнал, 5 – это число ребят, подписавшихся на два журнала, а 1 – число ребят, подписавшихся на все три журнала.
ЗАКЛЮЧЕНИЕ
Предмет математики настолько серьезен,
что нельзя упускать случая сделать
его немного занимательным.
Б. Паскаль
Среди математических задач логические задачи занимают особое место Решение таких задач способствует развитию математического мышления. Они отличаются от большинства математических задач тем, что для их решения часто не требуется запас каких-то специальных знаний, а нужна, как правило, сообразительность. Одна из характерных черт любой логики состоит в том, что она позволяет, получив некоторую информацию, извлечь (выявить) содержащиеся в ней новые знания.
Оказывается приемов, с помощью которых можно решать текстовые логические задачи, несколько. Они разнообразны и каждый из них имеет свою область применения.
В моей работе рассмотрены задачи, которые состоят из множества данных. Найденные решения подчиняются одному и тому же способу: составляем рисунок; заносим первоначальные данные в круги; анализируя и рассуждая, записываем результаты в части кругов; ищем и записываем ответ. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению. Кроме того с их помощью можно ответить на множество вопросов, поставленных к одному условию задачи.
Данная тема расширила мой математический кругозор, обогатила арсенал средств, используемых в решении разнообразных задач.
Список используемых источников:
1. Гаврилова Т. Д..Занимательная математика. 5 — 11 классы. Волгоград: Учитель, 2005.-96 с.
2. Германович П.Ю. «Сборник задач по математике на сообразительность».
3. Гетманова А. Д. Логические основы математики 10 – 11 класс: учебное пособие. – М.: Дрофа, 2005.
4. Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — С. 232.
5. Гусев В.А., Орлов А.И., Розенталь А.Л. «Внеклассная работа по математике». М.: Просвещение, 1984.
6. Нелин Е.П., Долгова О.Е.. Учебник алгебра и начала анализа 11 класс.
Тезисы к работе
Тема моей исследовательской работы «Решение задач с помощью кругов Эйлера ». При подготовке к олимпиаде я столкнулась с задачами, в которых большое количество данных. Оказывается, упростить решение таких задач помогают так называемые круги Эйлера, с помощью которых можно изобразить множество элементов, обладающих определённым свойством. Целью данной работы является изучение этого способа и умение применять его для решения задач.
В работе рассмотрены задачи, решение которых подчиняются одному алгоритму: составляем рисунок; заносим первоначальные данные в круги, начиная с условия которое содержит больше свойств; анализируя и рассуждая записываем результаты в части круга; записываем ответ.
Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь. Способ, рассмотренный в работе доступен и легок в понимании, что позволяет расширить круг его применения. Круги Эйлера можно встретить и в истории, и в биологии, и при изучении других предметов.
Материал,который был исследован в работе ,а также практическая часть, могут быть применены на дополнительных занятиях, при подготовке к математическим олимпиадам .
infourok.ru
Решение. Воспользуемся кругами Эйлера — Решение
Занятие по подготовке к ГИА по математике по решению задач с помощью кругов Эйлера. Теория графов. ( учитель Артемова Л.И.)
С
портивный
класс
В классе 38 человек. Из них 16 играют в баскетбол, 17 — в хоккей, 18 — в футбол. Увлекаются двумя видами спорта — баскетболом и хоккеем — четверо, баскетболом и футболом — трое, футболом и хоккеем — пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом.
Сколько ребят увлекаются одновременно тремя видами спорта?
Сколько ребят увлекается лишь одним из этих видов спорта?
Решение.
В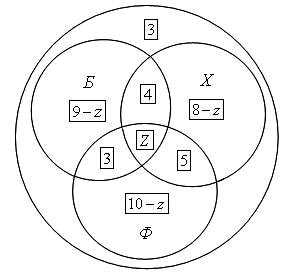
оспользуемся
кругами Эйлера.
Пусть большой круг изображает всех учащихся класса,
а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов.
Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта.
Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта —
баскетболом занимаются
16 — (4 + z + 3) = 9 — z;
одним лишь хоккеем
17 — (4 + z + 5) = 8 — z;
одним лишь футболом
18 — (3 + z + 5) = 10 — z.
Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам:
3 + (9 — z) + (8 — z) + (10 — z) + 4 + 3 + 5 + z = 38,
z = 2.
Таким образом, двое ребят увлекаются всеми тремя видами спорта.
Складывая числа 9 — z, 8 — z и 10 — z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек.
Ответ.
Двое ребят увлекаются всеми тремя видами спорта человека.
Увлекающихся лишь одним видом спорта: 21 человек.
Круги Эйлера – задачи на пересечение или объединение множеств
Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.
«Обитаемый остров» и «Стиляги»
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение
Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».
11 – 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:
Ответ. 5 человек смотрели только «Стиляги».
Любимые мультфильмы
Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?
Решение
В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:
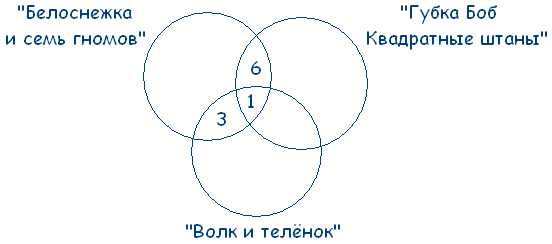
Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:
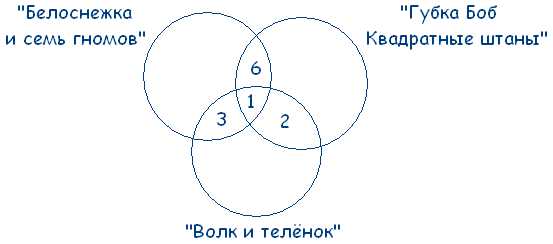
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Получаем:
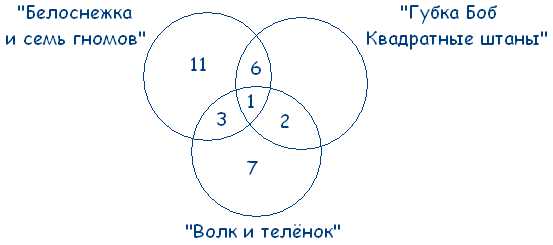
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».
«Мир музыки»
В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?
Решение
Изобразим эти множества на кругах Эйлера.
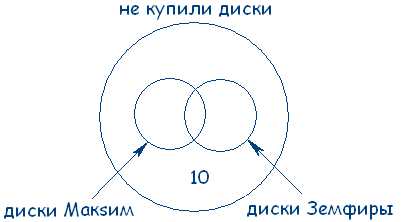
Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:
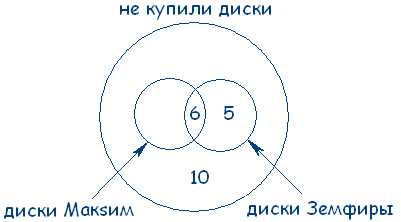
Ответ: 6 покупателей купили диски и Максим, и Земфиры.
Гарри Поттер, Рон и Гермиона
На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон?
Решение
Учитывая условия задачи, чертеж будет таков:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон.
Ответ. 8 книг прочитал Рон.
Пионерский лагерь
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение
Изобразим множества следующим образом:
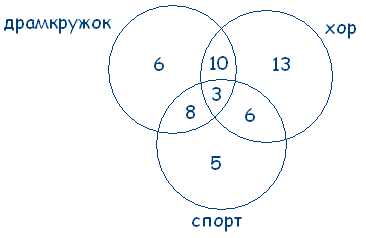
70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом заняты 5 человек.
Ответ. 5 человек заняты только спортом.
Экстрим
Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Решение
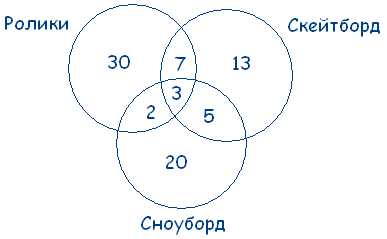
Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.
Задача: В классе учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по физике – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека и по физике – 11 человек. Семь человек имеют «тройки» и по математике и по физике, из них пятеро имеют тройки и по русскому языку. Сколько человек учатся без «троек». Сколько человек имеют «тройки» по двум из трёх предметов. Рассмотрим решение с помощью следующего слайда


Теория графов
Теория графов – наука сравнительно молодая. Первая работа по теории графов принадлежит Леонарду Эйлеру. Она появилась в 1736 году в публикациях Петербургской Академии Наук и начиналась с рассмотрения задачи о кенигсбергских мостах. Графы придали условиям наглядность, упростили решение и выявили сходство задач. Сейчас почти в любой отрасли науки и техники встречаешься с графами: в электротехнике при построении электрических схем, в химии – при изучении молекул и их цепочек, в экономике – при решении задач выбора оптимального пути для потоков грузового транспорта. Граф – это фигура, состоящая из точек и линий.
Решим следующую задачу:
В школьном драматическом кружке решили ставить гоголевского «Ревизора». И тут разгорелся жаркий спор. Всё началось с Ляпкина-Тяпкина.
– Ляпкиным-Тяпкиным буду я! Решительно заявил Дима. С раннего детства я мечтал воплотить этот образ на сцене.
– Ну хорошо, согласен уступить эту роль, если мне дадут сыграть Хлестакова, проявил великодушие Гена.
– … А мне – Осипа, – не уступил ему в великодушии Дима.
– Хочу быть Земляникой или Городничим, – сказал Вова.
– Нет, Городничим буду я, – хором закричали Алик и Боря. – или Хлестаковым, добавили они одновременно.
Удастся ли распределить роли так. Чтобы исполнители были довольны?

Изобразим каждого участника драматического кружка точкой, а все их пожелания будем изображать линиями. Видно, что Осипа будет играть Дима, Вова – Землянику, Гена – Ляпкина – Тяпкина, Алик и Боря – Хлестакова и Городничего.
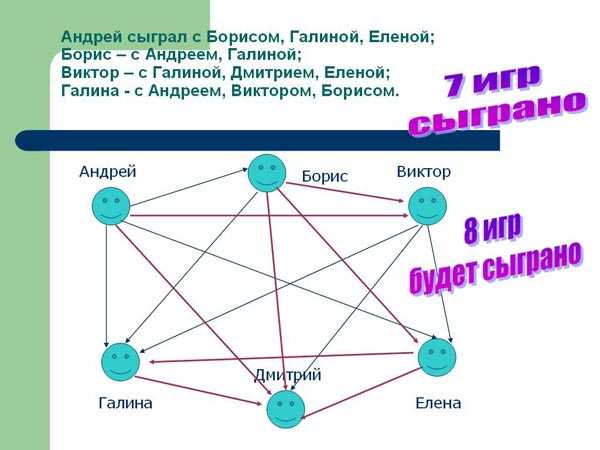
Решите с помощью графов следующую задачу: В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз.
13 Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским и немецким одновременно владеют 8 человек, английским и французским — 10, немецким и французским — 5, всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?
Выразим условие этой задачи графически. Обозначим кругом тех кто знает английский, другим кругом — тех, кто знает французский, и третим кругом — тех, кто знают немецкий. Тогда, например, те, кто владеет и английским и немецким, «попадут» в общую часть первого и третьего круга.

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языками владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.
Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста. Вносим эти данные в соответствующие части.
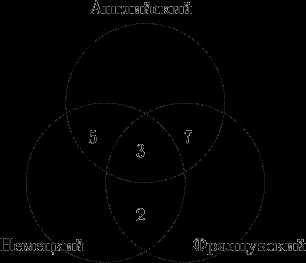
Определим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским — 30 человек.
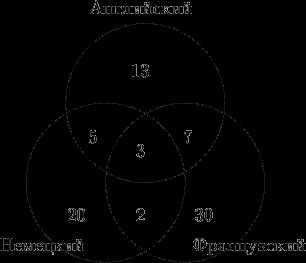
По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.
Ответ: только английским владеет 13 человек, только французским — 30, только немецким — 20 человек. 20 человек не знают ни одного из этих языков.
Задачи на круги Эйлера
Задача 1. Про учеников школы, которые участвовали в физико-математическом конкурсе, известно, что 7 из них справились с задачами и по математике и по физике, 11 из них справились с задачами по математике, 9 из них справились с задачами по физике. Сколько учеников принимали участие в конкурсе?
Задача 2. В одной семье было много детей. 7 из них любили капусту, 6 — морковь, 5 — горох, 4 — капусту и морковь, 3 — капусту и горох, 2 — морковь и горох, один — и капусту, и морковь, и горох. Сколько детей было в семье?
Задача 3. На полу комнаты площадью 24 м2 лежат три ковра. Площадь одного из них — 10 м2, другого — 8 м2, третьего — 6 м2. Каждые два ковра перекрываются по площади 3 м2, а площадь участка пола, покрытого всеми тремя коврами, составляет 1 м2. Найдите площадь участка пола: а) покрытого первым и вторым коврами, но не покрытого третьим ковром; б) покрытого только одним первым ковром; в) не покрытого коврами.
Задача 4. На спортивные соревнования в Летней математической школе ходили 220 школьников. При этом некоторые из них участвовали в чемпионатах, а остальные были зрителями. В легкоатлетической эстафете приняли участие 30 человек, в соревнованиях по волейболу — 26, пионерболу — 32, футболу — 31, шахматам — 28 и теннису — 36 человек. 53 школьника приняли участие более чем в одном соревновании; из них 24 школьника участвовали 3 или более раз, 9 школьников — не менее 4 раз и 3 школьника — даже 5 раз (в последнюю тройку входит и один чудак, который выступал во всех шести соревнованиях). Сколько школьников были зрителями?
Разнобой
Задача 5. Дано 6 гирь: две зеленых, две красных, две синих. В каждой паре одна гиря тяжелая, а другая легкая, причём все тяжелые гири весят одинаково и все легкие тоже. Можно ли за 2 взвешивания на чашечных весах найти все тяжелые гири?
Задача 6. На плоскости расположено 11 шестерёнок, соединенных в кольцо. Могут ли все шестерёнки вращаться одновременно?
gigabaza.ru
Логические задачи и круги Эйлера
Круги Эйлера – это геометрическая схема. С ее помощью можно изобразить отношения между подмножествами (понятиями), для наглядного представления.
Способ изображения понятий в виде кругов позволяет развивать воображение и логическое мышление не только детям, но и взрослым. Начиная с 4-5 лет детям доступно решение простейших задач с кругами Эйлера, сначала с разъяснениями взрослых, а потом и самостоятельно. Овладение методом решения задач с помощью кругов Эйлера формирует у ребенка способность анализировать, сопоставлять, обобщать и группировать свои знания для более широкого применения.
Пример
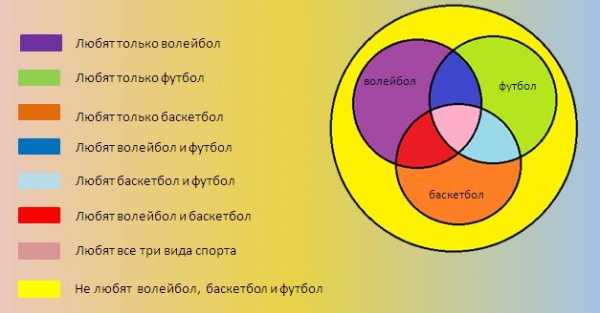
На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.Вот несколько задач для маленьких детей на логическое мышление:
- Определить круги, которые подходят к описанию предмета. При этом желательно обратить внимание на те качества, которыми предмет обладает постоянно и которыми временно. Например, стеклянный стакан с соком всегда остается стеклянным, но сок в нем есть не всегда. Или существует какое-то обширное определение, которое включает в себя разные понятия, подобную классификацию тоже можно изобразить с помощью кругов Эйлера. Например, виолончель – это музыкальный инструмент, но не каждый музыкальный инструмент окажется виолончелью.


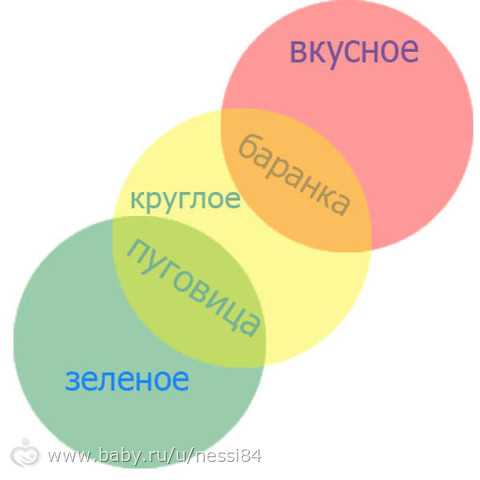
- Определение круга, который не подходит к описанию предмета. Например, баранка – она круглая и вкусная, а определение зеленая к ней не подходит. Можно также придумать, какой предмет подойдет для пересечения другой пары кругов. Пример – круглая и зеленая может быть пуговица.

- Определить предмет, который подходит под описание всех кругов. Для каждого круга выбирается какое-либо качество (например – сладкое, оранжевое, круглое). Ребенок должен назвать предмет, который одновременно соответствует всем этим описаниям (в данном примере подойдет апельсин), также можно спросить ребенка, какие предметы могут соответствовать двум описаниям из трех, то есть будут находиться на пересечении каждой пары кругов (например, сладкое и оранжевое – карамелька, оранжевое и круглое – мяч, круглое и сладкое – арбуз).

Для детей постарше можно предлагать варианты задач с вычислениями – от достаточно простых до совсем сложных. Причем самостоятельное придумывание этих задач для детей обеспечит родителям очень хорошую разминку для ума.
- 1.Из 27 пятиклассников все изучают иностранные языки – английский и немецкий. 12 изучают немецкий язык, а 19 – английский. Необходимо определить, сколько пятиклассников заняты изучением двух иностранных языков; сколько не изучают немецкий; сколько не изучают английский; сколько изучают только немецкий и только английский?
При этом первый вопрос задачи намекает в целом на путь к решению этой задачи, сообщая, что некоторые школьники изучают оба языка, и в этом случае использование схемы также упрощает понимание задачи детьми.

источник http://shkolazhizni.ru/school/articles/71462/
автор Леонид Серый
Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.
И еще одна табличка…
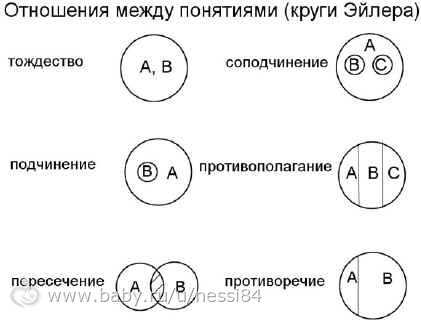
www.baby.ru
Проблемно-реферативная работа «Круги Эйлера в решении задач»
Министерство образования и науки Российской Федерации
Муниципальное образовательное учреждение
Краснопресненская средняя общеобразовательная школа
им. В.П.Дмитриева
проблемно-реферативная работа
Тема: Круги Эйлера в решении задач
Выполнила:
учащаяся 6 класса
Гунбетова Карина
Руководитель: Глазунова В.Г., учитель математики высшей квалификационной категории
2012
ОГЛАВЛЕНИЕ
Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Глава 1. Круги Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
1.1. Леонард Эйлер. Биография. . . . . . . . . . . . . . . . . . . . . . . . . . ..4
1.2. Круги Эйлера. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7
Глава 2. Круги Эйлера в задачах. . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
Список литературы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
ВВЕДЕНИЕ
«…Нет ученого, имя которого упоминалось бы в учебной литературе по математике столь же часто, как имя Эйлера. В Энциклопедии можно найти сведения о шестнадцати формулах, уравнениях, теоремах и т. д., носящих имя Эйлера…».
Леонард Эйлер жил в 18 веке, но его метод решения целого ряда задач актуален и сегодня, в 21-ом веке.
Один из величайших математиков, петербургский академик Леонард Эйлер за свою долгую жизнь написал более 850 научных работ.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера». Эйлер писал, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Венн и его назвали «диаграммы Венна».
Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах. Задачи таким способом решаются значительно быстрее, решение понятно.
Цель: научиться решать задачи с помощью кругов Эйлера и научить других.
Задачи:
Изучить теоретический материал: биографию Леонарда Эйлера, «круги Эйлера».
Научиться применять круги в решении задач.
Создать задачник для учащихся «Круги Эйлера в задачах».
Подвести итоги.
ГЛАВА 1. КРУГИ ЭЙЛЕРА
Леонард Эйлер. Биография
Леонард Эйлер 1 родился 15 апреля 1707 года в семье пастора, жившей в
швейцарском городке Базеле. Рано обнаружил математические способности. Отец Леонарда пастор Пауль Эйлер был хорошо образован и увлекался математикой. Именно под руководством отца Эйлер получил начальное обучение. Отец хотел дать Леонарду духовное образование и занимался с ним математикой только для развлечения и для развития логического мышления. 20 октября 1720 года 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета, где преподавались и математика и астрономия. Занятия по этим предметам вел прославленный математик Иоганн Бернулли. Проявив интерес к математике, Эйлер привлек к себе внимание Иоганна Бернулли. Профессор стал лично руководить самостоятельными занятиями юноши и вскоре публично признал, что от проницательности и остроты ума юного Эйлера он ожидает самых больших успехов.
Не забывал Эйлер и другие университетские курсы, поэтому и был широко образован. 8 июня 1724 года 17-летний Леонард Эйлер произнёс на латыни речь о сравнении философских воззрений Декарта и Ньютона и был удостоен учёной степени магистра. В последующие два года юный Эйлер написал несколько научных работ. Одна из них, «Диссертация по физике о звуке», получившая благоприятный отзыв, была представлена на конкурс для замещения неожиданно освободившейся в Базельском университете должности профессора физики (1725). Но, несмотря на положительный отзыв, 19-летнего Эйлера сочли слишком юным, чтобы включить в число кандидатов на профессорскую кафедру. Число научных вакансий в Швейцарии было совсем невелико. Поэтому братья Даниил и Николай Бернулли, сыновья Иоганна Бернулли, уехали в далёкую Россию, где как раз шла организация Академии наук. Своих ученых в России тогда не было совсем. Пришлось привлекать иностранных. В числе первых были приглашены братья Бернулли. По их рекомендации через три года после открытия Петербургской академии наук получил приглашение и двадцатилетний Эйлер на должность адъюнкта по физиологии. 5 апреля 1727 года Эйлер навсегда покинул родную Швейцарию. Одной из важнейших задач Академии стала подготовка отечественных кадров. Позднее при Академии были созданы университет и гимназия. В силу острой
нехватки учебников на русском языке Академия обратилась к своим членам с
просьбой составить такие руководства. Эйлер, хотя и числился физиологом, составил на немецком языке очень добротное «Руководство к арифметике», которое тут же было переведено на русский и служило не один год в качестве начального учебника. Перевод первой части выполнил первый русский,
ученик Эйлера Василий Адодуров. Это было первое систематическое изложение арифметики на русском языке. К всеобщему удивлению, Эйлер уже в следующем по приезде году стал бегло говорить по-русски. Эйлер отличался феноменальной работоспособностью. По отзывам современников, для него жить означало заниматься математикой. А работы у молодого профессора было много: картография, всевозможные экспертизы, консультации для кораблестроителей и артиллеристов, составление учебных руководств, проектирование пожарных насосов и т. д. За первый период пребывания в России (14лет), он написал более 90 крупных научных работ по математике, гидравлике, архитектуре, навигации, картографии и механике. Значительная часть академических «Записок» заполнена трудами Эйлера. Он делал доклады на научных семинарах, читал публичные лекции, участвовал в выполнении различных технических заказов правительственных ведомств. Петербургская академия по достоинству оценила молодого ученого, в двадцать три года он уже профессор физики, а еще через три года Леонард Эйлер получает кафедру высшей математики. В 1735 году Академия получила задание выполнить срочное и очень громоздкое астрономическое (по другим данным, картографическое) вычисление. Группа академиков просила на эту работу три месяца, а Эйлер взялся выполнить работу за 3 дня — и справился самостоятельно. Однако перенапряжение не прошло бесследно: он заболел и потерял зрение на правый глаз. Однако учёный отнёсся к несчастью с величайшим спокойствием: «Теперь я меньше буду отвлекаться от занятий математикой», — философски заметил он. В 1730-е годы Эйлер становится известен и в Европе. Двухтомное сочинение «Механика, или наука о движении, в аналитическом изложении», изданное в 1736 году, принесло ему мировую славу. Начиная с этого момента, теоретическая механика становится прикладной частью математики. Осенью 1740 внутренняя обстановка в России осложнилась. Это побудило Эйлера принять приглашение прусского короля, и летом 1741 он переехал в Берлин, где вскоре возглавил математический класс в Берлинской Академии наук и словесности. Годы, проведенные Эйлером в Берлине, были наиболее плодотворными в его научной деятельности. Переезд в Берлин не прервал, однако, тесных связей Эйлера с Петербургской Академией наук. Он по-прежнему регулярно посылал в Россию свои сочинения, участвовал в экспертизах различного рода, обучал посланных к нему из России учеников, подбирал ученых на замещение вакантных должностей в Академии и выполнял много других поручений. В 1762 году на русский престол вступила Екатерина II, которая хорошо понимая значение науки, как для прогресса государства, так и для собственного престижа, провела ряд важных, благоприятных для науки, преобразований в системе народного просвещения и культуры. Императрица предложила Эйлеру управление математическим классом (отделением), звание конференц-секретаря Академии.
После двадцати пяти лет проживания в Берлине, 60-летний Эйлер снова возвращается в Россию, в Петербург. Эйлер полон энергии и душевных сил, желания работать на благо России. К несчастью, после возвращения в Петербург у Эйлера образовалась катаракта второго, левого глаза — он перестал видеть. Вероятно, по этой причине обещанный пост вице-президента Академии он так и не получил. Однако слепота не отразилась на его работоспособности. Эйлер диктовал свои труды мальчику — портному, который всё записывал по-немецки. Число опубликованных им работ даже возросло; за полтора десятка лет второго пребывания в России он продиктовал более 400 статей и 10 книг. В 1773 году по рекомендации Даниила Бернулли в
Петербург приехал из Базеля ученик Бернулли, Никлаус Фусс. Это было большой удачей для Эйлера. Фусс обладал редким сочетанием математического таланта и умения вести практические дела, что и дало ему возможность сразу же после приезда взять на себя заботы о математических трудах Эйлера. В последующие десять лет — до самой своей смерти — Эйлер преимущественно ему диктовал свои труды, хотя иногда пользовался «глазами старшего сына» и других своих учеников. Эйлер активно трудился до последних дней. В сентябре 1783 года 76-летний учёный стал ощущать головные боли и слабость.
7 сентября после обеда, Эйлер почувствовал себя плохо, успел произнести: «Я умираю», — и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг.
Великий ученый Леонард Эйлер занимает одно из первых мест в истории мировой науки. Полное собрание его трудов составляет 72 тома, более 850 научных работ. Этот тихий и скромный человек, полностью ослепший, много работал, совершив великое множество научных открытий.
Круги Эйлера
Круги Эйлера2 — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами. Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. Используется в математике, логике, менеджменте и других прикладных направлениях. А впервые Эйлер их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления».
При решении задач Леонард Эйлер использовал идею изображения множеств с помощью кругов, и они получили название «круги Эйлера».
Строгого определения понятия множества не существует.
Множество — совокупность элементов, обладающих некоторым общим свойством, т. е. как единое целое (множество натуральных чисел, множество треугольников на плоскости).
Множества, состоящие из конечного числа элементов, называют конечными, а остальные множества – бесконечными. Например, множество китов в океане конечно, а множество рациональных чисел бесконечно. Конечное множество может быть задано перечислением его элементов (множество учеников в данном классе задается их списком в классном журнале).
Понятие подмножества в определении кругов Эйлера – это, например, во
множестве учеников класса можно выделить множество ударников, которые входят во множество всех учеников (ударники – подмножество).
Множество всех действительных чисел Эйлер изобразил с помощью этих
кругов: N — множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество всех действительных чисел.
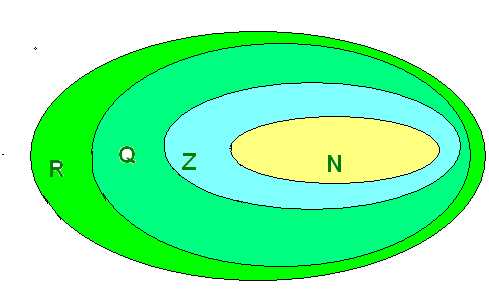
Метод Эйлера является незаменимым при решении целого ряда задач, а также упрощает рассуждения.
ГЛАВА 2. КРУГИ ЭЙЛЕРА В ЗАДАЧАХ3
Алгоритм решения задач
1. Внимательно изучи условия задач.
2. Построй пересечения множеств.
3. Расставь исходные данные.
4. Найдите недостающие данные.
5. Проверь решение.
1. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?
Решение:
Так как 26 половина детей любит пирожные, а 20 — и пирожные, и мороженое, то исключительно пирожное любят ровно 6 человек. Всего ребят 52, из них 6 — любители только пирожных, значит, 52 – 6 = 46 человек, которые любят мороженое.
2. Часть жителей нашего города умеет говорить только по-русски, часть – только по-башкирски и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?
Решение: Составим схему –
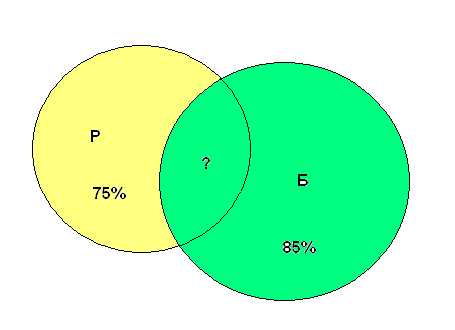
В кружке под буквой «Б» обозначим жителей, говорящих по-башкирски, под буквой
«Р» — по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «Б» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).
3. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?
Решение: Обратимся к кругам Эйлера: 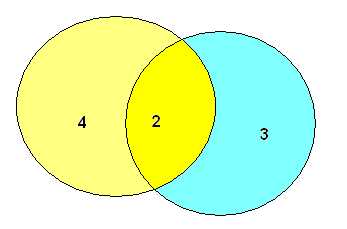
Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом — фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
4. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и
холодильник и микроволновку, 19 — и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Решение:
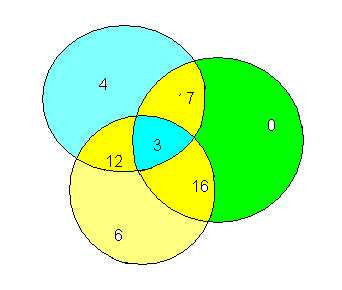
Купили только холодильники: 35-(20-3)-(15-3)-3=4.
Купили только микроволновки: 36-(20-3)-(19-3)-3=0.
Купили только телевизоры: 37-(15-3)-(19-3)-3=6.
Тогда всего покупателей было: 4+17+3+16+12+6=58.
65-58=7 посетителей магазина не купили ничего.
5. На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон?
Учитывая условия задачи, чертеж будет таков:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал толькоРон. А всего Рон прочитал 12 книг.
Ответ: 12 книг прочитал Рон.
6. Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу – 8 человек, спортивную школу – 12 человек, музыкальную и художественную школу– 3, художественную и спортивную школу– 2, музыкальную и спортивную школу– 2, все три школы посещает 1 человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают?
В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

Только музыкальную школу посещают 10-3-2-1=4 учащихся. Только художественную школу посещают 8-3-2-1=2 учащихся. Только спортивную школу посещают 12-2-2-1=7 учащихся.
Только одну школу посещают 4+2+7=13 учеников.
Ни в чем себя не развивают 24-(4+2+7+3+2+2+1)=3 учащихся.
Ответ: 13 учеников посещают только одну школу, 3 учащихся себя не развивают.
7. В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?
Решение: 1 способ. Для решения опять воспользуемся кругами Эйлера:
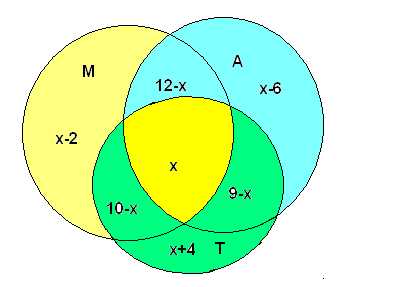
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3
8. Из 100 отдыхающих на турбазе «Графское»,
30 детей — отличники учебы,
28 — участники олимпиад,
42 — спортсмены.
8 учащихся одновременно участники олимпиад и спортсмены,
10 – участники олимпиад и отличники,
5 – спортсмены и отличники учебы,
3 – и отличники, и участники олимпиад, и спортсмены.
С колько отдыхающих не относятся ни к одной из групп?
колько отдыхающих не относятся ни к одной из групп?
Решение:
20+13+30+3+5+7+2=80 (детей)
100-80=20 (детей не входят ни в одну из групп)
Ответ: 20 детей.
ЗАКЛЮЧЕНИЕ
На уроках математики учитель знакомит нас, учеников, с историей развития математических понятий, символов, идей, методов. Но из-за нехватки учебного времени ему не всегда удается рассказать о жизни великих творцов математики – интенсивной, целенаправленной, поучительной, хотя подчас и драматичной; раскрыть все стороны древнейшей и, в то же время, современной науки.
Одно из первых мест в истории мировой науки занимает Леонард Эйлер.
Полное собрание его трудов составляет 72 тома, более 850 научных работ.
Леонард Эйлер жил в 18 веке, но его метод решения целого ряда задач актуален и сегодня, в 21-ом веке. Эйлер использовал идею изображения множеств с помощью кругов. Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах. Задачи таким способом решаются значительно быстрее, решение понятно.
Поэтому была поставлены задачи: изучить биографию Леонарда Эйлера и научиться решать задачи, применяя правила и круги Эйлера.
Для этого был разобран весь теоретический материал, решены задачи, используя круги Эйлера и составлен задачник для учащихся «Круги Эйлера в задачах».
Применение кругов Эйлера позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
Цель работы считаю достигнутой.
СПИСОК ЛИТЕРАТУРЫ
Академия математики «Леонард Эйлер» научно-практический журнал Математика для школьников №3 2007г., с.41-48
Интернет ресурсы http://logika.vobrazovanie.ru/index.php?link=kr_e.html – Учимся решать логические задачи
Интернет – ресурсы http://olymp.ifmo.ru/archive/problems/inf/ – архив задач по информатике.
Босова Л.Л. Информатика: Учебник для 6 класса / Л. Л. Босова. –5-е изд–М.: БИНОМ. Лаборатория знаний, 2007. – 208 с.: ил.
Босова Л.Л. Информатика: Рабочая тетрадь для 6 класса /Л. Л. Босова, – 2-е изд., испр. – М.: БИНОМ. Лаборатория знаний, 2005. – 117 с.: ил.
Угринович Н.Д. Информатика и ИКТ: Учебник для 10 класс. БИНОМ. Лаборатория знаний, 2010. – 371 с.: ил.
Глейзер Г. И. История математики. М., Наука, 1982 г.
1 Биографический очерк Е.Ф. Литвиновой в сокращенном варианте опубликован в научно-практическом журнале «Математика для школьников»№3 2007
infourok.ru
Урок на тему; «Круги Эйлера»
Класс: 10
Предмет: информатика и математика
Учитель: Сусанина Ирина Викторовна, Боталова Ольга Викторовна
Тема урока: Решение задач по теме: «Круги Эйлера»
Тип урока: интегрированный урок информатики и математики, урок обобщения и систематизации знаний, умений и навыков.
Вид урока: урок теоретических и практических работ, анализ ситуации.
Методы обучения: диалогический, наглядный, объяснительно – иллюстративный.
Формы обучения: коллективная и индивидуальная.
Оборудование: интерактивная доска, ПК, проектор, презентация «Круги Эйлера»
Цели урока:
обобщить знания и умения обучающихся по применению кругов Эйлера;
познакомить и сформировать у обучающихся принцип реализации диаграмм Вена-Эйлера для решения логических задач;
развить коммуникативно — технические умения, умения оценивать результаты выполненных действий;
развить аналитическо-логическое мышление;
воспитать самостоятельность, инициативность, толерантность, ответственное отношение к информации, информационную культуру.
Задачи урока:
повторить изученный материал по теме «Логика»;
научить обучающихся использовать круги Эйлера при решении логических задач;
продемонстрировать решение типовых задач из ЕГЭ;
закрепить изученный материал решением подобных задач.
Ход урока
1.Организационный момент. Приветствие обучающихся.
2. Этап мотивации обучающихся. Ставится цель и задачи занятия перед учащимися, говоря о том, что данные задания используются в ЕГЭ по информатике и математике.
3.Прорверка домашнего задания. Выборочная проверка Д/З. Правильные ответы на ИД. (Слайд 2-3)
4.Повторение изученного материала. Вспомнить основные логические операции, повторить правила работы со множествами, то есть логические операции с кругами Эйлера. (Слайд 4-5)
5. Объяснение нового материала. Круги Эйлера.
Учитель информатики (Слайд 6)
— Леонард Эйлер (1707 — 1783). Эйлеру повезло: он родился в маленькой тихой Швейцарии, куда изо всей Европы приезжали мастера и ученые. В Базеле жила семья Бернулли: уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. По воле случая юный Эйлер попал в эту компанию и вскоре сделался достойным членом базельского питомника гениев. (Д/з: подготовить сообщение о Якобе и Иоганне Бернулли).
Учитель математики
— Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Студенты проходят высшую математику под руководством, первыми образцами которых явились классические монографии Эйлера. Он был, прежде всего, математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный.
Его называли идеальным математиком 18 века. Леонард Эйлер написал более 850 научных работ. В одной из них и появились круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления».
Учитель математики
— А теперь давайте разберем несколько примеров заданий на определение объема найденной информации и на отработку навыков решения задач с логическими высказываниями с математической точки зрения.
(Слайд 7) Отношения между множествами чисел наглядно демонстрирует геометрическая иллюстрация – круги Эйлера Леонард Эйлер (Россия, середина XYΙΙΙ века).
5.1.Решение задач на математическую логику. Объяснить принцип решения задач такого типа и дать рекомендации по решению (работать цветными ручками, чтобы представить принцип и суть задачи, а также для того чтобы структурировать информацию и обозначать каждую часть круга латинскими буквами для большего освоения материала).
Задача 1. (Слайд 8-9) В автобусе «Кропоткин-Кавказская» едет 30 пассажиров. Все они являются жителями Кавказского района. Из них 20 человек являются жителями только города Кропоткин, 15 – живут только в станице Кавказской. Сколько человек не являются жителями нашего города?
Решение: Пусть круг Г изображает жителей только города Кропоткин, круг С — только жителей станицы Кавказской. Тогда ГС — изображение жителей и города, и станицы одновременно. Из рисунка следует, что число, не являющихся жителями Кропоткина, равно:
(не Г) = С — ГС. Всего 30 человек, Г = 20 человек, С = 15 человек. Тогда значение ГС может быть найдено так (см. рисунок): ГС = (Г + С) — 30 = (20 + 15) — 30 = 5, т.е. 5 человек живут и в городе и в станице одновременно.
Тогда (не Г) = = С — ГС= 15 — 5= 10.
Ответ: 10 пассажиров не являются жителями города Кропоткин.
Задача 2. (Задание В6. ЕГЭ). (Слайд 10)
Три друга – Петр, Роман и Сергей – учатся на математическом (М), физическом (Ф) и химическом (Х) факультетах.
Если Петр математик, то Сергей не физик. Если Роман не физик, то Петр – математик. Если Сергей не математик, то Роман – химик.
Определите специальность каждого. Ответ запишите в виде строки из трех символов, соответствующих первым буквам названия специальностей Петра, Романа и Сергея (в указанном порядке). Так, например, строка МФК соответствует тому, что Петр – математик, Роман – физик, Сергей – химик.
Решение: A Петр – математик; B Сергей-не физик; C Роман физик; D Сергей математик D=¬B; E Роман химик E= ¬C
(A ¬B) • ( ¬C A) • ( ¬D E)=
= (¬ A+¬B) • ( C +A) • ( D + E)=
= (¬ A+¬B) • ( C +A) • ( ¬B +¬C)=
= ¬ B+(¬ A • ¬C) • ( A + C )= ¬ B=1 ,
Значит B=0, D=1 Сергей математик,
Следовательно, A=0 ¬C A=1 C+A=1
C=1 Роман физик, а Петр химик
Ответ: ХФМ
5.2.Этап решения заданий у доски учениками.
Задача. (Слайд 11) Один из учеников решает около доски. Весь класс решает вместе с учеником.
Для какого имени истинно высказывание: ¬ (Первая буква согласная →Последняя буква гласная) Вторая буква согласная?
1) ИРИНА 2) СТЕПАН 3) МАРИНА 4) ИВАН
Для какого имени истинно высказывание: (Первая буква согласная → Вторая буква согласная) Последняя буква гласная?
1) КСЕНИЯ 2) МАКСИМ 3) МАРИЯ 4) СТЕПАН
Самостоятельная работа. Те ученики, которые хорошо усвоили материал и идут вперед, работают по карточкам. (Приложение 1)
5.3… Это интересно.
Учитель информатики
— В наше время Круги Эйлера приобретают все большую популярность.
Вам никогда не приходило в голову, как это классно, вставать каждое утро и сгорать от нетерпения поскорее взяться за любимые дела? Вставать, и чётко знать, что делать и как это делать? Знать, что получится в итоге, быть уверенным, что вы это сделаете лучше всех и горячо верить, что именно в этом и состоит смысл вашей жизни?
А вечерами с огромной неохотой и досадой ложиться спать с одной лишь мыслью, что завтра встанете пораньше и сразу же возьметесь за любимое дело!
Как вам это? Скажете, такого не бывает?
Жители северной части острова Окинава (Япония) с вами не согласятся. Не согласятся, поскольку они проживают так каждый свой день. Они знают один важный секрет, имя которому икигай. Жители северной части острова Окинава (Япония) с вами не согласятся. Не согласятся, поскольку они проживают так каждый свой день. Они знают один важный секрет, имя которому икигай.
Икигай (яп. 生き甲斐, «смысл жизни») (Слайд 12)
(Д/з: подготовить свою схему Икигая при помощи кругов Эйлера)
6. Подведение итогов урока.
7. Домашнее задание по информатике: (Слайд 13-14) Сообщение о Якобе и Иоганне Бернулли; схема Икигая.
Информационные ресурсы
«Информатика. Задачник- практикум в 2 т.», Под ред. И.Г. Семакина, Е.К. Хеннера, М.: Бином. Лаборатория знаний, 2012
«Информатика: готовимся к ЕГЭ», Зеленко Л.С., Сопченко Е.В., Самара, 2012
«ЕГЭ 2014. Информатика.», Ярцева, Цикина, 2014
Готовимся к ЕГЭ по математике — Самылкина Н.Н.2014
ЕГЭ Информатика : Раздаточный материал тренировочных тестов, Гусева И.Ю.
ЕГЭ 2014 Информатика, ЕГЭ 2014 по математике от ФИПИ
http://kpolyakov.narod.ru
http://www.ctege.org — Подготовка к ЕГЭ
http://www.websib.ru/noos — Предметный сайт для учителей.
http://pedsovet.su — » Сообщество взаимопомощи учителей»
Приложение 1
Уровень 1. У учеников 9А класса есть братья и сестры. У шестерых есть братья, а у пятерых — сестры. И только у двоих есть и те и другие. Угадайте, сколько таких ребят учатся в классе?
Уровень 2. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский (А), немецкий (Н), французский (Ф). 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
_______________________________________________________________________
Уровень 1. У учеников 9А класса есть братья и сестры. У шестерых есть братья, а у пятерых — сестры. И только у двоих есть и те и другие. Угадайте, сколько таких ребят учатся в классе?
Решение: Изобразим два круга. В одном обозначим ребят, у которых есть братья, в другом — сестры. Поскольку у некоторых учеников есть и те, и другие, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как братья и сестры есть у двоих. В оставшейся части «братского» круга ставим цифру 4 (6 — 2 = 4). В свободной части «сестринского» круга ставим цифру 3 (5 — 2 = 3). А теперь рисунок сам подсказывает, что всего 4 + 2 + 3 = 9 человек.
Ответ. 9 учеников.
Уровень 2. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский (А), немецкий (Н), французский (Ф). 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
Решение. При решении данной задачи недостаточно метода «Круги Эйлера-Венна». Удобно применить составление уравнения по условию задачи, а круги Эйлера-Венна в данной задаче наглядно показывают решение А + Н = 34
Ф + Н = 25
Н = 6 По условию: А + Н = на 3 чел >, чем Ф + Н = х изучают одновременно 2 языка.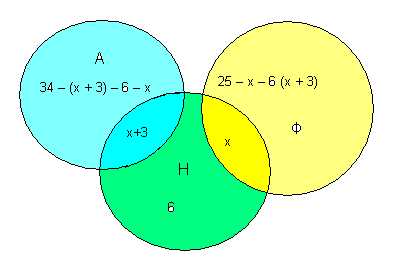
34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 – х – 3 = 40
– 2х = 40 – 34 + 3 – 25
– 2х = –10; х = 5
Ф + Н = 5 чел; А + Н = 8 чел; А = 34 – 8 – 6 – 5 =15 чел.
Н = 6 чел.; Ф =25 – 5 – 6 –8 = 6 чел.
Ответ: всего 40 человек.
infourok.ru