5. Производная сложной функции.
Теорема. Пусть функция 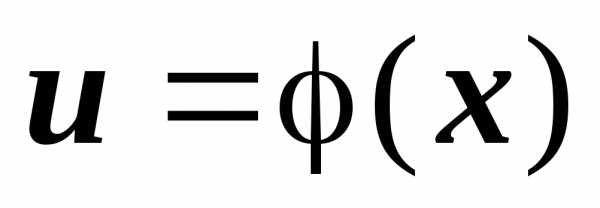 имеет в точкеxпроизводную
,
функция
имеет в точкеxпроизводную
,
функция 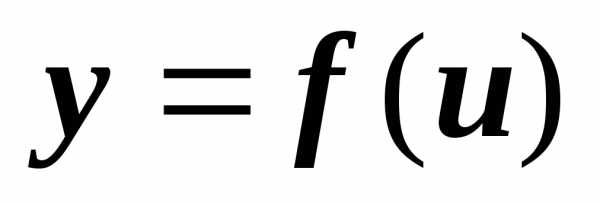 имеет в точкеuпроизводную
.
Тогда сложная функция
имеет в точкеxпроизводную,
равную произведению производных функций
имеет в точкеuпроизводную
.
Тогда сложная функция
имеет в точкеxпроизводную,
равную произведению производных функций 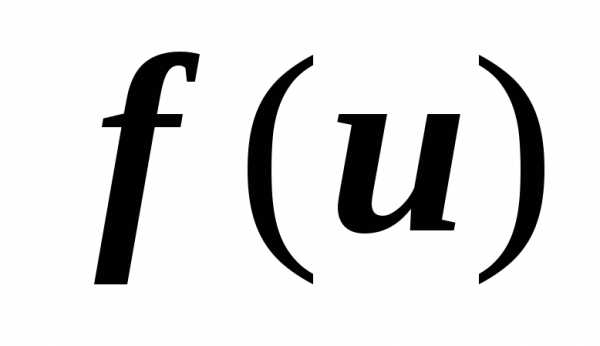 и
и 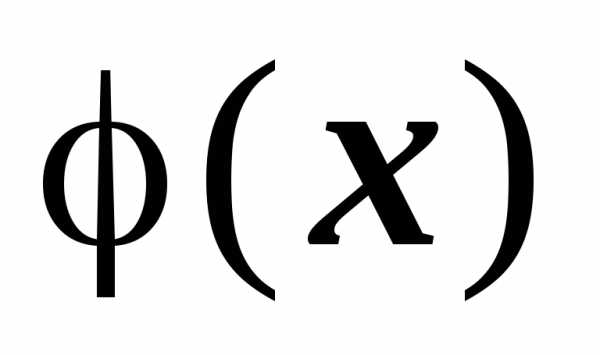 :
.Пример а) Найти производную функцииб) Найти производную функции
:
.Пример а) Найти производную функцииб) Найти производную функции
6. Неявная функция и ее дифференцирование.
Неявным заданием зависимости уотхназывается уравнение видаF(x,y) = 0, связывающее эти две переменные. Общая формула дляy‘(x), следующая из неявного уравнения
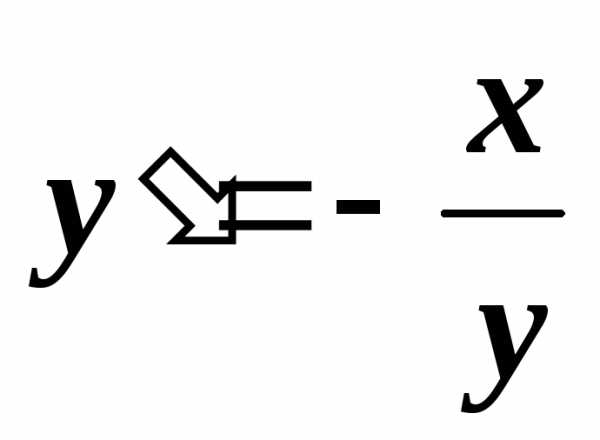 .
Производная найдена, она совпадает с
полученной в предыдущем разделе (с
учётом явного выражения).
.
Производная найдена, она совпадает с
полученной в предыдущем разделе (с
учётом явного выражения).7. Дифференцирование сложной показат ф-ии. Метод логариф дифф.
логарифмическое дифференцирование. Иногда проще продифференцировать логарифм данной функции, чем саму эту функцию. Это может быть, например, если функция представляет собой произведение большого числа сомножителей, или показательно-степенное выражение. Выведем формулу для производной показательно-степенной функции:
. Логарифмируем это выражение:. Дифференцируем обе части этого равенства пох, учитывая сложную зависимость отхв логарифмах:Окончательно:. Пример:
Показательная ф-я.Сложной показательной
функцией наз-ся ф-я, у кот и основание и
показатель степени является ф-ми от х.
Функция называется показательной, если
независимая переменная входит в
показатель степени, и степенной, если
переменная является основанием. Если
же и основание и показатель степени
зависят от переменной, то такая функция
будет показательно – степенной. Пустьu=f(x)
иv=g(x)
– функции, имеющие производные в точке
х,f(x)>0.
Найдем производную функцииy=uv.
Логарифмируя, получим:lny=vlnu,,, Пример.Найти
производную функции.
По полученной выше формуле получаем:Производные этих функций:
8. Обратная функция и ее дифференцирование, тригоном.
Пусть дана возрастающая или убыв ф-я y=f(x), определенная на интервале (a,b). Пустьf(a)=c,f(b)=d. Рассмотрим возрастающую ф-ю. Для х и у есть взаимное соответствие. Рассматривая у, как значение аргумента, а х – ф-ии, получаем х как ф-ю от у.х =g(у) – обратная ф-яy=f(x).(для убыв аналогично). Если возраст или убыв ф-яy=f(x) непрерывна на [a,b], причемf(a)=c,f(b)=d, то обратная ф-я определена и непрерывна на [c,d]. Если ф-ииy=f(x) их =g(у) являются взаимно обратными, то графиком явл одна и та же прямая.
Теорема. Пусть дляf(x):
1. выполняются условияТеор.5.6.5об
обратной функции(непрерывность и
строгая монотонность на отрезке [ a,b]).
2. в точкех0существует
неравная нулю производнаяf‘(х0).
Тогда обратная функциях =g(у)
в точкеу0= f(х0)
также имеет производную, равную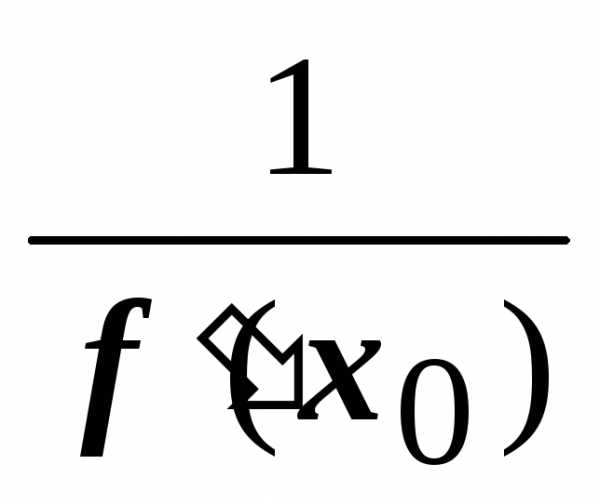 .
.
Док-во. Придадим переменнойуприращениеу0.
Тогда переменнаяхполучит
приращение
.
Вследствие строгой монотонностих0;
вследствие непрерывностих0у0. 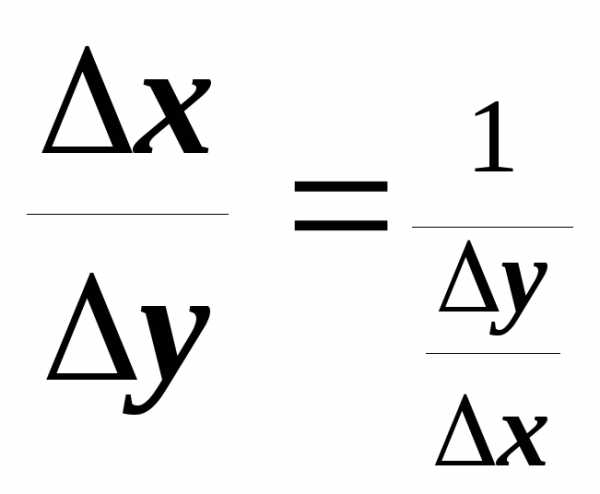 .
Устремиму0,
тогдах0
и, по условию теоремы, существует
(предел дроби), т.е.
.
Устремиму0,
тогдах0
и, по условию теоремы, существует
(предел дроби), т.е.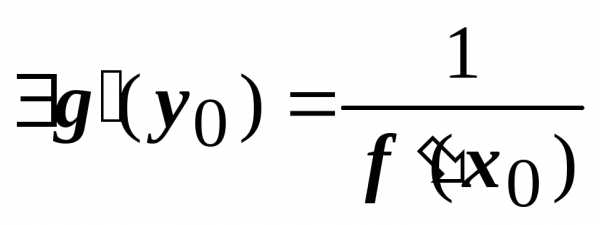 .
.
Итак, производные взаимно обратных
функций связаны соотношением 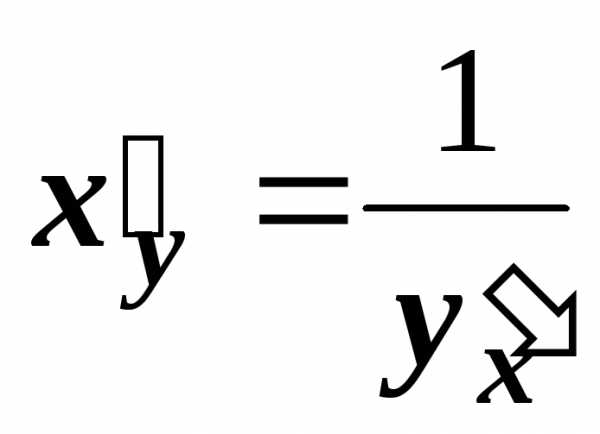
Применим эту формулу для вывода производных обратных тригонометрических функций.
1..
Обратная функция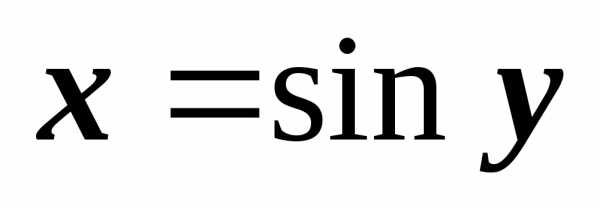 имеет производную
имеет производную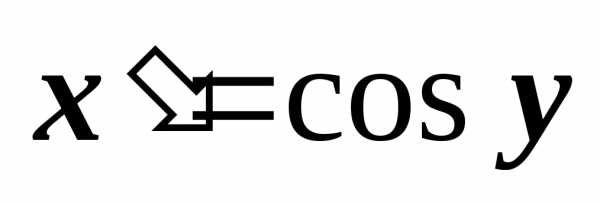 .
Так как,
получим:.
.
Так как,
получим:.
2.Для функциисовершенно аналогично получается .
.
studfiles.net
Производная сложной функции — Мегаобучалка
На данном уроке мы научимся находить производную сложной функции. Урок является логическим продолжением занятия Как найти производную?, на котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень или какие-нибудь моменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.
На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.
Смотрим в таблицу на правило (№5) дифференцирования сложной функции:
Разбираемся. Прежде всего, обратим внимание на запись . Здесь у нас две функции – и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию я буду называть внешней функцией, а функцию – внутренней (или вложенной) функцией
! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.
Для того, чтобы прояснить ситуацию, рассмотрим:
Пример 1
Найти производную функции
Под синусом у нас находится не просто буква «икс», а целое выражение , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
В данном примере уже из моих объяснений интуитивно понятно, что функция – это сложная функция, причем многочлен является внутренней функцией (вложением), а – внешней функцией.
Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.
В случае простых примеров вроде понятно, что под синус вложен многочлен . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
Представим, что нам нужно вычислить на калькуляторе значение выражения при (вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: , поэтому многочлен и будет внутренней функцией :
Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией:
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции .
Начинаем решать. С урока
Сначала находим производную внешней функции (синуса), смотрим на таблицу производных элементарных функций и замечаем, что . Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:
Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем.
Ну и совершенно очевидно, что
Результат применения формулы в чистовом оформлении выглядит так:
Далее мы берем производную внутренней функции, она очень простая:
Постоянный множитель обычно выносят в начало выражения:
Готово
Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.
Пример 2
Найти производную функцииЭто пример для самостоятельного решения (ответ в конце урока).
Пример 3
Найти производную функции
Как всегда записываем:
Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:
И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция:
Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения. Таким образом, результат применения правила дифференцирования сложной функции следующий:
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:
Готово.
Пример 4
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?
Пример 5
а) Найти производную функции
б) Найти производную функции
Пример 6
Найти производную функции
Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :
Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:
Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Пример 7
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного , но такое решение будет выглядеть как извращение забавно. Вот характерный пример:
Пример 8
Найти производную функции
Здесь можно использовать правило дифференцирования частного , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:
Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило :
Находим производную внутренней функции, косинус сбрасываем обратно вниз:
Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
Пример 9
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрешки, одна в другую, вложены сразу 3, а то и 4-5 функций.
Пример 10
Найти производную функции
Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения . Как бы мы считали на калькуляторе?
Сначала нужно найти , значит, арксинус – самое глубокое вложение:
Затем этот арксинус единицы следует возвести в квадрат :
И, наконец, семерку возводим в степень :
То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.
Начинаем решать
Согласно правилу сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции: Единственное отличие – вместо «икс» у нас сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий:
Под штрихом у нас снова сложная функция! Но она уже проще. Легко убедиться, что внутренняя функция – арксинус, внешняя функция – степень. Согласно правилу дифференцирования сложной функции сначала нужно взять производную от степени:
Теперь все просто, находим по таблице производную арксинуса и немного «причесываем» выражение:
Готово.
Пример 11
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
На практике правило дифференцирования сложной функции почти всегда применяется в комбинации с остальными правилами дифференцирования.
Пример 12
Найти производную функции
Сначала используем правило дифференцирования суммы , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу :
В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило :
Замечаем, что под некоторыми штрихами у нас находятся сложные функции , . Каламбур, но это простейшие из сложных функций, и при определенном опыте решения производных Вы будете легко находить их устно.
А пока запишем подробно, согласно правилу , получаем:
Готово.
! Обратите внимание на приоритет (порядок) применения правил: правило дифференцирования сложной функции применяется в последнюю очередь.
Пример 13
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Пожалуй, хватит на сегодня. Хочется еще привести пример с дробью и сложной функцией, но такой пример принципиально ничем не отличается от двух последних заданий, единственное отличие – вместо правила применяем правило .
Для закрепления темы рекомендую статью Сложные производные. Логарифмическая производная. Помимо рассмотрения дополнительных примеров, есть и новый материал! После изучения третьего урока вы будете очень уверенно себя чувствовать в ходе дальнейшего изучения математического анализа. Если задания покажутся слишком трудными (у всех разный уровень подготовки), то сначала посетите страницу Простейшие типовые задачи с производной, там рассмотрено ещё порядка 15-ти производных.
Желаю успехов!
Решения и ответы:
Пример 2:
Пример 4: Указание: перед дифференцированием необходимо перенести степень наверх, сменив у показателя знак .
Пример 7:
Пример 9:
Пример 11:
Пример 13:
megaobuchalka.ru
Производная сложной функции
⇐ ПредыдущаяСтр 5 из 11Следующая ⇒Рассмотрим суперпозицию двух функций: , где . В этом случае – называют промежуточным аргументом, – независимой переменной.
Функцию, заданную в виде суперпозиции функций, называют сложной функцией. Таким образом, прилагательное «сложная» характеризует не функцию, а способ ее задания.
Теорема (о дифференцировании сложной функции). Если функция дифференцируема в точке , а функция дифференцируема в соответствующей точке , то сложная функция дифференцируема в точке , причем
.
Последнее равенство можно записать в виде
.
Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
Физическая интерпретация формулы: производная есть скорость изменения переменной по отношению к изменению переменной , а производная – скорость изменения переменной по отношению к изменению переменной . Ясно, что скорость изменения переменной по отношению к изменению переменной равна произведению скоростей . (Если движется быстрее в раз, а – быстрее в раз, то движется быстрее в раз).
Правило нахождения производной сложной функции распространяется на композицию любого конечного числа функций. Например, если , т. е. если , то
.
Если функция, которую надо продифференцировать, не является сложной, то мы в сводке формул для вычисления производных будем полагать, что , т. е. – независимая переменная. Тогда (производная независимой переменной равна единице), и поэтому, применяя указанные формулы, умножать на не придется, так как такое умножение равносильно умножению на единицу, а, как известно, умножение на единицу не изменяет произведения.
Обычно путают степенную и показательную функции и совсем не знают степенно-показательной функции.
Функция называется степенной, если она имеет вид
,
где основание степени – переменная величина, показатель степени .
Например, . Здесь .
Функция называется показательной, если она имеет вид
,
где основание , а показатель – переменная величина.
Например, . Здесь .
Функция называется степенно-показательной, если она имеет вид
,
где основание и показатель – переменные величины.
Например, . Здесь .
| Производная степенной функции | Производная показательной функции |
Производная степенно-показательной функции состоит из суммы:
Поучитесь вычленять в сложной функции основные элементарные функции, которые ее составляют, и пользоваться правилом дифференцирования сложной функции.
Пример 1. Функция состоит из пяти основных элементарных функций, которые можно записать в виде цепочки простых функций таким образом:
.
Продифференцируем эту функцию по правилу
Продифференцируем каждую из основных элементарных функций:
.
Теперь подставим вместо их значения из цепочки и производная от сложной функции получена:
.
Так будет выглядеть результат дифференцирования без упрощения.
При дифференцировании рекомендуется сразу писать результат дифференцирования без введения промежуточных аргументов. Все промежуточные операции следует выполнять в уме.
Пример 2. Найти производную функции .
▲ В уме: – Функция состоит из пяти основных элементарных функций: степенная, котангенс, арккосинус, показательная и .
▼
При дифференцировании можно руководствоваться следующим правилом:
1. Все функции считать сложными.
2. Научиться определять основные элементарные функции и их промежуточные аргументы.
3. Умножать на производную основной элементарной функции по промежуточному аргументу до тех пор, пока в результате дифференцирования не будет получена .
Порядок дифференцирования обратный порядку вычисления значения функции в точке.
Вычисление значения функции начинается справа налево, а дифференцирование наоборот – слева направо.
Первой дифференцируется та основная элементарная функция, которая вычислялась бы последней – это самое главное!
Чтобы обратить ваше внимание на порядок дифференцирования, в следующем примере основные элементарные функции подчеркнуты в соответствии с их порядковым номером при дифференцировании.
Пример 3. Найти производную функции .
▲ . ▼
mykonspekts.ru
