График функции y = -e^x
Решение
$$f{\left (x \right )} = — e^{x}$$
График функции[LaTeX]
Точки пересечения с осью координат X[LaTeX]
График функции пересекает ось X при f = 0значит надо решить уравнение:
$$- e^{x} = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X Точки пересечения с осью координат Y
[LaTeX]
График пересекает ось Y, когда x равняется 0:подставляем x = 0 в -E^x.
$$- 1$$
Результат:
$$f{\left (0 \right )} = -1$$
Точка:
(0, -1)Экстремумы функции
[LaTeX]
Для того, чтобы найти экстремумы, нужно решить уравнение$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Первая производная
$$- e^{x} = 0$$
Решаем это уравнение
Решения не найдены,
возможно экстремумов у функции нет Точки перегибов
[LaTeX]
Найдем точки перегибов, для этого надо решить уравнение$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Вторая производная
$$- e^{x} = 0$$
Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет Горизонтальные асимптоты
[LaTeX]
Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo$$\lim_{x \to -\infty}\left(- e^{x}\right) = 0$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты слева:
$$y = 0$$
$$\lim_{x \to \infty}\left(- e^{x}\right) = -\infty$$
Возьмём предел
значит,
горизонтальной асимптоты справа не существует Наклонные асимптоты
[LaTeX]
Наклонную асимптоту можно найти, подсчитав предел функции -E^x, делённой на x при x->+oo и x ->-oo$$\lim_{x \to -\infty}\left(- \frac{e^{x}}{x}\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой справа
$$\lim_{x \to \infty}\left(- \frac{e^{x}}{x}\right) = -\infty$$
Возьмём предел
значит,
наклонной асимптоты справа не существует Чётность и нечётность функции
[LaTeX]
Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$- e^{x} = — e^{- x}$$
— Нет
$$- e^{x} = — -1 e^{- x}$$
— Нет
значит, функция
не является
ни чётной ни нечётной
www.kontrolnaya-rabota.ru
График функции y = 8*e^x
Решение
$$f{\left (x \right )} = 8 e^{x}$$
График функции[LaTeX]
Точки пересечения с осью координат X[LaTeX]
График функции пересекает ось X при f = 0значит надо решить уравнение:
$$8 e^{x} = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X Точки пересечения с осью координат Y
[LaTeX]
График пересекает ось Y, когда x равняется 0:подставляем x = 0 в 8*E^x.
$$8 e^{0}$$
Результат:
$$f{\left (0 \right )} = 8$$
Точка:
(0, 8)Экстремумы функции
[LaTeX]
Для того, чтобы найти экстремумы, нужно решить уравнение$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Первая производная
$$8 e^{x} = 0$$
Решаем это уравнение
Решения не найдены,
возможно экстремумов у функции нет Точки перегибов
[LaTeX]
Найдем точки перегибов, для этого надо решить уравнение$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Вторая производная
$$8 e^{x} = 0$$
Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет Горизонтальные асимптоты
[LaTeX]
Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo$$\lim_{x \to -\infty}\left(8 e^{x}\right) = 0$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты слева:
$$y = 0$$
$$\lim_{x \to \infty}\left(8 e^{x}\right) = \infty$$
Возьмём предел
значит,
горизонтальной асимптоты справа не существует Наклонные асимптоты
[LaTeX]
Наклонную асимптоту можно найти, подсчитав предел функции 8*E^x, делённой на x при x->+oo и x ->-oo$$\lim_{x \to -\infty}\left(\frac{8 e^{x}}{x}\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой справа
$$\lim_{x \to \infty}\left(\frac{8 e^{x}}{x}\right) = \infty$$
Возьмём предел
значит,
наклонной асимптоты справа не существует Чётность и нечётность функции
[LaTeX]
Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$8 e^{x} = 8 e^{- x}$$
— Нет
$$8 e^{x} = — 8 e^{- x}$$
— Нет
значит, функция
не является
ни чётной ни нечётной
www.kontrolnaya-rabota.ru
График функции y = 1/(1+e^x)
Решение
$$f{\left (x \right )} = \frac{1}{e^{x} + 1}$$
График функции[LaTeX]
Точки пересечения с осью координат X[LaTeX]
График функции пересекает ось X при f = 0значит надо решить уравнение:
$$\frac{1}{e^{x} + 1} = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X Точки пересечения с осью координат Y
[LaTeX]
График пересекает ось Y, когда x равняется 0:подставляем x = 0 в 1/(1 + E^x).
$$\frac{1}{1 + e^{0}}$$
Результат:
$$f{\left (0 \right )} = \frac{1}{2}$$
Точка:
(0, 1/2)Экстремумы функции
[LaTeX]
Для того, чтобы найти экстремумы, нужно решить уравнение$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Первая производная
$$- \frac{e^{x}}{\left(e^{x} + 1\right)^{2}} = 0$$
Решаем это уравнение
Решения не найдены,
возможно экстремумов у функции нет Точки перегибов
[LaTeX]
Найдем точки перегибов, для этого надо решить уравнение$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Вторая производная
$$\frac{e^{x}}{\left(e^{x} + 1\right)^{2}} \left(-1 + \frac{2 e^{x}}{e^{x} + 1}\right) = 0$$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = 0$$
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
[0, oo)
Выпуклая на промежутках
(-oo, 0]Горизонтальные асимптоты
[LaTeX]
Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo$$\lim_{x \to -\infty} \frac{1}{e^{x} + 1} = 1$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты слева:
$$y = 1$$
$$\lim_{x \to \infty} \frac{1}{e^{x} + 1} = 0$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты справа:
$$y = 0$$ Наклонные асимптоты
[LaTeX]
Наклонную асимптоту можно найти, подсчитав предел функции 1/(1 + E^x), делённой на x при x->+oo и x ->-oo$$\lim_{x \to -\infty}\left(\frac{1}{x \left(e^{x} + 1\right)}\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой справа
$$\lim_{x \to \infty}\left(\frac{1}{x \left(e^{x} + 1\right)}\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой слева Чётность и нечётность функции
[LaTeX]
Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$\frac{1}{e^{x} + 1} = \frac{1}{1 + e^{- x}}$$
— Нет
$$\frac{1}{e^{x} + 1} = — \frac{1}{1 + e^{- x}}$$
— Нет
значит, функция
не является
ни чётной ни нечётной
www.kontrolnaya-rabota.ru
График функции y = e^(-3*x)
Решение
$$f{\left (x \right )} = e^{- 3 x}$$
График функции[LaTeX]
Точки пересечения с осью координат X[LaTeX]
График функции пересекает ось X при f = 0значит надо решить уравнение:
$$e^{- 3 x} = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X Точки пересечения с осью координат Y
[LaTeX]
График пересекает ось Y, когда x равняется 0:подставляем x = 0 в E^(-3*x).
$$e^{- 0}$$
Результат:
$$f{\left (0 \right )} = 1$$
Точка:
(0, 1)Экстремумы функции
[LaTeX]
Для того, чтобы найти экстремумы, нужно решить уравнение$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Первая производная
$$- 3 e^{- 3 x} = 0$$
Решаем это уравнение
Решения не найдены,
возможно экстремумов у функции нет Точки перегибов
[LaTeX]
Найдем точки перегибов, для этого надо решить уравнение$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Вторая производная
$$9 e^{- 3 x} = 0$$
Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет Горизонтальные асимптоты
[LaTeX]
Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo$$\lim_{x \to -\infty} e^{- 3 x} = \infty$$
Возьмём предел
значит,
горизонтальной асимптоты слева не существует
$$\lim_{x \to \infty} e^{- 3 x} = 0$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты справа:
$$y = 0$$ Наклонные асимптоты
[LaTeX]
Наклонную асимптоту можно найти, подсчитав предел функции E^(-3*x), делённой на x при x->+oo и x ->-oo$$\lim_{x \to -\infty}\left(\frac{1}{x} e^{- 3 x}\right) = -\infty$$
Возьмём предел
значит,
наклонной асимптоты слева не существует
$$\lim_{x \to \infty}\left(\frac{1}{x} e^{- 3 x}\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой слева Чётность и нечётность функции
[LaTeX]
Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$e^{- 3 x} = e^{3 x}$$
— Нет
$$e^{- 3 x} = — e^{3 x}$$
— Нет
значит, функция
не является
ни чётной ни нечётной
www.kontrolnaya-rabota.ru
Число e. Функция y=e^x, ее свойства, график, дифференцирование
Дополнительные сочиненияНа данном уроке мы определим число е. Выясним свойства функции 〖y= e〗^x, построим график, и научимся ее дифференцировать. Также разберем несколько примеров классических задач, в которых используется число е.
1. Повторение основных свойств функции y=e^x,
Напомним, что показательной называется функция вида . График выглядит так:
Рис. 1. График показательной функции
График функции возрастает, если ; если основание лежит в пределах то функция убывает.
Вспомним основные свойства.
1. . x может принимать любые действительные значения;
2. может принимать любые положительные значения;
3. Графики всех функций при любом значении проходят через эту точку;
4. Функция возрастает, если ;
5. Функция убывает, если .
Итак, мы вспомнили, что такое показательная функция и каковы ее основные свойства.
2. Определение числа e
Число
Рассмотрим две конкретные показательные функции с основанием
Вот график функции :
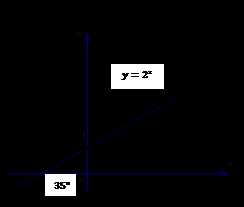
Рис. 2. График функции
Вот график функции :
Рис. 3. График функции
В точке , если проведем касательную к одному и второму графику, обнаружим, что касательная к первому графику наклонена к оси примерно на (меньше ).
Во втором случае касательная наклонена к оси примерно на (больше ).
Предполагаем, и вообще это доказано, что существует между основаниями такое число , что график имеет касательную в точке , которая наклонена к оси ровно на .
Рис. 4. Касательная к графику функции
Итак, в первом случае касательная наклонена под углом меньше , во втором случае касательная наклонена под углом больше . И, оказывается, есть такое число , что касательная в точке наклонена к оси под углом ровно Это число , во-первых, расположено и, во-вторых, иррационально. Вот выписано несколько десятичных знаков этого числа: . Таким образом, мы ввели очень важное число
Теперь рассмотрим свойства показательной функции с основанием
3. Свойства функции y=e
График функции выглядит так:
Рис. 5. График функции
Свойства аналогичны свойствам функции с основанием:
;
Функция возрастает;
Функция не ограничена сверху, но ограничена снизу;
Не существует ни наибольшего ни наименьшего значений;
Функция непрерывна;
Принимает все значения, когда ;
Функция выпукла вниз;
Функция дифференцируема. Что это значит практически? Что касательную к экспоненте можно провести в любой точке.
Таковы свойства данной функции.
4. Производная функции
Поговорим о производной этой функции. Что мы на данный момент о ней знаем и без доказательства понимаем?
Мы говорили, что функция дифференцируема. Это значит, что касательная в любой точке существует, то есть производная существует в любой точке. Но как ее найти? Мы знаем, что производная в точке Доказан важный факт:
При любом действительном значении То есть отсюда видна особенность числа . Производная, то есть скорость роста функции в точке равна значению функции в этой же точке. Это основная формула, которая позволит нам дифференцировать все показательные функции.
5. Некоторые типовые задачи
Теперь рассмотрим некоторые типовые задачи на производную функции
Пример 1.
Дано:
Найти: Производную
Решение.
Вот основная формула , мы умеем дифференцировать сложную функцию.
Ответ:=
Пример 2.
Дано:
Найти: Производную
Решение.
По тем же правилам, по которым мы дифференцируем все функции, продифференцируем и эту.
Ответ:=
Итак, зная основную формулу , мы можем решать примеры на нахождение производных.
6. Задача на касательную
Следующая стандартная задача на касательную.
Пример 3.
Дано:, абсцисса точки касания;
Найти: Уравнение касательной к данной кривой с абсциссой в .
Решение.
Вспоминаем уравнение касательной и стандартную методику ее построения:
Какие действия нужно сделать, чтобы составить уравнение касательной?
Найти координаты точки касания:
Итак, точка с координатами – это точка касания (рис. 6).
Рис. 6. Точка касания
Найти производную в любой точке
Найти конкретное значение производной в точке :
У нас все есть, чтобы заполнить уравнение касательной.
Заполняем, получаем:
Ответ:
Небольшой анализ:
Тангенс угла наклона
Ордината пересечения точки с осью :
Задача решена.
7. Задача на нахождение наименьшего значения функции
Пример 4.
Найти наименьшее значение функции.
Решение.
Имеем производную произведения:
Приравниваем производную к нулю и убеждаемся, что , так как по свойству показательной функции всегда больше нуля.
Итак, имеем единственную критическую точку (рис. 7).
Рис. 7. Критическая точка
Если , то и функция убывает. Если , то .
Мы уже говорили, что – единственная критическая точка. Посчитаем значение функции в ней:
Рис. 8. Точка наименьшего значения функции
И получаем ответ: наименьшее значение функции достигается в точке . Рис. 8.
Ответ:
Итак, мы познакомились с числом , показательной функцией с основанием . На следующем уроке мы рассмотрим логарифмическую функцию с основанием .
Список литературы
Мордкович А. Г. Алгебра и начала математического анализа. – М.: Мнемозина. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа. – М.: Дрофа. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Uztest. ru . Schoolife. ru . Terver. ru .
Домашнее задание
1. Найти производные функция в указанных точках:
а) ;
б) .
2. Найдите тангенс угла наклона касательной к графику функции в точке с абсциссой :
а) ;
б) .
3. Алгебра и начала анализа, Мордкович А. Г.: № 1616, 1618, 1621, 1624.
dp-adilet.kz
Число е. Функция y=e^x ее свойства, график, дифф.
Вопросы занятия:
• рассмотреть число е как основание показательной функции;
• рассмотреть функцию y = ex, её свойства, график и производную.
Материал урока
Прежде чем перейти к изучению нового материала, давайте вспомним основные свойства и график показательной функции.
Давайте рассмотрим график функции:
Проведем касательную к точке x = 0.
Если строить точно, а затем измерить угол между касательной и положительным направлением оси Ox, то можно убедиться в том, что:
Теперь давайте построим график функции:
Проведем касательную к точке x = 0.
Если измерить этот угол, то получится:
Если же мы построим график функции:
Проведем касательную к точке x = 0.
Измерим получившийся угол, то получим:
То есть:
То есть, логично предположить, что есть такое основание а, для которого соответствующий угол между касательной к точке x = 0 и осью абсцисс равен 45°.
Очевидно, что это основание заключено в промежутке от 2 до 3.
Было доказано, что такое число существует, его принято обозначать буквой е. Установлено, что число е – иррациональное, то есть представляет собой бесконечную десятичную непериодическую дробь:
На практике обычно полагают:
Существует множество способов запоминания несколько первых знаков после запятой числа е.
Изобразим график этой функции:
Ее отличие от остальных экспонент будет только в том, что угол между касательной к графику в точке x = 0 и осью абсцисс равен 45°.
По графику легко записать основные свойства функции игрек равно е в степени икс.
Без доказательства примем, что:
Рассмотрим несколько примеров.
Пример.
Рассмотрим еще один пример.
Рассмотрим еще один пример.
Давайте еще раз повторим основные свойства функции:
Исследовать и построить график функции y=x*e^x Помогите, кто чем может) Плиииииз
1. область определения — любое число 2. Не является ни четной, ни нечетной 3. Не является периодической 4. Асимптота одна горизонтальная у=0 (см. ниже) 4. точки экстремума y’ = e^x+x*e^x=e^x*(1+x) надо приравнять производную к и найти точки экстремума. y’ = 0 => x=-1единственная точка экстремума, у (-1)=-1/е=0,37 На числовой оси отметить эту точку и расставить знаки производной на двух получившихся интервалах: от (-беск. ) до (-1) знак «-«, значит функция убывает, от (-1) до (+беск) знак «+», значит функция возрастает, х=-1 точка минимума 6. Вторая производная и точки перегиба y» = e^x*(1+x)+e^x=e^x*(x+2) Аналогично, точка перегиба одна: х=-2, до нее знак второй производной «-«, функция выпукла вверх, после нее знак «+», функция выпукла вниз. у (-2)=-2/(е^2)=-0,27 7. Точки пересечения с осями координат она одна: (0,0) 8. ГРАФИК: <img src=»//otvet.imgsmail.ru/download/bee8afa680b85239daf876dbcc3464b0_i-47.jpg» >
Найти производные следующих функций: y=arcsin /x
touch.otvet.mail.ru
