Область значений функции как определить: виды, свойства, примеры решения задач

Функции. Понятие. Множество значений. Область определения. Свойства функции.

Функция — зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y.

1) Область определения функции и область значений функции.

Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.

Область значений функции — это множество всех действительных значений y, которые принимает функция.

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.

7) Периодическость функции.

Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.

Общий вид функции Преобразования

y = f(x − a) Параллельный перенос графика вдоль оси абсцисс на | a | единиц

вправо, если a > 0;

влево, если a < 0.

y = f(x) + a Параллельный перенос графика вдоль оси ординат на | a | единиц

вверх, если a > 0,

вниз, если a < 0.

y = f( − x) Симметричное отражение графика относительно оси ординат.

y = − f(x) Симметричное отражение графика относительно оси абсцисс.

y = f(kx) При k > 1 — сжатие графика к оси ординат в k раз,

при 0 < k < 1 — растяжение графика от оси ординат в 1 / k раз.

y = kf(x) При k > 1 — растяжение графика от оси абсцисс в k раз,

при 0 < k < 1 — cжатие графика к оси абсцисс в 1 / k раз.

y = | f(x) | При — график остаётся без изменений,

при f(x) < 0 — график симметрично отражается относительно оси абсцисс.

y = f( | x | ) При — график остаётся без изменений,

при x < 0 — график симметрично отражается относительно оси ординат.

определение диапазона+функции+а+по The Free Dictionary

Диапазон+функции+а+ — определение диапазона+функции+а+по The Free Dictionary

Range+of+a+function — определение диапазона+of+a+функции в The Free Dictionary

---

Слово, не найденное в Словаре и Энциклопедии.

Пожалуйста, попробуйте слова отдельно:

диапазон из а функция

Некоторые статьи, соответствующие вашему запросу:

Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.

Полный браузер ?

• ▲
• диапазон жесткости
• диапазон жесткости
• диапазон жесткости
• Диапазон Штормер
• проблесковый маячок
• Центр поддержки ассортимента
• дальность наблюдения
• развертка диапазона
• Трансформационная лаборатория Range Systems
• Таблица диапазонов
• Блок регулирования температуры диапазона
• Тендер для ассортимента
• Верхняя часть диапазона
• Верхняя часть диапазона
• Верхняя часть диапазона
• Range Township, округ Мэдисон, штат Огайо
• Система отображения дальности действия
• Секция обслуживания полигона для тренировок
• Офицер полигона
• Диапазонный блок

• Диапазон Версия Класс Класс
• Выбор диапазона
• Диапазон войны
• Диапазон, где применимо
• Диапазон во время поиска
• дальность ветра
• Крыло диапазона
• Диапазон работы
• нулевой диапазон
• зона дальности
• диапазон+функции+а+
• Диапазон, азимут, высота
• Диапазон, Эфемериды, GMT
• дисплей диапазона-амплитуды
• указатель дальности
• Диапазон-азимут-высота
• Ограничение диапазона
• Критерий изменения границы диапазона
• Транспортир дальности отклонения
• Диапазонно-доплеровская интерферометрия
• Дальномер

• Дальномер
• Импульсный допплер со стробированием по дальности
• Шаговая частота со стробированием по диапазону
• Индикатор диапазона-высоты
• Индикатор дальности-высоты
• дальномерный датчик
• диапазон в
• упражнение на диапазон движений (ROM)
• упражнение на диапазон движений
• упражнение на диапазон движений
• упражнение на диапазон движений
• упражнение на диапазон движений
• упражнение на диапазон движений
• упражнение на диапазон движения ROM
• Система корреляции только диапазона
• Радар только для дальнего действия
• Система слежения за дальностью полета
• дальнобойный
• дальнобойный
• дальнобойный
• ▼

Сайт: Следовать:

Делиться:

Открыть / Закрыть

 

Домен и диапазон функции – объяснение и примеры

В этой статье объясняются домен и диапазон среднего значения функции, а также способы расчета этих двух величин. Прежде чем перейти к теме домена и диапазона, давайте кратко опишем, что такое функция.

В математике мы можем сравнить функцию с машиной, которая генерирует некоторый результат в соответствии с данным вводом . На примере машины для чеканки монет мы можем проиллюстрировать значение функции следующим образом.

Когда вы вставляете монету в монетоштамповочную машину, в результате получается отштампованный и сплющенный кусок металла. Рассматривая функцию, мы можем связать монету и сплющенный кусок металла с доменом и диапазоном. В этом случае функцией считается машина для чеканки монет.

Точно так же, как машина для чеканки монет, которая может производить только один сплющенный кусок металла за раз, функция работает таким же образом, выдавая один результат за раз.

История функции

Идея функции была введена в начале семнадцатого века, когда Рене Декарт (1596-1650) использовал эту концепцию в своей книге «Геометрия» (1637) для моделирования математических задач.

Пятьдесят лет спустя, после публикации «Геометрии», Готфрид Вильгельм Лейбниц (1646–1716) ввел термин «функция». Позже Леонард Эйлер (1707-1783) сыграл большую роль, введя технику понятия функции, y = f (x).

Применение функции в реальной жизни

Функции очень полезны в математике, поскольку они позволяют нам моделировать реальные проблемы в математическом формате.

Вот несколько примеров применения функции.

Длина окружности зависит от ее диаметра или радиуса. Мы можем математически представить это утверждение как:

C(d) =dπ или C(r)=2π⋅r

• Тень

Длина тени объекта является функцией его высоты.

Местоположение движущегося объекта, например автомобиля, зависит от времени.

• Температура

Температура тела зависит от нескольких факторов и исходных данных.

• Деньги

Сложный или простой процент зависит от времени, основной суммы и процентной ставки.

• Высота объекта

Высота объекта зависит от его/ее возраста и массы тела.

Узнав о функции, теперь можно перейти к вычислению домена и диапазона функции.

Что такое домен и диапазон функции?

Домен функции — это входные числа, которые при подключении к функции определяют результат. Проще говоря, мы можем определить область определения функции как возможные значения x, которые сделают уравнение верным.

Некоторые из случаев, когда функция не будет работать, — это когда уравнение делится на ноль или отрицательный квадратный корень.

Например, f( x ) =  x ² — допустимая функция, поскольку независимо от того, какое значение x можно подставить в уравнение, всегда есть правильный ответ. По этой причине мы можем заключить, что областью определения любой функции являются все действительные числа.

Диапазон функции определяется как набор решений уравнения для данного входа. Другими словами, диапазон — это результат или значение y функции. Для данной функции существует только один диапазон.

Как использовать обозначения интервалов для указания домена и диапазона?

Поскольку диапазон и область значений функции обычно выражаются в виде интервалов, важно обсудить концепцию представления интервалов.

Процедура записи интервалов включает:

• Запишите числа, разделенные запятой, в порядке возрастания.
• Заключите числа в круглые скобки (), чтобы показать, что значение конечной точки не включено.
• Используйте квадратные скобки [] для заключения чисел, когда включено значение конечной точки.

Как найти домен и диапазон функции?

Мы можем определить область определения функции либо алгебраическим, либо графическим методом. Чтобы вычислить область определения функции алгебраически, вы решаете уравнение для определения значений x.

Различные типы функций имеют свои методы определения области определения.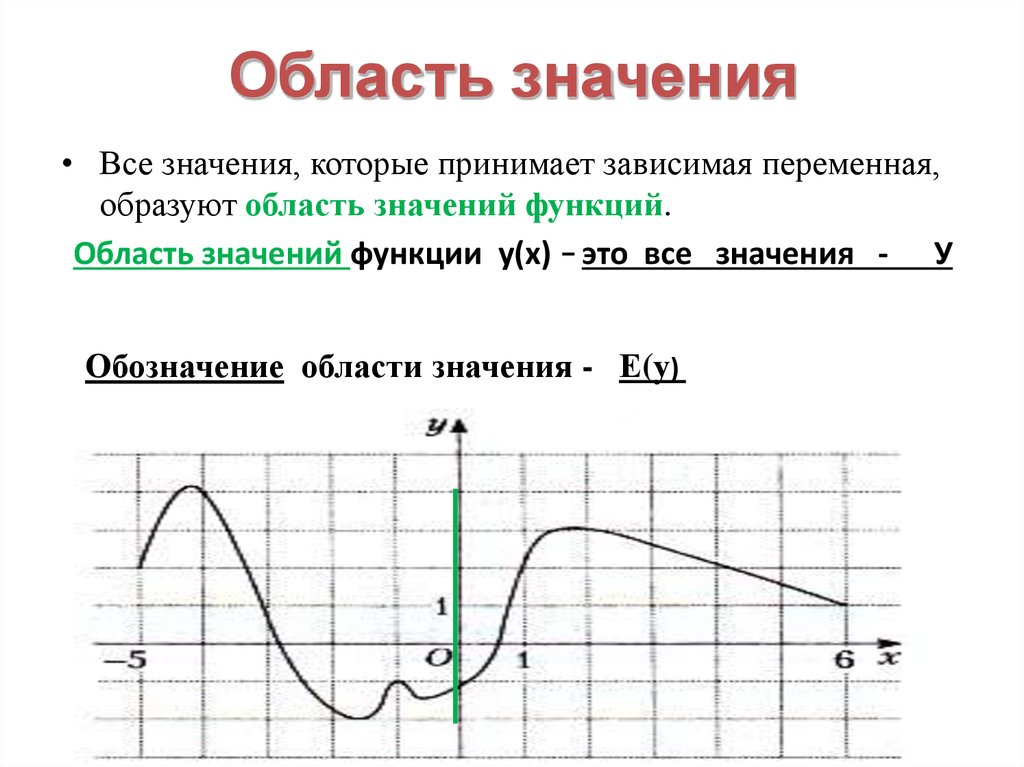

Давайте рассмотрим эти типы функций и то, как вычислить их домен.

Как найти область определения функции без знаменателя и радикалов?

Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.

Пример 1

Найдите область определения f (x) = 5x − 3 ∞)

Диапазон: (−∞, ∞)

Функция с радикалом

Пример 2

Найти область определения функции f(x)=−45×2 90 + 12x + 5

Решение

Функция f(x) = −2x ² + 12x + 5 является квадратичным полиномом, следовательно, областью определения является (−∞, ∞)

Как найти область определения рациональной функции с переменной в знаменателе?

Чтобы найти область определения функции этого типа, приравняйте знаменатель к нулю и вычислите значение переменной.

Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.

Пример 3

Определить область определения x−4/ (x ² −2x−15)

Решение

Приравнять знаменатель к нулю и найти x

− 5x 4 x 2 (x − 5) (x + 3) = 0

Следовательно, x = −3, x = 5

Чтобы знаменатель не был равен нулю, нам нужно избегать чисел −3 и 5. Следовательно, область определения все действительные числа, кроме −3 и 5.

Пример 4

Вычислите область определения и диапазон функции f(x) = -2/x.

Решение

Установите знаменатель равным нулю.

⟹ x = 0

Следовательно, домен: все действительные числа, кроме 0.

Диапазоном являются все действительные значения x, кроме 0.

Пример 5

Найдите домен и диапазон следующей функции .

f(x) = 2/(x + 1)

Решение

Приравняйте знаменатель к нулю и найдите x.

х + 1 = 0

= -1

Поскольку при x = -1 функция не определена, областью определения являются все действительные числа, кроме -1. Точно так же диапазоном являются все действительные числа, кроме 0

. Как определить домен для функции с переменной внутри подкоренного знака?

Чтобы найти область определения функции, члены внутри корня задают неравенство > 0 или ≥ 0. Затем определяется значение переменной.

Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.

Пример 6

Найдите область определения f(x) = √ (6 + x – x ² )

Решение

Чтобы избежать квадратных корней из отрицательных чисел, мы устанавливаем выражение внутри знака радикала на ≥ 0.

6 + x – x ² ≥ 0 ⟹ x ² – x – 6≤ 0

⟹ x ² – x – 6= (x – 3) (x +2) = 0

Следовательно, функция равна нулю, если x = 3 или x = -2

Следовательно, домен: [−2, 3]

Пример 7

Найти область определения f(x) =x/√ (x ² – 9)

Решение

Придать выражению под знаком радикала значение x ² – 91 > 0 90 переменная, которую нужно получить;

x = 3 или – 3

Следовательно, область определения: (−∞, −3) & (3, ∞)

Пример 8

Найдите область определения f(x) = 1/√ ( x ²  -4)

Решение

Разлагая знаменатель на множители, получаем x ≠ (2, – 2).

Проверьте свой ответ, подставив -3 в выражение перед знаком корня.

⟹ (-3) ²  – 4 = 5

также попробуйте с нулем

⟹ 0 ²  – 4 = -4, поэтому числа между 2 и -2 недействительны

9005

Попробуйте число выше 0 2 ⟹ 3 ²  – 4 = 5. Это верно.

Следовательно, область определения = (-∞, -2) U (2, ∞)

Как найти область определения функции с помощью натурального логарифма (ln)?

Чтобы найти область определения функции с помощью натурального логарифма, присвойте членам в скобках значение >0, а затем решите.

Давайте рассмотрим пример ниже, чтобы понять этот сценарий. Пример 9 + 8

⟹ x > 8

Домен:(8, ∞)

Как найти домен и диапазон отношения?

Отношение — это актив координат x и y. Чтобы найти домен и диапазон в отношении, просто перечислите значения x и y соответственно.

Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.

Пример 10

Укажите область определения и область значений отношения {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3) }

Решение

Список значений x.