Тангенс посчитать: Тангенс угла tg(α) | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Расчет и нанесение уклона на обмерных чертежах » Лазерное сканирование и архитектурные обмеры в Санкт-Петербурге | НПП «Фотограмметрия»

С необходимостью посчитать уклон постоянно сталкиваются проектировщики, строители, архитекторы, а также люди ряда других профессий, в силу того, что на земной поверхности очень трудно найти идеально ровный участок. Уклон выражается в градусах или в процентах. Обозначение в градусах показывает угол кривизны поверхности. Но уклон может быть представлен и в виде тангенса этого угла, умноженного на 100%.

Как рассчитать уклон поверхности?
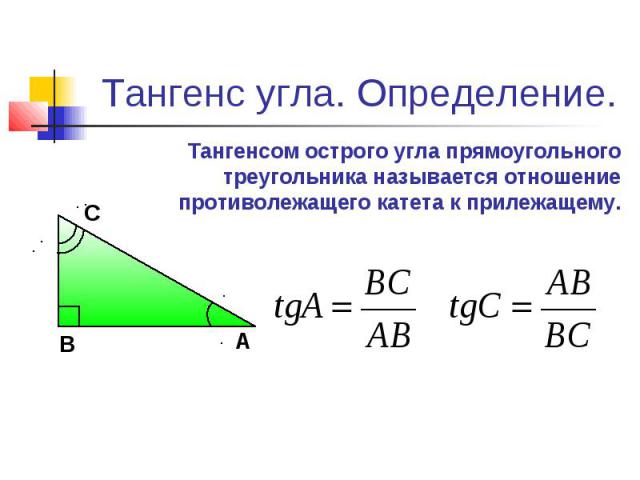
Уклон – это отношение превышения (ВС) к заложению (АС) и обозначается в текстовых документах буквой i.
Например, i=1:6

Разделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам нужно получить уклон в процентах, умножьте полученное число на 100%. Чтобы получить уклон в промилле, умножьте результат деления на 1000‰.

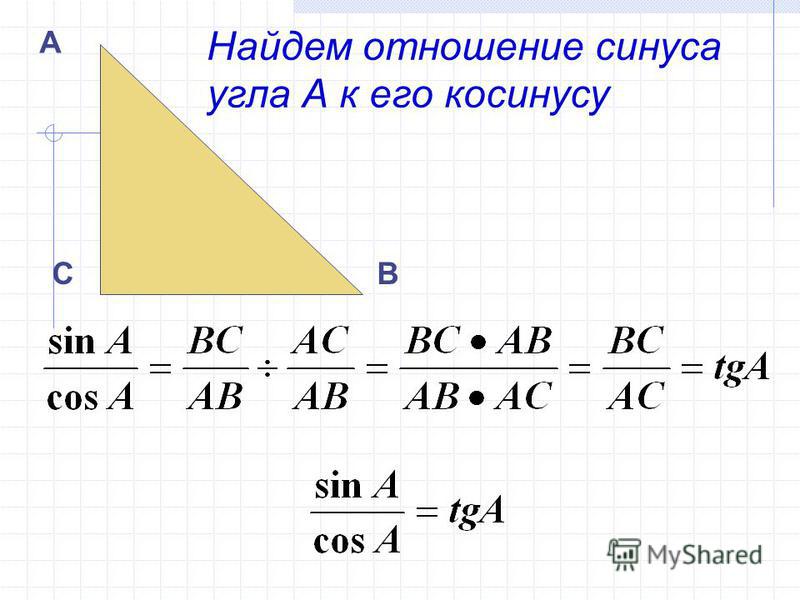
Если вам необходимо получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов результат – тангенс угла наклона.

Посчитайте его арктангенс при помощи инженерного калькулятора, в результате вы получите значение уклона в градусах.

На видах (фасадах), разрезах, сечениях и схемах перед размерным числом, определяющим величину уклона, наносят знак , острый угол которого должен быть направлен в сторону уклона.
Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
На планах направление уклона плоскостей указывают стрелкой, на которой, при необходимости, проставляют величину уклона (см.рис.).

Построение и обозначение уклона. Пример изображения уклона на планах.

Величину уклона (тангенс угла наклона) указывают в виде простой или десятичной дроби с точностью до третьего знака.

Уклон (в строительстве) — показатель крутизны склона (а также ската кровли).

Укло́н (в геодезии) — показатель крутизны склона; отношение превышения местности к горизонтальному проложению, на котором оно наблюдается.

Иными словами, величина уклона равна тангенсу угла между поверхностью склона и горизонталью.

Уклон поверхности равен тангенсу угла α, tgα = h/l — отношение перпендикуляра, опущенного из точки поверхности на прямую поверхность, к длине прямой поверхности от начала склона (при вершине угла α) до перпендикуляра.

Например, подъёму 12 м на 100 м перемещения по горизонтали соответствует уклон, равный 0,12 (12 % или 120 ‰).
При чтении нотации знак «%» произносится «сотых», а «‰» — «тысячных».

Источник:

книга: Единые требования по выполнению строительных чертежей.
М.: Изд-во «Архитектура-С», 2004.
Справочное пособие.
Автор: Георгиевский О.В.

Аннотация:
Справочное пособие по строительному черчению для студентов средних и высших учебных заведений. Пособие выполнено в соответствии с требованиями ГОСТов.

Настоящее справочное пособие выполнено в соответствии с требованиями ГОСТов ЕСКД (Единой системы конструкторской документации) и СПДС (Системы проектной документации для строительства).
Пособие может быть использовано при выполнении заданий по архитектурно-строительному черчению, а также при выполнении курсовых и дипломных проектов студентами всех строительных специальностей средних и высших учебных заведений.

Распечатать

Коэффициент наклона прямой

Что такое линейная функция и как выглядит ее график мы подробно разбирали здесь.

В этой статье мы остановимся на том, как находить коэффициент наклона прямой.

Как мы знаем, уравнение прямой имеет вид . В этом уравнении коэффициент при отвечает за наклон прямой и называется коэффициентом наклона. Он равен тангенсу угла между прямой и положительным направлением оси .

Внимание! Не просто между прямой и осью , а именно между прямой и положительным направлением оси .

Например, в прямой коэффициент наклона равен , в прямой  коэффициент наклона равен .

В уравнении прямой  слагаемое, содержащее отсутствует, следовательно, коэффициент при  равен нулю. Угол наклона этой прямой к оси  равен нулю — прямая  параллельна оси .

 

Если прямая наклонена вправо, то угол между прямой и положительным направлением оси — острый, соответственно, тангенс этого угла больше нуля, и коэффициент .

Например:

Здесь

Если прямая наклонена влево, то угол между прямой и положительным направлением оси — тупой, соответственно, тангенс этого угла меньше нуля, и коэффициент :

Здесь .

Решим две задачи на нахождение коэффициента наклона прямой.

1. Най­ди­те уг­ло­вой ко­эф­фи­ци­ент пря­мой, про­хо­дя­щей через точки с ко­ор­ди­на­та­ми (-1;-1) и (1;3).

Решим эту задачу  двумя способами.

А). Так как прямая проходит через точки (-1;-1) и (1;3), координаты этих точек удовлетворяют уравнению прямой . То есть если мы координаты каждой точки подставим в уравнение прямой, то получим верное равенство. Так как у нас две точки, получаем систему:

или

Вычтем из второго уравнения первое, и получим , отсюда .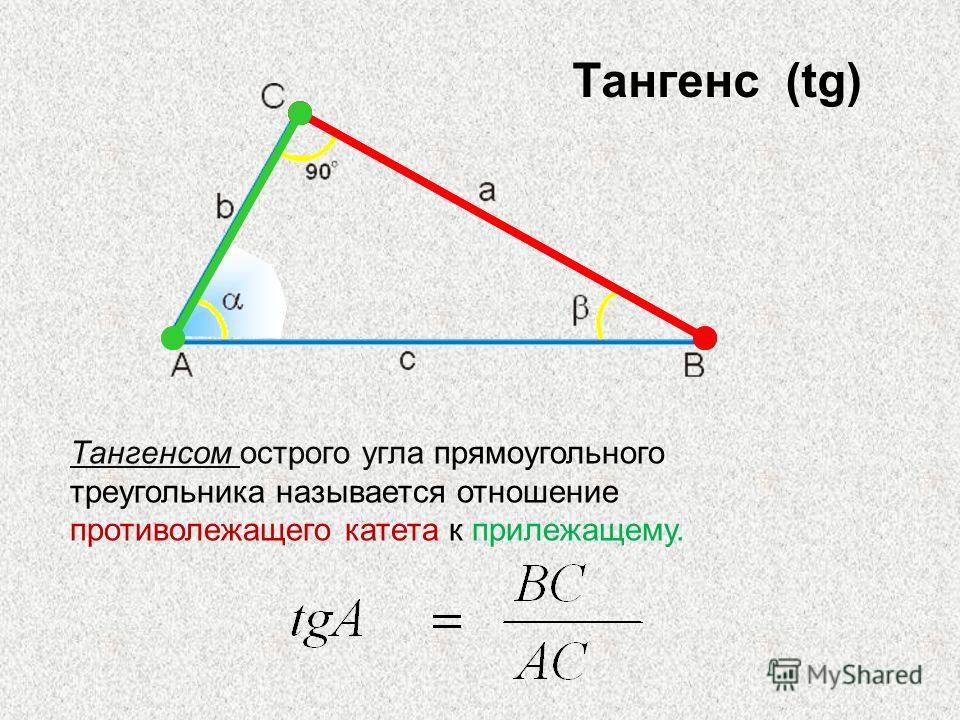

Б). Построим график этой функции. Для этого нанесем данные точки А(-1;-1) и В(1;3) на координатную плоскость и проведем через них прямую:

Коэффициент равен тангенсу угла наклона между прямой и положительным направлением оси , на чертеже это угол :

Чтобы найти рассмотрим прямоугольный треугольник АВС с вершинами в данных точках.

Угол прямоугольного треугольника АВС равен углу (соответственные углы, полученный при пересечении параллельных прямых АС и ОХ секущей АВ):

равен отношению противолежащего катета к прилежащему, то есть

Отсюда

2. Най­ди­те уг­ло­вой ко­эф­фи­ци­ент пря­мой, про­хо­дя­щей через точки с ко­ор­ди­на­та­ми (4;0) и (0;8).

Решение с помощью системы уравнений абсолютно аналогично решению предыдущей задачи, можете воспроизвести его самостоятельно.

Выполним это задание с помощью графика.

Нанесем данные токи на координатную плоскость и проведем через них прямую:

Угол между прямой и положительным направлением оси ОХ — это угол :

Коэффициент наклона прямой  . Чтобы найти , построим прямоугольный треугольник ВОА: 

В этом прямоугольном треугольнике угол    — внешний. Мы можем найти тангенс внутреннего угла  .  .

. Отсюда  .

Еще раз! Если прямая наклонена влево, то коэффициент наклона прямой отрицательный.

 

И.В. Фельдман, репетитор по математике.

Как найти угол с касательной

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский мандарин
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочие

  • Бухгалтерия
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

ACT Math Help » Тригонометрия » Тангенс » Как найти угол с касательной

Для приведенного выше треугольника  и .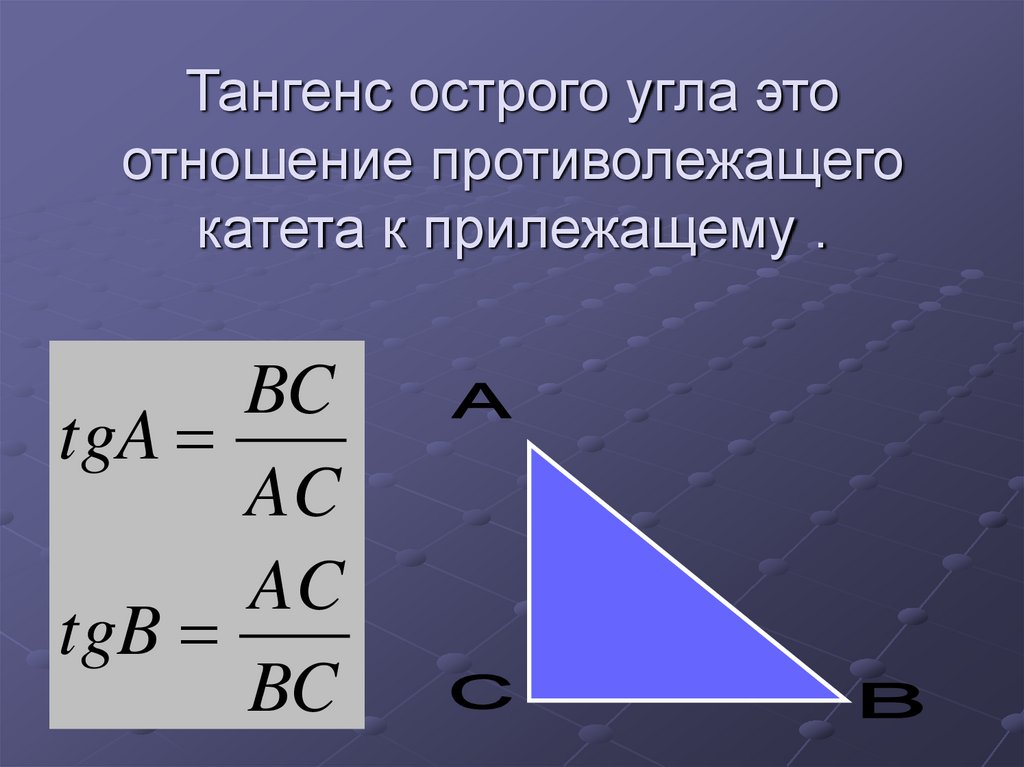 Находить .

Возможные ответы:

Этот треугольник не может существовать.

Правильный ответ:

Пояснение:

Для прямоугольных треугольников мы можем использовать SOH CAH TOA для нахождения неизвестных длин сторон и углов. Для этой задачи нам даны противолежащие и смежные стороны треугольника относительно угла. Имея эту информацию, мы можем использовать функцию касательной, чтобы найти угол.

Сообщить об ошибке

В приведенном выше треугольнике и . Находить .

Возможные ответы:

Правильный ответ:

Пояснение:

Для прямоугольных треугольников мы можем использовать SOH CAH TOA для нахождения неизвестных длин сторон и углов.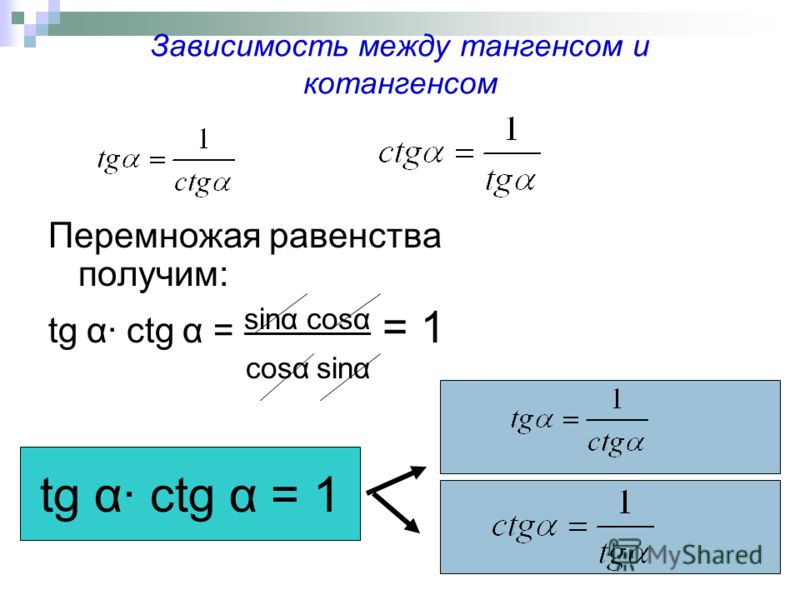 Для этой задачи нам даны противолежащие и смежные стороны треугольника относительно угла. Имея эту информацию, мы можем использовать функцию касательной, чтобы найти угол.

 

Сообщить об ошибке

Для приведенного выше треугольника и . Находить .

Возможные ответы:

Этот треугольник не может существовать.

Правильный ответ:

Пояснение:

Для прямоугольных треугольников мы можем использовать SOH CAH TOA для нахождения неизвестных длин сторон и углов. Для этой задачи нам даны противолежащие и смежные стороны треугольника относительно угла. Имея эту информацию, мы можем использовать функцию касательной, чтобы найти угол.

Сообщить об ошибке

Лазер размещен на расстоянии   от основания высокого здания.

Каков угол лазера (при условии, что он находится на уровне земли), чтобы он был направлен на вершину здания?

Возможные ответы:

Правильный ответ:

Объяснение:

Вы можете нарисовать свой сценарий, используя следующий прямоугольный треугольник:

Напомним, что тангенс угла равен отношению противолежащей стороны треугольника к прилежащей. Вы можете найти угол, используя функцию арктангенса:

 или .

Сообщить об ошибке

Каково значение  в правом треугольнике выше? Округлите до сотых долей градуса.

Возможные ответы:

Правильный ответ:

Объяснение:

Напомним, что тангенс угла равен отношению противолежащей стороны к прилежащей стороне треугольника. Вы можете найти угол, используя функцию арктангенса:

 или .

Сообщить об ошибке

Уведомление об авторских правах

Посмотреть репетиторы математики ACT

Уильям
Сертифицированный репетитор

Салезианский колледж Дона Боско, бакалавр естественных наук. Universidad Rafael Landívar, бакалавр искусств, бизнес-реклама…

View ACT Math Tutors

Sita
Сертифицированный репетитор

Калифорнийский университет в Беркли, бакалавр искусств, математика. Портлендский государственный университет, магистр наук, математика.

View ACT Math Tutors

Mark
Сертифицированный репетитор

Главный кампус Университета Сент-Луиса, бакалавр искусств, преподавание в начальной школе. Университет Вебстера, магистр преподавания…

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Учитесь по концепции

Калькулятор касательной окружности

Этот калькулятор касательной окружности вычисляет длину касательной окружности. Касательная линия окружности — очень универсальное свойство окружности, которое не изменится даже при различных преобразованиях, отображении и масштабировании . Касательная очень важна для различных геометрических построений и теорем.

Касательная может использоваться для различных приложений в дифференциалах и приближениях, сопротивлении материалов, движении, расстоянии и так далее. В этой статье вы узнаете больше о том, что такое касательная и как найти касательную окружности, и завершите обсуждением нескольких применений касательных.

В этом инструменте мы используем формулу расстояния. Вы можете узнать больше об этом на нашем калькуляторе расстояния.

Что такое касательная окружности?

Касательная окружности определяется как линия, начинающаяся из точки на окружности и перпендикулярная радиусу. Касательная окружности касается не пересекается с , окружность только в одной точке .

Рассмотрим окружность с центром O и точкой A на окружности. Линия, соединяющая точки O и A , будет OA . Касательная окружности из точки A перпендикулярна прямой OA . Теперь, если вы проведете линию между точкой O и точкой T на касательной.

Обратите внимание, что касательная окружности перпендикулярна радиусу, т. е. линиям, соединяющим точки 92.(x−a)2+(y−b)2=r2.

Уравнение может быть расширено до трех измерений, подробнее по теме в калькуляторе радиуса сферы. Линия, соединяющая центр и касательную, перпендикулярна, вы можете изучить эту тему с помощью нашего калькулятора перпендикулярных линий.

Тогда уравнение касательной к точке (x1,y1)(x_1, y_1)(x1​,y1​) задается уравнением:

(x−x1)(x1−a)+(y−y1) (y1-b)=0.\scriptsize (x — x_1)(x_1 — a) + (y-y_1)(y_1 — b) = 0.(x-x1​)(x1​-a)+(y- y1​)(y1​−b)=0.

Как найти касательную окружности?

Чтобы найти касательную окружности в точке:

1. Вставьте радиус окружности , r .
2. Введите расстояние d между центром и точкой касательной.
3. Калькулятор касательной окружности теперь рассчитает длину касательной l для вас.

Пример: использование калькулятора касательной окружности

Теперь, когда вы знаете, что такое касательная окружности, давайте попробуем решить задачу о реальной касательной окружности. Определите длину касательной окружности, имеющей радиус 10 м и точку касательной, находящуюся на расстоянии 15 м от центра.

Чтобы найти длину касательной:

1. Введите радиус окружности, r = 10 м .
2. Введите расстояние d между центром и точкой касательной как 15 м .
92}\\ &=11.18~\mathrm{м} \end{align*}l​=d2−r2

​=152−102

​=11,18 м​

Применение касательной к окружности

Касательная к окружности широко используется в различных передовых концепциях например:

• Аппроксимации и дифференциал – Наклон касательной в точке на кривой, определяемой функцией f(x)f(x)f(x), может быть задан первой производной f′(x)f’(x)f′(x).
• Геометрия – Сочетание различных касательных к окружности может быть использовано для построения касательного многоугольника . Окружность тогда называется 90 517 вписанной окружностью 90 520 многоугольника.
• Силовая передача – Две окружности, соединенные парой взаимных касательных, могут быть использованы для решения задачи длины ремня над шкивами. Сумму длин касательных линий и образуемой ими дуги можно использовать для нахождения длины ремня.
• Механика – Наклон касательной к кривой, представляющей скорость объекта, дает мгновенную скорость объекта.

Часто задаваемые вопросы

Определить касательную окружности?

Касательная окружности определяется линией, проведенной из точки на окружности перпендикулярно линии радиуса.

Как рассчитать длину касательной окружности?

Для расчета длины касательной:

1. Найдите квадрат расстояния между центром и точкой касательной.

   No related posts.