Найти обратную матрицу — онлайн калькулятор
Обратная матрица – это такая матрица, которая при умножении на исходную в результате дает единичную матрицу. Чтобы сэкономить время на расчеты и избежать описок, неточностей во время вычислений, воспользуйтесь нашим сервисом. Нахождение обратной матрицы онлайн-калькулятором осуществляется бесплатно.
Найти искомое значение потребуется студентам для подготовки к занятиям, преподавателям для быстрой проверки выполненных заданий, школьникам, изучающим математику на углубленном уровне. Быстро вычислить ответ понадобится также инженерам, работающим над проектами с большим количеством расчетов. Определить обратную матрицу с калькулятором надежнее, чем самостоятельно.
Для вычисления с помощью калькулятора обратной матрицы онлайн необходимо учитывать следующие условия:
- нахождение обратной матрицы онлайн доступно только для квадратных матриц;
- определитель матрицы должен быть отличным от нуля.

Чтобы найти обратную матрицу для матрицы онлайн, используется формула, позволяющая получить быстрый и точный ответ. Использование сервиса предполагает выбор числа столбцов и строк и введения значения матрицы в соответствующие пустые графы. Отправить пример на расчет вы сможете кнопкой «Рассчитать».
Найти обратную матрицу онлайн-калькулятором помогает заложенный алгоритм расчета:
- Происходит проверка, относится ли матрица к квадратным. В случае отрицательного ответа обратной матрицы не существует.
- Рассчитывается определитель матрицы. При его равенстве нулю обратной матрицы не существует. В остальных случаях расчеты продолжаются.
- Происходит поиск транспонированной матрицы.
- Вычисляются алгебраические дополнения. На них заменяется каждый элемент матрицы соответственно.
- Из алгебраических дополнений составляется обратная матрица. Находится частное между элементами полученной матрицы и определителем исходной матрицы.
 Полученная матрица обратная для исходной.
Полученная матрица обратная для исходной. - В качестве проверки происходит перемножение матриц онлайн-калькулятором. Результатом является единичная матрица.
Если вы пользуетесь калькулятором, то получаете не просто готовый ответ, но и подробную расшифровку расчета. Порядок вычислений помогает понять общий алгоритм и применять его при решении аналогичных задач.
Решение уравнений методом обратной матрицы онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Метод обратной матрицы применяется в математике для решения систем линейных алгебраических уравнений в том случае, когда число неизвестных равно количеству уравнений в системе.
Так же читайте нашу статью «Решить показательное уравнение онлайн»
Допустим, дана следующая система линейных уравнений:
\[\left\{\begin{matrix} 2x_1-x_2+3x_3=1\\ -2x_2+2x_3=2\\ 3x_1+x_2+x_3=0 \end{matrix}\right. -1=1/4 \begin{pmatrix} -4 & 4 & 4\\ 6 & -7 & -4\\ 6 & -5 & -4 \end{pmatrix}\]
-1=1/4 \begin{pmatrix} -4 & 4 & 4\\ 6 & -7 & -4\\ 6 & -5 & -4 \end{pmatrix}\]
Найдем матрицу неизвестных:
\[x=\frac{1}{4} \begin{pmatrix} -4 & 4 & 4\\ 6 & -7 & -4\\ 6 & -5 & -4\\ \end{pmatrix} \begin{pmatrix} 1\\ 2\\ 0 \end{pmatrix} = \begin{pmatrix} 1\\\ -2\\ -1 \end{pmatrix}\]
Решением систему методом обратной матрицы является:
\[x_1=1\]
\[x_2=2\]
\[x_3=-1\]
Проверить правильность ответа можно, подставив данные значения на место неизвестных в систему.
Где можно решить уравнение с помощью обратной матрицы онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Калькулятор матриц. Решение матриц онлайн. Решение матричных уравнений
Решение матриц онлайн является одним из самых востребованных запросов в интернете среди студентов, причём сервисов, где можно решить онлайн матрицу, практически нет. И снова на помощь придёт многофункциональный математический калькулятор. В его арсенал входит калькулятор матриц онлайн, который выполняет все основные операции над матрицами!
Матрица — это совокупность значений, записанных в прямоугольную таблицу. Каждый элемент матрицы имеет двойной порядковый номер в этой таблице, а именно номер столбца и номер строки. Размер матрицы определяется количеством строк и столбцов в таблице. Например, размер матрицы 3 на 5 значит, что она состоит из трёх строк и пяти столбцов.
Обратите внимание, 5 x 5 — это максимальный размер матрицы, которую может решить бесплатный калькулятор, предлагаемый на нашем сайте.
Как решать матрицы в онлайн калькуляторе
Чтобы вызвать калькулятор матриц, нажмите кнопку Matrix.
Кнопка, открывающая калькулятор матриц
Панель управления дополнится инструментами, с помощью которых выполняется решение матриц онлайн. Калькулятор позволяет выполнять следующие онлайн действия над матрицами: вычитание, сложение и умножение матриц, векторное произведение, решение матричных уравнений, транспонирование, нахождение обратной матрицы и вычисление определителя матрицы.
Кнопки калькулятора, выполняющие основные действия над матрицами
Помимо панели с кнопками онлайн калькулятор матриц содержит удобную форму для быстрого ввода выражения. В левой и правой частях задаются матрицы, их размер выбирается из выпадающего списка. В середине выпадающее меню для выбора операции, которую нужно выполнить калькулятору с заданными матрицами. Другие возможности калькулятора можно посмотреть здесь Функции калькулятора.
Вычисление матриц онлайн с помощью формы быстрого ввода
Если элемент матрицы не указан, онлайн калькулятор подставляет значение «0».
Обратите внимание, при вызове меню решения матриц вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I», чтобы увидеть дисплей в полный размер.Вектор столбец
Кнопки калькулятора для ввода вектора
(2, 6, 8)
Вектор-столбец из 3х строк
Квадратная матрица
Матрица называется квадратной, если число её строк равно числу столбцов. Следует отметить, что только у квадратной матрицы может быть главная диагональ матрицы — линия, проходящая через элементы матрицы с одинаковыми индексами, начиная с ячейки первой строки первого столбца и заканчивая элементом, стоящем в последнем столбце последней строки.
Для быстрой записи квадратных матриц 2, 3 или 4-го порядка используйте специальные кнопки, которые предлагает калькулятор онлайн.
Кнопки калькулятора для ввода квадратных матриц
[[ 8, 4, 1, 8][ 7, 1, 8, 8][ 8, 4, 1, 6][ 4, 8, 3, 1]]
Пример квадратной матрицы 4 порядка
Квадратные матрицы, у которых все элементы, исключая элементы главной диагонали, равны нулю, называются диагональные матрицы. Симметричная матрица чисел представляет собой таблицу, в которой все элементы, симметричные относительно главной диагонали, равны.
[[ 1, 2, 8, 11][ 2, 3, 24, 5][ 8, 24, 6, 4][ 11, 5, 4, 9]]
Пример симметричной матрицы
Есть ещё такие виды матриц в математике.
Единичная матрица чисел — это таблица, в которой элементы главной диагонали равны единице, а все остальные элементы являются нулевыми.
[[ 1, 0, 0, 0][ 0, 1, 0, 0][ 0, 0, 1, 0][ 0, 0, 0, 1]]
Пример единичной матрицы
Таблица, у которой значение всех элементов равно 0, называется нулевая матрица.
[[ 0, 0, 0, 0][ 0, 0, 0, 0][ 0, 0, 0, 0][ 0, 0, 0, 0]]
Пример нулевой матрицы
Матрицы и действия над ними
Сложение и вычитание матриц онлайн
С помощью калькулятора можно произвести сложение матриц онлайн, а также найти разность матриц онлайн. Чтобы вычислить сумму матриц или найти их разность, выполняются соответствующие операции над их элементами. Например, найти сумму матриц значит определить такую матрицу, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц.
Найти сумму элементов матриц или их разность можно только в том случае, если исходные матрицы одинакового размера, т. е. число их строк и столбцов соответственно равно. Вычитание и сложение матриц разного размера невозможно.
Для выполнения этих операций в калькуляторе используйте форму быстрого ввода или запишите выражение вручную.
Сложение матриц примеры
[[1, 2, 3][3, 1, 2][5, 0, 6]]+[[1, 2, 5][6, 3, 2][9, 9, 9]]
Сложение двух матриц
[[2, 7][4, 5]]+[[2, 10][6, 8]]
Сумма двух матриц
Векторное произведение матриц
Для выполнения этой операции используйте клавишу Cross Product.
(2, 6, 4)#(8, 2, 5)
Пример произведения векторов
Умножение матриц
Умножение матриц онлайн калькулятор производит с помощью клавиши Vector/Matrice-Multiplication.
Перемножение матриц возможно только в том случае, если количество столбцов одной матрицы равняется количеству строк другой. Чтобы матрицу умножить на число, нужно каждый элемент матрицы умножить на это число.
[[2, 8][4, 2]]*[[8, 8][7, 1]]
Умножение матриц пример
[[5, 6][7, 8]]*9
Умножение матрицы на число онлайн
Решение матричных уравнений
Эта функция калькулятора позволяет находить неизвестные матрицы, которые описаны уравнением зависимости одной матрицы от другой. Решение матричных уравнений осуществляется с помощью кнопки Solve Ecuation System.
[[6, 1, 8],[7, 5, 3],[2, 9, 4]]*x=(1, 2, 3)
Пример решения системы уравнений матриц
Транспонирование матрицы
Используйте клавишу Matrix Transponent, когда нужно выполнить транспонирование матрицы — действие, в котором строки со столбцами меняются местами. -1
-1
Нахождение обратной матрицы пример
Нахождение определителя матрицы
В калькуляторе матриц нет специальной кнопки для того, чтобы найти определитель матрицы. Но вычислить его можно, написав в поле ввода специальную функцию — оператор det(Determinant).
det( [ [-2, 2, -3], [-1, 1, 3], [2, 0, -1] ] )
Пример, как найти определитель матрицы онлайн
Бесплатный калькулятор онлайн может не только решить онлайн матрицу, в его возможностях также: возведение в степень, калькулятор корней, тригонометрические функции, решение логарифмов и другие дополнительные функции.
Калькулятор Инструкция — обзор всех функций калькулятора и общее описание, как пользоваться калькулятором.
Обратная матрица 3*3. Калькулятор
Как найти обратную матрицу подробно описано в предыдущих уроках. Напомню лишь последовательность вычислений:
- находим определитель главной матрицы;
- дальше вычисляем алгебраические дополнения к матрице;
- последним шагом нужно транспонировать матрицу алгебраических дополнений и разделить на определитель.

Результатом вычислений и будет обратная матрица.
Ниже приведены примеры пошагового вычисления матрицы 3х3.
Пример 1. Найти обратную матрицу
Решение: Вычисляем определитель матрицы 3 * 3 по правилу треугольников
Определитель отличен от нуля, следовательно матрица А не вырожденная и существует обратная к ней.
Алгебраические дополнения равны минорам умноженным на (-1) в степени суммы номера строки и столбца элемента матрицы.
Для простоты можно использовать приведенную ниже схему знаков миноров
Миноры равны определителю на единицу меньшего порядка чем матрица и образуются вычеркиванием строки и столбца на пересечении которых находится элемент.
Более понятно станет с вычислений алгебраических дополнений
Из найденных значений выписываем матрицу алгебраических дополнений
Транспонирует ее чтобы получить присоединенную (союзное) матрицу
На этом этапе будьте внимательны — можно выполнить правильно приведенные выше вычисления и из-за неумения транспонировать получить неверный результат.
Делим на определитель и получаем обратную матрицу
Найти обратную матрицу Вам поможет калькулятор обратной матрицы YukhymCalc. Для этого заходите в меню калькулятора и выбираете вычисления обратных матриц
Далее задаете размер матрицы
и вводить элементы матрицы.
После вычислений Вы получите элементы матрицы дополнений
союзной матрицы, и обратной, а также определитель.
Все действия расписаны подробно в отдельном окне
и результаты вычислений можно сохранить в текстовый файл
Используйте калькулятор для нахождения обратной матрицы и проверки правильности вычислений.
Пример 2. Найти обратную матрицу
Решение: Вычисляем определитель матрицы разложив его по первой строке. Это довольно удобно так как имеем два элемента которые равны нулю
Алгебраические дополнения находим воспользовавшись приведенной выше схемой знаков миноров
Если в определителе строка или столбец содержит элементы = 0 то он равен 0.
Записываем матрицу алгебраических дополнений
Присоединенную матрицу находим транспонированием найденной
Находим обратную матрицу по известной формуле
Калькулятор обратной матрицы дает следующий результат
Сравнением убеждаемся что обратную матрицу найдено правильно. Используйте приведенную методику в обучении и с опытом у Вас не будет проблем с обратной матрицей.
Матрицы и действия над ними — определитель матрицы, умножение и сложение матриц, транспонирование матриц, обратная матрица
Что такое матрица
Таблица чисел вида
состоящая из строк и столбцов называется матрицей. Числа называются ее элементами.
Под решением матрицы обычно понимают проведение таких операций как нахождение обратной матрицы, нахождение определителя, умножение матрицы на число и другое.
Кроме того действия могут проводиться сразу над несколькими матрицами. То есть матрицы могут между собой складываться, перемножаться. Все эти так называемые решения матриц проводятся по определенным схемам или алгоритмам.
Обратите внимание что действия над матрицами выполняются по определенным правилам и дело тут не в сложности этих правил, а в старательности и внимательности при вычислениях.
То есть матрицы могут между собой складываться, перемножаться. Все эти так называемые решения матриц проводятся по определенным схемам или алгоритмам.
Обратите внимание что действия над матрицами выполняются по определенным правилам и дело тут не в сложности этих правил, а в старательности и внимательности при вычислениях.
Определитель матрицы и его вычисление
Рассмотрим квадратную матрицу:
порядка . Из элементов этой матрицы составим всевозможные произведения так, чтобы они содержали по одному и только по одному элементу из каждой строки и каждого столбца. В каждом из этих произведений сомножители (которых будет ) расположим таким образом, чтобы первые индексы образовали перестановку . В результате полученные произведения будут иметь вид:
где
– некоторая
перестановка чисел 1,2,3…n. Очевидно, что число всевозможных
произведений составленных из элементов матрицы по приведенному выше правилу
будет равно числу всевозможных перестановок из множества вторых индексов
сомножителей произведений, то есть из чисел
, или то же самое, числу
перестановок из чисел
, а таких перестановок будет
. Каждая перестановка будет иметь
некоторое число инверсий, образованных вторыми индексами сомножителей
произведений. Условимся перед
произведением ставить плюс если число инверсий четное (то есть перестановка
вторых индексов четная), и минус, если число инверсий нечетное (то есть
перестановка вторых индексов нечетная).
Каждая перестановка будет иметь
некоторое число инверсий, образованных вторыми индексами сомножителей
произведений. Условимся перед
произведением ставить плюс если число инверсий четное (то есть перестановка
вторых индексов четная), и минус, если число инверсий нечетное (то есть
перестановка вторых индексов нечетная).
Просуммировав все произведения вида (*) составленные из матрицы и взятые с указанными знаками, получим число, называемое определителем.
Для определителя, как и для матрицы, используются такие понятия, как строка, столбец, главная и побочная диагонали и т. п. Квадратная матрица, определитель которой отличен от нуля, называется невырожденной, а матрица с определителем, равным нулю,— вырожденной.
Рассмотрим частные случаи определителей:
Определитель 2-го порядка:
Определитель третьего порядка:
Для его вычисления удобно пользоваться следующей схемой:
Для определителей порядка выше
третьего неудобно запоминать какую-либо символическую схему, так как, например,
определитель уже четвертого порядка есть алгебраическая сумма 24 слагаемых,
каждое из которых является произведением четырех сомножителей.
Минором какого-либо элемента определителя называется определитель, полученный из данного вычерчиванием той строки и того столбца, которым принадлежит этот элемент.
Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком .
В общем случае определителем порядка, соответствующим квадратной матрице порядка можно назвать число, равное сумме парных произведении элементов какой-либо строки (столбца) на их алгебраические дополнения.
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля.
Обратная матрица
Пусть – квадратная невырожденная матрица n-го порядка. Обратной матрицей для матрицы называется матрица, для которой справедливо равенство:
где – единичная матрица
Обратная матрица определена только для квадратных невырожденных матриц и вычисляется по формуле:
где
– определитель
матрицы
, а матрица
(союзная
матрица) получается из матрицы
заменой всех ее
элементов соответствующими им алгебраическими дополнениями.
Транспонирование матрицы
Замена каждой строки матрицы ее столбцов называется транспонированием. Транспонированная по отношению к матрице матрица обозначается .
Если задана матрица
то ее транспонированная матрица имеет вид:
Сумма матриц и произведение матрицы на число
Суммой матриц и называется матрица , элементы которой вычисляются по формуле:
Для суммы матриц используют обозначение
Произведением матрицы на число называется матрица , элементы которой вычисляются по формуле:
Для произведения матрицы на число используют обозначение .
Произведение матриц
Произведением матрицы на матрицу называется матрица , элементы которой вычисляются по формуле:
Из определения умножения матриц
следует, что элемент
в матрице
является суммой
произведений соответствующих элементов i-й строки матрицы
и j-го столбца матрицы
. {-1}\), где \(\mathbb{A}\) – первая матрица, \(\mathbb{B}\) – вторая матрица. То есть это умножение на обратную матрицу. Следует иметь ввиду, что вторая матрица должна быть квадратной.
{-1}\), где \(\mathbb{A}\) – первая матрица, \(\mathbb{B}\) – вторая матрица. То есть это умножение на обратную матрицу. Следует иметь ввиду, что вторая матрица должна быть квадратной.
При поэлементном возведении в степень вместо второй матрицы должно быть просто число. Каждый элемент матрицы возводится в степень, равную этому числу.
Матричное возведение в степень \(n\) – это матричное умножение матрицы саму на себя \(n\) раз. То есть во второе поле ввода должно быть вписано целое число. Для получения обратной матрицы введите в правую часть «\(-1\)»
Решение линейных уравнений – в этом режиме первая матрица содержит коэффициенты уравнения в левой части, вторая – в правой части. Например, чтобы решить систему уравнений \[\left\lbrace\begin{aligned}2x+3y&=5;\\10x-y&=6,\end{aligned}\right.\] нужно ввести в левое поле ввода:
2 3 10 -1в правое:
5 6
Вычисление обратной матрицы в EXCEL. Примеры и описание
Для вычисления обратной матрицы в MS EXCEL существует специальная функция
МОБР()
или англ. MINVERSE
.
MINVERSE
.
Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.
СОВЕТ : О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL
Матрица А -1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А -1 *А=Е и А*А -1 =Е, где Е единичная матрица порядка n.
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() .
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9 , то для получения транспонированной матрицы нужно (см. файл примера ):
- выделить диапазон 2 х 2, который не пересекается с исходным диапазоном А8:В9 , например, Е8:F9
- в
Cтроке формул
ввести формулу
=
МОБР
(A8:B9)
и нажать комбинацию клавиш CTRL+SHIFT+ENTER , т.
 е. нужно ввести ее как
формулу массива
(формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2 )
е. нужно ввести ее как
формулу массива
(формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2 )
Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.
Массив может быть задан не только как интервал ячеек, например A8:B9 , но и как массив констант , например =МОБР({5;4: 3;2}) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Ссылка на массив также может быть указана как ссылка на именованный диапазон .
Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция
МОБР()
возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.
Матрицы не могут быть обращены, у которых определитель равен 0.
Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ() ), а как ошибочное значение.
Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений
СОВЕТ : Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОБР() .
В файле примера приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.
Порядок действий при вычислении обратной матрицы:
В качестве проверки можно
перемножить исходную и обратную матрицы
. В результате должна получиться единичная матрица.
В результате должна получиться единичная матрица.
— Бесплатный онлайн-калькулятор обратной матрицы
Калькулятор обратной матрицывычисляет значение обратной матрицы для заданной матрицы. Матрица — это сеточная функция, которая имеет упорядоченный прямоугольный массив чисел. Числа расположены в ряды и столбцы. Вертикальное расположение называется столбцами, а горизонтальное расположение чисел — строками.
Что такое калькулятор обратной матрицы?
Калькулятор обратной матрицы— это онлайн-инструмент, который помогает найти обратные матрицы заданной матрицы.Это поможет вам рассчитать окончательную матрицу за несколько секунд. Чтобы использовать этот калькулятор обратной матрицы, введите число до 3 цифр.
Как пользоваться калькулятором обратной матрицы?
Выполните следующие действия, чтобы найти обратную матрицу с помощью онлайн-калькулятора обратной матрицы:
- Шаг 1: Перейти к онлайн-калькулятору обратной матрицы Cuemath
- Шаг 1: Введите значение матрицы в указанные поля ввода калькулятора обратной матрицы.

- Шаг 2: Нажмите кнопку «Рассчитать» , чтобы найти результирующую обратную матрицу
- Шаг 3: Нажмите кнопку «Сброс» , чтобы найти результирующую обратную матрицу с другими матрицами.
Как работает калькулятор обратной матрицы?
Матрица определяется как математическая функция для представления набора данных, обычно используемая матрица является двумерной матрицей и используется для целей сложения векторов, умножения векторов и т. Д.{-1} = \ frac {1} {ad-bc} [\ begin {matrix} d & -b \\ -c & a \ end {matrix}] \)
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. Cuemath находит решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенный пример на обратных матрицахНайдите результирующую обратную матрицу A = \ ([\ begin {matrix} 1 & 2 \\ 3 & 4 \ end {matrix}] \) и проверьте ее с помощью калькулятора обратной матрицы
Решение:Дано: A = \ ([\ begin {matrix} 1 & 2 \\ 3 & 4 \ end {matrix}] \)
Обратная матрица \ (A ^ {- 1} = \ frac {1} {ad-bc} [\ begin {matrix} d & -b \\ -c & a \ end {matrix}] \)
\ (A ^ {- 1} = \ frac {1} {4-6} [\ begin {matrix} 4 & -2 \\ -3 & 1 \ end {matrix}] \)
\ (A ^ {- 1} = \ frac {1} {- 2} [\ begin {matrix} 4 & -2 \\ -3 & 1 \ end {matrix}] \)
\ (A ^ {- 1} = [\ begin {matrix} -2 & 1 \\ 1. 5 & -0.5 \ end {matrix}] \)
5 & -0.5 \ end {matrix}] \)
Аналогично, вы можете попробовать калькулятор обратной матрицы и найти обратную матрицу для заданных матриц:
- Матрицы = \ (\ begin {matrix} 2 & 1 \\ 4 & 2 \ end {matrix} \)
- Матрицы = \ (\ begin {matrix} 1 & 2 \\ 3 & 4 \ end {matrix} \)
☛ Статьи по теме:
Калькулятор обратной матрицы Добро пожаловать в калькулятор обратной матрицы , где у вас будет возможность узнать все об инвертировании матриц.Эта операция аналогична поиску дробной части заданного числа, за исключением того, что теперь мы перемножаем матрицы и хотим, чтобы в результате была получена единичная матрица . Но не волнуйтесь, прежде чем мы дадим, скажем, обратную матрицу 4×4, мы рассмотрим некоторые основные определения, включая сингулярную матрицу и невырожденную матрицу . Затем мы перейдем к общей формуле обратной матрицы с аккуратным упрощением для обратной матрицы 2×2 и некоторыми полезными обратными свойствами матрицы. И последнее, но не менее важное: мы даем пример с подробными вычислениями того, как найти обратную матрицу 3×3.
И последнее, но не менее важное: мы даем пример с подробными вычислениями того, как найти обратную матрицу 3×3.
Так что налейте себе стакан воды и наслаждайтесь поездкой!
Что такое матрица?
В начальной школе вас учат натуральным числам , 1 , 2 или 143 , и они имеют смысл — у вас есть 1 игрушечная машинка , 2 комиксов и ужасно длинные 143 дней до Рождества.Затем они сообщают вам, что существуют дроби (или рациональных чисел, , как они их называют), например, ½ , или десятичные дроби, например, 1,25 , что все еще кажется разумным. В конце концов, вы дали брату ½ плитки шоколада, а она стоила $ 1,25 . Затем вы встречаетесь с отрицательными числами , такими как -2 или -30 , и их немного сложнее понять. Но если подумать, один парень из вашего класса получил -2 баллов на тесте на читерство, а в Черную пятницу была скидка –30 долларов на джинсы.
Наконец, школа вводит вещественных чисел и некоторых странных червеобразных символов, которые продолжают называть квадратными корнями. Что еще хуже, в то время как √4 - это простой 2 , √3 - это что-то вроде 1.73205 ... , и цифры продолжаются бесконечно. Они убеждают вас, что такие числа описывают, например, диагональ прямоугольника. И еще есть π , который каким-то образом появился из ниоткуда, когда вы говорили о кругах. Честно говоря, может быть, эти числа в каком-то смысле являются реальными .Но это почти все, что может быть , не так ли?
Неправильно. Математики заняты выяснением различных интересных и, не поверите, полезных расширений действительных чисел . Самый важный из них - комплексные числа, которые являются отправной точкой для любого современного физика. К счастью, мы здесь не в этом направлении. Есть еще один.
Матрица - это массив элементов (обычно чисел), , который имеет заданное количество строк и столбцов. Пример матрицы:
| А | = |
|
Более того, мы говорим, что матрица имеет ячеек или ячеек , в которые мы записываем элементы нашего массива. Например, матрица
Например, матрица A выше имеет значение 2 в ячейке, которая равна во второй строке и втором столбце . Отправной точкой здесь являются матрицы с одной ячейкой, которые в основном аналогичны действительным числам.
Как видите, матрицы - это инструмент, используемый для лаконичной записи нескольких чисел и работы со всей партией как с единым объектом . Таким образом, они чрезвычайно полезны при работе с:
Вычисления с матрицами намного сложнее, чем с числами .Например, если мы хотим добавить их, мы сначала должны убедиться, что можем. Но, поскольку мы здесь, на калькуляторе обратной матрицы , мы оставляем сложение на потом. Однако сначала давайте познакомимся с несколькими определениями.
Сингулярная и невырожденная матрица, единичная матрица
Если вы хотите найти обратную матрицу 2x2 или обратную матрицу 4x4, вы должны сначала понять одну вещь: не всегда существует . Придумайте дробь, скажем,
Придумайте дробь, скажем, a / b .Это нормально , пока b ненулевое значение . Если это так, выражение не имеет смысла, и то же самое происходит с матрицами.
Сингулярная матрица - это матрица, у которой нет обратной. Неособая матрица (неожиданный сюрприз) справляется. Поэтому всякий раз, когда вы сталкиваетесь с упражнением с обратной матрицей, вам следует начинать с проверки, является ли оно невырожденным. В противном случае нет смысла заниматься расчетами. Это просто невозможно.
По определению, инверсия матрицы A - это матрица A⁻¹ , для которой
A * A⁻¹ = A⁻¹ * A = I ,
, где I обозначает единичную матрицу , то есть квадратную матрицу, которая имеет 1 с на главной диагонали и 0 с в другом месте. Например, единичная матрица 3x3 равна
| I | = |
|
Другими словами, когда дана произвольная матрица A , мы хотим найти другую, для которой произведение двух (в любом порядке) дает единичную матрицу . Подумайте о
Подумайте о I как о 1 (элемент идентичности) в мире матриц. В конце концов, для дроби a / b обратное значение равно b / a , но не только потому, что мы « переворачиваем его на » (по крайней мере, не по определению). Это из-за аналогичного свойства умножения:
(а / б) * (б / а) = (б / а) * (а / б) = 1 .
Это было достаточно времени, потраченного на чтение определений, вам не кажется? Давайте, наконец, посмотрим формулу обратной матрицы и узнаем, как найти обратную матрицу 2x2, 3x3 и 4x4.
Как найти обратную матрицу: формула обратной матрицы
Прежде чем мы перейдем к частным случаям, таким как обратная матрица 2x2, давайте взглянем на , общее определение .
Пусть A - квадратная невырожденная матрица размером n . Тогда обратная величина A⁻¹ (если она существует) дается формулой:
| * |
|
Модель | A | - это определитель A (не путать с абсолютным значением числа).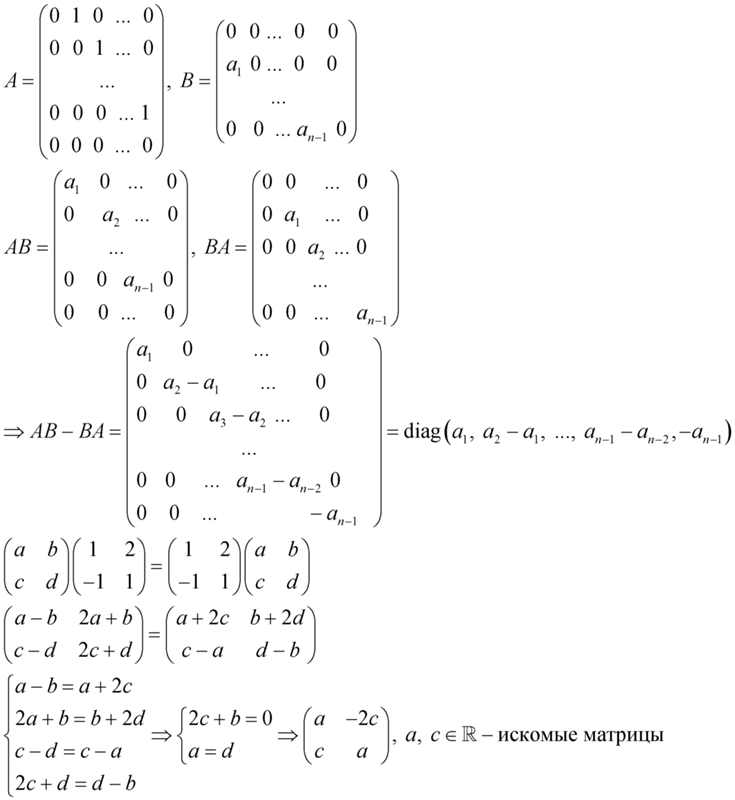
Aᵢⱼ обозначает i, j -минор A , то есть определитель матрицы, полученный из A , если забыть о его i -й строке и j -м столбце (это квадратная матрица размером n-1 ). Наконец, ᵀ вне массива - это транспонирование. Это означает, что как только мы узнаем ячейки внутри, мы должны « перевернуть их на », чтобы строка i стала его столбцом i и наоборот.
Уф, это было , много символов и много технической ерунды , но это именно то, что нравится математикам. Некоторые из нас заканчивают просмотр ромкомов, другие записывают определения, которые кажутся умными. Кто мы такие, чтобы их судить?
В следующем разделе мы укажем на несколько важных фактов, которые следует учитывать при поиске обратной матрицы 4x4 или любого ее размера. Но прежде чем мы их увидим, давайте посмотрим на , что приведенная выше формула обратной матрицы превращается в , когда это обратная матрица 2x2, которую мы ищем.
Пусть
Затем миноры ( Aᵢⱼ с выше) получаются из вычеркивания одной из строк и одного из столбцов. Но если мы это сделаем, у нас останется , одна ячейка ! И определитель такой вещи (матрица 1x1) - это просто число в этой ячейке. Например, A₁₂ получается из-за того, что забывают первую строку и второй столбец, что означает, что остается только c (или, скорее, [c] , поскольку это матрица). Следовательно,
| A⁻¹ | = | * |
|
Кроме того, в этом частном случае определитель достаточно простой : | A | = а * г - б * с . Итак, после учета минусов и перестановки, мы приходим к - красивой и красивой формуле для обратной матрицы 2x2:
Итак, после учета минусов и перестановки, мы приходим к - красивой и красивой формуле для обратной матрицы 2x2:
| A⁻¹ | = | * |
|
Возможно, обратную матрицу 4x4 не так просто вычислить, как в случае 2x2. Существует альтернативный способ вычисления обратной матрицы ; метод включает элементарных операций со строками и так называемое исключения Гаусса (для получения дополнительной информации обязательно ознакомьтесь с калькулятором (сокращенной) эшелонированной формы строк). В качестве примера ниже мы опишем, как найти обратную матрицу 3x3, используя альтернативный алгоритм.
В качестве примера ниже мы опишем, как найти обратную матрицу 3x3, используя альтернативный алгоритм.
Допустим, вы хотите вычислить обратную матрицу
|
Затем мы строим матрицу с тремя строками и вдвое большим количеством столбцов, как показано ниже:
|
и используйте гауссово исключение в строках с 6 элементами матрицы, чтобы преобразовать их в нечто вроде
|
, где x , y и z получаются в процессе преобразований.Тогда
| A⁻¹ | = |
|
Какой бы метод вы ни предпочли, может быть полезно проверить несколько обратных свойств матрицы , чтобы сделать наши исследования немного проще.
Обратные свойства матрицы
Ниже мы перечисляем несколько наблюдений и обратные свойства матрицы.
Не всегда существует обратная матрица. Давайте подробнее рассмотрим формулу обратной матрицы в раздел выше. Он содержит определитель матрицы. Это означает, что, прежде всего, нам нужно иметь квадратную матрицу даже для того, чтобы задуматься о ее инверсии. Во-вторых, определитель появляется в знаменателе дроби в формуле обратной матрицы.
 Следовательно, если этот определитель равен
Следовательно, если этот определитель равен 0, тогда это выражение не имеет никакого смысла, и обратное выражение не существует.Матрица, обратная обратной, является исходной матрицей. Другими словами, если вы дважды перевернете матрицу, вы получите то, с чего начали. Символически это свойство можно записать как
(A⁻¹) ⁻¹ = Aдля произвольной невырожденной матрицыA.Обратное произведение - произведение обратных чисел в обратном порядке. Это означает, что если у вас есть две квадратные матрицы
AиBодинакового размера и вы хотите вычислить обратное их произведение, то, в качестве альтернативы, вы можете найти их отдельные обратные и умножить их, но в обратном порядке. Короче говоря,(A * B) ⁻¹ = B⁻¹ * A⁻¹.Обратное транспонирования - это транспонирование обратного. По сути, не имеет значения, если вы сначала транспонируете матрицу, а затем вычислите ее обратную, или сначала найдете обратную матрицу и только потом ее транспонируете.
 В символической записи это переводится как
В символической записи это переводится как (Aᵀ) ⁻¹ = (A⁻¹) ᵀ. В частности, обратите внимание, что это основано на том факте, что определитель матрицы остается неизменным после транспонирования .
Мы надеемся, что вы достаточно заинтригованы теорией и не можете дождаться, чтобы рассказать о ней своим друзьям за чашкой кофе. Однако, прежде чем вы начнете распространять знания, давайте вместе рассмотрим пример и посмотрим, как найти на практике обратную матрицу 3x3 .
Пример: использование калькулятора обратной матрицы
Теперь мы, , пошагово изучим, как найти обратную матрицу 3x3. Скажите, что вам дан массив
| А | = |
|
Прежде чем мы перейдем к вычислениям, давайте посмотрим, как мы можем использовать калькулятор обратной матрицы , чтобы сделать все это за нас.
Прежде всего, мы имеем дело с матрицей 3x3, поэтому мы должны указать калькулятору, что это , выбрав соответствующий вариант в « Размер матрицы ». Это покажет нам символический пример такого массива с ячейками, обозначенными a₁ , a₂ и так далее. Мы должны ввести числа, указанные в нашей матрице, под правильными символами на картинке. Например, a₃ находится в первой строке третьего столбца, поэтому мы находим соответствующую ячейку в нашей матрице и проверяем, что там 5 .Поэтому в вычислителе обратной матрицы мы кладем a₃ = 5 . Аналогично получаем остальные ячейки:
a₁ = 1 , a₂ = 0 , a₃ = 5 ,
b₁ = 2 , b₂ = 1 , b₃ = 6 ,
c₁ = 3 , c₂ = 4 , c₃ = 0 .
В тот момент, когда мы введем последнее число, калькулятор обратной матрицы выдаст ответ или сообщит нам, что обратной матрицы не существует. Но, если вам не нужны спойлеры, мы также можем произвести расчеты вручную .
Но, если вам не нужны спойлеры, мы также можем произвести расчеты вручную .
Априори мы даже не знаем, существует ли A⁻¹ , может это просто сказка про вампиров? Для уверенности вычислим его определитель:
| A | = 1 * 1 * 0 + 0 * 6 * 3 + 5 * 2 * 4-5 * 1 * 3-0 * 2 * 0-1 * 6 * 4 = 0 + 0 + 40-15-0-24 = 1 .
Уф, сегодня нет вампиров , просто невырожденная матрица и старая добрая математика .
Вспомните формулу обратной матрицы и обратите внимание, что теперь пора вычислить Aᵢⱼ с для i и j между 1 и 3 .В качестве примера возьмем, скажем, A₁₁ и A₂₃ . Первый из двух является определяющим фактором того, что мы получим, если забудем первую строку и первый столбец A . Это означает, что
Аналогично, A₂₃ получается при вычеркивании второй строки и третьего столбца:
Это дает
A₁₁ = 1 * 0 - 6 * 4 = -23 ,
A₂₃ = 1 * 4-0 * 3 = 4 .
Итого получаем
A₁₁ = -23 , A₁₂ = -18 , A₁₃ = 5 ,
A₂₁ = -20 , A₂₁ = -15 , A₂₃ = 4 ,
A₃₁ = -5 , A₃₂ = -4 , A₃₃ = 1 .
Остается только использовать формулу обратной матрицы и подставить все числа, которые мы вычислили выше:
| A⁻¹ | = | * |
| = |
| = | * |
| = |
| = | 1 | * |
| = |
| = |
|
Было не так уж плохо, правда? Тем не менее, калькулятор обратной матрицы весьма полезен , поскольку он избавляет нас от лишних хлопот. Теперь, когда мы кое-чему научились, мы заслуживаем короткого сна в гамаке, не так ли?
Теперь, когда мы кое-чему научились, мы заслуживаем короткого сна в гамаке, не так ли?
Калькулятор обратной матрицы
Калькулятор обратной матрицы - это онлайн-инструмент, который находит обратную матрицу для заданных значений матрицы. Он может вычислять обратные матрицы 2x2, 3x3, 4x4 и 5x5.
Давайте узнаем, как вычислить обратную матрицу без использования калькулятора обратной матрицы.
Как найти обратную матрицу (3x3)?
Систему уравнений в матрице можно решить с помощью правила Краммера.Калькулятор матриц может быть удобным инструментом для сложения, вычитания или умножения матриц.
Обратную матрицу можно рассчитать с помощью вышеуказанного калькулятора, но здесь мы возьмем обратную матрицу вручную.
Пример:
Найдите матрицу, обратную следующей: A .
Решение:
Шаг 1: Дополните матрицу матрицей идентичности.
Шаг 2: Обнулить столбец 1, кроме записи в строке 1, столбце 1 (сводная запись).
Разделить строку 1 на 5 (R 1 /5)
R 2 => R 2 - 15R 1
R 3 => R 3 - 10 R 1
Шаг 3: Обнулить столбец 2, кроме записи в строке 2, столбец 2.
Разделить строку 2 на - 25 (R 2 / -25)
R 1 => R 1 - 2R 2
R 3 3 => - 5R 2
Шаг 4: Сделайте нули в столбце 3, кроме записи в строке 3, столбце 3 (сводная запись).
Разделить строку 3 на -20 (R 3 / -20)
R 1 => R 1 - 1R 3
R 2 => R 2 - 1R 3Окончательный A -1 может быть записан как,
В десятичной форме,
Калькулятор обратной матрицы
Калькулятор, приведенный в этом разделе, может быть использован для нахождения обратной матрицы 3x3. Он не только дает обратную матрицу 3x3, но также дает вам определитель и сопряженную матрицу 3x3, которую вы вводите.
Он не только дает обратную матрицу 3x3, но также дает вам определитель и сопряженную матрицу 3x3, которую вы вводите.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по скорости за единицу
задачи по сравнению ставок
Преобразование обычных единиц словесные задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами 00 00 00 Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями в словах
Словесные задачи с линейным неравенством
03 Задачи со словами
Проблемы со словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами по теореме Пифагора
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
Домен и диапазон 9163 рациональных функций
1 Область и диапазон 9163 рациональных функций1 функции с отверстиямиГрафики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
видение
Л. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении в степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Матрица, обратная
Матрица, обратная матрице, играет в матричной алгебре те же роли, что и обратная величина числа и деления в обычной арифметике: так же, как мы можем решить простое уравнение типа \ (4 x = 8 \) для \ (x \) умножив обе части на обратную \ [4 x = 8 \ Rightarrow 4 ^ {- 1} 4 x = 4 ^ {- 1} 8 \ Rightarrow x = 8/4 = 2 \], мы можем решить матричное уравнение типа \ (\ mathbf {A x} = \ mathbf {b} \) для вектора \ (\ mathbf {x} \) путем умножения обеих сторон на обратную матрицу \ (\ mathbf {A} \ ), \ [\ mathbf {A x} = \ mathbf {b} \ Rightarrow \ mathbf {A} ^ {- 1} \ mathbf {A x} = \ mathbf {A} ^ {- 1} \ mathbf {b} \ Rightarrow \ mathbf {x} = \ mathbf {A} ^ {- 1} \ mathbf {b} \]
Следующие примеры иллюстрируют основные свойства обратной матрицы. {-1} = а / а = 1 \).
{-1} = а / а = 1 \).
NB: Иногда вы получаете очень маленькие недиагональные значения (например, 1.341e-13 ). Функция zapsmall () округляет их до 0.
## [, 1] [, 2] [, 3]
## [1,] 1 0 0
## [2,] 0 1 0
## [3,] 0 0 1 3. Обратный -
рефлексивный : inv (inv (A)) = A Дважды взяв обратное, вы вернетесь к тому, с чего начали.
## [, 1] [, 2] [, 3]
## [1,] 5 1 0
## [2,] 3 -1 2
## [3,] 4 0 -1 4.
inv (A) является симметричным тогда и только тогда, когда A является симметричным ## [, 1] [, 2] [, 3]
## [1,] 0,0625 0,6875 0,25
## [2,] 0,0625 -0,3125 0,25
## [3,] 0,1250 -0,6250 -0,50 ## [1] ЛОЖЬ ## [1] ЛОЖЬ Вот симметричный случай:
B <- матрица (c (4, 2, 2,
2, 3, 1,
2, 1, 3), nrow = 3, byrow = TRUE)
inv (B) ## [, 1] [, 2] [, 3]
## [1,] 0. 50 -0,25 -0,25
## [2,] -0,25 0,50 0,00
## [3,] -0,25 0,00 0,50
50 -0,25 -0,25
## [2,] -0,25 0,50 0,00
## [3,] -0,25 0,00 0,50 ## [, 1] [, 2] [, 3]
## [1,] 0,50 -0,25 -0,25
## [2,] -0,25 0,50 0,00
## [3,] -0,25 0,00 0,50 ## [1] ИСТИНА ## [1] ИСТИНА ## [1] ИСТИНА Дополнительные свойства обратной матрицы
1. матрица, обратная диагонали = диагональ (1 / диагональ)
В этих простых примерах часто бывает полезно показать результаты матричных вычислений в виде дробей, используя MASS :: fractions () .
## [, 1] [, 2] [, 3]
## [1,] 1 0,0 0,00
## [2,] 0 0,5 0,00
## [3,] 0 0,0 0,25 ## [, 1] [, 2] [, 3]
## [1,] 1 0 0
## [2,] 0 1/2 0
## [3,] 0 0 1/4 2. Обратное обратное:
inv (inv (A)) = A A <- матрица (c (1, 2, 3, 2, 3, 0, 0, 1, 2), nrow = 3, byrow = TRUE)
AI <- inv (A)
inv (AI) ## [, 1] [, 2] [, 3]
## [1,] 1 2 3
## [2,] 2 3 0
## [3,] 0 1 2 3.
 инверсия транспонировать :
инверсия транспонировать : inv (t (A)) = t (inv (A)) ## [, 1] [, 2] [, 3]
## [1,] 1,50 -1,0 0,50
## [2,] -0,25 0,5 -0,25
## [3,] -2,25 1,5 -0,25 ## [, 1] [, 2] [, 3]
## [1,] 1,50 -1,0 0,50
## [2,] -0,25 0,5 -0,25
## [3,] -2,25 1,5 -0,25 4. инверсия скалярной * матрицы:
inv (k * A) = (1 / k) * inv (A) ## [, 1] [, 2] [, 3]
## [1,] 0.3 -0,05 -0,45
## [2,] -0,2 0,10 0,30
## [3,] 0,1 -0,05 -0,05 ## [, 1] [, 2] [, 3]
## [1,] 0,3 -0,05 -0,45
## [2,] -0,2 0,10 0,30
## [3,] 0,1 -0,05 -0,05 5. инверсия матричного произведения:
inv (A * B) = inv (B)% *% inv (A) B <- матрица (c (1, 2, 3, 1, 3, 2, 2, 4, 1), nrow = 3, byrow = TRUE)
C <- B [, 3: 1]
А% *% В ## [, 1] [, 2] [, 3]
## [1,] 9 20 10
## [2,] 5 13 12
## [3,] 5 11 4 ## [, 1] [, 2] [, 3]
## [1,] 4. 0 -1,50 -5,50
## [2,] -2,0 0,70 2,90
## [3,] 0,5 -0,05 -0,85
0 -1,50 -5,50
## [2,] -2,0 0,70 2,90
## [3,] 0,5 -0,05 -0,85 ## [, 1] [, 2] [, 3]
## [1,] 4,0 -1,50 -5,50
## [2,] -2,0 0,70 2,90
## [3,] 0,5 -0,05 -0,85 Это распространяется на любое количество членов: обратное произведение - произведение обратных чисел в обратном порядке.
## [, 1] [, 2] [, 3]
## [1,] 77 118 49
## [2,] 53 97 42
## [3,] 41 59 24 ## [, 1] [, 2] [, 3]
## [1,] 1.{-1} \)
Определитель обратного является обратным (обратным) определителем
## [1] 0,25
## [1] 0,25
Геометрические интерпретации
Некоторые из этих свойств обратной матрицы легче понять из геометрических диаграмм. Здесь мы берем невырожденную матрицу \ (2 \ times 2 \) \ (A \),
## [, 1] [, 2]
## [1,] 2 1
## [2,] 1 2
## [1] 3
Чем больше определитель \ (A \), тем меньше определитель \ (A ^ {- 1} \).
## [, 1] [, 2]
## [1,] 2/3 -1/3
## [2,] -1/3 2/3
## [1] 0,3333
Теперь постройте строки \ (A \) как векторы \ (a_1, a_2 \) от начала координат в двухмерном пространстве. Как показано в виньетке ("det-ex1") , определяющим фактором является площадь параллелограмма, определяемая этими векторами.
номинал (мар = c (3,3,1,1) +. 1)
xlim <- c (-1,3)
ylim <- c (-1,3)
plot (xlim, ylim, type = "n", xlab = "X1", ylab = "X2", asp = 1)
сумма <- A [1,] + A [2,]
# рисуем параллелограмм, определяемый строками A
многоугольник (rbind (c (0,0), A [1,], sum, A [2,]), col = rgb (1,0,0 ,.{-1} = I \).
Можно задаться вопросом, зависят ли эти свойства от симметрии \ (A \), поэтому вот еще один пример для матрицы A <- matrix (c (2, 1, 1, 1), nrow = 2) , где \ (\ det (A) = 1 \).
## [, 1] [, 2]
## [1,] 2 1
## [2,] 1 1
## [, 1] [, 2]
## [1,] 1 -1
## [2,] -1 2
Площади двух параллелограммов одинаковы, потому что \ (\ det (A) = \ det (A ^ {- 1}) = 1 \).
Нахождение обратной матрицы 3x3
Постановка задачи
Зачем вам вообще нужно искать обратную матрицу 3x3? Что ж, матрицы и обратные матрицы находят множество применений в геометрии, естественных науках и особенно в информатике. Допустим, вы компьютерный дизайнер или когда-нибудь хотите им стать, и вам нужно взять приведенную ниже матрицу и найти ее обратную.
Чтобы найти обратную матрицу 3x3, мы сначала должны знать, что такое обратная матрица.Математически это определение довольно просто. Просто посмотрите на уравнение ниже:
Давайте посмотрим на все члены в приведенном выше матричном уравнении и посмотрим, что они означают на простом английском языке. M - это просто наша исходная матрица. M в степени -1 - это математический символ матрицы, обратной M. И, наконец, I - это единичная матрица , у которой единицы на главной диагонали и нули везде. Выглядит это так:
Выглядит это так:
Итак, обратная матрица - это матрица, на которую нам придется умножить нашу исходную матрицу, чтобы получить единичную матрицу.Достаточно простая концепция, не так ли? Но как вычислить обратную матрицу? Для этого обратимся к другому матричному уравнению:
Это уравнение показывает нам, что для нахождения обратной матрицы мы должны найти сопряженную матрицу и разделить ее на определитель. Давайте посмотрим на них по очереди, начиная с определителя.
Определитель
Определитель матрицы - это единственное число, которое является характеристикой этой матрицы.Определитель можно найти несколькими способами. В этом упражнении мы будем использовать метод, который использует расширение по строке или столбцу. Почему? Потому что этот метод сокращает количество вычислений, если в вашей матрице есть нули. Поскольку у нас есть оба нуля в нашей матрице и мы хотели бы сократить количество вычислений, этот метод нам подойдет.
Поскольку у нас есть оба нуля в нашей матрице и мы хотели бы сократить количество вычислений, этот метод нам подойдет.
Чтобы использовать метод раскрытия, нам нужно умножить каждый член в строке или столбце, который мы выбираем, на его кофактор. Кофакторы являются определителями подматрицы матричного элемента, который не включает в себя строки или столбец этого элемента.Звучит запутанно, но на самом деле все довольно просто.
Например, кофактор матричного элемента M в первой строке и первом столбце будет определителем подматрицы, которая не включает никаких элементов ни из первой строки (1, 2, 3), ни из первого столбца (1 , 0, 1). Первая строка, расширение элемента первого столбца, умноженное на его сомножитель, выглядит следующим образом:
Продолжая наше расширение по первому столбцу, у нас будет элемент первого столбца (1, 0, 1), второй строки (0, 1, -2), умноженный на кофактор. Но ждать! Этот элемент равен 0, а все, что умножается на 0, равно 0. Нам не нужно ничего вычислять для этого члена. Это экономит нам шаг, чего мы и хотели в первую очередь.
Но ждать! Этот элемент равен 0, а все, что умножается на 0, равно 0. Нам не нужно ничего вычислять для этого члена. Это экономит нам шаг, чего мы и хотели в первую очередь.
Последний член в нашем расширении будет первым столбцом (1, 0, 1), третьей строкой (1, 2, 5) и будет выглядеть так:
Когда мы складываем все элементы раскрытия, мы получаем 9 + 0 - 7 = 2. Это означает, что определитель нашей матрицы равен 2.Много работы для небольшого числа, но мы добиваемся прогресса.
Матричный калькулятор в App Store
Калькулятор матриц
Это приложение включает в себя:
Калькулятор сложения матриц
Калькулятор вычитания матриц
Калькулятор умножения матриц 2x2
Калькулятор умножения матриц 3x3
Калькулятор определителя матрицы
3x3 Калькулятор обратных матриц215 Калькулятор вычитания матриц 2x16 215 Калькулятор сложения и вычитания матриц 4x4
Калькулятор умножения матриц 4x4
Калькулятор обратной матрицы 4x4
Калькулятор квадратной матрицы
Калькулятор матрицы транспонирования
Калькулятор определителя матрицы 4x4
Калькулятор определителя правила Крамера
Калькулятор определения матрицы Гаусса 1516 Калькулятор исключающей матрицы 916
вычислитель обратной матрицы
вычислитель умножения матрицы
обратный вычислитель
обратная матрица
обратная матрица
вычислитель rref
генератор матриц
обратная матрица 9 1615 онлайн-калькулятор матриц
обратимая матрица
обратная матрица 3x3
расширенная матрица калькулятор
матричный калькулятор онлайн
обратная 3x3 матрица
вычислитель определителя
редуктор матрицы
редуктор
обратная матрица 3x3
вычислитель определителя матрицы
обратная 2x2 матрица
обратная матрица
обратная матрица 2x2
вычислитель уменьшения матрицы
обратная матрица 3x3
инвертор матрицы
матричная формула
решатель матриц онлайн
обратный вычислитель матрица
вычислитель собственных значений
2x2 матрица обратная
найти обратную матрицу
обратная матрица
3x3 матрица обратная
вычисление матриц умножения 1615
вычислитель матриц
обратная матрица вычислителя 3x3
обратная матрица вычислителя
мультипликативный обратный вычислитель
определитель вычислителя 3x3
обратная матрица вычислителя 3x3
найти обратную матрицу
вычислитель матрица 9 1615 онлайн-решатель матриц
обратная матрица 3x3
обратная матрица 3x3-матричный калькулятор
матричный калькулятор
матричный калькулятор
матричный онлайн-калькулятор
решающий матричный калькулятор
матричный калькулятор rref
поиск обратной матрицы
матричный обратный онлайн
комплексный матричный калькулятор
Калькулятор матриц 3x3
калькулятор для матриц
формула обратной матрицы
калькулятор с матрицей
онлайн-матрица
вычислитель ранга матрицы
вычислитель матричных операций
метод инверсии матриц
вычислитель сопряженной матрицы
матрица обратная 3x3
вычислитель решающих матриц
вычислитель определителя 4x4
обратная матрица 3x3
вычислить обратную матрицу
обратная матрица онлайн
метод обратной матрицы
вычислитель обратной матрицы 3x3
математическая матрица вычислитель
кофакторный вычислитель матрицы
вычислитель произведения матрицы
3x3 обратная матрица 9161 5 найти обратную матрицу 3x3
инвертировать матрицу
матричные компьютеры
инвертировать матрицу 2 на 2
решатель определителя
решить матрицы онлайн
найти обратный калькулятор
онлайн матричный обратный
графический калькулятор
найти обратный матричный калькулятор
найти обратный матрицы 3x3
научный калькулятор
калькулятор собственных векторов
генератор матриц онлайн
калькулятор сокращения строк матрицы
калькулятор диагонализации
калькулятор переходной матрицы
обратная матрица 2x2
решение матрицы онлайн
детерминантный матричный калькулятор
матричный калькулятор диагонализации
матричный математический матричный калькулятор
Поддерживаемые операции с матрицей :
- Матрица инверсная.
- Определитель матрицы.
- Матричное скалярное умножение.
- Добавление матрицы.
- Матричное вычитание.
- Умножение матриц.
- Транспонирование матриц.
Приложение может работать с:
- целыми числами (-2, -1, 0, 1, 2 и т. Д.).
- Десятичные дроби (1,5, 3,14 и т. Д.).
- Обычные дроби (1/2, 3/4, 7/3 и т. Д.).
- Комплексные числа (i, 1 + i, 1 / 2-2i, 0,5 + 2 / 3i и т. Д.).
Проверьте результаты сложения матриц 2x2, 3x3, 4x4, nxn, вычитания, умножения, определителя, обратной или транспонированной матрицы или выполните такие вычисления, используя эти формулы и калькуляторы.Основная цель этих матричных инструментов - помочь студентам, специалистам и исследователям быстро выполнять такие вычисления или проверять результаты таких вычислений для анализа, определения и решения линейных функций и уравнений. Эти матричные формулы и калькуляторы могут дать ответы на многие сложные алгоритмы приложений обработки цифровой информации, изображений и видео.


 Полученная матрица обратная для исходной.
Полученная матрица обратная для исходной.
 е. нужно ввести ее как
формулу массива
(формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2 )
е. нужно ввести ее как
формулу массива
(формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2 )


 Следовательно, если этот определитель равен
Следовательно, если этот определитель равен  В символической записи это переводится как
В символической записи это переводится как  50 -0,25 -0,25
## [2,] -0,25 0,50 0,00
## [3,] -0,25 0,00 0,50
50 -0,25 -0,25
## [2,] -0,25 0,50 0,00
## [3,] -0,25 0,00 0,50  0 -1,50 -5,50
## [2,] -2,0 0,70 2,90
## [3,] 0,5 -0,05 -0,85
0 -1,50 -5,50
## [2,] -2,0 0,70 2,90
## [3,] 0,5 -0,05 -0,85 

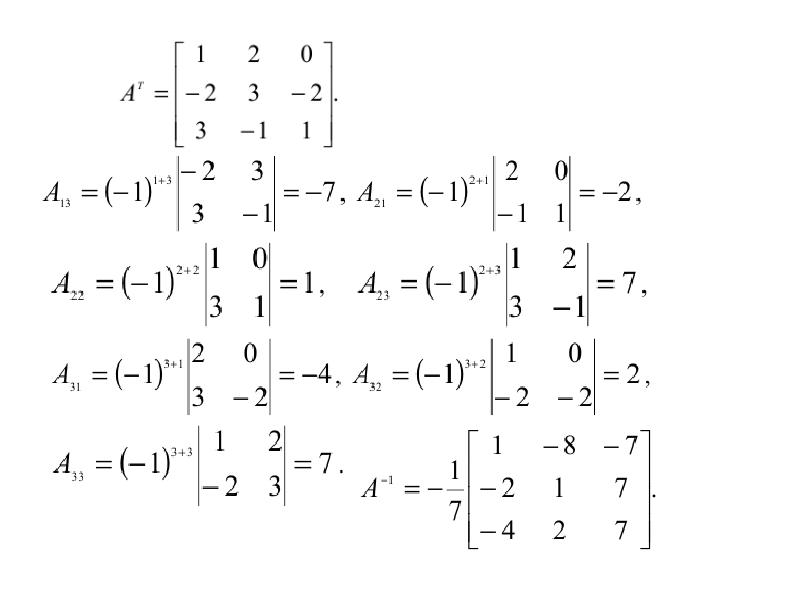 Выглядит это так:
Выглядит это так: Поскольку у нас есть оба нуля в нашей матрице и мы хотели бы сократить количество вычислений, этот метод нам подойдет.
Поскольку у нас есть оба нуля в нашей матрице и мы хотели бы сократить количество вычислений, этот метод нам подойдет. Но ждать! Этот элемент равен 0, а все, что умножается на 0, равно 0. Нам не нужно ничего вычислять для этого члена. Это экономит нам шаг, чего мы и хотели в первую очередь.
Но ждать! Этот элемент равен 0, а все, что умножается на 0, равно 0. Нам не нужно ничего вычислять для этого члена. Это экономит нам шаг, чего мы и хотели в первую очередь.
