T test в статистике – t-критерий Стьюдента

Занятие 7.Тест Стьюдента для независимых выборок — Основы доказательной медицины. Биомедицинская статистика. — Внауке.by

Критерий Стьюдента для независимых выборок

Критерий Стьюдента (t-тест Стьюдента или просто «t-тест») применяется, если нужно сравнить только две группы количественных признаков с нормальным распределением (частный случай дисперсионного анализа). Примечание: этим критерием нельзя пользоваться, сравнивая попарно несколько групп, в этом случае необходимо применять дисперсионный анализ. Ошибочное использование критерия Стьюдента увеличивает вероятность «выявить» несуществующие различия. Например, вместо того, чтобы признать несколько методов лечения равно эффективными (или неэффективными), один из них объявляют лучшим.

Два события называются независимыми, если наступление одного из них никак не влияет на наступление другого. Аналогично, две совокупности можно назвать независимыми, если свойства одной из них никак не связаны со свойствами другой. 

Пример выполнения  t-теста в программе STATISTICA.

Женщины в среднем ниже мужчин, однако, это не является результатом того, что мужчины оказывают какое-либо влияние на женщин — дело здесь в генетических особенностях пола. С помощью t-теста необходимо проверить, имеется ли статистически значимое различие между средними значениями роста в группах мужчин и женщин. (В учебных целях мы допускаем, что данные о росте подчиняются закону нормального распределения и поэтому t-тест применим).

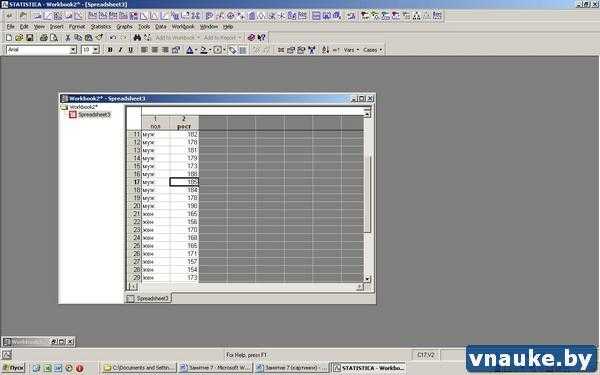
Рисунок 1. Пример оформления данных для выполнения t-теста для независимых выборок

Обратите внимание на то, как оформлены данные на рисунке 1. Как и при построении графиков типа Whisker plot или Box-whisker plot, в таблице имеются две переменные: одна из них — группирующая (

Grouping variable) («Пол») — содержит коды (муж и жен), позволяющие программе установить, какие из данных о росте принадлежат какой группе; вторая — т.н. зависимая переменная (Dependent variable) («Рост») — содержит собственно анализируемые данные. Однако при выполнении t-теста для независимых выборок в программе STATISTICA возможен и другой вариант оформления — данные для каждой из групп («Мужчины» и «Женщины») можно ввести в отдельные столбцы (рисунок 2).

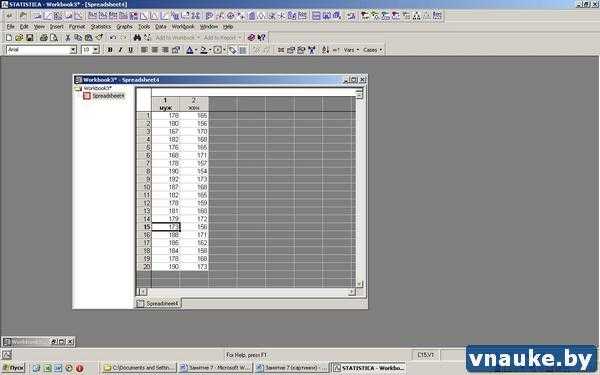
Рисунок 2. Еще один вариант оформления данных для выполнения t-теста для независимых выборок

Для выполнения t-теста для независимых выборок необходимо выполнить следующие действия:

1-а. Запустить модуль t-теста из меню  Statistics > Basic statistics/Tables > t

-test, independent, by groups (если в таблице с данными есть группирующая переменная, см.рисунок 3)​

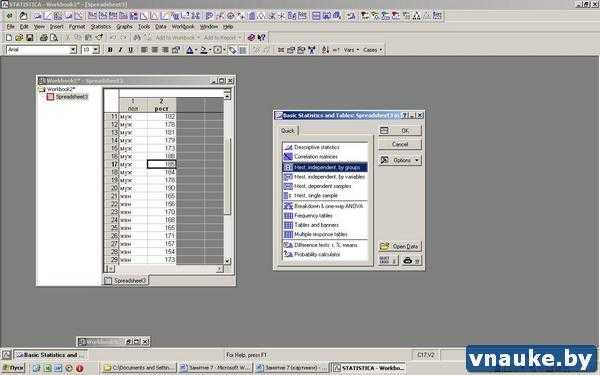
ИЛИ

1-б. Запустить модуль t-теста из меню  Statistics > Basic statistics/Tables > t-test, independent, by variables (если данные внесены в самостоятельные столбцы, см. рисунок 4).

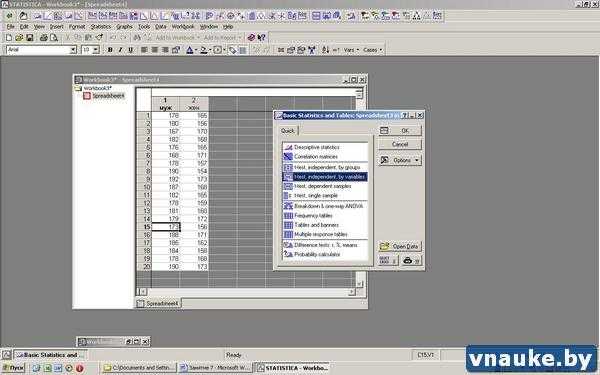
Ниже описывается вариант теста, при котором в таблице с данными имеется группирующая переменная. 

2. В открывшемся окне нажать кнопку Variables и указать программе, какая из переменных таблицы Sreadsheet является группирующей, а какая — зависимой (рисунки 5-6).

Рисунок 5. Выбор переменных для включения в t

-тест

Рисунок 6. Окно с выбранными переменными для проведения t-теста

3. Нажать на кнопку Summary: T-tests.

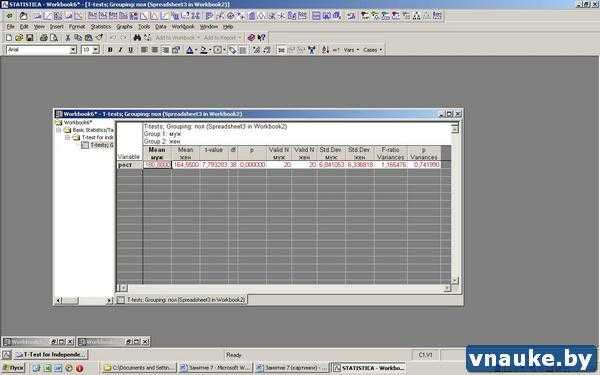
Рисунок 7. Результы t-теста для независимых выборок

В итоге программа выдаст рабочую книгу Workbook, содержащую таблицу с результатами t-теста (рисунок 7). Эта таблица имеет несколько столбцов:

• Mean (муж) — среднее значение роста  в группе «Мужчины»;
• Mean (жен) — среднее значение роста в группе «Женщины»;
• t-value: значение рассчитанного программой t-критерия Стьюдента;
• df — число степеней свободы;
• P — вероятность справедливости гипотезы о том, что сравниваемые средние значения не различаются. Фактически, это самый главный результат анализа, поскольку именно значение P говорит, верна ли проверяемая гипотеза. В нашем примере P > 0.05, из чего можно сделать вывод о том, что статистически значимые различия между ростом мужчин и женщин отсутствуют.
• Valid N (муж) — объем выборки «Мужчины»;
• Valid N (жен) — объем выборки «Женщины»;
• Std. dev. (муж) — стандартное отклонение выборки «Мужчины»;
• Std. dev. (жен) — стандартное отклонение выборки «Женщины»;
• F-ratio, Variances — значение F-критерия Фишера, с помощью которого проверяется гипотеза о равенстве дисперсий в сравниваемых выборках;
• P, Variances — вероятность справедливости гипотезы о том, что дисперсии сравниваемых выборок не различаются.

 

 

---

---

---

Добавление комментариев доступно только зарегистрированным пользователям

vnauke.by

T-критерии

t-критерий для одной выборки

t-критерии для двух независимых выборок

t-критерии для двух зависимых выборок

t-критерий для одной выборки

t-критерий для одной выборки позволяет проверить гипотезу о равенстве выборочного среднего некоторому заданному числу.

В так называемых одновыборочных t-критериях, наблюдаемое среднее (вычисленное по реализации выборки) сравнивается с ожидаемым (или эталонным) средним выборки μ (т.е. с некоторым теоретическим средним).

Статистика критерия: имеет t-распределение Стьюдента с (n-1) степенью свободы.

Выборочное стандартное отклонение s оценивается по наблюдаемой реализации выборки:

Вычисленное значение t проверяют на предмет попадания в критическую область (критическое значение можно найти по таблицам).

Если вычисленное значение t попадает в критическую область, то говорят, что отвергается на уровне α в пользу альтернативы.

Например, пусть установлены некоторые фиксированные показатели эффективности деятельности торговой компании: уровень рентабельности товарооборота — 20% . Таким образом, имея данные о рентабельности (скажем, по месяцам) мы можем применить одновыборочный t-критерий для проверки гипотезы о равенстве среднего уровня рентабельности заданному значению.

Отметим, что в данном случае необходимо применить односторонний критерий, т.к. нарушение эффективности коммерческой деятельности произойдет только в случае снижения показателя рентабельности относительно нормативного.

t-критерий для двух независимых выборок

t-критерий для двух независимых выборок (двухвыборочный t-критерий) проверяет гипотезу о равенстве средних в двух выборках (предполагается нормальность распределения переменных, а также равенство дисперсий выборок). Критерий применяется, например, если необходимо сравнить результаты баллов ЕГЭ в двух разных школах.

,

где

Алгоритм принятия решения об отклонении или не отклонении нулевой гипотезы аналогичен рассмотренному выше

t-критерий для двух зависимых выборок

t-критерий для двух зависимых (парных) выборок применяется, например, для оценки состояния больного до и после лечения. Нулевая гипотеза также гласит об отсутствии различий (среднее значение разности наблюдений в двух группах равно нулю).

,

где

Алгоритм принятия решения об отклонении или не отклонении нулевой гипотезы аналогичен рассмотренному выше

Связанные определения:
Параметрические методы статистики

В начало

Содержание портала

statistica.ru

2. Реализация в statistica

STATISTICA позволяет применять четыре варианта t-критерия:

• критерий для независимых выборок по группам (t-test, independent by groups),

• критерий для независимых переменных (t-test, independent by variables),

• критерий для зависимых выборок (t-test, dependent samples),

• критерий для одной выборки (t-test, single sample).

2.1. Применение t-критерия для независимых выборок

Данный метод сравнения позволяет проверить гипотезу о том, что средние значения двух генеральных совокупностей, из которых извлечены сравниваемые независимые выборки, отличаются друг от друга.

В программе STATISTICA реализовано два способа сравнения данных с помощью данного метода, которые основаны на обработке двух разных матриц данных: по группам (by groups), если в таблице с данными есть группирующая переменная и по переменным (by variables), если данные внесены в самостоятельные столбцы.

Для применения t-критерия для независимых выборок по группам необходимо использовать следующую последовательность команд:

Statistics (Статистики) – Basic Statistics and Tables (Основные статистики и таблицы) — t—test, independent by

groups (t-критерий для независимых выборок по группам)

В результате чего откроется диалоговое окно (рис.12), в котором необходимо указать зависимую переменную (Dependent) и группирующую переменную (Grouping), градациям которой соответствуют независимые выборки для вычисления t-критерия. Группирующая переменная должна быть дискретной и иметь две градации.

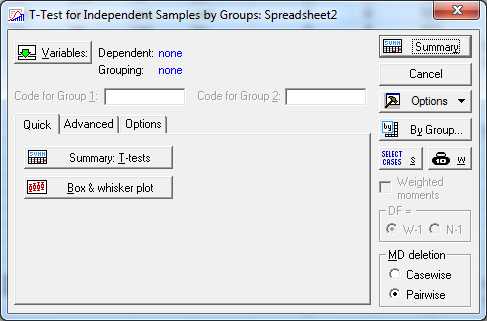
Рис.12.ДиалоговоеокноT-Test for independent Samples by groups

После выбора группирующей перемен в поле Code for Group 1 и Code for Group 2 появятся градации группирующей переменной. Чтобы рассчитать значение теста Левана для проверки равенства дисперсии в двух группах, необходимо перейти на вкладку Options (Опции) и установить флажок Levene’s test. Также в STATISTICA доступен критерий Брауна – Форсайта (Brown&Forsythe test). После нажатия на кнопку Summary на экран будет выведена таблица результатов вычисления t-критерия:

• Mean — среднее значение в каждой группе;

• t-value — значениеt-критерия Стьюдента;

• df — число степеней свободы;

• P — вероятность справедливости гипотезы о том, что сравниваемые средние значения не различаются;

• Valid N — объем каждой выборки;

• Std. dev.- стандартное отклонение для каждой выборки;

• F-ratio, Variances- значение F-критерия Фишера, с помощью которого проверяется гипотеза о равенстве дисперсий в сравниваемых выборках;

• P, Variances- вероятность справедливости гипотезы о том, что дисперсии сравниваемых выборок не различаются.

Анализ данных с помощью t—критерия, сравнения средних и меры отклонения от среднего в группах можно производить с помощью диаграмм размаха. Эти графики позволяют визуально оценить степень зависимости между группирующей и зависимой переменными.

Для того, чтобы на экран была выведена коробчатая диаграмма необходимо, в диалоговом окне T—Test for independent Samples by groups (рис.12), щелкнуть на кнопке Box&whisker plot, после чего на экран будет выведен ящик с усами.

Пример сравнения среднего значения индекса массы тела до программы похудения для мужчин и женщин представлен соответствующая диаграмма размаха представлены на рис.13. и рис.14.

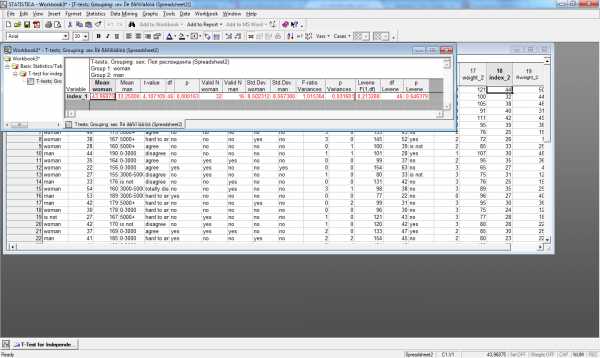
Рис.13. Применение t-критерия для независимых выборок

(по одной переменной)

Из результатов следует, что выборка из 32 женщин имеет средний индекс массы тела до программы похудения 43,9687, выборка из 16 мужчины — средний индекс массы тела до программы похудения 33,2500. Различия статистически достоверны на высоком уровне значимости (p = 0,000136). Критерий равенства дисперсий Ливиня указывает на то, что дисперсии двух распределений статистически значимо не различаются (p = 0,646), следовательно, применение t-критерия корректно.

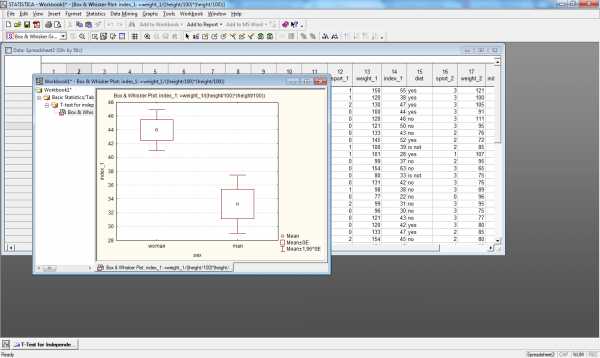
Рис.14. Коробчатая диаграмма для переменной index_1, сгруппированной по переменой sex

На рис.15. приведен пример сравнения индексов массы тела до и после программы похудения для мужчин и женщин, а на рис.16. коробчатые диаграммы отдельно для переменной index_1 и index_2 сгруппированные по переменной sex

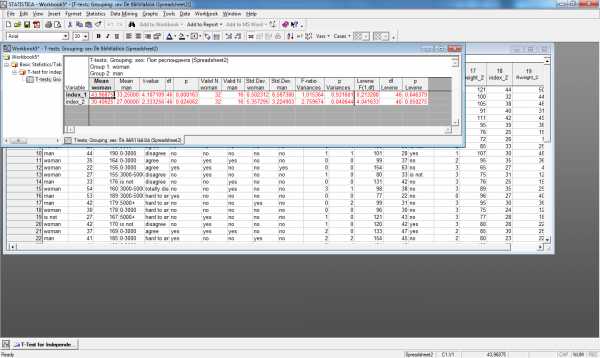
Рис.15. Применение t-критерия для независимых выборок

(по двум переменным)

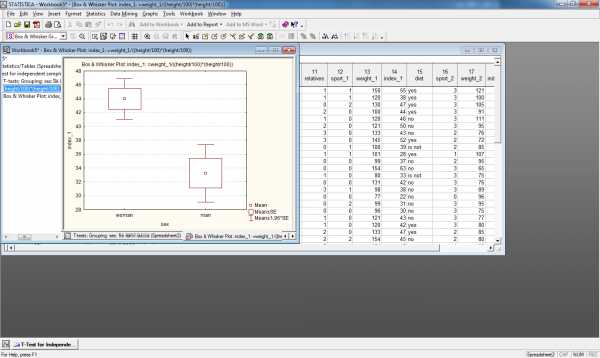
Рис.16. Коробчатые диаграммы для переменной index_1 и index_2 сгруппированные по переменной sex

studfiles.net

Z-тест и Т-тест 2019

Z-тест Vs T-test

Иногда измерение каждого отдельного предмета просто нецелесообразно. Вот почему мы разработали и использовали статистические методы для решения проблем. Самый практичный способ сделать это — измерить только выборку населения. Некоторые методы проверяют гипотезы путем сравнения. Двумя наиболее известными статистическими гипотезами являются T-тест и Z-тест. Попробуем разбить два.

Т-тест является статистическим критерием гипотезы. В таком тесте тестовая статистика следует Т-распределению ученика, если нулевая гипотеза верна. T-статистика была введена W.S. Госсетт под псевдонимом «Студент». Т-тест также упоминается как «Студенческий Т-тест». Весьма вероятно, что T-тест является наиболее часто используемой процедурой статистического анализа данных для тестирования гипотез, поскольку она проста и проста в использовании. Кроме того, он гибкий и адаптируемый к широкому спектру условий.

Существуют различные Т-тесты, и два наиболее часто применяемых теста — это однокаскадные и парные образцы T-тестов. Однокаскадные Т-тесты используются для сравнения среднего значения выборки с известным средним значением. С другой стороны, тесты с двумя образцами, с другой стороны, используются для сравнения независимых выборок или зависимых выборок.

Т-тест лучше всего применять, по крайней мере теоретически, если у вас ограниченный размер выборки (n <30), если переменные примерно нормально распределены, а изменение баллов в двух группах не является достоверно иным. Это также здорово, если вы не знаете стандартное отклонение населения. Если стандартное отклонение известно, тогда было бы лучше использовать другой тип статистического теста — Z-тест. Z-тест также применяется для сравнения образцов и популяций, чтобы знать, существует ли существенная разница между ними. Z-тесты всегда используют нормальное распределение и также идеально применяются, если известно стандартное отклонение. Z-тесты часто применяются, если выполняются определенные условия; в противном случае другие статистические тесты, такие как T-тесты, применяются в замене. Z-тесты часто применяются в больших образцах (n> 30). Когда T-тест используется в больших образцах, t-тест становится очень похожим на Z-тест. Существуют флуктуации, которые могут возникать при отклонениях образцов T-тестов, которых нет в Z-тестах. Из-за этого в обоих тестах есть различия.

Резюме:

1. Z-тест — это статистический тест гипотезы, который следует за нормальным распределением, тогда как T-тест следует за T-распределением Стьюдента. 2. Т-тест подходит, когда вы обрабатываете небольшие образцы (n <30), в то время как Z-тест подходит, когда вы обрабатываете отмеренные до больших образцов (n> 30). 3. Т-тест более адаптируется, чем Z-тест, поскольку Z-тест часто требует определенных условий, чтобы быть надежным. Кроме того, T-тест имеет множество методов, которые подходят для любой потребности. 4. Т-тесты чаще используются, чем Z-тесты. 5. Z-тесты предпочтительнее, чем T-тесты, когда известны стандартные отклонения.

ru.esdifferent.com

СТЬЮДЕНТ.ТЕСТ (функция СТЬЮДЕНТ.ТЕСТ) — Служба поддержки Office

Примечание:  Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке) .

Возвращает вероятность, соответствующую t-тесту Стьюдента. Функция СТЬЮДЕНТ.ТЕСТ позволяет определить вероятность того, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.

Синтаксис

СТЬЮДЕНТ.ТЕСТ(массив1;массив2;хвосты;тип)

Аргументы функции СТЬЮДЕНТ.ТЕСТ описаны ниже.

• Массив1     Обязательный. Первый набор данных.

• Массив2     Обязательный. Второй набор данных.

• Хвосты     Обязательный. Число хвостов распределения. Если значение «хвосты» = 1, функция СТЬЮДЕНТ.ТЕСТ возвращает одностороннее распределение. Если значение «хвосты» = 2, функция СТЬЮДЕНТ.ТЕСТ возвращает двустороннее распределение.

• Тип     Обязательный. Вид выполняемого t-теста.

Параметры

Тип	Выполняемый тест
1	Парный
2	Двухвыборочный с равными дисперсиями (гомоскедастический)
3	Двухвыборочный с неравными дисперсиями (гетероскедастический)

Замечания

• Если аргументы «массив1» и «массив2» имеют различное число точек данных, а «тип» = 1 (парный), то функция СТЬЮДЕНТ.ТЕСТ возвращает значение ошибки #Н/Д.

• Аргументы «хвосты» и «тип» усекаются до целых значений.

• Если аргумент «хвосты» или «тип» не является числом, то функция СТЬЮДЕНТ.ТЕСТ возвращает значение ошибки #ЗНАЧ!.

• Если аргумент «хвосты» принимает любое значение, отличное от 1 и 2, то функция СТЬЮДЕНТ.ТЕСТ возвращает значение ошибки #ЧИСЛО!.

• Функция СТЬЮДЕНТ.ТЕСТ использует данные аргументов «массив1» и «массив2» для вычисления неотрицательной t-статистики. Если «хвосты» = 1, СТЬЮДЕНТ.ТЕСТ возвращает вероятность более высокого значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими к генеральной совокупности с одним и тем же средним. Значение, возвращаемое функцией СТЬЮДЕНТ.ТЕСТ в случае, когда «хвосты» = 2, вдвое больше значения, возвращаемого, когда «хвосты» = 1, и соответствует вероятности более высокого абсолютного значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими к генеральной совокупности с одним и тем же средним.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные 1	Данные 2
3	6
4	19
5	3
8	2
9	14
1	4
2	5
4	17
5	1
Формула	Описание	Результат
=СТЬЮДЕНТ.ТЕСТ(A2:A10;B2:B10;2;1)	Вероятность, соответствующая парному критерию Стьюдента, с двусторонним распределением	0,196016

support.office.com

t-критерий Стьюдента — это… Что такое t-критерий Стьюдента?

t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.

t-статистика строится обычно по следующему общему принципу: в числителе случайная величина с нулевым математическим ожиданием (при выполнении нулевой гипотезы), а в знаменателе — выборочное стандартное отклонение этой случайной величины, получаемое как квадратный корень из несмещенной оценки дисперсии.

История

Данный критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).

Требования к данным

Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.

Требование нормальности распределения данных является необходимым для точного -теста. Однако, даже при других распределениях данных возможно использование -статистики. Во многих случаях эта статистика асимптотически имеет стандартное нормальное распределение — , поэтому можно использовать квантили этого распределения. Однако, часто даже в этом случае используют квантили не стандартного нормального распределения, а соответствующего распределения Стьюдента, как в точном -тесте. Асимптотически они эквивалентны, однако на малых выборках доверительные интервалы распределения Стьюдента шире и надежнее.

Одновыборочный t-критерий

Применяется для проверки нулевой гипотезы о равенстве математического ожидания некоторому известному значению .

Очевидно, при выполнении нулевой гипотезы . С учётом предполагаемой независимости наблюдений . Используя несмещенную оценку дисперсии получаем следующую t-статистику:

При нулевой гипотезе распределение этой статистики . Следовательно, при превышении критического значения нулевая гипотеза отвергается.

Двухвыборочный t-критерий для независимых выборок

Пусть имеются две независимые выборки объемами нормально распределенных случайных величин . Необходимо проверить по выборочным данным нулевую гипотезу равенстве математических ожиданий этих случайных величин .

Рассмотрим разность выборочных средних . Очевидно, если нулевая гипотеза выполнена . Дисперсия этой разности равна исходя из независимости выборок: . Тогда используя несмещенную оценку дисперсии получаем несмещенную оценку дисперсии разности выборочных средних: . Следовательно, t-статистика для проверки нулевой гипотезы равна

Эта статистика при справедливости нулевой гипотезы имеет распределение , где

Случай одинаковой дисперсии

В случае, если дисперсии выборок предполагаются одинаковыми, то . Тогда t-статистика равна:

Эта статистика имеет распределение

Двухвыборочный t-критерий для зависимых выборок

Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:

где  — средняя разность значений,  — стандартное отклонение разностей, а n — количество наблюдений

Эта статистика имеет распределение .

Проверка линейного ограничения на параметры линейной регрессии

С помощью t-теста можно также проверить произвольное (одно) линейное ограничение на параметры линейной регрессии, оцененной обычным методом наименьших квадратов. Пусть необходимо проверить гипотезу . Очевидно, при выполнении нулевой гипотезы . Здесь использовано свойство несмещенности МНК-оценок параметров модели . Кроме того, . Используя вместо неизвестной дисперсии ее несмещенную оценку получаем следующую t-статистику:

Эта статистика при выполнении нулевой гипотезы имеет распределение , поэтому если значение статистики выше критического, то нулевая гипотеза о линейном ограничении отклоняется.

Проверка гипотез о коэффициенте линейной регрессии

Частным случаем линейного ограничения является проверка гипотезы о равенстве коэффициента регрессии некоторому значению . В этом случае соответстующая t-статистика равна:

где  — стандартная ошибка оценки коэффициента — квадратный корень из соответствующего диагонального элемента ковариационной матрицы оценок коэффициентов.

При справедливости нулевой гипотезы распределение этой статистики — . Если значение статистики выше критического значения, то отличие коэффициента от является статистически значимым (неслучайным), в противном случае — незначимым (случайным, то есть истинный коэффициент вероятно равен или очень близок к предполагаемому значению )

Замечание

Одновыборочный тест для математических ожиданий можно свести к проверке линейного ограничения на параметры линейной регрессии. В одновыборочном тесте это «регрессия» на константу. Поэтому регрессии это и есть выборочная оценка дисперсии изучаемой случайной величины, матрица равна , а оценка «коэффициента» модели равна выборочному среднему. Отсюда и получаем выражение для t-статистики, приведенное выше для общего случая.

Аналогично можно показать, что двухвыборочный тест при равенстве дисперсий выборок также сводится к проверке линейных ограничений. В двухвыборочном тесте это «регрессия» на константу и фиктивную переменную, идентифицирующую подвыборку в зависимости от значения (0 или 1): . Гипотеза о равенстве математических ожиданий выборок может быть сформулирована как гипотеза о равенстве коэффициента b этой модели нулю. Можно показать, что соответствующая t-статистика для проверки этой гипотезы равна t-статистике, приведенной для двухвыборочного теста.

Также к проверке линейного ограничения можно свести и в случае разных дисперсий. В этом случае дисперсия ошибок модели принимает два значения. Исходя из этого можно также получить t-статистику, аналогичную приведенной для двухвыборочного теста.

Непараметрические аналоги

Аналогом двухвыборочного критерия для независимых выборок является U-критерий Манна–Уитни. Для ситуации с зависимыми выборками аналогами являются критерий знаков и T-критерий Вилкоксона

Литература

Student. The probable error of a mean. // Biometrika. 1908. № 6 (1). P. 1-25.

Столбчатая диаграмма · Совмещённая диаграмма · Диаграмма управления · Лесная диаграмма · Гистограмма · Q-Q диаграмма · Диаграмма выполнения · Диаграмма разброса · Стебель-листья · Ящик с усами

dic.academic.ru

Занятие 8. Тест Стьюдента для зависимых выборок — Основы доказательной медицины. Биомедицинская статистика. — Внауке.by

t-тест для зависимых выборок

С зависимыми выборками исследователь имеет дело каждый раз, когда измерения значений какого-либо признака выполняются на одних и тех же объектах. Распределение обоих выборок должно быть нормальным! В противном случае использование критерия Стьюдента недопустимо.

Рассмотрим следующий пример. Для сравнения эффективности двух антиаритмических лекарственных средств, 20 условным добровольцам (сопоставимым по возрасту, полу, росту, массе тела) дали  лекарство А, и через 1 час измерили частоту сердечных сокращений (ЧСС). Через 3 дня той же группе добровольцев дали лекарство Б в той же дозе и также через 1 час измерили ЧСС. Задача: выяснить, зависит ли ЧСС от вида используемого лекарственного средства.

Рисунок 1. Пример оформления данных для выполнения t-теста для зависимых выборок

Поскольку лекарства давались одним и тем же добровольцам, выборки, полученные в результате двух описанных выше экспериментов, являются зависимыми. Это объясняется тем, что уровень ЧСС через 1 час после дачи лекарства Б вполне мог испытывать определенное последействие лекарства А, т.е. ЧСС зависела от того, что происходило с добровольцами ранее. Для сравнения ЧСС в данном случае следует использовать t-тест для зависимых выборок. В учебных целях предполагается, что данные об ЧСС подчиняются закону нормального распределения.

Для выполнения t-теста для зависимых выборок необходимо:

1. Запустить соответствующий модуль из меню Statistics > Basic statistics/Tables > t-test, dependent samples.  Вместо использования меню Statistics можно нажать кнопку на дополнительной панели инструментов (Занятие 1).

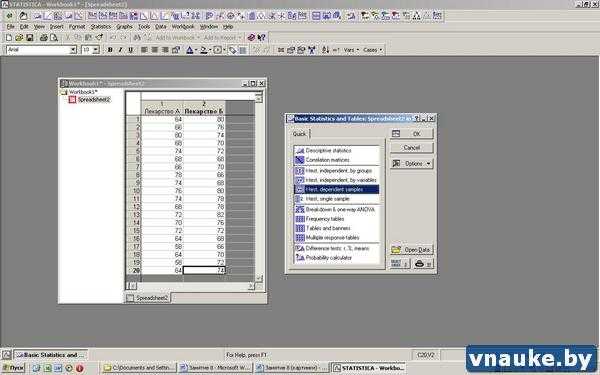
Рисунок 2.Запуск модуля t-test, dependent sample из меню Statistics > Basic statistics/Tables

В открывшемся окне нажать на кнопку Variables и указать программе первую (First variable) и вторую (Second variable) переменные, участвующие в анализе.

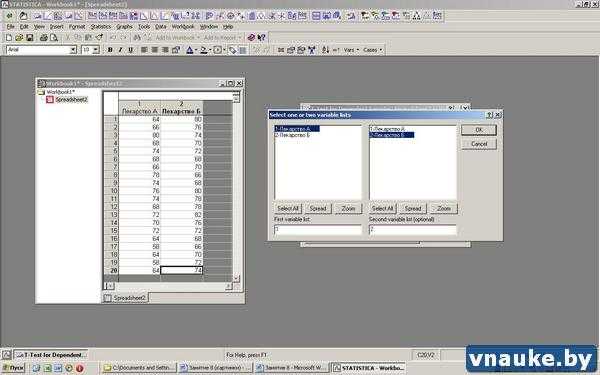
Рисунок 3-а. Выбор переменных, участвующих в анализе

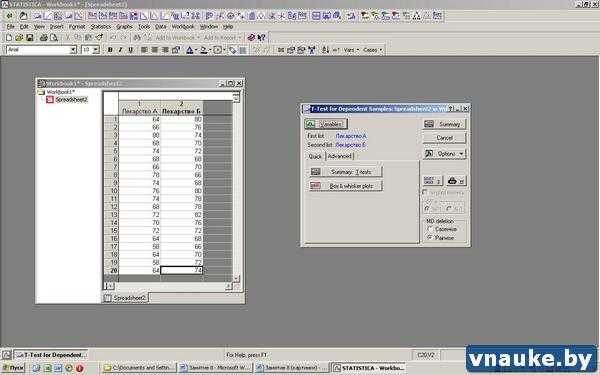
Рисунок 3-б. Выбор переменных, участвующих в анализе

3. Нажать на кнопку Summary: T-tests.

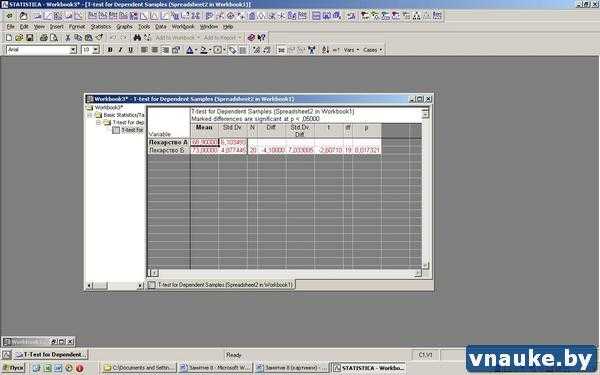
Рисунок 4. Рабочая книга с результатами t-теста для зависимых выборок

Программа откроет рабочую книгу, очень похожую на ту, с которой мы столкнулись при выполнении t-теста для независимых выборок. Она содержит следующие столбцы:

• Mean — средние значения ЧСС для каждой из сравниваемых групп;
• Std. dv. — стандартные отклонения для каждой из групп;
• N — число наблюдений;
• Diff. — средняя разница ЧСС;
• Std. dv. diff. — стандартное отклоение для средней разницы;
• t — значение t-критерия;
• df — число степенй свободы;
• Р — вероятность справедливости гипотезы о том, средние величины урожайности в сравниваемых группах не различаются. Как видно из таблицы, Р << 0.05. Это говорит о том, что ЧСС при использовании условных лекарства А и лекарства Б значительно различается (кстати, при наличии различий, результаты анализа в STATISTICA выделяются красным цветом).

В модулях обеих рассмотренных нами вариантов t-теста есть очень удобная возможность — построить график типа Box-whisker plot и визуально оценить, насколько велика разница между сравниваемыми группами. Достаточно нажать кнопку Box & Whisker Plots (см. рисунок 5)

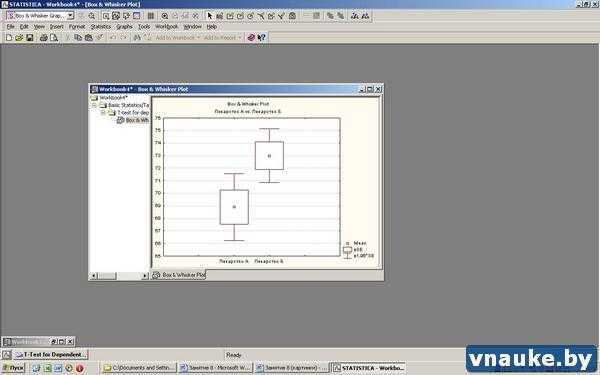
Рисунок 5. График Box & whisker plot, построенный на основе данных о ЧСС.

 

---

---

---

Добавление комментариев доступно только зарегистрированным пользователям

vnauke.by