1.3.3. Обратная матрица | Контрольные работы по математике и другим пред
Пусть А – квадратная матрица порядка П. Матрица А-1 называется Обратной к матрице А, если
Из того, что матрица А-1 может быть умножена на А как справа, так и слева, вытекает, что А-1 – тоже квадратная матрица порядка П.
Упражнение 1. Доказать, что (А-1)-1 = А.
Решение.
Пусть В = А-1. Тогда, поскольку по определению обратной матрицы
АВ = ВА = Е, матрица А является обратной для матрицы В, то есть
(А-1)-1 = А.
Из теоремы 3.1 следует, что |A||A-1| = |E| = 1. Таким образом, если у матрицы А существует обратная, то |A| ≠ 0 (такие матрицы называются Невырожден-ными) и
|A-1| = |A|-1.
Теорема 3.2 (о фальшивом разложении). Для любой квадратной матрицы А = ||Aij|| Порядка п справедливы равенства
Доказательство.
В случае I = J эти формулы вытекают из формул (5) темы «Определители». Докажем равенство (1) при I ≠ J. Пусть для определенности I < J. Рассмотрим определитель матрицы, которая получена из А заменой J-ой строки на I-ую. По следствию 2.1 определитель такой матрицы равен нулю. Тем не менее напишем его разложение по J-ой строке:
Остается заметить, что алгебраические дополнения Bjk совпадают с Ajk. Аналогично доказывается равенство (2) при I ≠ J (здесь вместо строк надо рассматривать столбцы и разлагать нулевой определитель по столбцу).
Для квадратной матрицы А = ||Aij|| порядка П присоединенной называется матрица
Пример 2. Найдем для матрицы
Присоединенную. Имеем
Из теоремы 3.2 непосредственно вытекает
Следствие 3.1.
Теорема 3. 3 (об обратной матрице). Для любой невырожденной матрицы А обратная матрица единственна и имеет вид
3 (об обратной матрице). Для любой невырожденной матрицы А обратная матрица единственна и имеет вид
Доказательство.
В силу следствия 3.1 имеем:
Тем самым матрица, определенная равенством (3.3), действительно является обратной. Докажем единственность обратной матрицы. Предположим, что нашлись две обратные матрицы А1-1 и А2-1. Тогда, умножив равенство
АА1-1 = Е
Слева на А2-1, получим:
Отсюда, в силу того, что А2-1А = Е, вытекает равенство
А1-1 = А2-1.
Пример 3. Найдем обратную матрицу для
Для нахождения присоединенной матрицы найдем сначала все алгебраические дополнения:
Следовательно (напомним, что алгебраические дополнения для элементов строк в присоединенной матрице надо расположить в соответствующем столбце),
Поскольку |A| = 1· A11 + 0· A12 + 1· A13 = — 9, получаем:
Упражнение 2. Найти обратную матрицу для
Найти обратную матрицу для
Решение.
Проверим невырожденность матрицы А:
Следовательно, обратная матрица существует. Вычислим алгебраические дополнения к элементам матрицы А:
Построим присоединенную матрицу:
Используя теорему 3.3, находим обратную матрицу:
Упражнение 3. Доказать, что (АВ)-1 = В-1А-1.
Решение.
Пусть С = В
-1А-1. Тогда, применяя свойство 1 произведения матриц, понятие единичной матрицы (лекция 1) и определение обратной матрицы, получим:Следовательно, матрица С = В-1А-1 удовлетворяет определению обратной матрицы для матрицы АВ. Значит, (АВ)-1 = В-1А-1.
| < Предыдущая | Следующая > |
|---|
| Алгебраические дополнения. | ∆ 1,2 = -(2·4-(-2·(-2))) = -4 | ∆ 2,1 = -(2·4-5·3) = 7 | ∆ 2,3 = -(-1·5-(-2·2)) = 1 | ∆ 3,2 = -(-1·(-2)-2·3) = 4 |
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .

Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Определение 1: матрица называется вырожденной, если её определитель равен нулю.
Определение 2: матрица называется невырожденной, если её определитель не равен нулю.
Матрица «A» называется обратной матрицей , если выполняется условие A*A-1 = A-1 *A = E (единичной матрице).
Квадратная матрица обратима только в том случае, когда она является невырожденной.
Схема вычисления обратной матрицы:
1) Вычислить определитель матрицы «A», если ∆ A = 0, то обратной матрицы не существует.
2) Найти все алгебраические дополнения матрицы «A».
3) Составить матрицу из алгебраических дополнений (Aij )
4) Транспонировать матрицу из алгебраических дополнений (Aij )T
5) Умножить транспонированную матрицу на число, обратное определителю данной матрицы.
6) Выполнить проверку:
На первый взгляд может показаться, что это сложно, но на самом деле всё очень просто. Все решения основаны на простых арифметических действиях, главное при решении не путаться со знаками «-» и «+», и не терять их.
Все решения основаны на простых арифметических действиях, главное при решении не путаться со знаками «-» и «+», и не терять их.
А теперь давайте вместе с Вами решим практическое задание, вычислив обратную матрицу.
Задание: найти обратную матрицу «A», представленную на картинке ниже:
Решаем всё в точности так, как это указано в план-схеме вычисления обратной матрицы.1. Первое, что нужно сделать, это найти определитель матрицы «A»:
Пояснение:
Мы упростили наш определитель, воспользовавшись его основными функциями. Во первых, мы прибавили ко 2 и 3 строке элементы первой строки, умноженные на одно число.
Во-вторых, мы поменяли 2 и 3 столбец определителя, и по его свойствам поменяли знак перед ним.
В-третьих, мы вынесли общий множитель (-1) второй строки, тем самым, снова поменяв знак, и он стал положительным. Также мы упростили 3 строку также, как в самом начале примера.
У нас получилась треугольный определитель, у которого элементы ниже диагонали равны нулю, и по 7 свойству он равен произведению элементов диагонали. В итоге мы получили ∆ A = 26, следовательно обратная матрица существует.
В итоге мы получили ∆ A = 26, следовательно обратная матрица существует.
А11 = 1*(3+1) = 4
А12 = -1*(9+2) = -11
А13 = 1*1 = 1
А21 = -1*(-6) = 6
А22 = 1*(3-0) = 3
А23 = -1*(1+4) = -5
А31 = 1*2 = 2
А32 = -1*(-1) = -1
А33 = 1+(1+6) = 7
3. Следующий шаг — составление матрицы из получившихся дополнений:
5. Умножаем эту матрицу на число, обратное определителю, то есть на 1/26:
6. Ну а теперь нам просто нужно выполнить проверку:
В ходе проверки мы получили единичную матрицу, следовательно, решение было выполнено абсолютно верно.
2 способ вычисления обратной матрицы.
1. Элементарное преобразование матриц
2. Обратная матрица через элементарный преобразователь.
Элементарное преобразование матриц включает:
1. Умножение строки на число, не равное нулю.
2. Прибавление к любой строке другой строки, умноженной на число.
3. Перемена местами строк матрицы.
4. Применяя цепочку элементарных преобразований, получаем другую матрицу.
А-1 = ?
1. (A|E) ~ (E|A-1 )
2. A-1 * A = E
Рассмотрим это на практическом примере с действительными числами.
Задание: Найти обратную матрицу.
Решение:
Выполним проверку:
Небольшое разъяснение по решению:
Сперва мы переставили 1 и 2 строку матрицы, затем умножили первую строку на (-1).
После этого умножили первую строку на (-2) и сложили со второй строкой матрицы. После чего умножили 2 строку на 1/4.
Заключительным этапом преобразований стало умножение второй строки на 2 и прибавлением с первой. В результате слева у нас получилась единичная матрица, следовательно, обратная матрица — это матрица справа.
После проверки мы убедились в правильности решения.
Как вы видите, вычисление обратной матрицы — это очень просто.
В заключении данной лекции хотелось бы также уделить немного времени свойствам такой матрицы.
Функция МОБР — Служба поддержки Office
Функция МОБР возвращает обратную матрицу для матрицы, храняной в массиве.
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Синтаксис
МОБР(массив)
Аргументы функции МОБР описаны ниже.
Замечания
-
Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива.
-
Если какие-либо ячейки в массиве пустые или содержат текст, функции МОБР возвращают #VALUE! ошибку «#ВЫЧИС!».
-
МоБР также возвращает #VALUE! если массив не имеет равного числа строк и столбцов.

-
Обратные матрицы, такие как определители, обычно используются для решения систем математических уравнений с несколькими переменными. Произведением матрицы и обратной является матрица удостоверений — квадратный массив, в котором диагональные значения равны 1, а все остальные — 0.
-
В качестве примера вычисления обратной матрицы, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В таблице приведена обратная матрица для массива A1:B2.
|
Столбец A |
Столбец B |
|
|---|---|---|
|
Строка 1 |
d/(a*d-b*c) |
b/(b*c-a*d) |
|
Строка 2 |
c/(b*c-a*d) |
a/(a*d-b*c) |
-
Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.

-
Некоторые квадратные матрицы невозможно инвертировать и возвращают #NUM! в функции МОБР. Определител непревратимой матрицы 0.
Примеры
Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка. в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.
Нужна дополнительная помощь?
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.
Основные сведения о матрицах
В этом разделе мы даем основные сведения о матрицах, необходимые для понимания статистики и анализа данных.
Матрицей размера m x n (читается m на n) называется прямоугольная таблица чисел, содержащая m строк и n столбцов.
Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,….
Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например: aij, где i — номер строки, j — номер столбца.
Например, матрица:
В сокращенной записи обозначаем A=(aij); i=1,2,…m; j=1,2,…,n
Приведем пример матрицы 2 на 2:
Вы видите, что a11 = 1, a12 = 0, a21 = 2, a22=5
Наряду с круглыми скобками используются и другие обозначения матрицы:
Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, aij = bij для любых i=1,2,…m; j=1,2,…n
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором) — строкой, а из одного столбца — матрицей (вектором)- столбцом:
A=(a11,a12,…,a1n) — матрица — строка
B=
Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.
Например,
Элементы матрицы aij, у которых номер столбца равен номеру строки образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a11, a22,…,ann.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциями над числами, а некоторые — специфические.
1. Умножение матрицы на число. Произведение матрицы А на число называется матрица B=A, элементы которой bij=aij для i=1,2,…m; j=1,2,…n
Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.
В частности, произведение матрицы А на число 0 есть нулевая матрица.
2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой cij=aij+bijдля i=1,2,…m; j=1,2,…n (т. е. матрицы складываются поэлементно).
е. матрицы складываются поэлементно).
3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)∙B.
4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц Am∙B kназывается такая матрица Cm, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:
i=1,2,…,m; j=1,2,…,n
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из этих операций):
A+B=B+A
(A+B)+C=A+(B+C)
λ (A+B)= λA+ λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ (AB)=( λA)B=A(λB)
A(BC)=(AB)C
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
a) Если АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать.
b) Если АВ и ВА существуют, то они могут быть матрицами разных размеров.
5. Транспонирование матрицы — переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А’ называется транспонированной относительно матрицы А:
Из определения следует, что если матрица А имеет размер m, то транспонированная матрица А’ имеет размер n
В литературе встречаются и другие обозначения транспонированной матрицы, например, АТ
Связанные определения:
Вырожденная матрица
Обобщенная обратная матрица
Обратная матрица
Плохо обусловленная матрица
Псевдообратная матрица
Эрмитова матрица
Эрмитово-сопряженная матрица
В начало
Содержание портала
Как найти обратную матрицу в Excel
Excel обладает мощным инструментарием, позволяющим выполнять множество математических, статистических, логических и прочих задач. В программе также можно выполнить такое действие, как нахождение обратной матрицы. Ниже мы на практическом примере рассмотрим, как именно это сделать.
В программе также можно выполнить такое действие, как нахождение обратной матрицы. Ниже мы на практическом примере рассмотрим, как именно это сделать.
Примечание: Найти обратную матрицу можно только при условии, что исходная является квадратной (количество столбцов и строк одинаковое). К тому же, ее определитель не должен равняться цифре 0.
Этап 1. Вычисляем определитель
В программе данное действие выполняется с помощью функции МОПРЕД.
- Переходим в свободную ячейку, в которой планируем производить расчеты, после чего кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.
- В открывшемся окне вставки функций выбираем категорию “Математические”, в которой кликаем по оператору “МОПРЕД”, затем – по кнопке OK.
- В следующем окне нужно заполнить единственный аргумент функции – “Массив”, в значении которого указываем координаты нашей матрицы.
 Сделать это можно вручную, прописав адреса ячеек, используя клавиши клавиатуры. Либо можно сначала кликнуть внутри области ввода информации, затем зажав левую кнопку мыши выделить диапазон ячеек непосредственно в самой таблице. Когда все готово, нажимаем кнопку OK.
Сделать это можно вручную, прописав адреса ячеек, используя клавиши клавиатуры. Либо можно сначала кликнуть внутри области ввода информации, затем зажав левую кнопку мыши выделить диапазон ячеек непосредственно в самой таблице. Когда все готово, нажимаем кнопку OK. - В выбранной ячейке отобразился результат, а именно, определитель матрицы. С учетом наших данных получилось число 157894, что значит, что у нашей матрицы обратная матрица существует, так как определитель не равен нулю.
Этап 2. Находим обратную матрицу
Итак, после того, как мы вычислили, что определитель матрицы не равен нулю, можно приступить к нахождению обратной.
- Встаем в ячейку, которая станет самым верхним левым элементом новой обратной матрицы. Заходим в окно Вставки функции, нажав на соответствующую кнопку.
- В категории “Математические” выбираем функцию “МОБР”, после чего щелкаем по кнопке OK.
- Аналогично заполнению значения аргумента “Массив” для функции МОПРЕД, рассмотренной в первом разделе, указываем координаты первичной матрицы, после чего нажимаем OK.
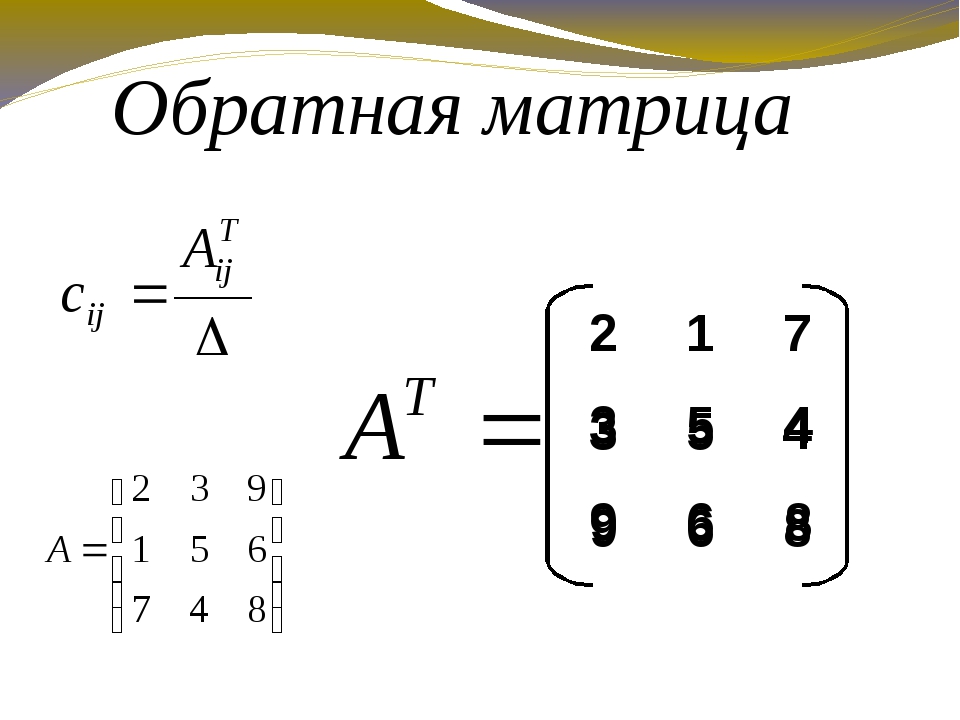
 {-1}\cdot A= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix} \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}=$ $\begin{pmatrix} -5\cdot1 + 3\cdot2 & -5\cdot3 + 3\cdot 5\\ 2\cdot1 +(-1)\cdot2 & 2\cdot3 +(-1)\cdot5 \end{pmatrix}= \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}=I_{2}$
{-1}\cdot A= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix} \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}=$ $\begin{pmatrix} -5\cdot1 + 3\cdot2 & -5\cdot3 + 3\cdot 5\\ 2\cdot1 +(-1)\cdot2 & 2\cdot3 +(-1)\cdot5 \end{pmatrix}= \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}=I_{2}$Как записать простейшее матричное уравнение
«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»
Д. Пойа (1887-1985 г.)(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)
Обратные матрицы используются при решении матричных уравнений.
Простейшими матричными уравнениями называются соотношения вида: АХ=В и ХА=В, где А,В– известные матрицы, Х – неизвестная.
Если дано уравнение вида АХ=В, то решение выглядит так Х=А -1 В.

Если уравнение вида ХА=В, то Х=ВА -1 .
Непосредственной подстановкой легко установить, что найденное Х является решением соответствующего уравнения.
ПРИМЕРЫ: Решить матричные уравнения.
РЕШЕНИЕ:
Тогда нам дано уравнение вида ХА=В, следовательно Х=ВА -1 . Найдем A -1 .
Тогда нам дано уравнение вида АX=В, следовательно Х=А -1 B. Найдем A -1 .
Как вычислить определитель смотреть здесь.
Как умножать матрицы можно посмотреть здесь.
Как найти обратную матрицу можно посмотреть здесь.
Упражнения к уроку:Решить матричные уравнения:
Автор: Аникина Анна
Комментарии к этой заметке:
Как можно решить логарифм матрицы простейшем способом?
все очень хорошо. Мог бы переслать Вам ,разработанный мной калькулятор для решения матричных уравнений, но не знаю как это исполнить.
 Хочется узнать Ваше мнение о нем
Хочется узнать Ваше мнение о немА как решить уравнение вроде ХА=В+2Х. Вот что делать с 2Х?
Доброго времени суток, Юлия! Необходимо представить 2Х=Х2Е (Е-единичная матрица соответствующего размера). А далее использовать свойства действий с матрицами.
Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
где x – неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы – это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B – известные матрицы, X – неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:
.

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому
.
Так как E – единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :
.
Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:
,
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X .
 То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .
То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
.
Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева.
 Найдём матрицу, обратную матрице A .
Найдём матрицу, обратную матрице A .Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :
.
Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение
.
Пример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :
.

Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :
.
Находим матрицу, обратную матрице B :
.
; ;
Причем элементы матриц А и В заданы, а Х1, Х2, Х3 – неизвестные.
Тогда уравнение А × Х = В называется простейшим матричным уравнением.
Чтобы его решить, т.е. найти элементы матрицы неизвестных Х, поступим следующим образом:
1. Умножим обе части уравнения на матрицу А -1 , обратную для матрицы А, слева:
А -1 (А × Х) = А -1 × В
2. Используя свойство умножения матриц, запишем
(А -1 × А) Х = А -1 × В
3. Из определения обратной матрицы
(А -1 × А = Е) имеем Е × Х = А -1 × В.
4. Используя свойство единичной матрицы (Е × Х = Х), окончательно получим Х = А -1 × В
Замечание.
 Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С -1 справа.
Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С -1 справа.Пример. Решить матричное уравнение
Решение. Введем обозначения
А = ; В = ,
Их определения умножения матриц с учетом размерностей А и В матрица неизвестных Х будет иметь вид
Х =
С учетом введенных обозначений имеем
А × Х = В откуда Х = А -1 × В
Найдем А -1 по алгоритму построения обратной матрицы
Тогда для Х получим
Х = откуда х1 = 3, х2 = 2
Ранг матрицы
Рассмотрим матрицу А размера (m x n)
Минором к-ого порядка матрицы А будем называть определитель порядка к, элементами которого являются элементы матрицы А, стоящие на пересечении любых К строк и любых К столбцов. Очевидно, к £ min (m, n).
Определение. Рангом r(A) матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля.

Определение. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется базисным минором.
Определение. Матрицы, имеющие одинаковые ранги, называются эквивалентными.
Вычисление ранга матрицы
Определение. Матрица называется ступенчатой, если под первым ненулевым элементом каждой ее строки стоят нули в нижележащих строках.
Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Таким образом, преобразуя матрицу к ступенчатому виду, несложно определить ее ранг. Эта операция осуществляется с помощью элементарных преобразований матрицы, которые не изменяют ее ранга:
– умножение всех элементов ряда матрицы на число l ¹ 0;
– замена строк столбцами и наоборот;
– перестановка местами параллельных рядов;
– вычеркивание нулевого ряда;
– прибавление к элементам некоторого ряда соответствующих элементов параллельного ряда, умноженных на любое действительное число.

Пример. Вычислить ранг матрицы
А =
Решение. Преобразуем матрицу к ступенчатому виду. Для этого к третьей строке прибавим вторую, умноженную на (-3).
К четвертой строке прибавим третью.
А
Число ненулевых строк в полученной эквивалентной матрице равно трем, следовательно r(А) = 3.
Системы n линейных уравнений с n неизвестными.
Методы их решения
Рассмотрим систему n линейных уравнений с n неизвестными.
а11х1 + а12х2 + … + а1nxn = b1
Определение: Решением системы (1) называется совокупность чисел (х1, х2, …, хn), которая обращает каждое уравнение системы в верное равенство.
Матрица А, составленная из коэффициентов при неизвестных, называется основной матрицей системы (1).
A =
Матрица В, состоящая из элементов матрицы А и столбца свободных членов системы (1), называется расширенной матрицей.

В =
Матричный метод
Х = – матрица неизвестных;
С = – матрица свободных членов системы (1).
Тогда по правилу умножения матриц систему (1) можно представить в виде матричного уравнения
Решение уравнения (2) изложено выше, то есть Х = А -1 × С, где А -1 – обратная матрица для основной матрицы системы (1).
Метод Крамера
Система n линейных уравнений с n неизвестными, главный определитель которой отличен от нуля, всегда имеет решение и притом единственное, которое находится по формулам:
где D = det А – определитель основной матрицы А системы (1), который называется главным, Dхi получаются из определителя D заменой i-ого столбца столбцом из свободных членов, т.е.
D = ;
Dх1 = ;
Dх2 = ; … ;
Dхn = ;
Пример. Решить систему уравнений методом Крамера
2х1 + 3х2 + 4х3 = 15
Решение.

Вычислим определитель основной матрицы системы
D = det A = = 44 ¹ 0
Вычислим вспомогательные определители
Dх1 = = 0;
Dх2 = = 44;
Dх3 = = 132.
По формулам Крамера найдем неизвестные
; ; .
Метод Гаусса
Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. в приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули. Это достигается с помощью элементарных преобразований матрицы над строчками. В результате таких преобразований не нарушается равносильность системы и она приобретает также треугольный вид, т.е. последнее уравнение содержит одну неизвестную, предпоследнее две и т.д. Выражая из последнего уравнения n-ую неизвестную и с помощью обратного хода, используя ряд последовательных подстановок, получают значения всех неизвестных.
Пример. Решить систему уравнений методом Гаусса
3х1 + 2х2 + х3 = 17
Решение.
 Выпишем расширенную матрицу системы и приведем, содержащуюся в ней матрицу А к треугольному виду.
Выпишем расширенную матрицу системы и приведем, содержащуюся в ней матрицу А к треугольному виду.В =
Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных выражений при последующих вычислениях
Первую строку полученной матрицы умножим последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом В будет иметь вид:
После умножения второй строки на и сложения ее с третьей строкой матрица А примет треугольный вид. Однако чтобы упростить вычисления можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим:
Далее, умножая вторую строку матрицы на 10 и складывая с третьей, окончательно получим:
Восстановим из полученной матрицы В систему уравнений, равносильную данной
х1 + 4х2 – 3х3 = 9
Из последнего уравнения находим Найденное значение х3 = 1 подставим во второе уравнение системы, из которого х2 = 2х3 = 2 × 1 = 2.

После подстановки х3 = 1 и х2 = 2 в первое уравнение для х1 получим х1 = 9 – 4х2 + 3х3 = 9 – 4 × 2 + 3 × 1 = 4.
Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.
3 × 4 + 2 × 2 + 1 = 17 верно
Матрица, обратная
В этом уроке определяется обратная матрица, и показано, как определить ли инверсия матрица существует.
Инверсия матрицы
Предположим, A — это матрица n x n . Обратный из A — это еще одна матрица n x n , обозначается A -1 , что удовлетворяет следующему условия.
A A -1 = А -1 А = I n
, где I n — это единичная матрица.
 Ниже на примере проиллюстрируем взаимосвязь между матрицей
и его обратное.
Ниже на примере проиллюстрируем взаимосвязь между матрицей
и его обратное.Не каждая квадратная матрица имеет обратную; но если матрица имеет обратную, это уникально.
Существует ли обратное?
Есть два способа определить, является ли обратная квадратная матрица существуют.
- Определить его ранг . Ранг матрицы — уникальное число, связанное с квадратной матрицей. Если ранг n x n матрица меньше n , матрица не имеет обратное.Мы показали как определить ранг матрицы ранее.
- Вычислить его определитель . Определитель — еще одно уникальное число, связанное с квадратной матрицей. Когда определитель для квадратной матрицы равен нулю, обратный для этого матрица не существует. Мы показали как найти определитель матрицы ранее.
Квадратная матрица, имеющая обратную называется неособым числом или обратимый ; квадратная матрица, не имеющая инверсия называется в единственном числе .

Проверьте свое понимание
Проблема 1
Рассмотрим матрицу A , показанную ниже.
Какое из следующих утверждений верно?
(A) Ранг матрицы A равен 1.
(B) Определитель матрицы A равен 0.
(C) Матрица A является сингулярным.
(D) Все вышеперечисленное.
(E) Ничего из вышеперечисленного.Решение
Правильный ответ — (D).
Примечание: Если квадратная матрица меньше полного ранга, ее определитель равно нулю; и наоборот.
Обращение матрицы
Мультипликативная обратная квадратная матрица называется ее обратной матрицей. Если матрица А имеет обратное, то А как говорят неособый или обратимый. А единственное число матрица не имеет инверсии. Чтобы найти обратную квадратную матрицу А , вам нужно найти матрицу А — 1 так что продукт А а также А — 1 — единичная матрица.

Другими словами, для каждой квадратной матрицы А которая является невырожденной, существует обратная матрица, обладающая тем свойством, что А А — 1 знак равно А — 1 А знак равно я , где я — единичная матрица подходящего размера.
Вы можете использовать любой из следующих методов, чтобы найти обратную квадратную матрицу.
Способ 1:
Позволять А быть п × п матрица.
1. Напишите дважды расширенную матрицу [ А | я п ] .
2. Примените элементарные операции со строками, чтобы записать матрицу в сокращенной форме строки-эшелона.
3. Решите, будет ли матрица А обратима (неособа).
4.
 Если
А
сводится к единичной матрице
я
п
, тогда
А
—
1
— матрица справа от преобразованной расширенной матрицы.
Если
А
сводится к единичной матрице
я
п
, тогда
А
—
1
— матрица справа от преобразованной расширенной матрицы.5. Если А не сводится к единичной матрице, то А единственное число.
Способ 2:
Вы можете использовать следующую формулу при нахождении обратной величины п × п матрица.
Если А является невырожденной матрицей, существует обратная матрица, которая задается формулой А — 1 знак равно 1 | А | ( прил А ) , где | А | — определитель матрицы.
Пример :
Находить А — 1 , если он существует.
 Если
А
—
1
не существует, пишите в единственном числе.
Если
А
—
1
не существует, пишите в единственном числе.А знак равно [ 1 2 1 1 ]
Шаг 1:
Напишите дважды расширенную матрицу [ А | я п ] .
[ А | я ] знак равно [ 1 2 1 0 1 1 0 1 ]
Шаг 2:
Примените элементарные операции со строками, чтобы записать матрицу в сокращенной форме строки-эшелона.

[ 1 2 1 0 0 1 1 — 1 ] р 2 знак равно р 1 — р 2 [ 1 0 — 1 2 0 1 1 — 1 ] р 1 знак равно — 2 р 2 + р 1 [ 1 0 — 1 2 0 1 1 — 1 ] знак равно [ я | А — 1 ]
У системы есть решение.

Следовательно, А обратима и А — 1 знак равно [ — 1 2 1 — 1 ]
Mathwords: инверсия матрицы
Инверсия матрицы
Инверсия матрицы
Мультипликативная обратная матрицаДля квадратной матрицы A обратная записывается A -1 . Когда А умножается на -1 А. результатом является единичная матрица I. Неквадратные матрицы не имеют обратных.
Примечание. Не все квадратные матрицы имеют обратные. Квадратная матрица, имеющая обратную, называется обратимой или невырожденной, а квадратная матрица без обратной называется необратимой или сингулярной.

AA -1 = A -1 A = I
Пример: Для матрицы это обратное значение, так как
AA -1 =и А -1 А =.
Вот три способа найти обратную матрицу:
1. Ярлык для матриц 2×2
Для, обратное значение можно найти по следующей формуле:
Пример :
2.
 Метод дополненной матрицы
Метод дополненной матрицы Используйте метод исключения Гаусса-Жордана для преобразования [A | I] в [I | А -1 ].
Пример : Следующие шаги приводят к.
Итак, мы это видим.
3. Сопряженный метод
A -1 = (примыкает к A) или A -1 = (матрица кофакторов A) T
Пример : Следующие шаги приводят к A -1 для.
Матрица сомножителей для A, значит, сопряженная. Поскольку det A = 22, получаем
.
См. также
Определитель матрица, сомножитель
Нахождение обратной матрицы с помощью графического калькулятора
Пройдя любой углубленный курс математики или даже просканировав этот веб-сайт, вы быстро узнаете, насколько мощным может быть графический калькулятор.
 Более «теоретический» курс, такой как линейная алгебра, не исключение. Фактически, как только вы научитесь делать что-то вроде поиска обратной матрицы вручную, калькулятор освободит вас от этого вычисления и позволит сосредоточиться на общей картине.
Более «теоретический» курс, такой как линейная алгебра, не исключение. Фактически, как только вы научитесь делать что-то вроде поиска обратной матрицы вручную, калькулятор освободит вас от этого вычисления и позволит сосредоточиться на общей картине.реклама
Помните, что не каждая матрица имеет инверсию. Матрица, выбранная ниже, — это обратимая , что означает, что у нее действительно есть обратная матрица. О том, что происходит, когда он не обратим, мы поговорим чуть позже.Вот матрица, которую мы будем использовать в нашем примере:
\ (\ left [\ begin {array} {cccc} 8 & 2 & 1 & 6 \\ 8 & 4 & 1 & 1 \\ 0 & 2 & 6 & 4 \\ 15 & 8 & 9 & 20 \ end { array} \ right] \)
Примечание. Чтобы просмотреть видео с этими шагами, прокрутите вниз.
Шаг 1. Войдите в меню редактирования матрицы
Это гораздо более сложный шаг, чем кажется! Если у вас TI 83, есть просто кнопка с надписью «MATRIX». Это кнопка, которую вы нажмете, чтобы попасть в меню редактирования.
 {-1} \)]. Вы попадете в меню, которое вы видите ниже. Наведите курсор на «РЕДАКТИРОВАТЬ» вверху.
{-1} \)]. Вы попадете в меню, которое вы видите ниже. Наведите курсор на «РЕДАКТИРОВАТЬ» вверху.
Теперь вы выберете матрицу A (технически вы можете выбрать любую из них, но пока с A проще иметь дело). Для этого просто нажмите [ENTER].Шаг 2. Войдите в матрицу
Во-первых, вы должны сообщить калькулятору, насколько велика ваша матрица. Только не забудьте сохранить его в порядке «строки» и «столбцы». Например, матрица нашего примера имеет 4 строки и 4 столбца, поэтому я набираю 4 [ENTER] 4 [ENTER].
Теперь вы можете вводить числа слева направо. После каждого числа нажимайте [ENTER], чтобы перейти к следующему месту.
Теперь, прежде чем мы перейдем к следующему шагу. На некоторых калькуляторах вы попадете в странный цикл, если не выйдете из этого меню сейчас. Итак, нажмите [2ND] и [MODE], чтобы выйти. Когда вы это сделаете, он вернется на главный экран.Шаг 3. Выберите матрицу в меню ИМЕНА
После выхода, нажав [2ND] и [MODE], вернитесь в меню матрицы, нажав [2ND] и [\ (x ^ {- 1} \)] (или просто кнопку матрицы, если у вас TI83 ).
 {-1} \)] и нажмите Enter
{-1} \)] и нажмите EnterСамый простой шаг! Все, что вам нужно сделать сейчас, это указать калькулятору, что делать с матрицей A. Поскольку мы хотим найти обратную матрицу, мы будем использовать эту кнопку.
На этом этапе вы можете нажать клавишу со стрелкой вправо, чтобы увидеть всю матрицу. Как видите, наш обратный здесь действительно беспорядочный. Следующий шаг может помочь нам, если нам это нужно.Шаг 5: (НЕОБЯЗАТЕЛЬНО) преобразовать все в дроби
Пока на экране отображается инверсия, если вы нажмете [MATH], 1: Frac, а затем ENTER, вы преобразуете все в матрице в дроби.Затем, как и раньше, вы можете щелкнуть клавишу со стрелкой вправо, чтобы увидеть все.
Вот и все! Звучит много, но на самом деле к этому легко привыкнуть. Это тоже полезно — возможность вводить матрицы в калькулятор позволяет добавлять их, умножать и т. Д.! Хороший! Если вы хотите увидеть все это в действии, посмотрите видео справа, где я прохожу шаги с другим примером. Даже с необязательным шагом у меня уходит меньше 3 минут.
Даже с необязательным шагом у меня уходит меньше 3 минут.Ах да — а что будет, если ваша матрица сингулярна (или НЕ обратима)? Другими словами, что произойдет, если в вашей матрице нет обратной?
Как вы можете видеть выше, ваш калькулятор СКАЖЕТ ВАМ.Как это хорошо?Видео прохождение
Следующее видео проведет вас через шаги, указанные выше.
Дополнительное чтение
Также может оказаться полезным иметь возможность сокращать матрицу по строкам с помощью калькулятора или даже умножать матрицы.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
Связанныеlinear algebra — ярлык для поиска обратной матрицы
Итак, мы хотим найти способ вычислить $ 2 \ times 2 ~ \ text {или} ~ 3 \ times 3 $ матричных систем наиболее эффективным способом.
 {T} $.
{T} $.Для элементов матрицы $ A = \ left | \ begin {array} {rrr} а_ {11} и а_ {12} и а_ {13} \\ а_ {21} и а_ {22} и а_ {23} \\ а_ {31} и а_ {32} и а_ {33} \ end {array} \ right |, ~~ $ его можно расширить для решений $ x_ {1}, ~ x_ {2}, ~ x_ {3} $
, зная, что $ {\ bf | {A} | =} ~ | a_ {ij} | ~ \ not = ~ 0. $
$ x_ {1} = \ dfrac {1} {| {\ bf {A}} |} \ left | \ begin {array} {rrr} b_1 & a_ {12} & a_ {13} \\ b_2 & a_ {22} & a_ {23} \\ b_3 и a_ {32} и a_ {33} \ end {array} \ right | $,
$ x_ {2} = \ dfrac {1} {| {\ bf {A}} |} \ left | \ begin {array} {rrr} a_ {11} & b_1 & a_ {13} \\ a_ {21} и b_2 и a_ {23} \\ a_ {31} и b_3 и a_ {33} \ end {array} \ right | $,
$ x_ {3} = \ dfrac {1} {| {\ bf {A}} |} \ left | \ begin {array} {rrr} a_ {11} и a_ {12} & b_1 \\ a_ {21} и a_ {22} & b_2 \\ a_ {31} и a_ {32} и b_3 \ end {array} \ right | $.
Альтернативный способ сделать это — использовать методы сокращения строк, известные как исключение Гаусса (ref) или исключение Гаусса-Жордана (rref).

Надеюсь, это помогло. Дайте мне знать, если вы чего-то не понимаете.
Спасибо.
Удачи.
Определитель и обратная матрица
Определитель и обратная матрицаПоиск обратной матрицы очень важен во многих областях науки. Например, для дешифрования закодированного сообщения используется обратная матрица.Определитель может быть использован для решения этой проблемы. Действительно, пусть A будет квадратной матрицей. Мы знаем, что A обратимо тогда и только тогда, когда . Также, если A имеет порядок n, то кофактор A i , j определяется как определитель квадратной матрицы порядка (n-1), полученной из A путем удаления номера строки i и номер столбца j, умноженный на (-1) i + j . Отзывать
для любых фиксированных и , и
для любых фиксированных j .Определите , сопряженный к A , обозначенный adj ( A ), как транспонирование матрицы, чья запись ij th равна A ij .
Пример. Пусть
У нас есть
Давайте оценим . У нас есть
Обратите внимание, что . Следовательно, мы имеемВерна ли эта формула только для этой матрицы, или аналогичная формула существует для любой квадратной матрицы? Фактически, у нас есть похожая формула.
Теорема. Для любой квадратной матрицы A порядка n имеем
В частности, если , тогдаДля квадратной матрицы порядка 2 имеем
который дает
Это формула, которую мы использовали на предыдущей странице.На следующей странице мы обсудим применение приведенных выше формул к линейным системам.
[Геометрия] [Алгебра] [Тригонометрия] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра]С.O.S MATH: Домашняя страница
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.
 O.S. Математика CyberBoard.
O.S. Математика CyberBoard.Автор : М.А.Хамси
Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователя онлайн за последний час Матрицыи матричная алгебра — Статистика Как к
Матрицы и содержание матричной алгебры (щелкните, чтобы перейти к этому разделу):
- Матричная алгебра: введение
- Добавление матрицы: больше примеров
- Умножение матриц
- Определение сингулярной матрицы
- Матрица идентичности
- Что такое обратная матрица?
- Собственные значения и собственные векторы
- Расширенные матрицы
- Определитель матрицы
- Диагональная матрица
- Что такое симметричная и кососимметричная матрицы?
- Что такое матрица транспонирования?
- Что такое матрица дисперсии-ковариации?
- Корреляционные матрицы
- Идемпотентная матрица.

Матрица — это прямоугольный массив чисел, упорядоченный по столбцам и строкам (как в электронной таблице). Матричная алгебра используется в статистике для выражения наборов данных. Например, ниже представлен рабочий лист Excel со списком оценок за экзамены:
Матрицы
Преобразование в матричную алгебру в основном включает удаление идентификаторов столбцов и строк. Добавляется идентификатор функции (в данном случае «G» для оценок):
Числа, которые появляются в матрице, называются элементами матрицы .: Обозначение
Почему странная нотация?
Мы используем другую нотацию (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений упрощает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть список, подобный этому: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a + 3b + 5g, чтобы придерживаться соглашения.
Некоторые из наиболее распространенных терминов, с которыми вы можете встретиться при работе с матрицами:
- Размер (также называемый порядком): сколько строк и столбцов имеет матрица.Сначала перечислены строки, за ними следуют столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
- Элементы : числа, которые появляются внутри матрицы.
- Матрица идентичности (I): Диагональная матрица с нулями в качестве элементов, за исключением диагонали, у которой есть единицы.
- Скаляр : любое действительное число.
- Матрица Функция: скаляр, умноженный на матрицу, чтобы получить другую матрицу.
Матрицы идентичности. Изображение: Википедия.com.
Матричная алгебра: сложение и вычитание
Размер матрицы (т. Е. 2 x 2) также называется размером матрицы или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размерность должна быть точно так же, как .
 Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одном и том же месте (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).
Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одном и том же месте (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).Примечание к обозначениям: рабочий лист (например, в Excel) использует буквы столбцов (ABCD) и номера строк (123), чтобы указать расположение ячейки, например A1 или D2. Для матриц типично использование обозначений типа g ij , что означает i-ю строку и j-й столбец матрицы G.
Вычитание матриц работает точно так же.
Вернуться к началуМатричное дополнение — это всего лишь серия дополнений. Для матрицы 2 × 2:
- Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом положении.
- Сложите верхние правые числа и запишите сумму в верхнем правом углу.
- Сложите нижние левые числа вместе и запишите сумму в нижнем левом углу.

- Сложите нижние правые числа вместе и запишите сумму в правом нижнем углу:
Используйте ту же процедуру для матрицы 2 × 3:
Фактически, вы можете использовать этот базовый метод для добавления любых матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк).Другими словами, , если матрицы одинакового размера, вы можете их добавить. Если они разного размера, вы не можете их добавить.
- Матрица с 4 строками и 2 столбцами может быть добавлена к матрице с 4 строками и 2 столбцами.
- Матрица с 4 строками и 2 столбцами не может быть добавлена к матрице с 5 строками и 2 столбцами.
Вышеупомянутый метод иногда называют «начальным суммированием», поскольку вы просто складываете элементы и фиксируете результат.
Другой способ подумать об этом…
Подумайте, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z.
 И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.Добавление матрицы для неравных размеров
Если у вас неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод.Один из таких приемов — прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q представляет собой матрицу размера (m + p) × (n + q):
Например:В начало
Относительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:
Просто умножьте каждое число в матрице на 2, и вы получите новую матрицу. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14Результат четырех умножений дает числа в новой матрице справа.
Умножение матриц: две матрицы
Когда вы хотите перемножить две матрицы, процесс становится немного сложнее.
 Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.Если все это звучит немного сложно, это (очень короткое) видео показывает, как это делается:
Вы можете выполнить матричное умножение для двух матриц, только если количество столбцов в первой матрице равно количеству строк во второй матрице.Например, вы можете умножить матрицу 2 x 3 (две строки и три столбца) на матрицу 3 x 4 (три строки и четыре столбца).
Очевидно, что это может стать очень сложным (и утомительным) процессом. Тем не менее, вы можете найти множество достойных инструментов для умножения матриц в Интернете. Мне нравится этот от Матрицы Решиш. После расчета вы можете умножить результат на другую матрицу и другую, что означает, что вы можете умножить несколько матриц вместе.

Microsoft Excel также может выполнять матричное умножение с использованием функций «массива».Вы можете найти инструкции здесь, на сайте Стэнфорда. Прокрутите вниз до места, где написано Матричные операции в Excel.
Вернуться к началуБыстрый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец с нулями или , два равных столбца или две равные строки, то это особая матрица. Например, следующие десять матриц являются единственными (изображение: Wolfram):
Существуют и другие типы сингулярных матриц, некоторые из которых не так-то легко обнаружить.Следовательно, необходимо более формальное определение.
Следующие три свойства определяют сингулярную матрицу:
- Матрица квадратная и
- Не имеет инверсии.
- Имеет определитель 0.
1. Квадратная матрица
Квадратная матрица имеет (как следует из названия) равное количество строк и столбцов.
 Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Особая матрица — это квадратная матрица, но не все квадратные матрицы сингулярны.Необратимые матрицы
Если квадратная матрица не имеет обратной, то это особая матрица.
Обратная матрица — это то же самое, что и обратная величина числа. Если умножить матрицу на обратную, получится единичная матрица , , матричный эквивалент 1. Идентификационная матрица в основном представляет собой последовательность единиц и нулей.Идентификационная матрица различается в зависимости от размера матрицы.
Матрицы идентичности. Изображение: Wikipedia.com.
Если вы не знакомы с поиском инверсий, вы можете посмотреть это короткое видео:
Определитель нуля
Определитель — это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений.
 Формула для вычисления определителя различается в зависимости от размера матрицы.Например, матрица 2 × 2, формула ad-bc.
Формула для вычисления определителя различается в зависимости от размера матрицы.Например, матрица 2 × 2, формула ad-bc.Эта простая матрица 2 × 2 сингулярна, потому что ее определитель равен нулю:
К началуЕдиничная матрица — это квадратная матрица с единицами в качестве элементов на главной диагонали сверху слева направо снизу и нулями в остальных местах. Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:
По идее аналогичен айдентике. В базовой математике элемент идентичности оставляет число неизменным.Например, кроме того, тождественный элемент равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. Д., А при умножении тождественный элемент равен 1, потому что любое число, умноженное на 1, равно этому числу (т. Е. 10 * 1 = 10 ). Говоря более формально, если x — действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x.
 По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .
По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .В матричной алгебре единичный элемент различается в зависимости от размера матрицы, с которой вы работаете; в отличие от сингулярной единицы для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I n * n . На главной диагонали всегда будут единицы, а оставшиеся пробелы — нули. На следующем изображении показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:
Дополнительная идентификационная матрица
Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности.Однако есть и другой тип: аддитивная единичная матрица.
 Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах — нули. Поэтому их иногда называют нулевой матрицей .
Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах — нули. Поэтому их иногда называют нулевой матрицей . Аддитивная единичная матрица для матрицы 3 * 3.
Вернуться к началуОбратные матрицы — это то же самое, что и обратные. В элементарной алгебре (а может быть, и раньше) вы столкнулись с идеей обратного: одно число, умноженное на другое, может равняться 1.
Изображение предоставлено LTU
Если вы умножите одну матрицу на ее обратную, вы получите матричный эквивалент 1: Identity Matrix , которая по сути представляет собой матрицу с единицами и нулями.Поиск обратной матрицы состоит из нескольких шагов. Посмотрите это короткое видео о том, как найти обратную матрицу, или выполните следующие действия:
Шаг 1: Найдите адъюгат матрицы.
 Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:
Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой: Чтобы найти сопряжение матрицы 2 × 2, поменяйте местами диагонали a и d, а затем поменяйте местами знаки c и d.
Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. Изображение выше) определитель равен (a * d) — (b * c).
Шаг 3: Умножить 1 / детерминант * адъюгат. .Проверка ответа
Вы можете проверить свой ответ умножением матриц. Умножьте свою матрицу ответов на исходную матрицу, и вы получите единичную матрицу. Вы также можете воспользоваться онлайн-калькулятором здесь.
Вернуться к началуСобственное значение (λ) — это специальный скаляр, используемый при матричном умножении и имеющий особое значение в нескольких областях физики, включая анализ устойчивости и небольшие колебания колеблющихся систем.Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственным значением .
 Основное уравнение:
Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенное выше уравнение говорит о том, что , если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, как если бы вы взяли собственное значение и умножили его по вектору x .Пример собственного значения
В следующем примере 5 — собственное значение A, а (1,2) — собственный вектор:
Давайте рассмотрим это по шагам, чтобы наглядно продемонстрировать, что такое собственное значение.В обычном умножении, если вы умножаете матрицу размера n x n на вектор n x 1, в результате вы получаете новый вектор n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
Что если бы вместо новой матрицы nx 1 можно было получить ответ с тем же вектором, который вы умножили на вместе с новым скаляром?
Когда это возможно, вектор умножения (то есть тот, который также есть в ответе) называется собственным вектором, а соответствующий скаляр — собственным значением.
 Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в так называемом разложении на собственные числа . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.
Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в так называемом разложении на собственные числа . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.Расчет
Найдите собственные значения для следующей матрицы:
Шаг 1: Умножьте единичную матрицу на λ.Единичная матрица для любой матрицы 2 × 2 равна [1 0; 0 1], поэтому:
Шаг 2: Вычтите ответ из шага 1 из матрицы A, используя вычитание матрицы:
Шаг 3: Найдите определитель матрицы, вычисленной на шаге 2:
det = (5- λ) (- 1-λ) — (3) (3)
Упрощая, получаем:
-5 — 5λ + λ + λ 2 — 9
= λ 2 — 4λ — 14Шаг 4: Установите уравнение, которое вы нашли на шаге 3, равным нулю и решите для λ:
0 = λ 2 — 4λ — 14 = 2
Мне нравится использовать свой TI-83, чтобы найти корни, но вы можете также воспользуйтесь алгеброй или этим онлайн-калькулятором. Находя корни (нули), получаем x = 2 + 3√2, 2 — 3√2
Находя корни (нули), получаем x = 2 + 3√2, 2 — 3√2Ответ : 2 + 3√2 и 2-3√2
Математика для больших матриц такая же, но вычисления могут быть очень сложными. Для матриц 3 × 3 используйте калькулятор внизу этого раздела; для больших матриц попробуйте этот онлайн-калькулятор.
Вернуться к началуНа изображении выше показана расширенная матрица (A | B) внизу. Расширенные матрицы обычно используются для решения систем линейных уравнений и, собственно, именно поэтому они были впервые разработаны.Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (т. Е. Значений справа от знака равенства в наборе уравнений). Она называется расширенной матрицей , потому что матрица коэффициентов была «дополнена» значениями после знака равенства.
Например, следующая система линейных уравнений:
x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11Может быть помещен в следующую расширенную матрицу:
После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.

У вас нет , у вас нет , чтобы использовать вертикальную черту в расширенной матрице. Обычно матрицы вообще не содержат линий. Полоса просто упрощает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Если вы вообще используете вертикальную полосу, зависит от учебника, который вы используете, и от предпочтений вашего преподавателя.
Написание системы уравнений
Вы также можете работать в обратном направлении, чтобы написать систему линейных уравнений, заданную расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.Шаг 1: Запишите коэффициенты для первого столбца, за которым следует «x». Обязательно запишите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Напишите коэффициенты для второго столбца, а затем укажите «y». Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Напишите коэффициенты для второго столбца, после чего укажите «z. «Сложите, если это положительное число, и вычтите, если оно отрицательное:
«Сложите, если это положительное число, и вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y — 7
6x + 2y + 9
Шаг 3. Запишите константы в третьем столбце со знаком равенства.
-1x + 7y + 3 = 0
2x + 4y — 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом этапе у вас стоит отрицательный знак, просто сделайте константу отрицательным числом.
Вернуться к началуОпределитель матрицы — это просто специальное число, которое используется для описания матриц для нахождения решений систем линейных уравнений, нахождения обратных матриц и для различных приложений в исчислении.Определить на простом английском языке невозможно; обычно его определяют в математических терминах или в терминах того, что он может вам помочь. Определитель матрицы имеет несколько свойств:
- Это действительное число. Сюда входят отрицательные числа.
- Определители существуют только для квадратных матриц.
- Обратная матрица существует только для матриц с ненулевыми определителями.

Символ для определителя матрицы A — | A |, который также является тем же самым символом, который используется для абсолютного значения, хотя эти два символа не имеют ничего общего друг с другом.
Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.
Определитель матрицы 2 × 2
Формула определителя матрицы 2 × 2 — ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.
Определитель матрицы 3 × 3
Определитель матрицы 3 × 3 находится по следующей формуле:
| A | = a (ei — fh) — b (di — fg) + c (dh — eg)
Это может показаться сложным, но если вы пометили элементы с помощью a, b, c в верхнем ряду, d, e, f во второй строке и g, h, i в последней, становится основной арифметикой.
Пример :
Найдите определитель следующей матрицы 3 × 3:
= 3 (6 × 2-7 × 3) –5 (2 × 2-7 × 4) +4 (2 × 3-6 × 4)
= -219
По сути, здесь происходит умножение a, b и d на детерминанты меньших 2×2 в матрице 3×3. Этот шаблон продолжается для поиска определителей матриц более высокого порядка.
Этот шаблон продолжается для поиска определителей матриц более высокого порядка.Определитель матрицы 4 × 4
Чтобы найти определитель матрицы 4 × 4, вам сначала нужно найти определители четырех матриц 3 × 3, которые находятся в матрице 4 × 4.В виде формулы:
Вернуться к началуДиагональная матрица — это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая проходит от верхнего левого угла до нижнего правого.
Записи на самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями еще можно назвать диагональной матрицей.
Единичная матрица, которая имеет все 1 на диагонали, также является диагональной матрицей. Любая матрица с равными элементами по диагонали (т. Е. 2,2,2 или 9,9,9) является скалярным кратным единичной матрице и также может быть классифицирована как диагональная.
Диагональная матрица имеет максимум n чисел, которые не равны нулю, где n — порядок матрицы.
 Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.Обозначение
Обозначение, обычно используемое для описания диагональной матрицы: diag (a, b, c) , где abc представляет собой числа в первой диагонали. Для приведенной выше матрицы это обозначение будет diag (3,2,4)..
Верхняя и нижняя треугольные матрицы
Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхние треугольные матрицы. В нижнетреугольной матрице числа под диагональю; верхнетреугольная матрица имеет числа над диагональю.
Диагональная матрица — это матрица с нижней диагональю и с нижней диагональю.
Прямоугольные диагональные матрицы
Для наиболее распространенного использования диагональная матрица представляет собой квадратную матрицу с порядком (размером) n .
 Существуют и другие формы, которые обычно не используются, например прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
Существуют и другие формы, которые обычно не используются, например прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
В началоТранспонирование матрицы (или транспонирование матрицы) — это как раз то место, где вы переключаете все строки матрицы в столбцы. Матрицы транспонирования полезны при комплексном умножении.
Альтернативный способ описания транспонированной матрицы состоит в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r».Например, элемент в строке 2, столбце 3 будет транспонирован в столбец 2, строку 3. Размер матрицы также изменится. Например, если у вас есть матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.
Симметричная матрица — это частный случай транспонированной матрицы; он равен своей транспонированной матрице.

Говоря более формальным языком, A = A T .Символы для матрицы транспонирования
Обычный символ для транспонированной матрицы — A T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ‘ и.
Свойства матриц транспонирования
Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы столкнулись в базовой алгебре (например, ассоциативным и коммутативным). Основные свойства матриц:
- (A T ) T = A: транспонированная матрица транспонирования является исходной матрицей.
- (A + B) T = A T + B T : Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы, сложенной вместе.
- (rA) T = rA T : когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент — это величина, которая может умножать матрицу).

- (AB) T = B T A T : транспонирование двух матриц, умноженных вместе, совпадает с произведением их транспонированных матриц в обратном порядке.
- (A -1 ) T = (A T ) -1 : транспонирование и инверсия матрицы могут выполняться в любом порядке.
В начало
Симметричная матрица — это квадратная матрица, имеющая симметрию относительно ведущей диагонали, сверху слева направо. Представьте себе складку в матрице по диагонали (не включайте числа в действительную диагональ). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:
Если вы можете сопоставить числа друг с другом по линии симметрии ( всегда ведущая диагональ), как в примере справа , у вас симметричная матрица.Альтернативное определение
Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна ее транспонированной.
 транспонирование матрицы — это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
транспонирование матрицы — это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы. Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда и альтернативное определение, что симметричная матрица равна ее транспонированию.С математической точки зрения, M = M T , где M T — матрица транспонирования.
Максимальное количество номеров
Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ — это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.

Диагональные матрицы
Диагональная матрица — это частный случай симметричной матрицы. Диагональная матрица имеет все нули, кроме ведущей диагонали.
Что такое асимметричная матрица?
Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является асимметричной:
Математически асимметричная матрица удовлетворяет условию a ij = -a ji .Например, возьмите запись в строке 3, столбце 2, которая равна 4. Его симметричный аналог — -4 в строке 2, столбце 3. Это условие также можно записать в терминах его транспонированной матрицы: A T = — А. Другими словами, матрица является кососимметричной, только если A T = -A, где A T — это транспонированная матрица.
Все старшие диагональные элементы в кососимметричной матрице должны быть нулевыми.
 Это потому, что из i, i = −a i, i следует i, i = 0.
Это потому, что из i, i = −a i, i следует i, i = 0.Еще одним интересным свойством этого типа матрицы является то, что если у вас есть две кососимметричные матрицы A и B одинакового размера, вы также получите кососимметричную матрицу, если сложите их вместе:
Добавление двух кососимметричных матриц все вместе.
Этот факт может помочь вам доказать, что две матрицы кососимметричны. Первый шаг — убедиться, что все элементы на ведущей диагонали равны нулю (что невозможно «доказать» математически!).Второй шаг — сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что a ij = — a ji .
Косоэрмитский
Косоэрмитова матрица по сути такая же, как кососимметричная матрица, за исключением того, что косоэрмитова матрица может содержать комплексные числа.
Косоэрмитова матрица, показывающая комплексные числа.
Фактически, кососимметричный и кососимметричный эквивалентны для вещественных матриц (матрицы, которая почти полностью состоит из действительных чисел).
Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в мнимой сфере ноль считается мнимым числом.
Вернуться к началуМатрица ковариации и дисперсии (также называемая матрицей ковариации или матрицей дисперсии) — это квадратная матрица, которая отображает дисперсию и ковариацию двух наборов двумерных данных вместе. Дисперсия — это мера того, насколько разбросаны данные. Ковариация — это мера того, насколько две случайные величины перемещаются вместе в одном направлении.
Дисперсии отображаются в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсии находятся в диагоналях ковариативной матрицы, потому что, по сути, эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.
Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.
Ковариации для каждой пары показаны в других ячейках.
 Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.
Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.Создание матрицы дисперсии-ковариации
Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать ковариативно-вариативные матрицы. Обратите внимание, что Excel вычисляет ковариацию для генеральной совокупности (знаменатель n), а не для выборки (n-1).Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.
Если вы хотите сделать один вручную:
Шаг 1: Вставьте отклонения для ваших данных в диагонали матрицы.
Шаг 2: Рассчитайте ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A / B в приведенном выше примере появляется в двух местах (A B и B A).

 Как найти обратную матрицу Матричная алгебра — Обратная матрица
Как найти обратную матрицу Матричная алгебра — Обратная матрица
 Вычислить матрицу, обратную данной.
Вычислить матрицу, обратную данной. д.).
д.). Мы
получим сдвоенную матрицу .
Умножим обе части этой матрицы на ,
тогда получим
Мы
получим сдвоенную матрицу .
Умножим обе части этой матрицы на ,
тогда получим Начинаем преобразования.
Начинаем преобразования.
 е. для тех матриц, у которых число строк и столбцов совпадают.
е. для тех матриц, у которых число строк и столбцов совпадают.

 …,m) .
…,m) . Обратная матрица может существовать только для квадратных матриц.
Обратная матрица может существовать только для квадратных матриц. Результирующая матрица является обратной для исходной матрицы.
Результирующая матрица является обратной для исходной матрицы.
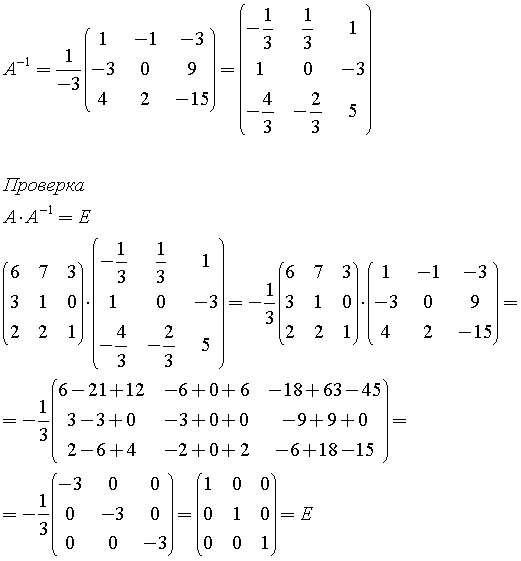

 Сделать это можно вручную, прописав адреса ячеек, используя клавиши клавиатуры. Либо можно сначала кликнуть внутри области ввода информации, затем зажав левую кнопку мыши выделить диапазон ячеек непосредственно в самой таблице. Когда все готово, нажимаем кнопку OK.
Сделать это можно вручную, прописав адреса ячеек, используя клавиши клавиатуры. Либо можно сначала кликнуть внутри области ввода информации, затем зажав левую кнопку мыши выделить диапазон ячеек непосредственно в самой таблице. Когда все готово, нажимаем кнопку OK. {-1}\cdot A= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix} \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}=$ $\begin{pmatrix} -5\cdot1 + 3\cdot2 & -5\cdot3 + 3\cdot 5\\ 2\cdot1 +(-1)\cdot2 & 2\cdot3 +(-1)\cdot5 \end{pmatrix}= \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}=I_{2}$
{-1}\cdot A= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix} \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}=$ $\begin{pmatrix} -5\cdot1 + 3\cdot2 & -5\cdot3 + 3\cdot 5\\ 2\cdot1 +(-1)\cdot2 & 2\cdot3 +(-1)\cdot5 \end{pmatrix}= \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}=I_{2}$
 Хочется узнать Ваше мнение о нем
Хочется узнать Ваше мнение о нем
 То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .
То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A . Найдём матрицу, обратную матрице A .
Найдём матрицу, обратную матрице A .



 Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С -1 справа.
Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С -1 справа.
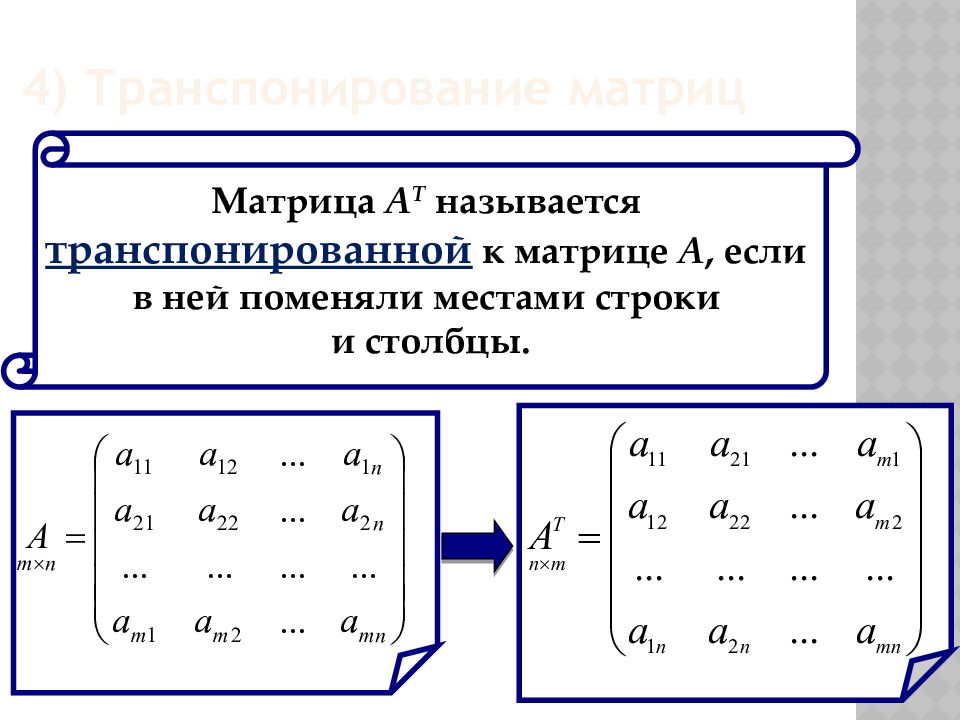


 Выпишем расширенную матрицу системы и приведем, содержащуюся в ней матрицу А к треугольному виду.
Выпишем расширенную матрицу системы и приведем, содержащуюся в ней матрицу А к треугольному виду.
 Ниже на примере проиллюстрируем взаимосвязь между матрицей
и его обратное.
Ниже на примере проиллюстрируем взаимосвязь между матрицей
и его обратное.

 Если
А
сводится к единичной матрице
я
п
, тогда
А
—
1
— матрица справа от преобразованной расширенной матрицы.
Если
А
сводится к единичной матрице
я
п
, тогда
А
—
1
— матрица справа от преобразованной расширенной матрицы. Если
А
—
1
не существует, пишите в единственном числе.
Если
А
—
1
не существует, пишите в единственном числе.


 Метод дополненной матрицы
Метод дополненной матрицы  Более «теоретический» курс, такой как линейная алгебра, не исключение. Фактически, как только вы научитесь делать что-то вроде поиска обратной матрицы вручную, калькулятор освободит вас от этого вычисления и позволит сосредоточиться на общей картине.
Более «теоретический» курс, такой как линейная алгебра, не исключение. Фактически, как только вы научитесь делать что-то вроде поиска обратной матрицы вручную, калькулятор освободит вас от этого вычисления и позволит сосредоточиться на общей картине. {-1} \)]. Вы попадете в меню, которое вы видите ниже. Наведите курсор на «РЕДАКТИРОВАТЬ» вверху.
{-1} \)]. Вы попадете в меню, которое вы видите ниже. Наведите курсор на «РЕДАКТИРОВАТЬ» вверху.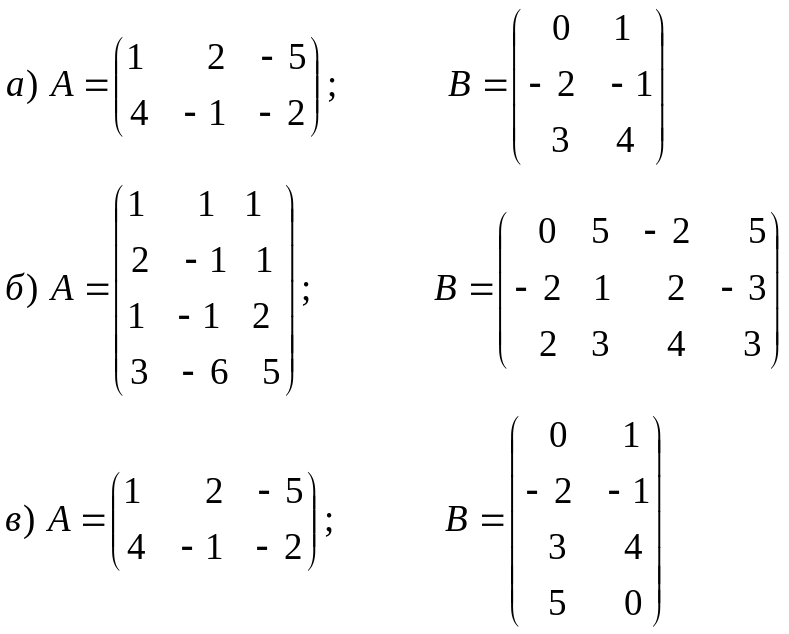 {-1} \)] и нажмите Enter
{-1} \)] и нажмите Enter Даже с необязательным шагом у меня уходит меньше 3 минут.
Даже с необязательным шагом у меня уходит меньше 3 минут. {T} $.
{T} $.

 O.S. Математика CyberBoard.
O.S. Математика CyberBoard.

 Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одном и том же месте (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).
Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одном и том же месте (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).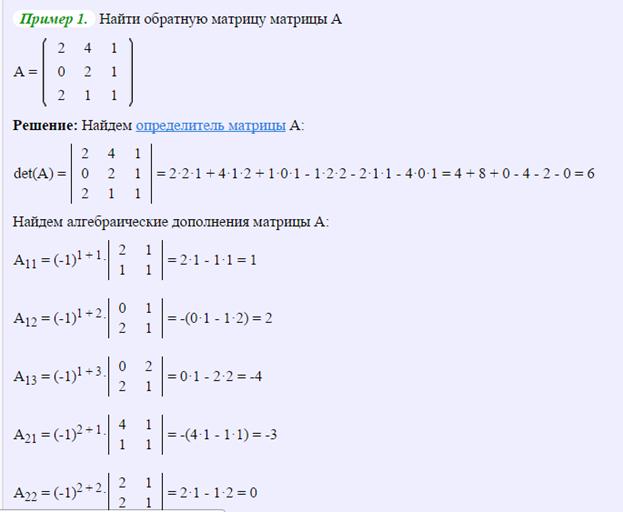
 И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:  Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
 Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.  Формула для вычисления определителя различается в зависимости от размера матрицы.Например, матрица 2 × 2, формула ad-bc.
Формула для вычисления определителя различается в зависимости от размера матрицы.Например, матрица 2 × 2, формула ad-bc. По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .
По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A . Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах — нули. Поэтому их иногда называют нулевой матрицей .
Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах — нули. Поэтому их иногда называют нулевой матрицей .  Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:
Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:  Основное уравнение:
Основное уравнение: 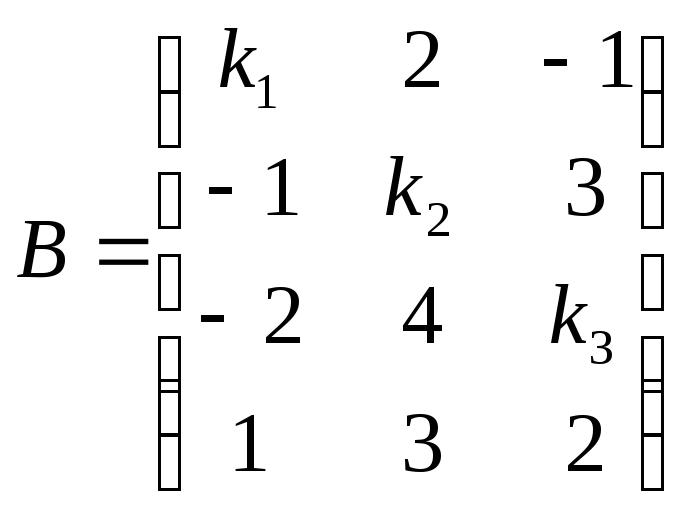 Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в так называемом разложении на собственные числа . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.
Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в так называемом разложении на собственные числа . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной. Находя корни (нули), получаем x = 2 + 3√2, 2 — 3√2
Находя корни (нули), получаем x = 2 + 3√2, 2 — 3√2
 «Сложите, если это положительное число, и вычтите, если оно отрицательное:
«Сложите, если это положительное число, и вычтите, если оно отрицательное: 
 Этот шаблон продолжается для поиска определителей матриц более высокого порядка.
Этот шаблон продолжается для поиска определителей матриц более высокого порядка. Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.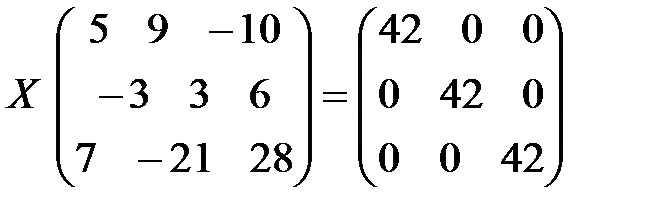 Существуют и другие формы, которые обычно не используются, например прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
Существуют и другие формы, которые обычно не используются, например прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы. 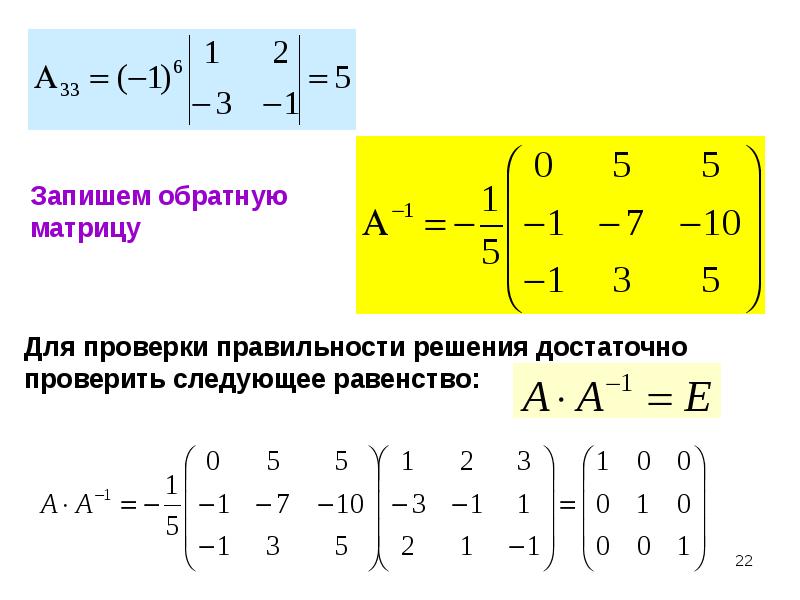

 транспонирование матрицы — это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
транспонирование матрицы — это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы. 
 Это потому, что из i, i = −a i, i следует i, i = 0.
Это потому, что из i, i = −a i, i следует i, i = 0.
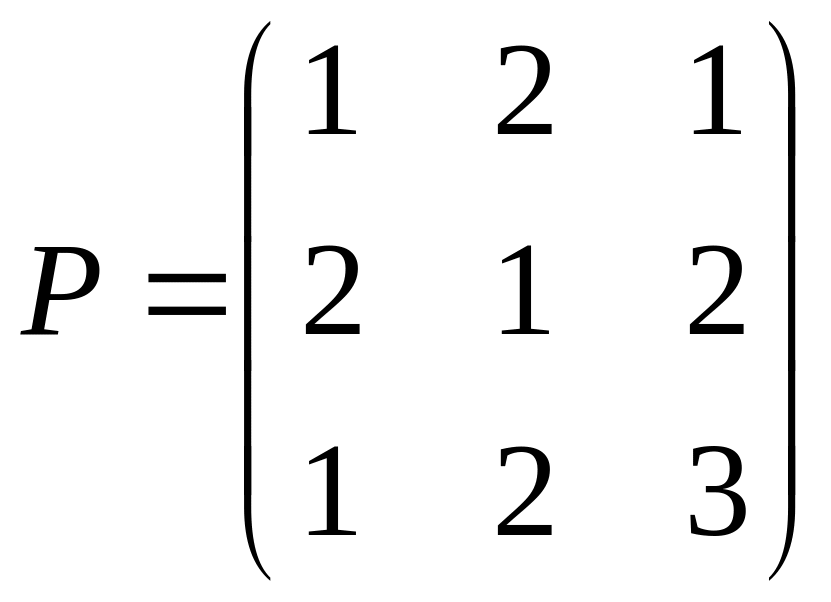 Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.
Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.