Показательные уравнения и неравенства
Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения ах = аb, где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:
Теорема. Если а > 0, а ≠ 1 и ах1 = ах2, то х1 = х2.
Обоснуем рассмотренное утверждение.
Предположим, что равенство х1 = х2 не выполняется, т.е. х1 < х2 или х1 = х2. Пусть, например, х1 < х2. Тогда если а > 1, то показательная функция у = ах возрастает и поэтому должно выполняться неравенство ах1 < ах2; если 0 < а < 1, то функция убывает и должно выполняться неравенство а
Рассмотрим несколько задач.
Задача 1.
Решить уравнение 4 ∙ 2х = 1.
Решение.
Запишем уравнение в виде 22 ∙ 2х = 20 – 2х+2 = 20, откуда получаем х + 2 = 0, т.е. х = -2.
Ответ. х = -2.
Задача 2.
Решить уравнение 23х ∙ 3х = 576.
Решение.
Так как 23х = (23)х = 8х, 576 = 242, то уравнение можно записать в виде 8х ∙ 3х = 242 или в виде 24х = 242.
Отсюда получаем х = 2.
Ответ. х = 2.
Задача 3.
Решить уравнение 3х+1 – 2∙3х — 2 = 25.
Решение.
Вынося в левой части за скобки общий множитель 3 х — 2, получаем 3х — 2 ∙ (33 – 2) = 25 – 3х — 2∙ 25 = 25,
откуда 3х — 2 = 1, т.е. х – 2 = 0, х = 2.
Ответ. х = 2.
Задача 4.
Решить уравнение 3х = 7х.
Решение.
Так как 7х ≠ 0, то уравнение можно записать в виде 3х/7х = 1, откуда (3/7)х = 1, х = 0.
Ответ. х = 0.
Задача 5.
Решить уравнение 9х – 4 ∙ 3х – 45 = 0.
Решение.
Заменой 3х = а данное уравнение сводится к квадратному уравнению а2 – 4а – 45 = 0.
Решая это уравнение, находим его корни: а1 = 9, а2 = -5, откуда 3х = 9, 3х = -5.
Уравнение 3х = 9 имеет корень 2, а уравнение 3х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ. х = 2.
Решение показательных неравенств часто сводится к решению неравенств ах > аb или ах < аb. Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции.
Рассмотрим некоторые задачи.
Задача 1.
Решить неравенство 3х < 81.
Решение.
Запишем неравенство в виде 3х < 34. Так как 3 > 1, то функция у = 3х является возрастающей.
Следовательно, при х < 4 выполняется неравенство 3х < 34, а при х ≥ 4 выполняется неравенство 3х ≥ 34.
Таким образом, при х < 4 неравенство 3х < 34 является верным, а при х ≥ 4 – неверным, т.е. неравенство
3х < 81 выполняется тогда и только тогда, когда х < 4.
Ответ. х < 4.
Задача 2.
Решить неравенство 16 х +4х – 2 > 0.
Решение.
Обозначим 4х = t, тогда получим квадратное неравенство t2 + t – 2 > 0.
Это неравенство выполняется при t < -2 и при t > 1.
Так как t = 4х, то получим два неравенства 4х < -2, 4х > 1.
Первое неравенство не имеет решений, так как 4х > 0 при всех х € R.
Второе неравенство запишем в виде 4х > 40, откуда х > 0.
Ответ. х > 0.
Задача 3.
Графически решить уравнение (1/3)х = х – 2/3.
Решение.
1) Построим графики функций у = (1/3)х и у = х – 2/3.
2) Опираясь на наш рисунок, можно сделать вывод, что графики рассмотренных функций пересекаются в точке с абсциссой х ≈ 1. Проверка доказывает, что
х = 1 – корень данного уравнения:
(1/3)1 = 1/3 и 1 – 2/3 = 1/3.
Иными словами, мы нашли один из корней уравнения.
3) Найдем другие корни или докажем, что таковых нет. Функция (1/3)х убывающая, а функция у = х – 2/3 возрастающая. Следовательно, при х > 1 значения первой функции меньше 1/3, а второй – больше 1/3; при х < 1, наоборот, значения первой функции больше 1/3, а второй – меньше 1/3. Геометрически это означает, что графики этих функций при х > 1 и х < 1 «расходятся» и потому не могут иметь точек пересечения при х ≠ 1.
Ответ. х = 1.
!!! Заметим, что из решения этой задачи, в частности, следует, что неравенство (1/3)х > х – 2/3 выполняется при х < 1, а неравенство (1/3)х < х – 2/3 – при х > 1.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
6. Показательные уравнения и неравенства
6.1. Показательные уравнения
Определение 6.1. Показательными называются уравнения, у которых переменная содержится в показатели степени.
Рассмотрим основные методы решения показательных уравнений.
1. Приведение обеих частей уравнения к одинаковому основанию:
,
где  ,
,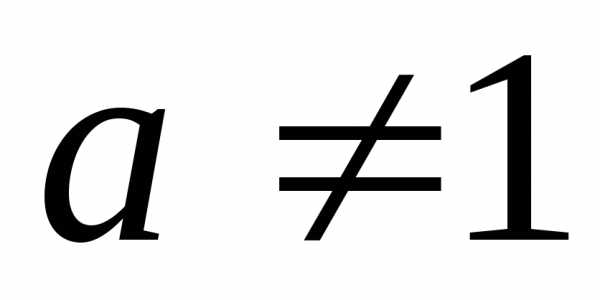 .
.
2. Вынесение общего множителя за скобки.
3. Уравнения, в которых правая и левая часть не приводится к одному основанию, можно решить логарифмированием:
.
4. Введение новой переменной.
5. Уравнение вида
,
где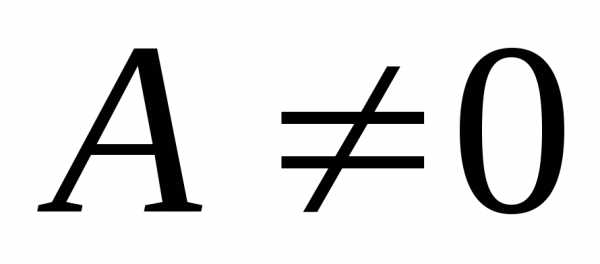 ,
, ,
,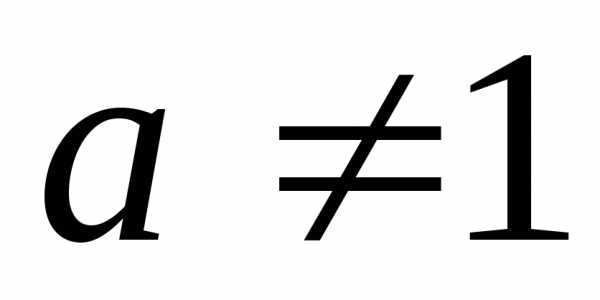 ,
, ,
,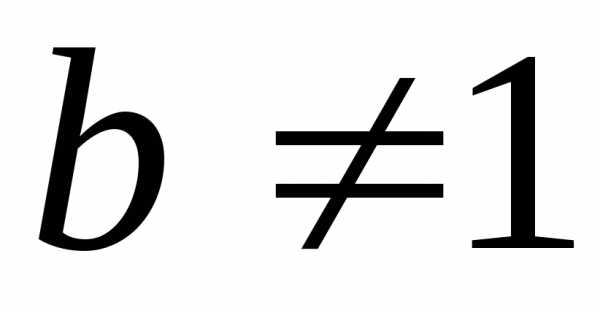 .
.
6. Показательно-степенные уравнения
7. Функциональный метод.
Пример 6.1. Решить уравнение .
Решение.
Ответ: 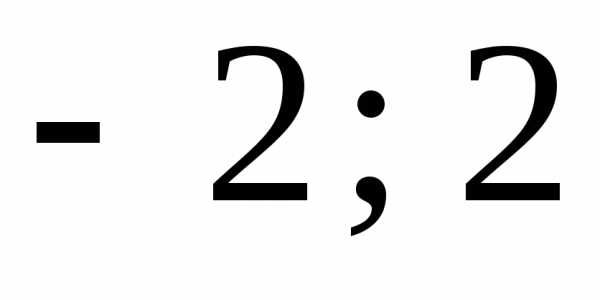 .
.
Пример 6.1.
Решить уравнение .Решение. Найдем предварительно ОДЗ уравнения:
.
Тогда на ОДЗ получим:
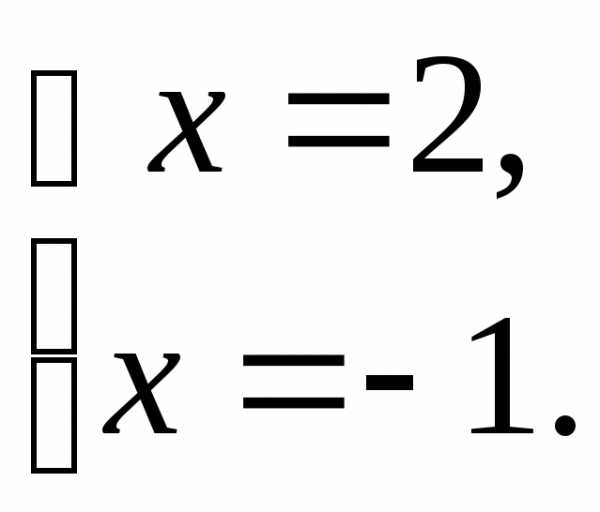
Оба корня принадлежат ОДЗ.
Ответ: 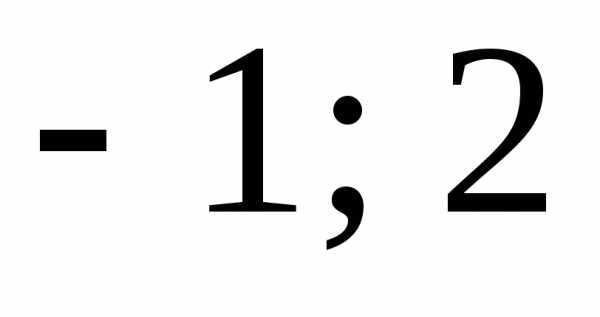 .
.
Пример 6.2. Решить уравнение  .
.
Решение. Так как левая часть является строго
убывающей функцией, то любое положительное
значение эта функция принимает ровно
один раз. Следовательно, уравнение имеет
единственное решение. Подбором получаем,
что решением уравнения является 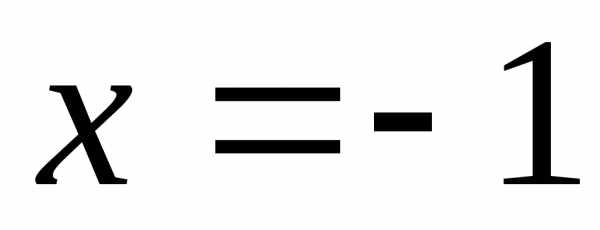
Ответ: 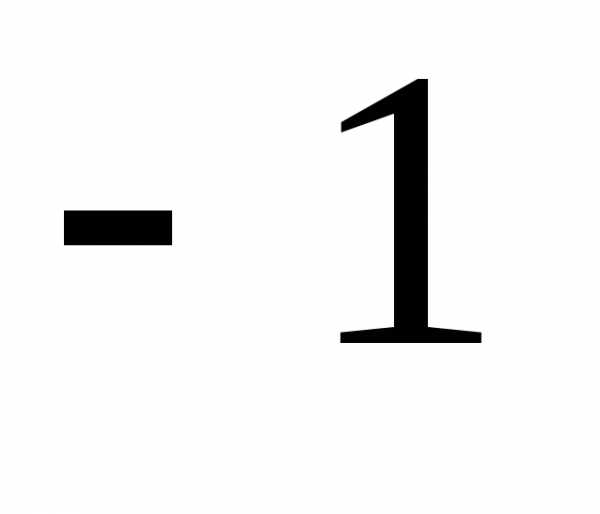 .
.
Пример 6.3. Решить уравнение .
Решение. Прологарифмируем уравнение по основанию 4:
.
Ответ:  .
.
Пример 6.4. Решить уравнение: .
Решение. Прологарифмируем уравнение, например, по основанию 4. Тогда:
Ответ: .
Пример 6.5. Решить уравнение
.
Решение. Отметим, что
, ,.
Введем замену
,
Сделаем замену: 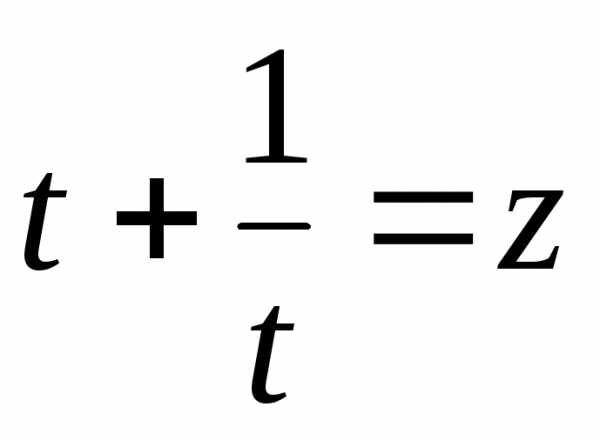 ,,
тогда
,,
тогда
.
Переходя обратно
к переменной 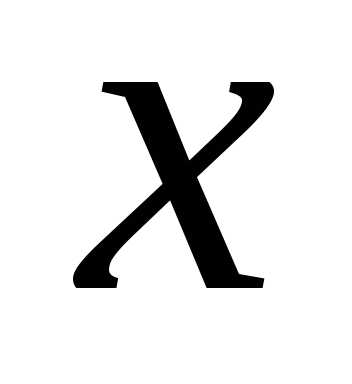 ,
получаем
,
получаем
Ответ: .
Пример 6.6. Решить уравнение
Решение. Проведем предварительно преобразование правой части уравнения
.
Тогда исходное уравнение привет вид:
Ответ: 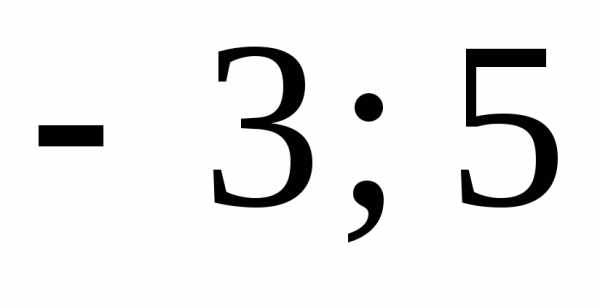 .
.
6.2. Показательные неравенства
Решение показательных
неравенств основывается на свойствах
монотонности показательной функции 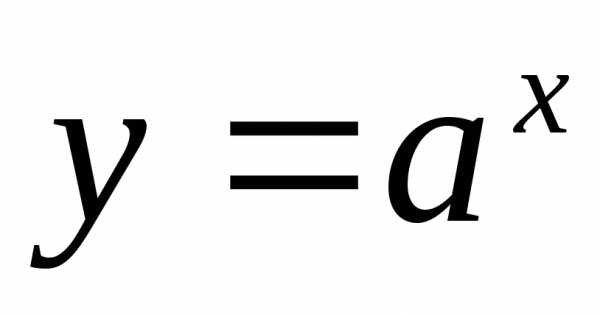
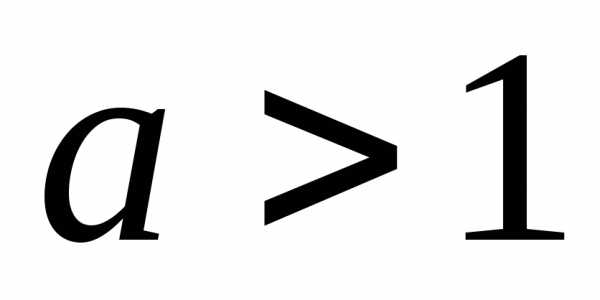 функция строго возрастает, а прифункция убывает.
функция строго возрастает, а прифункция убывает.Перечислим основные методы решения показательных неравенств.
1. Приведение обеих частей неравенства к одинаковому основанию:
;
2. Вынесение общего множителя за скобки.
3. Введение новой переменной.
4. Логарифмирование обеих частей неравенства по выбранному основанию.
5. Неравенства вида
,
где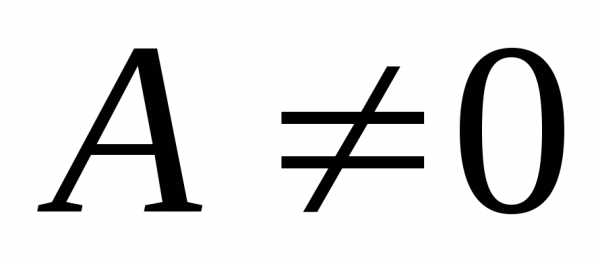 ,
, ,
,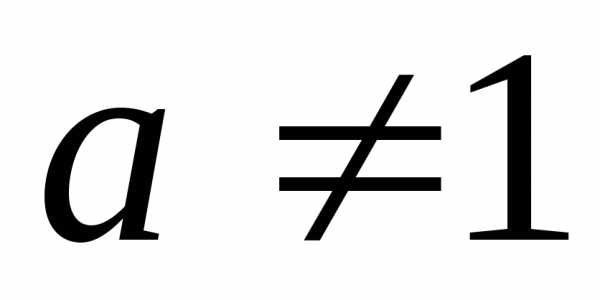 ,
, ,
,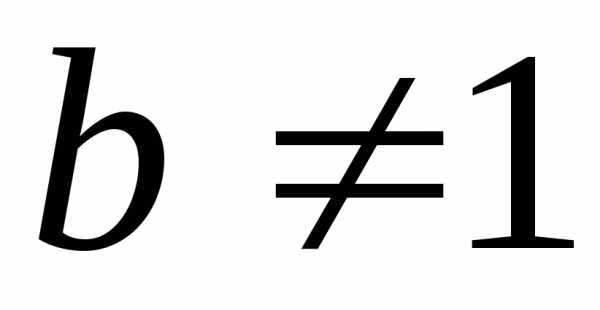 .
.
6. Неравенства
вида 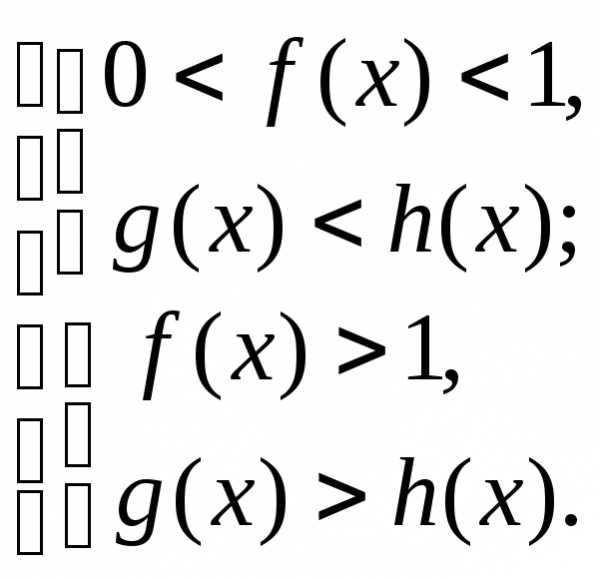
Пример 6.7. Решить неравенство .
Решение. Так как 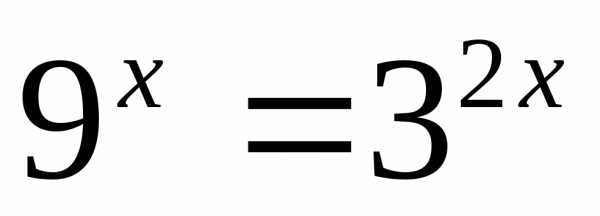 ;,
то, учитывая, что основание
;,
то, учитывая, что основание ,
исходное неравенство перепишется в
виде:
,
исходное неравенство перепишется в
виде:
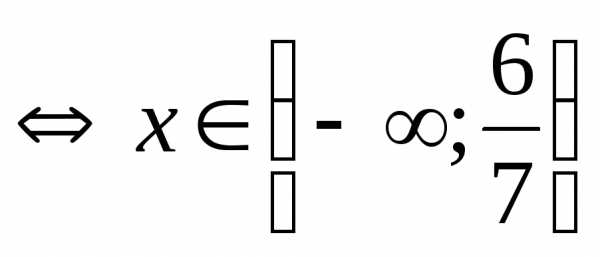 .
.
Ответ: 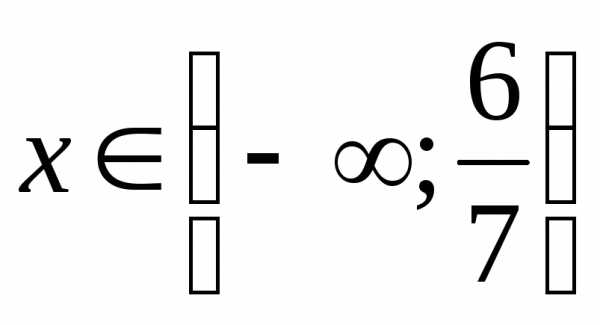 .
.
Пример 6.8. Решить неравенство .
Решение. Так как основание , то
 .
.
Ответ: 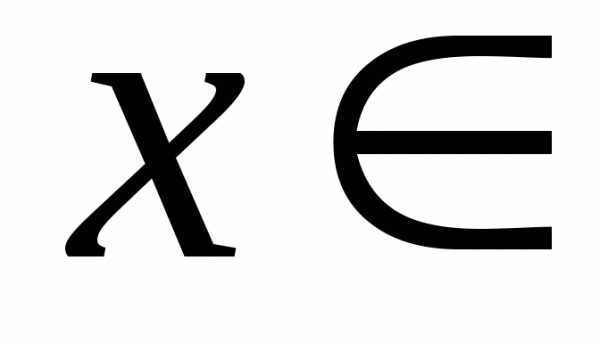
 .
.
Пример 6.9. Решить неравенство 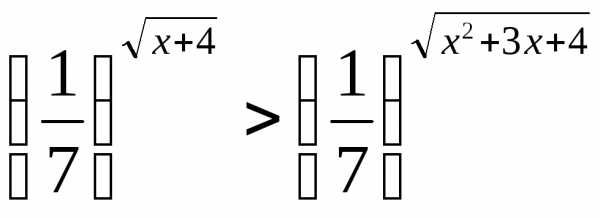 .
.
Решение. Так
как основание 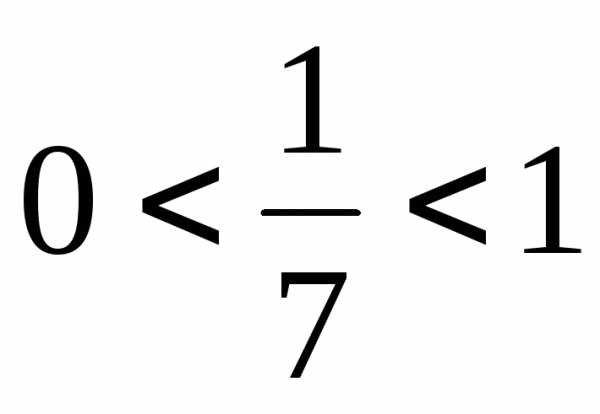 ,
то
,
то
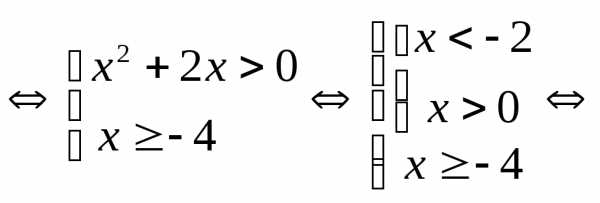 .
.
Ответ: .
Пример 6.10. Решить неравенство .
Решение.
.
Ответ: 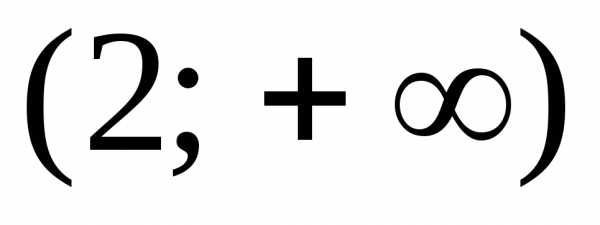 .
.
Пример 6.11. Решить неравенство .
Решение.
.
Ответ: 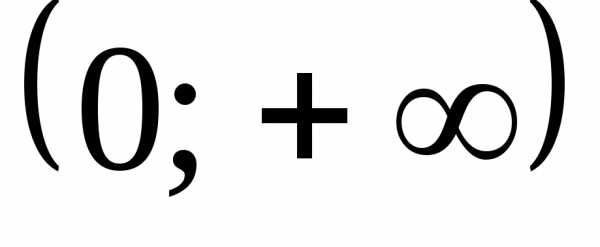 .
.
Пример 6.12. Решить неравенство .
Решение. .
Сделаем замену 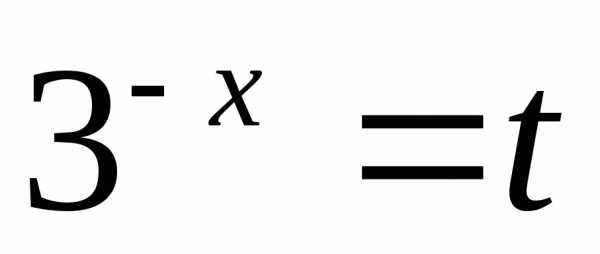 ,
, ,
тогда исходное неравенство примет вид:
,
тогда исходное неравенство примет вид:
.
Ответ: 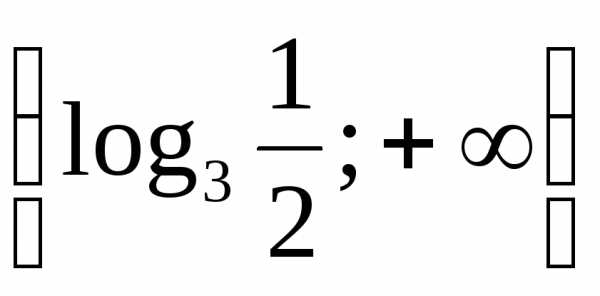 .
.
Пример 6.13. Решить неравенство
Решение. 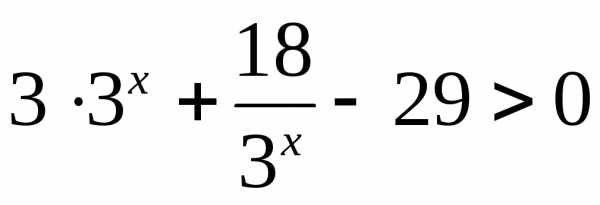 .
.
Сделаем замену: 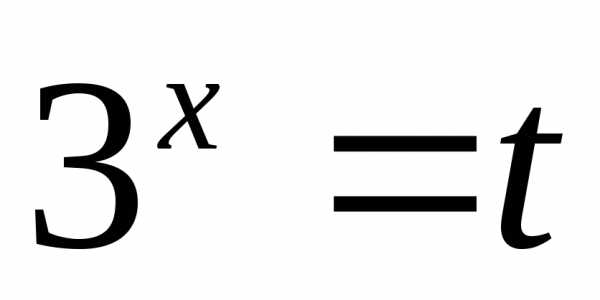 ,
,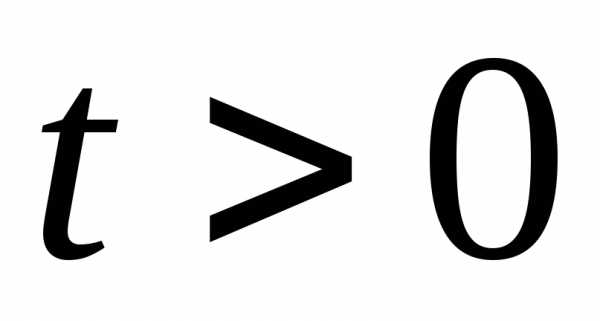 ,
тогда
,
тогда
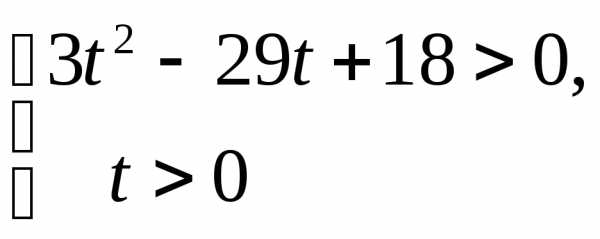
.
Ответ: .
Пример 6.14. Решить неравенство:
Решение.
Разделим обе части
неравенства на  ,
получаем
,
получаем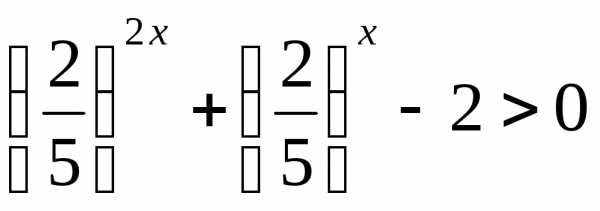 .
.
Сделаем замену 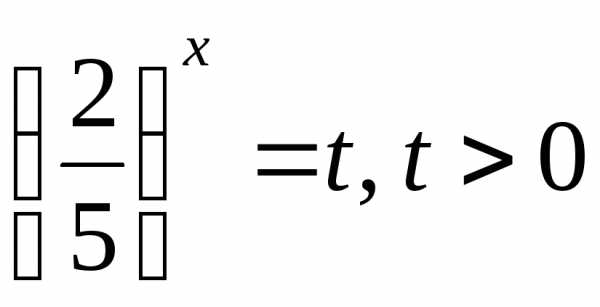 ,
тогда
,
тогда
 .
.
Ответ: 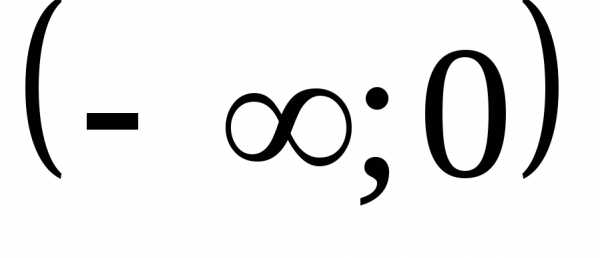 .
.
Пример 6.15. Решить неравенство:
Решение: Исходное неравенство равносильно совокупности двух систем:
.
Ответ: .
Пример 6.16. Решить неравенство:
Решение. 
Решим первую систему полученной совокупности:
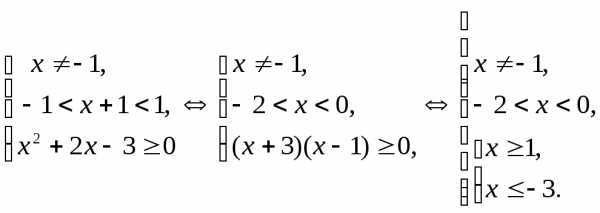
Данная система решений не имеет.
Решим вторую систему совокупности:
.
Ответ: .
Пример 6.17. Решить неравенство .
Решение.
.
.
Последнее неравенство равносильно совокупности двух систем:
1.
2.
Сравним числа 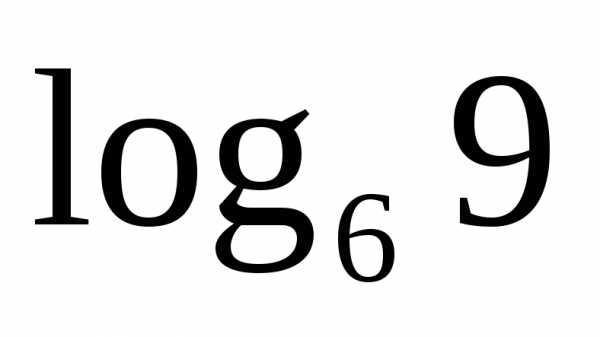 и
и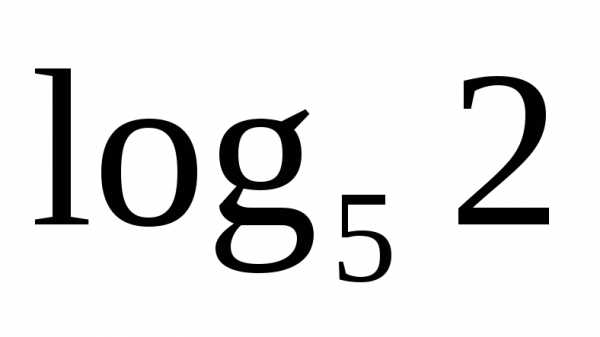 .
Так как
.
Так как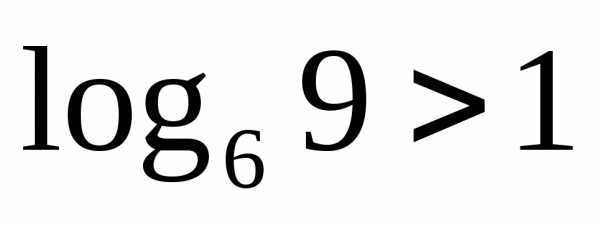 ,
а
,
а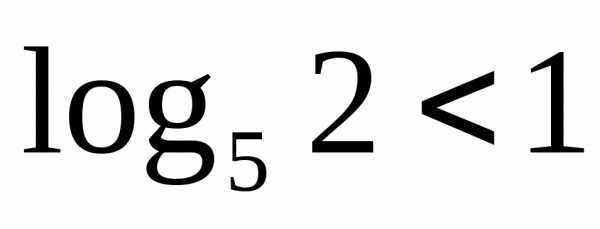 ,
то,
значит.
Тогда получаем, что первая система
решений не имеет, а решением второй
служит промежуток.
,
то,
значит.
Тогда получаем, что первая система
решений не имеет, а решением второй
служит промежуток.
Ответ: .
Пример 6.18. Решить неравенство: .
Решение. Область определения неравенства определяется условием . Исходное неравенство равносильно совокупности:
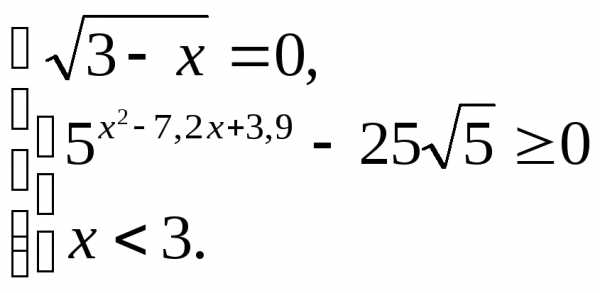 .
.
Из уравнения
получаем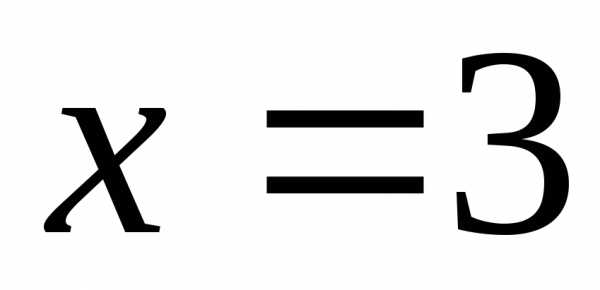 .
.
Так как , то первое неравенство системы можно записать в виде
Учитывая условие 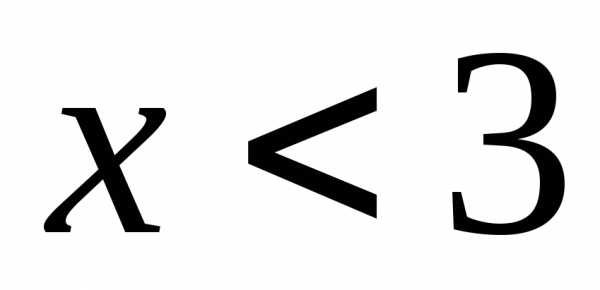 ,
получаем решение системы – промежуток
,
получаем решение системы – промежуток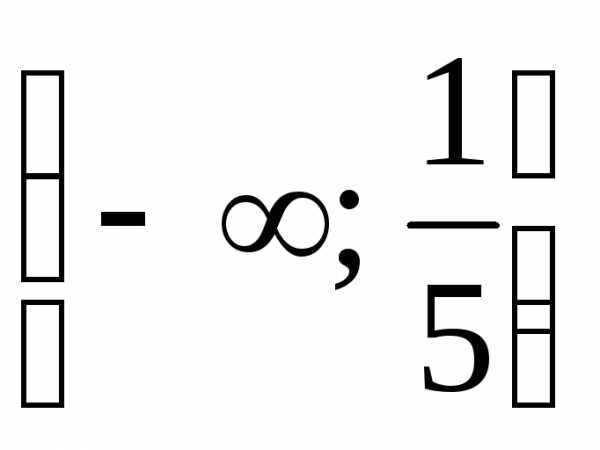 .
Тогда решение исходного неравенства
имеет вид
.
Тогда решение исходного неравенства
имеет вид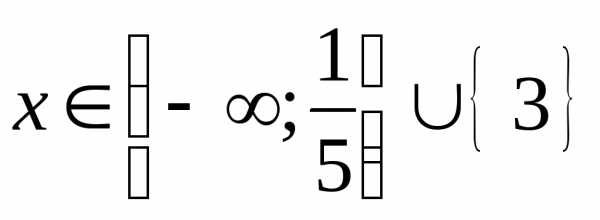 .
.
Ответ:  .
.
Пример 6.19. Решить неравенство 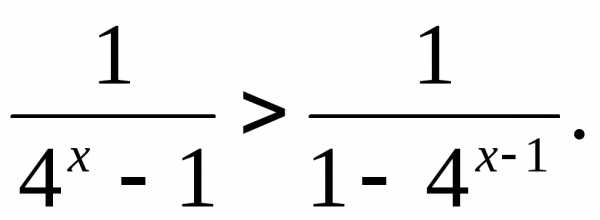
Решение. .
Сделаем замену , тогда
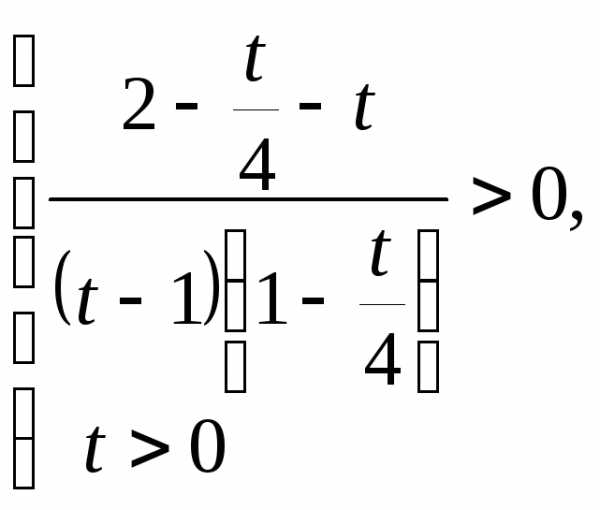
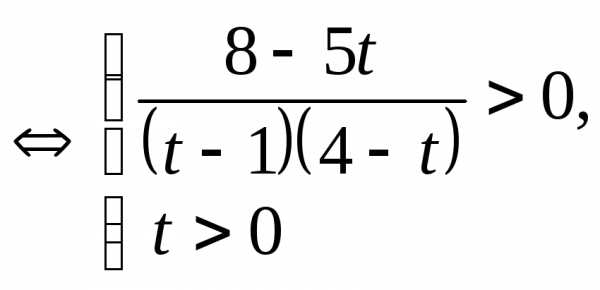
.
Ответ: .
studfiles.net
Решение показательных уравнений и неравенств.
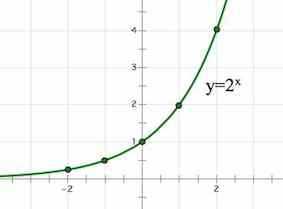
Функцию вида y = ax, где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции y = ax:
График показательной функцииГрафиком показательной функции является экспонента:
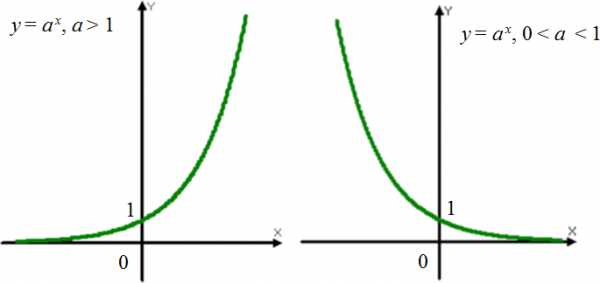
Графики показательных функций (экспоненты)
Решение показательных уравнений
Показательными называются уравнения, в которых неизвестная переменная находится только в показателях каких-либо степеней.
Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
Теорема 1. Показательное уравнение af(x) = ag(x) (где a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).
Помимо этого, полезно помнить об основных формулах и действиях со степенями:

Пример 1. Решите уравнение:
Решение: используем приведенные выше формулы и подстановку:
Уравнение тогда принимает вид:
Дискриминант полученного квадратного уравнения положителен:
Это означает, что данное уравнение имеет два корня. Находим их:
Переходя к обратной подстановке, получаем:
Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:
С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию.
Ответ: x = 3.
Пример 2. Решите уравнение:
Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 94-x положительна и не равна нулю).
Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней:
Последний переход был осуществлен в соответствии с теоремой 1.
Ответ: x = 6.
Пример 3. Решите уравнение:
Решение: обе части исходного уравнения можно поделить на 0,2x. Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид:
Ответ: x = 0.
Пример 4. Решите уравнение:
Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней:
Деление обеих частей уравнения на 4x, как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x.
Ответ: x = 0.
Пример 5. Решите уравнение:
Решение: функция y = 3x, стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет.
Ответ: x = -1.
Пример 6. Решите уравнение:
Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи:
Ответ: x = 2.
Решение показательных неравенств
Показательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней.
Для решения показательных неравенств требуется знание следующей теоремы:
Теорема 2. Если a > 1, то неравенство af(x) > ag(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 < a < 1, то показательное неравенство af(x) > ag(x) равносильно неравенству противоположного смысла: f(x) < g(x).
Пример 7. Решите неравенство:
Решение: представим исходное неравенство в виде:
Разделим обе части этого неравенства на 32x, при этом (в силу положительности функции y = 32x) знак неравенства не изменится:
Воспользуемся подстановкой:
Тогда неравенство примет вид:
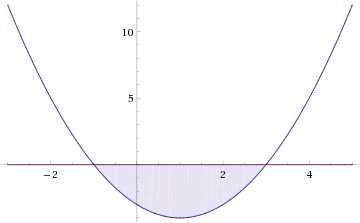
Итак, решением неравенства является промежуток:
переходя к обратной подстановке, получаем:
Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:
Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательно получаем ответ:
Пример 8. Решите неравенство:
Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде:
Введем новую переменную:
С учетом этой подстановки неравенство принимает вид:
Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство:
Итак, неравенству удовлетворяют следующие значения переменной t:
Тогда, переходя к обратной подстановке, получаем:
Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству:
Окончательно получаем ответ:
Пример 9. Решите неравенство:
Решение:
Делим обе части неравенства на выражение:
Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем:
Воспользуемся заменой переменной:
Исходное уравнение тогда принимает вид:
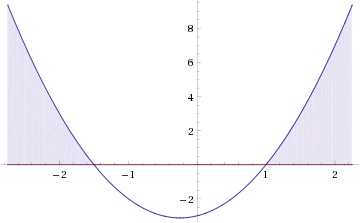
Итак, неравенству удовлетворяют значения t, находящиеся в промежутке:
Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая:
Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе:
Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательный ответ:
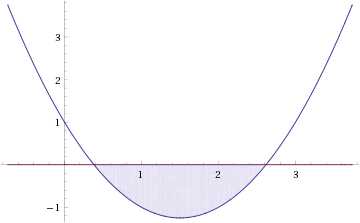
Пример 10. Решите неравенство:
Решение:
Ветви параболы y = 2x+2-x2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:
Ветви параболы y = x2-2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:
Вместе с этим ограниченной снизу оказывается и функция y = 3x2-2x+2, стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 31 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1.
Ответ: x = 1.
infourok.ru
Основные типы показательных неравенств | Подготовка к ЕГЭ по математике
 Сегодня решаем показательные неравенства.
Сегодня решаем показательные неравенства.
Рассмотрим основные типы показательных неравенств.
При решении показательных неравенств мы будем использовать следующие переходы:
и
Поясним, первый переход возникает в силу возрастания показательной функции , второй – в силу убывания функции .
Показательные неравенства, сводящиеся к простейшим
Задание 1.
Решить неравенство .
Решение:
Перепишем неравенство следующим образом:
А далее вот так:
Так как – возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:
Ответ: .
Задание 2.
Решить неравенство:
Решение:
Перепишем неравенство следующим образом:
Заметим, что .
В силу того, что основание степени () меньше 1, то есть мы имеем дело с убывающей функцией, переходим к следующему неравенству (не забывая поменять знак на ):
Ответ:
Однородные показательные неравенства
Задание 3.
Решить неравенство:
Решение:
Вынесем за скобку
Тогда переходим к следующему неравенству (в силу того, что основание степени больше 1, знак неравенства не меняется):
Ответ:
Показательные неравенства, сводящиеся к квадратным
Задание 4.
Решить неравенство
Решение:
Разделим обе части неравенства на 3:
Мы видим квадратное неравенство относительно которое будем решать методом интервалов.
Имеем:
или
или
Ответ:
Задание 5.
Решить неравенство
Решение:
Мы видим квадратное неравенство относительно , которое будем решать методом интервалов.
Находим при помощи дискриминанта корни квадратного трехчлена . Переходим к следующему неравенству:
Получаем: или . Заметьте, нет смысла указывать, что , так как по определению положительно.
Итак,
Ответ:
Задание 6.
Решить неравенство
Решение:
Разделим обе части неравенства на (можно и на , – как хотите…). Заметим, .
Заметим, что . Аналогично с .
Мы имеем квадратное неравенство относительно
которое будем решать методом интервалов.
Воспользуемся следующим способом превращения суммы в произведение:
где – корни уравнения (в случае неотрицательного дискриминанта квадратного трехчлена).
Заготавливаем шаблончик и находим корни при помощи дискриминанта, тогда
То есть
Ответ:
Задание 7.
Решить неравенство
Решение:
Перепишем неравенство следующим образом:
Домножим обе части неравенства на (заметим, ):
Ответ:
Показательные неравенства, сводящиеся к рациональным
Задание 8.
Решить неравенство:
Решение:
Переносим все в левую сторону неравенства и приводим к общему знаменателю:
Мы можем “отбросить” сумму в силу ее положительности:
Неравенство равносильно следующему:
Ответ:
Неравенства, решаемые графическим методом
Задание 9.
Решить неравенство:
Решение:
Рассмотрим функции и Обе они определены на . Первая – возрастает, вторая – убывает. Значит, уравнение имеет не более одного решения. Несложно заметить, что является корнем указанного уравнения.
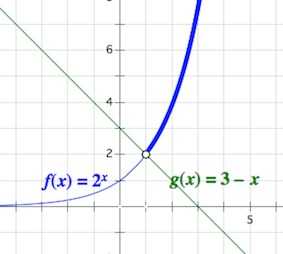
А значит, если вернуться к неравенству и посмотреть на него с графической точки зрения, мы должны взять те значения , которые отвечают за ту часть графика , что лежит выше графика , то есть .
Ответ:
Для самостоятельной работы:
Решить неравенства:
1.
Ответ: + показать
2.
Ответ: + показать
3.
Ответ: + показать
4.
Ответ: + показать
{-2}
5.
Ответ: + показать
6.
Ответ: + показать
7.
Ответ: + показать
(-1;1]
8.
Ответ: + показать
.
egemaximum.ru
Показательные уравнения и неравенства.
Инструкционная карта № 14
Тақырыбы/ Тема: «Решение простейших и сводящихся к ним показательных уравнений и неравенств».
Мақсаты/ Цель:Познакомить учащихся с методами решения простейших и сводящихся к ним показательных уравнений и неравенств. Уметь применять эти методы при решении упражнений.
Создать условия для развития умения устанавливать единые общие признаки и свойства целого, составлять план деятельности (сравнивать, анализировать).
Создать атмосферу коллективного поиска, эмоциональной приподнятости, радости познания трудностей.
Теоретический материал:
Основные методы и приемы решения показательных уравнений
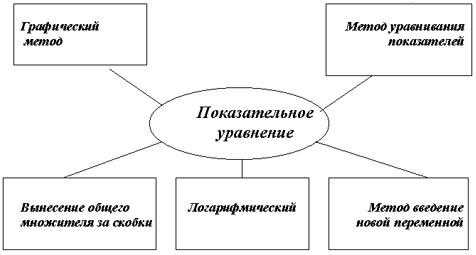
Пример 1. 3х2-х-2=81— Метод уравнивания показателей.
Решение:
3х2-х-2=34
Приравниваем показатели:
х2-х-2=4
х2-х-6=0
Получили квадратное уравнение:
D=1+24=25, D0, следовательно, уравнение имеет два действительных корня
х1=(1+5)/2=3
х2=(1-5)/2=-2
Ответ: х=3 и х=-2
Пример 2. 4х+1+4х=320— Метод вынесения общего множителя за скобки
Решение:
В таких случаях выносится основание с наименьшим показателем. В данном уравнении наименьшим показателем является х. Вынесем 4х за скобки:
4х(4+1)=3204х∙5=320
Представим 320 в виде 5∙43, тогда:4х∙5=5∙43
Поделим левую и правую часть уравнения на 5:4х=43
Приравняем показатели: х=3
Ответ: 3
Пример 3. 4х — 3·2х +2 = 0 — Метод замены переменных
Сначала — как обычно. Переходим к одному основанию. К двойке. 4х = (22)х = 22х
Получаем уравнение: 22х — 3·2х +2 = 0
А вот тут и зависнем. Предыдущие приёмы не сработают, как ни крутись. Придётся доставать из арсенала ещё один могучий и универсальный способ. Называется он замена переменной.
Суть способа проста до удивления. Вместо одного сложного значка (в нашем случае — 2х) пишем другой, попроще (например — t).
Итак, пусть 2х = t. Тогда 22х = 2х2 = (2х)2 = t2
Заменяем в нашем уравнении все степени с иксами на t: t2 — 3t+2 = 0
Квадратные уравнения не забыли ещё? Решаем через дискриминант, получаем: t1 = 2 ; t2 = 1
Тут, главное, не останавливаться, как бывает… Это ещё не ответ, нам икс нужен, а не t. Возвращаемся к иксам, т.е. делаем обратную замену. Сначала для t1: t1 = 2 = 2х
Стало быть, 2х = 2; х1 = 1 Один корень нашли. Ищем второй, из t2: t2 = 1 = 2х ; 2х = 1
Гм… Слева 2х, справа 1… Неувязочка? Да вовсе нет! Достаточно вспомнить (из действий со степенями, да…), что единичка — это любое число в нулевой степени. Любое. Какое надо, такое и поставим. Нам нужна двойка. Значит: 1 = 20 2х = 20 х2 = 0
Вот теперь всё. Получили 2 корня: х1 = 1 х2 = 0 — Это ответ.
Практические советы:
1. Первым делом смотрим на основания степеней. Соображаем, нельзя ли их сделать одинаковыми. Пробуем это сделать, активно используя действия со степенями. Не забываем, что числа без иксов тоже можно превращать в степени!
2. Пробуем привести показательное уравнение к виду, когда слева и справа стоят одинаковые числа в каких угодно степенях. Используем действия со степенями и разложение на множители. То, что можно посчитать в числах — считаем.
3. Если второй совет не сработал, пробуем применить замену переменной. В итоге может получиться уравнение, которое легко решается. Чаще всего — квадратное. Или дробное, которое тоже сводится к квадратному.
4. Для успешного решения показательных уравнений надо степени некоторых чисел знать «в лицо».
Рассмотрим решение показательных неравенств вида , где b – некоторое рациональное число.
Если a1, то показательная функция монотонно возрастает и определена при всех х. Для возрастающей функции большему значению функции соответствует большее значение аргумента. Тогда неравенстворавносильно неравенству .
Если 0 монотонно убывает и определена при всех х. Для убывающей функции большему значению функции соответствует меньшее значение аргумента. Тогда неравенстворавносильно неравенству
Пример 4. Решим неравенство
Запишем неравенство в виде . Т. к. , то показательная функция возрастает. Поэтому данное неравенство равносильно неравенству . Ответ: .
Пример 5. Решим неравенство .
Запишем неравенство в виде .
Показательная функция убывает. Поэтому данное неравенство равносильно неравенству х
Ответ: .
Практическая часть:
I Вариант.
Решите уравнения:
а) 0,8; б) ; в) 3; г) 4.
Решите неравенства:
а) 2 .
3. Решите систему уравнений: .
II Вариант.
Решите уравнения:
а) 3; б) 2; в) 2; г) 9.
Решите неравенства.
а) 51; б) 0,7х.
3. Решите систему уравнений: .
III Вариант.
Решите уравнения:
а) 9-х=27; б) ; в) 5; г) 9.
Решите неравенства:
а) ; б) 48.
3. Решите систему уравнений: .
IV Вариант.
Решите уравнения:
а) 8-х=16; б) 102х=0,1; в) 3; г) 4.
Решите неравенства:
а) -0,5; б) 9
3. Решите систему уравнений: .
V Вариант.
1. Решите уравнения:
а) 2х+2х-3=18; б) ; в) ; г) 8.
2.Решите неравенства:
а) 5; б) 3
3. Решите систему уравнений: .
Контрольные вопросы:
Всегда ли можно решить показательное уравнение способом приведения степеней к одинаковым основаниям?
В чем заключается основной смысл способа решения показательного уравнения введением новой переменной?
Что общего в ходе решения показательных уравнений и решения линейных уравнений с одной переменной?
Перечислите основные требования, соблюдение которых является обязательным в решении показательных неравенств?
multiurok.ru
Показательная функция. Решение показательных уравнений и неравенств
Разделы: Математика
Цели и задачи:
— обобщить и закрепить знание основных свойств показательной функции и применение их при решении задач;
— закрепить умение распознавать виды показательных уравнений и неравенств и находить методы их решения;
— развивать навыки логического мышления и вычислительные навыки;
— воспитывать внимательность, аккуратность при выполнении графических работ.
План проведения урока.
I. Проверка домашней работы.
II. Устная работа.
III. Решение задач.
IV. Подведение итогов урока.
V. Домашнее задание.
Работа на уроке: дифференцированная. Уровни дифференциации: I — учащиеся с низкой степенью успешности обучения, II – учащиеся со средней степенью успешности обучения, III – учащиеся с высокой степенью успешности.
I. Проверка домашней работы
1. У доски проверяются задания, вызвавшие затруднения, и задания, которые необходимо обсудить.
2. Нескольким ученикам предлагаются карточки индивидуальной работы (желательно, дифференцированные). Примеры заданий для индивидуального опроса, где карточки №1 и №2 предназначены для учащихся I уровня, №3 и №4 – II уровня, №5 и №6 – III уровня.
№1. 1) Решите уравнение .
2) Сколько корней имеет уравнение ?
№2. 1) Решите неравенство .
2) Сколько решений имеет система уравнений .
№3. 1) Решите уравнение .
2) Простройте график функции .
Укажите множество значений функции.
№4. 1) Решите неравенство .
2) Постройте график функции .
№5. 1) Решите неравенство .
2) При каких значениях параметра m уравнение
не имеет решений?
№6. 1) Решите неравенство .
3. При каких значениях параметра n уравнение имеет решение?
II. Устная работа
Проводится одновременно с проверкой домашней работы. Устную работу лучше проводить в парах. Ответы на вопросы записываются каждым учеником пары, По окончании работы один экземпляр ответов сдаётся на проверку учителю, второй остаётся у учащихся для проверки правильности выполнения заданий при разборе результатов устной работы.
I вариант
1. Какие из указанных функций являются: 1) возрастающими; 2) убывающими?
а) ; б) ; в) ; г) ; д)
2. Найдите область определения функции:
а) ;
б) ;
в) .
3. Решите уравнение:
а) ; б) ; в) ; г) ; д) .
4. Решите неравенство:
а) ; б) ; в) ; г) .
II вариант
1. Найдите область определения функции:
а) ; б) ; в) ; г) , где .
2. Какому из промежутков при надлежит корень уравнения:
а) ; б) ; в) ?
3. Решите уравнение:
а) ; б) ; в) ; г) .
4. Решите неравенство:
а) ; б) ; в) ; г) .
III вариант
1. Найдите область определения функции:
а) ; б) ; в) ; г) .
2. Найдите множество значений функции:
а) ; б) ; в) ; г) .
3. Решите уравнение:
а) ; б) ; в) ; г) .
4. Решите неравенство:
а) ; б) ; в) ; г) .
III. Решение задач
Этот этап урока также проводится дифференцированно. Для выполнения каждого задания вызывается по одному ученику с каждого варианта. Ученик работает у доски, при этом учащиеся этого варианта, работающие индивидуально, имеют возможность контролировать правильность выполнения задания как у себя в тетради, так и у вызванного к доске школьника.
I вариант
1. Решите уравнения:
а) ; б) и найдите сумму корней уравнения.
2. Решите неравенства:
а) . Является ли число -1 решением этого неравенства?
б) ; в) .
3. Решите графически неравенство .
II вариант
1. Решите уравнения:
а) . Если уравнение имеет более одного корня, укажите их произведение.
б) .
2. Решите неравенства:
а) . Укажите сумму наименьшего и наибольшего целых решений неравенства.
б) .
3. Решите графически неравенство: .
III вариант
1. Решите уравнения:
а) на отрезке ;
б) .
2. Решите неравенства:
а) ; б) .
3. Постройте график функции . Сколько корней имеет уравнение при всех значениях параметра k?
IV. Подведение итогов урока
Ученикам объявляются оценки, даются рекомендации по исправлению недостатков в знаниях и работе, выслушивается мнение учеников о составляющих урока.
V. Домашнее задание
№ 210 (2,3), № 211 (1), № 213 (1) — для учащихся I уровня;
№ 210 (5,6), №211 (4), №213 (4) — для учащихся II уровня;
№214 (1,4), № 218 (2), № 222 (1) — для учащихся III уровня.
9.02.2015
xn--i1abbnckbmcl9fb.xn--p1ai
Решение показательных уравнений и неравенств: алгоритм решения и примеры
аx = b — простейшее показательное уравнение. В нем a больше нуля и а не равняется единице.
Решение показательных уравнений
Из свойств показательной функции знаем, что ее область значений ограничена положительными вещественными числами. Тогда если b = 0, уравнение не имеет решений. Такая же ситуация имеет место быть, в уравнении где b
Теперь положим, что b>0. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0<a
Исходя из этого и применяя теорему о корне, получим, что уравнение ax = b иметь один единственный корень, при b>0 и положительном a не равном единице. Чтобы его найти, необходимо представить b в виде b = ac.
Тогда очевидно, что с будет являться решением уравнения ax = ac.
Рассмотрим следующий пример: решить уравнение 5(x2 — 2*x — 1) = 25.
Представим 25 как 52, получим:
5(x2 — 2*x — 1) = 52.
Или что равносильно :
x2 — 2*x — 1 = 2.
Решаем полученное квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1.
Ответ: 3;-1.
Решим уравнение 4x – 5*2x + 4 = 0. Сделаем замену: t=2x и получим следующее квадратное уравнение:
t2 — 5*t + 4 = 0.
Решаем это уравнение любым из известных способов. Получаем корни t1 = 1 t2 = 4
Теперь решаем уравнения 2x = 1 и 2x = 4.
Ответ: 0;2.
Решение показательных неравенств
Решение простейших показательных неравенств основывается тоже на свойствах возрастания и убывания функции. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0<a<1, то данная функция будет убывающей на всем множестве вещественных чисел.
Рассмотрим пример: решить неравенство (0.5)(7 — 3*x) < 4.
Заметим, что 4 = (0.5)2. Тогда неравенство примет вид (0.5)(7 — 3*x) < (0.5)(-2). Основание показательной функции 0.5 меньше единицы, следовательно, она убывает. В этом случае надо поменять знак неравенства и не записывать только показатели.
Получим: 7 — 3*x>-2.
Отсюда: х<3.
Ответ: х<3.
Если бы в неравенстве основание было больше единицы, то при избавлении от основания, знак неравенства менять было бы не нужно.
Нужна помощь в учебе?
Предыдущая тема: Показательная функция: график и основные свойства функции
Следующая тема:   Логарифмы и их свойства: определение и алгоритм решения
Все неприличные комментарии будут удаляться.
www.nado5.ru
