стереть
| TRIG: | sin | cos | tan | cot | csc | sec | назад | |||
| INVERSE: | arcsin | arccos | arctan | acot | acsc | asec | стереть |
|||
| HYPERB: | sinh | cosh | tanh | coth | x | π | ↑ | ↓ | ||
| OTHER: | ‘ | , | y | = | < | > | ← | → | ||
 уравнений онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
уравнений онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
Полезные ссылки:
Типы дифференциальных уравнений и методы их решения
Решить дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение — это уравнение, в котором свзяны между собой переменные, постоянные коэффициенты, искомая функция и производные от функции любого порядка. При этом максимальный порядок производной функции, который присутствует в уравнении, определяет порядок всего дифференциального уравнения. Решить диф уравнение — это определить искомую функцию, как зависимость от переменной.
Современные компьютеры позволяют решать сложнейшие диф уравнения численно. Нахождение же аналитического решения является сложной задачей. Существует множество типов уравнений и для каждого теория предлагает свои методы решения. На сайте matematikam.ru  д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям. Мы предлагаем для решения заполнить два поля: само собственно уравнение и при необходимости — начальные условия (задачу Коши) — то есть информацию о граничных условиях искомой функции. Ведь как известно, диф уравнения имеют бесконечное количество решений, поскольку в ответе присутствуют константы, которые могут принимать произвольное значение. Задав задачу Коши, мы из всего множества решений выбираем частные.
д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям. Мы предлагаем для решения заполнить два поля: само собственно уравнение и при необходимости — начальные условия (задачу Коши) — то есть информацию о граничных условиях искомой функции. Ведь как известно, диф уравнения имеют бесконечное количество решений, поскольку в ответе присутствуют константы, которые могут принимать произвольное значение. Задав задачу Коши, мы из всего множества решений выбираем частные.
Данный онлайн калькулятор разработан компанией WolframAlpha и позволяет решать как стандартные дифференциальные уравнения, так и уравнения, не имеющие стандартного подхода для решения.
Похожие сервисы:
Solve differential equation online
Онлайн решение интеграла
Что делать, если решение не появляется (пустой экран)?Данный калькулятор по решению интегралов онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
Все права на его использование принадлежат компании Wolfram Alpha LLC!
Решение интеграла онлайн
Неопределенный интеграл
Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно
Решить неопределенный интеграл
Онлайн сервис на matematikam.ru позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте. Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт matematikam.ru поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте matematikam.ru, вы всегда получите точный ответ.
Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте. Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт matematikam.ru поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте matematikam.ru, вы всегда получите точный ответ.
Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу.
Похожие сервисы:
Решение неопределенного интегралаCalculate indefinite integral online
Онлайн калькулятор метод изоклин | stud-baza.bitballoon.com
Рассмотрим геометрический метод, который вытекает из геометрического истолкования дифференциального уравнения первого порядка и его решений. Метод изоклин нам интересен тем, что он позволяет приближенно отыскать решение задачи Коши в виде графика. Однако для серьезной работы он непригоден; он дает лишь наглядное представление.
Итак, установим связь между уравнением и его интегральными кривыми. Предположим, что правая часть уравнения (3. 1. 1) определена и непрерывна в области G и пусть есть интегральная кривая этого уравнения, проходящая через точку М(х, у). Проведем касательную к интегральной кривой (3. 1. 2) в точке М и обозначим через угол образованный касательной МТ с положительным направлением оси ОХ. Тогда
Предположим, что правая часть уравнения (3. 1. 1) определена и непрерывна в области G и пусть есть интегральная кривая этого уравнения, проходящая через точку М(х, у). Проведем касательную к интегральной кривой (3. 1. 2) в точке М и обозначим через угол образованный касательной МТ с положительным направлением оси ОХ. Тогда
Т. о., если через точку М(х, у) проходит интегральная кривая (3. 1. 2), то наклон касательной к ней в этой точке определяется формулой
так что наклон касательной к интегральной кривой определен заранее самим дифференциальным уравнением.
Наклон касательной (как и всякой прямой) есть тангенс угла , образованного касательной с положительным направлением оси ОХ.
Наклоны касательных можно указать, не находя интегральных кривых. Для этого построим в каждой точке М области G отрезок (для определенности — единичной длины) с центром в точке М(рис.), составляющий с положительным направлением оси ОХ угол , тангенс которого определяется формулой (3. 1.
Чтобы найти угол, под которым интегральные кривые могут пересекать ось ОХ, достаточно подставить в правую часть уравнения (3. 1. 1) у = 0, и получим тангенс угла . Аналогично интегральные кривые уравнения (3. 1. 1) в точках их пересечения с осью ОУ образуют с осью ОХ угол :
Вообще, если надо узнать, какой угол с осью ОХ образуют интегральные кривые уравнения (3. 1. 1) в точках их пересечения с заданной кривой у = (х), то достаточно подставить у = (х) в правую часть уравнения (3. 1. 1). Получим
Кривая = (х, у), в каждой точке которой направление поля, определяемое дифференциальным уравнением (3. 1. 1), одно и тоже, называется изоклиной этого уравнения.
Уравнения изоклин дифференциального уравнения (3. 1. 1) имеют вид
С увеличением наклон интегральных кривых возрастает.
Если в точке М(х, у) правая часть уравнения (3. 1. 1) обращается в , то естественно считать, что направление поля в такой точке параллельно оси ОУ. В этом случае надо рассматривать перевернутое уравнение
В этом случае надо рассматривать перевернутое уравнение
Т. о., во всякой точке М(х, у), в которой правая часть уравнения (3. 1. 1) имеет конечное значение или обращается в , это уравнение задает вполне определенное направление поля. Интегральные кривые перевернутого уравнения (3. 1. 4), которое надо рассматривать наряду с уравнением (3. 1. 1) в окрестности точек, где f (х, у) обращается в , будем присоединять к интегральным кривым уравнения (3. 1. 1).
Когда правая часть уравнения (3. 1. 1) не определена в точке (хо, уо), но определена в окрестности этой точки, говорят, что поле направлений в точке (хо, уо) не задано. Такие точки называются особыми точками дифференциального уравнения. Если при этом существует интегральная кривая у = у(х) (х =х(у)), обладающая свойством у(х)уо при ххо (х(у) хо при ууо), то будем говорить, что эта интегральная кривая примыкает к точке (хо, уо).
Построив достаточно густое семейство изоклин, можно получить сколь угодно точное представление об интегральных кривых, в связи с этим рассмотрим следующий пример.
Пример. Дано дифференциальное уравнение. Определить поле направлений и построить изоклины.
Решение. Правая часть уравнения определена на всей плоскости, кроме начала координат, где она обращается в неопределенность вида . Т. о., поле направлений задано всюду, кроме начала координат; причем в точках, не лежащих на оси ОУ (х0), имеем. Отсюда ясно, что соответствующими интегральными кривыми будут полупрямые примыкающие к началу координат. В точках полуосей оси ОУ направление поля параллельно оси ОУ. Из рассмотрения перевернутого уравнения ясно, что эти полуоси являются интегральными кривыми.
Итак, интегральными кривыми исходного уравнения являются все полупрямые примыкающие к началу координат. Они являются изоклинами исходного уравнения.
Если в какой — либо задаче требуется выделить из общего решения одно частное решение, удовлетворяющее заданным начальным условиям (3. 0. 2), то геометрически это сводится к тому, что требуется из семейства интегральных кривых на плоскости выделить одну интегральную кривую, проходящую через заданную точку плоскости М (хо, уо). Теорема Коши указывает, в каких случаях можно ручаться за то, что через данную точку плоскости проходит только одна интегральная кривая.
Теорема Коши указывает, в каких случаях можно ручаться за то, что через данную точку плоскости проходит только одна интегральная кривая.
Действительно, теорему Коши можно прочитать следующим образом: Если даны дифференциальное уравнение (3. 0. 1) и начальные условия (3. 0. 2) и его правая часть непрерывна в окрестности точки (хо, уо), то через точку плоскости М(хо, уо) проходит одна и только одна кривая уравнения (3. 0. 1).
Теперь перейдем непосредственно к рассмотрению метода изоклин для задачи Коши.
Еще раз отметим, что метод изоклин для решения задачи Коши позволяет построить приближенно график интегральной кривой, проходящей через точку (хо, уо).
1. Строим густое поле направлений, т. е., другими словами, сеть изоклин, соответствующих различным значениям угловых коэффициентов (=tg) касательных поля направлений.
2. Выбираем изоклину о, на которой лежит точка (хо, уо) с угловым коэффициентом . В этой точке строим малый участок кривой, которая касается направления поля в точке (хо, уо) до пересечения с близлежащей изоклиной 1.
3. Через точку пересечения вновь проводим участок кривой, так, чтобы направление изоклины 1 было касательной для этого участка кривой, и т. д. В результате мы получим кривую — график искомой интегральной кривой.
Рассмотрим несколько примеров, иллюстрирующих применение метода изоклин для решения задачи Коши.
Темы для курсового проекта по программированию
Функции комплексного переменного аналитичность
ИСПОЛЬЗОВАНИЕ МЕТОДА ИЗОКЛИН ПРИ РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
1 Веретеников А.С. 1 Потапов Д.Н. 11 Самарская государственная сельскохозяйственная академия
1. Пискунов Н.С. Дифференциальное и интегральное исчисления: учебник в 2-х томах. Том 2. – М.: Наука – Главная редакция физико-математической литературы, 1985. – 560 с.
2. Пушкарь Е. А. Дифференциальные уравнения в задачах и примерах: учебно-методическое пособие. – М.: МГИУ, 2007. – 158 с.
А. Дифференциальные уравнения в задачах и примерах: учебно-методическое пособие. – М.: МГИУ, 2007. – 158 с.
Дифференциальное уравнение первого порядка ý = f(x, y) имеет общее решение , которое определяет собой семейство интегральных кривых на плоскости хОу.
Если переменные х и у правой части дифференциального уравнения рассматривать как координаты точки М(х, у) плоскости хОу, то производная выражает угловой коэффициент касательной к интегральной кривой в точке М(х, у). Таким образом, дифференциальное уравнение ý = f(x, y) определяет в каждой точке плоскости хОу, принадлежащей области существования функции , направление интегральной кривой, проходящей через эту точку, или определяет поле направлений на плоскости хОу.
Изображая направление в каждой точке области существования функции маленькой стрелкой, выходящей из этой точки, можно построить поле направлений дифференциального уравнения, которое дает приближенное представление о расположении интегральных кривых этого уравнения.
Изоклинами дифференциального уравнения ý = f(x, y) называются геометрические места точек плоскости хОу, в которых интегральные кривые уравнения имеют одно и то же направление. Уравнение является уравнением изоклины, соответствующей заданному направлению , где – параметр. Придавая близкие числовые значения, получается достаточно густая сеть изоклин – семейство изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального уравнения. Нулевая изоклина дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения, т.е. такими точками, в которых правая часть уравнения ý = f(x, y) не определена.
Метод изоклин состоит в следующем:
1. Строится достаточно густая сетка изоклин для различных значений k и на каждой изоклине изображаются небольшие отрезки с наклоном k.
2. Начиная из точки (x0, y0), поводится линия, которая, будет пересекать каждую изоклину под углом, заданным полем направлений. Полученная таким образом кривая и будет приближенным изображением (эскизом) интегральной кривой уравнения, проходящей через точку (x0, y0).
Пусть дано уравнение и требуется построить поле направлений и интегральные кривые, определяемые этим уравнением.
Сначала строятся графики изоклин. Уравнение семейства изоклин данного уравнения или . Изоклины представляют собой семейство квадратичных парабол с осями, совпадающими с осью Ох. Меняя параметр k, получается семейство графиков изоклин, на них строится поле направлений.
При k=0 получается изоклина , во всех точках которой направление поля параллельно оси Ох (Рис. 1).
При k=1 получается изоклина , во всех точках которой направление поля образует с осью Ох угол .
При k=-1 получается изоклина , во всех точках которой направление поля образует с осью Ох угол .
Рис. 1. Поле направлений уравнения .
Задается определенная точка (x0, y0) и поводится линия, которая, будет пересекать каждую изоклину под углом, заданным полем направлений. На рис. 2 показаны интегральные кривые, касающиеся поля направлений.
Метод изоклин как метод приближенного решения задачи Коши устарел. В его в основе лежит алгоритм изображения фрагмента поля направления, а современные компьютеры могут мгновенно и как угодно подробно нарисовать поле направлений, и достаточно точно изобразить интегральную кривую.
Рис. 2. Интегральные кривые уравнения .
Однако, метод изоклин эффективно работает как инструмент исследования поведения решений. Он позволяет изобразить области характерного поведения интегральных кривых и как средство эскизного представления интегральных кривых сохраняет свое значение и в нынешнюю эпоху бурного развития вычислительных машин и вычислительных методов.
Библиографическая ссылка
Веретеников А.С., Потапов Д.Н. ИСПОЛЬЗОВАНИЕ МЕТОДА ИЗОКЛИН ПРИ РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА // Международный студенческий научный вестник. – 2015. – № 3-4.;URL: http://eduherald.ru/ru/article/view?id=14105 (дата обращения: 04.06.2021).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Для данного дифференциального уравнения методом изоклин построить
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения первого порядка.
Основные понятия
Дифференциальным уравнением(ДУ) называется уравнение, связывающее независимую переменную , искомую функцию и её производные или дифференциалы.
– – дифференциальное уравнение первого порядка, неявный вид.
– – уравнение, разрешённое относительно производной.
– – дифференциальная форма записи дифференциального уравнения первого порядка.
ДУ с одной независимой переменной называется обыкновенным.
ПорядкомДУ называется порядок наивысшей производной (или дифференциала), входящей в уравнение.
Всякая функция, удовлетворяющая ДУ, т.е. при подстановке в уравнение обращающая его в тождество, называется решением уравнения. Бесконечное множество решений уравнения называется общим решением ДУ. Общее решение имеет вид , где C – произвольная постоянная. Если решение задано в неявном виде, то оно обычно называется интегралом. Множество интегралов называется общим интегралом и имеет вид .
Каждому решению уравнения соответствует линия (график), называемая интегральной кривой этого уравнения.
Задача отыскания решения ДУ первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши.
Теорема (существования и единственности задачи Коши). Если функция непрерывна в области, содержащей точку , то уравнение имеет решение такое, что . Если, кроме того, непрерывна и частная производная , то это решение – единственное.
Условие, при котором значение искомой функции равно при , называется начальным условием уравнения и записывается .
Решение ДУ, удовлетворяющее заданному начальному условию, называется частным решением.
а) – ДУ 1-го порядка в неявном виде.
б) – ДУ 1-го порядка в дифференциальной форме.
в) – ДУ 1-го порядка разрешенное относительно производной.
Пример 1.Выяснить, является ли функция решением уравнения ?
Решение. . Полученную производную подставим в уравнение. Тогда , . Получили верное тождество, следовательно, данная функция является решением данного ДУ.
Тогда , . Получили верное тождество, следовательно, данная функция является решением данного ДУ.
Дифференциальные уравнения первого порядка
и методы их решения. Метод изоклин (графическое решение)
Геометрическое истолкование ДУ первого порядка. Уравнение устанавливающее связь (зависимость) между координатами точки и угловым коэффициентом касательной интегральной кривой, проходящей через эту точку. Следовательно, ДУ дает совокупность направлений (поле направлений) на плоскости Оху.
Поле направлений изображаетсяпри помощисистемы чёрточек или стрелок с углом наклона .
Кривые (где ), в точках которых наклон поля имеет постоянное значение, равное k, называются изоклинами. Построив изоклины и поле направлений, можно приближённо нарисовать интегральные кривые, рассматривая последние как кривые, которые в каждой своей точке имеют заданное направление поля.
Пример 2. Методом изоклин построить приближенно поле интегральных кривых для дифференциальног уравнения .
Методом изоклин построить приближенно поле интегральных кривых для дифференциальног уравнения .
Решение. Здесь изоклинами являются прямые линии:
, где
, , ;
, , ;
, , .
На каждой из прямой изображаем систему черточек под найденным углом. Проводя линии таким образом, чтобы черточки являлись касательными к интегральным кривым, получим параболы (рис. 12)
Пусть задано дифференциальное уравнение y ′ = f ( x , y ) .
Если обозначить α угол между касательной к интегральной
кривой y = ϕ ( x ) и положительным направлением оси
принимая во внимание, что tg α = y ′ , y ′ = f ( x , y ) ,
Из этого следует, что дифференциальное уравнение в каждой точке плоскости ( x , y ) задает направление касательных к
интегральным кривым или поле направлений .
Поле направлений можно построить, проводя в каждой точке ( x , y ) из области определения функции f ( x , y ) отрезок (для определенности единичной длины) с центром в этой точке, образующий с положительным направлением оси Ox угол α , для которого tg α = f ( x,y ) .
Если в точке ( x 0 , y 0 ) значение функции f ( x 0 , y 0 ) = ∞ , то направление поля параллельно оси Oy . В этом случае нужно
Дифференциальное уравнение первого порядка
Если в каждой точке области задано значение некоторой величины, то говорят, что в области задано поле этой величины. Таким образом, дифференциальное уравнение (1) определяет поле направлений.
Тройка чисел определяет направление прямой, проходящей через точку . Совокупность отрезков этих прямых дает геометрическую картину поля направлений.
Задача интегрирования дифференциального уравнения (1) может быть теперь истолкована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.
Задача построения интегральной кривой часто решается введением изоклин . Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и тоже направление. Семейство изоклин дифференциального уравнения (1) определяется уравнением
где — параметр.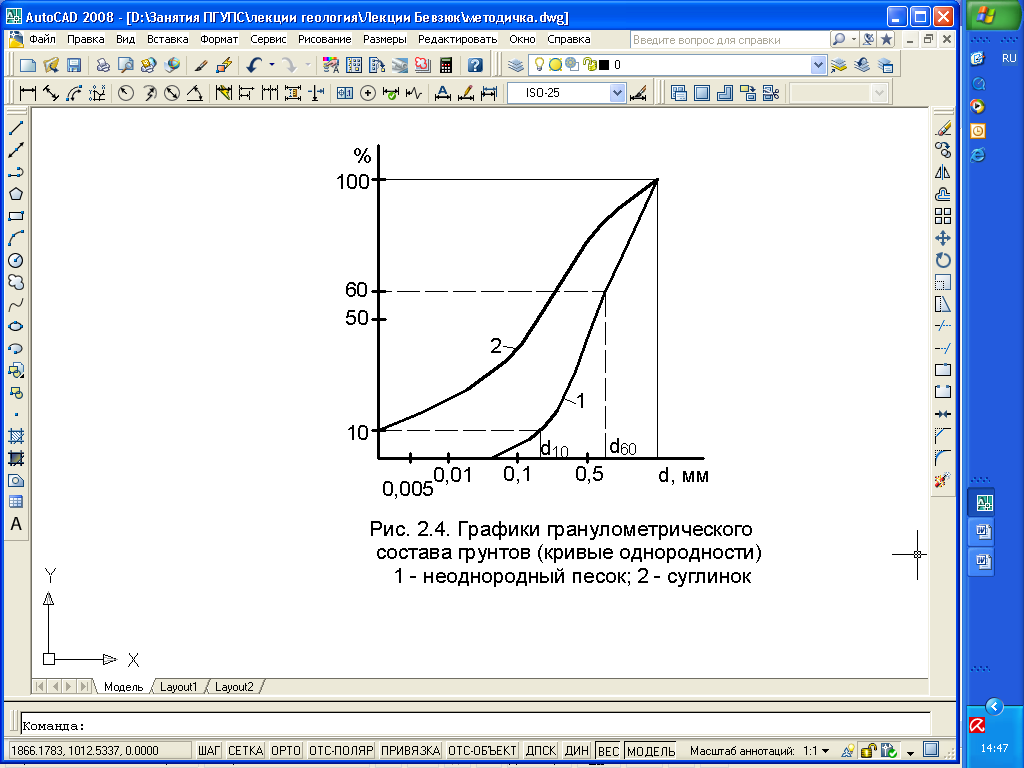 Придавая параметру близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения (1).
Придавая параметру близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения (1).
Замечание 1. Нулевая изоклина дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых.
Для большей точности построения интегральных кривых находят также геометрическое место точек перегиба. Для этого находят в силу уравнения (1):
и приравнивают ее нулю. Линия, определяемая уравнением
и есть возможное геометрическое место точек перегиба.
Пример 1. С помощью изоклин построить приближенно интегральные кривые дифференциального уравнения .
Решение. Для получения уравнения изоклин положим , тогда или .
Изоклинами являются параллельные прямые. При получим изоклину . Эта прямая делит плоскость на две части, в каждой из которых производная имеет один и тот же знак (рис. 6).
Интегральные кривые, пересекая прямую , переходят из области убывания функции в область возрастания, и наоборот, а значит на этой прямой находятся точки экстремума интегральных кривых, именно точки минимума.
Возьмем еще две изоклины: и .
Касательные, проведенные к интегральным кривым в точках пересечения с изоклинами и , образуют с осью углы в и соответственно. Найдем далее вторую производную .
Прямая , на которой , является изоклиной, получаемой при , и в то же время интегральной линией, в чем можно убедиться подстановкой в уравнение. Так как правая часть данного уравнения удовлетворяет условиям теоремы существования и единственности во всей плоскости , то остальные интегральные кривые не пересекают эту изоклину. Изоклина , на которой находятся точки минимума интегральных кривых, расположена над изоклиной , а поэтому интегральные кривые, проходящие ниже изоклины , не имеют точек экстремума.
Прямая делит плоскость на две части, в одной из которых (расположенной над прямой) 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFE />, а значит интегральные кривые обращены вогнутостью вверх, а в другой и, значит, интегральные кривые обращены вогнутостью вниз.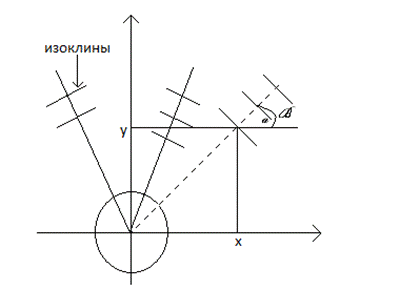 Интегральные кривые не пересекают прямой , значит, она не является геометрическим местом точек перегиба. Интегральные кривые данного уравнения не имеют точек перегиба.
Интегральные кривые не пересекают прямой , значит, она не является геометрическим местом точек перегиба. Интегральные кривые данного уравнения не имеют точек перегиба.
Проведенное исследование позволяет нам приближенно построить семейство интегральных кривых уравнения (рис.6).
Пример 2. Методом изоклин построить приближенно интегральные кривые дифференциального уравнения .
Решение. Полагая , где , получаем уравнение изоклин , причем . При получим , откуда
Интегральные кривые в точках пересечения с этими изоклинами имеют горизонтальные касательные.
Определим, имеют ли интегральные кривые на изоклинах экстремум. Для этого найдем вторую производную:
Если четное, то 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFE />, и, значит, в точках пересечения с изоклинами , интегральные кривые имеют минимум; если же нечетное, то и интегральные кривые в точках пересечения с изоклинами имеют максимум. Находим изоклины:
Находим изоклины:
Изоклинами являются параллельные прямыми с угловым коэффициентом, равным –1 , т. е. изоклины пересекают ось под углом . Легко убедиться в том, что изоклины , являются интегральными кривыми данного дифференциального уравнения (для этого достаточно подставить функции в уравнение ).
Во всех точках плоскости правая часть данного уравнения, т.е. функция , удовлетворяет всем условиям теоремы существования и единственности, а поэтому интегральные кривые не пересекаются, и, следовательно, не пересекают изоклины . Производная обращается в ноль при , т.е. на изоклинах (6), и при , т. е. на изоклинах (6) и (7). При переходе (слева направо) через изоклины (7) меняет знак с плюса на минус. Например, если рассмотреть полосу, заключенную между изоклинами и , то на изоклине производная , причем под изоклиной 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFE />. Значит, интегральные кривые обращены вогнутостью вверх, а над изоклиной , значит, интегральные кривые обращены вогнутостью вниз. Таким образом, изоклины (7) являются геометрическим местом точек перегиба интегральных кривых. Полученные данные позволяют приближенно построить семейство интегральных кривых данного уравнения. Для более точного построения следует нанести еще несколько изоклин (рис. 7).
Таким образом, изоклины (7) являются геометрическим местом точек перегиба интегральных кривых. Полученные данные позволяют приближенно построить семейство интегральных кривых данного уравнения. Для более точного построения следует нанести еще несколько изоклин (рис. 7).
Пример 3. Методом изоклин построить интегральные кривые уравнения .
Решение. Положим . Тогда уравнение изоклин будет
Изоклинами являются параболы с вертикальной осью симметрии . Среди изоклин нет интегральных кривых. В самом деле, подставляя в данное уравнение и , будем иметь , или . Но это равенство ни при каком значении не может выполняться тождественно относительно .
Пусть , тогда в точках пересечения с изоклиной интегральные кривые будут иметь горизонтальные касательные. Изоклина разбивает плоскость на две части: в одной из них (решения убывают), а в другой 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADQAAAAXBAMAAAC2bnFAAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAncEhYUEQgTHg8NGxUXFruPrBAAAA30lEQVQoz2NgIB8wr8MpxfIFpxTjAnSRDh /> (решения возрастают). И так как эта изоклина не является интегральной кривой, то на ней находятся точки экстремума интегральных кривых, именно на той части параболы , где — точки минимума, а на другой части этой параболы, где 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcChQSFZMdCB6RCQsVNol/AAAACdSURBVBjTY2AgCbDjEBexE8Aqzrl2HbJEZQCcKaiHLMGiDJdhBEvs0dymDJVxQJbgVpForkqAyBg5IEnwOPC+ngeRYGA1SkRIsDFIKWyHGc5qlQCXYGSImwB3AOsJhAQDY54DXBzZKGaDewISEGezGzkIIiTqtFcxZEIcpQvTKtAHVMBxwsPoAKoHWd69ewe0t5AhEMwtRgoSQUEGAFJBHb3FaZBuAAAAAElFTkSuQmCC» /> — точки максимума. Интегральная кривая, проходящая через точку , т.е. через вершину параболы , в этой точке не имеет экстремума. В точках изоклин и касательные к интегральным кривым имеют угловые коэффициенты, соответственно равные 1 и –1.
И так как эта изоклина не является интегральной кривой, то на ней находятся точки экстремума интегральных кривых, именно на той части параболы , где — точки минимума, а на другой части этой параболы, где 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcChQSFZMdCB6RCQsVNol/AAAACdSURBVBjTY2AgCbDjEBexE8Aqzrl2HbJEZQCcKaiHLMGiDJdhBEvs0dymDJVxQJbgVpForkqAyBg5IEnwOPC+ngeRYGA1SkRIsDFIKWyHGc5qlQCXYGSImwB3AOsJhAQDY54DXBzZKGaDewISEGezGzkIIiTqtFcxZEIcpQvTKtAHVMBxwsPoAKoHWd69ewe0t5AhEMwtRgoSQUEGAFJBHb3FaZBuAAAAAElFTkSuQmCC» /> — точки максимума. Интегральная кривая, проходящая через точку , т.е. через вершину параболы , в этой точке не имеет экстремума. В точках изоклин и касательные к интегральным кривым имеют угловые коэффициенты, соответственно равные 1 и –1.
Для исследования направления вогнутости интегральных кривых найдем вторую производную:
Она обращается в ноль только в точках, лежащих на параболе . 2″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADkAAAAYCAMAAAB3NqUkAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEXRSTlMA0KEwwGKBBhD6IUGwkHFR4HWSoZwAAAD0SURBVDjLvVTZrsQgCBVBAnVp//9rB6fJ1FJz78Sh5alBD/YsGsLvSpjzGrBsu/IKMukWmq4gsUjYFRepRlgE4uqRQtt8gdM/wCghydwv+AsrUJlPnlJp7z/fRiz7oTsVxFjQPqziu1eQuz10jIOTw1Y2E0GIhl6uoXSkRuc4xEsItMWsKWsZkZvo2X+kBaJ8NplyFp4sLk/Gs+pD6kxx3Hijc1bRWT8d8T7L0+kgevadQonsgh />, они вогнуты вверх 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFE />. Точки пересечения интегральных кривых с параболой являются точками перегиба этих кривых. Итак, парабола есть геометрическое место точек перегиба интегральных кривых.
2″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADkAAAAYCAMAAAB3NqUkAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEXRSTlMA0KEwwGKBBhD6IUGwkHFR4HWSoZwAAAD0SURBVDjLvVTZrsQgCBVBAnVp//9rB6fJ1FJz78Sh5alBD/YsGsLvSpjzGrBsu/IKMukWmq4gsUjYFRepRlgE4uqRQtt8gdM/wCghydwv+AsrUJlPnlJp7z/fRiz7oTsVxFjQPqziu1eQuz10jIOTw1Y2E0GIhl6uoXSkRuc4xEsItMWsKWsZkZvo2X+kBaJ8NplyFp4sLk/Gs+pD6kxx3Hijc1bRWT8d8T7L0+kgevadQonsgh />, они вогнуты вверх 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFE />. Точки пересечения интегральных кривых с параболой являются точками перегиба этих кривых. Итак, парабола есть геометрическое место точек перегиба интегральных кривых.
Правая часть исходного уравнения во всех точках плоскости удовлетворяет условиям теоремы существования и единственности, поэтому через каждую точку плоскости проходит единственная интегральная кривая уравнения.
Используя полученные сведения, строим приближенно семейство интегральных кривых данного уравнения (рис.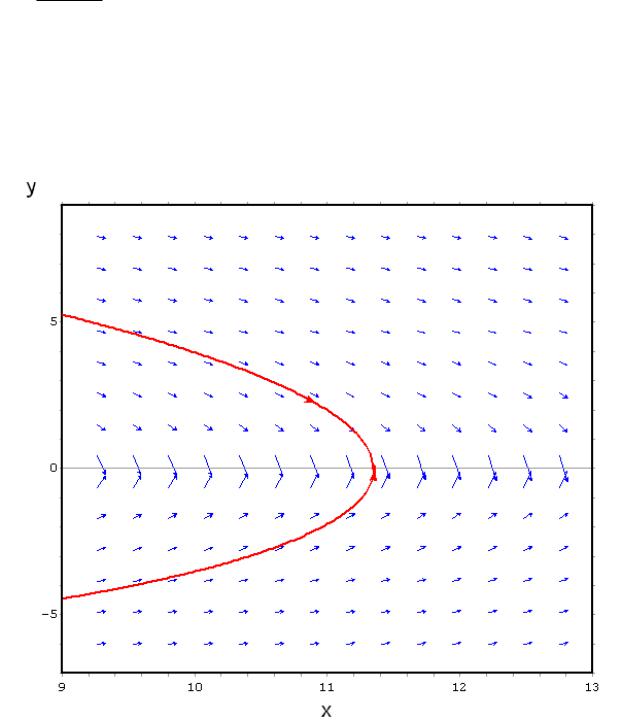 8).
8).
Замечание 2. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.
Рассмотрим уравнение . Семейство изоклин определяется уравнением . Это семейство прямых, проходящих через начало координат, так что в начале координат пересекаются изоклины, отвечающие различным наклонам касательных к интегральным кривым. Нетрудно убедиться, что общее решение данного уравнения имеет вид и точка является особой точкой дифференциального уравнения. Здесь изоклины являются интегральными кривыми уравнения (рис. 9).
Пример 4. Методом изоклин построить интегральные кривые уравнения .
Решение. Полагая , получаем уравнение семейства изоклин . Таким образом, изоклинами являются прямые, проходящие через начало координат .
При получим изоклину , при — изоклину , при — изоклину .
Рассматривая обратное уравнение найдем изоклину , во всех точках которой интегральные кривые имеют вертикальные касательные.
В точке пересекаются все изоклины данного уравнения (особая точка уравнения). С помощью полученных изоклин строим интегральные кривые (рис. 10).
Применение интегральных кривых к определению скорости горения
Имеем
При измерении 10-20 зерен пороха определится среднее значение толщины 21ср , но не соответствует средней толщине зерна , т.к. этот интеграл соответствует тому случаю , пока самый толстый порох не сгорит . Необходимо подкорректировать , на рис…( фиг.3,44 ) показано среднее значение Јkcр. Для трубчатых и ленточных порохов откорректированное значение будет (5,8)
Т.к. пороха с узкими каналами горят с разной скоростью внутри канала и на наружной поверхности , то определение U1 для этих порохов является условным , зависит от плотности заряжания для таких порохов обычно берут U1 при = 0,23 кг/дм3 . В таблице … для некоторых порохов приведены значения Ik
| Пироксилиновые пороха | Нитроглицериновые пороха | ||||
| марка пороха | Ik, кг*сек/дм2 | марка пороха | Ik, кг*сек/дм2 | марка пороха | Ik, кг*сек/дм2 |
| Сокол | 4/7 | Х | |||
| Барс | 5/7 | отсутств.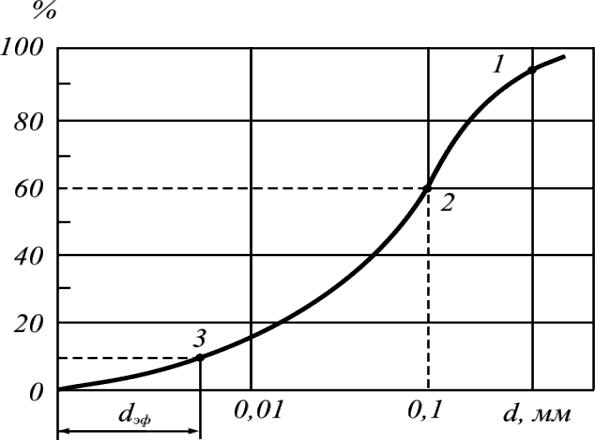 | 9/1НГВ | ||
| Сунар | 6/7 | НДТ-2 16/1 | |||
| ВТ | 7/7 | НДТ-3 16/1 | |||
| 4/1 | 9/7 | 130/55НГВ | |||
| 18/1 | 12/7 | 100/50Н | |||
| 100/50 | 14/7 | 100/50НУ | |||
| 130/55 | 15/7 | НДТ-3 18/1 | |||
| 120/50 | 17/7 | 305/52НГВ | |||
| 203/50 | |||||
| 22/1 |
Примечание : для семиканальных порохов Јk подбирают условно
8.Особенности горения комбинированных зарядов .
Значительная часть артиллерийских орудий обладает комбинированными зарядами из смеси двух порохов . Эти пороха разной толщины ( тонкий и толстый ) могут иметь так же разную форму и разную природу : Силу пороха, коволюм , скорость горения . Обычно основной заряд состоит из трубчатого пороха , дополнительный – из 7-ми канального пороха .
Статическая остойчивость — Построение диаграммы ДСО
Для определения угла крена, возникающего в результате действия на судно кренящего момента, строят кривую, выражающую зависимость плеч статической остойчивости от угла крена судна. Построение выполняют в прямоугольной системе координат: на оси абсцисс откладывают углы крена (положительные – вправо, отрицательные – влево от начала координат), а по оси ординат – плечи статической остойчивости.
СодержаниеСвернуть
В точках на оси абсцисс, соответствующих конкретным углам крена, восстанавливают перпендикуляры и на них откладывают снятые со специальной универсальной диаграммы отрезки плеч статической остойчивости. Полученные точки соединяют плавной кривой, которая называется диаграммой статической остойчивости (ДСО) (Stability cross curves). Диаграмма статической остойчивости имеет вид кривой с ярко выраженным максимумом.
Полученные точки соединяют плавной кривой, которая называется диаграммой статической остойчивости (ДСО) (Stability cross curves). Диаграмма статической остойчивости имеет вид кривой с ярко выраженным максимумом.
На ней можно отметить три точки, характерные для неповрежденного судна, обладающего положительной остойчивостью:
- точку 0 (начало координат), определяющую положение устойчивого равновесия;
- точку А, где плечо статической остойчивости и восстанавливающий момент имеют максимальные значения;
- точку В, определяющую так называемый угол заката диаграммы.
Равновесие накренившегося судна наступает при равенстве кренящего и восстанавливающего моментов. Чтобы воспользоваться диаграммой статической остойчивости для определения угла крена, возникающего под действием заданного кренящего момента МКР, необходимо найти плечо кренящего момента lКР = МКР/D’. Условие равновесия судна можно написать и в таком виде:
ιКР=Iθ.
Плечо lКР откладывают в соответствующем масштабе на оси ординат диаграммы и проводят горизонтальную линию до пересечения с кривой. В точке пересечения восстанавливающий момент равен кренящему, и, следовательно, судно находится в равновесии в наклоненном положении. Точка пересечения перпендикуляра, опущенного из точки С, с горизонтальной осью диаграммы определяет угол крена.
Диаграмма статической остойчивости строится для конкретного судна и соответствует определенным водоизмещению и положению Ц.В. по высоте. Если у данного судна изменится водоизмещение или аппликата Ц.Т., то диаграмма статической остойчивости приобретает другой вид. Это обстоятельство всегда следует иметь в виду, и, прежде чем воспользоваться диаграммой для решения каких-либо вопросов, касающихся остойчивости данного судна, необходимо обратить внимание на ее соответствие имеющейся нагрузке судна. Каждое судно должно быть снабжено комплектом диаграмм статической остойчивости, характеризующих остойчивость его при наиболее часто встречающихся случаях загрузки.
Диаграммы статической остойчивости отличаются большим разнообразием форм кривых, но все они обладают некоторыми общими свойствами:
- Начальный участок диаграммы статической остойчивости представляет собой прямую наклонную линию. Это видно, если приравнять две формулы восстанавливающего момента; метацентрическую формулу поперечной остойчивости, применимую только для малых углов крена, и формулу восстанавливающего момента, справедливую для любых углов крена, т. e.
Мθ=D‘·h·θ и Мθ=D‘·Iст,
Iст=h·θ
При малых углах крена поперечная метацентрическая высота – постоянная величина, поэтому зависимость между плечом статической остойчивости lcm и углом крена θ при малых углах крена является линейной и изображается прямой линией.
Рис. 2- Отрезок перпендикуляра, восстановленного из точки на оси абсцисс, находящейся на расстоянии одного радиана (57,3 град) от начала осей координат, до точки пересечения его с начальной касательной к кривой, определяет на диаграмме статической остойчивости поперечную метацентрическую высоту h, взятую в масштабе плеч статической остойчивости.
 Однако только графически определять метацентрическую высоту h по диаграмме статической остойчивости не рекомендуется, т. к. проведение касательной к кривой не может быть выполнено с необходимой точностью. Этот метод может использоваться только как дополнительный (контрольный).
Однако только графически определять метацентрическую высоту h по диаграмме статической остойчивости не рекомендуется, т. к. проведение касательной к кривой не может быть выполнено с необходимой точностью. Этот метод может использоваться только как дополнительный (контрольный). - Восходящая часть кривой диаграммы статической остойчивости характеризует устойчивое положение равновесия судна, а нисходящая – неустойчивое.
Универсальная диаграмма остойчивости
В судовых условиях часто возникает необходимость произвести расчет и оценку остойчивости судна. Для построения диаграмм статической остойчивости суда снабжаются разного рода документацией. К числу такой вспомогательной документации относятся интерполяционные кривые плеч формы, или пантокарены, и универсальные диаграммы статической остойчивости, составляемые в процессе проектирования судна на основании систематизированных расчетов.
Универсальные диаграммы позволяют строить диаграммы статической остойчивости судна без каких-либо дополнительных расчетов. Они представляют собой набор диаграмм статической остойчивости для различных водоизмещений судна в пределах от водоизмещения судна порожнем до полного водоизмещения. Пример таких диаграмм приведен ниже на рисунках 3, 4.
Они представляют собой набор диаграмм статической остойчивости для различных водоизмещений судна в пределах от водоизмещения судна порожнем до полного водоизмещения. Пример таких диаграмм приведен ниже на рисунках 3, 4.
Как уже отмечалось ранее данные для построения диаграмм статической остойчивости могут быть приведены в виде таблицы. Например:
| Диаграмма статистической остойчивости | ||||||||
|---|---|---|---|---|---|---|---|---|
| HydroSHIP | STABILITY CROSS CURVES | PAGE: 38 | ||||||
| DISPL (t) | KZ (m) | |||||||
| 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | |
| 6000 | 1.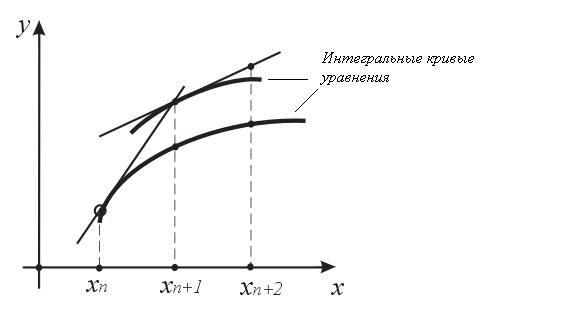 196 196 | 2.428 | 3.536 | 4.557 | 5.301 | 5.697 | 5.821 | 5.717 |
| 6050 | 1.196 | 2.424 | 3.529 | 4.552 | 5.294 | 5.690 | 5.815 | 5.713 |
| 6100 | 1.196 | 2.421 | 3.522 | 4.547 | 5.287 | 5.683 | 5.810 | 5.709 |
| 6150 | 1.196 | 2.417 | 3.515 | 4.542 | 5.280 | 5.676 | 5.803 | 5.705 |
| 6200 | 1.195 | 2.414 | 3.508 | 4.537 | 5.273 | 5.670 | 5.797 | 5.701 |
| 6250 | 1.195 | 2.411 | 3.501 | 4.532 | 5.266 | 5.663 | 5.791 | 5.697 |
| 6300 | 1.195 | 2.407 | 3.495 | 4.526 | 5.259 | 5.656 | 5.785 | 5.693 |
| 6350 | 1.195 | 2.404 | 3.488 | 4.519 | 5.253 | 5. 650 650 | 5.779 | 5.689 |
| 6400 | 1.195 | 2.401 | 3.462 | 4.512 | 5.246 | 5.641 | 5.773 | 5.686 |
| 6450 | 1.195 | 2.397 | 3.475 | 4.505 | 5.237 | 5.633 | 5.767 | 5.682 |
| 6500 | 1.195 | 2.394 | 3.469 | 4.499 | 5.228 | 5.625 | 5.762 | 5.678 |
| 6550 | 1.195 | 2.389 | 3.463 | 4.492 | 5.219 | 5.617 | 5.756 | 5.674 |
| 6600 | 1.197 | 2.385 | 3.457 | 4.486 | 5.210 | 5.609 | 5.750 | 5.670 |
| 6650 | 1.198 | 2.380 | 3.452 | 4.479 | 5.201 | 5.601 | 5.744 | 5.667 |
| 6700 | 1.199 | 2.376 | 3.447 | 4.473 | 5.192 | 5.594 | 5.738 | 5.663 |
| 6750 | 1.200 | 2.372 | 3.442 | 4.467 | 5.184 | 5.586 | 5.731 | 5.660 |
| 6800 | 1.202 | 2.367 | 3.437 | 4.461 | 5.176 | 5.579 | 5.725 | 5.656 |
| 6850 | 1.203 | 2.363 | 3.433 | 4.455 | 5.167 | 5.571 | 5.719 | 5.652 |
| 6900 | 1.203 | 2.359 | 3.428 | 4.449 | 5.159 | 5.564 | 5.713 | 5.649 |
| 6950 | 1.203 | 2.355 | 3.423 | 4.443 | 5.151 | 5.557 | 5.708 | 5.645 |
| 7000 | 1.203 | 2.351 | 3.419 | 4.437 | 5.143 | 5.550 | 5.702 | 5.642 |
| 7050 | 1.204 | 2.347 | 3.414 | 4.431 | 5.136 | 5.541 | 5.696 | 5.638 |
| 7100 | 1.204 | 2.343 | 3.410 | 4.425 | 5.128 | 5.532 | 5.690 | 5.635 |
| 7150 | 1.205 | 2.339 | 3.405 | 4.416 | 5.120 | 5.524 | 5.684 | 5.631 |
| 7200 | 1.206 | 2.335 | 3.401 | 4.408 | 5.110 | 5.515 | 5,678 | 5.628 |
| 7250 | 1.207 | 2.332 | 3.397 | 4.400 | 5.100 | 5.507 | 5.671 | 5.625 |
| 7300 | 1.208 | 2.328 | 3.393 | 4.391 | 5.090 | 5.499 | 5.665 | 5.621 |
| 7350 | 1.209 | 2.324 | 3.389 | 4.383 | 5.080 | 5.491 | 5.659 | 5.618 |
| 7400 | 1.210 | 2.321 | 3.386 | 4.375 | 5.071 | 5.483 | 5.653 | 5.614 |
| 7450 | 1.211 | 2.317 | 3.383 | 4.368 | 5.061 | 5.475 | 5.648 | 5.611 |
| 7500 | 1.212 | 2.314 | 3.379 | 4.360 | 5.052 | 5.467 | 5.642 | 5.608 |
| 7550 | 1.213 | 2.311 | 3.376 | 4.352 | 5.042 | 5.459 | 5.636 | 5.604 |
| 7600 | 1.214 | 2.308 | 3.373 | 4.345 | 5.033 | 5.452 | 5.630 | 5.601 |
| 7650 | 1.215 | 2.305 | 3.370 | 4.337 | 5.024 | 5.443 | 5.623 | 5.598 |
| 7700 | 1.215 | 2.302 | 3.367 | 4.330 | 5.015 | 5.434 | 5.617 | 5.595 |
| 7750 | 1.215 | 2.299 | 3.364 | 4.323 | 5.006 | 5.425 | 5.611 | 5.591 |
| 7800 | 1.215 | 2.296 | 3.361 | 4.316 | 4.997 | 5.416 | 5.605 | 5.588 |
| 7850 | 1.215 | 2.293 | 3.358 | 4.309 | 4.989 | 5.407 | 5.599 | 5.585 |
| 7900 | 1.215 | 2.290 | 3.355 | 4.300 | 4.980 | 5.399 | 5.593 | 5.582 |
| 7950 | 1.215 | 2.287 | 3.332 | 4.291 | 4.969 | 5.390 | 5.587 | 5.579 |
| 8000 | 1.213 | 2.284 | 3.349 | 4.282 | 4.958 | 5.382 | 5.581 | 5.575 |
Построение диаграммы статической остойчивости (ДСО) по универсальной диаграмме
Рис. 5 а)Пример построения диаграммы статической остойчивости по универсальной диаграмме остойчивости для конкретного случая загрузки судна при D = 8 500 т, h = 0,8 м.
Для каждого угла крена снимаем значение плеч статической остойчивости как показано на рис. 5 а) для угла крена 30 град. Составляем таблицу:
| Значение плеч статистической остойчивости | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| θ | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| Iст | 0 | 0,25 | 0,44 | 0,7 | 0,77 | 0,63 | 0,24 | – 0,39 | – |
С помощью составленной таблицы строим диаграмму статической остойчивости для своего случая загрузки судна при h = 0,8 м.
Использование пантокарена для построения (ДСО)
Использование пантокарен для построения диаграмм статической остойчивости требует дополнительных расчетов, но несмотря на это приводимый ниже метод получил самое широкое распространение на флоте.
Сами пантокарены могут иметь следующий вид.
Рис. 6Рис. 7Зависимость плеч остойчивости формы от осадок судна и углов крена также может быть выражена в виде таблицы. Пример такой таблицы приводим ниже.
| Плечи остойчивости формы (м) относительно точки киля | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| V,м3 | Т,м | Углы крена, θ | |||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | ||
| 9000 | 5,02 | 1,58 | 3,21 | 4,83 | 6,22 | 7,26 | 7,93 | 8,17 | 8,07 |
| 10000 | 5,50 | 1,54 | 3,13 | 4,76 | 6,17 | 7,21 | 7,87 | 8,11 | 8,05 |
| 11000 | 5,94 | 1,52 | 3,07 | 4,70′ | 6,12 | 7,16 | 7,79 | 8,06 | 8,01 |
| 12000 | 6,43 | 1,50 | 3,05 | 4,65 | 6,07 | 7,10 | 7,72 | 8,00 | 7 |
| 13000 | 6,90 | 1,50 | 3,03 | 4,61 | 6,02 | 7,04 | 7,66 | 7,95 | 7,93 |
| 14000 | 7,35 | 1,50 | 3,03 | 4,58 | 5,96 | 6,97 | 7,59 | 7,89 | 7,89 |
| 15000 | 7,80 | 1,50 | 3,03 | 4,54 | 5,90 | 6,91 | 7,53 | 7,85 | 7,86 |
| 16000 | 8,23 | 1,51 | 3,04 | 4,52 | 5,84 | 6,84 | 7,47 | 7,80 | 7,82 |
| 17000 | 8,65 | 1,52 | 3,05 | 4,49 | 5,78 | 6,77 | 7,42 | 7,75 | 7,79 |
| 18000 | 9,08 | 1,53 | 3,05 | 4,46 | 5,72 | 6,70 | 7,36 | 7,70 | 7,77 |
| 19000 | 9,50 | 1,55 | 3,06 | 4,44 | 5,65 | 6,63 | 7,29 | 7,65 | 7,74 |
| 20000 | 9,91 | 1,57 | 3,05 | 4,41 | 5,59 | 6,55 | 7,22 | 7,60 | 7,72 |
Расчет плеч и построение диаграмм статической и динамической остойчивости с помощью пантокарен
Пантокарены – это кривые плеч остойчивости формы lф, выражающие зависимость значений плеч формы от водоизмещения судна и угла крена. Пантокарены могут иметь следующий вид:
Рис. 8С помощью пантокарен определяем значения плеч формы lф для различных углов крена θ при заданном водоизмещении судна, а затем находим плечи статической остойчивости по формуле:
lст=lф–a·sin θ,
a=ZG–ZC
Такая формула для расчета плеч статической остойчивости применяется, если пантокарены рассчитаны относительно центра величины т.С. Если кривые или таблицы плеч формы рассчитаны относительно точки киля, то применяется такая формула:
lст=lф–ZG·sin θ
Затем рассчитываем плечи динамической остойчивости lꝺ через lcm и θ, учитывая, что диаграмма динамической остойчивости является интегральной кривой от диаграммы статической остойчивости. Для этого можно использовать формулу:
lД=1/2 Δθрад Σинт lст.
Удобнее всего необходимые расчеты плеч статической и динамической остойчивости делать в табличном виде:
| Плечи статистической и динамической остойчивости | ||||||||
|---|---|---|---|---|---|---|---|---|
| Расчетные величины | Численные значения величин | |||||||
| θ | 00 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
| lф | 0 | |||||||
| sin θ | 0 | |||||||
| a · sin θ или ZG · sin θ | 0 + +↑ | + ↓ | + +↑ | + ↓ | ||||
| lст = lф – a · sin θ или lст=lф–ZG·sin θ | 0 ↑ | |||||||
| Σинт lст | 0 | |||||||
| lд=1/2ΔθрадΣинт lст | ||||||||
Δθ=10°; Δθрад=0,174; 1/2 Δθрад = 0,087.
Определение интегральных сумм плеч статической остойчивости производится путем суммирования плеч и интегральных сумм по схеме, как показано в таблице. На основании полученных значений плеч lcm и lꝺ строим диаграммы статической и динамической остойчивости.
Предлагается к прочтению:
Определение поперечной метацентрической высоты судна путем выполнения опыта кренования
Влияние на остойчивость судна подвешенных грузов
Сноски
Sea-Man
Геометрический вид DE: поля направлений, интегральные кривые | Геометрические методы | Раздел I: Дифференциальные уравнения первого порядка | Дифференциальные уравнения | Математика
Хорошо, приступим. Я предполагаю, что, A, вы вчера читали B, что даже если вы этого не сделали, вы знаете, как разделять переменные, и вы знаете, как строить простые модели, решать физические задачи с помощью дифференциальных уравнений и, возможно, даже решать их. Итак, вы должны были выучить это либо в старшей школе, либо в 18.01 здесь, или да. Итак, я собираюсь начать с этого момента, предположим, вы это знаете.
Я не собираюсь рассказывать вам, что такое дифференциальные уравнения или что такое моделирование. Если вы все еще не уверены в этих вещах, в книге есть очень подробное и хорошее объяснение. Просто прочтите это.
Итак, мы говорим об ODE первого порядка.
ODE: Я использую только два акронима.
ODE — обыкновенные дифференциальные уравнения.
Я думаю, что весь Массачусетский технологический институт знает это, независимо от того, проходили ли они курс обучения или нет.Итак, мы говорим об ОДУ первого порядка, которые в стандартной форме записываются, вы выделяете производную y по x, скажем, в левой части, а в правой части вы пишете все остальное. Вы не всегда можете делать это очень хорошо, но на сегодняшний день я предполагаю, что это было сделано и это выполнимо. Так, например, некоторые из тех, которые будут рассматриваться сегодня или в наборе задач, — это такие вещи, как y, простое число равно x над y.
Это довольно просто.
В наборе задач y простое число равно, давайте посмотрим, x минус y в квадрате.
Кроме того, у него простое число y равно y минус x в квадрате.
Есть и другие. Теперь, когда вы посмотрите на это, вы, конечно же, можете решить эту проблему, разделив переменные. Итак, это решаемо.
Это — и ни одна из них не может разделить переменные. И внешне они очень похожи. Но они крайне непохожи. Самое непохожее на них то, что эта легко решаемая.
И вы узнаете, если еще не знаете, в следующий раз в следующую пятницу, как решить эту задачу.
Эта, которая выглядит почти так же, в определенном смысле неразрешима. А именно, нет элементарных функций, которые можно было бы записать, которые давали бы решение этого дифференциального уравнения. Итак, сразу же сталкиваешься с наиболее существенным фактом, что даже для самых простых возможных дифференциальных уравнений, которые включают только первую производную, можно записать чрезвычайно выглядящих простых людей.
Я выделю это синим цветом, чтобы указать, что он плохой.
Ой, извините, я имею в виду, неплохо, но непокорно. Это не разрешимо в обычном смысле, в котором вы думаете, что уравнение разрешимо. И поскольку эти уравнения являются скорее правилом, чем исключением, в этот первый день я собираюсь не решать ни одно дифференциальное уравнение, а указывать вам, что вы делаете, когда встречаетесь с таким синим уравнением. Что ты с этим делаешь?
Итак, этот первый день будет посвящен геометрическим подходам к рассмотрению дифференциальных уравнений и численных расчетов.
В самом конце я немного расскажу о числовых способах. И вы будете работать над обоими из них для первого набора задач. Итак, каков наш геометрический взгляд на дифференциальные уравнения? Что ж, это то, что отличается от обычных процедур, с помощью которых вы решаете проблемы и находите элементарные функции, которые их решают.
Я назову это аналитическим методом.
Итак, с одной стороны, у нас есть аналитические идеи, в которых вы явно записываете уравнение, y простое число равно f x, y.
И вы ищете определенные функции, которые называются ее решениями. Итак, вот ODE.
И y1 из x, обратите внимание, я не использую отдельную букву. Я не использую g, h или что-то в этом роде для решения, потому что буквы умножаются так быстро, то есть умножаются в смысле кроликов, что через некоторое время, если вы продолжите использовать разные буквы для каждой новой идеи, вы можете Не понимаю, о чем ты говоришь. Итак, я использую y1 означает, что это решение этого дифференциального уравнения.
Конечно, дифференциальное уравнение имеет множество решений, содержащих произвольную константу.
Итак, назовем это решением.
Итак, геометрический вид, геометрический парень, который соответствует этой версии написания уравнения, является чем-то, что называется полем направления.
И решение, с геометрической точки зрения, называется интегральной кривой.
Итак, позвольте мне объяснить, если вы не знаете, что такое поле направления. Я знаю, что для некоторых из вас я пересматриваю то, что вы узнали в старшей школе.
Те из вас, кто учился в средней школе по программе BC, должны знать эти вещи. Но никогда не помешает немного больше практики. И, в любом случае, я думаю, что компьютерные вещи, которые вы будете делать с набором задач, в некоторой степени должны быть для вас в новинку.
Для меня это было в новинку, почему не для вас?
Итак, что такое поле направления? Ну, поле направления таково: вы берете самолет, и в каждой точке плоскости — конечно, это невозможно.
Но вы выбираете некоторые точки плоскости.
Вы рисуете так называемый маленький линейный элемент.
Итак, есть смысл. Это небольшая линия, и единственное, что ее отличает за пределами ее положения на плоскости, поэтому точка (x, y), в которой мы рисуем этот линейный элемент, — это его наклон. И каков ее уклон?
Его наклон должен быть равен f от x, y.
А теперь вы заполняете самолет этими вещами, пока не устанете вставлять их. Так что я довольно быстро устану. Итак, я не знаю, давайте не будем заставлять их всех идти одним и тем же путем.
Это вроде жульничества. Как насчет здесь?
Вот несколько случайно выбранных линейных элементов, которые я вставил, и я произвольно поставил наклоны, так как у меня не было в голове какого-либо конкретного дифференциального уравнения.
Теперь интегральная кривая, это линейные элементы.
Интегральная кривая — это кривая, которая проходит через плоскость и в каждой точке касается элемента линии.
Итак, это интегральная кривая. Эй, подождите минутку, я думал, что касательные — это линейный элемент, который даже не касался его.Ну, я не могу заполнить плоскость линейными элементами. Здесь, в этот момент, был элемент линии, который я не стал рисовать. И это касалось этого.
Здесь то же самое: если бы я нарисовал здесь линейный элемент, я бы обнаружил, что кривая имеет именно там правильный наклон. Итак, точка — это интеграл, интегральная кривая отличает то, что везде она имеет направление, именно так я укажу, что она касательная, имеет направление поля везде, во всех точках кривой, конечно, где это не идет.У него нет никакой миссии. Теперь я говорю, что эта интегральная кривая является графиком решения дифференциального уравнения. Другими словами, аналитическая запись дифференциального уравнения геометрически такая же, как рисование этого поля направления, а аналитическое решение для решения дифференциального уравнения — то же самое, что геометрическое рисование интегральной кривой. Итак, что я говорю?
Я говорю, что интегральная кривая, хорошо, позвольте мне написать ее так. Я сделаю из этого небольшую теорему, что y1 of x является решением дифференциального уравнения тогда и только тогда, когда график, кривая, связанная с этим, график y1 of x является интегральной кривой.
Интегральная кривая чего? Ну, о поле направления, связанном с этим уравнением. Но на доске недостаточно места, чтобы написать это. Но вы можете записать это в свои заметки, если будете делать заметки. Итак, это соотношение между двумя интегральными кривыми графиков или решений. Итак, почему это так?
Ну, на самом деле, все, что мне нужно сделать, чтобы доказать это, если вы вообще можете это назвать доказательством, — это просто перевести то, что на самом деле означает каждая сторона. Что на самом деле означает сказать, что данная функция является решением дифференциального уравнения? Что ж, это означает, что если вы включите его в дифференциальное уравнение, оно ему удовлетворит.
Хорошо, что это? Итак, как мне подключить его к дифференциальному уравнению и проверить, что оно ему удовлетворяет?
Ну, делая это абстрактно, я сначала вычисляю его производную. И как это будет выглядеть после того, как я включу его в дифференциальное уравнение?
Ну, я ничего не делаю с x, но везде, где я вижу y, я подключаю именно эту функцию.
Итак, в обозначениях это было бы записано так.
Итак, чтобы это было решением, это означает, что это уравнение удовлетворяется.Хорошо, что означает, что график является интегральной кривой? Ну, это означает, что в каждой точке наклон этой кривой означает, что наклон y1 для x должен быть в каждой точке x1 y1.
Он должен быть равен наклону поля направления в этой точке.
И затем, каков наклон поля направления в этой точке? Ну, это f этого конкретного, ну, в точке x, y1 точки x. Если хотите, вы можете поставить там нижний индекс, единицу, отправить единицу сюда или ноль туда, чтобы указать, что вы имеете в виду конкретную точку.Но будет лучше, если вы этого не сделаете. Но есть вероятность путаницы. Я признаю это.
Итак, наклон поля направления, что это за наклон?
Ну, кстати, я вычислил поле направления. Его наклон в точке должен был быть равен x, независимо от значения x и значения y1 для x, подставляемого в правую часть уравнения. Итак, какой наклон этой функции этой кривой графика должен быть равен наклону поля направления.Что здесь говорится?
Ну, а каков наклон y1 для x?
Это y1 простое число x.
Это с первого дня 18.01, исчисление.
Какой наклон поля направления?
Это? Ну вот это.
И это с правой стороны.
Итак, сказать, что эти два парня равны или равны, с аналитической точки зрения, то же самое, что сказать, что эти два парня равны. Другими словами, доказательство состоит в том, что это на самом деле означает?
Что это на самом деле означает? И после того, как вы поймете, что они на самом деле значат, вы скажете: да, они одно и то же.
Итак, я не знаю, как это писать. Ничего страшного: то же самое, как это? Это то же самое.
Хорошо, это оставляет нам интересный вопрос о том, как вы черпаете направление из… ну, это был 2003 год, в основном компьютеры рисуют их для вас.
Тем не менее, вы должны знать определенную сумму. Я дал вам пару упражнений, в которых вы должны сами нарисовать поле направления.
Это для того, чтобы вы почувствовали это, а также потому, что люди не рисуют поля направлений так, как это делают компьютеры.
Итак, давайте прежде всего, как компьютеры это сделали?
Они очень тупые. Нет проблем.
Поскольку они работают очень быстро и тратят неограниченное количество энергии, компьютерный метод наивен.
Вы выбираете точку. Вы выбираете точку, и обычно они расположены на одинаковом расстоянии. Вы определяете некоторый интервал, этот: бла, бла, бла, бла, бла, бла, бла, равный интервал.
И в каждой точке он вычисляет f для x, y в точке, находит, встречает и вычисляет значение f для (x, y), этой функции, и следующее на экране это рисует в точке (x, y) маленький линейный элемент, имеющий наклон f равный x, y.
Другими словами, он выполняет то, что говорит ему дифференциальное уравнение. И единственное, что он делает, это то, что вы можете, если вы говорите объекту нарисовать поле направления, единственный вариант, который у вас есть, — это указать, каким должен быть интервал, а иногда людям не нравится видеть всю линию.
Им нравится видеть только половину строки.
И иногда, согласно программе, вы можете сказать компьютеру, какой длины вы хотите, чтобы эта линия была, если вы хотите, чтобы она была маленькой или немного больше.
Время от времени вы хотите, чтобы он был уже, но не сейчас. Хорошо, это то, что делает компьютер. Что делает человек?
Вот что значит быть человеком.
Вы используете свой интеллект. С человеческой точки зрения, все это было сделано в неправильном порядке.
Причина, по которой это было сделано в неправильном порядке: потому что для каждой новой точки требуется пересчет f из (x, y).
Это ужасно. Компьютер не возражает, но человек возражает.Итак, для человека способ сделать это — не начать с выбора точки, а начать с выбора наклона, который вы хотели бы увидеть. Итак, вы начинаете с уклона. Назовем это значением наклона C. Итак, вы выбираете число.
C — два. Я хочу увидеть, где все точки на плоскости, где наклон этого линейного элемента будет равен двум? Что ж, они удовлетворят уравнению. Уравнение f из (x, y) равно, в общем случае, это будет C.
Итак, что вы делаете, это строите это, строите уравнение, строите это уравнение.Обратите внимание, это не дифференциальное уравнение. Вы не можете точно построить дифференциальное уравнение. Это кривая, обычная кривая. Но какая кривая будет зависеть; Фактически, с точки зрения 18.02, это кривая уровня C, извините, это кривая уровня f для (x, y), функция f от x и y, соответствующая уровню значения C. Но мы не будем называть это так, потому что это не 18.02. Вместо этого мы будем называть это изоклиной. А потом вы замышляете, ну, вы это сделали. Итак, у вас есть эта изоклина, за исключением того, что я собираюсь использовать кривую решения, сплошные линии, только для интегральных кривых.
Когда мы строим изоклины, чтобы указать, что они не являются решениями, мы будем использовать пунктирные линии для их выполнения.
Один компьютер работает, а другой нет.
Но они тоже используют разные цвета.
Есть разные способы сказать вам, что такое изоклина, а что кривая решения. Итак, а что вы делаете?
Итак, это все точки, где наклон будет C. А теперь вы рисуете столько элементов линии, сколько хотите, имеющих наклон C.
Обратите внимание, насколько это эффективно. Если вы хотите их 50 миллионов и у вас есть время, возьмите 50 миллионов.
Если двух или трех достаточно, возьмите два или три.
Вы будете смотреть на картинку.
Вы увидите, как выглядит кривая, и это даст вам ваше суждение о том, как вы должны это делать.
Итак, в общем, изображение, нарисованное таким образом, скажем, изоклина, соответствующая C, равна нулю. Линейные элементы, и я думаю, что для изоклины для целей этой лекции было бы неплохо поставить изоклины.
Хорошо, я собираюсь выделить кривые раствора розовым или другим цветом, а изоклины, я думаю, будут оранжевыми. Итак, изоклина, представленная пунктирной линией, и теперь вы вставите элементы линии, для этого нам понадобится много мела. Итак, я воспользуюсь белым мелом.
Y горизонтально? Потому что согласно этому там наклон должен быть нулевым.
А как насчет изоклины с отрицательным наклоном? Предположим, здесь C равно отрицательному.Хорошо, тогда это будет выглядеть так. Предполагается, что это линии с отрицательным наклоном. Не стреляйте в меня, если это не так.
Итак, это принцип. Итак, вот как вы заполните плоскость, чтобы нарисовать поле направления: сначала вычерчивая изоклины. И затем, когда у вас есть изоклины, у вас будут линейные элементы.
А можно нарисовать поле направления.
Хорошо, в течение следующих нескольких минут я хотел бы поработать для вас пару примеров, чтобы показать, как это работает на практике.
Итак, первое уравнение будет иметь простое y, равное минус x над y. Хорошо, во-первых, что такое изоклины? Что ж, изоклины будут у. Ну, отрицательное x по y равно C. Может быть, мне лучше сделать два шага из этого. Минус x над y равен C.
Но, конечно, никто не рисует кривую в таком виде. Вы хотите, чтобы это было в форме y равно минус единице по C умножить на x.
Итак, вот наша изоклина. Почему бы мне не поставить это оранжевым цветом, раз уж он будет таким, я его нарисую.Другими словами, для разных значений C теперь эта вещь выровнена.
Фактически, он выровнен через начало координат.
Это выглядит довольно просто. Хорошо, вот и наш самолет.
Изоклины будут линиями, проходящими через начало координат.
А теперь вставим их, допустим, например, C равно единице. Ну, если C равно единице, то это прямая, y равно минус x.
Итак, это изоклина. Я поставлю здесь, C равно минус один. И, вместе с тем, нет, что-то не так.Мне жаль?
C — один, а не отрицательный, да, спасибо.
Спасибо. Итак, C равно единице.
Итак, это должны быть небольшие отрезки линии первого наклона, которые будут элементами линии, элементы первого наклона.
Хорошо, а как насчет того, чтобы C равно отрицательному?
Если C равно отрицательному, то это прямая, y равно x. Итак, это изоклина.
Обратите внимание, по-прежнему прочерк, потому что это изоклины.
Здесь C отрицательная. Итак, элементы откоса выглядят так.Обратите внимание, они перпендикулярны.
Теперь обратите внимание, что они всегда будут перпендикулярны линии, потому что наклон этой линии минус один над C.
Но наклон линейного элемента будет C.
Эти числа, минус один над C и C, являются отрицательными обратными. И вы знаете, что две линии с отрицательным обратным наклоном перпендикулярны.
Итак, линейные элементы будут перпендикулярны им.
И поэтому мне даже не приходится заморачиваться с расчетами, делать какие-то еще вычисления.
Вот будет, ну как насчет этого?
Вот спорная изоклина.
Это изоклина? Подожди минутку.
Это не соответствует ничему подобному.
А-ха, но это было бы, если бы я умножил C на C.
И тогда это будет соответствовать нулю C.
Другими словами, не пишите так.
Умножить на C. Будет прочитано, что C y равно отрицательному x. И затем, когда C равно нулю, у меня x равно нулю, что в точности совпадает с осью y.
Итак, это действительно включено. Как насчет оси x?
Ну ось абсцисс не входит.
Однако большинство людей все равно включают его.
Это очень часто бывает неаккуратно и немного загибает края углов, надеясь, что никто этого не заметит.
Скажем, что C равно бесконечности.
Надеюсь, никто не хочет спорить из-за этого.
Если да, сразись с кем-нибудь еще.
Итак, если C равно бесконечности, это означает, что маленький отрезок линии должен иметь бесконечный наклон, и, по общему мнению, это означает, что он должен быть вертикальным.
Итак, мы можем даже считать это своего рода изоклиной.
И, я сделаю тире меньше, чтобы указать, что он имеет более низкий статус, чем другие. И, я вставлю это, сделаю эту ласковую штуку, заключив это в кавычки, чтобы указать, что я не несу ответственности за это.
Хорошо, теперь мы должны построить интегральные кривые.
Что ж, нет ничего проще. Я ищу кривые, которые везде перпендикулярны этим лучам.
Ну, из геометрии вы знаете, что это круги.
Итак, интегральные кривые представляют собой окружности.
И это элементарное упражнение, от которого я бы не стал лишать вас удовольствия. Решите ОДУ путем разделения переменных. Другими словами, мы получили, поэтому круги — это круги с центром в начале координат, конечно, равные некоторой константе.
Я назову его C1, чтобы его не путали с этим C. Они выглядят так, и теперь вы должны решить эту проблему, разделив переменные и просто подтвердив, что решения на самом деле являются этими кругами.Одна интересная вещь, и я подтверждаю это, я не буду этого делать, потому что сегодня я хочу заниматься геометрическими и числовыми вещами.
Итак, если вы решите это путем разделения переменных, следует отметить одну интересную вещь: если я напишу решение как y равно y1 из x, оно будет выглядеть примерно как квадратный корень из C1 минус, давайте возведем это в квадрат потому что так люди обычно ставят радиус минус x в квадрат.
Итак, решение, типичное решение выглядит так.
Ну, а какое здесь решение?
Что ж, одно решение будет идти отсюда сюда.
Если хотите, у него есть и отрицательная сторона.
Итак, сделаю, скажем так, плюс.
Есть еще одно решение, имеющее отрицательное значение.
Но давайте использовать тот, у которого положительное значение квадратного корня. Я хочу сказать, что это решение, область этого решения, действительно идет только отсюда сюда.
Это не вся ось абсцисс. Это всего лишь ограниченный участок оси x, на котором определяется это решение.
Нет возможности продлить его дальше.
И, глядя на дифференциальное уравнение, невозможно предсказать, что типичное решение будет иметь такую ограниченную область.
Другими словами, вы можете найти решение, но как далеко оно зайдет?
Иногда это невозможно сказать, кроме как найти его явно или попросить компьютер нарисовать его изображение и посмотреть, дает ли это какое-то представление. Это одна из многих трудностей при работе с дифференциальными уравнениями.
Вы не знаете, какой будет область решения, пока не рассчитаете ее.
Теперь немного более сложный пример, давайте посмотрим, y простое число равно единице плюс x минус y.
Это не намного сложнее, и в качестве компьютерного упражнения вы будете работать с еще более сложными. Но что здесь изоклины? Ну, я установил это равным C.
Можете ли вы решить алгебру в уме?
Изоклина будет иметь уравнение: это равно C.
Итак, я собираюсь поместить y справа, а букву C — слева.
Итак, уравнение y равно единице плюс x минус C, или, что лучше, это будет x плюс один минус C. Я думаю, это действительно не имеет значения. Итак, есть уравнение изоклины. Давайте быстро нарисуем поле направления. И обратите внимание, кстати, это простое уравнение, но вы не можете разделить переменные. Так что сегодня я, во всяком случае, не смогу проверить ответ.
Я не смогу получить аналитический ответ.
Все, что мы теперь сможем сделать, это получить геометрический ответ.
Но обратите внимание, как быстро, относительно быстро это можно получить. Итак, я чувствую, как ведут себя решения этого уравнения.
Хорошо, давайте посмотрим, что нам в первую очередь построить?
Мне нравится, что C равно единице, нет, не делайте C равно единице.
Давайте сначала сделаем C равным нулю.
C равно нулю. Это линия.
y равно x плюс 1.
Хорошо, позволь мне побежать и взять этот мел.
Итак, изоклины оранжевого цвета.
Если да, то когда C равно нулю, y равно x плюс один.
Итак, допустим, это кривая. C равно нулю.
Как насчет того, чтобы C равно отрицательному?
Тогда y равно x плюс два.
Вот эта кривая. Что ж, давайте обозначим это здесь.
Итак, C равно отрицательному.
C равно отрицательным двум будет y равно x, нет, что я делаю? C равно отрицательному, если y равно x плюс два. Верно.
Ну а как насчет другой стороны? Если C равно плюс один, тогда он пройдет через начало координат.
Похоже, здесь немного больше места.
Как насчет того, если это будет C равно единице, то я вроде как уловил идею. C равно двум будет выглядеть так. Все они будут параллельными линиями, потому что все, что меняется, — это точка пересечения по оси Y, как я это делаю. Итак, здесь C равно двум.
Наверное, хватит. Хорошо, давайте поместим это в элементы строки.Хорошо, C равно отрицательному. Они будут перпендикулярны.
C равно нулю, вот так.
C равно единице. О, это интересно.
Я даже не могу нарисовать линейные элементы, потому что они, кажется, совпадают с самой кривой, с самой линией.
Они пишут y вдоль линии, и из-за этого их трудно нарисовать. Как насчет того, чтобы C равно двум?
Ну вот, линейные элементы будут скошенными.
У них будет второй уклон, поэтому довольно крутой.
И я точно так же вижу, равно ли C трем.
Там будет еще более клеветнической.
А здесь они будут еще более наклонными.
Это не очень научная терминология или математика, но идею вы поняли. Хорошо, вот наша быстрая версия поля направления. Все, что нам нужно сделать, это ввести несколько интегральных кривых. Ну, похоже, он это делает. Здесь становится менее наклонным.
Выравнивается, имеет нулевой наклон.
А теперь в этой части равнины склон кажется поднимающимся. Итак, он должен делать что-то подобное. Этот парень должен сделать что-то вроде этого. Я немного сомневаюсь, что мне здесь делать. Или как насчет того, чтобы пойти с другой стороны? Ну, он поднимается, немного поднимается, должно ли оно пересекать это?
Что мне делать? Что ж, есть одна интегральная кривая, которую легко увидеть. Это один.
Эта линия одновременно является изоклиной и интегральной кривой.
Это все, кроме возможности рисования, [СМЕХ] Итак, вы понимаете, что это одна и та же линия.Он одновременно оранжевый и розовый. Но я не знаю, какое сочетание цветов из этого получится.
Это не похоже на строчку, но проявите сочувствие.
Теперь вопрос в том, что происходит в этом коридоре? В коридоре, это тоже не математическое слово, между изоклинами, ну что они такое? Это изоклины, где C равно двум, а C равно нулю. Как выглядит этот коридор?
Ну примерно так. Здесь все линии выглядят так.А здесь все они выглядят вот так. Склон два.
И вот тут оказывается неудачное решение.
Что делать? Хорошо, вы видите, что если решение попадает в этот коридор, интегральная кривая попадает в этот коридор, выхода нет. Это как ловушка для омаров.
Лобстер может войти. Но он не может выйти, потому что вещи всегда идут внутрь. Как он мог сбежать?
Что ж, ему нужно как-то удвоить назад, и помнить, что для побега, он должен быть, чтобы убежать с левой стороны, он должен идти горизонтально.
Но как он мог это сделать, не повернувшись назад и не имея неправильного наклона? Уклон всего в этом коридоре положительный, и чтобы вернуться назад и уйти, в какой-то момент он должен иметь отрицательный уклон.
Он не может этого сделать. Что ж, могло ли оно сбежать с правой стороны? Нет, потому что в тот момент, когда он захочет перейти, у него должен быть наклон меньше этой линии. Но все эти острые ребята указывают пальцем; он не может убежать и этим путем.
Итак, побег невозможен.Это должно продолжаться. Но более того, правда.
Итак, от решения никуда не деться. Попав туда, он не может сбежать. Это что-то типа того, как они называют эти растения, я забыл, кувшинками.
Все, что они слышат, это то, что они падают.
Так вот, похоже. И вот бедное маленькое насекомое падает внутрь. Они могут взбираться по стенам, но все волосы идут не в том направлении, и оно не может их преодолеть. Что ж, давайте подумаем об этом так: об этой плохой ловушке.Итак, он делает то, что должен.
И это еще не все.
Потому что здесь задействованы два принципа, которые вы должны знать, которые очень помогают при рисовании этих изображений. Принцип номер один заключается в том, что две интегральные кривые не могут пересекаться под углом.
Две интегральные кривые не могут пересекаться, я имею в виду, пересекаясь под таким углом.
Я поясню, что я имею в виду под такой картинкой.
А почему бы и нет? Это важный принцип.
Поместим это в белый ящик.
Они не могут пересекаться, потому что если две интегральные кривые пытаются пересечься, ну, одна будет выглядеть так.
Это интегральная кривая, потому что у нее такой наклон.
И другая интегральная кривая имеет этот наклон.
А теперь они дерутся друг с другом.
Каков истинный уклон в этой точке?
Ну, поле направления позволяет иметь только один уклон.
Если в этой точке есть линейный элемент, он имеет определенный уклон. А значит, у него не может быть и наклона, и этого.
Это так просто. Итак, причина в том, что у вас не может быть двух спусков. Поле направления не позволяет этого. Что ж, это большая, большая помощь, потому что, если я знаю, вот интегральная кривая, и если я знаю, что ни одна из этих розовых интегральных кривых не может пересекать ее, как еще я могу это сделать?
Что ж, им не сбежать. Они не могут перейти.
Понятно, что надо подходить к нему все ближе и ближе. Знаете, мне пришлось бы немного поработать, чтобы это оправдать. Но я думаю, что никто не усомнится в этом, кто бы немного поэкспериментировал.
Другими словами, все эти кривые соединяются с этой маленькой трубочкой и становятся все ближе и ближе к этой линии, y равно x. И там, не решая дифференциального уравнения, понятно, что все эти решения, как они себя ведут? Когда x стремится к бесконечности, они становятся асимптотическими, они становятся все ближе и ближе к решению x.
Является ли x решением? Да, потому что y равно x, это интегральная кривая. Является ли x решением?
Да, потому что если я вставлю y, равное x, что я получу?
С правой стороны у меня один.
А с левой стороны я получаю один.
Один равен одному. Итак, это решение.
Укажем, что это решение.
Итак, аналитически мы обнаружили аналитическое решение дифференциального уравнения, а именно, Y равно X, только с помощью этого геометрического процесса.
Есть еще один такой принцип, менее очевидный. Но вы должны это знать.
Итак, переход запрещен.
Это понятно. Но гораздо, намного, намного, намного, гораздо менее очевидно, что две интегральные кривые не могут соприкасаться.То есть они не могут даже касаться друг друга. Две интегральные кривые не могут касаться друг друга.
Я обозначу это словом «прикосновение», как многие говорят. Другими словами, если это незаконно, то и это.
Этого не может быть. Вы знаете, без этого, например, могло бы быть, я мог бы чувствовать, что в этом не было бы ничего, что препятствовало бы соединению этих кривых. Почему эти розовые кривые не могли соединиться с линией, y равно x?
Вы знаете, это решение. Они как бы просто устроили поездку.Ответ заключается в том, что они не могут этого сделать, потому что им нужно просто подойти к нему асимптотически, когда-либо, еще ближе. Они не могут присоединиться к y равно x, потому что в точке, где они присоединяются, возникает такая ситуация.
А почему ты не можешь этого получить?
Это намного сложнее, чем это, и причина кроется в так называемой теореме существования и единственности, которая гласит, что через точку x ноль y ноль, что простое y, равное f из (x, y), имеет только одно, и только одно решение.Есть одно решение.
На языке математики это означает хотя бы одно решение. Это не значит, что у него есть только одно решение. Это математическое соглашение.
Имеет одно решение, по крайней мере, одно решение.
Но убийца — только одно решение.
Это то, что вы должны сказать в математике, если хотите только одно, одно и только одно решение через точку x ноль y ноль. Итак, тот факт, что он есть, это часть существования. Тот факт, что он имеет только один, является частью теоремы об уникальности.
Теперь, как и во всех хороших математических теоремах, у этой есть гипотезы. Так что это не будет курс, я предупреждаю вас, тех из вас, кто склонен к теории, очень богат гипотезами.
Но, гипотезы для той или иной f of (x, y) должны быть непрерывной функцией.
Теперь, как и многочлен, знаки должны быть непрерывными рядом с этой точкой.
Гарантия существования и уникальность — это гипотеза, о которой вы даже не догадывались.
Я тоже. Что гарантирует уникальность, так это то, что ее частная производная по y должна быть непрерывной, должна быть непрерывной около x ноль y ноль.
Что ж, мне нужно принять решение.
У меня нет времени говорить о методе Эйлера.
Я отсылаю вас к, там одна страница заметок, и я ничего не мог сделать, кроме как просто повторить то, что в этих заметках. Итак, я доверяю вам это прочитать. А вместо этого позвольте мне привести вам пример, который немного укрепит эти вещи в вашем уме.Думаю, это лучший вариант.
Пример отсутствует в ваших заметках, поэтому помните, что вы впервые услышали его здесь.
Хорошо, а какой пример? Итак, вот это дифференциальное уравнение. Теперь давайте просто решим это, разделив переменные. Можете ли вы сделать это в своей голове?
dy поверх dx, поместите все y слева.
Это будет выглядеть как dy над единицей минус y.
Поместите все dx слева. Итак, dx здесь скорее идет справа. Это будет dx.
Затем x переходит в знаменатель.
Итак, это выглядит так. И, если я объединю обе стороны, я получу логарифм один минус y, я думаю, может быть, с a, я никогда не беспокоился об этом, но вы можете.
Это должны быть абсолютные значения. Хорошо, поставьте абсолютное значение плюс константу. А теперь, если я возведу в степень обе стороны, константа будет положительной. Итак, это будет выглядеть как y. Один минус y равен x And, константа будет равна e для C1. И я просто сделаю это новой константой Cx.И теперь, позволив C быть отрицательным, вы можете избавиться от абсолютных значений, если вы позволите C иметь отрицательные значения, а также положительные значения. Напишем это в более человечной форме. Итак, y равно единице минус Cx.
Хорошо, ладно, давайте просто нанесем их на график. Итак, вот решения.
Это довольно простое уравнение, довольно простой метод решения, просто разделение переменных. На что они похожи?
Ну, это все линии, пересечение которых находится в одном месте.
Причем, наклон у них любой.
Итак, вот строки, которые выглядят вот так.
Хорошо, теперь позвольте спросить, существование и уникальность.
Существование: через какие точки плоскости проходит решение? Ответ: через каждую точку плоскости, через любую точку здесь я могу найти одну и только одну из этих линий, за исключением этих глупых парней здесь, на стебле цветка. Здесь для каждой из этих точек не существует. У этого дифференциального уравнения нет решения, которое проходит через любую из этих волнообразных точек на оси Y, за одним исключением.
Эта точка избыточна. На этом этапе не существование терпит поражение. Неудача только в уникальности: нет уникальности. Здесь много чего происходит. Итак, является ли это нарушением теоремы существования и единственности?
Это не может быть нарушением, потому что теорема не имеет исключений. В противном случае это не было бы теоремой. Итак, давайте посмотрим.
Что не так? Мы думали, что решили его по модулю, поставив в журнал знаки абсолютного значения.
Что не так? Ответ: неправильно то, что, используя теорему, вы должны написать дифференциальное уравнение в стандартной форме, в зеленой форме, которую я вам дал.
Давайте запишем дифференциальное уравнение так, как мы должны были. В нем говорится, что dy / dx равно единице минус y, деленной на x.
И теперь, я вижу, правая часть не является непрерывной, на самом деле, даже не определена, когда x равно нулю, когда вдоль оси y. Следовательно, существование и уникальность вдоль линии не гарантируется, x равен нулю оси y. И, по сути, мы видим, что это не удалось. С практической точки зрения, это то, как существование и уникальность терпят неудачу во всей повседневной жизни, работа с дифференциальными уравнениями происходит не из-за сложных примеров, которые могут построить математики.
Но обычно, потому что f of (x, y) где-то не может быть определено, и это будут плохие моменты.
Спасибо.
Некоторые интегральные кривые с новой рамкой
В этой статье некоторые новые интегральные кривые определены в трехмерном евклидовом пространстве с использованием новой системы отсчета полиномиальной пространственной кривой. Векторы Френе, кривизна и кручение этих кривых получены с помощью новой системы отсчета и кривизны. Мы даем характеристики и свойства этих интегральных кривых, при которых они являются общей спиралью.Кроме того, вводятся отношения между этими кривыми как некоторые виды связанных кривых. Наконец, проиллюстрирован пример.
1 Введение
Дифференциальная геометрия использует технику исчисления для понимания форм и их свойств. Теория кривых — важный раздел дифференциальной геометрии в том смысле, в котором она имеет форму. Поскольку общие типы кривых необходимы для понимания, чтобы выйти за рамки этой теории, исследователи работают в этой области долгое время.
Между тем, изучая теорию кривых, рамки кривых необходимы для исследования их характеристик. Для пространственной кривой α в трехмерном евклидовом пространстве E 3 , адаптированные кадры представляют собой набор троек { v 1 , v 2 , v 3 } , где v я образуют ортонормированный базис E 3 такой, что v 1 касается α а также v 2 , v 3 разрешено собирать в плоскости, которая нормальна для v 1 .Несколько примеров адаптированных рамок уже были рассчитаны. Самая известная и широко используемая — это рама Frenet, которая представляет собой подвижную раму. Хотя это хорошо заявлено, в случае, когда вторая производная кривой равна нулю, она не определена, и ее вращение вокруг касательной к общей кривой позвоночника часто приводит к нежелательному повороту в дизайне движения или моделировании поверхности сдвига. Подвижная рамка, которая не вращается вокруг мгновенной касательной к кривой позвоночника, называется вращающейся минимизирующей рамкой (RMF).RMF определяется непрерывно для любой правильной кривой позвоночника. Благодаря своей минимальной скручиваемости и устойчивому поведению в присутствии точек перегиба, RMF предпочтительнее рамки Френе во многих приложениях в компьютерной графике [1]. Несмотря на свою предпочтительность, RMF сложно вычислить. Кроме того, альтернативный фрейм, который называется фреймом Бишопа, определен Р. Л. Бишопом [2]. Фрейм Bishop — это параллельный транспортный фрейм. Параллельная транспортная система отсчета — это альтернативный подход к определению подвижной системы отсчета, которая четко определена, даже когда кривая имеет исчезающую вторую производную [3].
Недавно Деде [4] определил новый фрейм, который назван фреймом кривой Френе. Этот новый кадр легко вычисляется с точки зрения использования перекрестного произведения производных первого и высшего порядка кривой для вычисления вектора бинормали кривой. Преимущество этого фрейма состоит в том, что он уменьшает количество особых точек, где они не могут быть определены в фрейме Френе. Кроме того, это уменьшает нежелательное вращение вокруг касательного вектора кривой. Кроме того, Dede et al.[5] указывает q-шкалу вдоль пространственной кривой, но эта шкала не инвариантна относительно евклидова вращения.
Сопутствующие кривые в основном изучались многими исследователями. Связанная кривая образуется с помощью другой кривой, и ее поведение можно исследовать с помощью связи между основной кривой и связанной с ней кривой. Некоторыми иллюстрациями этих кривых являются сопряжения эвольвент-эволюции, сопряжения Бертрана, пары Мангейма, сферические изображения и интегральные кривые.
В [6] Чой и Ким ввели соответствующие кривые кривой Френе, которые они назвали главной (бинормальной) кривой направления и главной (бинормальной) кривой донора.Они дали соотношение между направленными кривыми и основной кривой. В [7] Macit и Düldül определили новые связанные кривые, которые являются кривой W-направления и W-выпрямляющей кривой с помощью вектора Дарбу кривой Френе, кривой V-направления, которая связана с кривой, лежащей на ориентированной поверхности в E 3 . Более того, Körpinar et al. исследовали ассоциированные кривые с репером Бишопа в E 3 [8].Соответствующие кривые согласно системе Бишопа типа 2 были даны Йылмазом в [9].
Интегральные кривые — интересная тема, поскольку они касаются в каждой точке векторного поля, которое используется для формирования кривой. Интегральная кривая — это параметрическая кривая, которая изображает конкретное решение дифференциального уравнения или системы уравнений. В случае X — векторное поле и α ( т ) параметрическая кривая, α ( т ) является интегральной кривой X , если это решение дифференциального уравнения α ′ ( т ) знак равно Икс ( α ( т ) ) .В литературе есть различные исследования по этому поводу (см. [6–10]).
С точки зрения дифференциальной геометрии спираль — это кривая, касательный вектор которой составляет постоянный угол с фиксированным направлением, которое называется осью спирали. Хорошо известный результат, указанный Ланкре в 1802 г. (см. [11]), состоит в том, что необходимым и достаточным условием того, что кривая является общей спиралью, является соотношение (гармоническая кривизна) τ κ постоянно где κ а также τ обозначают кривизну и кручение кривой соответственно.Если оба κ а также τ ненулевые константы, то кривая называется круговой спиралью. Спираль была обобщенной, которую Хайден назвал «обобщенной спиралью» [12]. Баррос определил общую спираль в трехмерной реальной пространственной форме, используя концепцию векторного поля Киллинга вдоль кривой, и доказал теорему Ланкре для общих спиралей в этой пространственной форме [13]. В литературе о спиралях можно найти множество исследований [14–18].
В этой статье мы изучаем некоторые новые интегральные кривые, которые являются ассоциированными кривыми.Строим их по новому каркасу полиномиальной пространственной кривой. Мы даем им свойства с помощью аппарата Френе и нового каркаса и кривизны. Мы также характеризуем их в терминах пар Бертрана, пар Мангейма, эвольвентно-эволютных пар и кривых Сальковского.
2 Предварительные сведения
Пусть α ( т ) — регулярная пространственная кривая и невырожденное условие α ′ × α ″ ≠ 0 .Тогда три ортогональных векторных поля, которые называются кадром Френе, определяются как
.(2.1) т знак равно α ′ ∥ α ′ ∥ , п знак равно б × т , б знак равно α ′ × α ″ ∥ α ′ × α ″ ∥ ,
где t — касательная, п главная нормаль и б — бинормальное векторное поле.Хорошо известные формулы Френе даются(2.2) т ′ п ′ б ′ знак равно ∥ α ′ ( т ) ∥ 0 κ 0 — κ 0 τ 0 — τ 0 т п б ,
где кривизна κ и кручение τ кривой (см. [ 19– 21])(2.3) κ знак равно ∥ α ′ × α ″ ∥ ∥ α ′ ∥ 3 а также τ знак равно Det ( α ′ , α ″ , α ′ ″ ) ∥ α ′ × α ″ ∥ 2 .
Новый фрейм, который называется Flc-фреймом (фрейм кривой типа Френе), определен Деде в [ 4]. Концепция Flc-рамы представлена ниже.Пусть α ( т ) — полиномиальная пространственная кривая степени n (а именно, α кривая в пространстве с полиномиальными компонентами). Мы предполагаем, что α ( т ) регулярно и α ′ ( т ) ≠ 0 .Векторные поля Flc-кадра следующие:
(2.4) т знак равно α ′ ∥ α ′ ∥ , D 1 знак равно α ′ × α ( п ) ∥ α ′ × α ( п ) ∥ , D 2 знак равно D 1 × т ,
где t — единичный касательный вектор, D 1 — бинормальный вектор и D 2 — главный нормально-подобный вектор.Здесь штрих указывает на производную по т и ( п ) это n -я производная.Кривизны Flc-рамки d 1 , d 2 а также d 3 даются
(2.5) d 1 знак равно 〈 т ′ , D 2 〉 v , d 2 знак равно 〈 т ′ , D 1 〉 v а также d 3 знак равно 〈 D ′ 2 , D 1 〉 v ,
где v знак равно ∥ α ′ ∥ .Кроме того, формулы типа Френе выражены в [4] как
(2,6) т ′ D 2 ′ D 2 ′ знак равно v 0 d 1 d 2 — d 1 0 d 3 — d 2 — d 3 0 т D 2 D 1 .
Соотношения между кривой Френе и аппаратом кривой Френе следующие:
(2,7) d 1 знак равно κ потому что θ , d 2 знак равно — κ грех θ , d 3 знак равно d θ + τ
и(2.8) D 2 знак равно потому что θ п + грех θ б , D 1 знак равно — грех θ п + потому что θ б ,
где θ угол между вектором главной нормали п и главный нормально-подобный вектор D 2 .Определение 2.1
Две кривые, которые имеют общий вектор главной нормали, называются парами кривых Бертрана [21].
Определение 2.2
Если существует соответствующая взаимосвязь между пространственными кривыми α а также α * такие, что в соответствующих точках кривых главные нормальные линии α совпадает с бинормальными линиями α * , тогда α называется кривой Мангейма и α * Кривая партнера Мангейма из α .Пара { α , α * } называется парой Мангейма [22].
Определение 2.3
Кривая, имеющая постоянную кривизну и непостоянное кручение, называется кривой Сальковского [23,24].
Определение 2.4
Эвольвента кривой — это геометрическое место точки на отрезке струны, когда струна либо разворачивается от кривой, либо наматывается вдоль кривой.Эволюция эвольвенты — это исходная кривая [25].
Кроме того, Хаджисалихоглу [26] дал пары эвольвентно-эвольвентных кривых следующим образом: если касательные векторы двух кривых ортогональны (а именно, 〈 Т , Т * 〉 знак равно 0 , где T и Т * являются касательными векторами кривых), то они называются эвольвентно-эволютными кривыми.
3 Новые интегральные кривые
В этом разделе мы определяем некоторые новые интегральные кривые, которые называются «направленными кривыми». Затем мы даем аппарату Френе эти кривые с помощью новой системы отсчета и кривизны.
Определение 1
Пусть α — полиномиальная пространственная кривая и D 2 — главное нормальное векторное поле α .Интегральная кривая D 2 называется D 2 -направленная кривая α . А именно D 2 -направленная кривая α дается
(3.1) λ ( т ) знак равно ∫ D 2 ( т ) или же D 2 ( т ) знак равно λ ′ ( т ) .
Теорема 1
Пусть λ быть D 2 — направление полиномиальной пространственной кривой α с d 1 , d 3 ≠ 0 . Тогда векторные поля Френе, кривизна и кручение λ выдает
(3.2) т λ знак равно D 2 , п λ знак равно — d 1 d 1 2 + d 3 2 т + d 3 d 1 2 + d 3 2 D 1 , б λ знак равно d 3 d 1 2 + d 3 2 т + d 1 d 1 2 + d 3 2 D 1
и(3.3) κ λ знак равно v d 1 2 + d 3 2 , τ λ знак равно d 3 d 1 ′ d 1 2 d 1 2 + d 3 2 — v d 2 .
Проба
Используя уравнения. (2.6) и (3.1) и взяв производные, получаем
λ ′ знак равно D 2 , λ ″ знак равно v ( — d 1 т + d 3 D 1 ) , λ ′ ″ знак равно ( — v ′ d 1 — v d 1 ′ — v 2 d 2 d 3 ) т — v 2 ( d 1 2 + d 3 2 ) D 2 + ( v ′ d 3 + v d 3 ′ — v 2 d 1 d 2 ) D 1
и простые вычисления дают результат:λ ′ × λ ″ знак равно v d 3 т + v d 1 D 1 Det ( λ ′ , λ ″ , λ ′ ″ ) знак равно v 2 ( d 1 d 3 ′ — d 1 ′ d 3 ) — v 3 d 2 ( d 1 2 + d 3 2 ) .
Тогда из уважения к уравнениям. ( 2.1) и ( 2.3) результаты очевидны.Теорема 2
Пусть α — полиномиальная пространственная кривая, а — λ быть D 2 — кривая направления α . Если α — это общая спираль и θ — константа, затем D 2 Кривая направления — это общая спираль.
Проба
Гармоническая кривизна D 2 Кривая направления — рассчитывается по формуле. (3.3) следующим образом:
τ λ κ λ знак равно d 3 d 1 ′ d 1 2 v ( d 1 2 + d 3 2 ) 3 / 2 — d 2 d 1 1 + d 3 d 1 2 .
Также из уравнения. ( 2.7), получаемd 2 d 1 знак равно — загар θ , d 3 d 1 знак равно d θ + τ κ потому что θ .
Если α это общая спираль, то τ κ постоянно и если θ постоянно, отношения d 2 d 1 а также d 3 d 1 постоянны. Таким образом, результат очевиден.□Следствие 1
Если v , d 1 и d 3 полиномиальной пространственной кривой α постоянны, затем D 2 Кривая направления — кривая Сальковского.
Определение 2
Пусть α — полиномиальная пространственная кривая и D 1 — главное нормальное векторное поле α .Интегральная кривая D 1 называется D 1 -направленная кривая α . А именно D 1 -направленная кривая α дается
(3,4) β ( т ) знак равно ∫ D 1 ( т ) или же D 1 ( т ) знак равно β ′ ( т ) .
Теорема 3
Пусть β быть D 1 — направление полиномиальной пространственной кривой α с d 2 , d 3 ≠ 0 . Тогда векторные поля Френе, кривизна и кручение β выдает
(3.5) т β знак равно D 1 , п β знак равно — d 2 d 2 2 + d 3 2 т — d 3 d 2 2 + d 3 2 D 2 , б β знак равно d 3 d 2 2 + d 3 2 т — d 2 d 2 2 + d 3 2 D 2
и(3.6) κ β знак равно v d 2 2 + d 3 2 , τ β знак равно d 3 d 2 ′ d 2 2 d 2 2 + d 3 2 + v d 1 .
Проба
Учитывая уравнение. (3.4) и дифференцируя, получаем:
β ′ знак равно D 1 , β ″ знак равно v ( — d 2 т — d 3 D 2 ) , β ′ ″ знак равно ( — v ′ d 2 — v d 2 ′ + v 2 d 1 d 3 ) т + ( — v ′ d 3 — v d 3 ′ — v 2 d 1 d 2 ) D 2 — v 2 ( d 2 2 + d 3 2 ) D 1
и затем вычисляемβ ′ × β ″ знак равно v d 3 т — v d 2 D 2 , Det ( β ′ , β ″ , β ′ ″ ) знак равно v 2 ( d 2 d 3 ′ — d 2 ′ d 3 ) + v 3 d 1 ( d 2 2 + d 3 2 ) .
Из приведенных выше расчетов и формул. ( 2.1) и ( 2.3), мы, по-видимому, достигаем результатов. □Теорема 4
Пусть α — полиномиальная пространственная кривая, а — β быть D 1 — кривая направления α . Если α — общая спираль и θ является постоянным, тогда D 1 Кривая направления — общая спираль.
Проба
Гармоническая кривизна β , из уравнения. (3.6) выглядит следующим образом:
τ β κ β знак равно d 3 d 2 ′ d 2 2 v ( d 2 2 + d 3 2 ) 3 / 2 + d 1 d 2 1 + d 3 d 2 2 .
Тогда у нас есть d 1 d 2 знак равно — детская кроватка θ а также d 3 d 2 знак равно d θ + τ — κ грех θ .Как и при доказательстве теоремы 2, следствие очевидно. □Следствие 2
Если v , d 2 и d 3 полиномиальной пространственной кривой α постоянны, затем D 1 Кривая направления — кривая Сальковского.
Теперь сформулируем теоремы, касающиеся обоих D 2 — направление кривой и D 1 — направленная кривая.
Теорема 5
Пусть α — полиномиальная пространственная кривая. α образует пару эвольвентно-эвольвентной кривой как с D 2 — кривая направления β и D 1 — кривая направления λ .Также D 2 — кривая направления β и D 1 — кривая направления λ — эвольвентно-эволютные пары.
Проба
Поскольку касательные векторы α , β а также λ находятся т , т λ знак равно D 2 а также т β знак равно D 1 , соответственно, тогда:
〈 т , т λ 〉 знак равно 0 , 〈 т , т β 〉 знак равно 0 а также 〈 т β , т λ 〉 знак равно 0 .
Доказательство завершено с использованием определения пар эвольвентно-эвольвентных кривых. □Теперь переформулируем векторные поля Френе D 2 — направление кривой β а также D 1 — направление кривой λ . Используя уравнения. (3.2) и (3.5) и связь между аппаратом Френе и новыми векторными полями, существующими в уравнении.(2.8) имеем
(3,7) т λ знак равно потому что θ п + грех θ б , п λ знак равно — d 1 d 1 2 + d 3 2 т — d 3 грех θ d 1 2 + d 3 2 п + d 3 потому что θ d 1 2 + d 3 2 б , б λ знак равно d 3 d 1 2 + d 3 2 т — d 1 грех θ d 1 2 + d 3 2 п + d 1 потому что θ d 1 2 + d 3 2 б
и(3.8) т β знак равно — грех θ п + потому что θ б , п β знак равно — d 2 d 2 2 + d 3 2 т — d 3 потому что θ d 2 2 + d 3 2 п — d 3 грех θ d 2 2 + d 3 2 б , б β знак равно d 3 d 2 2 + d 3 2 т — d 2 потому что θ d 2 2 + d 3 2 п — d 2 грех θ d 2 2 + d 3 2 б .
Теорема 6
Пусть α — полиномиальная пространственная кривая, λ и β быть D 2 — кривая направления и D 1 — кривая направления α соответственно.Удовлетворены следующие утверждения:
- (1)
Если третья кривизна α равно нулю ( d 3 знак равно 0 ), затем D 2 — направление и D 1 — кривые направления α — пары кривых Бертрана.
- (2)
Если θ знак равно π 2 + k π ; ( k ∈ Z ), затем кривая α и D 2 — кривая направления α — пары кривых Бертрана.
- (3)
Если θ знак равно 2 k π ; ( k ∈ Z ), затем кривая α и D 1 — кривая направления α — пары кривых Бертрана.
Проба
- (1)
Если d 3 знак равно 0 , затем, рассматривая уравнение. (3.7) и (3.8), п λ знак равно а ⋅ п β , что означает, что п λ а также п β линейно зависимы.Кроме того, следующие уравнения предоставляются в случае d 3 знак равно 0 :
〈 т β , п λ 〉 знак равно 0 а также 〈 т λ , п β 〉 знак равно 0 , 〈 б β , п λ 〉 знак равно 0 〈 б λ , п β 〉 знак равно 0 .
Следовательно, это означает, что D 2 — направление и D 1 Кривые направления — представляют собой пары кривых Бертрана. - (2)
Принимая во внимание тот факт, что θ знак равно π 2 + k π , что также означает, что d 1 знак равно 0 , мы получили п знак равно c ⋅ п λ .Тогда уравнения
〈 т , п λ 〉 знак равно 0 а также 〈 т λ , п 〉 знак равно 0 , 〈 б , п λ 〉 знак равно 0 〈 б λ , п 〉 знак равно 0
довольны.Так что результат очевиден. - (3)
По аналогии с предыдущим доказательством, если θ знак равно 2 k π , что значит d 2 знак равно 0 , у нас есть п знак равно d ⋅ п β .Тогда ясно, что:
〈 т , п β 〉 знак равно 0 а также 〈 т β , п 〉 знак равно 0 , 〈 б , п β 〉 знак равно 0 〈 б β , п 〉 знак равно 0 .□
Теорема 7
Пусть α — полиномиальная пространственная кривая, λ и β быть D 2 — кривая направления и D 1 — кривая направления α соответственно. D 2 — кривая направления и D 1 — кривая направления, α и D 2 — кривая направления, α и D 1 Кривая направления никогда не составляет пары кривых Мангейма с Flc-подобной рамкой . α .
Проба
Если D 2 — направление кривой и D 1 Кривая направления — считается парами кривых Мангейма, тогда мы должны иметь п β знак равно б λ и уравнения 〈 т β , б λ 〉 знак равно 0 , 〈 б β , б λ 〉 знак равно 0 , 〈 т λ , п β 〉 знак равно 0 а также 〈 п λ , п β 〉 знак равно 0 должен быть доволен.Они удовлетворяются при условии, что d 1 знак равно 0 а также d 3 знак равно 0 . Но в этом случае векторные поля Френе D 2 Кривая направления — не существует. Итак, самое верхнее утверждение не соответствует действительности.
Аналогично для пар α а также D 2 — направленная кривая должна быть удовлетворена п знак равно б λ а также 〈 т , б λ 〉 знак равно 0 , 〈 б , б λ 〉 знак равно 0 , 〈 т λ , п 〉 знак равно 0 а также 〈 п λ , п 〉 знак равно 0 , у нас должно быть условие θ знак равно π 2 + k π ; k ∈ Z (что значит d 1 знак равно 0 ) а также d 3 знак равно 0 .
Для пар α а также D 1 — направленная кривая должна быть удовлетворена п знак равно б β а также 〈 т , б β 〉 знак равно 0 , 〈 б , б β 〉 знак равно 0 , 〈 т β , п 〉 знак равно 0 , 〈 п β , п 〉 знак равно 0 , у нас должно быть условие θ знак равно 2 k π ; k ∈ Z (что значит d 2 знак равно 0 ) а также d 3 знак равно 0 .
Но в обоих условиях аппарат кривых Френе λ а также β не может быть сформирован. Следовательно, очевидно, что мы имеем результат. □
Замечание 1
Сопряженная кривая как интегральная кривая бинормального вектора в системе Френе была исследована Нурканом и др. [27]. Мы можем провести сравнение с нашей новой интегральной кривой и этой сопряженной кривой. Сопряженная кривая сравнивается с нашей интегральной кривой D 1 -направленная кривая, потому что сопряженная кривая и D 1 -направленная кривая — это интегральные кривые бинормального вектора в системе Френе и бинормального вектора в системе Френе, соответственно.Если α является общей спиралью, то присоединенная кривая α является общей спиралью [27], а если α это общая спираль и θ постоянна, то D 1 -направленная кривая — общая спираль (теорема 4). Условие » θ постоянно »- другое. Кроме того, кривая α а сопряженная к нему кривая — пары кривых Бертрана и эвольвентно-эволютные кривые [27].Также такой же результат дается между α а также D 1 -направленные кривые, которые представляют собой пары эвольвентно-эволютных кривых (теорема 6). Но если θ знак равно 2 k π , ( k ∈ Z ), то кривая α а также D 1 -направленная кривая α являются парами кривых Бертрана (теорема 7).
Пример
Полиномиальная пространственная кривая степени 4 равна
α ( т ) знак равно т 2 , 2 т 3 3 , т 4 4 .
Кривизна и кручение α ( т ) находятсяκ знак равно 2 т ( т 2 + 2 ) 2 а также τ знак равно 2 т ( т 2 + 2 ) 2 .
С τ κ знак равно 1 (постоянный), α ( т ) — общая спираль.Касательные, главные нормальные и бинормальные векторные поля α следующие:
т знак равно 2 т 2 + 2 , 2 т т 2 + 2 , т 2 т 2 + 2 , D 2 знак равно — т 2 ( т 2 + 2 ) т 2 + 1 , — т 3 ( т 2 + 2 ) т 2 + 1 , 2 т 2 + 1 т 2 + 2 , D 1 знак равно т т 2 + 1 , — 1 т 2 + 1 , 0 .
D 1 — направление кривой α ( т ) составляет:β ( т ) знак равно ( т 2 + 1 + c 1 , — пер т 2 + 1 + т + c 2 , c 3 ,
где c 1 , c 2 а также c 3 реальные константы.D 2 — направление кривой α ( т ) выглядит следующим образом:
λ ( т ) знак равно 2 арктан час т 2 т 2 + 1 — Arcsin час ( т ) + d 1 , 2 арктан т 2 + 1 — т 2 + 1 + d 2 , 2 Arcsin час ( т ) — 2 арктан час т 2 т 2 + 1 + d 3 ,
где d 1 , d 2 а также d 3 реальные константы.Кривизны α ( т ) по отношению к Flc-кадру следующие:
d 1 знак равно 2 ( т 2 + 2 ) 2 т 2 + 1 , d 2 знак равно — 2 т ( т 2 + 2 ) 2 т 2 + 1 , d 3 знак равно т ( т 2 + 2 ) 2 ( т 2 + 1 ) .
Используя уравнение. ( 2.7) угол θ получается какθ знак равно — 1 4 ( потому что 2 θ + пер ( 2 — потому что 2 θ ) — 2 пер ( потому что θ ) + 1 ) + c ,
где c — действительная константа.Рисунок 2
D 1 — кривая направления α .
Рисунок 3
D 2 — кривая направления α .
Ссылки
[1] Вэньпин Ван, Берт Юттлер, Дайю Чжэн и Ян Лю, Вычисление кадров минимизации вращения, ACM Trans.График. 27 (2008), нет. 1, арт. 2, 10.1145 / 1330511.1330513. Поиск в Google Scholar
[2] Ричард Л. Бишоп, Существует несколько способов обозначить кривую, амер. Математика. Месяц 82 (1975), вып. 3, 246–251. Поиск в Google Scholar
[3] Эндрю Дж. Хансон и Хуэй Ма, Параллельный транспортный подход к криволинейному каркасу, Tech. Представитель, Университет Индианы, Блумингтон, Индиана, 1995. Поиск в Google Scholar
[4] Мустафа Деде, Новое представление о трубчатых поверхностях, Хьюстон Дж.Математика. 45 (2019), нет. 3, 707–720. Поиск в Google Scholar
[5] Мустафа Деде, Кумали Экичи и Али Горгюлю, Направленная q-рамка вдоль пространственной кривой, IJARCSSE 5 (2015), no. 12, 775–780. Поиск в Google Scholar
[6] Джин Хо Чой и Янг Хо Ким, Ассоциированные кривые кривой Френе и их приложения, Прил. Математика. Comput. 218 (2012), нет. 18, 9116–9124. Поиск в Google Scholar
[7] Несибе Мацит и Мустафа Дюльдул, Некоторые новые связанные кривые кривой Френе в E3 и E4, Turkish J.Математика. 38 (2014), 1023–1037. Искать в Google Scholar
[8] Талат Кёрпынар, Мухаммед Т. Сарыайдын и Эссин Турхан, Ассоциированные кривые согласно системе Бишопа в евклидовом 3-пространстве, Adv. Модель. Оптим. 15 (2013), нет. 3, 713–717. Поиск в Google Scholar
[9] Сюха Йылмаз, Характеризация некоторых связанных и специальных кривых в системе Бишопа типа 2 в E3, Университет Кыркларели J. Eng. Sci. 1 (2015), 66–77. Поиск в Google Scholar
[10] Джон М. Ли, Введение в гладкие многообразия — интегральные кривые и потоки, Тексты для выпускников по математике., Нью-Йорк, 2003, стр. 205–248. Поиск в Google Scholar
[11] Дирк Дж. Струик, Лекции по классической дифференциальной геометрии, Довер, Нью-Йорк, 1988. Поиск в Google Scholar
[12] Х. А. Хайден, Об общей спирали в римановом n-пространстве, Proc. Лондонская математика. Soc. 32 (1931), нет. 2, 37–45. Искать в Google Scholar
[13] Мануэль Баррос, Общие спирали и теорема Ланкре, Proc. Являюсь. Математика. Soc. 125 (1997), нет. 5, 1503–1509. Искать в Google Scholar
[14] Мануэль Баррос, Анхель Феррандес, Паскуаль Лукас и Мигель А.Мероно, Общие спирали в трехмерных лоренцевых пространственных формах, Rocky Mountain J. Math. 31 (2001), нет. 2, 373–388. Искать в Google Scholar
[15] Четин Камчи, Казым Иларслан, Левент Кула и Х. Хилми Хаджисалихоглу, Гармонические кривизны и обобщенные спирали в En, Chaos Solitons Fractals 40 (2009), no. 5, 2590–2596. Поиск в Google Scholar
[16] Надя Чуаиб, Ален Гориели и Джон Х. Мэддокс, Helices, PNAS 103 (2006), нет. 25, 9398–9403. Искать в Google Scholar
[17] Юнвер Чифтчи, Обобщение теоремы Ланкре, J.Геом. Phys. 59 (2009), нет. 12, 1597–1603. Искать в Google Scholar
[18] Эртугрул Оздамар и Х. Хилми Хаджисалихоглу, Характеристика наклонных кривых в евклидовом n-пространстве, Comm. Фак. Sci. Univ. Анкара, Ser A1 24 (1975), 15–23. Искать в Google Scholar
[19] Альфред Грей, Современная дифференциальная геометрия кривых и поверхностей с помощью Mathematica, 2-е изд., CRC Press, Бока-Ратон, Флорида, 1993. Искать в Google Scholar
[20] Вольфганг Кюнель, Дифференциальная геометрия Кривые-поверхности-многообразия, 2-е изд., AMS, Провиденс, 2006.Поиск в Google Scholar
[21] Джон Опреа, Дифференциальная геометрия и ее приложения, 2-е изд., The Math. Доц. of America, Washington, 2006. Поиск в Google Scholar
[22] Хуэли Лю и Фань Ван, партнерские кривые Мангейма в 3-м пространстве, J. Geom. 88 (2008), 120–126. Поиск в Google Scholar
[23] Хуан Монтерде, Кривые Сальковского еще раз: семейство кривых с постоянной кривизной и непостоянным кручением, Comput. Помощь Geom. Дизайн 26 (2009), 271–278. Искать в Google Scholar
[24] Эрих Сальковски, преобразование Цура фон raumkurven, Math.Аня. 66 (1909), 517–557. Искать в Google Scholar
[25] Джон В. Раттер, Геометрия кривых, CRC Press, Бока-Ратон, Флорида, 2000. Искать в Google Scholar
[26] Х. Хилми Хасисалихоглу, Diferansiyel Geometri, Ankara Üniversitesi Fen Fakültesi, Анкара, 2000. Поиск в Google Scholar
[27] Семра К. Нуркан, Илькай А. Гювен и Мурат К. Каракан, Характеризация сопряженных кривых в трехмерном евклидовом пространстве, Proc. Nat. Акад. Sci. Индия, секта. А 89 (2019), вып. 1, 155–161.Искать в Google Scholar
Поступила: 2020-03-10
Пересмотрено: 21.08.2020
Принято: 2020-08-31
Опубликовано в сети: 2020-11-24
© 2020 Илькай Арслан Гювен, опубликовано De Gruyter
Это произведение находится под международной лицензией Creative Commons Attribution 4.0.
Анализ— Векторное поле с ограниченными интегральными кривыми
Я думаю о гладких векторных полях на некотором (открытом множестве) евклидова пространства $ \ mathbb {R} ^ n $.n $ такое, что $ \ gamma (t) \ in K, \ \ \ forall t \ in] -T, T [$. Может ли кто-нибудь привести пример или намек на его создание?
Редактировать из комментариев: было указано, что по лемме о побеге такое векторное поле не может существовать, потому что, если максимальная область не является всей $ \ mathbb {R} $, тогда кривые вынуждены «уходить» «любой компакт.
Итак, позвольте мне немного изменить свой вопрос: пусть в приведенных выше обозначениях $ T = + \ infty $, так что максимальная область равна $ \ mathbb {R} $, а интегральные кривые могут быть априори ограничены.n $), которое ограничено в компакте $ K $ (и таким образом определено глобально леммой о побеге). Это возможно? (возможно, есть другой результат, который я не знаю, который доказывает, что это не так).
В чем разница между интегральной кривой и решением дифференциального уравнения?
В чем разница между интегральной кривой и решением дифференциального уравнения? — Обмен математическими стекамиСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 6к раз
$ \ begingroup $Не могли бы вы объяснить, в чем разница между интегральной кривой и решением дифференциального уравнения? В моей книге приведен пример того, что $$ \ frac {dy} {dx} = \ frac {y} {x} $$ определяет поле направления везде, кроме начала координат.функция $ y = kx $ является решением этого уравнения, а интегральная кривая задается как $ ax + by = 0 $, где $ a, b $ — произвольные постоянные. Затем книга приходит к выводу, что ось y — это интегральная кривая дифференциального уравнения, а не график решения. Я знаю определение интегральной кривой и решение уравнения.
Будем очень признательны за подробную помощь!
Заранее спасибо!
Создан 22 июн.
Фрэнк БутФрэнк Бут60511 золотой знак66 серебряных знаков1717 бронзовых знаков
$ \ endgroup $ 1 $ \ begingroup $Учитывая ОДУ, у вас есть бесконечно много интегральных кривых, соответствующих различным начальным условиям.Думайте о начальном состоянии как о бесплатном параметр.
После того, как вы укажете начальное состояние, у вас будет решение для ODE.
Итак, вы можете думать о решении ODE среди множества интегральных кривых, которые удовлетворяют вашей IC.
По указанной выше причине в некоторых текстах вместо интегральных кривых используются кривые решения.
Создан 22 июн.
felasfafelasfa1,9288 серебряных знаков1414 бронзовых знаков
$ \ endgroup $ $ \ begingroup $Решение — это интеграл, который также является непрерывным в заданной области ($ \ mathbf {Differential} $ $ \ mathbf {Equations} $ от Lomen & Lovelock).$ y = kx $ на $ (- \ infty, 0) \ cup (0, \ infty) $ является решением, потому что его производная в данной области ($ (- \ infty, 0) \ cup (0 , \ infty) $, и он также непрерывен в этой области. Но $ x = 0 $ не является решением, потому что он не определен в области, следовательно, не является непрерывным там.
Создан 14 ноя.
$ \ endgroup $ $ \ begingroup $Уравнение $ \ dot {x} = -y $, $ \ dot {y} = x $ имеет общее решение $ (x, y) = A (\ cos (t — \ phi), \ sin (t — \ phi)) $.2 $, которые представляют собой круги. Однако эти круги также допускают параметризации, такие как $ (x, y) = A (\ cos 2t, \ sin 2t) $, которые не удовлетворяют ОДУ. Следовательно, не каждая параметризация интегральной кривой дает решение, но существует одна параметризация интегральной кривой, которая является решением.
Создан 15 мар.
питонист34733 серебряных знака1111 бронзовых знаков
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
диаграмм в теории дифференциальных уравнений (восемнадцатый-девятнадцатый века) на JSTOR
AbstractДиаграммы играли важную роль на протяжении всей истории дифференциальных уравнений.Геометрическая интуиция, визуальное мышление, эксперименты с диаграммами, концепции алгоритмов и инструментов для построения этих диаграмм, эвристические доказательства, основанные на диаграммах, взаимодействовали с развитием аналитических абстрактных теорий. Мы стремимся проанализировать эти взаимодействия в течение двух столетий, когда была разработана классическая теория дифференциальных уравнений. Они тесно связаны с трудностями, с которыми сталкиваются при определении того, что является решением дифференциального уравнения, и при описании глобального поведения такого решения.
Информация журналаSynthese охватывает темы эпистемологии, методологии и философии науки. Охват включает теорию познания; общие методологические проблемы науки, индукции и вероятности, причинности и роли математики, статистики и логики в науке; а также методологические и фундаментальные проблемы различных наук. Журнал исследует символическую логику и основы математики, имеющие отношение к философии и методологии науки; и те аспекты этики, истории и социологии науки, которые важны для современных актуальных исследований.Журнал фокусируется на роли математических, логических и лингвистических методов в общей методологии науки и в основах различных наук. В журнале есть раздел о знаниях, рациональности и действии как платформа для исследователей. Объем Знания, Рациональности и Действия междисциплинарный: будет интересен исследователям в области искусственный интеллект, агенты, информатика, представление знаний, теория игр, экономика, логика, философия, математика, когнитивная наука, криптографии и теории аукционов, а также специалистам по приложениям, использующим формальные и математические методы и инструменты.
Информация об издателеSpringer — одна из ведущих международных научных издательских компаний, издающая более 1200 журналов и более 3000 новых книг ежегодно, охватывающих широкий круг предметов, включая биомедицину и науки о жизни, клиническую медицину, физика, инженерия, математика, компьютерные науки и экономика.
Геометрическая теория обыкновенных дифференциальных уравнений
Страница из
НАПЕЧАТАНО ИЗ ОНЛАЙН-СТИПЕНДИИ ОКСФОРДА (Оксфорд.Universitypressscholarship.com). (c) Авторские права Oxford University Press, 2021. Все права защищены. Отдельный пользователь может распечатать одну главу монографии в формате PDF в OSO для личного использования. дата: 04 июня 2021 г.
- Глава:
- (стр.33) 6 Геометрическая теория обыкновенных дифференциальных уравнений
- Источник:
- Advanced Mechanics
- Автор (ы):
С.Г. Раджив
- Издатель:
- Oxford University Press
DOI: 10.1093 / acprof: oso / 9780199670857.003.0006
Вся физика основана на дифференциальных уравнениях. В механике появляются обыкновенные дифференциальные уравнения. Их можно рассматривать как интегральные кривые векторного поля на многообразии фазового пространства. Векторные поля — это производные алгебры функций. Особый интерес представляет векторное поле около фиксированной точки. Определены стабильные и нестабильные направления. В упражнении развивается динамика около двойного нуля на реальной прямой. Другое упражнение показывает бабочку Лоренца: проблеск грядущего хаоса.
Ключевые слова: векторное поле, интегральные кривые, неподвижная точка, бабочка Лоренца
Для получения доступа к полному тексту книг в рамках службы для получения стипендииOxford Online требуется подписка или покупка. Однако публичные пользователи могут свободно искать на сайте и просматривать аннотации и ключевые слова для каждой книги и главы.
Пожалуйста, подпишитесь или войдите для доступа к полному тексту.
Если вы считаете, что у вас должен быть доступ к этому заголовку, обратитесь к своему библиотекарю.
Для устранения неполадок, пожалуйста, проверьте наш FAQs , и если вы не можете найти там ответ, пожалуйста свяжитесь с нами .
Структура повторного использования данных интегральной кривой на основе сжатия для визуализации потоков (Журнальная статья)
Хун, Фань, Би, Чонгке, Го, Ханьци, Оно, Кэндзи и Юань, Сяору.Основанная на сжатии структура повторного использования данных интегральной кривой для визуализации потока. США: Н. П., 2017.
Интернет. https://doi.org/10.1007/s12650-017-0428-4.
Хун, Фань, Би, Чонгке, Го, Ханьци, Оно, Кэндзи и Юань, Сяору. Основанная на сжатии структура повторного использования данных интегральной кривой для визуализации потока. Соединенные Штаты. https://doi.org/10.1007/s12650-017-0428-4
Хун, Фань, Би, Чонгке, Го, Ханьци, Оно, Кэндзи и Юань, Сяору.Сидел .
«Основанная на сжатии структура повторного использования данных интегральной кривой для визуализации потока». Соединенные Штаты. https://doi.org/10.1007/s12650-017-0428-4. https://www.osti.gov/servlets/purl/1421954.
@article {osti_1421954,
title = {Структура повторного использования данных интегральной кривой на основе сжатия для визуализации потока},
author = {Hong, Fan and Bi, Chongke and Guo, Hanqi and Ono, Kenji and Yuan, Xiaoru},
abstractNote = {В настоящее время по умолчанию интегральные кривые повторно вычисляются в различных приложениях визуализации потоков, таких как вычисление полей FTLE, запросы источника-назначения и т. Д., что приводит к ненужным затратам ресурсов. Мы представляем основанную на сжатии структуру повторного использования данных для интегральных кривых, чтобы значительно снизить стоимость их извлечения, особенно в среде с ограниченными ресурсами. В нашем проекте предлагается иерархическая и гибридная схема сжатия, чтобы сбалансировать три цели, включая высокую степень сжатия, управляемую ошибку и низкую стоимость распаковки. В частности, мы используем и комбинируем разреженное представление оцифрованной кривой, сжатие данных с плавающей запятой и разделение пространства октодерева для адаптивного достижения целей.Результаты показали, что наша структура повторного использования данных может получить в десятки раз ускорение в среде с ограниченными ресурсами по сравнению с отслеживанием частиц «на лету» и сохранить управляемую потерю информации. Более того, наш метод может обеспечить быстрое извлечение интегральной кривой для более сложных данных, таких как данные неструктурированной сетки.

 Однако только графически определять метацентрическую высоту h по диаграмме статической остойчивости не рекомендуется, т. к. проведение касательной к кривой не может быть выполнено с необходимой точностью. Этот метод может использоваться только как дополнительный (контрольный).
Однако только графически определять метацентрическую высоту h по диаграмме статической остойчивости не рекомендуется, т. к. проведение касательной к кривой не может быть выполнено с необходимой точностью. Этот метод может использоваться только как дополнительный (контрольный).