Конспект урока математики в 6 классе по теме Деление обыкновенных дробей
Методическая разработка урока в 6 классе по теме: «Деление обыкновенных дробей».
Предмет: Математика
УМК: Н. Я. Виленкин и др.
Учитель: Бажина Агния Кирилловна
Класс: 6
Тема: Деление обыкновенных дробей
Метапредметная тема: Постановка проблемы.
Тип урока: Урок открытия нового знания
Цель: Развитие компетентности разрешения проблем.
Задачи * повторить основные действия с обыкновенными дробями, вывести правило деления обыкновенных дробей,
закрепить при выполнении заданий, проверить уровень усвоения материала;
способствовать развитию логического, аналитического, критического мышления, интереса к
математике;
способствовать формированию умений работать в парах, самостоятельно, коллективно;
способствовать формированию функциональной математической грамотности учащихся
Методы: Проблемно-диалогический
Оборудование: ПК, интерактивная доска, карточки для игры «Лото», карточки для самостоятельной работы по новой теме,
источники информации для выполнения работы в группах.
Формы работы: самостоятельная работа, работа в парах, работа в группах, фронтальная работа.
Ожидаемые результаты:
После проведенного урока учащиеся смогут:
Сформулировать правило деления обыкновенных дробей;
Выполнять деление обыкновенных дробей, применяя правило.
Сокращать обыкновенные дроби;
Выделять целую часть обыкновенных дробей;
Составить модель правила;
Выбрать информацию из источника.
Применить полученные знания в решении реальных ситуациях.
Деятельность учителя | Деятельность учащихся | Оформление доски |
1. Организационный момент — 1мин | ||
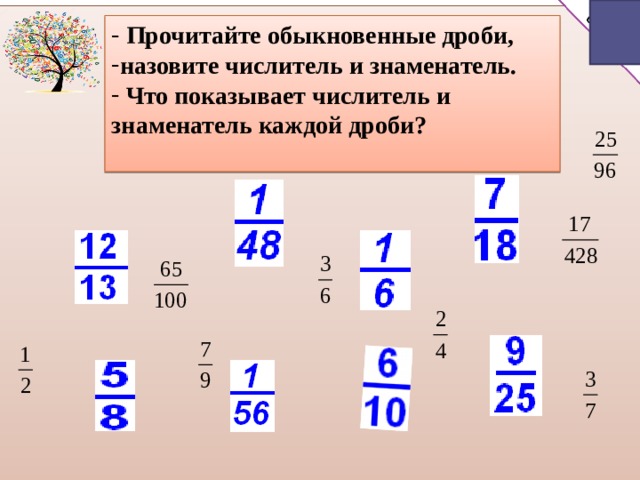
Здравствуйте, ребята! Садитесь! (приветствие) Я рада приветствовать Вас на уроке математики и прошу обратить внимание на доску. Прочитайте, что написано. Как вы понимаете эти слова? Сегодня мы с вами отправимся в путь за знаниями. Это высказывание будет девизом нашего сегодняшнего урока! Мы будем мыслить, рассуждать, исследовать только с хорошим настроением. Давайте вспомним, какие дроби вы знаете? Что мы умеем делать с дробями? Чтобы продуктивно работать на уроке нам нужно достать из наших сундучков знания, которые мы уже имеем. Предлагаю Вам игру «Лото». | (присаживаются) Чтобы переварить знания, надо поглощать их с аппетитом. (А. Франц). Для того, что бы усвоить материал, надо всегда делать это с хорошим настроением. Обыкновенные и десятичные С десятичными дробями мы умеем складывать, вычитать, умножать и делить. С обыкновенными — складывать дроби с одинаковыми, разными знаменателями, умножать и делить на натуральное число, умножать обыкновенные и смешанные дроби. | Слайд Чтобы переварить знания, надо поглощать их с аппетитом. (А. Франц). |
2. | |||||||||||
(Проводится инструктаж игры «Лото») Необходимо выполнить задания на листе, полученный результат найти на соответствующей карточке и приложить её обратной стороной к заданию. В результате получится шифр. Если какое-то задание Вы выполнить не можете, положите на него знак «?». (Контролирует выполнение заданий) (Фронтальная работа, вместе с учащимися заполняют табло на доске, анализируют шифр) Что у вас получилось? Вы смогли выполнить все задания? В чем затруднение? Почему не получается? Чем это задание не похоже на предыдущие? (Подводит учащихся к формулировке проблемного вопроса – как разделить обыкновенную дробь на дробь). Что ж, сегодня наши мыслительные операции будут направлены на то, чтобы найти ответ на этот проблемный вопрос, этому и посвятим наш урок. Тема нашего урока… ? Курс задан, какова цель урока? Итак, каждый сам для себя наметил поле деятельности. | (Внимательно слушают, задают вопросы, если они есть). (Выполняют задания, пара, заполнившая карточку «Лото» поднимает руку, после того как большинство выполнили задание – фронтальная проверка) КАК РАЗДЕЛИТЬ ОБЫКНОВЕННУЮ ДРОБЬ НА ? (В результате работы приходят к проблемному вопросу – как разделить обыкновенную дробь на дробь, так как решить последний пример им не удалось, в силу того, что задание новой не изученной темы) (формулируют с учителем тему урока, записывают её в тетрадь) Деление обыкновенных дробей! Несколько учащихся проговаривают цель, которую они ставят на этот урок. Научиться делить обыкновенные дроби, вывести правило деления обыкновенных дробей и закрепить. | Слайд «Игра «ЛОТО»
Тема урока: Деление обыкновенных дробей | |||||||||
3. | |||||||||||
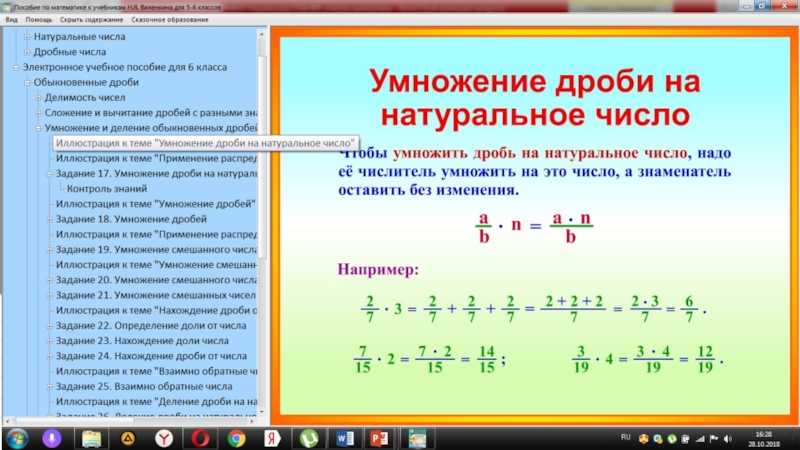
Для достижения цели и получения ответа на проблемный вопрос предлагаю Вам выполнить небольшое исследование. Обратите внимание на доску. Охарактеризуйте условие и данные. Как найти площадь данного прямоугольника? Что произойдет с шириной прямоугольника, если длину и площадь одновременно уменьшить в 10 раз? На какое число надо умножить, чтобы получить х? Чему равна ширина прямоугольника? Какое свойство уравнения мы использовали? Решим же это уравнение, находя неизвестный множитель. Проанализируйте выражение и предположите, как можно выполнить деление дроби на дробь? А сейчас посмотрим в учебник — правильно ли мы сформулировали правило деления обыкновенных дробей. Проговорите правило друг другу так, как вы его поняли. После того как проговорили в парах, несколько учащихся проговаривают правило для всех Как это правило можно записать с помощью букв? Запишите в тетрадь Молодцы!!! Вот и наше открытие! | Дан прямоугольник длина которого 4см, а площадь 20 см2. Для того, что бы найти ширину прямоугольника надо надо площадь прямоугольника разделить на длину. (Выслушиваются ответы) Ширина прямоугольника не изменится. Пусть ширина равна х см, тогда чтобы найти площадь надо ширину умножить на длину прямоугольника, т.е. 10/4 ( Х=5см Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю. Х= =5, поскольку корень один и тот же Х= = Чтобы разделить обыкновенные дроби нужно делимое умножить на число , обратное делителю. Открывают учебники и читают правило. Убеждаются, что правило сформулировано верно По схеме: УЧЕНИК-УЧИТЕЛЬ-УЧЕНИК формулируется правило Проговаривают правило в парах 4 человека рассказывают правило классу. (записывают) | Слайд «Исследование» S = 20 см2 Как найти ширину прямоугольника? Чему равна ширина данного прямоугольника? 20 см2 : 4см = 5 см дм2 Слайд «Результат исследования» Частное обыкновенных дробей – это дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй дроби, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби. | |||||||||
4.1. Закрепление (самостоятельная работа) – 4 мин | ||
Для закрепления правила, нужно… (3 ученика вызываются к доске, выполняют задания первого столбика, второй столбик — решают самостоятельно, затем проверяют). | решить примеры! (Остальные решают самостоятельно, затем проводят проверку решений через показ на доске) | З адания на закрепление 1) 4) 2) 5) 3) 6) |
4.2. Закрепление (фронтальная работа) – 2 мин | ||
А теперь, ребята, я предлагаю Вам стать настоящими экспертами! Найдите и проанализируйте ошибку в данных заданиях. (направляет деятельность учащихся на нахождение ошибок, выявление их характер) | (анализируют, находят ошибки и их характер) Арифметическая ошибка. Неправильную дробь нужно переводить в число. Не сокращена дробь. | (После определения ошибки, она выделяется анимацией в примере на доске) Слайд «Работа экспертов» 1 ) 2 ) 3 ) |
5. Проверочная работа (самостоятельная работа, взаимопроверка) – 5 мин | ||
(Раздаются карточки с заданиями, время работы 5 минут, затем взаимопроверка). Кто выполнил все 5 заданий правильно? Кто выполнил 4 задания правильно? (Проводится анализ: количество выполнивших на «5», «4», характер ошибок, выявляется степень усвоения материала) По желанию ребят оценки за проверочную работу могут быть выставлены в журнал | (Решают задания на карточке, подписывают их, затем обмениваются с соседом по парте и выполняют с помощью доски взаимопроверку). (Проводится анализ: количество выполнивших на «5», «4», характер ошибок) (поднимают руки) Проверочные работы уч-ся сдают учителю для определения уровня усвоения. | (Высвечиваются ответы на этапе взаимопроверки) |
6. | ||
А сейчас посмотрим, в каких жизненных ситуациях встречаются задания на деление обыкновенных дробей. Учитель руководит созданием групп Создаются 2 группы по 4 человека, | Ведут поиск информации из книг. Выполняют предложенное задание, выбирают из группы выступающего для объяснения решения задачи. Задают вопросы, если они возникают. Выполняют задания в группах. Представляют свое решение задач. | Слайд Поочередно высвечиваются задания и правильное их решенияе |
7. Рефлексия урока – 2 мин | ||
Какова была цель урока? Достигли ли вы цели урока? Сформулируйте правило деления обыкновенных дробей. Решена ли проблема, поставленная в начале урока? Какие трудности возникли? Соответствовал ли наш эпиграф уроку? Вопросы? | (Отвечают на поставленные вопросы, анализируя собственную деятельность на уроке) | Слайд: «Всякая хорошо решённая математическая задача доставляет умственное наслаждение. |
8. Домашнее задание – 1 мин | ||
Записываем домашнее задание. есть ли вопросы? (контролирует запись домашнего задания в дневник или тетрадь) | (записывают, задают вопросы при возникновении таковых) | № 617; 618 (а), 622 правило ИЛИ Провести самостоятельное исследование и вывести правило деления смешанных чисел. |
Приложение № 1: проверочная работа
Проверочная работа по теме «Деление обыкновенных дробей» Вариант 1 ФИ_______________________________ Выполнить деление: 4. 5. МОЛОДЕЦ! | Проверочная работа по теме «Деление обыкновенных дробей» Вариант 2 ФИ_______________________________ Выполнить деление: 4. 5. МОЛОДЕЦ! |
Приложение № 2 Работа в группах.
1 группа: Найти скорость ученика, измерив расстояние, пройденное за 2 минуты по прямой.
2группа: Придумать и решить задачу по данной схеме
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/31358-konspekt-uroka-matematiki-v-6-klasse-po-teme-
Разработки уроков | ПЕДАКАДЕМИЯ — конкурсы для учителей и воспитателей
Письменное умножение на числа, оканчивающиеся нулями
Автор: Гаранина Ольга ЮрьевнаСоздание условий для ознакомления обучающихся с письменным приемом умножения на числа, оканчивающиеся нулями, формирование данного умения посредством выполнения практических заданий
Опубликовано: 13.09.2022Разработка урока физики «Обобщение по теме «Электромагнитные явления», 9 класс
Автор: Мельник Елена ФедоровнаУрок построен по требованиям ФГОС. Учащиеся самостоятельно формулируют тему урока, ставят цель.
 На уроке используется фронтальная, индивидуальная работа, работа в парах, в группах. Задания по теме подобраны из ОГЭ по физике. В течение урока проводится самооценивание. Учащиеся повторяют следующие элементы темы: опыт Эрстеда; магнитное поле прямого проводника с током; действие магнитного поля на проводник с током; направление и модуль силы Ампера; электромагнитная индукция; опыты Фарадея. На данномОпубликовано: 06.04.2020
На уроке используется фронтальная, индивидуальная работа, работа в парах, в группах. Задания по теме подобраны из ОГЭ по физике. В течение урока проводится самооценивание. Учащиеся повторяют следующие элементы темы: опыт Эрстеда; магнитное поле прямого проводника с током; действие магнитного поля на проводник с током; направление и модуль силы Ампера; электромагнитная индукция; опыты Фарадея. На данномОпубликовано: 06.04.2020Презентация «Цветок лотоса»
Автор: Масленникова Надежда ЮрьевнаДанную презентацию можно использовать на уроках технологии и во внеурочной деятельности. В ней рассказывается изготовление цветка лотоса в технике оригами
Опубликовано: 08.10.2019«Мы в ответе за тех, кого приручили?» Презентация к уроку по рассказу Л. Андреева «Кусака». Литература, 7 класс
Автор: Бельмас Наталья НиколаевнаНазначение презентации — в информационной и иллюстративной поддержке важных этапов урока, основной задачей которого является развитие навыков анализа художественного текста.
 В презентации содержатся элементы образовательных технологий критического мышления и проблемного обучения, нацеленных на воспитание думающего ученика, способного работать и мыслить самостоятельно. Формы работы на уроке, по усмотрению учителя, могут быть различными: коллективной, групповой, индивидуальной. Для любой из них в пОпубликовано: 07.07.2019
В презентации содержатся элементы образовательных технологий критического мышления и проблемного обучения, нацеленных на воспитание думающего ученика, способного работать и мыслить самостоятельно. Формы работы на уроке, по усмотрению учителя, могут быть различными: коллективной, групповой, индивидуальной. Для любой из них в пОпубликовано: 07.07.2019Разработка урока математики. 5 класс. Делимость натуральных чисел
Автор: Царук Ольга НиколаевнаУрок обобщения и систематизации знаний по теме «Делимость натуральных чисел». Технологии: здоровьесберегающие, ИКТ. Приложение: рабочий лист.
Опубликовано: 18.12.2018Занятие по правовому воспитанию: «Мои личные документы»
Автор: Титова Наталья СергеевнаКонспект занятия по правовому воспитанию, в котором дети знакомятся со своими первыми документами (паспорт, свидетельство о рождении), правилами их пользования и хранения
Опубликовано: 07. 10.2018
10.2018Технологическая карта к уроку русского языка в 5 классе по теме «Путешествие в страну Орфография»
Автор: Вишнякова Татьяна АнатольевнаУрок повторения, обобщения, систематизации построен по требованиям ФГОС .Дети самостоятельно формулируют тему урока, ставят цель, определяют задачи. На уроке используются следующие методы : мозговой штурм, сравнение и аналогия, ролевая игра. Работают не только фронтально, но и в парах, группами, индивидуально. Задания разнообразные, отличаются по уровню сложности. В течение урока проводится самооценивание и взаимооценивание
Опубликовано: 13.07.2018Разработка урока «Разделение властей как главный принцип организации государственной власти»
Автор: Ситанова Алла НиколаевнаСоздать условия для личностной самореализации каждого обучающегося в процессе изучения темы «Принцип разделения властей как главный принцип организации государственной власти» и способствовать формированию информационных, коммуникативных, образовательных, рефлексивных компетенций у участников образовательного процесса
Опубликовано: 17. 05.2018
05.2018Разработка урока по географии на тему «Характеристика особенностей развития и размещения машиностроения мира»
Автор: Бикаева Наталья ЮрьевнаПлан-конспект урока на тему «Характеристика особенностей развития и размещения машиностроения мира» для студентов средних профессиональных учебных заведений, изучающих учебную дисциплину «География»
Опубликовано: 28.02.2018План-конспект к уроку «Россия на рубеже XIX-XX вв.» (2 часа)
Автор: Бабенко Елена ВладимировнаРазработка к уроку в 10 классе базового курса
Опубликовано: 13.02.2018Конспект урока по литературному чтению в 4 классе по теме «Мифы Древней Греции. Миф о деревянном коне» (УМК «Перспектива»)
Автор: Козырева Мария БорисовнаВашему вниманию предлагается план-конспект урока для 4 класса по теме « Мифы Древней Греции.
 Миф о деревянном коне» (УМК «Перспектива»).
Предложенный автором подход к структурированию урока и использование различных методических приемов создает условия для полноценного восприятия учащимися мифа «Деревянный конь».
Данная разработка урока по литературному чтению соответствует требованиям ФГОС НОООпубликовано: 14.11.2017
Миф о деревянном коне» (УМК «Перспектива»).
Предложенный автором подход к структурированию урока и использование различных методических приемов создает условия для полноценного восприятия учащимися мифа «Деревянный конь».
Данная разработка урока по литературному чтению соответствует требованиям ФГОС НОООпубликовано: 14.11.2017Урок окружающего мира «Петр Великий»
Автор: Проничева Светлана ПавловнаТехнологическая карта урока по окружающему миру в 4 классе
Опубликовано: 09.09.2017Презентация и самоанализ урока «Кислоты в свете ТЭД» 9класс
Автор: Волкова Татьяна НиколаевнаУрок химии проведен в 8 классе на тему «Кислоты в свете ТЭД, их классификация и свойства». Данная тема является 5 уроком в изучении раздела «Растворы. Растворение. Реакции ионного обмена и окислительно-восстановительные реакции» Вид урока: комбинированный Форма урока: форма обучения — классно-урочная, форма работы – индивидуальная, парная, групповая, форма опроса — фронтальная и индивидуальная Методы: проблемно-поисковый, словесно-иллюстративный, эксперимент, синтез, анализ.
 Опубликовано: 05.03.2017
Опубликовано: 05.03.2017Тема Детский музыкальный театр Балет «Щелкунчик» П.И. Чайковский
Автор: Бурмистрова Алла ИвановнаПредставлен ход урока и презентация по музыке для 2 класса: Автор разработки Бурмистрова Алла Ивановна, учитель музыки МОУ «СОШ No 63 с УИП» г. Саратов
Опубликовано: 19.02.2017План – конспект урока 10 класса по немецкому языку «Kinder- Eltern- Kontakte»
Автор: Муравьева Наталья СергеевнаУрок к учебнику немецкого языка 10 класса «Deutsch. Kontakte»
Опубликовано: 22.11.2016Великие навигаторы
Автор: Кривоносова Жанна ИвановнаУрок «Великие навигаторы» по учебнику Starlight 6 ( авторы Баранова К.М., Дули Д., Копылова В.В.).
Опубликовано: 18.10.2016Интеллектуальная игра – шоу «Tom Sawyer & Co»
Автор: Шестакова Фаина МихайловнаИнтеллектуальная игра – шоу «Tom Sawyer & Co»
Опубликовано: 18. 10.2016
10.2016Литературная викторина «Своя игра» по рассказу Л.Н. Толстого «После бала». (Презентация )
Автор: Криничная Ирина ИвановнаПознавательная игра для учеников 8-х классов, позволяющая в занимательной игровой форме обобщить изученное, показать важную роль детали в произведении, ещё раз обратиться к тексту рассказа Л.Н. Толстого.
Опубликовано: 14.10.2016План — конспект урока по русскому языку в 5 классе по теме: «Словосочетание. Повторение и обобщение изученного»
Автор: Криничная Ирина ИвановнаВ статье представлен план-конспект обобщающего урока по теме «Словосочетание». Материалы урока подобраны таким образом, чтобы ученик поработал со всеми единицами языка (слово-словосочетание –предложение-текст), увидел и почувствовал их взаимосвязь. А это мостик к следующей теме. В ходе работы каждый ученик оценивает не только свою работу, но и работу своего товарища.
 Тем самым развивается умение работать в парах (коммуникативные навыки общения).Опубликовано: 14.10.2016
Тем самым развивается умение работать в парах (коммуникативные навыки общения).Опубликовано: 14.10.2016План – конспект урока по окружающему миру во 2 классе по теме «Спутник Земли – Луна»
Автор: Боева Елена АнатольевнаТехнологическая карта урока по окружающему миру по требованиям ФГОС для 2 класса. Цель урока: формирование у учащихся научного представления о естественном спутнике Земли — Луне, о ее особенностях: движении Луны вокруг Земли, ее поверхности, размерах, расстоянии от Земли. В ходе урока используются разнообразные формы работы: фронтальная, групповая, работа в парах.
Опубликовано: 08.08.2016Общая базовая учебная программа по математике для 6 класса
Государственные школы Audubon Привлечение учащихся ~ воспитание достижения ~ Культивирование глобальных навыков 21 -го века Написано: Beth Canzanese Уровень 6
Привлечение учащих0008 Beth Canzanese Название курса: Математика для шестого класса Название раздела: Соотношения и пропорциональные отношения Класс: 6 3 9003 Заявления о содержании Представление числовых отношений в виде отношений; найти процент числа и, если дан процент или часть, найти число; использовать координатную плоскость для представления скорости или отношения; использовать отношения для преобразования измерений в длину, вес и мощность. | Общие базовые стандарты: 6.РП.1-3 6.EE.9 | ||||||||
Общие основные вопросы Что такое коэффициент?
| Всеобъемлющее прочное понимание Соотношение сравнивает два числа и описывает взаимосвязь между двумя количествами или элементами в целом. | ||||||||
Основные вопросы по устройству Как я могу выразить соотношение? Что такое процент? Чем процент похож на соотношение? Какая связь между процентом и дробью? Что такое ставка и удельная ставка? Как использовать графики при работе с коэффициентами? Как я могу использовать графики для преобразования одних единиц измерения в другие в обычной или метрической системе США?
| Блок прочного понимания Соотношения могут быть записаны тремя способами: 2 к 3, 2:3, 2/3. Процент означает из каждой сотни и представляет части целого, разделенные на 100 равных частей. Процент — это отношение к 100. Если я знаю процент и целое, я могу найти часть целого, которую представляет процент. Скорость — это отношение, которое сравнивает две разные единицы измерения. Единица измерения — это соотношение, сравнивающее две разные единицы измерения, в которых одно из измерений равно единице. Я могу использовать графики скорости или отношения, чтобы показать закономерности. Я могу использовать графики для преобразования одних единиц измерения в другие как в американской, так и в метрической системе. | ||||||||
Обоснование блока Учащиеся должны знать, как вычислять коэффициенты и коэффициенты, потому что они часто появляются в случаях, связанных со статистической информацией.
| Обзор устройства Учащиеся будут представлять пропорции; найти процент числа и, если дан процент или часть, найти число; использовать координатную плоскость для представления скорости или отношения; и используйте коэффициенты для преобразования измерений в длину, вес и вместимость. |
Audubon Public Schools
Engaging Students ~ Fostering Achievement ~ Cultivating 21st Century Global Skills
Written By: Beth Canzanese
Название курса Пятый класс Математика Название раздела: Выражения и уравнения Уровень класса: 6
Заявления о содержании Решение переменных в математических задачах; писать и оценивать переменные выражения, неравенства и писать и решать уравнения с переменными; определять и создавать эквивалентные выражения, используя свойства чисел; создавать таблицы, чтобы показать отношения между зависимыми и независимыми переменными. | Общие базовые стандарты:
6.EE: 1-9
|
Общие основные вопросы Что такое выражение? Что такое уравнение? | Всеобъемлющее прочное понимание Выражение — это фраза, состоящая из чисел, символов операций и иногда переменных. Есть два вида выражений — числовые и алгебраические. Уравнение — это математическое выражение, содержащее знак равенства, разделяющий уравнение на 2 эквивалентных выражения. |
Основные вопросы модуля Что такое переменная? Что такое коэффициент? Что такое термин? Как преобразовать словосочетание в математическое выражение? Как я могу вычислить выражение? Что такое эквивалентные выражения? Как узнать, эквивалентны ли два выражения? Как решить уравнение? Что такое неравенство?
| Блок прочного понимания Переменная — это буква, представляющая неизвестное число: когда значение одной переменной зависит от значения другой, она называется зависимой переменной; когда значение одной переменной не зависит от значения другой, она называется независимой переменной. Таблица может отображать взаимосвязь между зависимой и независимой переменной. Число, умноженное на переменную, называется коэффициентом. Термин представляет собой число или переменную; одинаковые термины имеют одну и ту же переменную, возведенную в один и тот же показатель степени. Мне нужно идентифицировать операции по их ключевым словам, чтобы преобразовать словесное выражение в математическое выражение. Я могу вычислить выражение с переменной или символами, подставив заданное число вместо переменной или символа; далее по порядку действий. Два выражения эквивалентны, если они выглядят по-разному, но представляют одну и ту же информацию. Я могу использовать дистрибутивные, коммутативные и ассоциативные свойства, чтобы выяснить, эквивалентны ли два выражения.
Я могу решить уравнение, изолируя переменную по одну сторону от знака равенства, применяя обратные операции. Решение можно проверить, подставив его в исходное уравнение, чтобы убедиться, что оно дает верное утверждение. Не каждое уравнение имеет решение. Неравенство — это математическое предложение, сравнивающее два выражения; используются символы <, < , > и > . Чтобы решить неравенство, я могу следовать тем же правилам решения уравнений. |
Обоснование блока В реальной жизни учащиеся сталкиваются со многими ситуациями, когда им нужно определить неизвестное число, чтобы вычислить сумму, которую им нужно знать.
| Обзор устройства Учащиеся найдут значения переменных в математических задачах; писать и находить решения выражений, неравенств и уравнений с переменными; определять и создавать эквивалентные выражения, используя свойства чисел; и создайте таблицы, чтобы показать отношения между зависимыми и независимыми переменными. |
Государственные школы Audubon
Привлечение студентов ~ Содействие достижению ~ Культивирование глобальных навыков 21 -го века
Написано: Beth Canzanese
Заявления о содержании Повторение нахождения площади и периметра двумерных фигур; найти площадь поверхности и объем трехмерных фигур; представлять объемные фигуры в двух измерениях с помощью сетки; чертить многоугольники на координатной плоскости и определять расстояние между их вершинами | Общие базовые стандарты: 6. 6.NS.8 |
Общие основные вопросы Что такое измерение? Как можно измерить внутреннюю часть двумерной фигуры? Как можно измерить площадь поверхности и объем трехмерной фигуры?
| Всеобъемлющее прочное понимание Размер — это мера ширины, высоты или длины фигуры. Внутреннюю часть двумерной фигуры можно измерить, определив квадратные единицы, покрывающие фигуру. Я могу измерить площадь поверхности трехмерной фигуры, найдя количество квадратных единиц всех ее сторон; объем трехмерной фигуры путем нахождения количества кубических единиц, заполняющих пространство.
|
Основные вопросы по устройству Что такое площадь? Как найти площадь двухмерной фигуры? Как найти площадь прямоугольника? Как найти площадь треугольника? Как найти площадь параллелограмма? Как найти площадь неправильного многоугольника? Что такое объем (V)? Как измерить объем? Что такое прямоугольная призма? Как измерить объем прямоугольной призмы? Что такое сеть? Что такое лицо? Что такое вершина? Что такое площадь поверхности? Как найти площадь поверхности твердого тела? Что такое координатная геометрия? Что такое абсолютное значение? Как нарисовать многоугольник?
| Блок прочного понимания Площадь — это мера области внутри двухмерной фигуры. Я могу найти площадь двухмерной фигуры, посчитав квадраты внутри фигуры. Я могу найти площадь прямоугольника, умножив его длину на ширину. Площадь треугольника равна половине площади прямоугольника той же высоты и длины. Площадь параллелограмма можно найти, умножив его основание на высоту. Основание и высота пересекаются под прямым углом. Я могу найти площадь неправильного многоугольника, разбив его на треугольники и прямоугольники и найдя площади этих частей, а затем сложив площади вместе. Объем — это мера пространства внутри твердого тела, трехмерной фигуры. Прямоугольная призма — объемная фигура, имеющая шесть граней, являющихся прямоугольниками; она называется призмой, потому что имеет одинаковое поперечное сечение по длине. Я могу измерить объем прямоугольной призмы в кубических единицах, используя формулу V=lwh или V=Bh. Сеть — это двумерное связное представление твердого тела, которое показывает все грани, ребра и вершины твердого тела. Грани — это плоские фигуры, образующие стороны и основание(я) твердого тела. Грани пересекаются, образуя ребра фигуры. Вершина — это угол фигуры; это точка пересечения трех или более ребер. Площадь поверхности — это площадь всех граней трехмерной фигуры. Я могу найти площадь поверхности тела, найдя сумму площадей всех граней в сети тела. Координатная геометрия дает мне возможность точно описать, где находится точка на координатной плоскости. Я могу использовать координатную геометрию для определения расстояния между двумя точками. Абсолютное значение — это расстояние числа от нуля. Я могу использовать абсолютное значение для определения расстояния между двумя точками. Я могу нарисовать многоугольник, используя координатную плоскость.
|
Обоснование блока Формы встречаются повсюду в мире природы. Учащиеся должны понимать, что рукотворный мир построен по геометрическим принципам.
| Обзор устройства Учащиеся повторят нахождение площади и периметра двумерных фигур. Они также найдут объем трехмерных фигур. Они будут представлять трехмерные фигуры в двух измерениях с помощью сетей и находить их площади поверхности; и создавать многоугольники и определять расстояние между их вершинами, используя координатные плоскости. |
Государственные школы Audubon
Привлечение учащих : Математика шестого класса Название раздела: Статистика и вероятность Уровень класса: 6
Заявления о содержании Определить, можно ли ответить на вопрос с помощью статистики; использовать различные меры для описания центра набора данных; наборы графических данных; и описывать наборы данных по-разному. | Общие базовые стандарты: 6.СП.1-5 |
Общие основные вопросы Что такое статистика? Что такое вероятность?
| Всеобъемлющее прочное понимание Статистика — это сбор и анализ данных. Вероятность — это вероятность того, что данное событие произойдет. |
Основные вопросы модуля Что такое статистическая изменчивость? Как я могу решить вопрос, который включает тему, имеющую вариативность? Что такое среднее значение, медиана и мода для данного набора данных? Как измерить набор данных? Что такое диапазон? Что такое межквартильный размах? Что такое среднее абсолютное отклонение? Как отображать данные? Что такое точечный график? Что такое коробочная диаграмма? Что такое гистограмма? Каковы шесть шагов решения статистического вопроса? Какова вероятность того, что данное событие произойдет?
| Блок прочного понимания Статистическая изменчивость — это когда значение чего-то может измениться. Если я решаю вопрос, который включает тему, имеющую вариативность, я могу использовать статистику. Среднее значение, медиана и мода являются индикаторами центра набора данных. Медиана — это среднее число в наборе данных, упорядоченном от наименьшего к наибольшему или от наибольшего к наименьшему. Мода — это число, которое чаще всего встречается в наборе данных. Я могу измерить набор данных, используя диапазон, межквартильный диапазон и среднее абсолютное отклонение. Диапазон — это разница между наименьшим и наибольшим числом в наборе данных. Межквартильный диапазон — это разница между первым и третьим квартилями набора данных. Среднее абсолютное отклонение — это средняя величина, на которую измерения в наборе данных отличаются от среднего значения. Я могу отображать данные в виде числовой линии, точечных диаграмм, коробчатых диаграмм и гистограмм. Точечный график показывает, сколько раз встречается каждое значение в наборе данных. Блочная диаграмма показывает диапазон значений и то, как они распределяются в наборе данных, включая минимальное и максимальное значение. Гистограмма показывает непрерывные данные в наборе. Чтобы решить статистический вопрос, я могу выполнить шесть шагов:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, представленное в виде дроби в виде числа от 0 до 1 или от 0% до 100%. |
Обоснование блока Анализ данных используется во многих повседневных ситуациях, от сельского хозяйства и дорожного движения до спорта и транспорта. Поскольку наш мир все больше зависит от производства, основанного на данных, скорее всего, студенты будут сталкиваться с данными и последующим анализом в своих классах колледжа и карьере.
| Обзор устройства Учащиеся определят, можно ли ответить на вопрос с помощью статистики; использовать различные меры для описания центра набора данных; наборы графических данных; и описывать наборы данных по-разному, используя проблемы и ситуации реального мира. |
4 распространенных заблуждения относительно математических дробей и способы их устранения
Примечание редактора:
Это обновленная версия сообщения в блоге, опубликованного 19 октября 2020 г.
Понимание дробей необходимо для понимания математики в целом. Но распространенные заблуждения могут оставить как учителей, так и учащихся более неуверенными, чем следовало бы.
Хотя это правда, что вы можете не замечать неверные представления на каждом уроке математики в начальной школе или у каждого ребенка, знание того, как выглядят распространенные заблуждения и как с ними бороться, может существенно изменить понимание ваших учащихся.
Давайте рассмотрим некоторые распространенные заблуждения относительно дробей и то, как самые ранние представления о дробях необходимы для формирования прочного фундамента.
Распространенное заблуждение 1: непонимание знаменателя
Распространенное заблуждение состоит в том, что учащиеся считают, что числитель и знаменатель одинаковы. Давайте начнем с основ дробей, чтобы помочь устранить это заблуждение.
«Знаменатель» означает «то, что именует» на латыни. Этот перевод идентифицирует знаменатель как имя так же, как «один», «два» и «три» являются именами.
Знаменатель также может указать размер частей. Дети узнают, что:
* ⁄ 2 показывает нам, что каждая часть называется половинкой и две из них составят одно целое.
* ⁄ 3 показывает нам, что каждая часть называется третьей и три из них составляют одно целое.
* ⁄ 4 показывает нам, что каждая часть называется четвертью и четыре из них составляют одно целое.
И так далее.
Дети должны использовать физические материалы, чтобы открыть это для себя, как в следующем примере из Математика — нет проблем! Учебник 1Б, глава 14, урок 1.
Откуда мы знаем, что партия Чарльза такая же, как партия Холли?
Мы могли бы положить кусок Чарльза на кусок Холли, чтобы увидеть, одинаковы ли они по размеру.
Сколько частей нужно, чтобы сделать один целый лист бумаги?
Чтобы сделать один лист бумаги, нужно две части.
Дети должны сначала обнаружить это, используя физические материалы, и развить язык, связанный с этой идеей.
Например, Математика — нет проблем! Учебник 1Б, глава 14, урок 2.
Если мы сосредоточимся на размерах фигур и поймем, что у каждого размера есть имя, в данном случае «четверть», обозначения станут более понятными.
Как только учащиеся поймут это, мы сможем найти название дроби.
Какая часть фигуры зеленая?
Используя идеи, впервые представленные в 1-м классе, ответить на этот вопрос будет довольно просто.
Чтобы закрыть желтую фигуру, нужно 6 зеленых кусочков. Есть одна зеленая деталь.
1 ⁄ 6 формы зеленого цвета. Мы можем развить эту идею дальше и спросить: «Сколько зеленых фишек потребуется, чтобы покрыть половину фигуры?» .
Если мы сначала сосредоточимся на знаменателе, понимание числителя станет более понятным. Числитель просто показывает нам количество частей.
3 ⁄ 4 показывает нам, что есть три части и четыре части составляют одно целое.
Распространенное заблуждение 2: почему
1 ⁄ 4 меньше, чем 1 ⁄ 2 ?Дети узнают, что 4 больше 2. И это правда. Верно ли также, что 1 ⁄ 4 больше, чем 1 ⁄ 2 ?
Если понимать роль знаменателя, то такого заблуждения дроби быть не должно. Однако, когда вы видите это заблуждение, есть шаги, которые вы можете предпринять:
Однако, когда вы видите это заблуждение, есть шаги, которые вы можете предпринять:
1. Составьте дробь, используя квадратную или прямоугольную бумагу.
2. Вырежьте детали.
3. Сравните части с написанными дробями.
Может ли учащийся установить связь между количеством частей, необходимых для создания одного целого, и размером частей? Как только эта связь будет установлена, и учащийся поймет, о чем говорит нам знаменатель, учащийся увидит, что одна четверть меньше половины. Мы могли бы обобщить и сказать: «Чем меньше часть, тем больше частей потребуется, чтобы составить одно целое».
Распространенное заблуждение 3: язык дробей
Мы можем выучить процедуры, которые эффективны и облегчают работу с дробями, но насколько хорошо они понятны?
Давайте посмотрим на этот пример для 6-го класса в Математика — нет проблем! Учебник 6A, Глава 3, Урок 15 , в котором предполагается, что 3 ⁄ 4 ÷ 2 равен 1 ⁄ 2 × 3 ós 4 .
Мы можем научить связи между ÷ 2 и × 1 ⁄ 2 с помощью процедуры. Но мы хотим, чтобы учащиеся поняли, почему это работает. В этом случае чтение математики полезно.
Почему ÷ 2 и × 1 ⁄ 2 эквивалентны в приведенном выше уравнении?
Заполним часть уравнения 3 ⁄ 4 ÷ 2 = 3 ⁄ 8 , а затем прочитаем его как предложение.
«Три четверти торта делятся между двумя людьми, и каждый получает 3 ⁄ 8 всего торта».
И еще одна часть уравнения.
1 ⁄ 2 × 3 ⁄ 4 = 3 ⁄ 8 9009
«Половина из трехэтажных», или «Остаток трехэтажных». целый торт.
Каждый получает по три восьмых части торта».
Если у детей возникают затруднения с этой идеей, мы можем сделать физическое представление или изобразить изображение в картинках, как указано ниже.

 В дорогу мы возьмем только самое необходимое: хорошее настроение и наши знания.
В дорогу мы возьмем только самое необходимое: хорошее настроение и наши знания. Актуализация знаний – игра «Лото» (работа в парах, фронтальная работа) – 4 мин
Актуализация знаний – игра «Лото» (работа в парах, фронтальная работа) – 4 мин Запишите в тетради цель, которую вы сегодня поставили.
Запишите в тетради цель, которую вы сегодня поставили. Изучение нового материала (фронтальная работа) – 10 мин
Изучение нового материала (фронтальная работа) – 10 мин Нужно найти ширину прямоугольника.
Нужно найти ширину прямоугольника.

 Решение практических задач (работа в группах) – 16 мин
Решение практических задач (работа в группах) – 16 мин » Г. Гессе
» Г. Гессе
 НС.2-7
НС.2-7 
 Упорядоченная пара (x, y) используется для определения местоположения этой точки.
Упорядоченная пара (x, y) используется для определения местоположения этой точки.






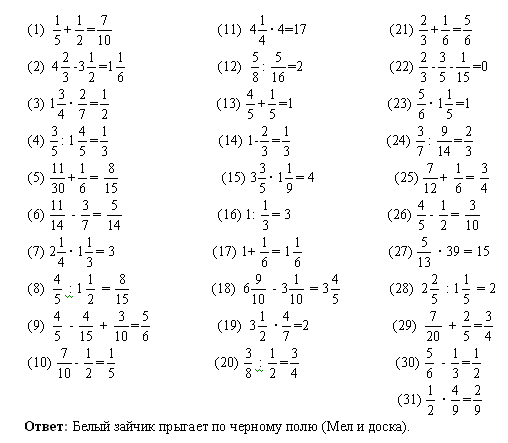 Г.1- 4
Г.1- 4


 Найти вероятность того, что данное событие произойдет.
Найти вероятность того, что данное событие произойдет.

 Вероятность используется для прогнозирования и получения статистики в таких областях, как прогнозирование погоды, контроль качества бизнеса и спортивная статистика.
Вероятность используется для прогнозирования и получения статистики в таких областях, как прогнозирование погоды, контроль качества бизнеса и спортивная статистика.