Десятичные дроби — как решать примеры 5, 6 класс
Поможем понять и полюбить математику
Начать учиться
381.8K
Оказывается, научиться работать с дробями полезно не только для школы, но и чтобы написать музыкальный трек или сверстать сайт. В этой статье разбираемся с теорией и учимся выполнять основные действия с дробями.
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,8
- 7,42
- 9,932
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья.
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Как решаем:- Знаменатель равен 10 — это один ноль.

- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Ответ: 16/10 = 1,6.
Пример 2. Перевести 37/1000 в десятичную дробь.
Как решаем:
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
и т. д. д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
1% = 1/100 = 0,01
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Быстрая напоминалка:
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе.
Пример 1. Перевести 5,4 в смешанное число.
Как решаем:
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Ответ: 5,4 = 5 2/5.
Пример 2. Перевести 4,005 в смешанное число.
Как решаем:
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как решаем:
- Читаем вслух: пять целых шестьдесят сотых.
 Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100. - Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули.
 На примере легче:
На примере легче:- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.
- Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.
Как решаем:
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
Как решаем:
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.

- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Как решаем:
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
Как решаем:
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.

- Разделить дробь по правилам:
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Как решаем:
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
Как решаем:
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.

- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
161.5K
Умножение и деление степеней
К следующей статье
175.7K
Умножение десятичных дробей
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Запись и чтение десятичных дробей
Десятичная дробь отличается от обыкновенной дроби тем, что знаменатель у нее — это разрядная единица.
Например:
Десятичные дроби выделены из обыкновенных дробей в отдельный вид, что привело к собственным правилам сравнения, сложения, вычитания, умножения и деления этих дробей. В принципе, с десятичными дробями можно работать и по правилам обыкновенных дробей. Собственные правила преобразования десятичных дробей упрощают вычисления, а правила преобразования обыкновенных дробей в десятичные, и наоборот, служат связкой между этими видами дроби.
Запись и чтение десятичных дробей позволяет их записывать, сравнивать и производить действия над ними по правилам, очень похожим на правила действий с натуральными числами.
Впервые система десятичных дробей и действий над ними была изложена в XV в. самаркандским математиком и астрономом Джемшид ибн-Масудаль-Каши в книге «Ключ к искусству счета».
Целая часть десятичной дроби отделена от дробной части запятой, в некоторых странах (США) ставят точку. Если в десятичной дроби нет целой части, то перед запятой ставят число 0.
К дробной части десятичной дроби справа можно дописывать любое количество нулей, это величину дроби не изменяет. Дробная часть десятичной дроби читается по последнему значащему разряду.
Например:
0,3 — три десятых
0,75 — семьдесят пять сотых
0,000005 — пять миллионных.
Чтение целой части десятичной дроби такое же, как и натуральных чисел.
Например:
27,5 — двадцать семь…;
1,57 — одна…
После целой части десятичной дроби произносится слово «целых».
Например:
10.7 — десять целых семь десятых
0,67 — ноль целых шестьдесят семь сотых.
Десятичные знаки — это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом. Разрядная система дробной части десятичной дроби несколько иная, чем у натуральных чисел.
- 1-й разряд после занятой — разряд десятых
- 2-й разряд после запятой — разряд сотых
- 3-й разряд после запятой — разряд тысячных
- 4-й разряд после запятой — разряд десятитысячных
- 5-й разряд после запятой — разряд стотысячных
- 6-й разряд после запятой — разряд миллионных
- 7-й разряд после запятой — разряд десятимиллионных
- 8-й разряд после запятой — разряд стомиллионных
В вычислениях чаще всего используются первые три разряда. Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.
Перевод десятичной дроби в смешанную дробь состоит н следующем: число, стоящее до запятой записать целой частью смешанной дроби; число, стоящее после запятой — числителем ее дробной части, а в знаменателе дробной части записать единицу со столькими нулями, сколько цифр стоит после запятой.
Например:
Перевод обыкновенной дроби в десятичную дробь — это вычисление частного отделения числителя дроби на знаменатель по правилам действий с десятичными дробями:
Но не все обыкновенные дроби можно перевести в десятичную дробь. Например: — нет такого множителя, который с множителем 3 даст в произведении разрядную единицу.
Запись опубликована в рубрике Математика с метками десятичная, дробь. Добавьте в закладки постоянную ссылку.
Что такое 1 1/3 в виде десятичной дроби? (Преобразовать 1 1/3 в десятичную)
Очень часто при изучении дробей возникает желание узнать, как преобразовать смешанную дробь, например 1 1/3, в десятичную. В этом пошаговом руководстве мы покажем вам, как очень легко превратить любую дробь в десятичную. Давайте взглянем!
Прежде чем мы начнем преобразование дроби в десятичную, давайте кратко рассмотрим некоторые основы дробей. Помните, что числитель — это число над дробной чертой, а знаменатель — число под дробной чертой. Мы будем использовать это позже в уроке.
Мы будем использовать это позже в уроке.
Когда мы используем смешанные дроби, у нас есть целое число (в данном случае 1) и дробная часть (1/3). Итак, что мы можем сделать здесь, чтобы преобразовать смешанную дробь в десятичную, это сначала преобразовать ее в неправильную дробь (где числитель больше знаменателя), а затем оттуда преобразовать неправильную дробь в десятичную/
Шаг 1: Умножьте целое число на знаменатель
1 x 3 = 3
Шаг 2: Добавьте результат шага 1 к числителю
3 + 1 = 4
Шаг 3: Разделите результат шага 2 на знаменатель
4 ÷ 3 = 1,3333333333333
Итак, ответ таков: 1 1/3 в виде десятичной дроби равно 1,3333333333.
И это все, что нужно для преобразования 1 1/3 в десятичную дробь. Преобразуем ее в неправильную дробь, которая в данном случае равна 4/3, а затем разделим новый числитель (4) на знаменатель, чтобы получить ответ.
Если вы хотите попрактиковаться, возьмите ручку, блокнот и калькулятор и попробуйте самостоятельно преобразовать несколько смешанных дробей в десятичные.
Надеемся, что это руководство помогло вам понять, как преобразовать дробь в десятичную, и заставило вас понять, насколько это просто на самом деле. Теперь вы можете пойти дальше и преобразовать смешанные дроби в десятичные столько, сколько пожелает ваше маленькое сердце!
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Что такое 1 1/3 в виде десятичной дроби?». VisualFractions.com . По состоянию на 14 апреля 2023 г. http://visualfractions.com/calculator/mixed-to-decimal/what-is-1-1-3-as-a-decimal/.
«Что такое 1 1/3 в виде десятичной дроби?».
 VisualFractions.com , http://visualfractions.com/calculator/mixed-to-decimal/what-is-1-1-3-as-a-decimal/. По состоянию на 14 апреля 2023 г.
VisualFractions.com , http://visualfractions.com/calculator/mixed-to-decimal/what-is-1-1-3-as-a-decimal/. По состоянию на 14 апреля 2023 г.Что такое 1 1/3 в виде десятичной дроби?. VisualFractions.com. Получено с http://visualfractions.com/calculator/mixed-to-decimal/what-is-1-1-3-as-a-decimal/.
Калькулятор преобразования смешанной дроби в десятичную
Введите целое число, числитель и знаменатель
Преобразование случайной смешанной дроби в десятичную дробь
- Что такое 34 350/734 в виде десятичной дроби?
Арифметика, математика и статистика – Набор академических навыков
Десятичные числа и округление (экономика)
ContentsToggle Главное меню 1 Определение 2 Сложение и вычитание 2.1 Примеры 3 Умножение и деление 3.1 Примеры 4 Деление десятичного числа на целое 5 Десятичные числа и дроби 5.1 Преобразование десятичных чисел в дроби 5.2 Преобразование дробей в десятичные числа 6 Округление 7 Значимость Рисунки 8 Проверьте себя 9 Внешние ресурсы
Определение
Десятичное число содержит десятичную точку. Мы используем десятичные дроби для записи дробей в виде единственного числа 9.0042 .
Мы используем десятичные дроби для записи дробей в виде единственного числа 9.0042 .
Десятичная точка показывает, где начинается дробная часть числа. Слева от запятой находится целая часть числа, а справа — дробная часть, состоящая из десятых, сотых, тысячных и так далее. Десятки в $10$ раз больше сотых, сотые в $10$ раз больше тысячных…
Например, $92,67$ состоит из $9$ десятков, $2$ единиц, $6$ десятых и $7$ сотых. Давайте посмотрим на это десятичное число на диаграмме позиционных значений, чтобы лучше понять, как работают десятичные дроби.
Повторяющееся десятичное число — это десятичное число, в котором последняя цифра или несколько последних цифр повторяются бесконечно. Например, «одна треть», записанная в виде десятичной дроби, равна $0,3333333\dotso$. Обозначение повторяющегося числа — точка над числом. Мы можем поставить точку над первыми $3$, чтобы более четко показать, что это повторяющееся значение: $0. \dot{3}$. Если группа чисел повторяется, мы пишем одну точку там, где числа начинают повторяться, и одну на последнем повторяющемся числе. Например, $\frac{452}{555}$ можно записать как $0,8144144144144\dotso$, но лучше записать как $0,8\dot{1}4\dot{4}$.
\dot{3}$. Если группа чисел повторяется, мы пишем одну точку там, где числа начинают повторяться, и одну на последнем повторяющемся числе. Например, $\frac{452}{555}$ можно записать как $0,8144144144144\dotso$, но лучше записать как $0,8\dot{1}4\dot{4}$.
Иррациональное число нельзя записать в виде дроби от целых чисел. При записи в десятичной форме цифры продолжаются вечно и не повторяются. Примеры таких чисел: $\pi = 3,1415926\dotso$ или $\sqrt{2} = 1,414213\dotso$.
Сложение и вычитание
Чтобы складывать или вычитать десятичные дроби, записывайте числа, располагая одно под другим и выстраивая десятичные точки (при необходимости поставьте нули в конце чисел, чтобы числа были одинаковой длины). Затем добавьте числа столбец за столбцом справа налево.
Примеры
a) Добавьте 0,055$ к 1,07$. Решение : \begin{align} &0,055\\ +&1,070\\ &\overline{1,125} \end{align}
b) Вычтите 0,035$ из 4,0729$. Решение : \begin{align} &4.0729\\ +&0.0350\\ &\overline{4.0379} \end{align}
Решение : \begin{align} &4.0729\\ +&0.0350\\ &\overline{4.0379} \end{align}
Умножение и деление
При умножении десятичного числа на $10$ цифры остаются то же самое, но десятичный разряд смещается на единицу вправо. Деление противоположно умножению, поэтому десятичная точка перемещается влево. Для умножения и деления на $100$ переместите запятую на два разряда; для $1,\!000$ переместите запятую на три позиции; и так далее.
Примеры
- 16,21 $ \ умножить на 10 = 162,1 $
- 1,09$ \умножить на 100 = 109$
- 0,74$ \дел 10 = 0,074$
Чтобы умножить десятичное число на другое десятичное число, умножьте числа как обычно (игнорируя десятичные точки), а затем поставьте десятичную точку в ответе — в нем будет столько знаков после запятой, сколько вместе взятых двух исходных чисел.
Пример 1
Умножьте 1,6$ на 0,12$.
Раствор
Сначала умножьте без десятичных знаков: \[16\times 12=192\] $1,6$ имеет $1$ десятичного разряда, а $0,12$ имеет $2$ десятичных разряда, поэтому ответ содержит 3 десятичных знака: \[1,6\times 0,12=0,192\ ]
Деление десятичного числа на целое число
Чтобы разделить десятичное число на целое, сначала выполните вычисление, игнорируя десятичную точку, а затем поставьте десятичную точку в том же месте, что и делимое число.
Пример 1
Разделите 0,124$ на 4$.
Решение
Сначала разделите $0,124$ на $4$, игнорируя десятичную точку. \[124\div 4=31\] $0,124$ имеет $3$ десятичных знаков, а $4$ не имеет десятичных знаков, поэтому ответ содержит $3$ десятичных знаков: \[0,124\div 4=0,031\]
Десятичные числа и дроби
Преобразование десятичных дробей в дроби
Дробную часть десятичной дроби можно рассматривать как сумму дробей, где каждая разрядная цифра представляет собой дробь над другим знаменателем. Например, $0,25$ имеет $2$ в десятых столбцах и $5$ в сотых, что совпадает с $\frac{2}{10} + \frac{5}{100} = \frac{25}{ 100} = \frac{1}{4}$. В качестве альтернативы, посмотрите на последний столбец цифр и напишите дробную часть как целое число над знаменателем этой цифры. Например, $0,331$ равно $3$ десятым, $3$ сотым и $1$ тысячным или $331$ тысячных, т.е. $\frac{331}{1000}$.
Преобразование дробей в десятичные
Чтобы преобразовать дробь в десятичную, разделите числитель на знаменатель.
Проработанный пример
Напишите следующие десятичные десятки в виде фракций, уменьшенной до самой простой формы:
a) $ 0,8 $
B) $ 0,275 $
Решение
a) . $0,8$ находится в десятом столбце, поэтому мы имеем: \[0,8 = \dfrac{8}{10} = \dfrac{4}{5}.\]
б) \[\dfrac{2}{10}+\dfrac{7}{100}+\dfrac{5}{1000} = \dfrac{200}{1000}+\dfrac{70}{ 1000}+\dfrac{5}{1000} = \dfrac{275}{1000}= \dfrac{11}{40}.\]
Рабочий пример
Преобразуйте следующие дроби в их десятичные эквиваленты:
а) $\frac{35}{10}$.
б) $\frac{11}{20}$.
Решение
а) Деление числителя на знаменатель дает: \[\frac{35}{100}=0,35\]
b) Деление числителя на знаменатель дает: \[\frac{35}{100}=0,55\]
Округление
Округление означает уменьшение количества знаков после запятой (d. p.) в числе, но сохранение его значение близко к тому, что было. Цель состоит в том, чтобы сделать число проще . Предположим, мы хотим округлить число до $2$ знаков после запятой (или $2$d.p.). Для этого смотрим только на следующую справа цифру (третья десятичная цифра). Если это:
p.) в числе, но сохранение его значение близко к тому, что было. Цель состоит в том, чтобы сделать число проще . Предположим, мы хотим округлить число до $2$ знаков после запятой (или $2$d.p.). Для этого смотрим только на следующую справа цифру (третья десятичная цифра). Если это:
- $\geq 5$ увеличиваем вторую десятичную цифру на $1$.
- $\lt 5$ вторую десятичную цифру оставляем как есть.
Рабочий пример
Округлите $251,6731$ до:
a) $3$ десятичных знаков
b) $2$ десятичных знаков
c) $1$ десятичных знаков.
Решение
а) Четвертая десятичная цифра — $1$. Поскольку $1\lt 5$, мы оставляем только третью десятичную цифру: от $251,6731$ до $3$d.p. составляет $ 2,673 $.
б) Третья десятичная цифра — $3$. Поскольку $3\lt 5$, мы оставляем только вторую десятичную цифру: от $251,6731$ до $2$d.p. составляет $ 2,67 $.
б) Вторая десятичная цифра $7$.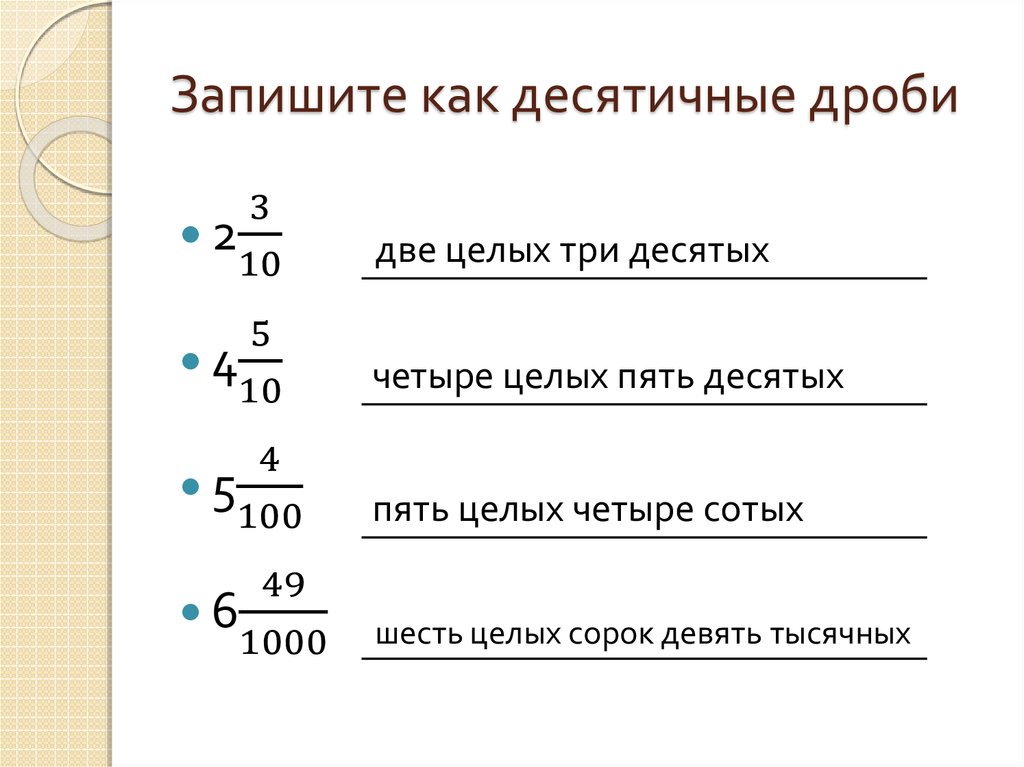 Поскольку $7\gt 5$, мы увеличиваем первую десятичную цифру на единицу: $251,6731$ до $1$d.p. составляет 2,7$.
Поскольку $7\gt 5$, мы увеличиваем первую десятичную цифру на единицу: $251,6731$ до $1$d.p. составляет 2,7$.
Значащие цифры
Иногда нас просят округлить число до заданного количества « значащих цифр » (с.ф.) или « значащих цифр ». Вот основные правила для значащих цифр:
1) Все ненулевые цифры являются значащими. 2) Все нули между значащими цифрами являются значимыми. 3) Все нули, которые стоят как справа от десятичной точки, так и справа от всех ненулевых значащих цифр, являются значащими.
Правила округления те же. Если следующее число:
- Равно или больше 5 долларов США, мы округляем его в большую сторону.
- $4$ или меньше, мы не округляем.
Рабочий пример 1
Раунд $702,019$ до
A) Пять значимых цифр
B) Четыре значимых цифр
C) Одна значимая цифра
Раствор
A) $ 702,02 $
B) $ 702,0 $
C) $
РАБОТА.




 Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100. На примере легче:
На примере легче: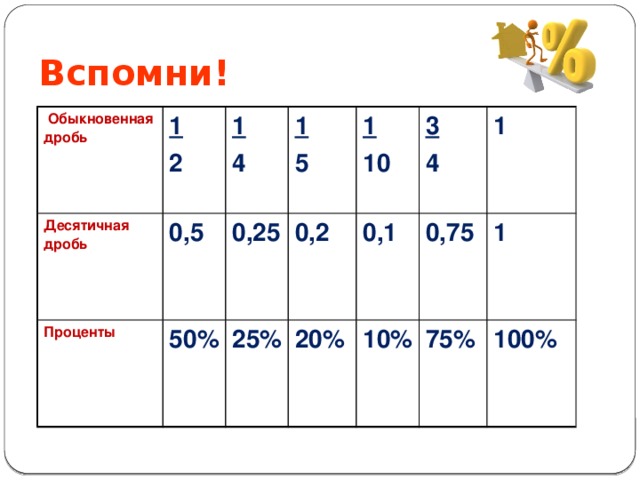



 VisualFractions.com , http://visualfractions.com/calculator/mixed-to-decimal/what-is-1-1-3-as-a-decimal/. По состоянию на 14 апреля 2023 г.
VisualFractions.com , http://visualfractions.com/calculator/mixed-to-decimal/what-is-1-1-3-as-a-decimal/. По состоянию на 14 апреля 2023 г.