Параметрически заданные функции
Связь между аргументом и функцией может быть записана через дополнительную переменную, называемую параметром, то есть в виде системы, в которой прописывается зависимость аргумента от параметра и зависимость функции от того же параметра:
, где– это параметр,.
В этом случае функция называетсяфункцией, заданной параметрически.
График функции
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).
ОСНОВНЫЕ ЭЛЕМЕНЫ ПОВЕДЕНИЯ ФУНКЦИИ
Функция y=f(x) называется четной, если она удовлетворяет следующим двум условиям:
1.
Область определения данной функции
должна быть симметрична относительно
точки О.
2. Значение функции в точке х, принадлежащей области определения функции должно равняться значению функции в точке -х. То есть для любой точки х, из области определения функции должно выполняться следующее равенство f(x) = f(-x).
Если построить график четной функции, он будет симметричен относительно оси Оу.
Например, тригонометрическая функция y=cos(x) является четной
Функция y=f(x) называется нечетной, если она удовлетворяет следующим двум условиям:
1. Область определения данной функции должна быть симметрична относительно точки О. То есть если некоторая точка a принадлежит области определения функции, то соответствующая точка -a тоже должна принадлежать области определения заданной функции.
2.
Для любой точки х, из области определения
функции должно выполняться следующее
равенство f(x) = -f(x).
График нечетной функции симметричен относительно точки О – начала координат.
Например, тригонометрические функции y=sin(x), y=tg(x), y=ctg(x) являются нечетными.
Функция у=f (х)называется периодической, если существует некоторое число Т !=0 (называемое периодом функции у=f (х) ), такое что при любом значении х, принадлежащем области определения функции, числа х+Т и х-Т также принадлежат области определения функции и выполняется равенство f(x)=f(x+T)=f(x-T).
Следует понимать, что если Т — период функции, то число k*T, где k любое целое число отличное от нуля, также будет являться периодом функции. Исходя из вышесказанного, получаем, что любая периодическая функции имеет бесконечно много периодов. Чаще всего разговор ведется о наименьшем периоде функции.
Тригонометрические функции sin(x) и cos(x) являются периодическими, с наименьшим периодом равным 2*π.
Тригонометрические
функции tg(x) и ctg(x) являются периодическими,
с наименьшим периодом равным π.
Ограниченность функций
Функция y=f(x), определенная на множестве X, называется ограниченной сверху, если множество её значений ограниченно сверху. Иначе говоря, функция fограничена сверху, если существует такая постоянная М, что для каждого выполняется неравенство.
Функция y=f(x), определенная на множестве Х, называется ограниченной снизу, если множество её значений ограниченно снизу, то есть если существует такая постоянная М, что для каждоговыполняется неравенство. Например, таковыми являются показательные функции, функцииy=x2n, y=x.
Функция f(x), определенная на множестве Х, называется ограниченной, если множество её значений ограниченно как сверху, так и снизу. Примерами функций, ограниченных на всей числовой прямой, являются функции y=sin x, y=cos x, y=arccos x, y=arcsin x, y=arctg x, y=arcctg x.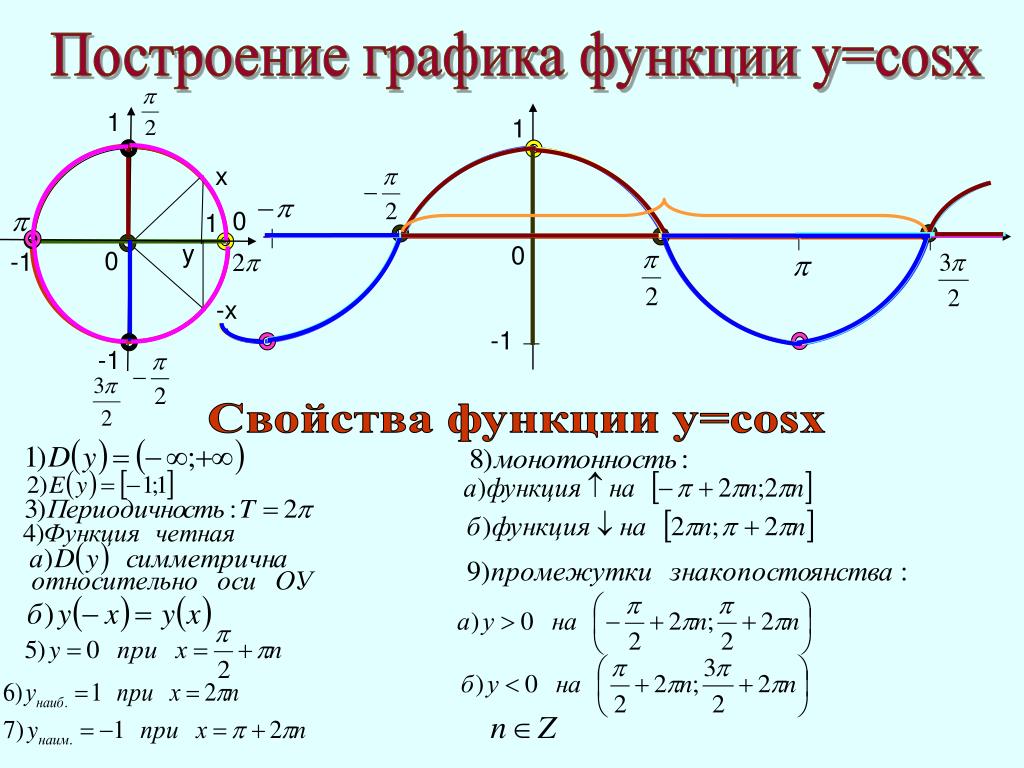
а) если для всех х из некоторого множества Х справедливы неравенства f(x)>M и g(x)<M, где М – некоторое число, то на множестве Х уравнение f(x)=g(x) и неравенство f(x)<g(x) решений не имеют;
б) если для всех х из некоторого множества Х справедливы неравенства f(x)
Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.
Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.
Действительно,
если x1 < x2 –
корни этого уравнения на промежутке D (f(x)),
то f (x1) = f (x2) = 0,
что противоречит условию монотонности.
Перечислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D).
Сумма нескольких возрастающих функций является возрастающей функцией.
Произведение неотрицательных возрастающих функций есть возрастающая функция.
Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.
Если функция f возрастает и сохраняет знак, то функция 1/f убывает.
Если функция f возрастает и неотрицательна, то где, также возрастает.
Если функция f возрастает и n – нечетное число, то f n также возрастает.
Композиция g (f (x)) возрастающих функций f и g также возрастает.

Основные элементарные функции
Функция | График | Свойства | |||||
| -четноеЧетная. Возрастает при. Убывает при. | -нечетноеНечетная. Возрастает при | |||||
|
| -четноеНи четная ни нечетная. Возрастает при | -нечетноеНечетная. | ||||
| , Ни четная ни нечетная. Возрастает при, еслиубывает, если. | ||||||
| , Ни четная ни нечетная. Возрастает, если. Убывает, если | ||||||
Четная. Возрастает. Убывает. Периодическая. | |||||||
Нечетная.
Возрастает .
Убывает. | |||||||
| .. Нечетная. Возрастает. Периодическая. | ||||||
| Нечетная. Убывает . Периодическая. | ||||||
| Нечетная. Возрастает . | ||||||
Ни четная ни нечетная. Убывает . . | |||||||
|
| Нечетная. | |||||
|
| Ни четная, ни нечетная. Убывает . | |||||
|
|
|
|
|
|
|
|
Определение. Функции,
составленные из основных элементарных
функций, называются элементарными,
если удовлетворяют двум условиям:
задаются одним аналитическим выражением
в области определения; представляют
результат конечного числа алгебраических
операций и операций взятия функции от
функции.
ГДЗ Четная или нечетная функция? Выясним! Упр 760 параграф 43 Алимов Алгебра 10-11 класс – Рамблер/класс
ГДЗ Четная или нечетная функция? Выясним! Упр 760 параграф 43 Алимов Алгебра 10-11 класс – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Прив) Друзья, делитесь ответами) Вот задание!
Выяснить, является ли данная функция чётной или нечётной:
1) у = х2 + cos х; 2) у = х3 — sin х;
3) у = (1 — х2) cos х; 4) у = (1 + sin х) sin х.
ответы
Привет! Вот делюсь:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
9 класс
11 класс
Химия
похожие вопросы 5
Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство
Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А. Н.Алгебра
Н.Алгебра
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?
Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
3



 Возрастает при
Возрастает при .
Периодическая.
.
Периодическая.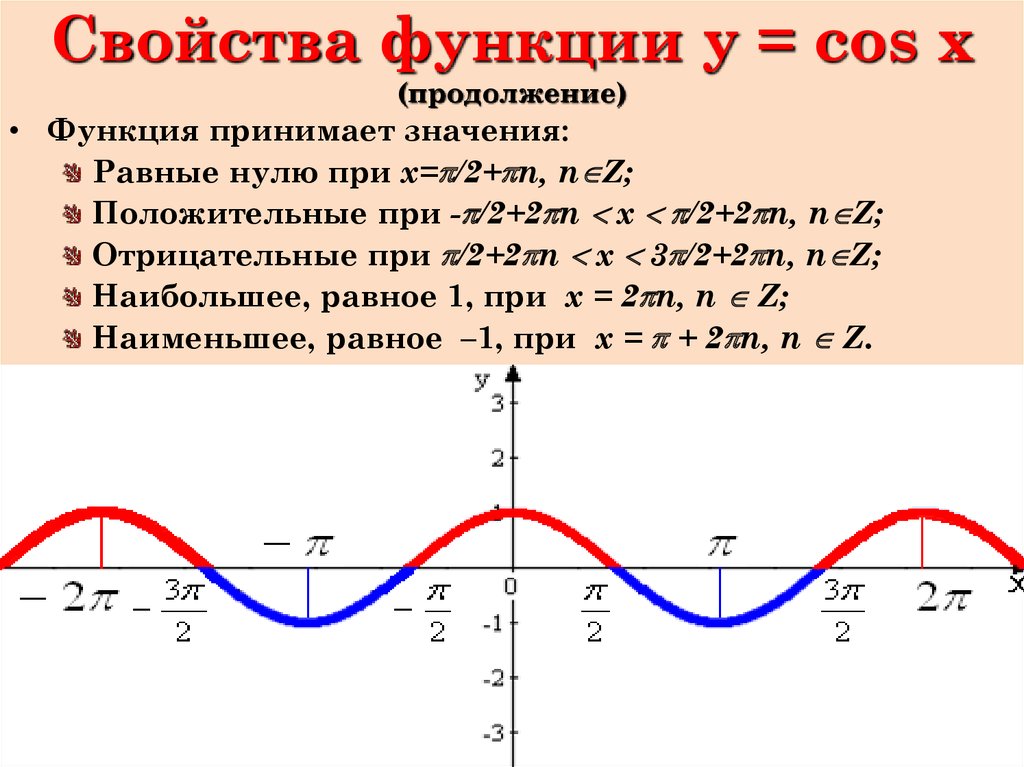 Возрастает
Возрастает