При вычитании степеней с одинаковыми основаниями: Свойства степеней с одинаковыми основаниями

Содержание

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

Ходить даже по полу с подогревом в ванной комнате после принятия водных процедур босыми ногами крайне не рекомендуется. Это чревато не только простудными заболеваниями.

Зачем стелить коврик в ванную комнату?

Причин не оставлять полы в ванной без покрытия несколько:

В качестве напольного покрытия здесь используется чаще всего устойчивая к влаге и долговечная керамическая плитка, отличающаяся довольно холодной поверхностью. Если не планируется монтировать «теплый пол», ходить по ней весьма некомфортно.
В ванной практически всегда влажно, а вероятность попадания воды на пол максимальна. Это делает плитку очень скользкой, повышает шанс скольжения и получения травмы от падения.
В интерьере ванных комнат порой не хватает некоторого уюта. Небольшой мягкий коврик для ванной способен буквально преобразить обстановку. Интерьер становится более комфортным.

Коврик в ванной выполняет не только функциональную, но и декоративную роль. Он снижает травмоопасность керамической плитки, защищает от холода, идущего от пола.

Какой коврик купить в ванную комнату?

Расцветка, размеры и фактура выбираются с учетом интерьера и личного вкуса. Особое внимание необходимо уделять следующим параметрам:

Чтобы коврик не скользил по кафелю, выбирают изделие с прорезиненной подложкой либо силиконовыми присосками.
Из-за слишком высокой влажности, предпочтение отдается материалам, которые хорошо впитывают влагу, легко отстирываются и быстро сохнут.
Предпочтение следует отдавать короткому и среднему ворсу. За слишком длинным потребуется сложный уход.
Края должны быть хорошо отработаны. Это позволяет гарантировать сохранность формы изделия.

Еще одним важным требованием является гигиеничность. Коврик должен быть безопасным, то есть не содержать вредных веществ, а также не вызывать аллергию.

Какому материалу отдать предпочтение?

Особое значение при выборе коврика в ванную имеет состав изделия.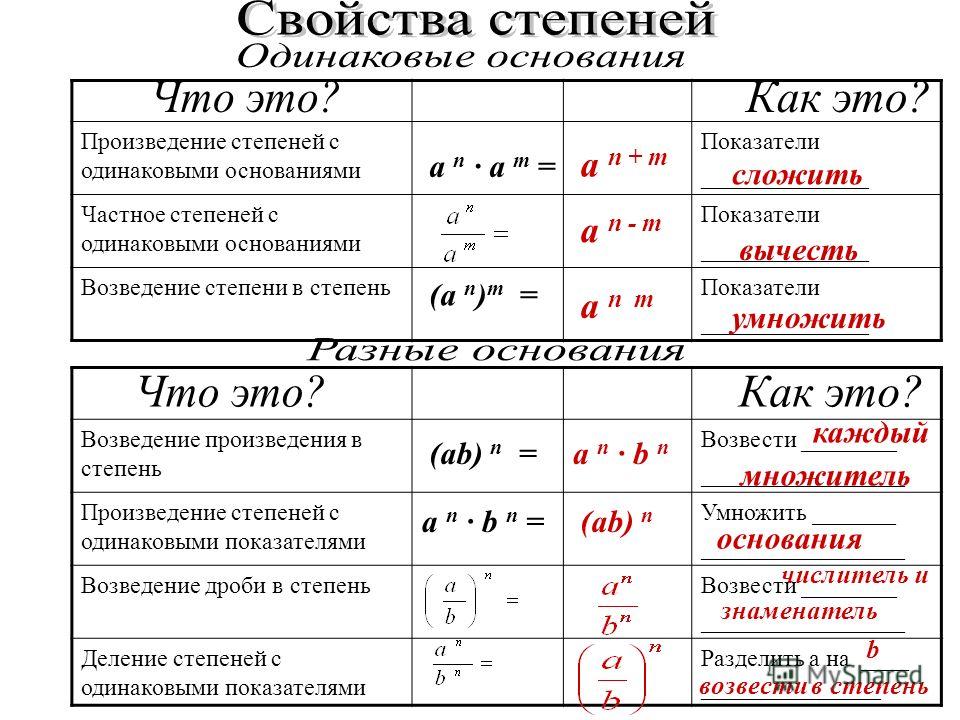 Он, как говорилось выше, должен хорошо чувствовать себя в условиях повышенной влажности. Наибольшей популярностью пользуются:

ПВХ. Отличается доступной стоимостью. Отлично моется, не скользит. Выпускается в рулонах, поэтому может отрезаться любой длины.
Силикон. Гигиеничный и гипоаллергенный. Силиконовые коврики представлены многообразием форм и оттенков, снабжены присосками. Они быстро сохнут и не доставляют неудобств в уходе.
Микрофибра. Внешне напоминает натуральный материал. Устойчива к образованию грибка, плесени. Не только хорошо отстирывается, но и оставляет после себя невероятно приятные тактильные ощущения.
Акрил. Из него выпускаются самые красивые коврики для ванной комнаты. Материал устойчив к образованию грибка и плесени. Изделия из акрила имеют прорезиненную либо силиконовую основу.

Предпочтение отдается именно синтетическим материалам, поскольку натуральные ткани не способны перенести условия повышенной влажности. Все перечисленные варианты обладают высокой гигиеничностью и безопасны для человека.

Показательные уравнения: вынесение | Логарифмы

Показательные уравнения: вынесение вынесение общего множителя за скобки — следующий шаг в рассмотрении видов показательных уравнений и способов их решения.

Признаки показательного уравнения, решаемого вынесением общего множителя за скобки:

1) все степени имеют одинаковые основания;

2) все показатели степеней имеют одинаковые коэффициенты при переменных.

Количество степеней может быть любым.

Выносить за скобки можно степень с любым показателем, но удобнее всего в качестве общего множителя вынести степень с наименьшим показателем если основание a>1, с наибольшим — при a<1.

Вынести за скобки общий множитель — значит, каждое слагаемое разделить на этот множитель. При делении степеней с одинаковыми основаниями показатели степеней вычитаем. При вычитании наименьшего показателя получим все степени с положительными показателями (в противном случае появятся степени с отрицательными показателями и придётся иметь дело с дробями, что менее удобно).

В общем виде решение показательных уравнений вынесением общего множителя за скобки схематически можно записать так:

Если

— наименьший из показателей, то в качестве общего множителя выносим за скобки степень с этим показателем:

Все слагаемые с иксами в показателях степеней — противоположные числа — взаимно уничтожаются:

Таким образом, с скобках получаем некоторое число

Разделив обе части уравнения на это число c, получим простейшее показательное уравнение:

Примеры.

5>1, выносим за скобки степень с меньшим показателем (он равен x):

Ответ: 1.

5>1, выносим за скобки общий множитель — степень с наименьшим показателем (1-2x):

Приравниваем показатели:

Ответ: 1.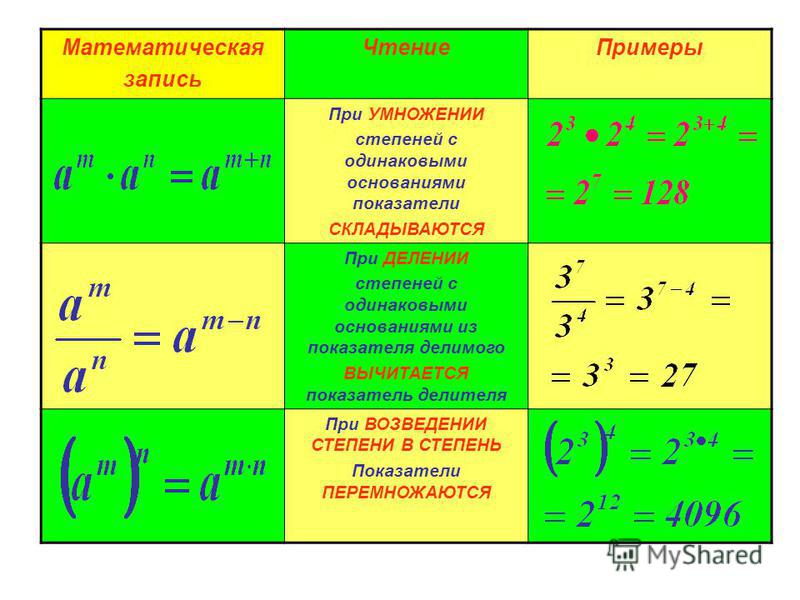

Приводим все степени к основанию 2:

Степень с наименьшим показателем (12x-4) выносим за скобки:

Приводим к степеням с одинаковыми основаниями

и приравниваем показатели

Ответ: 11/12.

Выносим за скобки степень с меньшим показателем (2x²-x-1):

Приравниваем показатели:

Находим корни квадратного уравнения:

Ответ: 1,5; -1.

Рубрика: Показательные уравнения | Комментарии

Изучите основы вычитания показателей степени

Образование

Пол — 14 сентября 2021 г.

801

Экспоненты — это степени или индексы.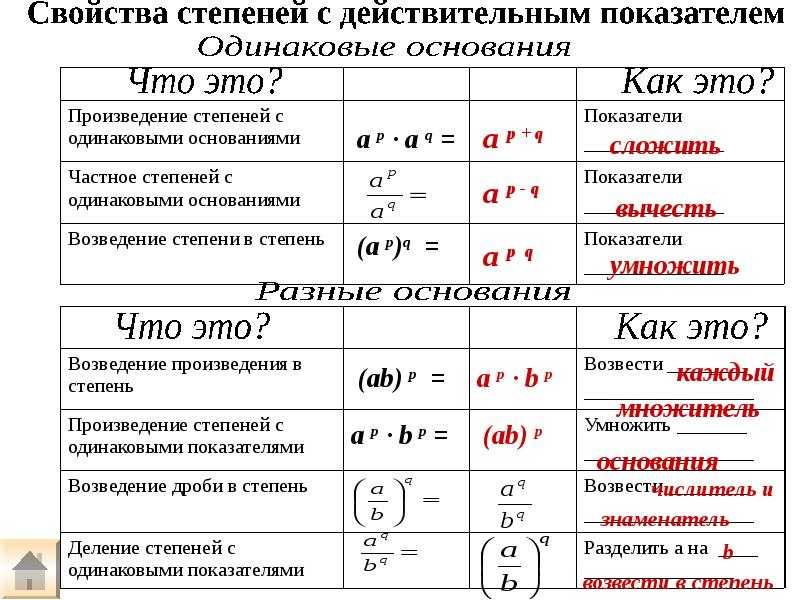 Экспоненциальное выражение состоит из двух компонентов, в частности основания, обозначаемого как b, и показателя степени, обозначаемого как n. Основная форма экспоненциального выражения — b n. Давайте узнаем больше о вычитании показателей степени.

Содержание

Операция вычитания показателей степени выполняется относительно легко, если вы хорошо понимаете показатели степени. В этой короткой статье вы узнаете правила и как их использовать, когда вам нужно вычитать с показателями.

Но прежде чем мы начнем вычитать с показателями, давайте напомним себе несколько стандартных терминов, касающихся показателей.

Что такое экспонента?

Ну, показатель степени или степень обозначает количество раз, когда число многократно увеличивается само по себе. Например, когда мы сталкиваемся с числом, записанным как 53, это просто предполагает, что пять увеличивается само по себе три раза. Проще говоря, 53 = 5 x 5 x 5 = 125

Тот же формат построения показателей степени используется с переменными. Переменные представлены буквами, а также символами. Например, когда x увеличивается, повторяется само по себе три раза, мы записываем это как; х3. Коэффициенты обычно сопровождают переменные. В результате коэффициент представляет собой целое число, которое умножается на переменную.

Например, в 2×3 коэффициентом является число 2, а x — переменная. Когда перед переменной нет числа, коэффициент постоянно равен 1. Это также верно, когда число не имеет степени. Коэффициентом 1 обычно можно пренебречь, и результат не может быть создан с помощью переменной.

Вычитание показателей степени не влечет за собой никакой политики. Предположим, что число возведено в степень. Вы просто вычисляете результат, а затем выполняете обычное вычитание. Если и показатели степени, и основания совпадают, их можно вычесть, как любые другие члены алгебры. Например, 3y– 2xy = x y.

Вычитание показателей степени с различным основанием

Показатели степени с различным основанием вычисляются отдельно, и результаты вычитаются.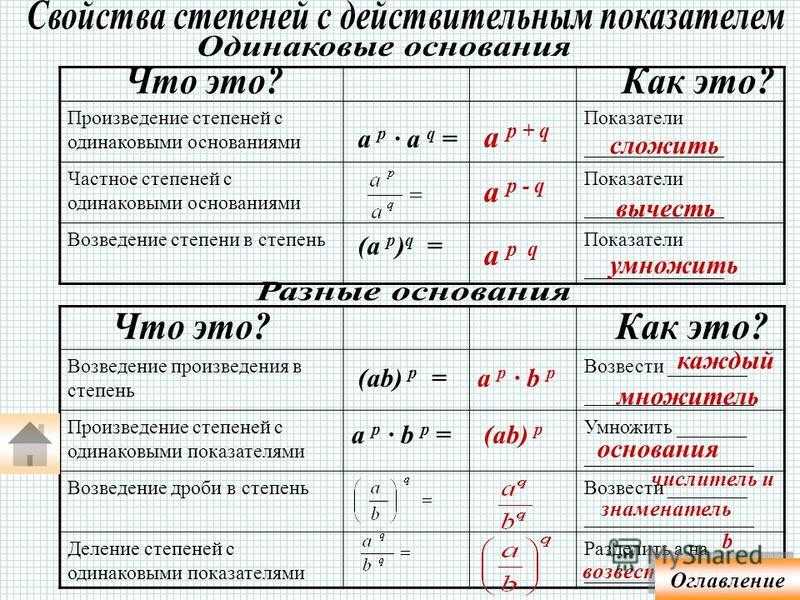 С другой стороны, переменные с разными основаниями никак не вычитаются. Например, преобразование экземпляра an и b не может быть выполнено, и результатом будет просто a -b.

Чтобы вычесть благоприятные показатели m и неблагоприятные показатели n, соединим оба слагаемых, изменив знак вычитания на многообещающее указание, и составим отведение к типу m + n.

Следовательно, сокращение как положительного, так и отрицательного различных показателей m, а также -n = m + n.

Пример

42 32 = 16 9 =7.

Вычет: 11x 7y -2x3x.

= 11x 2x 3x 7 лет.

= 6x 7 лет.

Обзор 3×2 7у2.

В этой ситуации два показателя степени 3x два и 7y2 отличаются друг от друга, поэтому все останется как есть.

Прямо здесь, 3x и 7y — разные термины, поэтому они останутся такими, какие они есть.

В результате решение 3×2 7y2.

Обзор 15x 12y 11x.

= 15×5 11×5 12y5.

= 4×5 12y5.

Теги: #сложение и вычитание показателей степени в дробях # добавление и вычитание показателей степени #добавление правил степени #добавление показателей степени с разными основаниями и степенями #экспонентные правила #Вычитание показателей степени #калькулятор вычитания степеней #вычитание показателей степени примеры #вычитание показателей степени в дробях #вычитание показателей степени в экспоненциальном представлении #правила вычитания степеней #вычитание показателей с разным основанием #вычитание показателей с одинаковым основанием и разной степенью #вычитание показателей с одинаковым основанием #вычитание дробных степеней с одинаковым основанием

Умножение с экспонентами Рон Куртус

SfC Home > Арифметика > Алгебра >

Рон Куртус (обновлено 18 января 2022 г. )

Когда вы умножаете экспоненциальные выражения , необходимо соблюдать несколько простых правил. Если они имеют одинаковую базу, вы просто добавляете показатели степени.

Примечание : основание экспоненциального выражения x ^y равно x
, а показатель степени равен y .

Это также верно для чисел и переменных с разными основаниями, но с одинаковым показателем степени. Вы можете применить правила, когда включены другие числа.

Это правило не применяется, когда числа или переменные имеют разные основания и разные степени.

У вас могут возникнуть следующие вопросы:

Как умножать степени с одинаковым основанием?
Как насчет разных оснований, но с одним и тем же показателем?
А с другими номерами?
Когда правило не применяется?

Этот урок ответит на эти вопросы.

Умножение показателей степени с одинаковым основанием

Когда вы умножаете две переменные или числа, имеющие одно и то же основание , вы просто добавляете показателей степени.

(х ^а )*(х ^б ) = х
а+б

Таким образом, x ³ *x ⁴ = x ³⁺⁴ = x ⁷ .

Доказательство: Так как x ³ = x*x*x и x ⁴ = x*x*x*x , тогда
(х*х*х)*(х*х*х*х) = х*х*х *х*х*х*х = х ⁷

Демонстрация с числами

Демонстрация этого правила видна при умножении 7 ³ раз 7 ² . Результат:

(7*7*7)*(7*7) =
7*7*7*7*7 = 7 ⁵

Вместо того, чтобы записывать числа, вы можете просто добавить показатели степени:

7 ³ *7 ² = 7 ³⁺² = 7 ⁵

Аналогично, 2 ³ *2 ⁵*2 ² = 2 ³⁺⁵⁺² = 2 ¹⁰ .

Вы видите, что когда вы умножаете числа с одинаковым основанием, возведенные в степень, вы добавляете их показателей степени.

Разные основания, но один и тот же показатель степени

Когда вы умножаете две переменные или числа или с разными основаниями , но с одним и тем же показателем степени , вы можете просто умножать основания и использовать один и тот же показатель степени. Например:

(х ^а )*(y ^a ) = (xy) ^a

Также:

(x ³ )*(y ³ ) = xxx*yyy = (xy) ³

Аналогично, с номерами:

3 ² *4 ²⁼ (3*4) ² = 12 ² = 144

Включая другие числа

Если у вас есть экспоненциальные числа, которые умножаются на другие числа, вы можете легко выполнить арифметику. Например, упростите:

(12*7 ⁵)*(2*7 ³)

Переставить числа:

(12*2)*(7 ⁵ *7 ³ )

Затем добавьте показатели степени:

24*7 ⁸

Другие числа или переменные также могут быть экспоненциальными. Некоторые примеры включают:

(3 ³ *5 ²)*(5 ³ *3 ³ ) = (3 ³⁺³ )*(5 ²⁺³ ) = 3 ⁶ *5 ⁵
(7*x ³ )*(y ² *x ⁵ ) = 7 лет ² x ⁸
(а ³ *б ³ )*(б ⁶ *а ⁵ ) = а ⁸ б ⁹

Когда правило не применяется

При умножении выражений с разными основаниями и разными показателями , нет правила для упрощения процесса.

Например, предположим, что вы хотите умножить 2 ³ *5 ² .

Вы видите, что 2 ³ = 8 и 5 ² = 25 . Таким образом, 8*25 = 200 . Но если вы попробуете (2*5) ³⁺² , вы получите 10 ⁵ , что неверно.

Резюме

Когда вы умножаете два числа или переменные с одинаковым основанием, вы просто складываете показатели степени. Когда вы умножаете выражения с одним и тем же показателем степени, но с разными основаниями, вы умножаете основания и используете один и тот же показатель степени.

Когда вы включаете в умножение другие числа или переменные, вы просто разбиваете его на несколько умножений, например (x*10 ⁵ )*(x*10 ³ ) = x ² * 10 ⁸ .

Когда вы умножаете выражения с разными основаниями и разными показателями, нет правила, упрощающего процесс.

Всегда делай все возможное

Ресурсы и ссылки

Полномочия Рона Куртуса

Веб -сайты

Экспоненты: Основные правила — purplemath.