Все что нужно знать об окружности
Эта статья содержит минимальный набор сведений об окружности, необходимый для успешной сдачи ЕГЭ по математике.
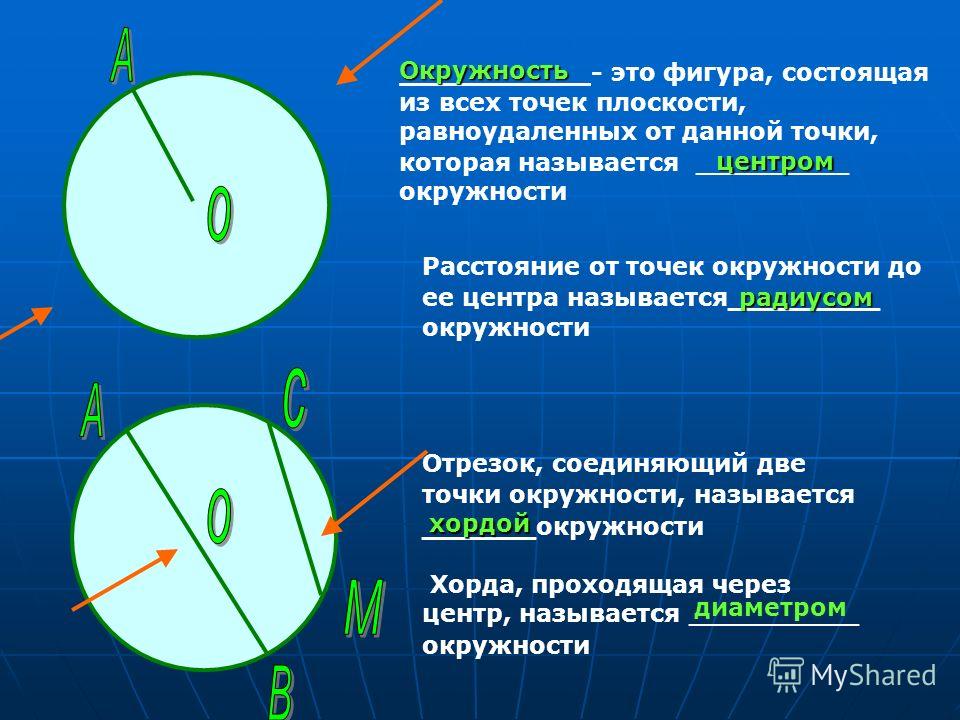
Окружностью называется множество точек, расположенных на одинаковом расстоянии от данной точки, которая называется центром окружности.
Для любой точки , лежащей на окружности выполняется равенство ( Длина отрезка равна радиусу окружности.
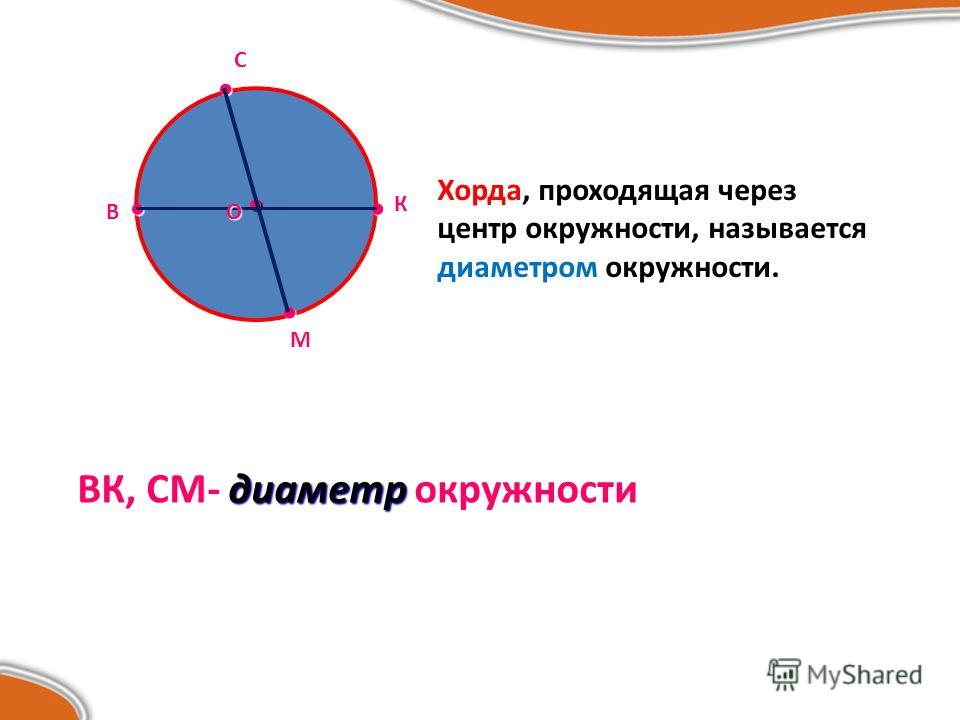
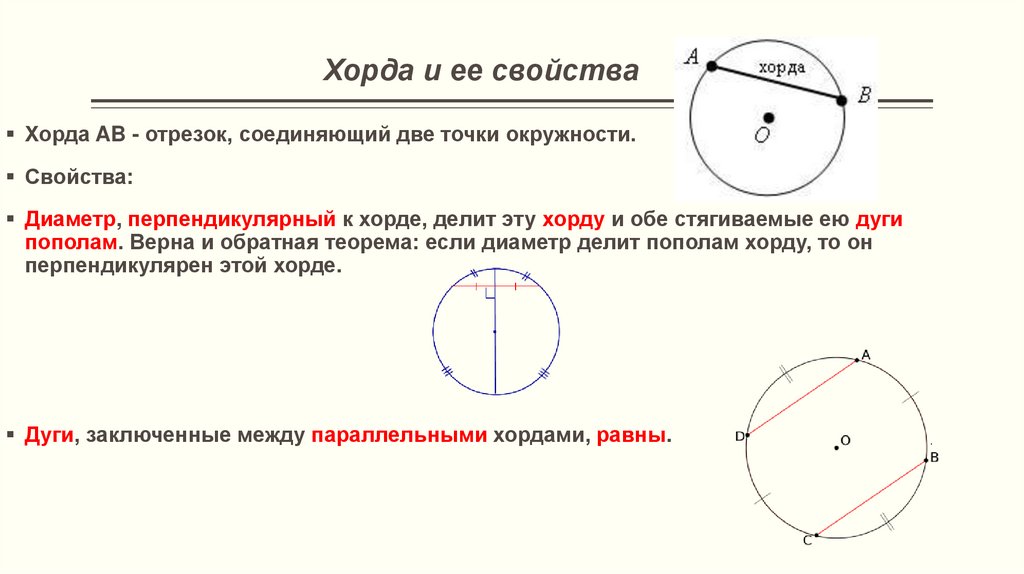
Отрезок, соединяющий две точки окружности называется хордой.
Хорда, проходящая через центр окружности называется диаметром окружности ().
Длина окружности:Площадь круга:Дуга окружности:
Часть окружности, заключенная между двумя ее точками называется дугой окружности. Две точки окружности определяют две дуги. Хорда стягивает две дуги: и . Равные хорды стягивают равные дуги.
Хорда стягивает две дуги: и . Равные хорды стягивают равные дуги.
Угол между двумя радиусами называется центральным углом:
Чтобы найти длину дуги , составляем пропорцию:
а) угол дан в градусах:
Отсюда
б) угол дан в радианах:
Отсюда
Диаметр, перпендикулярный хорде, делит эту хорду и дуги, которые она стягивает пополам:
Если хорды и окружности пересекаются в точке , то произведения отрезков хорд, на которые они делятся точкой равны между собой:
Касательная к окружности.Прямая, имеющая с окружностью одну общую точку называется касательной к окружности. Прямая, имеющая с окружностью две общие точки называется секущей.
Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.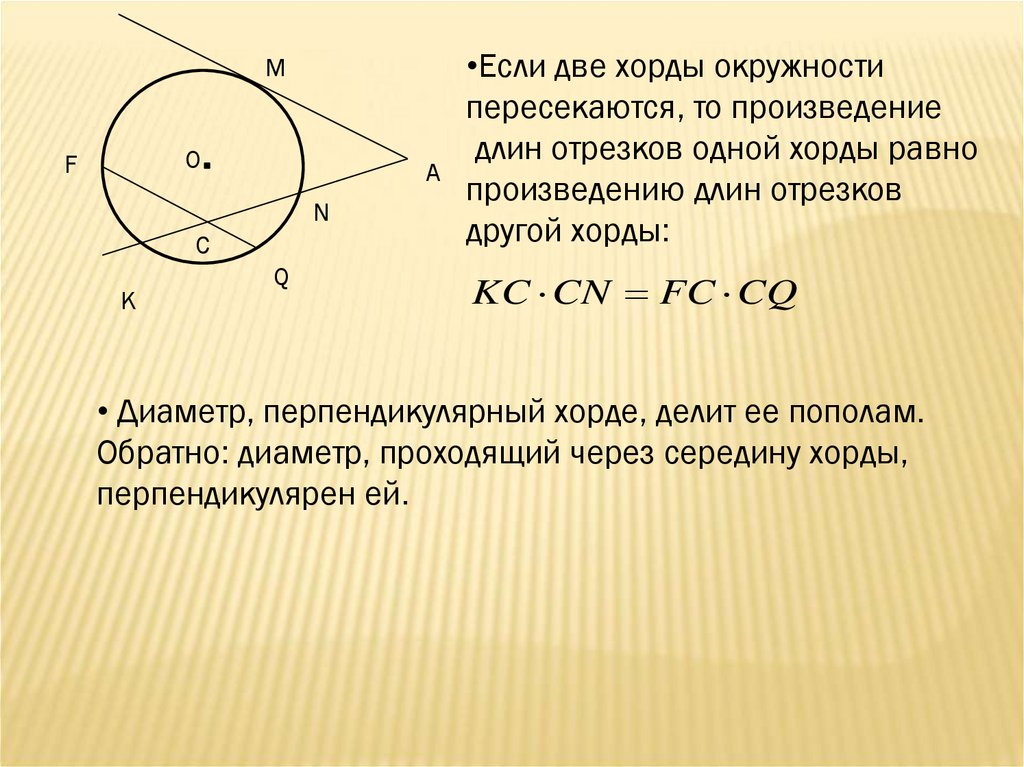
Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке:
Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть:
Следствие: произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть:
Углы в окружности.Градусная мера центрального угла равна градусной мере дуги, на которую он опирается:
∠ ⌣
Угол, вершина которого лежит на окружности, а стороны содержат хорды, называется вписанным углом. Вписанный угол измеряется половиной дуги, на которую он опирается:
∠∠
Вписанный угол, опирающийся на диаметр, прямой:
∠∠∠
Вписанные углы, опирающиеся на одну дугу, равны:
∠∠∠
Вписанные углы, опирающиеся на одну хорду равны или их сумма равна
∠∠
∠∠∠
Вершины треугольников с заданным основанием и равными углами при вершине лежат на одной окружности:
Угол между двумя хордами (угол с вершиной внутри окружности) равен полусумме угловых величин дуг окружности, заключенных внутри данного угла и внутри вертикального угла.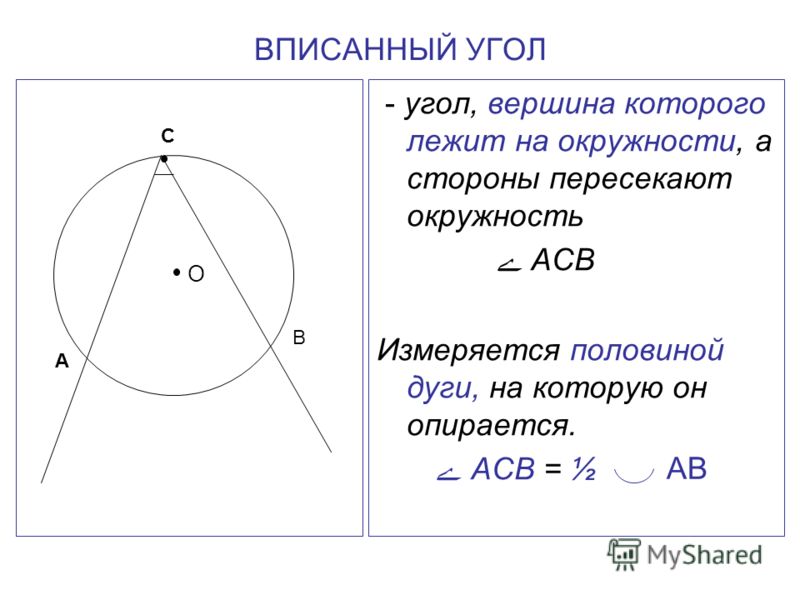
∠ ∠∠( ⌣ ⌣ )
Угол между двумя секущими (угол с вершиной вне окружности) равен полуразности угловых величин дуг окружности, заключенных внутри угла.
∠ ∠∠( ⌣ ⌣ )
Вписанная окружность.
Окружность называется вписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.
Не во всякий многоугольник можно вписать окружность.
Площадь многоугольника, в который вписана окружность можно найти по формуле
,
здесь — полупериметр многоугольника, — радиус вписанной окружности.
Отсюда радиус вписанной окружности равен
Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:
В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.
Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.
Радиус вписанной окружности равен . Здесь
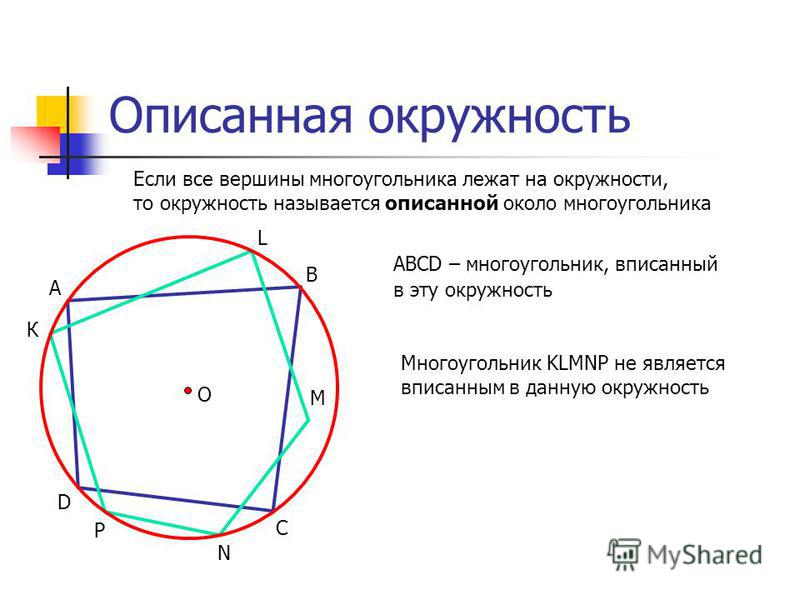
Описанная окружность.Окружность называется описанной около многоугольника, если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:
Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна .
∠+∠=∠+∠
Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника:
Радиус описанной окружности вычисляется по формулам:
Где — длины сторон треугольника, — его площадь.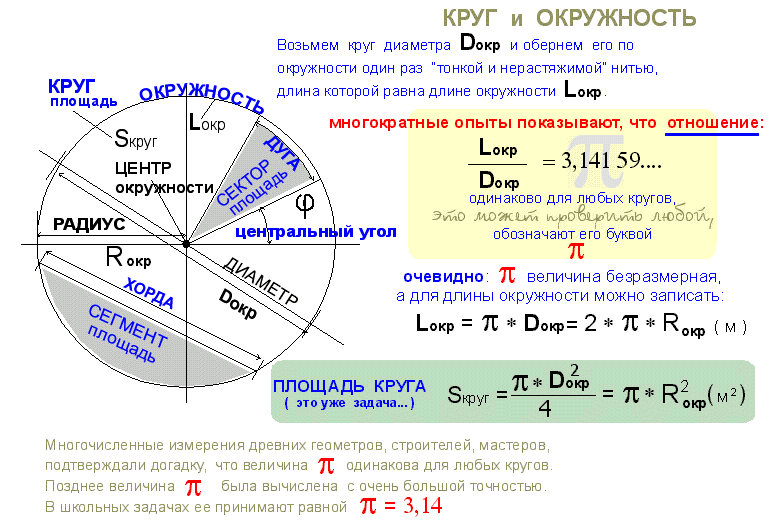
Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон:
Окружности и её элементы | ЕГЭ по математике (профильной)
Окружность и ее элементы
Окружность — это фигура, которая состоит из множества точек плоскости, равноудаленных от данной точки (центра).
Отрезок, соединяющий любую точку на окружности с центром окружности, называется радиусом $(R)$.
$ОС=OD=OE=R$.
Отрезок, соединяющий любые две точки на окружности, называется хордой, а хорда, проходящая через центр, — диаметром $(d)$.
$АВ$ и $ВС$ – хорды.
$СЕ$ — диаметр.
Свойства хорды и диаметра:
1. Диаметр равен двум радиусам $d=2R$; $СЕ=2СО$
2. Равные хорды стягивают равные дуги
Если $AB=CD$, то $∪AB=∪CD$.
3. Вся окружность составляет $360°$. Диаметр делит окружность на две полуокружности по $180°$. 2∙36°}/{360°}={π∙256∙36°}/{360°}$
2∙36°}/{360°}={π∙256∙36°}/{360°}$
Сокращаем полученную дробь на $36$
$S={π∙256}/{10}$
Данную дробь легко перевести в десятичную дробь, необходимо просто с конца числа $256$ отделить один знак.
$S=25,6π$
В результате надо указать ${S}/{π}$, следовательно, ${S}/{π}={25,6π}/{π}=25,6$
Ответ: $25,6$
Касательные и секущие:
Прямая, имеющая с окружностью только одну общую точку, называется касательной. $АВ$ — касательная
Прямая, имеющая с окружностью две общие точки, называется секущей. $CD$ — секущая
Свойства:
1. Касательная перпендикулярна радиусу, проведенному в точку касания. $ОА⊥АС$; $OB⊥BC$
2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
$АС=ВС$; $ОС$ — биссектриса
3. Если из точки к окружности проведены секущая и касательная , то произведение секущей на ее внешнюю часть равно квадрату касательной
$AB∙DB=BC^2$
4. Если из одной точки к окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на ее внешнюю часть.
Если из одной точки к окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на ее внешнюю часть.
$BD∙AB=BE∙CB$
Вписанные и описанные окружности.
В любой треугольник можно вписать окружность. Центром вписанной окружности (точка $О$) является точка пересечения биссектрис внутренних углов треугольника.
$OD$ – это радиус $(r)$ вписанной окружности
$r={2S_{ABC}}/{a+b+c}$
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности
$S={P∙r}/{2}$
В равнобедренном треугольнике вписанная окружность точкой касания делит основание пополам
Пример:
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны $10$ и $4$, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Решение:
Изобразим треугольник $АВС$. Окружность касается боковой стороны $CD$ в точке $М$.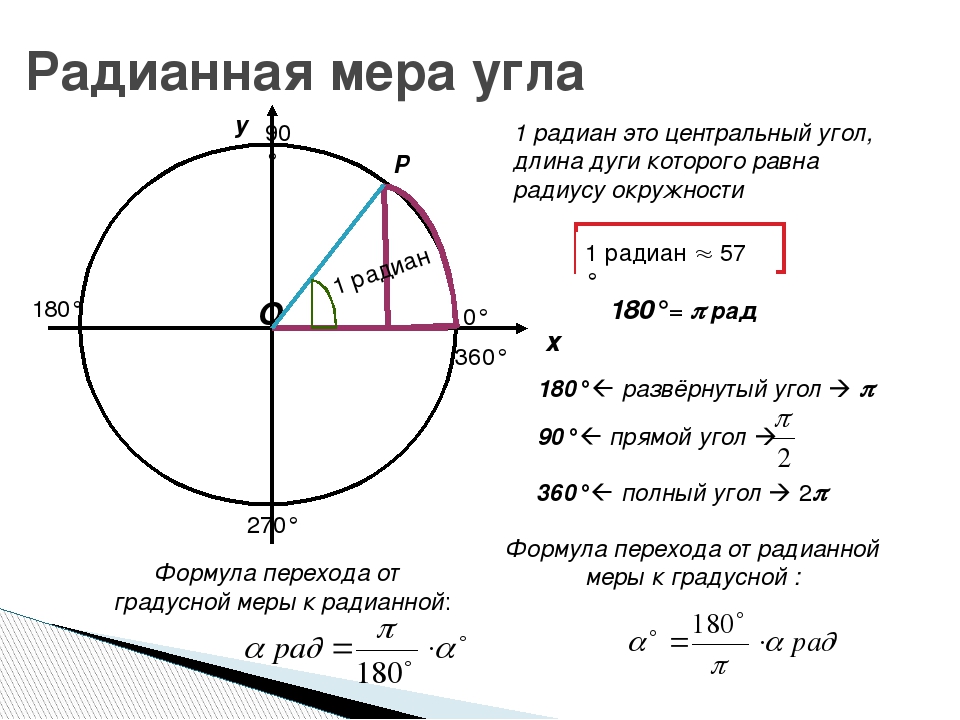
$СМ=10, МВ=4$, тогда вся сторона $СВ=14$.
Так треугольник $АВС$ равнобедренный, то $СВ=АС=14$
Стороны треугольника для окружности являются касательными. Отрезки касательных к окружности, проведенные из одной точки, равны. $МВ=ВН=4$
В равнобедренном треугольнике вписанная окружность точкой касания делит основание пополам, следовательно, $АН=НВ=4$. Вся сторона $АВ=8$.
Все стороны треугольника найдены, теперь можем найти периметр:
$Р=14+14+8=36$
Ответ: $36$
В равностороннем треугольнике радиус вписанной окружности равен трети высоты данного треугольника.
$r={h}/{3}$
В прямоугольном треугольнике радиус вписанной окружности равен:
$r={a+b-c}/{2}$, где $а$ и $b$ – это катеты, $с$ – гипотенуза
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
Площадь любого многоугольника можно найти как произведение полупериметра на радиус вписанной окружности.
$S={P∙r}/{2}$
Около любого треугольника можно описать окружность, причем только одну. Центром описанной окружности является точка $(О)$ пересечения серединных перпендикуляров к сторонам треугольника.
$ОА$ — радиус описанной окружности $(R)$
В равностороннем треугольнике радиус описанной окружности равен две трети высоты данного треугольника.
$R={2h}/{3}$
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы и радиус равен половине гипотенузы.
Радиус описанной окружности можно найти как:
$R={a}/{2sinA}={b}/{2sinB}={c}/{2sinC}$;
$R={a∙b∙c}/{4S}$, где $S$ — это площадь заданного треугольника
Около четырехугольника не всегда можно описать окружность. Если сумма
противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
В прямоугольнике и квадрате центр описанной окружности лежит в точке пересечения диагоналей, а радиус описанной окружности равен половине диагонали.
$R={d}/{2}$
Выпуклый многоугольник называется правильным, если у него все стороны и все углы
равны.
Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей:
$АВ=an$ — сторона правильного многоугольника
$R$ — радиус описанной окружности
$r$ — радиус вписанной окружности
$n$ — количество сторон и углов
$a_n=2Rsin{180°}/{n};$
$r=Rcos{180°}/{n};$
$a_n=2rtg{180°}/{n}.$
Углы в окружности:
1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается.
$∠О=∪BmA$
2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается.
$∠B={∪AmC}/{2}$
3. Угол между хордой и касательной равен половине дуги, заключенной внутри него.
$∠B={∪BmC}/{2}$
Практика: решай 3 задание и тренировочные варианты ЕГЭ по математике (профильной)
Окружность.
 — Математика — Подготовка к ОГЭ (ГИА)
— Математика — Подготовка к ОГЭ (ГИА)На этом занятии мы рассмотрим окружность, вписанные и центральные углы, свойства секущих и касательных, вспомним формулы для вычисления длины окружности и площади круга, площадь сектора. Вписанная окружность треугольника. Описанная окружность треугольника. Вписанные и описанные четырехугольники.
Конспект занятия «Окружность.»Теоретический материал по теме «Окружность»
Элементы окружности
Окружность — множество всех точек плоскости, удаленных на заданное расстояние (равное радиусу) от заданной точки этой же плоскости (центра окружности).
Радиусы — отрезки, соединяющие точки окружности с центром. Все радиусы данной окружности равны.
Хорда — отрезок, соединяющий любые две точки окружности.
Диаметр — хорда, проходящая через центр окружности. Диаметр, делящий хорду пополам, перпендикулярен этой хорде
Центральный угол — угол, образованный двумя радиусами.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Касательная — прямая, проходящая через точку окружности, перпендикулярно ее радиусу. Касательная имеет с окружностью только одну общую точку.
Длина окружности: C = 2R, R — радиус окружности, D — диаметр.
Длина дуги окружности: C= Ra =Rα/180˚ , a — радианная мера дуги, α — градусная мера.
Круг — часть плоскости, ограниченная окружностью.
Площадь круга: S = R² = D²/4 .
Сектор — часть круга, ограниченная двумя радиусами и дугой окружности.
Площадь сектора:S=R²α/360˚ .
Сегмент – часть круга, ограниченная хордой и дугой.
Свойства вписанных углов Вписанный угол измеряется половиной дуги, на которую он опирается: .
Вписанные углы, опирающиеся на одну и ту же дугу, равны: .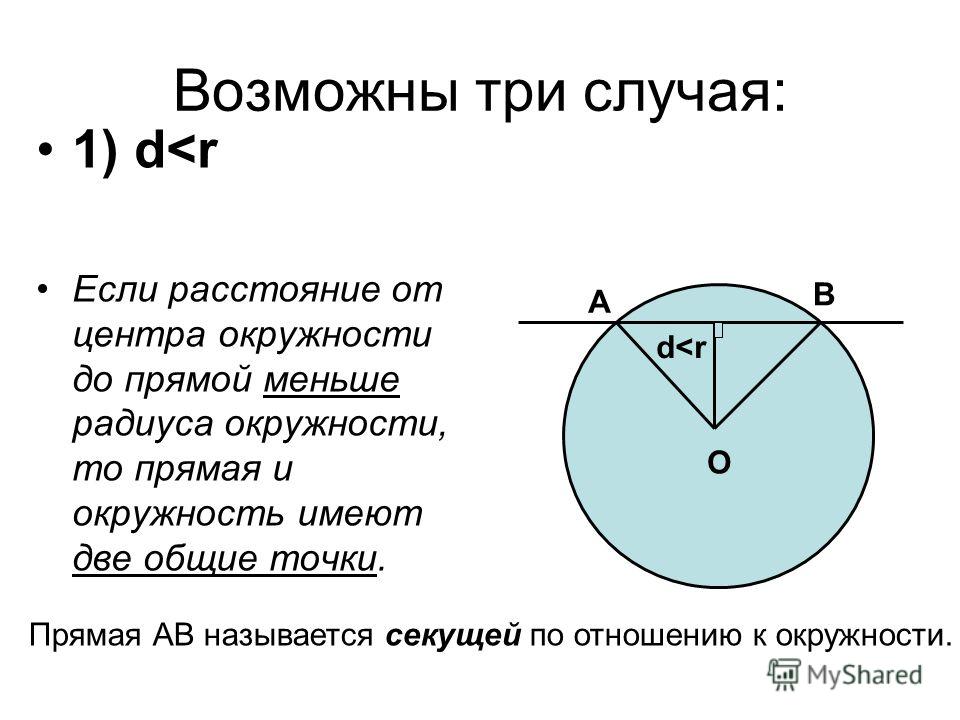
Вписанный угол, опирающийся на диаметр — прямой.
Углы, связанные с окружностью
Теорема (угол между касательной и хордой, проведенной через точку касания). Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой: .
Отрезки, связанные с окружностью
Теорема. Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Теорема. Произведение отрезков, на которые делится хорда данной точкой, есть для данной окружности величина постоянная и равная разности квадратов радиуса окружности и расстояния от точки M до центра окружности: .

Окружность, вписанная в многоугольник
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.
Теоремы:
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Из параллелограммов окружность можно вписать в ромб, квадрат.
-
Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон, а средняя линия — полусумме боковых сторон: , .
Окружность, описанная около четырехугольника
Если вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник — вписанным в эту окружность.
Теоремы:
Центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам.
В любом четырехугольнике, вписанном в окружность, сумма противоположных углов равна 180˚.
Из всех параллелограммов окружность можно описать около прямоугольника, квадрата.
Задание 1
(2 балла)
Длина хорды окружности равна 48, а расстояние от центра окружности до этой хорды равно 70. Найдите диаметр окружности.
Задание 2
(2 балла)
AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.
Задание 3
(2 балла)
Точка O — центр окружности, на которой лежат точки A, B и C.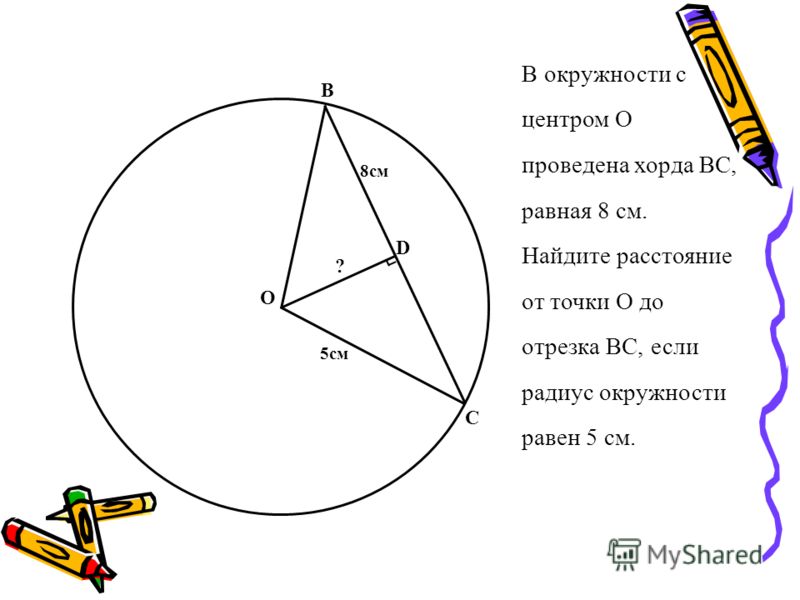 Известно, что ∠ABC=112° и ∠OAB=59°. Найдите угол BCO. Ответ дайте в градусах.
Известно, что ∠ABC=112° и ∠OAB=59°. Найдите угол BCO. Ответ дайте в градусах.
Проверить правильность выполнения заданий вы можете в автоматическом режиме в разделе домашние задания на странице с курсом «Математика Подготовка к ОГЭ 2016»
Следующий урок на тему » Решение геометрических задач»
Предыдущий урок на тему » Четырехугольник.»
Теория колец помогает нам обрести комфорт… и «выбросить» личные вещи – Центр горячей линии
Теория колец помогает нам обрести комфорт… и «выбросить» личные вещи , L.C.S.W., M.P.H.
Перепечатано с разрешения из Psychology Today, May, 2017
Несколько лет назад психолог Сьюзан Силк и ее друг Барри Голдман написали о концепции, которую они назвали «теорией колец». Это теория, которая поможет вам понять, что делать в кризис. Если с тобой происходит кризис, ты в центре ринга. Если кризис не происходит с вами, вы находитесь в одном из внешних кругов.
Вот основные принципы, перефразированные из Шелка и Гудмана:
1) Нарисуйте круг. В этом кружке напишите имя человека, оказавшегося в центре кризиса.
2) Теперь нарисуйте круг большего размера вокруг первого. В этом кольце поставьте имя человека, ближайшего к кризису.
3) В каждое большее кольцо поставьте следующих ближайших людей. Как заявляют Силк и Гудман: «Родители и дети важнее более дальних родственников. Близкие друзья в меньших кольцах, менее близкие друзья в больших. . . Когда вы закончите, у вас будет Kvetching* Order».
Вот правила:
Человек в центре кольца может говорить что угодно кому угодно и где угодно. Она может ворчать, жаловаться, ныть, стонать, проклинать небеса и говорить: «Жизнь несправедлива» и «Почему я?» Это единственная награда за то, что ты находишься в центре ринга. Все остальные тоже могут говорить то же самое, но только людям в больших кругах. Когда вы разговариваете с человеком в кольце меньшем, чем ваше, с кем-то, кто находится ближе к центру кризиса, цель состоит в том, чтобы помочь.
Слушать часто бывает полезнее, чем говорить. Но если вы собираетесь открыть рот, сначала спросите себя, может ли то, что вы собираетесь сказать, обеспечить утешение и поддержку. Если это не так, не говорите об этом. Не давайте, например, советов. Людям, пережившим травму, советы не нужны. Они нуждаются в утешении и поддержке. Поэтому скажите: «Извините», или: «Вам должно быть очень тяжело», или: «Могу ли я принести вам жаркое в горшочках?» Не говорите: «Вы должны услышать, что со мной случилось» или «Вот что бы я сделал на вашем месте». И не говорите: «Это действительно меня расстраивает». Если вы хотите кричать, плакать или жаловаться, если вы хотите рассказать кому-то, как вы потрясены или как вам противно себя чувствовать, или ныть о том, что это напоминает вам обо всех ужасных вещах, которые произошли с вами в последнее время, это нормально. Это совершенно нормальный ответ. Просто сделай это с кем-нибудь на большом ринге.
За то время, что я впервые прочитал их статью, я думал об этой теории много, много раз. Где я в кругу? Учитывая такое положение, что я должен сказать или что, я надеюсь, мне скажут? Кого из круга я мог бы утешить? Кому я могу «сбросить»?
Где я в кругу? Учитывая такое положение, что я должен сказать или что, я надеюсь, мне скажут? Кого из круга я мог бы утешить? Кому я могу «сбросить»?
Квечинг (жалобы) — важный инструмент для борьбы со стрессом, тревогой и депрессией, а также для укрепления связей между людьми и повышения эмпатии. Это также деликатный инструмент, требующий бережного обращения. Определение kvetch из идиш кветшн, означает сжимать, щипать или давить. Говоря современным американским языком, думайте об этом как о повседневных жалобах на большие и малые проблемы, которыми мы все занимаемся почти бессознательно. Речь идет о том, что мы должны выбросить из головы.
Вот список практических вещей, которые можно сделать для человека в кризисной ситуации:
1. Принесите еду
2. Принесите чашку кофе, чая или плитку шоколада.
3. Предложите прогуляться.
4. Предлагайте посмотреть/провести время с детьми, пожилыми родителями или домашними животными.
5. Приходи просто помыть посуду или постирать.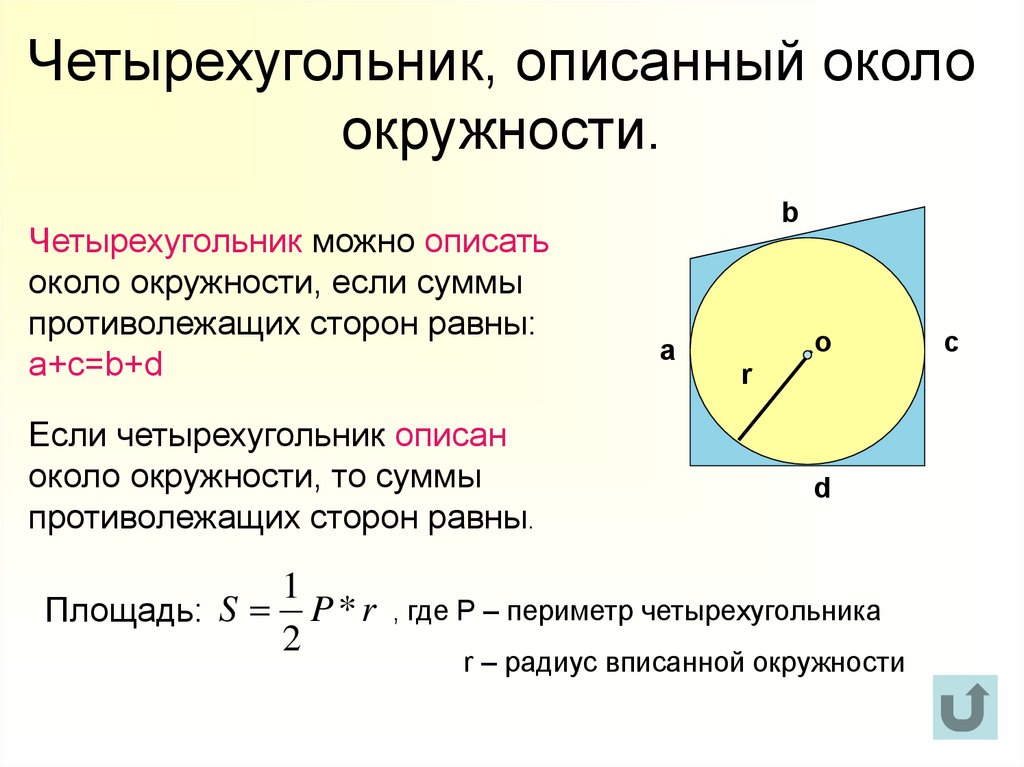
6. Возьмите с собой любимый компакт-диск или фильм.
7. Если личное присутствие кажется вам слишком сложным, отправьте сообщение по почте.
Что вы можете добавить к этому списку?
Что помогло вам или вашим близким?
Где ты сейчас в кругу?
Элана Премак Сандлер, L.C.S.W., MPH, подходит к вопросам здоровья с социальной точки зрения, рассматривая элементы социальной среды как решающие факторы в укреплении индивидуального здоровья и благополучия. Элана работала с национальным Ресурсным центром по предотвращению самоубийств, предоставляя организациям консультации по использованию доказательных вмешательств и передового опыта для разработки программ предотвращения самоубийств. Элана получила степень магистра социальной работы и магистра общественного здравоохранения в Бостонском университете и является преподавателем Школы социальной работы Симмонса.
Она является автором блога «Содействие надежде, предотвращение самоубийств». Он написан как с личной, так и с профессиональной точки зрения. В книге «Содействие надежде, предотвращение самоубийств» исследуется предотвращение самоубийств, вмешательство и поственция. Этот блог является форумом для новых взглядов на старые идеи и поощряет оспаривание догм. Элана выжила, потеряв отца в результате самоубийства 32 года назад, когда она была ребенком. Многие из ее сообщений в блоге касаются ее личного опыта, поскольку ее горе развивалось с годами.
Он написан как с личной, так и с профессиональной точки зрения. В книге «Содействие надежде, предотвращение самоубийств» исследуется предотвращение самоубийств, вмешательство и поственция. Этот блог является форумом для новых взглядов на старые идеи и поощряет оспаривание догм. Элана выжила, потеряв отца в результате самоубийства 32 года назад, когда она была ребенком. Многие из ее сообщений в блоге касаются ее личного опыта, поскольку ее горе развивалось с годами.
Теория золотого круга: узнайте, почему, как и что делает ваш бренд
Перейти к содержимому
Немногие предприятия сегодня могут процветать, просто заваливая клиентов сообщениями о возможностях и преимуществах своих продуктов или услуг. Людям нужна более глубокая причина, чтобы выбрать ваш бренд, а не другой. Если вы не уверены, что это за причина, ваш бизнес, скорее всего, будет бороться за процветание среди всех конкурентов.
Огромное количество компаний, стремящихся закрепиться и удержаться на современном рынке, означает, что вашему бизнесу нужно что-то особенное, чтобы преодолеть весь этот шум, и именно здесь вступает в действие теория Золотого круга.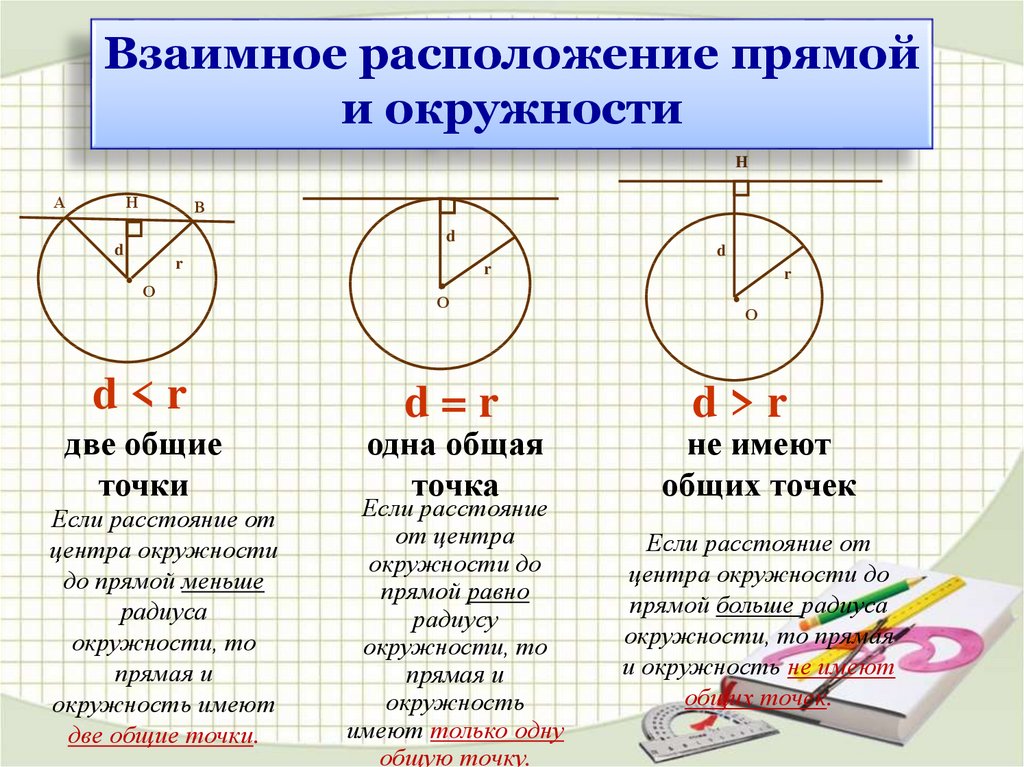
Первоначально предложенная Саймоном Синеком, экспертом в области лидерства и автором классической книги «Начните с того, почему», теория золотого круга утверждает, что многие из наиболее успешных современных компаний думают не только о практических, рациональных преимуществах продуктов и услуг, которые они предлагают. В то время как некоторые компании начинают с объяснения того, что они предлагают своим клиентам, крупные компании, такие как Apple, начинают с изучения того, как и почему они стоят за своим бизнесом.
Просто подумайте о лозунге Apple «Думай иначе» и о том, насколько неузнаваемым был бы этот технологический гигант сегодня, если бы вместо этого остановился на «Мы продаем компьютеры». С точки зрения Apple, клиенты выбирают бизнес по более расплывчатым эмоциональным причинам, чем просто потребность в MacBook или iPhone. Короче говоря, люди хотят поддерживать компании, движимые общими ценностями и убеждениями.
Компания Apple смогла добиться процветания, с самого начала обращаясь к покупателям более осмысленно. Но почему это связано с Золотым кольцом и как компании могут включить его в свои собственные маркетинговые планы? Читайте дальше, чтобы узнать об основах теории Золотого круга, о том, как она применима к маркетингу и почему она так важна для больших и малых предприятий.
Но почему это связано с Золотым кольцом и как компании могут включить его в свои собственные маркетинговые планы? Читайте дальше, чтобы узнать об основах теории Золотого круга, о том, как она применима к маркетингу и почему она так важна для больших и малых предприятий.
Узнать больше.
Что такое теория Золотого круга?Хотя может показаться, что причины, по которым люди предпочитают одну компанию другой, трудно определить, теория Золотого круга предполагает обратное. С точки зрения клиента может показаться, что компании просто хотят зарабатывать деньги, а ценности или «почему» — это второстепенные мысли.
Однако такие компании, как Apple, подходят к делу совершенно по-другому, начиная со своего «почему», прежде чем упоминать свои продукты, а также «как» и «что». Основы теории Золотого круга относительно просты и состоят из трех основных частей.
 «Почему»
«Почему» Поскольку, как говорит Синек, «люди покупают не то, что вы делаете, они покупают то, почему вы это делаете», вопрос «зачем мы занимаемся этим бизнесом?» должен быть фокусом любого бренда. Естественно, руководители малого бизнеса и некоммерческих организаций сосредоточены на практических результатах, но есть ценная история, которую можно рассказать через причины, по которым ваш бизнес или некоммерческая организация делает то, что делает.
Возможно, на рынке или в вашем сообществе есть неудовлетворенная потребность, которую ваш бизнес сможет удовлетворить, или, может быть, у вас просто есть новаторское видение будущего вашей отрасли. Возможно, у вашего бизнеса есть личное или ориентированное на миссию «почему».
«Почему», стоящее за вашим брендом, должно определять всеобъемлющую цель компании помимо итоговой прибыли, давая клиентам и сотрудникам более весомую причину поддерживать ваш бизнес.
Отличный пример признанного бренда, объясняющего свое «почему», можно увидеть в заявлении о миссии Tesla: «Tesla считает, что чем быстрее мир перестанет полагаться на ископаемое топливо и двинется к будущему с нулевым уровнем выбросов, тем лучше». Это простое предложение резюмирует основание компании Илона Маска, связывая его бренд с более благородным делом, чем просто продажа электромобилей или солнечных батарей.
Это простое предложение резюмирует основание компании Илона Маска, связывая его бренд с более благородным делом, чем просто продажа электромобилей или солнечных батарей.
Следующая часть теории Золотого круга посвящена тому, как ваш бренд достигает цели «почему». Это может включать процессы или системы, которые отличают ваш бизнес от конкурентов. Например, вы можете создать интернет-магазин одежды, в котором используются только ткани из этических источников, чтобы поддержать ваше «зачем» двигаться в моде в более устойчивом направлении.
Для Amazon Джефф Безос заявил, что цель «почему» состоит в том, чтобы «постоянно повышать планку качества обслуживания клиентов, используя Интернет и технологии, чтобы помочь потребителям находить, открывать и покупать что угодно».
Как его компании удалось достичь этой цели и стать таким мощным центром в индустрии электронной коммерции? Во-первых, Amazon создал надежную и простую в использовании платформу, которая объединила тысячи продавцов на едином онлайн-рынке.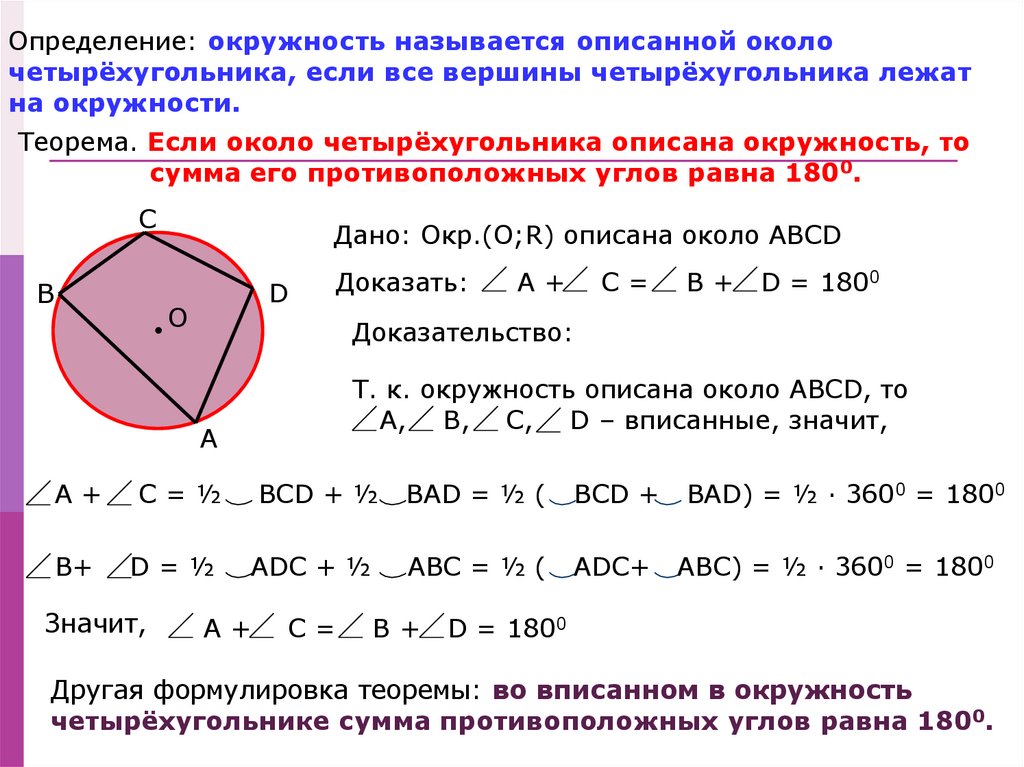 Чтобы обеспечить ускоренную доставку по более низкой цене для подписчиков, Amazon также создала собственный парк транспортных средств и открыла центры микроисполнения по всей территории Соединенных Штатов.
Чтобы обеспечить ускоренную доставку по более низкой цене для подписчиков, Amazon также создала собственный парк транспортных средств и открыла центры микроисполнения по всей территории Соединенных Штатов.
Последний аспект бренда Золотого круга — это то, что ваша компания фактически делает с точки зрения продуктов или услуг, которые она предоставляет. Эта часть теории Золотого круга должна позиционировать вашу компанию на рынке как уникального и инновационного лидера отрасли.
Хотя эта часть Золотого круга кажется самоочевидной, важно учитывать, как ваши предложения соответствуют тому, почему и как это определяет ваш бренд. Что такого в ваших продуктах или услугах, что поддерживает цель вашей компании? Для такой компании, как Tesla, продажа электромобилей — просто средство для достижения заявленной цели — сделать мир менее зависимым от ископаемого топлива.
Независимо от того, «что» вы продаете, ваши продукты или услуги должны соответствовать основному видению и мотивации компании. Если вы будете четко помнить «почему», за этим последуют убедительные сообщения бренда.
Если вы будете четко помнить «почему», за этим последуют убедительные сообщения бренда.
Учитывая значение «Золотого круга» в создании надежного и легко узнаваемого бренда, неудивительно, что некоторые из наиболее успешных современных компаний следуют этой модели. Чтобы проиллюстрировать, как эта теория работает на практике, полезно изучить, что делают основные отраслевые конкуренты. Вот несколько примеров теории Золотого круга, которые можно увидеть в реальном мире сегодня.
Amazon продолжает следовать своему видению предоставления наилучших услуг для клиентов. АмазонкаС момента своего основания в 1994 году Amazon остается верным своему первоначальному видению предоставления наилучших возможностей для всех своих клиентов. Это клиентоориентированное отношение служит центральным элементом бренда Golden Circle.
Но как компания достигает этого? Как упоминалось выше, они создали платформу, которая помогает клиентам находить, находить и покупать все, что сегодня означает все, от продуктов до фильмов для потоковой передачи.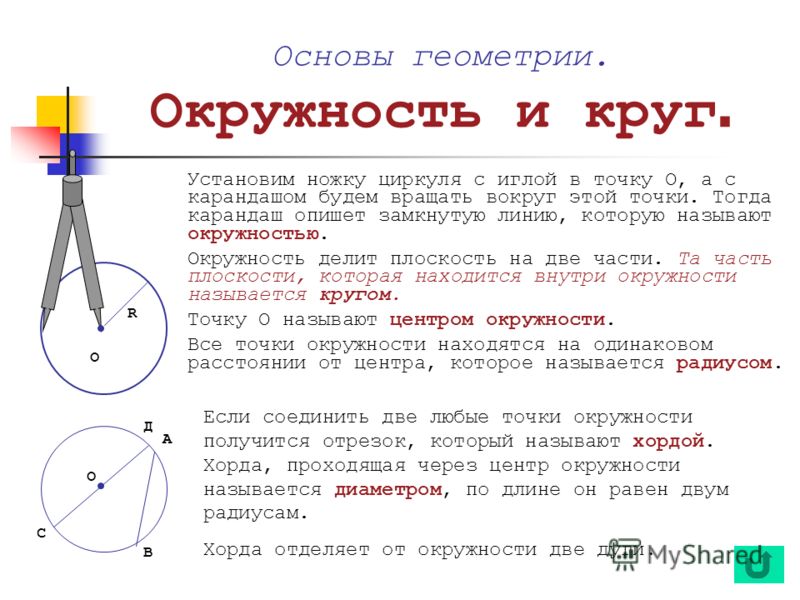 Для такой компании, как Amazon, которая продает практически все на свете, «что» ее бренда гораздо менее определено по сравнению с ее «почему» и «как».
Для такой компании, как Amazon, которая продает практически все на свете, «что» ее бренда гораздо менее определено по сравнению с ее «почему» и «как».
При этом все ее продукты имеют одну общую черту: вы можете купить все, что угодно, одним нажатием кнопки, с доставкой прямо к вашей двери. Это легкое удобство и, казалось бы, бесконечный ассортимент продуктов, которые предлагает Amazon, трудно воспроизвести другим компаниям. Сохранение приверженности своим основным ценностям и мотивации – главная причина, по которой Amazon удалось вырасти с менее чем 200 000 активных пользователей в 1996 году до крупнейшей компании в мире.
Домашний складЭтот бренд Golden Circle — еще один прекрасный пример того, как компания достигает своей цели, обслуживая своих клиентов. Первоначальные магазины Home Depot носили слоган «Склад в Атланте своими руками», и за четыре десятилетия с момента основания компания, безусловно, вышла далеко за пределы Атланты.
В книге, подробно описывающей скромное начало Home Depot, соучредитель Берни Маркус пишет: «В конце концов, мы работаем для людей».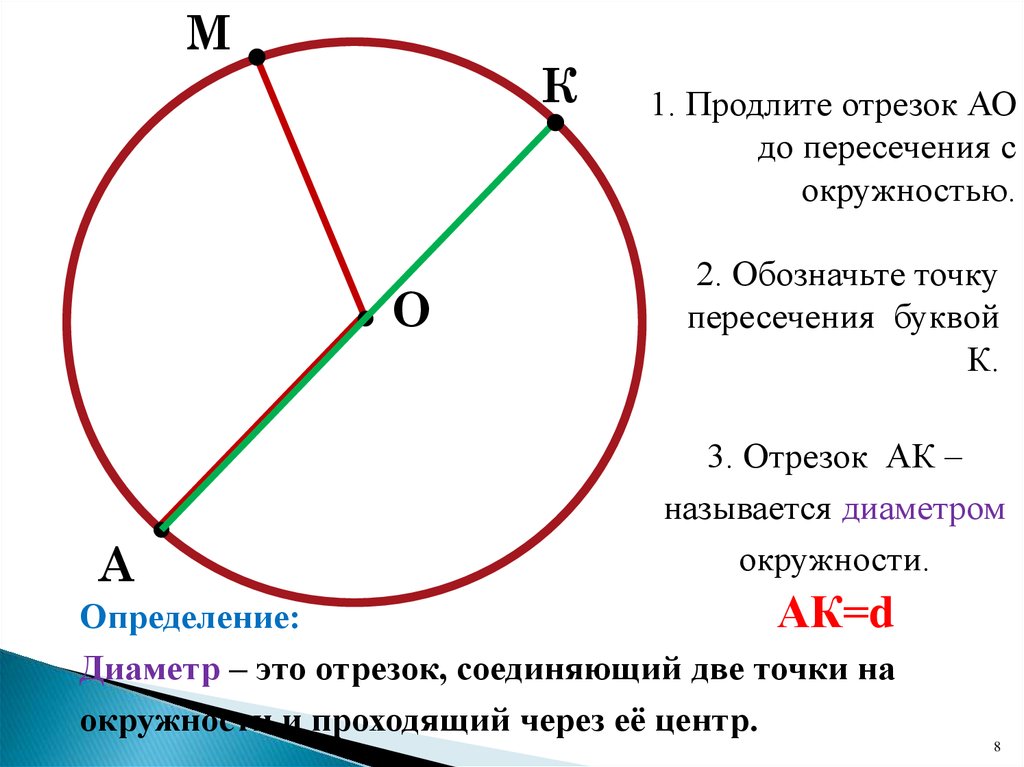 Эта приверженность клиентам отвечает на вопрос «почему», который продолжает продвигать компанию вперед. Его «как» включает в себя обучение сотрудников магазина строительным навыкам, чтобы они были максимально полезными, а также предоставление инструментов и материалов для удовлетворения любых потребностей в строительстве.
Эта приверженность клиентам отвечает на вопрос «почему», который продолжает продвигать компанию вперед. Его «как» включает в себя обучение сотрудников магазина строительным навыкам, чтобы они были максимально полезными, а также предоставление инструментов и материалов для удовлетворения любых потребностей в строительстве.
Home Depot поступать правильно также способствует активному улучшению сообществ, в которых он живет, через фонд Home Depot Foundation. Этот фонд помогает улучшить жилье для ветеранов, предоставляет финансирование сообществам, восстанавливающимся после стихийных бедствий, и поддерживает обучение торговцев в рамках своей программы Path to Pro.
Ставя людей на первое место, Home Depot зарекомендовала себя как один из самых надежных магазинов товаров для дома в Америке.
Tesla — отличный пример бренда Золотого кольца, который понимает свои цели и точно знает, как их достичь. Тесла «Почему» Тесла прост: полностью переосмыслить транспорт и энергию. Как он стремится достичь этой цели? Он ищет и поддерживает творческие решения, чтобы облегчить переход к устойчивым альтернативным источникам энергии как можно быстрее.
Как он стремится достичь этой цели? Он ищет и поддерживает творческие решения, чтобы облегчить переход к устойчивым альтернативным источникам энергии как можно быстрее.
Естественно, «что» в Золотом кольце Tesla состоит из инновационных продуктов, таких как Powerwall, Solar Roof и линейки привлекательных электромобилей. Склонность Tesla к инновациям в будущем — часто за счет краткосрочной прибыли — придает этой компании более высокий статус среди конкурентов, стимулируя непрерывный рост и успех.
СпотифайЭтот стриминговый сервис — отличный пример компании, построенной на идеях теории Золотого круга. Миссия Spotify — «раскрыть потенциал человеческого творчества», и она делает это, «предоставляя миллионам творческих художников возможность жить за счет своего искусства, а миллиардам поклонников — возможность наслаждаться и вдохновляться им».
Сегодня Spotify предлагает более 70 миллионов песен и подкастов, чтобы воплотить свое видение в жизнь, и является одной из крупнейших стриминговых компаний в мире. Как и другие компании в этом списке, Spotify признает, что то, что она предлагает, является второстепенным по сравнению с тем, почему она это делает, и это видно.
Как и другие компании в этом списке, Spotify признает, что то, что она предлагает, является второстепенным по сравнению с тем, почему она это делает, и это видно.
Лучше всего то, что пользователи Spotify могут чувствовать себя комфортно при использовании службы потоковой передачи, поскольку прослушивание песни напрямую способствует поддержке исполнителя, который ее создал. Эта беспроигрышная ситуация во многом объясняет, почему Spotify удалось добиться такого успеха.
Преимущества использования модели Golden Circle Правда в том, что многие компании, которые не понимают своих основных ценностей и мотивации, просто сосредоточатся на продаже продуктов, чтобы получить прибыль. Независимо от того, какой у вас бизнес, модель Золотого круга — это бесценный инструмент, который можно использовать для формирования более глубокого видения будущего вашей компании и общения с вашими клиентами на эмоциональном уровне. Вот основные преимущества использования теории Золотого круга. для создания уникального бренда для вашего бизнеса.
для создания уникального бренда для вашего бизнеса.
Понимание того, почему, как и что в вашей компании может служить путеводной звездой, которая ведет вашу компанию вперед. Ценности и мотивы, которых придерживается ваш бизнес, будут присутствовать во всех аспектах работы вашей компании, от обслуживания клиентов до культуры на рабочем месте.
Это означает, что вся ваша корреспонденция, реклама и пресс-релизы будут иметь последовательный, легко узнаваемый тон, уникальный для вашего бренда. Золотой круг также может помочь в разработке стратегий привлечения клиентов, оттачивая фокус контент-маркетинга, электронной почты и сообщений в социальных сетях.
Обеспечивает четкое направление Модель «Золотой круг» помогает определить курс будущего вашей компании, устанавливая основные правила и внутреннюю цель с самого начала. Настойчиво преследуя свои цели, ваша компания всегда будет иметь четкий путь вперед, чтобы ориентироваться на современном высококонкурентном рынке.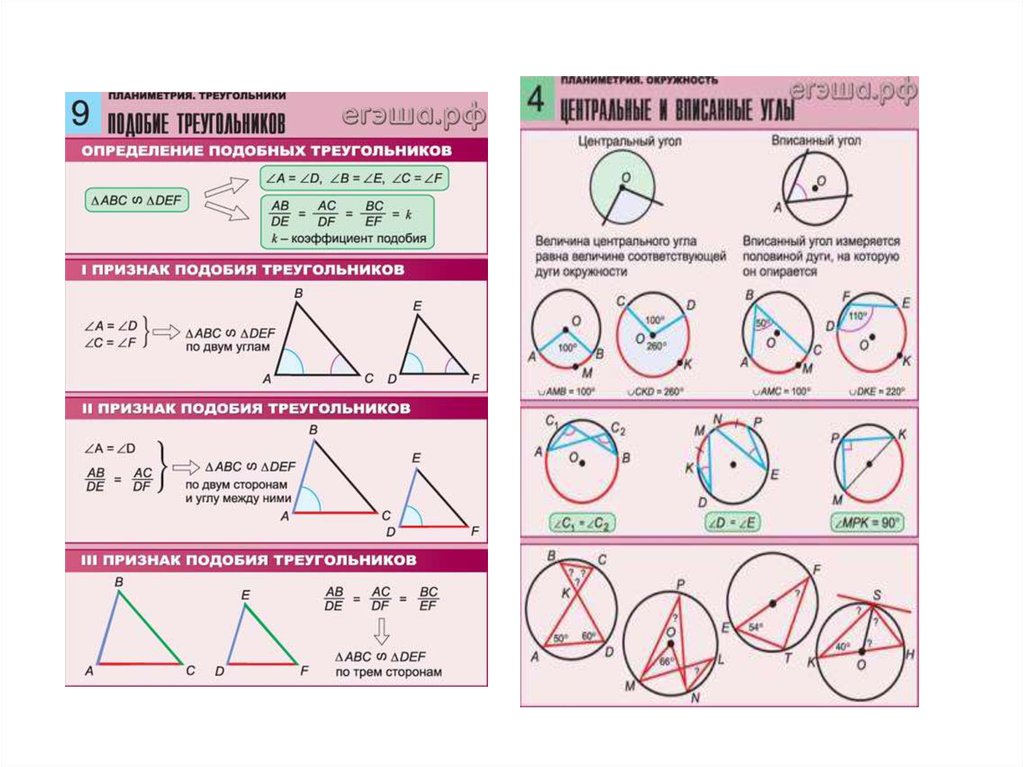
В то время как другие компании борются за узнаваемость своего бренда или увеличение прибыли, вы уже будете точно знать, за что выступает ваша компания, чего она надеется достичь и как она намерена добиться этого.
Помогает вашей компании выделитьсяЛюди знают, как отличить заботливый бизнес от бизнеса, который просто фокусируется на прибыли. Компании, которые следуют теории Золотого круга, с большей вероятностью будут выделяться из толпы и привлекать лояльных клиентов, которые поддерживают те же цели. Со временем ваша компания начнет повышать узнаваемость бренда, которая полностью отличается от конкурентов, и ваше сообщение никогда не потеряется в шуме.
Подумайте о том, «почему», «как» и «что» для вашего бизнеса Вспомните самые ранние дни своего бизнеса. Что побудило вас пойти именно по этому пути? Какие из ваших личных ценностей, интересов и убеждений привели вас в этот бизнес? У вас есть магазин натуральных продуктов, потому что вы заботитесь о здоровье своего сообщества? Возможно, у вас есть собственный бизнес по производству кроссовок, потому что вы цените моду и хотите вдохновлять на творчество.
Будет ли когда-нибудь цена ваших акций соответствовать цене Tesla или Apple? Может быть, а может и нет, но сообщения вашего бренда, безусловно, могут быть на одном уровне, если вы будете постоянно придерживаться своих «почему», «как» и «что» во всем, что вы говорите и делаете. Сосредоточение всей вашей маркетинговой деятельности на Золотом кольце вашей компании может помочь вам общаться с вашими клиентами гораздо более осмысленно и запоминающимся образом.
Прелесть этой теории в ее простоте. Это то, что может применить любой владелец бизнеса. Ваш первый шаг? Возьмите лист бумаги и ручку, нарисуйте диаграмму Золотого круга и напишите на ней свои «почему», «как» и «что». Поговорите об этом со своими сотрудниками, разместите на стене, где это будет видно каждый день, и присоединяйтесь к Apple, Tesla и другим лидерам в области брендинга в создании сильного и ценного бренда.
Зарегистрируйтесь бесплатно
org/Person»> Роберт КоулМеня зовут Роберт Коул, я писатель-фрилансер с более чем десятилетним стажем. Я подготовил контент, охватывающий широкий круг тем, включая финансы, технологии, малый бизнес, право, обслуживание дома, текущие новости и многое другое.
Аудиокнига недоступна | Audible.com
Приносим извинения за неудобства.
Что могло быть причиной этого?
Проблемы с качеством звука
Когда мы обнаруживаем проблему со звуком, она становится нашим приоритетом. Как только это будет исправлено, оно вернется в магазин как можно скорее.
Возможно, издатель потерял права
Когда у наших партнеров больше нет прав на название, мы должны удалить его из нашей коллекции.
Устаревшая ссылка
Если вы попали на эту страницу по сторонней ссылке, сообщите нам, где вы ее нашли, отправив электронное письмо по адресу [email protected].
Готовы к отличному прослушиванию? Выберите из этого списка фаворитов слушателей.

Опасный человек
- Роман Элвиса Коула и Джо Пайка, книга 18
- По: Роберт Крейс
- Рассказал: Люк Дэниэлс
- Продолжительность: 7 часов 23 минуты
- Полный
Джо Пайк не ожидал в тот день спасти женщину. Он пошел в банк так же, как все ходят в банк, и вернулся к своему джипу./918870b1bc4a305.s.siteapi.org/img/8aa195e2cfb8b8b18f3ad80023d4eae977f22c8f.jpg) Поэтому, когда Изабель Роланд, одинокая молодая кассирша, которая помогала ему, выходит из банка по пути на обед, Джо оказывается рядом, когда двое мужчин похищают ее. Джо преследует их, и двое мужчин арестованы. Но вместо того, чтобы положить конец драме, аресты — это только начало проблем для Джо и Иззи.
Поэтому, когда Изабель Роланд, одинокая молодая кассирша, которая помогала ему, выходит из банка по пути на обед, Джо оказывается рядом, когда двое мужчин похищают ее. Джо преследует их, и двое мужчин арестованы. Но вместо того, чтобы положить конец драме, аресты — это только начало проблем для Джо и Иззи.
Лето 69-го
- По: Элин Хильдербранд
- Рассказал: Эрин Беннетт
- Продолжительность: 13 часов 34 минуты
- Полный
Добро пожаловать в самое бурное лето 20 века. На дворе 1969 год, и для семьи Левиных времена меняются. Каждый год дети с нетерпением ждут возможности провести лето в историческом доме своей бабушки в центре Нантакета. Но, как и многое другое в Америке, здесь все по-другому.
На дворе 1969 год, и для семьи Левиных времена меняются. Каждый год дети с нетерпением ждут возможности провести лето в историческом доме своей бабушки в центре Нантакета. Но, как и многое другое в Америке, здесь все по-другому.
- 3 из 5 звезд
отличная история
- По Клиент Амазонки на 07-09-19
Внутренний
- Роман
- По: Теа Обрехт
- Рассказал: Анна Кламски, Эдоардо Баллерини, Юан Мортон
- Продолжительность: 13 часов 7 минут
- Полный
На беззаконных, засушливых землях Аризонской территории в 1893 году разворачиваются две необыкновенные жизни.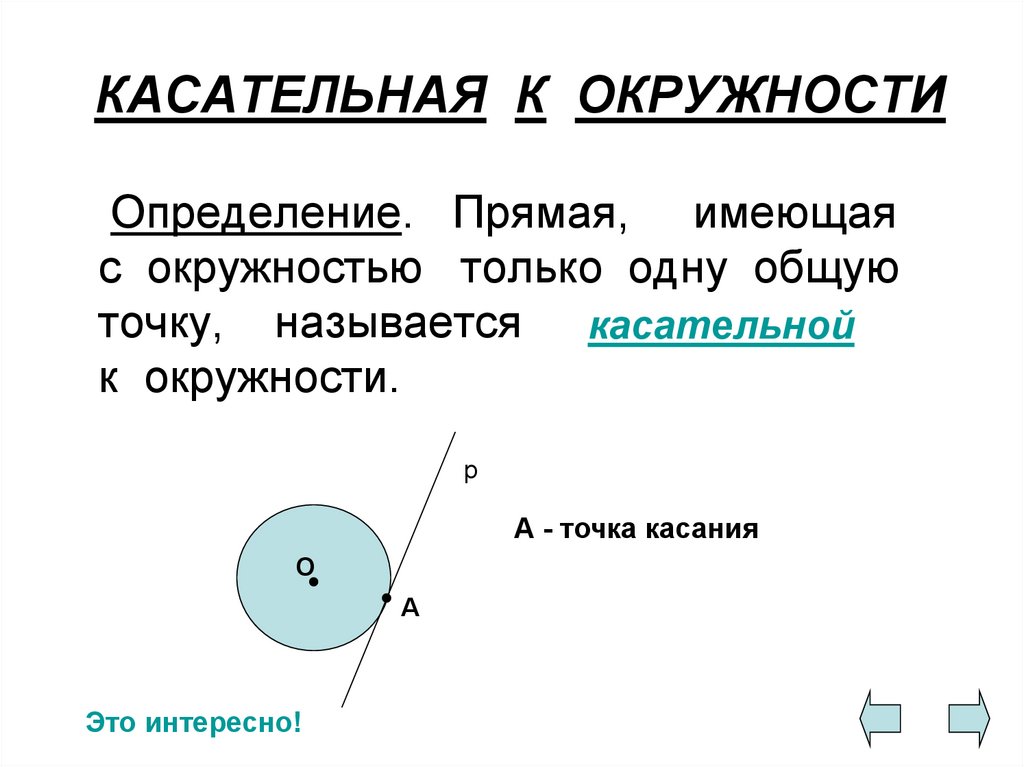 Нора — непоколебимая пограничница, ожидающая возвращения мужчин в своей жизни — своего мужа, отправившегося на поиски воды для выжженного дома, и старших сыновей, исчезнувших после бурной ссоры. Нора ждет своего часа со своим младшим сыном, который убежден, что таинственный зверь бродит по земле вокруг их дома.
Нора — непоколебимая пограничница, ожидающая возвращения мужчин в своей жизни — своего мужа, отправившегося на поиски воды для выжженного дома, и старших сыновей, исчезнувших после бурной ссоры. Нора ждет своего часа со своим младшим сыном, который убежден, что таинственный зверь бродит по земле вокруг их дома.
- 2 из 5 звезд
Я старался,
- По Джулианна на 10-09-19
В сонном приморском городке штата Мэн недавно овдовевшая Эвелет «Эвви» Дрейк редко покидает свой большой, мучительно пустой дом спустя почти год после гибели ее мужа в автокатастрофе. Все в городе, даже ее лучший друг Энди, думают, что горе держит ее взаперти, и Эвви не поправляет их. Тем временем в Нью-Йорке Дин Тенни, бывший питчер Высшей лиги и лучший друг детства Энди, борется с тем, что несчастные спортсмены, живущие в своих самых страшных кошмарах, называют «улюлюканьем»: он больше не может бросать прямо и, что еще хуже, он не может понять почему.
Все в городе, даже ее лучший друг Энди, думают, что горе держит ее взаперти, и Эвви не поправляет их. Тем временем в Нью-Йорке Дин Тенни, бывший питчер Высшей лиги и лучший друг детства Энди, борется с тем, что несчастные спортсмены, живущие в своих самых страшных кошмарах, называют «улюлюканьем»: он больше не может бросать прямо и, что еще хуже, он не может понять почему.
- 5 из 5 звезд
Хоумран
- По ДалласД на 30-06-19
Кэсси Хэнвелл родилась для чрезвычайных ситуаций. Как одна из немногих женщин-пожарных в своей пожарной части в Техасе, она повидала их немало и отлично справляется с чужими трагедиями.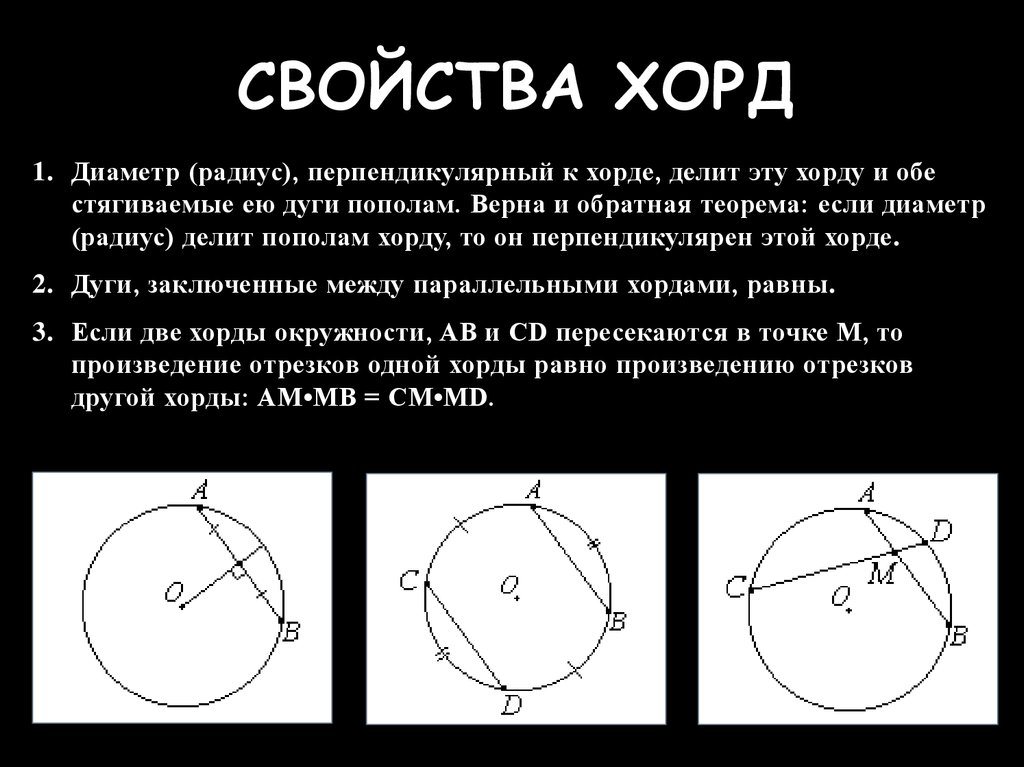 Но когда ее отчужденная и больная мать просит ее разрушить свою жизнь и переехать в Бостон, это чрезвычайное положение, которого Кэсси никогда не ожидала. Жесткая бостонская пожарная часть старой школы настолько отличается от старой работы Кэсси, насколько это возможно. Дедовщина, нехватка финансирования и плохие условия означают, что пожарные не очень рады видеть в бригаде «женщину».
Но когда ее отчужденная и больная мать просит ее разрушить свою жизнь и переехать в Бостон, это чрезвычайное положение, которого Кэсси никогда не ожидала. Жесткая бостонская пожарная часть старой школы настолько отличается от старой работы Кэсси, насколько это возможно. Дедовщина, нехватка финансирования и плохие условия означают, что пожарные не очень рады видеть в бригаде «женщину».
- 2 из 5 звезд
Здесь нет пламени
- По Дина на 09-07-19
Контрабанда
- Стоун Баррингтон, Книга 50
- По: Стюарт Вудс
- Рассказал: Тони Робертс
- Продолжительность: 7 часов 23 минуты
- Полный
Стоун Баррингтон получает столь необходимый отдых и расслабление под солнцем Флориды, когда с неба падает беда — буквально. Заинтригованный подозрительными обстоятельствами этого события, Стоун объединяет усилия с остроумным и привлекательным местным детективом для расследования. Но они сталкиваются с проблемой: улики продолжают исчезать.
Заинтригованный подозрительными обстоятельствами этого события, Стоун объединяет усилия с остроумным и привлекательным местным детективом для расследования. Но они сталкиваются с проблемой: улики продолжают исчезать.
Шансы есть…
- Роман
- По: Ричард Руссо
- Рассказал: Фред Сандерс
- Продолжительность: 11 часов 17 минут
- Полный
Одним прекрасным сентябрьским днем трое мужчин собираются на Мартас-Винъярд, друзья с тех пор, как встретились в колледже примерно в 60-х годах. Они не могли быть более разными ни тогда, ни даже сегодня: Линкольн был брокером по коммерческой недвижимости, Тедди — издателем крошечной прессы, а Микки — музыкантом не по возрасту. Но у каждого человека есть свои секреты, в дополнение к монументальной тайне, над которой никто из них не переставал ломать голову со времен Дня поминовения на выходных прямо здесь, на Винограднике, в 1971: исчезновение женщины, которую любил каждый из них — Джейси Кэллоуэй.
Они не могли быть более разными ни тогда, ни даже сегодня: Линкольн был брокером по коммерческой недвижимости, Тедди — издателем крошечной прессы, а Микки — музыкантом не по возрасту. Но у каждого человека есть свои секреты, в дополнение к монументальной тайне, над которой никто из них не переставал ломать голову со времен Дня поминовения на выходных прямо здесь, на Винограднике, в 1971: исчезновение женщины, которую любил каждый из них — Джейси Кэллоуэй.
Аутфокс
- По: Сандра Браун
- Рассказал: Виктор Слезак
- Продолжительность: 13 часов 59 минут
- Полный
Агент ФБР Дрекс Истон неустанно преследует одну цель: перехитрить мошенника, когда-то известного как Уэстон Грэм.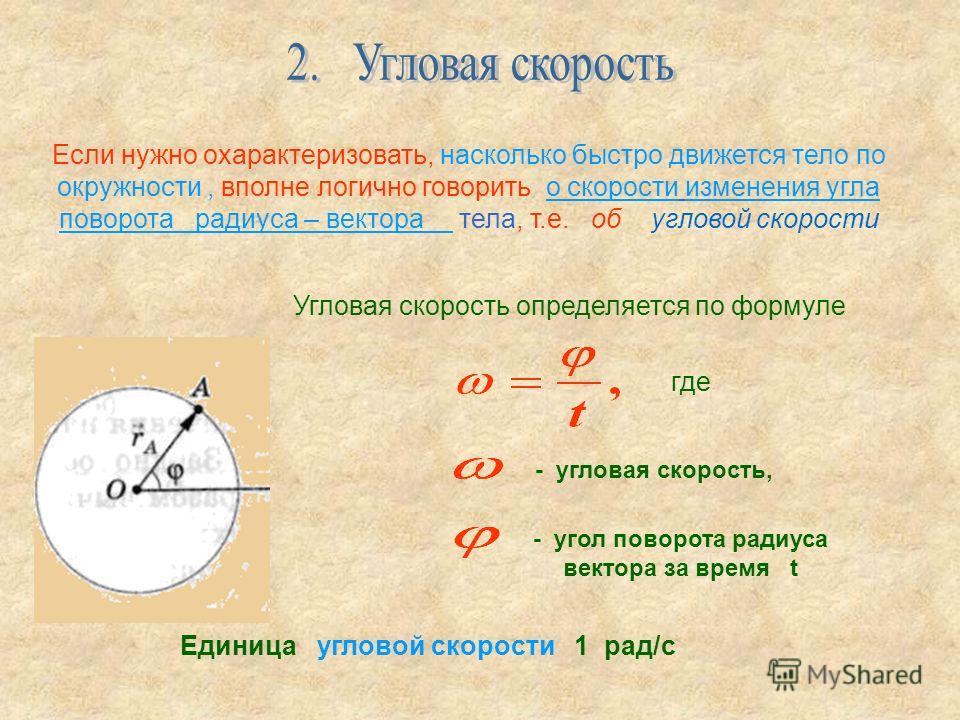 За последние 30 лет Уэстон сменил множество имен и бесчисленное количество маскировок, что позволило ему выманить восемь богатых женщин из своего состояния до того, как они бесследно исчезли, их семьи остались без ответов, а власти — без зацепок. Единственная общая черта среди жертв: новый человек в их жизни, который также исчез, не оставив после себя никаких свидетельств своего существования… кроме одного подписного обычая.
За последние 30 лет Уэстон сменил множество имен и бесчисленное количество маскировок, что позволило ему выманить восемь богатых женщин из своего состояния до того, как они бесследно исчезли, их семьи остались без ответов, а власти — без зацепок. Единственная общая черта среди жертв: новый человек в их жизни, который также исчез, не оставив после себя никаких свидетельств своего существования… кроме одного подписного обычая.
Новая девушка
- Роман
- По: Даниэль Сильва
- Рассказал: Джордж Гидалл
- Продолжительность: 10 часов 16 минут
- Полный
Она была с ног до головы покрыта дорогой шерстью и пледом, вроде того, что можно было увидеть в бутике Burberry в Harrods.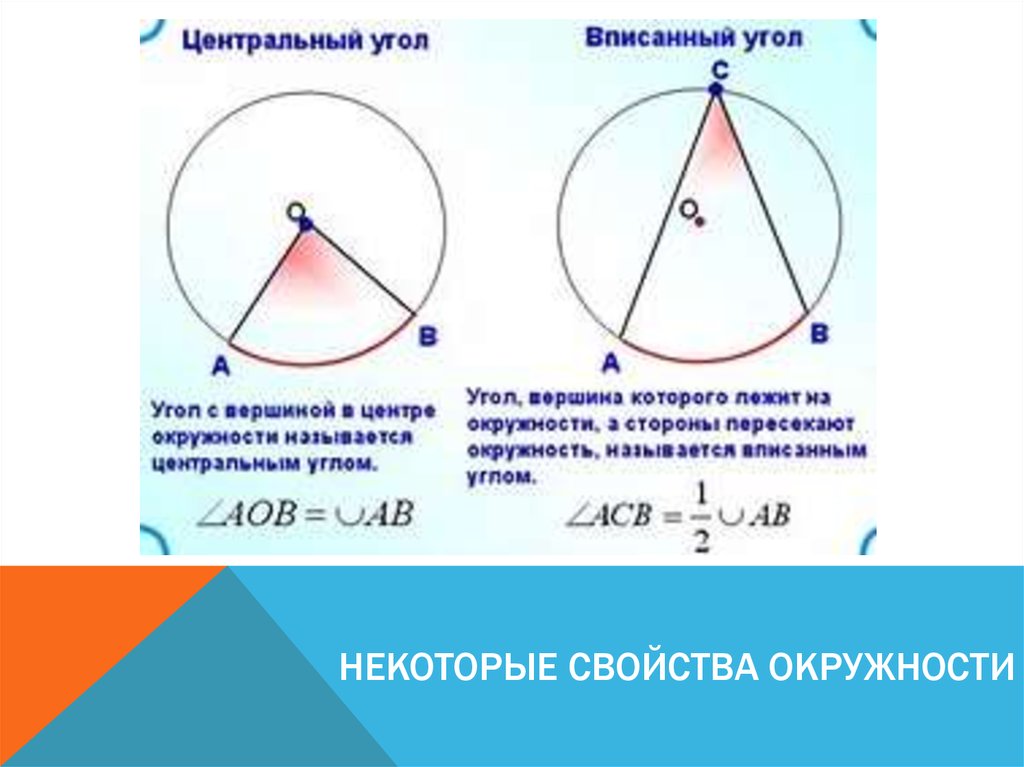 У нее была кожаная сумка для книг, а не нейлоновый рюкзак. Ее лакированные балетки были блестящими и яркими. Она была приличной, новенькой, скромной. Но было в ней кое-что еще… В эксклюзивной частной школе в Швейцарии тайна окружает личность красивой темноволосой девушки, которая каждое утро прибывает в кортеже, достойном главы государства. Говорят, что она дочь богатого международного бизнесмена.
У нее была кожаная сумка для книг, а не нейлоновый рюкзак. Ее лакированные балетки были блестящими и яркими. Она была приличной, новенькой, скромной. Но было в ней кое-что еще… В эксклюзивной частной школе в Швейцарии тайна окружает личность красивой темноволосой девушки, которая каждое утро прибывает в кортеже, достойном главы государства. Говорят, что она дочь богатого международного бизнесмена.
Опасный человек
- Роман Элвиса Коула и Джо Пайка, книга 18
- По: Роберт Крейс
- Рассказал: Люк Дэниэлс
- Продолжительность: 7 часов 23 минуты
- Полный
Джо Пайк не ожидал в тот день спасти женщину. Он пошел в банк так же, как все ходят в банк, и вернулся к своему джипу. Поэтому, когда Изабель Роланд, одинокая молодая кассирша, которая помогала ему, выходит из банка по пути на обед, Джо оказывается рядом, когда двое мужчин похищают ее. Джо преследует их, и двое мужчин арестованы. Но вместо того, чтобы положить конец драме, аресты — это только начало проблем для Джо и Иззи.
Он пошел в банк так же, как все ходят в банк, и вернулся к своему джипу. Поэтому, когда Изабель Роланд, одинокая молодая кассирша, которая помогала ему, выходит из банка по пути на обед, Джо оказывается рядом, когда двое мужчин похищают ее. Джо преследует их, и двое мужчин арестованы. Но вместо того, чтобы положить конец драме, аресты — это только начало проблем для Джо и Иззи.
Лето 69-го
- По: Элин Хильдербранд
- Рассказал: Эрин Беннетт
- Продолжительность: 13 часов 34 минуты
- Полный
Добро пожаловать в самое бурное лето 20 века. На дворе 1969 год, и для семьи Левиных времена меняются. Каждый год дети с нетерпением ждут возможности провести лето в историческом доме своей бабушки в центре Нантакета. Но, как и многое другое в Америке, здесь все по-другому.
На дворе 1969 год, и для семьи Левиных времена меняются. Каждый год дети с нетерпением ждут возможности провести лето в историческом доме своей бабушки в центре Нантакета. Но, как и многое другое в Америке, здесь все по-другому.
- 3 из 5 звезд
отличная история
- По Клиент Амазонки на 07-09-19
Внутренний
- Роман
- По: Теа Обрехт
- Рассказал: Анна Кламски, Эдоардо Баллерини, Юан Мортон
- Продолжительность: 13 часов 7 минут
- Полный
На беззаконных, засушливых землях Аризонской территории в 1893 году разворачиваются две необыкновенные жизни.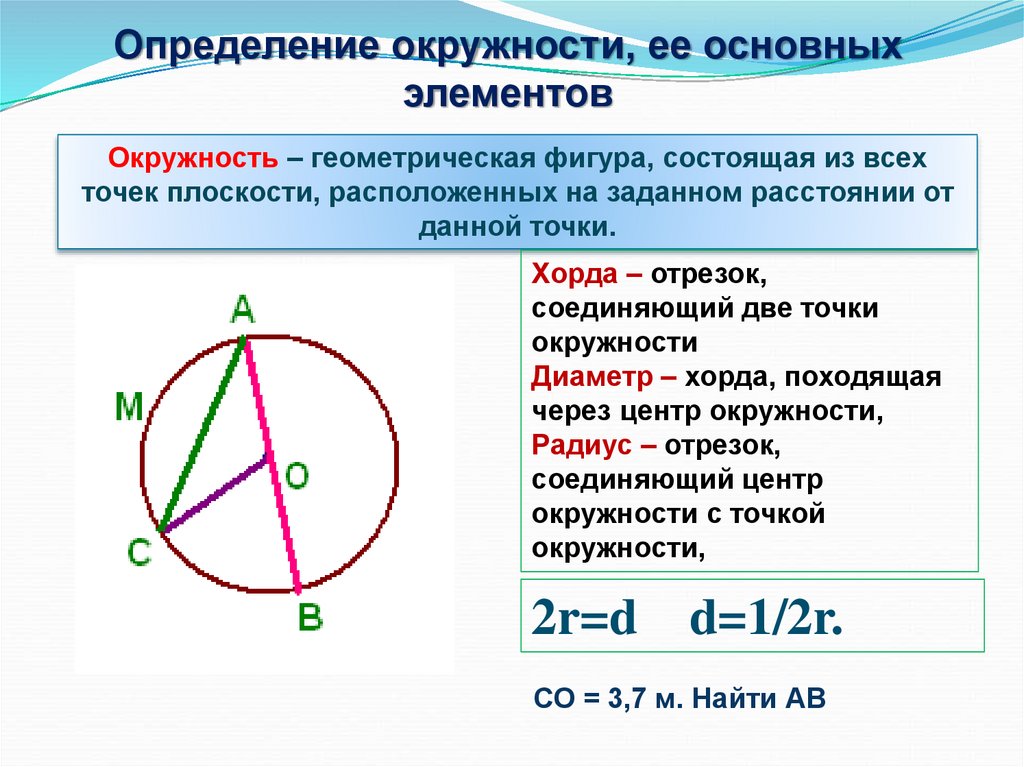 Нора — непоколебимая пограничница, ожидающая возвращения мужчин в своей жизни — своего мужа, отправившегося на поиски воды для выжженного дома, и старших сыновей, исчезнувших после бурной ссоры. Нора ждет своего часа со своим младшим сыном, который убежден, что таинственный зверь бродит по земле вокруг их дома.
Нора — непоколебимая пограничница, ожидающая возвращения мужчин в своей жизни — своего мужа, отправившегося на поиски воды для выжженного дома, и старших сыновей, исчезнувших после бурной ссоры. Нора ждет своего часа со своим младшим сыном, который убежден, что таинственный зверь бродит по земле вокруг их дома.
- 2 из 5 звезд
Я старался,
- По Джулианна на 10-09-19
В сонном приморском городке штата Мэн недавно овдовевшая Эвелет «Эвви» Дрейк редко покидает свой большой, мучительно пустой дом спустя почти год после гибели ее мужа в автокатастрофе. Все в городе, даже ее лучший друг Энди, думают, что горе держит ее взаперти, и Эвви не поправляет их. Тем временем в Нью-Йорке Дин Тенни, бывший питчер Высшей лиги и лучший друг детства Энди, борется с тем, что несчастные спортсмены, живущие в своих самых страшных кошмарах, называют «улюлюканьем»: он больше не может бросать прямо и, что еще хуже, он не может понять почему.
Все в городе, даже ее лучший друг Энди, думают, что горе держит ее взаперти, и Эвви не поправляет их. Тем временем в Нью-Йорке Дин Тенни, бывший питчер Высшей лиги и лучший друг детства Энди, борется с тем, что несчастные спортсмены, живущие в своих самых страшных кошмарах, называют «улюлюканьем»: он больше не может бросать прямо и, что еще хуже, он не может понять почему.
- 5 из 5 звезд
Хоумран
- По ДалласД на 30-06-19
Кэсси Хэнвелл родилась для чрезвычайных ситуаций. Как одна из немногих женщин-пожарных в своей пожарной части в Техасе, она повидала их немало и отлично справляется с чужими трагедиями. Но когда ее отчужденная и больная мать просит ее разрушить свою жизнь и переехать в Бостон, это чрезвычайное положение, которого Кэсси никогда не ожидала. Жесткая бостонская пожарная часть старой школы настолько отличается от старой работы Кэсси, насколько это возможно. Дедовщина, нехватка финансирования и плохие условия означают, что пожарные не очень рады видеть в бригаде «женщину».
Но когда ее отчужденная и больная мать просит ее разрушить свою жизнь и переехать в Бостон, это чрезвычайное положение, которого Кэсси никогда не ожидала. Жесткая бостонская пожарная часть старой школы настолько отличается от старой работы Кэсси, насколько это возможно. Дедовщина, нехватка финансирования и плохие условия означают, что пожарные не очень рады видеть в бригаде «женщину».
- 2 из 5 звезд
Здесь нет пламени
- По Дина на 09-07-19
Контрабанда
- Стоун Баррингтон, Книга 50
- По: Стюарт Вудс
- Рассказал: Тони Робертс
- Продолжительность: 7 часов 23 минуты
- Полный
Стоун Баррингтон получает столь необходимый отдых и расслабление под солнцем Флориды, когда с неба падает беда — буквально. Заинтригованный подозрительными обстоятельствами этого события, Стоун объединяет усилия с остроумным и привлекательным местным детективом для расследования. Но они сталкиваются с проблемой: улики продолжают исчезать.
Заинтригованный подозрительными обстоятельствами этого события, Стоун объединяет усилия с остроумным и привлекательным местным детективом для расследования. Но они сталкиваются с проблемой: улики продолжают исчезать.
Шансы есть…
- Роман
- По: Ричард Руссо
- Рассказал: Фред Сандерс
- Продолжительность: 11 часов 17 минут
- Полный
Одним прекрасным сентябрьским днем трое мужчин собираются на Мартас-Винъярд, друзья с тех пор, как встретились в колледже примерно в 60-х годах. Они не могли быть более разными ни тогда, ни даже сегодня: Линкольн был брокером по коммерческой недвижимости, Тедди — издателем крошечной прессы, а Микки — музыкантом не по возрасту. Но у каждого человека есть свои секреты, в дополнение к монументальной тайне, над которой никто из них не переставал ломать голову со времен Дня поминовения на выходных прямо здесь, на Винограднике, в 1971: исчезновение женщины, которую любил каждый из них — Джейси Кэллоуэй.
Они не могли быть более разными ни тогда, ни даже сегодня: Линкольн был брокером по коммерческой недвижимости, Тедди — издателем крошечной прессы, а Микки — музыкантом не по возрасту. Но у каждого человека есть свои секреты, в дополнение к монументальной тайне, над которой никто из них не переставал ломать голову со времен Дня поминовения на выходных прямо здесь, на Винограднике, в 1971: исчезновение женщины, которую любил каждый из них — Джейси Кэллоуэй.
Аутфокс
- По: Сандра Браун
- Рассказал: Виктор Слезак
- Продолжительность: 13 часов 59 минут
- Полный
Агент ФБР Дрекс Истон неустанно преследует одну цель: перехитрить мошенника, когда-то известного как Уэстон Грэм.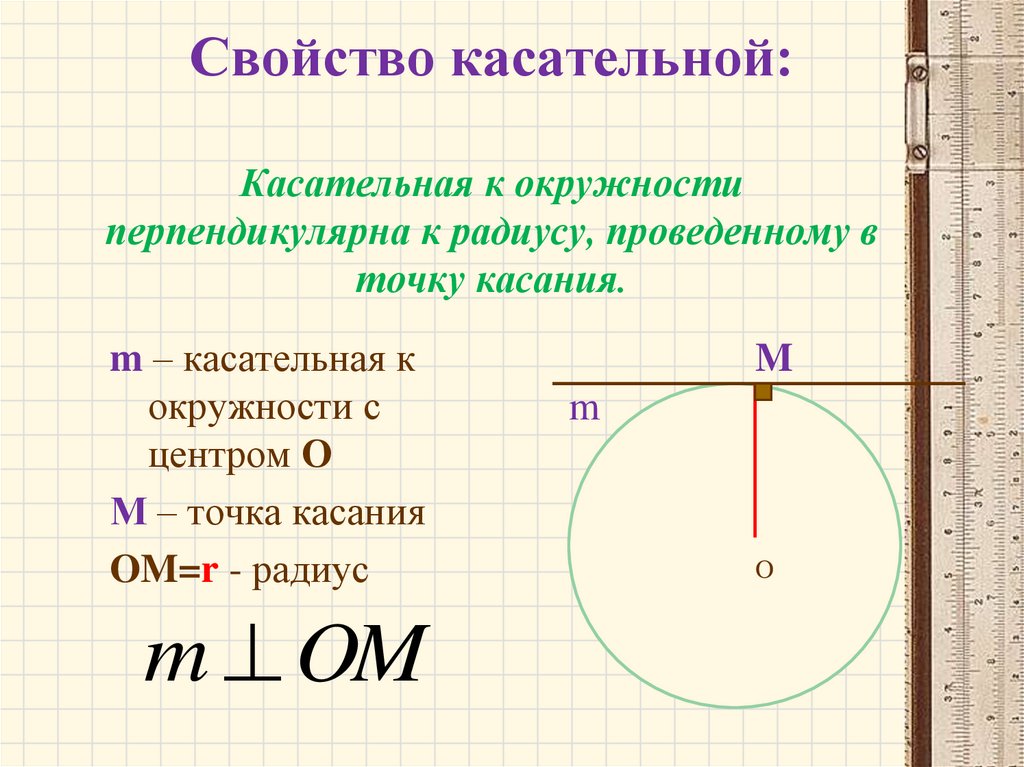 За последние 30 лет Уэстон сменил множество имен и бесчисленное количество маскировок, что позволило ему выманить восемь богатых женщин из своего состояния до того, как они бесследно исчезли, их семьи остались без ответов, а власти — без зацепок. Единственная общая черта среди жертв: новый человек в их жизни, который также исчез, не оставив после себя никаких свидетельств своего существования… кроме одного подписного обычая.
За последние 30 лет Уэстон сменил множество имен и бесчисленное количество маскировок, что позволило ему выманить восемь богатых женщин из своего состояния до того, как они бесследно исчезли, их семьи остались без ответов, а власти — без зацепок. Единственная общая черта среди жертв: новый человек в их жизни, который также исчез, не оставив после себя никаких свидетельств своего существования… кроме одного подписного обычая.
Новая девушка
- Роман
- По: Даниэль Сильва
- Рассказал: Джордж Гидалл
- Продолжительность: 10 часов 16 минут
- Полный
Она была с ног до головы покрыта дорогой шерстью и пледом, вроде того, что можно было увидеть в бутике Burberry в Harrods.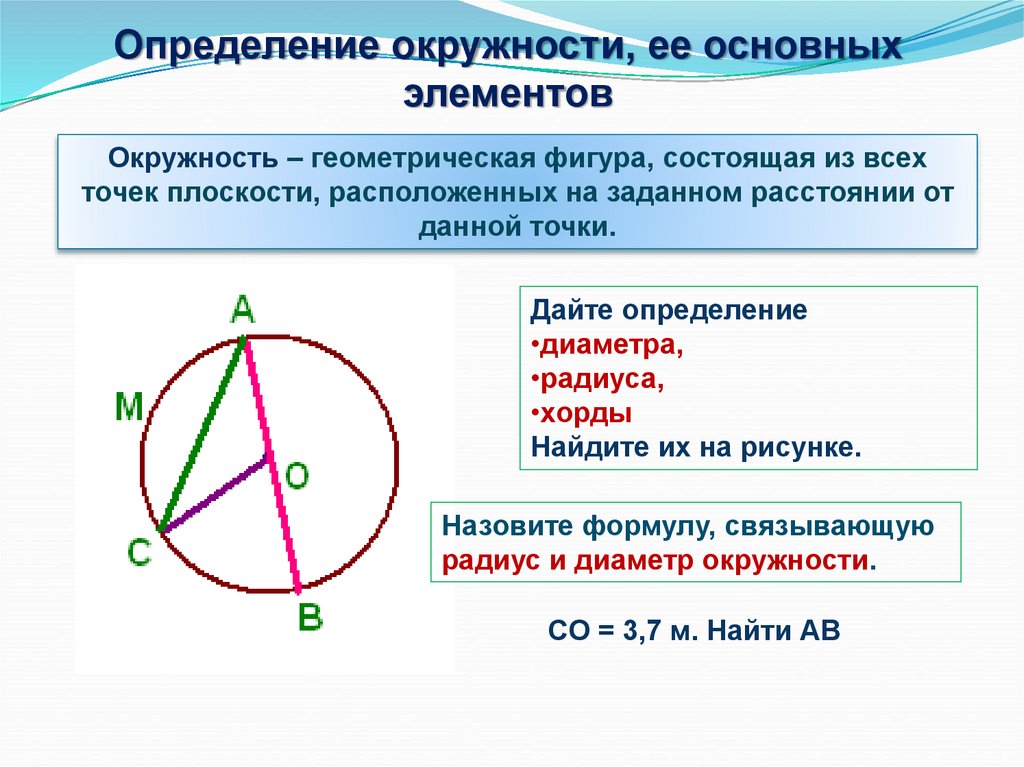 У нее была кожаная сумка для книг, а не нейлоновый рюкзак. Ее лакированные балетки были блестящими и яркими. Она была приличной, новенькой, скромной. Но было в ней кое-что еще… В эксклюзивной частной школе в Швейцарии тайна окружает личность красивой темноволосой девушки, которая каждое утро прибывает в кортеже, достойном главы государства. Говорят, что она дочь богатого международного бизнесмена.
У нее была кожаная сумка для книг, а не нейлоновый рюкзак. Ее лакированные балетки были блестящими и яркими. Она была приличной, новенькой, скромной. Но было в ней кое-что еще… В эксклюзивной частной школе в Швейцарии тайна окружает личность красивой темноволосой девушки, которая каждое утро прибывает в кортеже, достойном главы государства. Говорят, что она дочь богатого международного бизнесмена.
Когда Элвуда Кертиса, темнокожего мальчика, выросшего в 1960-х годах в Таллахасси, несправедливо приговаривают к исправительному учреждению для несовершеннолетних под названием Никелевая академия, он оказывается в ловушке в гротескной комнате ужасов. Единственное спасение Элвуда — его дружба с товарищем-правонарушителем Тернером, которая крепнет, несмотря на убежденность Тернера в том, что Элвуд безнадежно наивен, что мир извращен и что единственный способ выжить — это строить планы и избегать неприятностей.
Одно доброе дело
- По: Дэвид Балдаччи
- Рассказал: Эдоардо Баллерини
- Продолжительность: 11 часов 41 минута
- Полный
На дворе 1949 год. Когда ветеран войны Алоизиус Арчер выходит из тюрьмы Кардерок, его отправляют в Пока-Сити на условно-досрочное освобождение с коротким списком разрешений и гораздо более длинным списком запретов: регулярно отчитываться перед офицером по условно-досрочному освобождению, не Не ходи в бары, уж точно не пей алкоголь, найди работу и никогда не общайся с распутными женщинами. Маленький городок быстро оказывается более сложным и опасным, чем годы службы Арчера на войне или его время в тюрьме.
Когда ветеран войны Алоизиус Арчер выходит из тюрьмы Кардерок, его отправляют в Пока-Сити на условно-досрочное освобождение с коротким списком разрешений и гораздо более длинным списком запретов: регулярно отчитываться перед офицером по условно-досрочному освобождению, не Не ходи в бары, уж точно не пей алкоголь, найди работу и никогда не общайся с распутными женщинами. Маленький городок быстро оказывается более сложным и опасным, чем годы службы Арчера на войне или его время в тюрьме.
Горькие корни
- Роман Кэсси Дьюэлл
- По: Си Джей Бокс
- Рассказал: Кристина Делейн
- Продолжительность: 9 часов 55 минут
- Полный
Бывший полицейский Кэсси Дьюэлл пытается начать все сначала со своей частной детективной фирмой. Виновная в том, что она не видела своего сына и измученная ночами в засаде, Кэсси, тем не менее, справляется… пока старый друг не просит об одолжении: она хочет, чтобы Кэсси помогла оправдать человека, обвиняемого в нападении на молодую девушку из влиятельной семьи. Вопреки собственному здравому смыслу, Кэсси соглашается. Но в стране Большого Неба в Монтане извращенная семейная верность так же глубока, как и связи с землей, и в этой истории всегда есть что-то большее.
Виновная в том, что она не видела своего сына и измученная ночами в засаде, Кэсси, тем не менее, справляется… пока старый друг не просит об одолжении: она хочет, чтобы Кэсси помогла оправдать человека, обвиняемого в нападении на молодую девушку из влиятельной семьи. Вопреки собственному здравому смыслу, Кэсси соглашается. Но в стране Большого Неба в Монтане извращенная семейная верность так же глубока, как и связи с землей, и в этой истории всегда есть что-то большее.
Гостиница
- По: Джеймс Паттерсон, Кэндис Фокс
- Рассказал: Эдоардо Баллерини
- Продолжительность: 7 часов 17 минут
- Полный
Гостиница в Глостере стоит одиноко на скалистом берегу. Его уединение подходит бывшему детективу бостонской полиции Биллу Робинсону, начинающему владельцу и трактирщику. Пока дюжина жильцов платит арендную плату, Робинсон не задает никаких вопросов. Как и шериф Клейтон Спирс, живущий на втором этаже. Затем появляется Митчелл Клайн с новым смертельно опасным способом ведения бизнеса. Его команда местных убийц нарушает законы, торгует наркотиками и совершает насилие у дверей гостиницы.
Его уединение подходит бывшему детективу бостонской полиции Биллу Робинсону, начинающему владельцу и трактирщику. Пока дюжина жильцов платит арендную плату, Робинсон не задает никаких вопросов. Как и шериф Клейтон Спирс, живущий на втором этаже. Затем появляется Митчелл Клайн с новым смертельно опасным способом ведения бизнеса. Его команда местных убийц нарушает законы, торгует наркотиками и совершает насилие у дверей гостиницы.
- 5 из 5 звезд
Отличная Книга!!!!
- По Шелли на 08-06-19
Поворот ключа
- По: Рут Уэр
- Рассказал: Имоджен Черч
- Продолжительность: 12 часов 13 минут
- Полный
Когда она натыкается на объявление, она ищет что-то совершенно другое.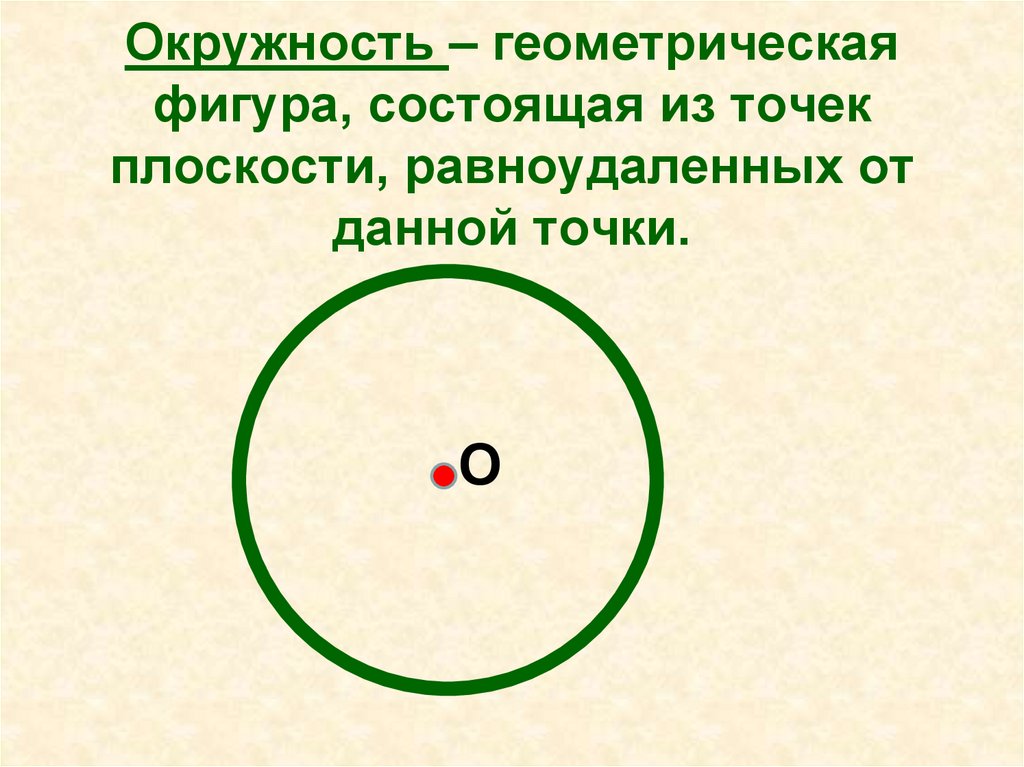 Но это кажется слишком хорошей возможностью, чтобы ее упустить — должность няни с проживанием и ошеломляюще щедрой зарплатой. И когда Роуэн Кейн приезжает в Heatherbrae House, она поражена — роскошным «умным» домом, оснащенным всеми современными удобствами, красивым шотландским нагорьем и этой идеальной семьей. Чего она не знает, так это того, что она вступает в кошмар, который закончится смертью ребенка, а она сама окажется в тюрьме в ожидании суда за убийство.
Но это кажется слишком хорошей возможностью, чтобы ее упустить — должность няни с проживанием и ошеломляюще щедрой зарплатой. И когда Роуэн Кейн приезжает в Heatherbrae House, она поражена — роскошным «умным» домом, оснащенным всеми современными удобствами, красивым шотландским нагорьем и этой идеальной семьей. Чего она не знает, так это того, что она вступает в кошмар, который закончится смертью ребенка, а она сама окажется в тюрьме в ожидании суда за убийство.
В течение многих лет слухи о «Болотной девочке» не давали покоя Баркли Коув, тихому городку на побережье Северной Каролины. Так в конце 1969 года, когда красавца Чейза Эндрюса находят мертвым, местные жители сразу подозревают Кию Кларк, так называемую Болотную девушку. Но Кия не то, что говорят. Чувствительная и умная, она годами выживала в одиночестве в болоте, которое называет своим домом, находя друзей среди чаек и уроки в песке.
Комар
- Человеческая история нашего самого смертоносного хищника
- По:
Тимоти С.
 Винегард
Винегард - Рассказал: Марк Дикинс
- Продолжительность: 19 часов 7 минут
- Полный
Почему джин-тоник был любимым коктейлем британских колонистов в Индии и Африке? Чем Starbucks обязана своему мировому господству? Что защищало жизнь пап на протяжении тысячелетий? Почему Шотландия передала свой суверенитет Англии? Что было секретным оружием Джорджа Вашингтона во время американской революции? Ответом на все эти и многие другие вопросы является комар. Благодаря неожиданным открытиям и стремительному повествованию, The Mosquito – это необыкновенная нерассказанная история о господстве комаров в истории человечества.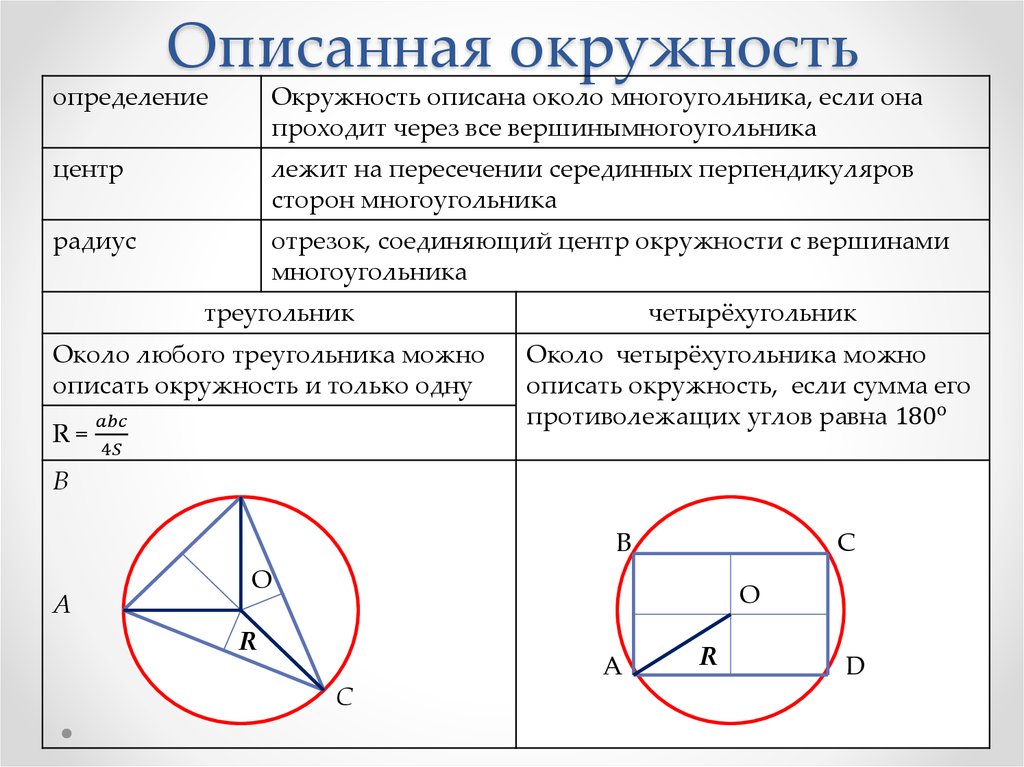
Возможно, самая знаменитая и почитаемая писательница нашего времени дарит нам новую коллекцию документальной литературы — богатое собрание ее эссе, речей и размышлений об обществе, культуре и искусстве за четыре десятилетия.
- 5 из 5 звезд
Освежающие мысли
- По Клиент Амазонки на 04-02-19
Однажды Лори Готлиб становится терапевтом, который помогает пациентам в своей практике в Лос-Анджелесе. Следующий кризис заставляет ее мир рушиться. Входит Венделл, причудливый, но опытный терапевт, в чей кабинет она внезапно попадает.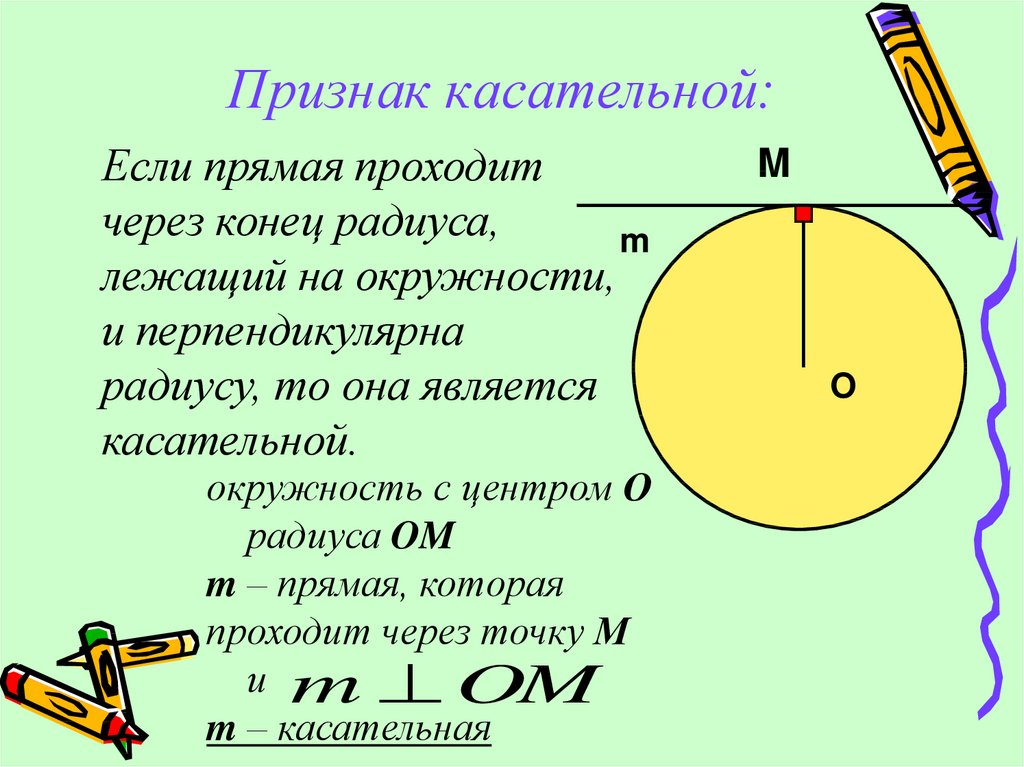 С его лысеющей головой, кардиганом и брюками цвета хаки он, кажется, пришел прямо из Центрального кастинга Терапевта. И все же он окажется совсем не таким.
С его лысеющей головой, кардиганом и брюками цвета хаки он, кажется, пришел прямо из Центрального кастинга Терапевта. И все же он окажется совсем не таким.
Кохланд
- Тайная история Koch Industries и корпоративной власти в Америке
- По: Кристофер Леонард
- Рассказал: Жак Рой
- Продолжительность: 23 часа 15 минут
- Полный
Так же, как Стив Колл рассказал историю глобализации через ExxonMobil, а Эндрю Росс Соркин рассказал историю избытка Уолл-Стрит до Слишком большой, чтобы потерпеть неудачу , Кристофер Леонард Kochland использует необычный рассказ о том, как крупнейшая частная компания в мире стала такой большой, чтобы рассказать историю современной корпоративной Америки.
Несвобода прессы — это не просто очередная книга о прессе. [Левин] показывает, как те, кому сегодня доверено сообщать новости, разрушают свободу прессы изнутри — не действиями государственных чиновников, а собственным отказом от репортерской честности и объективной журналистики. Обладая глубоким историческим фоном, которым славятся его книги, Левин приглашает вас в путешествие по ранней американской патриотической прессе, которая с гордостью продвигала принципы, изложенные в Декларации независимости и Конституции.
Диапазон
- Почему универсалы побеждают в специализированном мире
- По: Дэвид Эпштейн
- Рассказал: Уилл Дэмрон
- Продолжительность: 10 часов 17 минут
- Полный
Дэвид Эпштейн изучил самых успешных в мире спортсменов, художников, музыкантов, изобретателей, прогнозистов и ученых.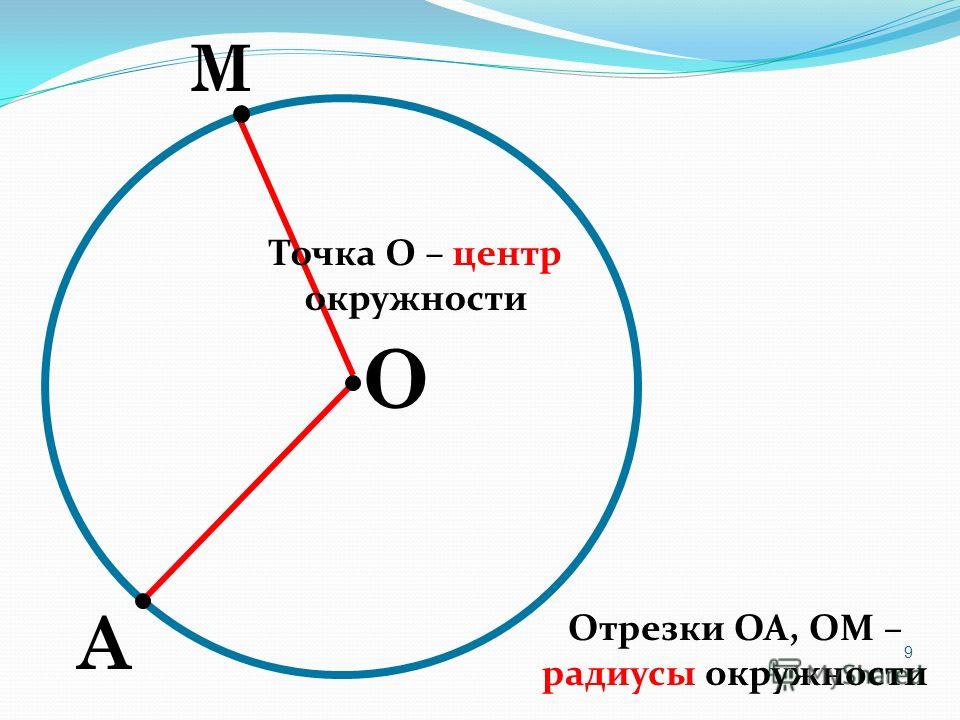 Он обнаружил, что в большинстве областей — особенно в сложных и непредсказуемых — универсалы, а не специалисты, стремятся преуспеть. Универсалы часто поздно находят свой путь и жонглируют многими интересами, а не сосредотачиваются на одном. Они также более креативны, более гибки и способны устанавливать связи, которые их более специализированные сверстники не видят.
Он обнаружил, что в большинстве областей — особенно в сложных и непредсказуемых — универсалы, а не специалисты, стремятся преуспеть. Универсалы часто поздно находят свой путь и жонглируют многими интересами, а не сосредотачиваются на одном. Они также более креативны, более гибки и способны устанавливать связи, которые их более специализированные сверстники не видят.
Фокусное зеркало
- Размышления о самообмане
- По: Джиа Толентино
- Рассказал: Джиа Толентино
- Продолжительность: 9 часов 46 минут
- Полный
Джиа Толентино — несравненный голос своего поколения, борющийся с конфликтами, противоречиями и коренными изменениями, которые определяют нас и наше время. Теперь, в этом ослепительном сборнике из девяти совершенно оригинальных эссе, написанных с редким сочетанием подачи и резкости, остроумия и бесстрашия, она углубляется в силы, искажающие наше видение, демонстрируя беспрецедентную стилистическую мощь и критическую ловкость.
Теперь, в этом ослепительном сборнике из девяти совершенно оригинальных эссе, написанных с редким сочетанием подачи и резкости, остроумия и бесстрашия, она углубляется в силы, искажающие наше видение, демонстрируя беспрецедентную стилистическую мощь и критическую ловкость.
Техасское наводнение
- Внутренняя история Стиви Рэя Вона
- По: Алан Пол, Энди Аледорт, Джимми Вон — эпилог
- Рассказал: Алан Пол, Энди Аледорт, полный состав
- Продолжительность: 11 часов 39 минут
- Полный
Texas Flood предоставляет чистую правду о Стиви Рэе Вогане от тех, кто знал его лучше всего: его брата Джимми, его товарищей по группе Double Trouble Томми Шеннона, Криса Лейтона и Риз Винанс, а также многих других близких друзей, членов семьи, подруг, коллеги-музыканты, менеджеры и члены экипажа.
Пионеры
- Героическая история поселенцев, принесших американский идеал Запада
- По: Дэвид Маккалоу
- Рассказал: Джон Бедфорд Ллойд
- Продолжительность: 10 часов 23 минуты
- Полный
Номер один New York Times Бестселлер лауреата Пулитцеровской премии историка Дэвида Маккалоу заново открывает важную главу в американской истории, которая «сегодня актуальна как никогда» ( The Wall Street Journal ) — заселение Северо-Западной территории мужественными первопроходцами, преодолевшими невероятные трудности, чтобы построить сообщество, основанное на идеалах, определяющих нашу страну.
Три женщины
- По: Лиза Таддео
- Рассказал: Тара Линн Барр, Марин Айрлэнд, Мена Сувари и другие
- Продолжительность: 11 часов 24 минуты
- Полный
В пригороде Индианы мы встречаем Лину, домохозяйку и мать двоих детей, чей брак спустя десять лет потерял свою страсть. Изголодавшись по привязанности, Лина ежедневно борется с приступами паники и, воссоединившись со старым увлечением через социальные сети, заводит роман, который быстро становится всепоглощающим. В Северной Дакоте мы встречаем Мэгги, 17-летнюю ученицу средней школы, у которой якобы есть тайные физические отношения с ее красивым женатым учителем английского языка; последующий уголовный процесс перевернет их тихое сообщество с ног на голову.
В Северной Дакоте мы встречаем Мэгги, 17-летнюю ученицу средней школы, у которой якобы есть тайные физические отношения с ее красивым женатым учителем английского языка; последующий уголовный процесс перевернет их тихое сообщество с ног на голову.
Становление
- По: Мишель Обама
- Рассказал: Мишель Обама
- Продолжительность: 19 часов 3 минуты
- Полный
В своих мемуарах, содержащих глубокие размышления и завораживающее повествование, Мишель Обама приглашает слушателей в свой мир, рассказывая о событиях, сформировавших ее — от детства в южной части Чикаго до лет, когда она работала руководителем, уравновешивая требования материнство и работа в ее время, проведенное на самом известном в мире адресе.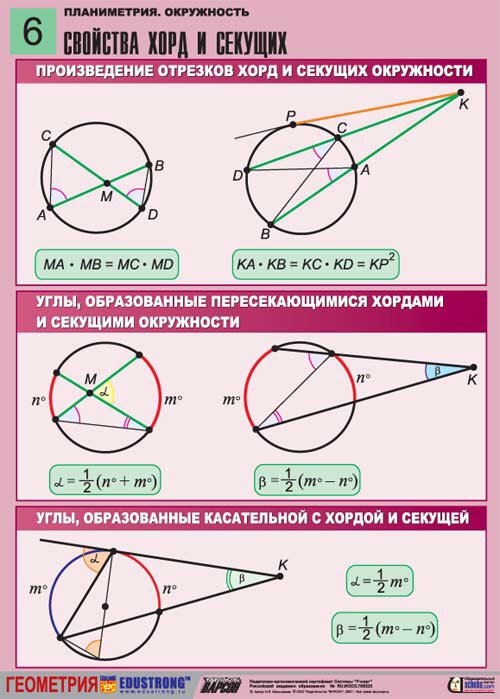

 Винегард
Винегард