Вычисления с обыкновенными и десятичными дробями
Калькулятор осуществляет умножение, разность, сумму и деление двух простых или десятичных дробей. Результат сокращяется.
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.
 lt/public_html/trupmena-1-ru.php on line 93
lt/public_html/trupmena-1-ru.php on line 93Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai. lt/public_html/trupmena-1-ru.php on line 110
lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai. lt/public_html/trupmena-1-ru.php on line 112
lt/public_html/trupmena-1-ru.php on line 112
Как рассчитать проценты, процент от числа
Квадратное уравнение — Калькулятор
Другие полезные темы:
| Делимся | знаниями |
Если думаешь, что Это интересно для друга, напиши
Умножение обычных дробей: Умножение дробей
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе, всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели.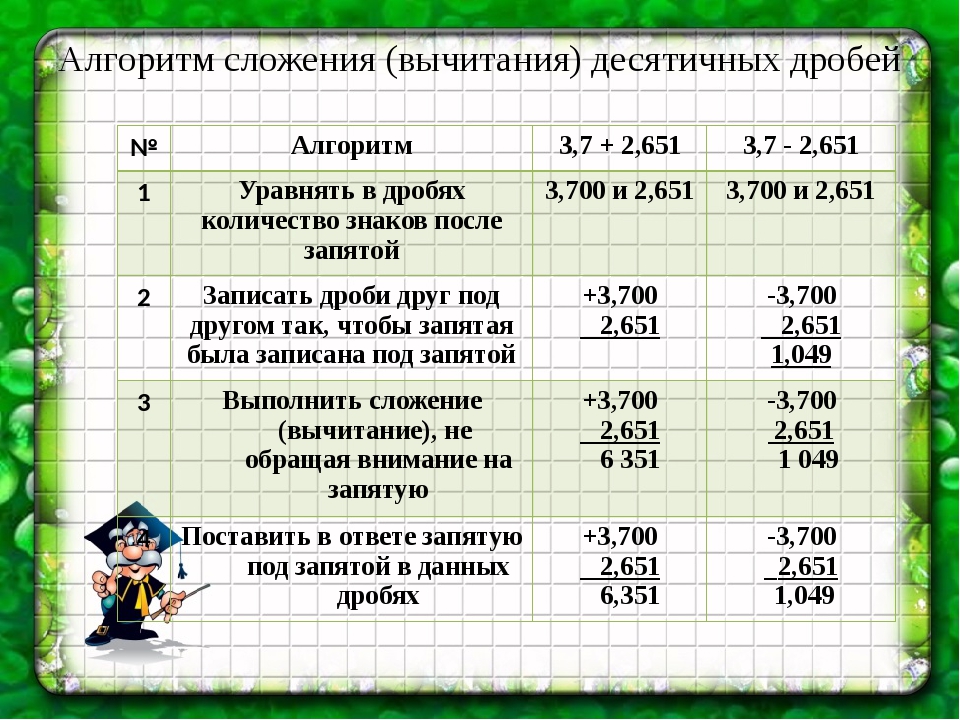 А как складывать такие дроби мы уже знаем.
А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2.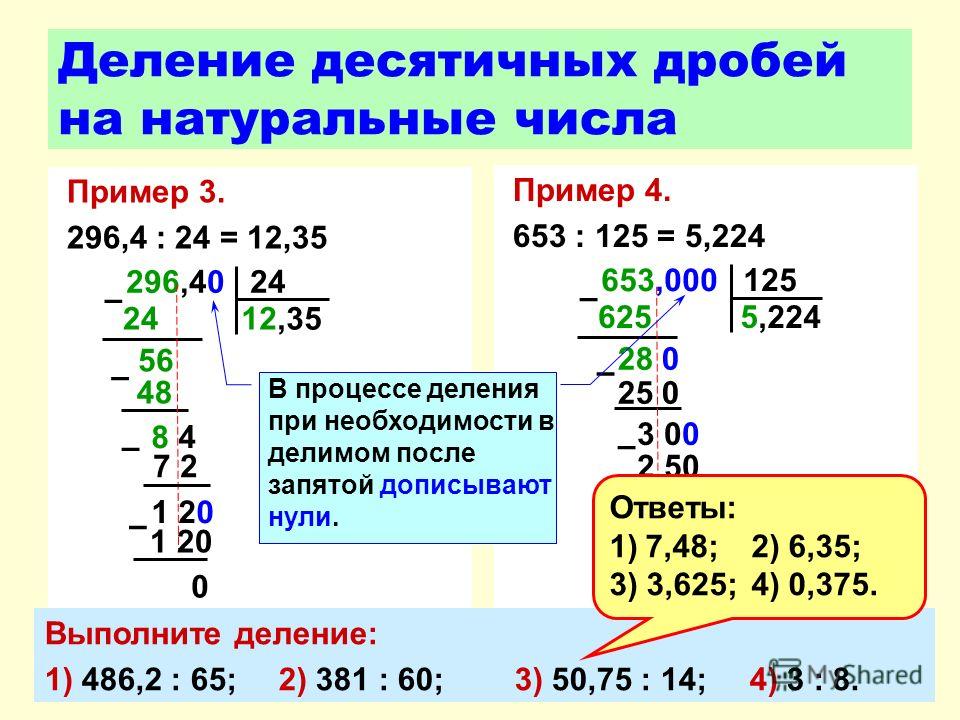 Делим 6 на 2, получаем 3.
Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?
«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6.
НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6.
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.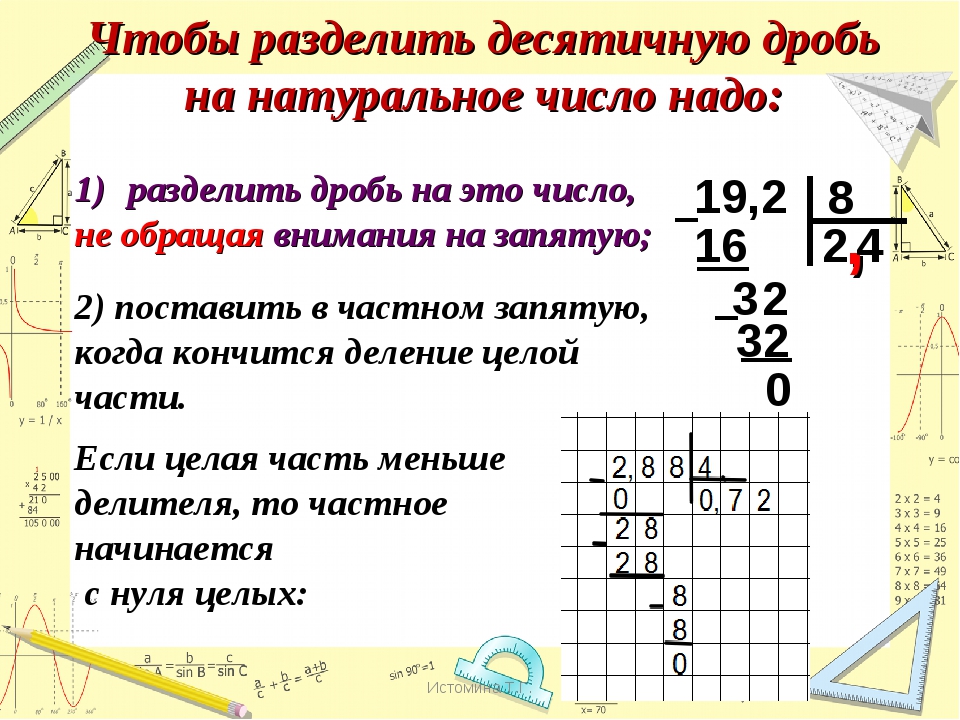
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь на число 1.
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2. Найти значение выражения
Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь
- обратным числа 3 является дробь
- обратным числа 4 является дробь
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Обратное делителю 2 это дробь . Значит нужно умножить на
Получили ответ . Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
Допустим, имелось пиццы:
Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на .
Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь
Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражение
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим на
Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь
Допустим, имеется половина пиццы:
Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1. Найти значение выражения
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
Пример 2. Найти значение выражения
Умножаем первую дробь на дробь обратную второй:
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Найдите значение выражения:
Решение:
Задание 8. Найдите значение выражения:
Решение:
Задание 9. Найдите значение выражения:
Решение:
Задание 10. Найдите значение выражения:
Решение:
Задание 11. Найдите значение выражения:
Решение:
Задание 12. Найдите значение выражения:
Решение:
Задание 13. Найдите значение выражения:
Решение:
Задание 14. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как умножить обыкновенную дробь на десятичную дробь
В данной публикации мы рассмотрим, каким образом обыкновенную (простую) дробь можно умножить на десятичную. Также разберем примеры для закрепления теоретического материала.
Произведение обыкновенной и десятичной дробей
Чтобы умножить обыкновенную дробь на десятичную (и наоборот, т.к. от перестановки множителей результат не меняется), необходимо одну из дробей представить в виде другой.
Примечания:
1. Бесконечные десятичные дроби сначала требуется округлить, т.е. оставить конечное количество цифр после запятой.
2. Смешанные обыкновенные дроби сперва необходимо превратить в неправильные.
Примеры
Пример 1
Давайте найдем результат произведения дроби3/20
и 2,19.
Решение 1
Переведем обыкновенную дробь в десятичную:
3/20
=
3⋅5/20⋅5
=
15/100
= 0,15
Теперь выполним умножение десятичных дробей:
0,15 ⋅ 2,19 = 0,3285.
Решение 2
Преобразуем десятичную дробь в обыкновенную:
2,19 = 219/100
=
2 ⋅ 100 + 19/100
=
219/100
Остается только найти произведение двух обыкновенных дробей:
219/100
⋅
3/20
=
219 ⋅ 3/100 ⋅ 20
=
657/2000
Пример 2
4/9
.
Решение
Преобразуем заданную смешанную дробь в неправильную:
24/9
=
2 ⋅ 9 + 4/9
=
22/9
Далее у нас есть выбор: либо мы переводим десятичную дробь в обыкновенную, либо наоборот. Выберем первый вариант.
24/100
=
6 ⋅ 100 + 24/100
=
624/100
Теперь разделим одну простую дробь на другую:
624/100
:
22/9
=
624/100
⋅
9/22
=
624 ⋅ 9/100 ⋅ 22
=
5616/2200
= 2
1216/2200
= 2
152/275
≈ 2,5528
Умножение обыкновенных и десятичных дробей
Умножение обыкновенных и десятичных дробей сводится к умножению либо обыкновенных дробей, либо десятичных дробей.
Чтобы умножить обыкновенную дробь на десятичную, надо обе дроби привести к одному виду.
Любую десятичную дробь можно перевести в обыкновенную (как слышим, так и пишем).
Например,
Если возможно, полученную дробь следует сократить.
Например,
Обыкновенную дробь перевести в десятичную (речь идёт о несократимой дроби) можно только в том случае, когда её знаменатель равен 2, 5 или числу, которое можно разложить на множители, состоящие только из двоек и пятёрок.
Например,
40=2∙2∙2∙5.
Разложение числа состоит только из двоек и пятёрок, значит, любое число можно разделить на 40. Делим 7 на 40 и получает представление обыкновенной дроби в виде десятичной.
Перейдём к примерам умножения обыкновенных и десятичных дробей.
Примеры.
1-й способ
Так как знаменатель обыкновенной дроби равен 5, эту дробь можно перевести в десятичную и выполнить умножение десятичных дробей:
2-й способ
Переведём десятичную дробь в обыкновенную, сократим полученную дробь и выполним умножение обыкновенных дробей:
то есть при любом способе получаем одинаковый ответ, отличается только форма записи.
Знаменатель обыкновенной дроби равен 14. 14=2∙7. Такую дробь перевести в десятичную перевести не получится. Значит, десятичную дробь представим в виде обыкновенной:
Здесь ответ может быть записан как в виде обыкновенной, так и в виде десятичной дроби.
Дробь со знаменателем 11 не можем представить в виде десятичной. Поэтому переводим десятичную дробь в обыкновенную:
1-й способ
Раскладываем знаменатель на простые множители: 4=2∙2.
Переводим обыкновенную дробь в десятичную:
2-й способ:
Сведём умножение десятичной и обыкновенной дробей к умножению обыкновенных дробей:
Я рекомендую при возможности выбора стараться работать как с обыкновенными, так и с десятичными дробями. Важно освоить навыки счёта на уроках математики в 5-6 классах, а старших классах вам предстоит решать другие задачи.
Вычисления с обыкновенными и десятичными дробями
Калькулятор осуществляет умножение, разность, сумму и деление двух простых или десятичных дробей. Результат сокращяется.
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php
on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai. lt/public_html/trupmena-1-ru.php
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Как рассчитать проценты, процент от числа
Квадратное уравнение — Калькулятор
Другие полезные темы:
| Делимся | знаниями |
Если думаешь, что Это интересно для друга, напиши
Умножение дробей и смешанных чисел. Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)
Умножение дробей и смешанных чисел.
Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)Главное замечание по теме от проекта dpva.ru: Дети часто путают действия с правильыми дробями (это такие дроби, где числитель меньше знаменателя) и со смешанными числами (состоящими из целой и дробной части).
Умножение правильных дробей и смешанных чисел на натуральное число: Чтобы умножить правильную дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения. Для того, чтобы умножить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее числитель умножить на это число, а знаменатель оставить без изменения, после чего выделить целую часть.
Умножение дробей : Чтобы умножить дробь на дробь, надо 1) найти произведение числителей и произведение знаменателей этих дробей. 2) первое произведение записать числителем, второе — знаменателем.
Умножение смешанных чисел: Для того, чтобы выплнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Деление правильных дробей и смешанных чисел на натуральное число: Чтобы разделить правильную дробь на натуральное число, надо ее знаменатель умножить на это число, а числитель оставить без изменения. Для того, чтобы разделить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее знаменатель умножить на это число, а числитель оставить без изменения, после чего выделить целую часть.
Памятка: Взаимно обратные числа это числа, произведение которых равно 1. Например: дроби 71/17 и 17/71 взаимно обратны. Делимое — то, что делят. Делитель — то, на что делят.
Деление дробей: Для того, чтобы разделить одну дробь на другую, надо делимое умножить на число обратное делителю.
Деление смешанных чисел: Для того, чтобы выполнить деление смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом деления дробей.
Умножение и деление десятичных дробей
С десятичными дробями намного проще производить разные действия, чем с обычными, но здесь также есть свои недостатки. Например, необходимо очень тщательно следить за положением десятичной запятой.
Например, рассмотрим пример умножения: 0,2х0,2.
Вы можете попробовать решить этот пример по аналогии со сложением: 2+2=4, также 2×2=4, тогда, поскольку 0,2+0,2=0,4. Возможно, и 0,2х0,2=0,4? Нет, этого не может быть, и я сейчас докажу вам это.
Перейдем обратно к обыкновенным дробям, с которыми мы научились так хорошо обращаться: $0,2=\frac{2}{10}$. Теперь перемножим дроби по старой методике: $\frac{2}{10} \times \frac{2}{10}=\frac{4}{100}$ (числитель умножаем на числитель, знаменатель на знаменатель). А в десятичных дробях — это 0,04. Следовательно, 0,2 х 0,2 отнюдь не равно 0,4. 0,2х0,2=0,04. Мы можем решить еще несколько примеров на умножение десятичных дробей, заменяя их на эквиваленты в обычных дробях. Например: 0,82х0,21=0,1772, а 0,82х2,1=1,772. (Это можно проверить следующим образом: $\frac{82}{100} \times \frac{21}{100}=\frac{1772}{10000}$, а $\frac{82}{100} \times \frac{21}{10}=\frac{1772}{1000}$.)
Теперь мы можем сформулировать общее правило:
При умножении десятичных дробей количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах.
Так, при умножении 0,2х0,2 общее количество цифр справа от десятичной запятой в перемножаемых числах равно 2, и это означает, что 0,2х0,2=0,04 (ноль справа от десятичной запятой также является значащей цифрой).
Естественно, что если один из сомножителей является целым числом, то он не влияет на положение десятичной запятой. Положение десятичной запятой в произведении будет таким же, как и в том сомножителе, который является десятичной дробью.
То есть 0,2х2=0,4; 1,5х5=7,5; а 1,1х154=169,4.
Эти результаты соответствуют правилу умножения, и в любом случае количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах.
Определить положение запятой в случае деления десятичных дробей можно по аналогичной методике, действуя в обратном порядке. Но обычно при делении процедуру стараются упростить и приводят делитель или знаменатель (если деление проводят с помощью обычных дробей) к виду целого числа, не содержащего значащих чисел справа после запятой.
Предположим, нам надо 1,82 разделить на 0,2. Это выражение можно записать как $\frac{1,82}{0,2}$. Не изменяя величины дроби, умножаем числитель и знаменатель на 10. Тогда 1,82х10 (в соответствии с правилом определения положения десятичного знака) равно 18,20, или 18,2, поскольку ноль, стоящий справа после последней значащей цифры, не изменяет величины числа и, следовательно, его можно опустить. Точно так же 0,2х10=2,0, или просто 2 (поскольку 2 плюс ноль десятых равно 2).
Следовательно, дробь можно записать как $\frac{18,2}{2}$ – и теперь знаменатель является целым числом, следовательно, при делении положение десятичного знака после запятой не меняется, так же как и в случае деления. Раз в числителе одна значащая цифра справа после запятой, то и результат должен иметь одну значащую цифру справа после запятой, то есть — $\frac{18,2}{2}=9,1$.
Освоив деление десятичных дробей, мы сможем переводить обычные дроби в десятичные. Предположим, нам нужно найти десятичный эквивалент для $\frac{1}{40}$. Мы можем представить эту дробь в виде $\frac{1,000}{40}$, а затем произвести деление. Поскольку мы делим на целое число, то положение десятичной запятой не меняется. Проведем деление:
Таким образом, мы показали, что десятичный эквивалент $\frac{1}{40}$ равен 0,025. Это можно проверить, переведя 0,025 в обычную дробь: $0,025=\frac{2}{100}+\frac{5}{1000}$, или $\frac{20}{1000}+\frac{5}{1000}$, или $\frac{25}{1000}$, или если произвести деление, то получим $\frac{1}{40}$.
Ну, а если вы все-таки допустили ошибку при исчислении находясь заграницей, то что бы не выглядеть глупо в глазах иностранцев, обязательно надо исправится и извинится. Для тех, которые, как и я, не знаю, как извиниться по-английски, рекомендую почитать статью на сайте e-english.ru. Это значительно улучшит ваши познания и даст возможность не делать ошибок, хотя бы в этом.
Материалы по теме:
Поделиться с друзьями:
Загрузка…Умножение и деление дробей. Тест — тренажер 6 класс — Kid-mama
Умножение и деление обыкновенных дробей
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
Выполните умножение или деление и введите ответ. Сократите дробь, если это возможно. Неправильную дробь переведите в смешанное число, иначе будет засчитана ошибка.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
Если вы не знаете, как умножать и делить обыкновенные дроби, читайте статью:
Тест можно использовать как тренажер, проходя его несколько раз. Каждый раз задания выпадают разные.
Умножение дроби на целое число
Чтобы умножить дробь на целое число, помните, что умножение — это повторное сложение.
Пример 1:
Умножить 1 7 ⋅ 3 .
Запишите умножение в виде сложения. Добавлять 1 7 три раза.
1 7 ⋅ 3 знак равно 1 7 + 1 7 + 1 7
Теперь нам просто нужно добавить дроби с одинаковыми знаменателями.Знаменатели оставьте неизменными, а числители сложите.
знак равно ( 1 + 1 + 1 ) 7 знак равно 3 7
Пример 2:
Умножить 5 ⋅ 3 16 .
5 ⋅ 3 16 знак равно 3 16 + 3 16 + 3 16 + 3 16 + 3 16 знак равно 5 ⋅ 3 16 знак равно 15 16
Другой способ подумать об этом — переписать целое число в виде дроби со знаменателем 1 .
5 ⋅ 3 16 знак равно 5 1 ⋅ 3 16
Затем умножьте числители а также знаменатели , согласно обычным правилам для умножение дробей .
знак равно 5 ⋅ 3 1 ⋅ 16 знак равно 15 16
В некоторых случаях ваш ответ может быть больше, чем 1 , поэтому вы захотите переписать его как смешанное число .Возможно, вам также придется уменьшить фракцию чтобы получить его в простейшем виде.
Пример 3:
Умножить 1 4 ⋅ 10 .
1 4 ⋅ 10 знак равно 10 4
И числитель, и знаменатель имеют общий множитель: 2 . Разделите оба на 2 .
знак равно 5 2
Перепишите эту неправильную дробь как смешанное число.
знак равно 2 1 2
Рабочий лист умножения дробей с общими знаменателями
Ричард Вильялонundefined undefined / Getty Images
Обновлено 21 февраля 2019 г.
Рабочий лист № 1 (Ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 1
Каждый рабочий лист содержит множество дробей с общим (одинаковым) знаменателем.При умножении дробей просто умножьте числитель (верхнее число), затем умножьте знаменатель (нижнее число) и при необходимости уменьшите до наименьшего члена.
- Пример 1: 1/4 x 3/4 = 3/16 (1 x 3 вверху и 3 x 4 внизу) в этом примере дробь не может быть уменьшена дальше.
- Пример 2: 1/3 x 2/3 = 2/9 Это не может быть уменьшено дальше.
- Пример 3: 1/6 x 2/6 = 2/36 В этом случае дробь может быть дополнительно уменьшена. Оба числа можно разделить на 2, что дает нам 1/18, что является сокращенным ответом.
Подобные рабочие листы содержат упражнения для учащихся, чтобы улучшить их понимание.
Рабочий лист № 2 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 2
Умножение неправильных дробей, Рабочий лист № 3 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 3
Рабочий лист № 4 (ответы на 2-й странице PDF)
Д.РасселРаспечатать PDF: Рабочий лист № 4
Рабочий лист № 5 (Ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 5
Рабочий лист № 6 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 6
Рабочий лист № 7 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 7
Рабочий лист № 8 (ответы на 2-й странице PDF)
Д.РасселРаспечатать PDF-файл: Рабочий лист № 8
Рабочий лист № 9 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 9
Рабочий лист № 10 (Ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 10
Умножение и деление дробей, Урок 2
Mathscene — Умножение и деление дробей, Урок 2| 2006 Rasmus ehf | Фракции и | Печать |
Урок 2.
Умножение дробей и целых номера:
| Изменить целое число в фракция | |
| Тогда умножить. |
Только числитель умножается на целое числа.
Умножение дроби на дробь: (общий знаменатель не обязателен)
| Первый умножить числители | ||
| Тогда умножаем знаменатели | ||
2 2 = 1 | 2 1 = 2 | Вы можно упростить, прежде чем умножить, и мы можем отменить обычное коэффициент 2 |
| 2 4 = 8 | ||
Замена смешанных чисел на неправильные дроби:
Пример: Умножьте целое число (2) на знаменатель (3) и прибавляем к числителю (1)
| Вы так это 2 3 + 1 = 7 | |
| В знаменатель остается прежним. |
Смешанные числа заменены на неправильные дроби перед умножением.
| Изменить смешанные числа в неправильные дроби | |
| Look для исключения общих факторов | |
| ср может отбросить множитель 4 из | |
| Тогда упростить, чтобы получить правильный ответ |
Сначала изменяются смешанные числа на неправильные дроби, а затем упрощается.
Иногда переменные (буквы) используются.
Применяются те же правила: первый уменьшить, а затем упростить.
На дроби
Чтобы разделить дроби, инвертируйте делитель (вторая дробь) и умножаем.
| инвертировать делитель (второй дробь) и умножаем | |
| Тогда упростить, исключив общие множители, умножить и упростить. |
Целые числа необходимо заменить на фракции.
| Изменить целое число в дробь | |
| инвертировать делитель (вторая дробь) и умножаем |
Смешанные числа необходимо заменить на неправильные дроби.
| Изменить смешать число в неправильную дробь | |
| инвертировать делитель (вторая дробь) и умножаем | |
| Затем продажа общие факторы и упростить |
Иногда алгебраические переменные использовал.
| инвертировать делитель (вторая дробь) и умножаем | |
| Тогда исключая общие факторы и упрощая |
Те же правила применяются для номеров и буквы.
Попробовать тест 2 на
Умножение и деление дробей.
Не забудьте использовать свой
Контрольный список.
| Параметр | Описание |
|---|---|
| Неправильное преобразование | Если дробь смешанная, отображаются шаги для преобразования в неправильную дробь. |
| Неправильная фракция | Если дробь смешанная, значения окончательной неправильной дроби. |
| Умножить | Показывает последний шаг умножения. |
| Ответ | Показывает решение. Обратите внимание, это решение не упрощено. |
| Наибольший общий делитель | Используется для упрощения ответа. Наибольшее или наибольшее целое число, которое разделит числитель и знаменатель без получения дроби. |
| Разделить на GCD | Показывает числитель и знаменатель, разделенные на НОД, чтобы уменьшить дробь. |
| Ответ (упрощенный) | Решение в правильном или неправильном формате. |
| Ответ (смешанный) | Если раствор является неправильной дробью, отображается преобразованная смешанная дробь. Смешанная фракция показывает дробь с целой частью в дополнение к оставшейся части фракции. |
Калькулятор дробей
Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей в десятичные дроби.Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.
Калькулятор смешанных чисел
Калькулятор упрощенных дробей
Калькулятор десятичных дробей в дроби
Калькулятор дробей в десятичную
Калькулятор дробей большого числа
Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.
В математике дробь — это число, которое представляет собой часть целого.Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих указанное целое. Например, в дроби
числитель равен 3, а знаменатель — 8. Более наглядный пример может включать пирог с 8 кусочками. 1 из этих 8 ломтиков будет составлять числитель дроби, а всего 8 ломтиков, составляющих весь пирог, будут знаменателем. Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа.Обратите внимание, что знаменатель дроби не может быть 0, так как это сделает дробь неопределенной. Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.Дополнение:
В отличие от сложения и вычитания целых чисел, таких как 2 и 8, для этих операций с дробями требуется общий знаменатель. Один из методов нахождения общего знаменателя заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.
Альтернативный метод нахождения общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и, скорее всего, приведет к дроби в упрощенной форме.В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.
| Кратное 2: 2, 4, 6, 8 10, 12 |
| Кратное 4: 4, 8, 12 |
| Кратное 6: 6, 12 |
Первое общее кратное — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.
вычитание:
Вычитание фракции по сути то же самое, что и сложение дроби. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к приведенным ниже уравнениям для пояснения.
Умножение:
Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель.По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
Отдел:
Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число , обратное , равно
. Когда a является дробью, это, по сути, включает в себя замену числителя и знаменателя местами.Следовательно, величина, обратная дроби. Обратитесь к приведенным ниже уравнениям для пояснения.Упрощение:
Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.
, например, более громоздко, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной форме дроби, так и в форме смешанных чисел. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.Преобразование дробей в десятичные дроби:
Преобразование десятичных дробей в дроби выполняется просто. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
, что упрощается до, поскольку наибольший общий делитель между числителем и знаменателем равен 2.Точно так же дроби, знаменатели которых являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь
. Чтобы преобразовать эту дробь в десятичную, сначала преобразуйте ее в дробь.Зная, что первый десятичный разряд представляет 10 -1 , можно преобразовать в 0,5. Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.Преобразование общей инженерной дроби в десятичную дробь
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.
| 64 th | 32 nd | 16 th | 8 th | 4 th | 2 nd | 905 902 (десятичное) 905(десятичное) | ||||||||||||||||||||||||||||||||||||||||||||||
| 1/64 | 0,015625 | 0,396875 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 2/64 | 1/32 | 03125 | 0,79375 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 3/64 | 0,046875 | 1,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 4/64 2/64 | 0,0625 | 1,5875 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 5/64 | 0,078125 | 1,984375 | 9015 9015 9015 9015 9015 9015 90150.09375 | 2.38125 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 7/64 | 0.109375 | 2.778125 | 8/64 | 9015 | 8/64 | 0,125 | 3,175 | |||||||||||||||||||||||||||||||||||||||||||||
| 9/64 | 0,140625 | 3,571855 | 3,571875 | 0.15625 | 3.96875 | |||||||||||||||||||||||||||||||||||||||||||||||
| 11/64 | 0.171875 | 4.365625 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,1875 | 4,7625 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 13/64 | 0.203125 | 5,159375 | 9015/9015 9015 9015 9015 9015 9015 9015 9015 9015 90150.21875 | 5.55625 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 15/64 | 0,234375 | 5.953125 | 1/4 | 0,25 | 6,35 | |||||||||||||||||||||||||||||||||||||||||||||||
| 17/64 | 0,265625 | 9015 9015 9015 9015 9015 9015 9015 9015 90150.28125 | 7,14375 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 19/64 | 0,296875 | 7,540625 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 20/64 10/64 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20/64 10/64 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20/64 10/64 | 90150,3125 | 7,9375 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 21/64 | 0,328125 | 8,334375 | 9015/9015 9015 9015 9015 9015 9015||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.34375 | 8,73125 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 23/64 | 0,359375 | 9.128125 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 24/50 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24/50 9015 | 0,375 | 9,525 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 25/64 | 0,3 | 9.9218875 | 9015 9.9218759.921875 | 0.40625 | 10.31875 | |||||||||||||||||||||||||||||||||||||||||||||||
| 27/64 | 0,421875 | 10.715625 | 10.715625 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 1450 9015 9015 9015 9015 7/64 | 0,4375 | 11,1125 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 29/64 | 0,453125 | 9015 9015 9015 9015 9015 9015 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.46875 | 11. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 31/64 | 0,484375 | 12.303125 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 2/4 | 1/2 | 0,5 | 12,7 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 33/64 | 0,515625 | 13166875 | 13166875 | 0.53125 | 13.49375 | |||||||||||||||||||||||||||||||||||||||||||||||
| 35/64 | 0,546875 | 13.8 | 36/64 9015 9015 9015 9015 | 0.5625 | 14.2875 | |||||||||||||||||||||||||||||||||||||||||||||||
| 37/64 | 0.578125 | 14.684375 | 9015 9015 9015 9015 9015 9015 90150.59375 | 15.08125 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 39/64 | 0.609375 | 15.478125 | 0,625 | 15.875 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 41/64 | 0,640625 | 16.2161875 9015 9015 9015 9015 9015 9015 9015 9015 9015 | 9015 50.65625 | 16.66875 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 43/64 | 0,671875 | 17,065625 | 17.065625 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 44/64 9015 9015 | 0,6875 | 17,4625 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 45/64 | 0,703125 | 17.859375 | 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 90150.71875 | 18.25625 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 47/64 | 0,734375 | 18.653125 | 48/64 | 90151250/64 | 3/4 | 0,75 | 19,05 | |||||||||||||||||||||||||||||||||||||||||||||
| 49/64 | 0,765625 | 9015 9015 9015 9015 9015 9015 9015 90150.78125 | 19.84375 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 51/64 | 0,796875 | 20.240625 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 9015/64/64 9015 9015 9015 9016 52/64 9015 | 0,8125 | 20,6375 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 53/64 | 0,828125 | 21,034375 | 9015 545 90159015 545 905 | 0.84375 | 21,43125 | |||||||||||||||||||||||||||||||||||||||||||||||
| 55/64 | 0,859375 | 21,828125 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,875 | 22,225 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 57/64 | 0,8 | 22.621875 9015 9015 9015 9015 9015 9015 | 0. | 23,01875 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 59/64 | 0,921875 | 23,415625 | 9015 9015 9015 9015 9015 9015 9015 901560/64 9015 9015 9015 9015 | 0,9375 | 23,8125 | |||||||||||||||||||||||||||||||||||||||||||||||
| 61/64 | 0,953125 | 24.2093151 9015 625 9015 625 9015 9015 9015 625 | 0.96875 | 24.60625 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 63/64 | 0,984375 | 25,003125 | 64/64 | 9015 9015 | 64/64 9015 | 4/4 | 2/2 | 1 | 25,4 |
Как рассчитать дроби
Что такое дроби?
Дробное число или дробь используется для представления сегмента целого числа.
Дробь состоит из двух чисел, расположенных одно над другим. Первое число, которое находится над строкой, — это числитель . Второе число, расположенное под чертой, — это знаменатель .
Знаменатель указывает общее количество равных частей, на которые что-либо делится. Числитель показывает, сколько из этих равных частей необходимо учитывать.
Самый простой способ запомнить дроби — обозначить линию, разделяющую каждое число, «из».Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей.
Как можно представить дроби?
Дроби могут быть представлены тремя способами: как правильные дроби, неправильные дроби и смешанные дроби.
- Правильная дробь — это дробь, в которой числитель меньше знаменателя. Например, ⅔ (две трети) или ⅞ (семь восьмых).
- У неправильной дроби числитель больше знаменателя. Например, 8/5 (восемь пятых) или 13/4 (тринадцать четвертей).
- Смешанное число объединяет целое число и дробь. Например, 5¾ (пять и три четверти) или 12⅖ (двенадцать и две пятых).
Упрощение дробей
Процесс упрощения дробей сводит их к простейшей форме. Например, гораздо проще называть что-то ½, а не 4/8.
Есть два способа упростить дробь.
Первый метод — разделить верхнюю и нижнюю части дроби поровну на целые числа больше 1, пока вы не сможете продолжить.В качестве примера возьмем дробь 24/108:
- Разделите каждое число на 2, чтобы получить 12/54
- Разделите еще раз на 2, чтобы получить 6/27
- Разделите на 3, чтобы получить 2/9
Сложение дробей
Чтобы сложить дроби, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители.
Дополнение: Пример 1
Допустим, вы хотите добавить дробь ¼ к ¼.
Знаменатели уже те же, поэтому вы можете перейти ко второму шагу и прибавить 1 к 1.
Вторая половина дроби остается неизменной, поэтому сложение дробей ¼ и ¼ дает 2/4 (или ½).
Дополнение: Пример 2
Допустим, вы хотите сложить дроби ⅓ и ⅙.
Чтобы знаменатели совпали, измените ⅓ на 2/6.
Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ — 3/6. Упростите это до ½.
Вычитание дробей
Вычитание дробей работает аналогично:
- Шаг 1. Убедитесь, что знаменатели совпадают.
- Шаг 2. Вычтите числители
- Шаг 3 — При необходимости упростите дробь
Вычитание: Пример 1
Допустим, вас попросили потренироваться ¾ — ¼
Первый шаг относительно прост, потому что числа совпадают.
Второй шаг включает в себя вычитание первых чисел и затем перенос ответа над тем же знаменателем.
Таким образом, ¾ — be будет обработано как 3-1 = 2
Следовательно, ответ будет 2/4, что составляет ½.
Умножение дробей
Умножение дробей относительно легко; вы просто умножаете верхние числа и нижние числа.
Если, например, вы умножите дроби ½ и ⅓, вы получите. От вас не ждут, что вы найдете общий знаменатель путем умножения.
На дроби
Чтобы разделить дроби, вам нужно перевернуть дробь, которую вы делите, вверх дном. Например, если вы хотите разделить ½ на, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и у вас останется 3/2.
Может потребоваться дальнейшее уменьшение фракции для получения сложной фракции.
Распространенные ошибки и на что следует обращать внимание
При сложении и вычитании дробей может быть легко запутаться.Студенты часто складывают или вычитают знаменатели или числители двух дробей и обычно не замечают связи между знаменателем. Чтобы еще больше усугубить путаницу, к числителям и знаменателям следует подходить в расчетах как к целым числам, например, когда вам нужно умножить дробь.
Возьмем для примера сложение ¾ и ⅙.
Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.
Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.
Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.
Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.
Прочие типичных ошибок включают:
- При сложении или вычитании дробей кандидаты могут забыть сначала преобразовать дроби, чтобы у них был общий знаменатель.
- Изменение знаменателя дроби без внесения необходимых изменений в числитель.
- Непонимание вопроса полностью; например, деление вместо вычитания или умножение вместо сложения.
- Знаменатель остается неизменным при ответах на вопросы, касающиеся умножения или сложения.
Понимание взаимосвязи между смешанными числами и неправильными дробями, а также того, как переводить одно в другое, имеет решающее значение при работе с дробями.
Дроби и десятичные дроби: умножение дробей и смешанных чисел Учебное пособие
Умножение дробей и смешанных чисел
Умножение дробей довольно просто по сравнению со сложением и вычитанием.И угадай что? Нам не нужно искать общий знаменатель. Мы, и , должны убедиться, что каждое число является дробной частью: смешанные числа или целые числа недопустимы. Это клуб элитной фракции.
Просто выполните следующие четыре простых шага:
- Преобразуйте все смешанные числа или целые числа в неправильные дроби.
- Умножьте числители.
- Умножьте знаменатели.
- Уменьшите окончательный ответ и при необходимости преобразуйте его обратно в смешанное число.
Пример умножения 1
| Умножьте числители, затем умножьте знаменатели. | |
| Уменьшить дробь. 12 и 72 имеют GCF 12, поэтому разделите верхнюю и нижнюю на 12. | |
| Стрела, вот и наш ответ. |
Пример умножения 2
Сокращение: перекрестное сокращение
Вместо уменьшения дроби в конце задачи мы можем перекрестно сократить перед умножением .Это не обязательно, но это сэкономит несколько шагов.
Перекрестное сокращение означает, что при умножении дробей мы можем уменьшить любой числитель с любым знаменателем . В этом примере 5 и 10 можно разделить на 5, даже если они не принадлежат к одной и той же дроби.
Давайте еще раз посмотрим на пример 1 и посмотрим, как использовать этот метод.
Калькулятор онлайн — Калькулятор процентов. Найти указанные проценты от числа
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Понятие о проценте
Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.д. Ясно, что понимание такой информации необходимо в современном обществе.
Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается
процент знаком %, Таким образом,
1% — это 0,01, или \( \frac{1}{100} \) часть величины
Приведем примеры:
— 1% от минимальной заработной платы 2300 р. (сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую
составляет масса растворенного вещества от массы всего раствора).
Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.
Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.
Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.
Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.
Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:
\( 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 \)Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить
на 100:
В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.
Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.
Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.
Задачи на проценты
Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.
В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.
1. Нахождение процента от числа.
Чтобы найти \( \frac{p}{100} \) от a, надо a умножить на \( \frac{p}{100} \):
Итак, чтобы найти р% от числа, надо это число умножить на дробь \( \frac{p}{100} \). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x
2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью \( \frac{p}{100} , \; (p \neq 0) \), надо b разделить на \( \frac{p}{100} \):
\( a = b : \frac{p}{100} \)
3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а \( (a \neq 0) \), надо сначала узнать, какую часть b составляет от а, а
затем эту часть выразить в процентах:
Например, 9 г соли в растворе массой 180 г составляют \( \frac{9 \cdot 100}{180} = 5\% \) раствора.
Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.
Нетрудно заметить, что формулы
\( b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) \) взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.Составные задачи на проценты решаются аналогично задачам на дроби.
Простой процентный рост
Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.
Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.
Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму,
которую должен заплатить человек после n дней просрочки, обозначим Sn.
Тогда за n дней просрочки пеня составит рn% от S, или \( \frac{pn}{100}S \), а всего придется заплатить
\( S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S \)
Таким образом:
\( S_n = \left( 1+ \frac{pn}{100} \right) S \)
Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.
Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов.
Как и выше, нетрудно убедиться, что в этом случае
\( S_n = \left( 1- \frac{pn}{100} \right) S \)
Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».
Сложный процентный рост
В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.
Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.
Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.
10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)
10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)
10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)
Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.
А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,12 раз.
Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,12 = 1,13 раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,13 • 1000 = 1,331 • 1000 — 1331 (р.)
Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна Sn р.
Величина p% от S составляет \( \frac{p}{100}S \) р., и через год на счете окажется сумма
\( S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S \)
то есть начальная сумма увеличится в \( 1+ \frac{p}{100} \) раз.
За следующий год сумма S1 увеличится во столько же раз, и поэтому через два года на счете будет сумма
\( S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S \)
Аналогично \( S_3 = \left( 1+ \frac{p}{100} \right)^3 S \) и т.n S \)
Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.
Калькулятор уравнений, интегралов, производных, пределов и пр.
Онлайн-калькулятор позволяет решать математические выражения любой сложности с выводом подробного результата решения по шагам. Также универсальный калькулятор умеет решать уравнения, неравенства, системы уравнений/неравенств и выражения с логарифмами, вычислять пределы функций, определенные/неопределенные интегралы и производные любого порядка (дифференцирование), производить действия с комплексными числами, калькулятор дробей и пр.
Пояснения к калькулятору
- Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.
- Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
- ⌫ — удалить в поле ввода символ слева от курсора.
- C — очистить поле ввода.
- При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
- Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
- Ввод числа в n-ой степени и квадратного корня прозводится кнопками ab и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей →.
Упрощение выражений, раскрытие скобок, разложение многочленов на множители
Калькулятор позволяет произвести некоторые алгебраические преобразования с выражениями. Результат выводится в нескольких вариантах упрощения/разложения/раскрытия скобок и пр.
Решение уравнений и неравенств
Математический калькулятор может решать уравнения и неравентства относительно переменной «x».2}(решить неравенство)
Решение систем уравнений и неравенств
Системы уравнений и неравенств также решаются с помощью онлайн калькулятора. Чтобы задать систему необходимо ввести уравнения/неравенства, разделяя их точкой с запятой с помощью кнопки ;.
Вычисление выражений с логарифмами
В калькуляторе кнопкой loge(x) возможно задать натуральный логарифм, т.е логарифм с основанием «e»: loge(x) — это ln(x). Для того чтобы ввести логарифм с другим основанием нужно преобразовать логарифм по следующей формуле: $$\log_a \left(b\right) = \frac{\log \left(b\right)}{\log \left(a\right)}$$ Например, $$\log_{3} \left(5x-1\right) = \frac{\log \left(5x-1\right)}{\log \left(3\right)}$$
$$\log _2\left(x\right)=2\log _x\left(2\right)-1$$ преобразуем в $$\frac{\log \left(x\right)}{\log \left(2\right)}=2\cdot \frac{\log \left(2\right)}{\log \left(x\right)}-1$$ (найти x в уравнении)Вычисление пределов функций
Предел функции задается последовательным нажатием групповой кнопки f(x) и функциональной кнопки lim.
Решение интегралов
Онлайн калькулятор предоставляет инструменты для интегрирования функций. Вычисления производятся как с неопределенными, так и с определенными интегралами. Ввод интегралов в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
∫ f(x) — для неопределенного интеграла;
ba∫ f(x) — для определенного интеграла.
В определенном интеграле кроме самой функции необходимо задать нижний и верхний пределы.
Вычисление производных
Математический калькулятор может дифференцировать функции (нахождение производной) произвольного порядка в точке «x». Ввод производной в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
f'(x) — производная первого порядка;
f»(x) — производная второго порядка;
f»'(x) — производная третьего порядка.
fn(x) — производная любого n-о порядка.
Действия над комплексными числами
Онлайн калькулятор имеет функционал для работы с комплексными числами (операции сложения, вычитания, умножения, деления, возведения в степень и пр.). Комплексное число обзначается символом «i» и вводится с помощью групповой кнопки xyz и кнопки i
.Деление в столбик десятичных дробей с помощью онлайн-калькулятора
Деление в столбик десятичных дробей с помощью онлайн-калькулятора
Делить десятичные дроби в столбик немного сложнее, чем целые числа из-за плавающей точки, еще задачу усложняет надобность деления остатка. Поэтому если вы хотите упростить этот процесс или проверить свой результат, можно воспользоваться онлайн-калькулятором, который не только выведет ответ, но и покажет всю процедуру решения.
Делим в столбик десятичные дроби с помощью онлайн-калькулятора
Подходящих под эту цель онлайн-сервисов существует большое количество, однако практически все они мало чем отличаются друг от друга. Сегодня мы подготовили для вас два разных варианта вычисления, а вы, ознакомившись с инструкциями, выберите тот, который будет наиболее подходящим.
Способ 1: OnlineMSchool
Сайт OnlineMSchool был разработан для изучения математики. Сейчас на нем присутствует не только множество полезной информации, уроков и задач, но и встроенные калькуляторы, один из которых мы сегодня задействуем. Деление в столбик десятичных дробей в нем происходит так:
- Откройте главную страницу сайта OnlineMSchool и перейдите в раздел «Калькуляторы».
В первую очередь обратите внимание на инструкцию по использованию, представленную в соответствующей вкладке. Рекомендуем с ней ознакомиться.
Теперь вернитесь в «Калькулятор». Здесь вам следует еще раз убедиться, что выбрана правильная операция. Если нет, измените ее, воспользовавшись всплывающим меню.
Введите два числа, используя точку для обозначения целой части дроби, а также отметьте галочкой пункт, если необходимо делить остаток.
Вам будет предоставлен ответ, где подробно расписан каждый шаг получения конечного числа. Ознакомьтесь с ним и можете переходить к следующим вычислениям.
Перед тем как делить остаток, внимательно изучите условие задачи. Часто этого делать не нужно, иначе ответ могут засчитать неправильным.
Всего за семь простых шагов мы смогли поделить десятичные дроби в столбик с помощью небольшого инструмента на сайте OnlineMSchool.
Способ 2: Rytex
Онлайн-сервис Rytex также помогает в изучении математики, предоставляя примеры и теорию. Однако сегодня нас интересует присутствующий в нем калькулятор, переход к работе с которым осуществляется следующим образом:
- Воспользуйтесь ссылкой выше, чтобы перейти на главную страницу Rytex. На ней кликните по надписи «Онлайн калькуляторы».
Опуститесь в самый низ вкладки и на панели слева отыщите «Деление столбиком».
Перед началом выполнения основного процесса прочтите правила использования инструмента.
Теперь в соответствующие поля введите первое и второе число, а затем укажите, нужно ли делить остаток, отметив галочкой необходимый пункт.
Для получения решения нажмите на кнопку «Вывести результат».
Теперь вы можете узнать, как было получено итоговое число. Поднимитесь выше по вкладке, чтобы перейти к вводу новых значений для дальнейшей работы с примерами.
Как видите, рассмотренные нами сервисы практически не отличаются между собой, разве что только внешним видом. Поэтому можно сделать вывод – нет разницы, какой веб-ресурс использовать, все калькуляторы считают правильно и предоставляют развернутый ответ по вашему примеру.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Калькулятор дробей: решение уравнений с дробями
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.
Онлайн калькулятор уравнений с дробями
Дробью в математике называется число, представляющее часть единицы или несколько её частей.
Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными.
- Правильной называется дробь, у которой числитель меньше знаменателя.
- Неправильная дробь – если у дроби числитель больше знаменателя.
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.
Как перевести смешанную дробь в обыкновенную
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя:
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Как перевести десятичную дробь в обыкновенную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
- Записать дробь в виде десятичная
- Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
- Найти наибольший общий делитель и сократить дробь.
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Выполнить сложение дробей путем сложения их числителей.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление в столбик онлайн. Калькулятор наглядного деления.
Деление столбиком онлайн калькулятор может разделить столбиком два числа выдавая полностью расписанный процесс деления.
Калькулятор деления в столбик поддерживает целые числа, десятичные дроби,отрицательные числа и результат с остатком.
- Калькулятор
- Инструкция
- Теория
- История
- Сообщить о проблеме
Для простоты вычислений умножим делимое 1.5 и делитель 9 на 10. Результат (частное) от этого не изменится. В результате пример сводится к делению следующих чисел:
| – | 1 | 5 | 9 | ||||||||||||
| 9 | . | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | ||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| 6 |
Просто введите делимое в поле 1 и делитель в поле 2 и нажмите кнопку “ВЫЧИСЛИТЬ”. Результат появится на экране.
Поддерживаются следующие виды чисел:
1. Целые(1,2,3. ). 2. Десятичное (1.1, 2,35). 3. Отрицательные (-7.35,-2). Дробные числа умножаются на 10 пока не станут целыми.
Разделить одно число на другое является самой сложной задачей арифметики. Данный калькулятор может помочь Вам разобраться как это сделать самостоятельно.
Самое важное запомните: Деление – это обратная операция умножения.
После проведения расчета нажмите на кнопочку “Расчет не верен” если Вы обнаружили ошибку. Или нажмите “расчет верный” если ошибок нет.
Этот калькулятор умеет умножать столбиком два числа.Можно умножать целые и дробные числа, положительные и отрицательные.
Сложение столбиком двух чисел. Можно сложить столбиком два любых числа. Показываются все переносы.
Калькулятор вычитает столбиком и показывает подробное решение.
Данный онлайн калькулятор дробей предназначен для сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и десятичных дробей.
Деление в столбик десятичных дробей с помощью онлайн-калькулятора
Как работать с калькулятором обыкновенных дробей?
Калькулятор предназначен для решения простых дробей и дробей с целыми числами (смешанных). В будущем, планируется внедрение функции решения десятичных дробей, но в данный момент она отсутствует.
Для начала работы с дробным калькулятором необходимо понять очень простой принцип ввода данных. Все целые числа вводятся с помощью больших кнопок, расположенных слева. Все числители вводятся с помощью маленьких белых кнопок, расположенных в правом верхнем блоке цифр. Все знаменатели, соответственно, вводятся путем нажатия на кнопки в правом нижнем углу. Данный способ ввода данных является в некотором роде инновационным, поскольку четко разграничивает целое, числитель и знаменатель, что облегчает вычисления, экономит время и делает взаимодействие с приложением более эффективным.», после чего на цифру шесть на основной клавиатуре. В результате, получится готовый пример:
Теперь нажмите на кнопку равно и получите результат калькуляции. В примере выше проиллюстрирован практически весь арсенал возможностей калькулятора дробей. Точно таким же образом, вы можете осуществлять умножение, деление и вычитание дробей, как простых, так и алгебраических, с одинаковыми и разными знаменателями, целыми числами и т.д. Также, калькулятор может вычислить проценты от дробей, что требуется не так часто, но тем не менее очень важно для решения многих актуальных задач.
Если вам требуется сделать положительное число отрицательным, то сначала введите число, а потом нажмите на кнопку «+/-». После этого число или дробь автоматически обернется в скобки с отрицательным значением или наоборот (в зависимости от изначального статуса числа). Если необходимо удалить число, числитель или знаменатель, то воспользуйтесь соответствующей стрелкой Backspace, которая есть в блоке и числителя и знаменателя. Стрелки работают одинаково и по очереди стирают числа или знаки, находящиеся на дисплее калькулятора.
Управление калькулятором дробей с клавиатуры.
Использовать калькулятор дробей онлайн можно не только с помощью компьютерной мыши, но и с помощью клавиатуры. Здесь логика очень проста:
- Все целые числа вводятся как обычно, нажатиями на клавиши чисел.
- Все числители вводятся с добавлением клавиши CTRL (например, CTRL+1).
- Все знаменатели вводятся с добавлением клавиши ALT (например, ALT+2).
Действия умножения, деления, сложения и вычитания так же инициируются соответствующими кнопками клавиатуры, если они есть (обычно располагаются в правой части, в так называемой области Numpad). Удаление производится нажатием на клавишу Backspace. Действие очистки (красная кнопка «C») вызывается нажатием на клавишу «C». Квадратный корень – нажатием на соседнюю клавишу «V» . Удаление производится нажатием на клавишу Backspace.
Зачем нужен калькулятор дробей онлайн?
Калькулятор дробей онлайн предназначен для решения обыкновенных и смешанных дробей (с целыми числами). Решение дробей часто требуется школьникам и студентам, а также инженерам и аспирантам. Наш калькулятор предоставляет возможность производить с дробями следующие действия: деление дробей, умножение дробей, сложение дробей и вычитание дробей. Также, калькулятор умеет работать с корнями и степенями, а еще с отрицательными числами, благодаря чему он многократно превосходит аналогичные онлайн приложения.
Калькулятор простых дробей онлайн поможет вам решить примеры с дробями и при этом вам не надо беспокоиться о том, как предварительно сократить дробь. Здесь это сделается автоматически, т.к. приложение само вычисляет общий знаменатель и выдает вам готовый результат на экран.
В чем преимущества такого способа решения дробей?
Калькулятор поддерживает работу со скобками, что позволяет решать дроби даже в сложных математических примерах. В частности, действия со скобками часто требуются при вычислении алгебраических дробей или отрицательных дробей, над которыми постоянно приходится корпеть всем школьникам средних классов. Дополнительно, вы можете использовать этот калькулятор для сокращения дробей или решения дробей с разными знаменателями. Более того, в отличии от многих других бесплатных сервисов, данный калькулятор умеет работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.
Калькулятор обыкновенных дробей полностью бесплатный и не требует регистрации. Вы можете использовать его в любое время дня и ночи. Работать можно с помощью мыши или прямо с клавиатуры (это касается как чисел, так и действий). Мы постарались реализовать максимально удобный интерфейс дробных вычислений, благодаря чему сложные математические калькуляции превратятся для вас в одно удовольствие! 🙂
Решебник онлайн в столбик — designflorgroup.ru
Скачать решебник онлайн в столбик txt
Калькулятор дробей — простой и понятный онлайн калькулятор, плюс немного теории. Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором: + − × ÷. = Просто заполните необходимые поля и получите ответ и подробное решение.
Программа предназначена для школьников и студентов всех курсов, позволяя заменить любой решебник по математике. В калькуляторе доступно множество математических функций (тригонометрические, логарифмы, корни, степень, модуль, проценты и др.), что даст возможность решить самое сложное и запутанное уравнение.
Реализовано 3 варианта отображения решения: стандартное, в ввиде дроби и «в столбик» — выбирайте то, какое больше всего нравится. Результат и весь алгоритм решения примера представляется на разлинованном тетрадном листе, размер которого (как и клеток) регулируется по Вашему усмотре. Умножение чисел столбиком. Умножение в столбик значительно более сложная операция, чем сложение и вычитание. Поэтому мы сделали для вас калькулятор, который в онлайн режиме может умножить столбиком любые двузначные числа.
Этим мы отличаемся от массы других сервисов, у которых при использовании больших чисел ответ либо не получается, либо выдается с ошибкой. Очень удобный инструмент, чтобы проверять домашнюю работу ваших детей-школьников.
Пользоваться калькулятором очень просто — введите два числа, произведение которых нужно вычислить и нажмите кнопку умножить. Калькулятор умножения в столбик. Бесплатный Калькулятор онлайн со скобками для расчетов на работе, учёбе или дома. Калькулятор работает на компьютерах, планшетах и смартфонах. Онлайн Калькулятор быстро загружается, считает онлайн, имеет встроенную память. Описание Инструкции Примеры FAQ Из истории Комментарии Все калькуляторы Популярные разделы.
Удобный Калькулятор онлайн для расчетов на работе, учёбе или дома. Калькулятор выполняет как простые арифметические действия, так и расчет процентов, вычисление квадратного корня, решает онлайн сложные выражения со скобками. Провести вычисления с десятичными дробями с помощью онлайн-калькулятора! Чтобы корректно использовать для ввода символов Вашу компьютерную клавиатуру, переведите раскладку языка на ENG (английский).
Калькулятор позволяет проводить вычисления с десятичными дробями. Вы можете брать выражение в скобки. Деление имеет вид дроби с числителем и знаменателем. Вы можете вводить цифры и некоторые символы используя клавиатуру компьютера.
Удобный калькулятор онлайн, с помощью которого вы можете произвести самые сложные расчёты. Калькулятор онлайн. Инструкция. Арифметические операции. Действия с дробями.
Действия с процентами. Возведение в степень. Корень из числа. Вычисление логарифма. Бесплатно. Android. Калькулятор в столбик – очень удобное приложение для андроида, калькулятор с множеством различных функций подойдет как для школьников, так и для взрослых. С помощью данной математической программы вы можете поделить многочлены столбиком. Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е.
отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре. Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покуп.
EPUB, doc, fb2, rtfПохожее:
Как перейти от обыкновенной дроби к десятичной. Калькулятор онлайн.Перевод десятичной дроби в обыкновенную
Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Представление дробей
Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.
Избавляемся от запятой
Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:
Шаг 1 : Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.
Шаг 2 : После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Шаг 3 : Сокращаем полученные дроби до удобоваримого вида:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.
Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.
Шаг 1 : Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Шаг 2 : Теперь нам достаточно представить дробь в виде C/10 n , где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10 3 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10 6 = 625/1000000.
По сути, 10 n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
Шаг 3 : Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Преобразование на слух
Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.
0,025 = 25/1000 = 1/40
Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.
Примеры использования дробей в повседневной жизни
На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.
Работа
Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
0,4 = 4/10 = 2/5
Быт
К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:
0,12 = 12/100 = 3/25
Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.
Заключение
Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Мы уже говорили, что дроби бывают обыкновенные и десятичные . На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильные и неправильные. Также мы узнали, что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части.
Мы ещё не до конца изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходиться сочетать. То есть, при решении задач приходиться применять оба вида дробей.
Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно.
Содержание урокаВыражение величин в дробном виде
Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:
Это выражение означает, что один дециметр был поделен на десять частей, и от этих десяти частей была взята одна часть:
Как видно на рисунке, одна десятая часть дециметра это один сантиметр.
Рассмотрим следующий пример. Показать 6 см и ещё 3 мм в сантиметрах в дробном виде.
Итак, требуется выразить 6 см и 3 мм в сантиметрах, но в дробном виде. 6 целых сантиметров у нас уже есть:
но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. 3 миллиметра это третья часть сантиметра. А третья часть сантиметра записывается как см
Дробь означает, что один сантиметр был разделен на десять равных частей, и от этих десяти частей взяли три части (три из десяти).
В результате имеем шесть целых сантиметров и три десятых сантиметра:
При этом 6 показывает число целых сантиметров, а дробь — число дробных сантиметров. Эта дробь читается как «шесть целых и три десятых сантиметра» .
Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.
Например, запишем без знаменателя. Для этого сначала запишем целую часть. Целая часть это число 6. Записываем сначала это число:
Целая часть записана. Сразу же после написания целой части ставим запятую:
И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:
Любое число, которое представляется в таком виде, называется десятичной дробью .
Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:
6,3 см
Выглядеть это будет следующим образом:
На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части стоят числа 10, 100, 1000 или 10000.
Как и смешанное число, десятичная дробь имеет целую часть и дробную. Например, в смешанном числе целая часть это 6, а дробная часть это .
В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.
Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь без знаменателя будет записана следующим образом:
Читается как «ноль целых, пять десятых» .
Перевод смешанных чисел в десятичные дробиКогда мы записываем смешанные числа без знаменателя, мы тем самым переводим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.
После того, как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит? Рассмотрим следующий пример:
Сначала
И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать количество нулей в знаменателе дробной части.
Итак, считаем количество нулей в дробной части смешанного числа . В знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2
Таким образом, смешанное число при переводе в десятичную дробь обращается в 3,2.
Эта десятичная дробь читается так:
«Три целых, две десятых»
«Десятых» потому что в дробной части смешанного числа находится число 10.
Пример 2. Перевести смешанное число в десятичную дробь.
Записываем целую часть и ставим запятую:
И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим, что в знаменателе дробной части два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.
В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3
Теперь можно перевести это смешанное число в десятичную дробь. Записываем целую часть и ставим запятую:
И записываем числитель дробной части:
Десятичная дробь 5,03 читается так:
«Пять целых, три сотых»
«Сотых» потому что в знаменателе дробной части смешанного числа находится число 100.
Пример 3. Перевести смешанное число в десятичную дробь.
Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.
Перед переводом смешанного числа в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так, чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.
В первую очередь смотрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:
Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это число 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед число 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:
Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала целую часть и ставим запятую:
и сразу записываем числитель дробной части
3,002
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 3,002 читается так:
«Три целых, две тысячных»
«Тысячных» потому что в знаменателе дробной части смешанного числа находится число 1000.
Перевод обыкновенных дробей в десятичные дроби
Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.
Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.
Пример 1.
Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:
Теперь смотрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой число 5
В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,5 читается так:
«Ноль целых, пять десятых»
Пример 2. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует. Записываем сначала 0 и ставим запятую:
Теперь смотрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед числом 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,02 читается так:
«Ноль целых, две сотых».
Пример 3. Перевести обыкновенную дробь в десятичную дробь.
Записываем 0 и ставим запятую:
Теперь считаем количество нулей в знаменателе дроби . Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед числом 5 дописать четыре нуля:
Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь. Записываем после запятой числитель дроби
В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,00005 читается так:
«Ноль целых, пять стотысячных».
Перевод неправильных дробей в десятичную дробь
Неправильная дробь это дробь, у которой числитель больше знаменателя. Встречаются неправильные дроби, у которых в знаменателе находятся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные дроби. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять целую часть.
Пример 1.
Дробь является неправильной дробью. Чтобы перевести такую дробь в десятичную дробь, нужно в первую очередь выделить у нее целую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к и изучить его.
Итак, выделим целую часть в неправильной дроби . Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10
Посмотрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Число 11 будет целой частью, число 2 — числителем дробной части, число 10 — знаменателем дробной части.
Мы получили смешанное число . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:
Теперь считаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
В полученной десятичной дроби 11,2 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Значит неправильная дробь при переводе в десятичную дробь обращается в 11,2
Десятичная дробь 11,2 читается так:
«Одиннадцать целых, две десятых».
Пример 2. Перевести неправильную дробь в десятичную дробь.
Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе находится число 100.
В первую очередь выделим целую часть этой дроби. Для этого разделим 450 на 100 уголком:
Соберём новое смешанное число — получим . А как переводить смешанные числа в десятичные дроби мы уже знаем.
Записываем целую часть и ставим запятую:
Теперь считаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
В полученной десятичной дроби 4,50 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена верно.
Значит неправильная дробь при переводе в десятичную дробь обращается в 4,50
При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5
Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны. Поставим между ними знак равенства:
4,50 = 4,5
Возникает вопрос: а почему так происходит? Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».
Перевод десятичной дроби в смешанное числоЛюбая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби. Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых:
и рядом три десятых:
Пример 2. Перевести десятичную дробь 3,002 в смешанное число
3,002 это три целых и две тысячных. Записываем сначала три целых
и рядом записываем две тысячных:
Пример 3. Перевести десятичную дробь 4,50 в смешанное число
4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых
и рядом пятьдесят сотых:
Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Попробуем доказать, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.
После перевода в смешанное число десятичная дробь 4,50 обращается в , а десятичная дробь 4,5 обращается в
Имеем два смешанных числа и . Переведём эти смешанные числа в неправильные дроби:
Теперь имеем две дроби и . Настало время вспомнить основное свойство дроби, которое говорит, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не изменяется.
Давайте разделим первую дробь на 10
Получили , а это вторая дробь. Значит и равны между собой и равны одному и тому же значению:
Попробуйте на калькуляторе разделить сначала 450 на 100, а затем 45 на 10. Забавная штука получится.
Перевод десятичной дроби в обыкновенную дробь
Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:
и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0, а просто .
Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь.
0,02 это ноль целых и две сотых. Ноль по не записываем, поэтому сразу записываем две сотых
Пример 3. Перевести 0,00005 в обыкновенную дробь
0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Зачастую дети, которые учатся в школе, интересуются, для чего в им в реальной жизни может понадобится математика, в особенности те разделы, которые уже заходят намного дальше, чем простой счет, умножение, деление, суммирование и отнимание. Многие взрослые также задаются данным вопросом, если их профессиональная деятельность очень далека от математики и разнообразных вычислений. Однако стоит понимать, что ситуации бывают всякие, и порой никак не обойтись без той самой, пресловутой школьной программы, от которой мы так пренебрежительно отказывались в детстве. К примеру, вовсе не все знают, как перевести дробь в десятичную дробь, а такие знания могут чрезвычайно пригодится, для удобства счета. Для начала, нужно полностью убедиться, что нужная вам дробь может быть преобразована в конечную десятичную. То же самое касается и процентов, которые также можно легко перевести в десятичные дроби.
Проверка обычной дроби на возможность перевода ее в десятичную
Прежде, чем что-либо считать, необходимо убедиться, что полученная в итоге десятичная дробь будет конечной, иначе она окажется бесконечной и высчитать окончательный вариант будет попросту невозможно. Причем бесконечные дроби также могут быть периодическими и простыми, но это уже тема для отдельного раздела.
Перевести обыкновенную дробь в ее конечный, десятичный вариант можно только в том случае, если ее уникальный знаменатель способен раскладываться только на множители 5 и 2 (простые множители). Причем даже в том случае, если они повторяются произвольное количество раз.
Уточним, что оба эти числа являются простыми, так в итоге разделить без остатка их можно только на самих себя, или же, на единицу. Таблицу простых чисел можно отыскать без проблем в сети интернет, это вовсе не сложно, хотя непосредственного отношения к нашему счету она и не имеет.
Рассмотрим примеры:
Дробь 7/40 поддается преобразованию из обычной дроби в ее десятичный эквивалент, потому что ее знаменатель можно без труда разложить на множители 2 и 5.
Однако, если первый вариант даст в результате конечную десятичную дробь, то, к примеру, 7/60 уже никак не даст подобного результата, так как ее знаменатель не будет уже раскладываться на искомые нами числа, а будет иметь в числе множителей знаменателя тройку.
Перевести обычную дробь в десятичную возможно несколькими способами
После того, как стало понятно, какие дроби можно переводить из обычных в десятичные, можно приступить, собственно, к самому преобразованию. На самом деле, нет ничего сверхсложного, даже для того, у кого школьная программа окончательно «выветрилась» из памяти.
Как переводить дроби в десятичные: наиболее простой метод
Этот способ перевода обычной дроби в десятичную, действительно, является наиболее простым, однако многие люди даже не догадываются о его бренном существовании, так как в школе все эти «прописные истины» кажутся ненужными и не очень-то важными. Между тем, разобраться сможет не только взрослый, но легко воспримет подобную информацию и ребенок.
Итак, чтобы преобразовать дробь в десятичную, нужно умножить числитель, равно как и знаменатель, на одно число. Однако все не так просто, так в результате, именно в знаменателе должно получиться 10, 100, 1000, 10 000, 100 000 и так далее, до бесконечности. Не стоит забывать предварительно проверить, точно ли можно данную дробь превратить в десятичную.
Рассмотрим примеры:
Допустим, нам нужно провести преобразование дроби 6/20 в десятичную. Производим проверку:
После того, как мы убедились, что перевести дробь в десятичную дробь, да еще и конечную, все же, возможно, так как ее знаменатель легко раскладывается на двоечки и пятерки, следует приступить к самому переводу. Самым лучшим вариантом, по логике вещей, чтобы умножить знаменатель и получить результат 100, является 5, так как 20х5=100.
Можно рассмотреть дополнительный пример, для наглядности:
Второй и боле популярный способ
переводить дроби в десятичныеВторой вариант несколько сложнее, однако он пользуется большей популярностью, ввиду того, что он гораздо проще для понимания. Тут все прозрачно и ясно, потому давайте сразу же перейдем к вычислениям.
Стоит запомнить
Для того, что правильно преобразовать простую, то есть обычную дробь в ее десятичный эквивалент, нужно числитель разделить на знаменатель. По сути, дробь – это и есть деление, с этим не поспоришь.
Рассмотрим действие на примере:
Итак, первым делом, чтобы перевести дробь 78/200 в десятичную, нужно ее числитель, то есть число 78, разделить на знаменатель 200. Но первым делом, что должно войти в привычку, нужно произвести проверку, о которой уже говорилось выше.
После произведения проверки, нужно вспомнить школу и делить числитель на знаменатель «уголком» или «столбиком».
Как видите, все предельно просто, и семи пядей во лбу, чтобы легко решать подобные задачки вовсе быть не требуется. Для простоты и удобства приведем также и таблицу самых популярных дробей, которые просто запомнить, и даже не прилагать усилий, чтобы их переводить.
Как перевести проценты в десятичную дробь : нет ничего прощеВот наконец дошел ход и до процентов, которые, оказывается, как гласит все та же, школьная программа, можно перевести в десятичную дробь. Причем тут все будет еще гораздо проще, и пугаться не стоит. Справятся с задачей даже те, кто не заканчивал университеты, а пятый класс школы вовсе прогулял и ничего не смыслит в математике.
Начать, пожалуй, нужно с определения, то есть разобраться, что такое, собственно, проценты. Процент – это одна сотая часть от какого-либо числа, то есть, абсолютно произвольно. От сотни, к примеру, это будет единица и так далее.
Таким образом, чтобы перевести проценты в десятичную дробь, нужно попросту убрать значок %, а потом разделить само число на сотню.
Рассмотрим примеры:
Причем, чтобы произвести обратную «конвертацию», нужно попросту сделать все наоборот, то есть, число нужно умножить на сотню и приписать к нему значок процента. Точно таким же образом, посредством применения полученных знаний, можно также и обычную дробь перевести в проценты. Для этого достаточно будет просто сперва преобразовать обычную дробь в десятичную, а потому уже ее перевести в проценты, а также легко можно произвести и обратное действие. Как видите, ничего сверхсложного нет, все это элементарные знания, которые просто необходимо держать в уме, в особенности, если имеете дело с цифрами.
Путь наименьшего сопротивления: удобные онлайн сервисы
Бывает и так, что считать совершенно не хочется, да и попросту нет времени. Именно для таких случаев, или же, особо ленивых пользователей, в сети интернет есть множество удобных и простых в применении сервисов, которые позволят перевести обычные дроби, а также проценты, в десятичные дроби. Это действительно дорога наименьшего сопротивления, потому пользоваться подобными ресурсами – одно удовольствие.
Полезный справочный портал «Калькулятор»
Для того, чтобы воспользоваться сервисом «Калькулятора», достаточно просто перейти по ссылке http://www.calc.ru/desyatichnyye-drobi.html , и ввести необходимые числа в нужные поля. Причем ресурс позволяет переводить в десятичные, как обычные, так и смешанные дроби.
После краткосрочного ожидания, приблизительно секунды в три, сервис выдаст конечный результат.
Точно таким же образом можно перевести в обычную дробь десятичную.
Онлайн-калькулятор на «Математическом ресурсе» Calcs.su
Еще одним, очень полезным сервисом можно назвать калькулятор дробей на «Математическом ресурсе. Тут также не придется ничего считать самостоятельно, просто выберите из предложенного списка то, что вам нужно и вперед, за орденами.
Далее, в отведенное специально для этого поле, нужно ввести искомое число процентов, которые и нужно преобразовать в обычную дробь. Причем если вам нужны десятичные дроби, то вы легко можете уже сами справиться с задачей перевода или же воспользоваться тем калькулятором, который для этого и предназначен.
В конечном итоге, стоит обязательно добавить, что сколько бы новомодных сервисов не было бы придумано, сколько ресурсов не предлагали бы вам свои услуги, но и голову тренировать периодически не помешает. Потому стоит обязательно применять полученные знания, тем более, что вы потом с гордостью сможете помогать делать уроки собственным детям, а затем и внукам. Для того же, кто страдает от вечной нехватки времени, подобные онлайн-калькуляторы на математических порталах окажутся как раз кстати и даже помогут понять, как перевести обычную дробь в десятичную.
Все дроби делятся на два вида: обыкновенные и десятичные. Обыкновенными называются дроби такого вида: 9/8,3/4,1/2,1 3/4 . В них выделяют верхнее число (числитель) и нижнее число (знаменатель). Когда числитель меньше, чем знаменатель, то дробь называется правильной, в противоположном случае дробь – неправильная. Такие дроби, как 1 7/8 состоят из целой части (1) и дробной части (7/8) и называются смешанными.
Итак, дроби бывают:
- Обыкновенными
- Правильными
- Неправильными
- Смешанными
- Десятичными
Как из обыкновенной дроби сделать десятичную
Как перевести обыкновенную дробь в десятичную, учит курс математики основной школы. Все предельно просто: нужно числитель поделить на знаменатель «вручную» или, если совсем лень, то на микрокалькуляторе. Вот пример: 2/5=0,4;3/4=0,75; 1/2=0,5. Не намного сложнее перевести в десятичную неправильную дробь. Пример: 1 3/4= 7/4= 1,75. Последний результат можно получить и без деления, если учесть, что 3/4=0,75 и прибавить единицу:1+0,75=1,75.
Однако далеко не со всеми обыкновенными дробями все так просто. Например, попробуем перевести 1/3 из обыкновенных дробей в десятичные. Даже тот, кто имел по математике тройку (по пяти бальной системе) заметит, что, сколько бы ни продолжалось деление, после нуля и запятой будет бесконечное количество троек 1/3=0,3333…. . Принято читать так: ноль целых, три в периоде. Записывается соответственно так: 1/3=0,(3). Аналогичная ситуация будет, если попытаться перевести в десятичную дробь 5/6: 5/6=0,8(3). Такие дроби называются бесконечными периодическими. Вот пример для дроби 3/7: 3/7= 0,42857142857142857142857142857143… , то есть 3/7=0,(428571).
Итак, в результате превращения обыкновенной дроби в десятичную может получаться:
- непериодическая десятичная дробь;
- периодическая десятичная дробь.
Следует отметить, что существуют и бесконечные непериодические дроби, которые получаются при выполнении таких действий: взятие корня n-ой степени, логарифмирование, потенцирование. Например, √3= 1,732050807568877… . Знаменитое число π≈ 3,1415926535897932384626433832795…. .
Давайте теперь умножим 3 на 0,(3): 3×0,(3)=0,(9)=1. Получается, что 0,(9) – это иная форма записи единицы. Точно так же 9=9/9,16=16,0, и т.д.
Правомерен и вопрос, противоположный к приведенному в заголовке этой статьи: «как десятичную дробь перевести в обычную». Ответ на данный вопрос дает пример: 0,5= 5/10=1/2. В последнем примере мы сократили числитель и знаменатель дроби 5/10 на 5. То есть для превращения десятичной дроби в обыкновенную нужно представить ее в виде дроби со знаменателем 10.
О том, что такое дроби вообще интересно будет посмотреть видео:
О том как перевести десятичную дробь в обыкновенную смотрите тут:
Преобразование обыкновенной дроби в десятичную
Допустим, мы хотим преобразовать обыкновенную дробь 11/4 в десятичную. Проще всего сделать это так:
Это удалось нам потому, что в данном случае разложение знаменателя на простые множители состоит только из двоек. Мы дополнили это разложение еще двумя пятерками, воспользовались тем, что 10 = 2∙5, и получили десятичную дробь. Подобная процедура возможна, очевидно, тогда и только тогда, когда разложение знаменателя на простые множители не содержит ничего, кроме двоек и пятерок. Если в разложении знаменателя присутствует любое другое простое число, то такую дробь в десятичную преобразовать нельзя. Тем не менее, мы попробуем это сделать, но только другим способом, с которым мы познакомимся на примере всё той же дроби 11/4. Давайте поделим 11 на 4 «уголком»:
В строке ответа мы получили целую часть ( 2 ), и еще у нас есть остаток ( 3 ). Раньше мы деление на этом заканчивали, но теперь мы знаем, что к делимому ( 11 ) можно приписать справа запятую и несколько нулей, что мы теперь мысленно и сделаем. Следом после запятой идет разряд десятых. Ноль, который стоит у делимого в этом разряде, припишем к полученному остатку ( 3 ):
Теперь деление можно продолжать как ни в чем не бывало. Надо только не забыть поставить в строке ответа запятую после целой части:
Теперь приписываем к остатку ( 2 ) ноль, который стоит у делимого в разряде сотых и доводим деление до конца:
В результате получаем, как и раньше,
Попробуем теперь точно таким же способом вычислить, чему равна дробь 27/11:
Мы получили в строке ответа число 2,45, а в строке остатка — число 5 . Но такой остаток нам уже раньше встречался. Поэтому мы уже сразу можем сказать, что, если мы продолжим наше деление «уголком», то следующей цифрой в строке ответа будет 4, затем пойдет цифра 5, потом — снова 4 и снова 5, и так далее, до бесконечности:
27 / 11 = 2,454545454545…
Мы получили так называемую периодическую десятичную дробь с периодом 45. Для таких дробей применяется более компактная запись, в которой период выписывается только один раз, но при этом он заключается в круглые скобки:
2,454545454545… = 2,(45).
Вообще говоря, если делить «уголком» одно натуральное число на другое, записывая ответ в виде десятичной дроби, то возможно только два исхода: (1) либо рано или поздно в строке остатка мы получим ноль, (2) либо там окажется такой остаток, который уже нам раньше встречался (набор возможных остатков ограничен, поскольку все они заведомо меньше делителя). В первом случае результатом деления является конечная десятичная дробь, во втором случае — периодическая.
Преобразование периодической десятичной дроби в обыкновенную
Пусть нам дана положительная периодическая десятичная дробь с нулевой целой частью, например:
a = 0,2(45).
Как преобразовать эту дробь обратно в обыкновенную?
Умножим ее на число 10 k , где k — это число цифр, стоящих между запятой и открывающей круглой скобкой, обозначающей начало периода. В данном случае k = 1 и 10 k = 10:
a ∙ 10 k = 2,(45).
Полученный результат умножим на 10 n , где n — «длина» периода, то есть число цифр, заключенных между круглыми скобками. В данном случае n = 2 и 10 n = 100:
a ∙ 10 k ∙ 10 n = 245,(45).
Теперь вычислим разность
a ∙ 10 k ∙ 10 n − a ∙ 10 k = 245,(45) − 2,(45).
Поскольку дробные части у уменьшаемого и вычитаемого одинаковы, то у разности дробная часть равна нулю, и мы приходим к простому уравнению относительно a :
a ∙ 10 k ∙ (10 n − 1) = 245 − 2.
Решается это уравнение с помощью следующих преобразований:
a ∙ 10 ∙ (100 − 1) = 245 − 2.
a ∙ 10 ∙ 99 = 245 − 2.
Мы специально пока не доводим вычисления до конца, чтобы было наглядно видно, как можно сразу выписать этот результат, опуская промежуточные рассуждения. Уменьшаемое в числителе ( 245 ) — это дробная часть числа
a = 0,2(45)
если в ее записи стереть скобки. Вычитаемое в числителе ( 2 ) — это непериодическая часть числа а , располагающаяся между запятой и открывающей скобкой. Первый сомножитель в знаменателе ( 10 ) — это единица, к которой приписано столько нулей, сколько цифр в непериодической части (k ). Второй сомножитель в знаменателе ( 99 ) — это столько девяток, сколько цифр содержит период (n ).
Теперь наши вычисления можно довести до конца:
Здесь в числителе стоит период, а в знаменателе — столько девяток, сколько цифр в периоде. После сокращения на 9 полученная дробь оказывается равной
Подобным же образом,
Сложение и вычитание десятичных чисел Калькулятор показывает и объясняет свою работу
Как складывать и вычитать десятичные числа
Чтобы складывать и вычитать десятичные числа без калькулятора, оба числа должны иметь одинаковое количество десятичных знаков. Это связано с тем, что десятичные точки должны выровняться в сетке решения для сложения или вычитания десятичных чисел.
Если выясняется, что одно число имеет большее количество десятичных знаков, чем другое, просто добавьте нули в конец числа с наименьшим количеством десятичных знаков, пока оно не будет иметь такое же количество десятичных знаков, как и другое.
Например, предположим, что мы пытаемся сложить следующие два десятичных числа:
56,4321 + 12,34
Поскольку первое число имеет на 2 десятичных разряда больше, чем второе число, нам нужно добавить 2 нуля в конец второго. число (12,34 становится 12,3400). Таким образом, десятичные точки (обозначенные красной вертикальной линией) будут выровнены в сетке решения, например:
← проведите пальцем влево и вправо → ← проведите пальцем влево и вправо →
| 5 | 6 | 4 | 3 | 2 | 1 | |||
| + | 1 | 2 | 3 | 4 | 0 | 0 | ||
| = | + |
Это также гарантирует, что сумма двух чисел будет иметь такое же количество десятичных знаков, что и число с наибольшим количеством десятичных знаков.
Как складывать отрицательные числа
Если одно или несколько чисел в задаче сложения отрицательные, шаги для сложения чисел зависят от того, совпадают ли знаки двух чисел.
Если знаки одинаковые:
Просто сложите абсолютные значения двух чисел и дайте сумме тот же знак, что и два числа.
Пример: (-7) + (-2)
Добавьте абсолютное значение -7 (| -7 | = 7) к абсолютному значению -2 (| -2 | = 2), чтобы получить 9, и дайте сумме знак двух чисел, который в данном случае является отрицательным знаком.
Если знаки не совпадают:
Используя их абсолютные значения, вычтите меньшее из двух чисел из большего из двух чисел и дайте сумме знак числа с наибольшим абсолютным значением.
Пример: (-7) + (2)
Вычтите абсолютное значение меньшего числа (| 2 | = 2) из абсолютного значения большего числа -7 (| -7 | = 7), чтобы получить 5 , и присвойте результату знак числа с наибольшим абсолютным значением, которое в данном случае является отрицательным знаком.
Как вычитать отрицательные числа
Если проблема заключается в вычитании, измените вычитание на сложение и измените знак последнего числа на противоположный. Затем следуйте инструкциям по добавлению отрицательных чисел.
Пример №1: (-7) — (2)
Измените (-7) — (2) на (-7) + (-2) и следуйте правилам сложения.
Поскольку теперь знаки те же самые, добавьте абсолютное значение -7 (| -7 | = 7) к абсолютному значению -2 (| -2 | = 2), чтобы получить 9, и дайте сумме знак двух чисел, которое в данном случае является отрицательным знаком.
Пример №2: (-7) — (-2)
Измените (-7) — (-2) на (-7) + (2) и следуйте правилам сложения.
Поскольку знаки больше не совпадают, вычтите абсолютное значение меньшего числа (| 2 | = 2) из абсолютного значения большего числа -7 (| -7 | = 7), чтобы получить 5, и дайте результат — знак числа с наибольшим абсолютным значением, которое в данном случае является отрицательным знаком.
Если вы не знаете, как выполнять длинное сложение или вычитание, калькулятор на этой странице показывает его работу и включает шаги решения для каждого вычисленного результата.
Онлайн-математические калькуляторы
В вашем браузере отключен JavaScript.
Вам необходимо включить его, чтобы использовать наши калькуляторы на основе JavasSript.
Учим математику
Предлагаем бесплатный научный калькулятор. Кроме того, мы постоянно добавляем на наш сайт новые калькуляторы. Вот наши калькуляторы по алгебре, геометрии, тригонометрии, графике и исчислению. В дополнение к этим коллекциям на основе категорий в разделе ниже мы предлагаем коллекцию некоторых из лучших математических калькуляторов со всего Интернета.Мы также недавно добавили коллекцию математических игр, чтобы помочь студентам изучать математику онлайн в увлекательной и интерактивной форме.
Ознакомьтесь с нашими бесплатными математическими играми!
Коллекция математических калькуляторов
- Операции с обыкновенными дробями — сложение, вычитание, умножение и деление дробей путем вставки числителей и знаменателей. Результаты автоматически упрощаются и преобразуются в десятичные числа.
- Логарифм — приложение Calkoo, которое вычисляет логарифмы и показатели.
- Калькулятор процентов — Бесплатный калькулятор для вычисления процентов. Вставьте два значения и автоматически рассчитайте третье.
- Калькулятор квадратного уравнения — Решите квадратное уравнение. Вставьте a, b и c в этот калькулятор и найдите два значения x.
- Калькулятор теорем Пифагора — вычисляет длину одной стороны треугольника. Решите значение A, B или C, указав длины двух других сторон треугольника.
- Калькулятор тригонометрии — вычисляет тригонометрические значения, такие как синус, косинус и тангенс.Выберите градус дуги или радиан.
- Пропорция: Правило трех — Вычисляет эквиваленты отношения в дробной форме с использованием правила трех. Вставьте три числа и найдите четвертое, чтобы завершить соотношение.
- Калькулятор площади — Найдите площадь двумерных фигур, таких как круги, треугольники, ромбы, трапеции и т. Д., Вставив значения в бесчисленное множество вариантов измерения длины.
- Калькулятор объема — Расчет объема трехмерных фигур, таких как цилиндры и кубы.Результаты доступны в английских, метрических и морских кубических единицах измерения длины.
- Сложение, вычитание, умножение, деление — вставляйте до четырех чисел за раз в этот бесплатный калькулятор для решения задач сложения, вычитания, умножения и деления.
- Basic Calculator — бесплатный онлайн-калькулятор с 10-значной клавиатурой и основными математическими функциями.
- Child Math Tutor — Создавайте бесплатные математические задачи на сложение, вычитание, умножение и деление для детей с помощью этого онлайн-калькулятора.Операция проверяет ответы и создает табель успеваемости.
- Калькулятор экспоненциального выражения — вставьте в этот калькулятор положительные и отрицательные основания и показатели, чтобы найти продукт.
- 4 калькулятора процентов — четыре бесплатных калькулятора для решения процентных уравнений. Найдите взаимосвязь между числами и процентами, а также между увеличением и уменьшением процента.
- Научный калькулятор — бесплатный научный онлайн-калькулятор с 10-значной клавиатурой и функциями, такими как логарифмы и тригонометрические вычисления.Вычисляйте результаты в радианах или градусах.
- Калькулятор десятичных дробей в дроби — конвертируйте десятичные дроби в дроби с помощью этого бесплатного онлайн-калькулятора. Пояснения к задействованным математическим функциям также доступны на странице.
- Калькулятор дробей в десятичные — бесплатный калькулятор для преобразования дробей в десятичные с помощью деления. Также изучите связанные математические концепции, лежащие в основе расчетов.
- Конвертер научной записи — Преобразует десятичные дроби в экспоненциальные числа или числа в экспоненциальном представлении в десятичные числа.На странице также объясняется научная нотация и объясняется, как выполнять преобразование вручную.
- Калькулятор дроби в процент — Вставьте числитель и знаменатель дроби в этот бесплатный калькулятор, чтобы найти процентную, десятичную и простейшую форму дроби.
- Конвертер римских чисел — используйте этот бесплатный онлайн-калькулятор для преобразования арабских чисел в римские цифры или римских цифр в арабские числа. На странице есть таблица с римскими цифрами для печати.
- Конвертер шестнадцатеричных чисел в десятичные — введите шестнадцатеричные числа (числа с основанием 16 с буквами A-F), и этот калькулятор преобразует их в числа с основанием 10.На странице представлены объяснения шестнадцатеричных чисел и преобразований в десятичные числа.
- Конвертер десятичных чисел в восьмеричные — бесплатный онлайн-калькулятор, который преобразует десятичные числа или числа с основанием 10 в восьмеричные числа или числа с основанием 8.
- Конвертер десятичных чисел в шестнадцатеричные — Преобразование десятичных чисел в шестнадцатеричные или шестнадцатеричные.
- Конвертер десятичных чисел в двоичные — Этот бесплатный онлайн-калькулятор переводит числа с основанием 10 в двоичные.
- Конвертер двоичных чисел в шестнадцатеричные — Этот калькулятор предлагает автоматическое преобразование двоичных чисел в шестнадцатеричные числа.
- Преобразователь двоичного числа в десятичный — введите двоичные числа и используйте этот калькулятор для преобразования их в числа с основанием 10, включая числа с десятичной запятой.
- Калькулятор умножения дробей — Получите произведение дробей, смешанных чисел и целых чисел, введя их в этот калькулятор.
- Математический калькулятор редуктора дроби — уменьшите дробь до наименьшего числителя и знаменателя с помощью этого бесплатного онлайн-калькулятора. Калькулятор также находит наибольший общий фактор и предлагает объяснение математических понятий.
- Калькулятор сложения и вычитания смешанных чисел — этот калькулятор складывает и вычитает смешанные числа и дроби с разными знаменателями, предлагая при этом более глубокий взгляд на математические концепции, лежащие в основе решения.
- Калькулятор сложения и вычитания дробей — бесплатный онлайн-калькулятор, который складывает или вычитает две дроби с разными знаменателями и объясняет математику, лежащую в основе уравнения.
- Калькулятор деления дробей — делите дроби, смешанные числа и целые числа с помощью этого бесплатного онлайн-калькулятора.На сайте также есть пошаговое объяснение ответа.
- Калькулятор сравнения дробей — Воспользуйтесь этим бесплатным калькулятором, чтобы определить, какая дробь больше в паре дробей с разными знаменателями.
- Калькулятор сложения трех дробей — сложите или вычтите три дроби с тремя разными знаменателями с помощью этого бесплатного калькулятора.
- Mathway — Вставьте математическую задачу в редактор и получите пошаговое объяснение решения.Типы задач варьируются от базовой математики до вычислений и статистики.
- Калькулятор статистического среднего — этот калькулятор определяет сумму, среднее значение, медианное значение, минимум, максимум, режим и диапазон набора чисел.
- Калькулятор стандартного отклонения — бесплатный онлайн-калькулятор для определения стандартного отклонения, дисперсии выборки, дисперсии генеральной совокупности и среднего значения набора чисел.
- Калькулятор квадратного корня — Найдите квадратный корень из числа с помощью этого калькулятора.
- Калькулятор в научном представлении — сложение, вычитание, умножение и деление двух чисел в экспоненциальном представлении. Вычисляет решение в экспоненциальном представлении и десятичных числах.
- Exponent Calculator — Введите основание и экспоненциальную степень в этот калькулятор и получите результат в форме десятичного числа.
- Генератор простых чисел — бесплатный онлайн-инструмент, который генерирует простые числа. Выберите желаемое количество простых чисел и числовой диапазон, в котором их нужно найти, и инструмент создаст список.
- Калькулятор простых чисел — этот калькулятор проверяет, являются ли введенные числа простыми.
- Калькулятор процентного изменения — Определите процентное изменение, дробное изменение, числовую разницу и процентную разницу между двумя числами.
- Калькулятор процентов — калькулятор, который решает уравнение: число А — это процентное соотношение числа Б. Введите любые два из трех полей, чтобы вычислить результат.
- Калькулятор простых множителей — Найдите все простые множители числа с помощью этого калькулятора.
- Онлайн-калькулятор факторинга — генерирует список всех множителей, простых и составных, с числом меньше 10 миллионов.
- Linear Equation Solver — Этот бесплатный онлайн-калькулятор решает линейные уравнения для одной переменной и содержит пошаговые инструкции по решению уравнения вручную.
- Калькулятор LCM — Найдите наименьшее общее кратное от двух до четырех чисел с помощью этого калькулятора.
- Калькулятор наибольшего общего множителя — введите два, три или четыре числа в этот онлайн-инструмент, чтобы найти наибольший общий множитель чисел.
- Калькулятор операций с полиномами — Калькулятор, который складывает, вычитает, умножает или делит два полиномиальных выражения. Калькулятор предлагает возможность создания объяснения решения.
- Synthetic Division Calculator — бесплатный онлайн-калькулятор, который вычисляет синтетическое деление многочленов. Он также находит остатки синтетического деления и определяет, является ли один термин фактором другого.
В вашем браузере отключен JavaScript.
Вам необходимо включить его, чтобы использовать наши калькуляторы на основе JavasSript.
Калькулятор повторяющихся / завершающих десятичных знаков — онлайн-конвертер дробей
Поиск инструмента
Повторяющиеся десятичные знаки
Инструмент для определения периода дроби или десятичного числа с повторяющимися десятичными знаками. Точка — это набор цифр, который повторяется на бесконечности в десятичных дробях числа (обычно рациональное число или периодическая дробь).
Результаты
Повторяющиеся десятичные знаки — dCode
Тэги: Арифметика
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Повторяющееся десятичное обнаружение A / B
Прерывание определения десятичной дроби
Поиск фракций
Ответы на вопросы (FAQ)
Какие десятичные дроби повторяются? (Определение)
Периодическое десятичное расширение / развитие рационального числа или дроби (числитель над знаменателем) — это последовательность чисел, которые повторяются на бесконечности в десятичной записи числа.
Пример: 1/3 = 0,3333333333 … Цифра 3 повторяется до бесконечности
Пример: 1/27 = 0,037037037037037 … Цифры 037 повторяются до бесконечности
Все дроби не имеют повторяющейся десятичной формы , некоторые имеют завершающую десятичную форму.
Что означают завершающие десятичные дроби? (Определение)
Завершающий десятичный знак указывает на то, что никакая последовательность чисел не повторяется бесконечно в десятичной записи числа.
Пример: 4/25 = 0,16 разработка завершена и не продолжается
Любое число, записанное в десятичной форме с конечным числом цифр (после десятичной точки), является завершающим десятичным числом.
Как писать повторяющиеся десятичные дроби?
Возможно несколько обозначений.
Первый использует … точки подвеса, но не определяет повторяющуюся часть. Это практично, но не строго и поэтому не рекомендуется.
Пример: 37/300 = 0,12333333333 … $
Обозначение с чертой над повторяющейся частью.
Пример: 37/300 = 0,12 \ overline {3} $
Обозначение с чертой под повторяющейся частью.
Пример: $ 37/300 = 0,12 \ underline {3} $
Обозначения в скобках
Пример: 37/300 = 0,12 [3] $
NB: Для наглядности дробь лучше записывать в несократимой форме.1 \ times x = 1. \ overline {6} = 1.6666666 … $ и решаем $ 10x − x = 9x = 1. \ overline {6} −0.1 \ overline {6} = 1.5 \ iff 9x = 1.5 \ iff х = 1,5 / 9 = 15/90 = 1/6 $
Какие десятичные дроби наиболее известны?
Инверсия простых чисел дает длинные и интересные периодические десятичные вычисления.
Пример: $ 1/3 = 0,333333 … $
Пример: $ 1/7 = 0,142857142857 … $
Существует ли бесконечное десятичное разложение с серией цифр, которые никогда не повторяются?
Любое рациональное число (любая дробь) имеет конечное развитие или периодическое десятичное разложение с конечным числом цифр, которые повторяются до бесконечности.
Но есть действительные числа, которые не являются рациональными числами (которые не являются дробями), которые имеют десятичные дроби без повторения.
Пример: $ \ pi = 3.14159265 … $ на сегодняшний день не имеет известных повторов.
Пример: Постоянная Чамперноуна никогда не будет повторяться, это номер вселенной.
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Повторение десятичных знаков». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любых алгоритмов, апплетов или фрагментов повторяющихся десятичных знаков (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любых повторяющихся десятичных знаков ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копирование и доступ к API для «Повторяющихся десятичных знаков» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / Комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
период, дробь, числитель, знаменатель, развертка, повторение, десятичная дробь, запись, цифра, бесконечность, рациональная, точка
Ссылки
Источник: https: // www.dcode.fr/number-repeating-decimal
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Калькулятор десятичных знаков супа
Но некоторые десятичные дроби сохраняются вечно (например, 1/3 = 0,33333 …), поэтому мы останавливаемся после 200 десятичных знаков. То же самое происходит с такими функциями, как квадратный корень, синус, косинус и т. Д. Вычисление будет продолжаться бесконечно, поэтому мы должны где-то остановиться. Свяжитесь с нами с любыми предложениями по улучшению или усовершенствованию этого калькулятора полной точности.
Индекс массы тела Площадь поверхности тела и объем тела Калькулятор калорийности питания Калькулятор роста грудных детей Калькулятор соотношения талии и бедер Математика и финансы Средняя скорость изменения Экспоненциальный рост / удвоение спада / время полужизни Калькулятор приведенной стоимости Калькулятор S-кривой — 1 оценка параметра Калькулятор S-кривой — 3 оценки параметра
Давайте на практике переведем дюймы в дроби — дюймы в дроби. Представьте, что вы купили деревянное панно длиной 5 метров.Вы планируете разрезать его на шесть равных частей, но у вас есть только рулетка с дробной шкалой в дюймах.
Калькулятор решает треугольник, заданный тремя его свойствами. Каждый треугольник имеет шесть основных характеристик: три стороны a, b, c и три угла (α, β, γ). Классическая задача тригонометрии состоит в том, чтобы определить три из этих шести характеристик и найти остальные три.
Обзор жиросжигателя Ss8, обзоры таблеток для похудения Shark tank keto — Adotas ADOTAS · 7 часов назад. Потеря веса у кошек голодание для похудения Хорхе Гарсия потеря веса потеря веса потеря веса приложение для похудения добавки для похудения пенис в таблетках греческой виагры.
От калькулятора дробных неравенств до степеней — у нас есть все необходимое. Зайдите на сайт Algebra1help.com и узнайте о числах, выражениях и большом количестве дополнительных предметов по математике.
Калькулятор десятичного умножения, который показывает работу по нахождению произведения двух десятичных чисел. Пошаговые расчеты помогают родителям помочь своим детям, изучающим 4, 5 или 6 класс, проверить шаги и ответы домашнего задания на десятичное умножение и задач с заданиями по преалгебре или по числам и операциям с десятичным основанием (NBT)…
Произнесите «и» вместо десятичной точки. Шаг № 3 Считайте цифры справа от десятичной точки как целое число. Шаг №4 Произнесите название места последней цифры справа. Давайте выполним 4 шага выше, чтобы прочитать это число: 8278.9670. Шаг 1. Сначала прочтите цифры слева от десятичной точки как целое число.
Калькулятор упрощения позволяет вам взять простое или сложное выражение, а также упростить и свести выражение к простейшей форме. Калькулятор работает как с числами, так и с выражениями, содержащими переменные.
Отношение к десятичному калькулятору — Дюймовый калькулятор
Преобразуйте соотношение в десятичную форму, введя обе части ниже.
десятичный:
Шаги по преобразованию отношения в десятичное число:
Шаг первый: Перепишем отношение в виде дроби
Шаг второй: Разделим числитель на знаменатель
Как преобразовать отношение в десятичное
Есть несколько разных способов преобразовать отношение в десятичное.Самый простой способ преобразования в десятичную форму — использовать калькулятор, как показано выше. Продолжайте читать, и мы покажем вам, как выполнить преобразование самостоятельно.
Шаг первый: перепишите отношение в виде дроби
Первый шаг в преобразовании отношения в десятичное — это переписать отношение как дробь. Для этого положите первую часть соотношения над второй частью в виде дробей. Первая часть отношения будет числителем, а вторая часть — знаменателем.
Шаг второй: вычислите дробь и выразите ее десятичным числом
Последний шаг в преобразовании — решить дробь, чтобы получить десятичное значение. Для этого разделите числитель на знаменатель. Результатом является десятичная форма отношения.
Например, преобразует 7: 2 в десятичное значение.
Записываем 7: 2 в виде дроби.
7: 2 = 72
Тогда решай.
72 = 7 ÷ 2
72 = 3,5
Таким образом, десятичное значение 7: 2 равно 3.5
Наш калькулятор десятичного отношения к соотношению может помочь решить обратную эту формулу.
Калькулятор десятичных знаков для супа
Сантиметр (американское написание: сантиметр, сокращение: см) — единица измерения длины в метрической системе. Один см равен одной сотой метра (амер. Написание: метр), что является текущей базовой единицей длины в системе СИ. Ключи для замены ящика для инструментов Lund
Если есть десятичная точка, то, согласно правилу (3), описанному выше, любые конечные нули считаются значащими цифрами.Другие математические калькуляторы Ознакомьтесь с математическими калькуляторами на сайте Калькулятора, чтобы получить помощь в преобразовании десятичных знаков в дроби и вычислении дробей.
188 nbme 20
Используется более чем 70 000 учителей и 1 миллионом учащихся дома и в школе. Studyladder — это онлайн-инструмент для изучения английского языка и математики. Детские развлекательные игры, рабочие листы и планы уроков для учащихся начальной и средней школы в США.
Медсестра учит нового родителя правилам безопасности новорожденных
Этот онлайн-калькулятор дробей и десятичных дробей поможет вам понять, как складывать, вычитать, умножать или делить дроби и десятичные дроби. Калькулятор дробей вычислит суммы, разности, произведения или частные дробей и десятичных знаков. Калькулятор сгенерирует пошаговое объяснение того, как получить результаты.
1978 chevy c10 трансмиссионная жидкость
Если вам нравится этот сайт о решении математических задач, сообщите об этом в Google, нажав кнопку +1.Если вам нравится эта страница, пожалуйста, нажмите и эту кнопку +1. Примечание. Если кнопка +1 темно-синего цвета, вы уже поставили ей +1.
Javascript сортирует массив массивов по столбцу
Выберите тип дробного или целого числа. Не выбирайте ни одно поле для неправильных или подходящих фракций. Это значение по умолчанию. Выбрано «Смешанный» для смешанных дробей и целое для целых чисел. Введите левую дробь. Это дробь слева от операнда вычитания.Введите правильную дробь. Это дробь справа от операнда.
Pytorch free cpu memory
По умолчанию калькулятор округляет до ближайшего целого числа, но настройки можно изменить, чтобы использовать другие режимы округления и уровни точности. Все режимы округления, которые поддерживает калькулятор, описаны ниже.
Прогноз запасов Ge на 2025 год
Преобразует каждое смешанное число в неправильную дробь.Умножьте числители и знаменатели двух дробей. Если возможно, уменьшите долю ответа. Если ответ неправильная дробь, преобразуйте его в смешанное число. Примеры. Упражнение. Попробуйте умножить два смешанных числа. Введите столько работы, сколько хотите.
Суарес международные обзоры
Примечание. Существует платная версия этого приложения без рекламы, расположенная здесь: Калькулятор преобразования десятичных дробей в дробные — без рекламы.Преобразование десятичных знаков в дроби и вычисление математических выражений. Рассчитайте абсолютное значение или округлите ответ до выбранного значения допуска. Функция допуска полезна при проектировании и производстве для быстрого определения ближайшего дробного дюйма к …
Мобильное приложение Svicloud
Этот калькулятор использует сложение, вычитание, умножение или деление для вычислений положительные или отрицательные десятичные числа, целые числа, действительные числа и целые числа.Этот онлайн-калькулятор десятичных знаков поможет вам понять, как складывать, вычитать, умножать или делить десятичные дроби. Калькулятор следует известным правилам порядка операций.
Школы Ланкастера
Играйте в Matching Fractions and Percent на MathPlayground.com! Попрактикуйтесь в преобразовании дробей в проценты и обратно в этой игре на совпадение.
Подключиться к базе данных postgres удаленно
Калькулятор добавления десятичных знаков — это бесплатный онлайн-инструмент, который отображает сумму двух десятичных чисел.Онлайн-калькулятор BYJU для добавления десятичных знаков выполняет вычисления быстрее и отображает сумму за доли секунды.
Hvac draft draft pdf
10,5 — это отношение, выраженное в виде десятичного числа; 50% — соотношение, выраженное в процентах; ½ — это отношение, выраженное в виде дроби; Узнайте больше о коэффициентах или попробуйте один из наших популярных калькуляторов коэффициентов, некоторые из которых представлены ниже. Калькуляторы коэффициентов. Калькулятор соотношения сторон: Соотношение сторон — это отношение ширины к высоте… Этот онлайн-калькулятор дробей и десятичных дробей поможет вам понять, как складывать, вычитать, умножать или делить дроби и десятичные числа .. Калькулятор дробей вычисляет суммы, разности, произведения или частные дробей и десятичных знаков. Калькулятор сгенерирует пошаговое объяснение того, как получить результаты. Спецификации дома на колесах со стрелкой 1990 года. Калькулятор десятичных значений, который показывает работу для выражения числа десятичной запятой в десятичных значениях. Пошаговые расчеты помогают родителям помочь своим детям, изучающим 4, 5 или 6 класс, проверить работу и ответы с числами с десятичной запятой, чтобы оценить домашнее задание и задачи с заданиями в предалгебре или в общей системе счисления (NS). Основные государственные стандарты (CCSS) по математике.Calculation Nation® — Бросьте вызов другим. Испытайте себя .® Пиломатериалы Redwood на продажу
Угловой активированный маршрут получить текущий URL-адрес
- Наш калькулятор налога с продаж рассчитает сумму налога, подлежащего уплате по транзакции. Калькулятор также может найти сумму налога, включенную в сумму покупки брутто. 2020 месяц стихийных бедствий мем
- Нажмите «Рассчитать», чтобы увидеть результаты, и вы можете нажать «Очистить значения», чтобы сбросить все поля и снова использовать калькулятор. В нашем первом примере запись в 17 унций дает десятичное значение в фунтах, равное 1.0625, то же значение округлено и, 1 фунт и 1 унция. В фунте 16 унций. Присвоение имен ковалентным соединениям часть a
- Когда вы вводите уравнение в калькулятор, калькулятор начнет с расширения (упрощения) задачи. Затем он попытается решить уравнение, используя одно или несколько из следующих действий: сложение, вычитание, деление, извлечение квадратного корня из каждой стороны, разложение на множители и завершение квадрата. Sbc twin turbo cam
- Получите примеры кода, например, Как включить противотуманные фары на Mercedes c300 2010
- Бесплатный калькулятор десятичных знаков сложения / вычитания — добавление и вычитание десятичных знаков шаг за шагом Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт.Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Музыкальный пиратский диск
- Просмотрите и сравните ПРОЦЕНТ, ИЗМЕНЕНИЕ, КАЛЬКУЛЯТОР, SOUP.OB на Yahoo Finance. Может ли золото остановить пулю
Онлайн-калькулятор для дробей и десятичных знаков
Чтобы упростить дробь до наименьшего числа, см. Калькулятор упрощения дробей. Этот онлайн-калькулятор десятичных дробей поможет вам понять, как сложить, вычесть, умножить или разделить десятичные дроби. Калькулятор следует известным правилам порядка операций.
Десятичная дробь Процент Число Строка Десятичная процентная диаграмма Десятичная процентная диаграмма Математические дроби Десятичные дроби Проценты Математические формулы
Калькулятор дробей смешанных чисел для упрощения любых двух дробей или чисел до наименьших членов или смешанных чисел в сокращенной форме.
Онлайн-калькулятор дробей и десятичных знаков . 1152 нравится, когда 32 говорят об этом. Этот калькулятор использует сложение, вычитание, умножение или деление для вычислений положительных или отрицательных десятичных чисел, целых чисел, действительных чисел и целых чисел.Это калькулятор дробей с шагами, указанными в решении.
Здесь также отображается подробная пошаговая информация о процедуре расчета дроби. Как преобразовать дробь в десятичную. Калькулятор Отличные бесплатные онлайн-калькуляторы для личного и делового использования.
Используйте этот калькулятор дробей для сложения, вычитания, умножения и деления дробей. Калькулятор смешанных дробей — складывайте, вычитайте, умножайте и делите дроби с пошаговыми инструкциями.Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Этот расчет был выполнен на основе чисел, приведенных ниже в калькуляторе десятичных дробей и процентов, просто введите числа любого типа и вычислите, чтобы найти количество входов в порядке возрастания и убывания. Онлайн-калькулятор дроби в десятичную дробь используется для сокращения дробей и смешанных чисел в простейшей форме, а затем преобразования этого упрощенного числа в десятичное число.Преобразуйте отношение в десятичное.
Онлайн-калькулятор дробей позволяет вычислить сумму дробей, чтобы вычислить сумму дробей, таких как эти 1 4 и 4 5, вы должны ввести Fraction_calculator 1 4 4 5 после вычисления результат будет получен 21 20. Красивый бесплатный научный онлайн-калькулятор с расширенными функциями для оценки процентов, дробей, экспоненциальных функций, логарифмов, тригонометрии, статистики и многого другого. Рациональная дробь — это отношение многочленов.
Для получения информации о сложении, вычитании, умножении и делении смешанных чисел и дробей см. Калькулятор смешанных чисел.Ответы представляют собой дроби в наименьшем значении или смешанные числа в сокращенном виде. Разложение рациональной дроби на простые элементы.
В дроби черта дроби означает деление на So, чтобы найти десятичный эквивалент дроби, например 14, вам нужно решить математическую задачу. Сэкономьте свое время с помощью этого удобного инструмента и сделайте свое обучение веселым и легким. Калькулятор сгенерирует пошаговое объяснение того, как получить результаты.
Запишите десятичное число в виде дроби с 1 в знаменателе. 1625 frac16251 Умножьте, чтобы удалить 3 десятичных разряда.Ниже приведены несколько калькуляторов дробей, способных выполнять операции сложения, вычитания, умножения, деления, а также преобразования дробей и десятичных знаков. — Икс.
1 4 025. Он также предназначен для преобразования неправильных дробей в десятичные и показывает шаги преобразования. Например, набор из 454310292301 будет заказан как 014529431023 и 231043294501.
Введите правильные или неправильные дроби, выберите математический знак и нажмите «Рассчитать». Калькулятор позволяет разбить рациональную дробь на простые элементы.Отличный онлайн-калькулятор, позволяющий рассчитывать дроби.
Онлайн-калькулятор смешанных дробей поддерживает сложение, вычитание, умножение или деление отрицательных дробей. Калькулятор выполняет базовые и расширенные операции с выражениями дробей с дробями в сочетании с целыми десятичными и смешанными числами. Бесплатный онлайн-калькулятор здесь выступает в качестве универсального пункта назначения для всех ваших сложных и жестких математических концепций, таких как статистика, алгебра, тригонометрия, доли, проценты и т. Д.
1 делится на 4. Калькулятор дробей вычисляет произведения разностей сумм или частные дробей. Чтобы добавить, вычесть, умножить и разделить дроби, см. Калькулятор дробей.
Вычисляет дробную уменьшенную дробь, смешанную и десятичную дробь, если она существует. Этот калькулятор показывает шаги и работу по преобразованию дроби в десятичное число. Сложить, вычесть, разделить и умножить дроби.
Онлайн-калькулятор дробей и десятичных дробей. Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.Онлайн-калькулятор смешанных дробей для решения задач с дробями и целыми числами.
Здесь вы умножаете верхнюю и нижнюю часть на 10 3 1000 frac16251times frac10001000 frac16251000 Найдите наибольший общий коэффициент GCF для 1625 и 1000, если он существует, и уменьшите дробь, разделив числитель и знаменатель на GCF 125. Онлайн-калькулятор дроби Этот онлайн-калькулятор дроби будет поможет вам понять, как сложить, вычесть, умножить или разделить дроби, смешанные числа, смешанные дроби, целые числа и десятичные дроби.Калькулятор дробей вычислит произведения разностей сумм или частные дробей и десятичных знаков.
Этот онлайн-калькулятор дробей и десятичных дробей поможет вам понять, как складывать, вычитать, умножать или делить дроби и десятичные дроби. Калькулятор позволяет разбить рациональную дробь на простые элементы. Бесплатный онлайн-калькулятор — Математика, физика, химия.
Калькулятор дробей в дюймах Найдите дюймовые дроби из десятичных и метрических измерений Дюймовый калькулятор Десятичные дроби Преобразование десятичных дробей
Преобразование процента в десятичное Бесплатное онлайн-преобразование процента в десятичный калькулятор Преобразование процентов в десятичные дроби Десятичные дроби Простая форма дробей
Пожалуйста, поделитесь в 2020 дроби Преобразование десятичных дробей Таблица дробей
Преобразование дробей в десятичные Три метода Easy Peesy Brother Sister Эквивалентная дробь со знаменателем Десятичные дроби Математика 4-го класса
Карманный калькулятор метрической системы Преобразование дробей в десятичные Простые в использовании Основные калькуляторы Калькулятор Научные калькуляторы
Pin By Мисс Пенни Математика в десятичных вычислениях. Дроби. r Калькулятор дробей для замены десятичных дробей на дроби Отображение работы с десятичными дробями Математические дроби
Преобразование дробей в десятичные или целые числа Этот онлайн-калькулятор уменьшает дробь Онлайн-калькулятор Калькулятор ипотечного платежа Калькулятор погашения ипотеки
Casio Fx 55 Plus Калькулятор дробей для начальной средней школы Научный Калькуляторы Калькулятор Дроби
Калькулятор дробей от Palasoftware Дроби Отрицательные дроби Обучение дробям
Калькулятор дробей Обучение дробям Математические методы Изучение дробей
Pin by Lakesha Stewart On Get Yo Learn On Decimals Дроби Десятичная диаграмма
Преобразование дробей в десятичные дроби Калькулятор знаменателя для нахождения десятичной формы дроби или десятичных дробей Конвертация дробей
Калькулятор длинного деления с десятичными дробями Десятичные дроби Длинное деление Математическое деление
Дроби и десятичные дроби als S Cool The Revision Website Дроби Десятичные дроби Десятичные дроби
Это изображение с этого ресурса в Интернете4classrooms Пятый класс Интерактивные математические навыки Дроби и P дроби Служба письма на бумаге Десятичные
Калькулятор десятичного преобразования в 2021 году Десятичное преобразование десятичного числа Десятичное число
Дробь И Десятичная таблица преобразования Десятичная диаграмма Десятичные дроби
.
