Математика и информатика в Плесской школ
Математика и информатика в Плесской школ — Построение логических схем и таблиц истинности в Excel| Приветствую Вас Гость | RSS |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Copyright MyCorp © 2022 |
Таблица истинности которая считывает функцию Python
Чтобы не парсить выражение, можно привлечь Питон вычислять введённую функцию и заполнять таблицу истинности.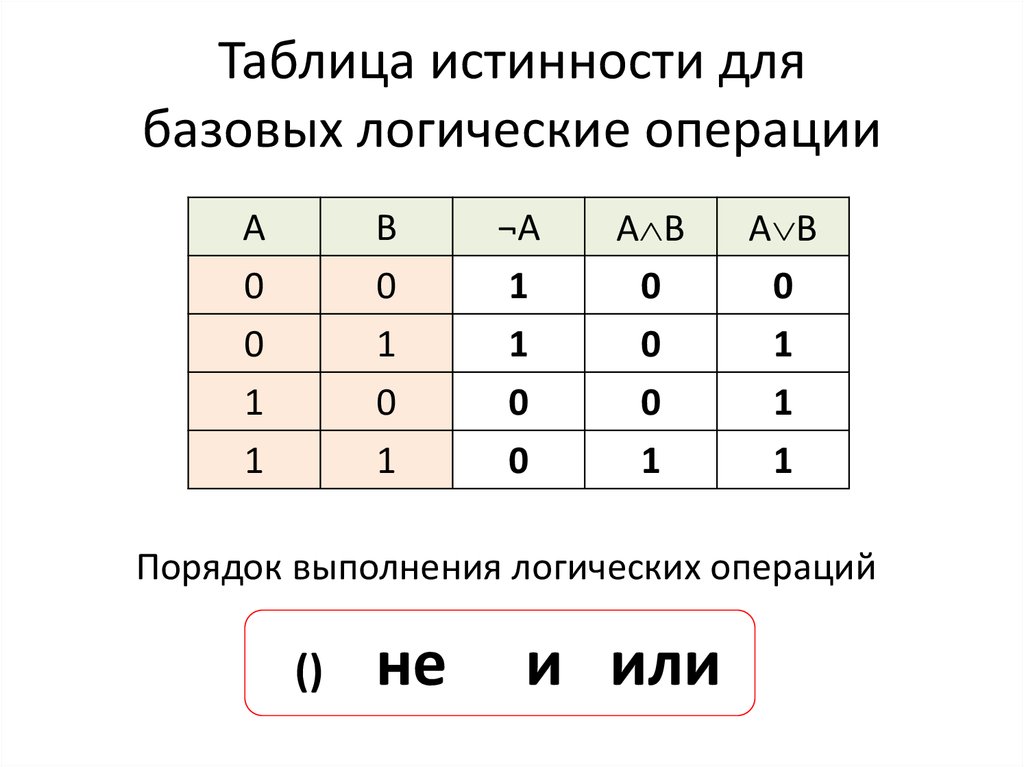 Для этого завести класс, который будет представлять переменные в выражении, и у него переопределить соответствующие операторы. А дальше инициализировать переменные всеми возможными значениями и получать результат введённой функции для каждого набора значений переменных при помощи штатной функции
Для этого завести класс, который будет представлять переменные в выражении, и у него переопределить соответствующие операторы. А дальше инициализировать переменные всеми возможными значениями и получать результат введённой функции для каждого набора значений переменных при помощи штатной функции eval().
import re
class BoolVar:
def __init__(self, value):
self.value = value
#print("INIT =", value)
# '-' — возражения "нет"
def __neg__(self):
return BoolVar(not self.value)
# '+' — дизъюнкция "или"
def __add__(self, other):
return BoolVar(self.value or other.value)
# '*' — конъюнкция "и"
def __mul__(self, other):
return BoolVar(self.value and other.value)
# '>' — импликация "если ..., тогда"
def __gt__(self, other):
return BoolVar((not self.value) or other.value)
# '=' — эквивалентность "ровно"
def __eq__(self, other):
return BoolVar(self.value == other.value)
# строковое представление значения
def __str__(self):
return "True" if self. value else "False"
def __format__(self, format_spec):
return format(str(self), format_spec)
infunc = input('Enter your function: ')
# в питоне знак эквивалентности - это '==', так что заменяем
infunc = infunc.replace("=", "==")
# находим переменные в функции, т.е. просто буквы
# set() делает этот набор уникальным, ну и сортируем
variables = sorted(set(re.findall(r"[A-Za-z]", infunc)))
# или так, если надо без использования регулярных выражений
# variables = sorted(set([c for c in infunc if c.isalpha()]))
# просто красивое оформление для таблицы
header = [""]*2
for key in variables:
header[0] += "-"*7 + "+"
header[1] += f" {key} |"
header[0] += "-+" + "-"*7
header[1] += " | Result"
print("\n".join(header + header[0:1]))
vars_for_eval = {}
# вариантов входных значений для таблицы - 2 в степени кол-ва переменных
for variant in range(1 << len(variables)):
# заполняем входной словарь c представлением переменных
# в виде экземпляров нашего класса для функции eval()
# key идут в прямом порядке, а i - в обратном
for i, key in reversed(list(enumerate(reversed(variables)))):
# используем биты этого числа для инициализыции булевых значений
vars_for_eval[key] = BoolVar(variant & (1 << i))
# вывод строки таблицы истинности
print(f" {vars_for_eval[key]:<5}", end=" |")
# вычисляем результат
result = eval(infunc, {}, vars_for_eval)
print(f" | {result:<5}")
print(header[0])
value else "False"
def __format__(self, format_spec):
return format(str(self), format_spec)
infunc = input('Enter your function: ')
# в питоне знак эквивалентности - это '==', так что заменяем
infunc = infunc.replace("=", "==")
# находим переменные в функции, т.е. просто буквы
# set() делает этот набор уникальным, ну и сортируем
variables = sorted(set(re.findall(r"[A-Za-z]", infunc)))
# или так, если надо без использования регулярных выражений
# variables = sorted(set([c for c in infunc if c.isalpha()]))
# просто красивое оформление для таблицы
header = [""]*2
for key in variables:
header[0] += "-"*7 + "+"
header[1] += f" {key} |"
header[0] += "-+" + "-"*7
header[1] += " | Result"
print("\n".join(header + header[0:1]))
vars_for_eval = {}
# вариантов входных значений для таблицы - 2 в степени кол-ва переменных
for variant in range(1 << len(variables)):
# заполняем входной словарь c представлением переменных
# в виде экземпляров нашего класса для функции eval()
# key идут в прямом порядке, а i - в обратном
for i, key in reversed(list(enumerate(reversed(variables)))):
# используем биты этого числа для инициализыции булевых значений
vars_for_eval[key] = BoolVar(variant & (1 << i))
# вывод строки таблицы истинности
print(f" {vars_for_eval[key]:<5}", end=" |")
# вычисляем результат
result = eval(infunc, {}, vars_for_eval)
print(f" | {result:<5}")
print(header[0])
Оно даже чего-то считает:
D:\Programming\Python\1>python bools.py Enter your function: a+b -------+-------+-+------- a | b | | Result -------+-------+-+------- False | False | | False False | True | | True True | False | | True True | True | | True -------+-------+-+------- D:\Programming\Python\1>python bools.py Enter your function: -x=y -------+-------+-+------- x | y | | Result -------+-------+-+------- False | False | | False False | True | | True True | False | | True True | True | | False -------+-------+-+------- D:\Programming\Python\1>python bools.py Enter your function: -p+(p*q)=q -------+-------+-+------- p | q | | Result -------+-------+-+------- False | False | | False False | True | | True True | False | | True True | True | | True -------+-------+-+-------
Кстати, программу заодно можно использовать как калькулятор. 🙂
D:\Programming\Python\1>python bools.py Enter your function: 55*23-16**5//16 -+------- | Result -+------- | -64271 -+-------
Генератор таблиц истинности с заключением
Краткий справочник по логическим операторам
Первым шагом в создании таблицы истинности является перевод вашего аргумента на язык символической логики.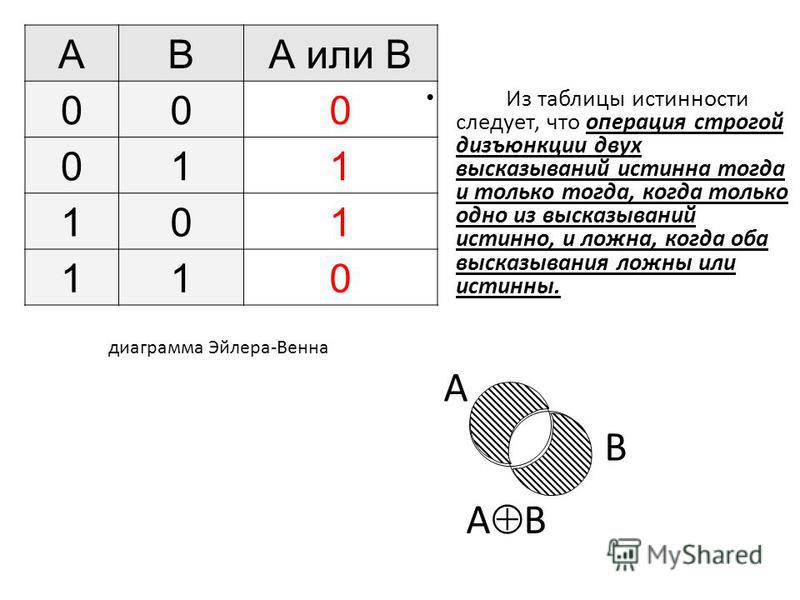 Вот шпаргалка по логическому переводу, чтобы помочь.
Вот шпаргалка по логическому переводу, чтобы помочь.
| Символ | Альтернатива | Название | Вид | Английские связки | 9 90 ! | Тильда | Отрицание (НЕ) | это не так, что А; не А; неверно, что А |
| & | &&, /\ | Амперсанд | Союз (И) | А и В; А, но Б; А еще Б; А пока Б; А кроме того Б; А однако Б; А тем не менее Б; А еще Б; А тем не менее Б; А также Б; А хотя Б; оба а и Б; А дополнительно В; A кроме того B |
| v | ||, \/ | Клин | Разъединение (OR) | A или B; А если Б |
| ⊃ | > | Подкова | Условное (ЕСЛИ) | если А, то В; В только если А; А является необходимым условием для В; B — необходимое условие для A; B при условии, что A; В при условии, что А; А подразумевает, что Б; В при условии, что А; B в случае, если A |
| ≡ | ==, = | Тройной стержень | Биусловный (IFF) | A тогда и только тогда, когда B; А на всякий случай, что Б; А является необходимым и достаточным условием для В; А эквивалентно В |
Что такое таблица истинности?
Таблица истинности — это таблица, которую можно использовать для работы с логическими утверждениями. Википедия говорит, что:
Таблица истинности — это математическая таблица, используемая в логике, особенно в связи с булевой алгеброй, булевыми функциями и исчислением высказываний, которая устанавливает функциональные значения логических выражений для каждого из их функциональных аргументов, то есть для каждой комбинации значений, принимаемых их логическими переменными. В частности, таблицы истинности можно использовать, чтобы показать, является ли пропозициональное выражение истинным для всех законных входных значений, то есть логически верным.
Но это не очень полезно, если вы еще не логик. По сути, таблица истинности показывает все возможные входы и выходы логического утверждения.
Что такое оператор символьной логики?
Оператор символьной логики — это способ представления логического аргумента с помощью символов. Итак, вы можете написать что-то вроде этого:
Итак, вы можете написать что-то вроде этого:
Я человек или я робот, и у меня есть процессор вместо мозга.
во что-то вроде этого:
H v (R & C)
Чтобы перевести это в символическую логику, мы превратили каждый из атомарных операторов оператора в однобуквенные константы, а такие слова, как или и и , в соответствующие логические операторы ( v и и ). Вы можете найти список всех логических операторов здесь.
Теперь, когда у нас есть оператор символьной логики, мы можем сгенерировать для него таблицу истинности. Для этого введите его в калькулятор. Вы должны увидеть вывод, подобный этому: В самом верху есть смайлик с большим пальцем вверх, указывающий, что утверждение правильно сформировано. Если вы добавите ошибку в оператор (например, замените «&» на «&&»), она исчезнет, и вы увидите сообщение об ошибке. Также есть кнопка «Prettify» для замены таких операторов, как 9. 0085 > или = с более красивыми версиями. Далее вы увидите индикаторы, показывающие, что оператор является непредвиденным обстоятельством . Это просто означает, что утверждение может быть либо истинным, либо ложным, в зависимости от того, являются ли входные данные (идентификаторы) истинными или ложными. Утверждения также могут быть тавтологиями (утверждение всегда истинно, независимо от входных данных) или противоречиями (всегда ложно). Например, A v ~A — это тавтология, потому что, если вы переведете это на английский язык, получится, что «A истинно или ложно», что, конечно, всегда верно, независимо от того, что такое A. A & ~A — это противоречие, потому что оно говорит, что «A истинно и ложно», и невозможно, чтобы что-то было одновременно и истинным, и ложным. Наш пример является случайным, потому что я могу быть ни человеком, ни роботом, или я могу быть роботом, но не иметь ЦП вместо мозга.
0085 > или = с более красивыми версиями. Далее вы увидите индикаторы, показывающие, что оператор является непредвиденным обстоятельством . Это просто означает, что утверждение может быть либо истинным, либо ложным, в зависимости от того, являются ли входные данные (идентификаторы) истинными или ложными. Утверждения также могут быть тавтологиями (утверждение всегда истинно, независимо от входных данных) или противоречиями (всегда ложно). Например, A v ~A — это тавтология, потому что, если вы переведете это на английский язык, получится, что «A истинно или ложно», что, конечно, всегда верно, независимо от того, что такое A. A & ~A — это противоречие, потому что оно говорит, что «A истинно и ложно», и невозможно, чтобы что-то было одновременно и истинным, и ложным. Наш пример является случайным, потому что я могу быть ни человеком, ни роботом, или я могу быть роботом, но не иметь ЦП вместо мозга.
Наконец, у нас есть таблица истинности для нашего утверждения.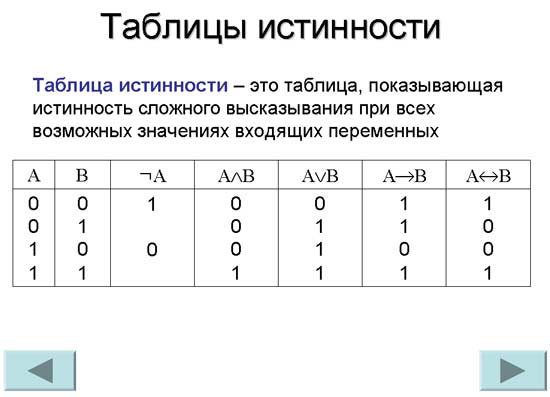 Каждый компонент нашего заявления разбит на столбец таблицы. Столбец главного оператора выделен; это «вывод» оператора. Давайте попробуем использовать его! Во-первых, мы должны определить, каково значение каждого идентификатора. Я человек, я не робот, и у меня нет процессора вместо мозга, так что H верно, R ложно, и C тоже ложно. В таблице мы можем найти строку, в которой каждый из наших идентификаторов имеет значение, которое мы определили: И мы видим, что в этой строке основной оператор истинен, что означает, что утверждение истинно!
Каждый компонент нашего заявления разбит на столбец таблицы. Столбец главного оператора выделен; это «вывод» оператора. Давайте попробуем использовать его! Во-первых, мы должны определить, каково значение каждого идентификатора. Я человек, я не робот, и у меня нет процессора вместо мозга, так что H верно, R ложно, и C тоже ложно. В таблице мы можем найти строку, в которой каждый из наших идентификаторов имеет значение, которое мы определили: И мы видим, что в этой строке основной оператор истинен, что означает, что утверждение истинно!
Как пользоваться таблицей истинности?
Подведение итогов, составление и использование таблицы истинности:
- Переведите свое утверждение в символьную логику
- Вставьте свое утверждение в калькулятор, чтобы сгенерировать таблицу истинности
- Найдите строку в таблице, в которой значения идентификаторов совпадают ваши входные значения
- Прочтите значение в главном столбце оператора (выделено), чтобы увидеть результат!
Часто задаваемые вопросы
Таблицы истинности сложны?
Таблицы истины поначалу могут показаться немного пугающими, но как только вы научитесь ими пользоваться, они станут очень простыми. Их использование — это просто вопрос подстановки значений и поиска соответствующей строки.
Их использование — это просто вопрос подстановки значений и поиска соответствующей строки.
Чем полезны таблицы истинности?
Таблицы истинности позволяют легко анализировать логические утверждения. Это позволяет вам видеть вывод оператора для всех комбинаций входных данных, что полезно, если оператор очень сложен и его трудно оценить вручную.
Какие еще есть термины для символической логики?
Символическая логика также может называться «формальной логикой» или, в более широком смысле, «математической логикой». Вы можете просмотреть больше синонимов на Power Thesaurus (отличный сайт тезауруса).
Создавайте таблицы LaTeX онлайн – TablesGenerator.com
- Латекс
- HTML
- Текст
- Уценка
- МедиаВики
Введите размер таблицы. Пожалуйста, помните, что текущее содержимое таблицы будет
Потерянный.
Пожалуйста, помните, что текущее содержимое таблицы будет
Потерянный.
Ряды
Допустимый диапазон: 1–500
Столбцы
Допустимый диапазон: 1-20
Вы можете импортировать данные таблицы, загрузив файл в формате CSV (запятая отдельное значение). Большинство программ для работы с электронными таблицами, как настольных, так и онлайн, позволяет сохранять табличные данные в формате CSV — обычно он доступен в меню «Файл» под названием «Сохранить как…» или «Экспорт».
Выбрать CSV-файл
Убедитесь, что кодировка символов вашего CSV-файла установлена на UTF-8. в противном случае некоторые символы могут отображаться неправильно.
Вставить (Ctrl + V) ниже существующей таблицы, скопированной (Ctrl + C) из
Электронная таблица (например, Microsoft Excel), текстовый документ 
Если вы хотите сохранить таблицу для дальнейшего редактирования, нажмите кнопку Кнопка «Скачать» ниже. Файл с таблицей можно загрузить обратно с помощью пункт меню «Загрузить таблицу».
Имя таблицы
Скачать
Основные клавиатурные команды
- ВВОД или двойной щелчок — для начала редактирования ячейки
- ESC — остановить редактирование ячейки
- CTRL+C, CTRL+X, CTRL+V — копировать, вырезать и паста соответственно
- TAB или клавиши со стрелками — для выбора другой ячейки
- CTRL+Z — отменить изменение
- CTRL+Y — повторить изменение
- Левая кнопка мыши — щелкните ячейку, чтобы выберите его (удерживайте левую кнопку, чтобы выбрать соседние ячейки)
- Удерживайте клавишу CTRL , чтобы выбрать несколько ячеек (не обязательно соседних).


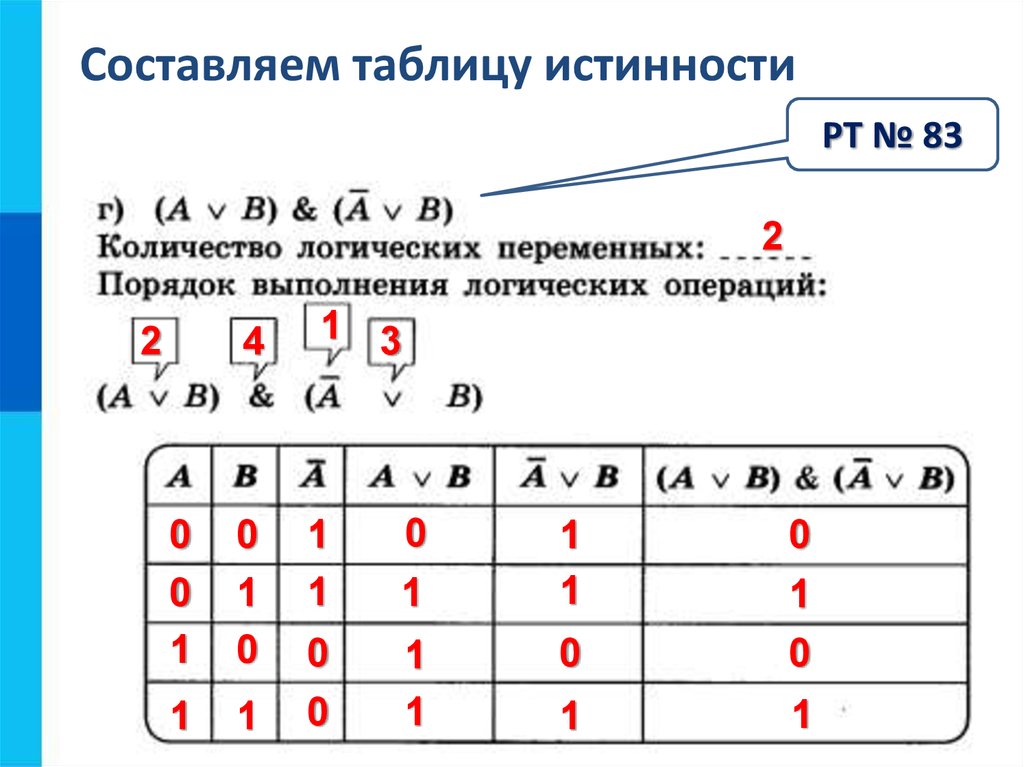
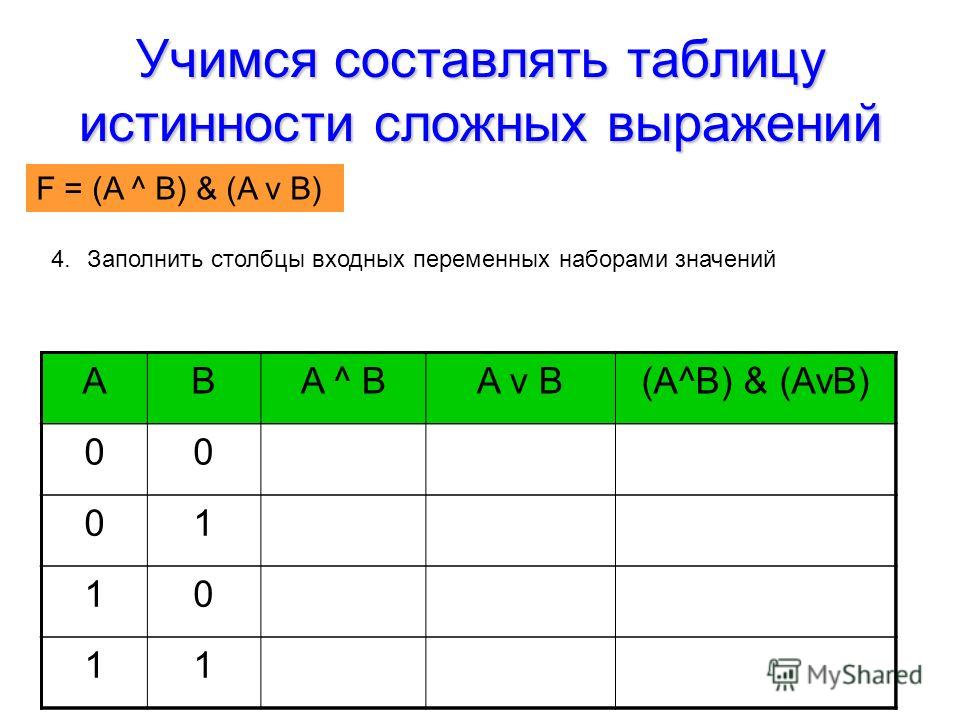
 По формуле построить таблицу истинности. Сложное выражение разбить на действия. Над таблицей написать эти действия, введя для каждого новую переменную. Столбцы в таблице лучше назвать именами вспомогательных переменных. В данном примере: в ячейку D5 вводится формула =И(A5;B5). В ячейку E5 вводится формула =НЕ(A5). В ячейку F5 вводится формула =И(E5;C5). В ячейку G5 — формула =ИЛИ(D5;F5). Дальше эти формулы размножаются по столбцам. Строится рамка и таблица готова
По формуле построить таблицу истинности. Сложное выражение разбить на действия. Над таблицей написать эти действия, введя для каждого новую переменную. Столбцы в таблице лучше назвать именами вспомогательных переменных. В данном примере: в ячейку D5 вводится формула =И(A5;B5). В ячейку E5 вводится формула =НЕ(A5). В ячейку F5 вводится формула =И(E5;C5). В ячейку G5 — формула =ИЛИ(D5;F5). Дальше эти формулы размножаются по столбцам. Строится рамка и таблица готова value else "False"
def __format__(self, format_spec):
return format(str(self), format_spec)
infunc = input('Enter your function: ')
# в питоне знак эквивалентности - это '==', так что заменяем
infunc = infunc.replace("=", "==")
# находим переменные в функции, т.е. просто буквы
# set() делает этот набор уникальным, ну и сортируем
variables = sorted(set(re.findall(r"[A-Za-z]", infunc)))
# или так, если надо без использования регулярных выражений
# variables = sorted(set([c for c in infunc if c.isalpha()]))
# просто красивое оформление для таблицы
header = [""]*2
for key in variables:
header[0] += "-"*7 + "+"
header[1] += f" {key} |"
header[0] += "-+" + "-"*7
header[1] += " | Result"
print("\n".join(header + header[0:1]))
vars_for_eval = {}
# вариантов входных значений для таблицы - 2 в степени кол-ва переменных
for variant in range(1 << len(variables)):
# заполняем входной словарь c представлением переменных
# в виде экземпляров нашего класса для функции eval()
# key идут в прямом порядке, а i - в обратном
for i, key in reversed(list(enumerate(reversed(variables)))):
# используем биты этого числа для инициализыции булевых значений
vars_for_eval[key] = BoolVar(variant & (1 << i))
# вывод строки таблицы истинности
print(f" {vars_for_eval[key]:<5}", end=" |")
# вычисляем результат
result = eval(infunc, {}, vars_for_eval)
print(f" | {result:<5}")
print(header[0])
value else "False"
def __format__(self, format_spec):
return format(str(self), format_spec)
infunc = input('Enter your function: ')
# в питоне знак эквивалентности - это '==', так что заменяем
infunc = infunc.replace("=", "==")
# находим переменные в функции, т.е. просто буквы
# set() делает этот набор уникальным, ну и сортируем
variables = sorted(set(re.findall(r"[A-Za-z]", infunc)))
# или так, если надо без использования регулярных выражений
# variables = sorted(set([c for c in infunc if c.isalpha()]))
# просто красивое оформление для таблицы
header = [""]*2
for key in variables:
header[0] += "-"*7 + "+"
header[1] += f" {key} |"
header[0] += "-+" + "-"*7
header[1] += " | Result"
print("\n".join(header + header[0:1]))
vars_for_eval = {}
# вариантов входных значений для таблицы - 2 в степени кол-ва переменных
for variant in range(1 << len(variables)):
# заполняем входной словарь c представлением переменных
# в виде экземпляров нашего класса для функции eval()
# key идут в прямом порядке, а i - в обратном
for i, key in reversed(list(enumerate(reversed(variables)))):
# используем биты этого числа для инициализыции булевых значений
vars_for_eval[key] = BoolVar(variant & (1 << i))
# вывод строки таблицы истинности
print(f" {vars_for_eval[key]:<5}", end=" |")
# вычисляем результат
result = eval(infunc, {}, vars_for_eval)
print(f" | {result:<5}")
print(header[0])
 py
Enter your function: a+b
-------+-------+-+-------
a | b | | Result
-------+-------+-+-------
False | False | | False
False | True | | True
True | False | | True
True | True | | True
-------+-------+-+-------
D:\Programming\Python\1>python bools.py
Enter your function: -x=y
-------+-------+-+-------
x | y | | Result
-------+-------+-+-------
False | False | | False
False | True | | True
True | False | | True
True | True | | False
-------+-------+-+-------
D:\Programming\Python\1>python bools.py
Enter your function: -p+(p*q)=q
-------+-------+-+-------
p | q | | Result
-------+-------+-+-------
False | False | | False
False | True | | True
True | False | | True
True | True | | True
-------+-------+-+-------
py
Enter your function: a+b
-------+-------+-+-------
a | b | | Result
-------+-------+-+-------
False | False | | False
False | True | | True
True | False | | True
True | True | | True
-------+-------+-+-------
D:\Programming\Python\1>python bools.py
Enter your function: -x=y
-------+-------+-+-------
x | y | | Result
-------+-------+-+-------
False | False | | False
False | True | | True
True | False | | True
True | True | | False
-------+-------+-+-------
D:\Programming\Python\1>python bools.py
Enter your function: -p+(p*q)=q
-------+-------+-+-------
p | q | | Result
-------+-------+-+-------
False | False | | False
False | True | | True
True | False | | True
True | True | | True
-------+-------+-+-------
 0)
0)