Онлайн построение графиков сложных функций: Построение графика функции онлайн

Содержание

Преобразование графиков функции. Приемы построения графиков

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

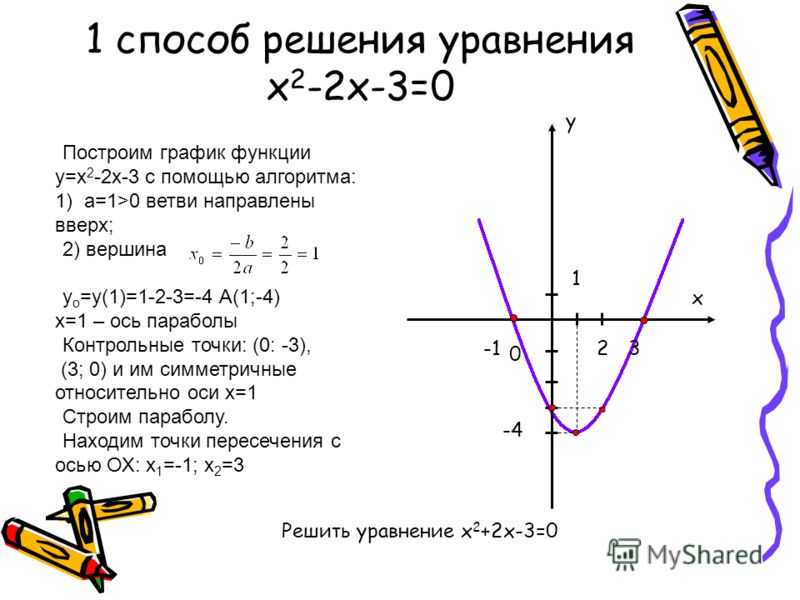
1. Тема: «Преобразование графиков функции»

2. Цели:

1) Систематизировать приемы
построения графиков.
2) Показать их применение при
построении:
а) графиков сложных функций;
б) при решении заданий ЕГЭ из
части C.

3. Рассмотрим основные правила преобразования графиков на примерах элементарных функций

4.

1) Преобразование симметрии относительно оси x f(x)-f(x)1) Преобразование симметрии относительно оси x
f(x) -f(x)
График функции y=-f(x)
получается
преобразованием
симметрии графика
функции y=f(x)
относительно оси x.
Замечание. Точки
пересечения графика с
осью x остаются
неизменными.

6. 2) Преобразование симметрии относительно оси y f(x)f(-x)

2) Преобразование симметрии относительно оси y
f(x) f(-x)
График функции y=f(-x) получается
преобразованием симметрии графика функции
y=f(x) относительно оси y.
Замечание. Точка пересечения графика с осью y
остается неизменной.
Замечание 1. График четной функции не изменяется при
отражении относительно оси y, поскольку для четной функции
f(-x)=f(x). Пример: (-x)²=x²
Замечание 2. График нечетной функции изменяется
одинаково как при отражении относительно оси x, так и при
отражении относительно оси y, поскольку для нечетной
функции f(-x)=-f(x).

Пример: sin(-x)=-sinx.

7. 3) Параллельный перенос вдоль оси x f(x)f(x-a)

3) Параллельный перенос вдоль оси x
f(x) f(x-a)
График функции y=f(x-a)
получается параллельным
переносом графика функции
y=f(x) вдоль оси x на |a|
вправо при a>0 и влево при
a<0.
Замечание.График периодической функции с периодом T не изменяется
при параллельных переносах вдоль оси x на nT, n Z.

8. 4) Параллельный перенос вдоль оси y f(x)f(x)+b

4) Параллельный перенос вдоль оси y
f(x) f(x)+b
График функции
y=f(x)+b получается
параллельным
переносом графика
функции y=f(x)
вдоль оси y на |b|
вверх при b>0 и
вниз при b<0.

9. 5) Сжатие и растяжение вдоль оси x f(x)f(x), где >0

5) Сжатие и растяжение вдоль оси x
f(x) f( x), где >0
0< <1 График
функции y=f( x)
получается
растяжением
графика функции
y=f(x) вдоль оси x в
1/ раз.
>1 График
функции y=а( x)
получается сжатием
графика функции
y=f(x) вдоль оси x в
раз.

Замечание. Точки с пересечения графика с осью y остаются неизменными.

10. 6) Сжатие и растяжение вдоль оси y f(x)kf(x), где k>0

6) Сжатие и растяжение вдоль оси y
f(x) kf(x), где k>0
k>1 График функции y=kf(x)
получается растяжением графика
функции y=f(x) вдоль оси y в k
раз.
0<k<1 График функции y=kf(x)
получается сжатием графика
функции y=f(x) вдоль оси y в
1/k раз.
Замечание. Точки пересечения графика с осью x остаются неизменными.

11. 7) Построение графика функции y=|f(x)|

Части графика функции y=f(x), лежащие выше оси x и на оси x,
остаются без изменения, а лежащие ниже оси x – симметрично
отображаются относительно этой оси (вверх).
Замечание. Функция y=|f(x)| неотрицательна (ее график расположен
в верхней полуплоскости).
Примеры:

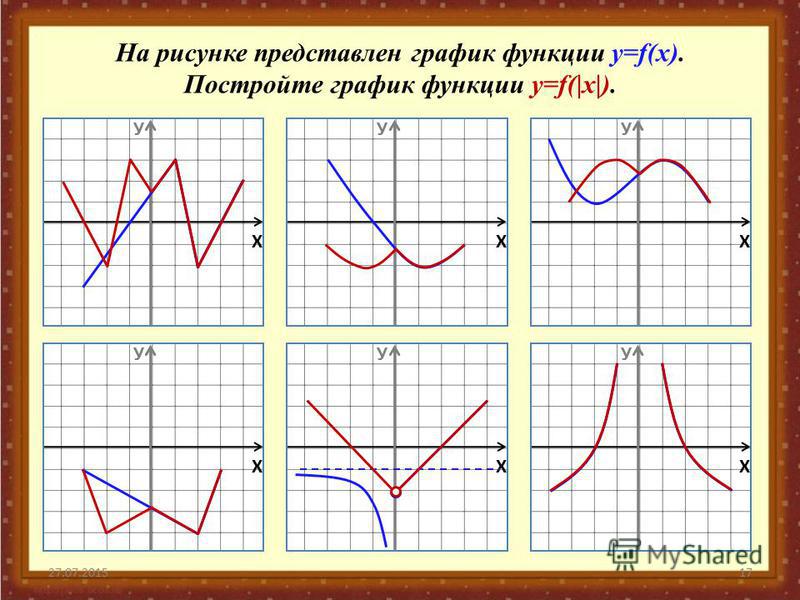
12. 8) Построение графика функции y=f(|x|)

Часть графика функции y=f(x), лежащая левее оси y, удаляется, а
часть, лежащая правее оси y – остается без изменения и, кроме
того, симметрично отражается относительно оси y (влево).

Точка
графика лежащая на оси y, остается неизменной.
Замечание. Функция y=f(|x|) четная (ее график симметричен
относительно оси y).
Примеры:

13. 9) Построение графика обратной функции

График функции y=g(x), обратной функции y=f(x),
можно получить преобразованием симметрии
графика функции y=f(x) относительно прямой y=x.
Замечание. Описанное построение производить
только для функции, имеющей обратную.
Построение графиков сложных
функций с помощью
последовательных
преобразований графиков
элементарных функций (на
примерах)

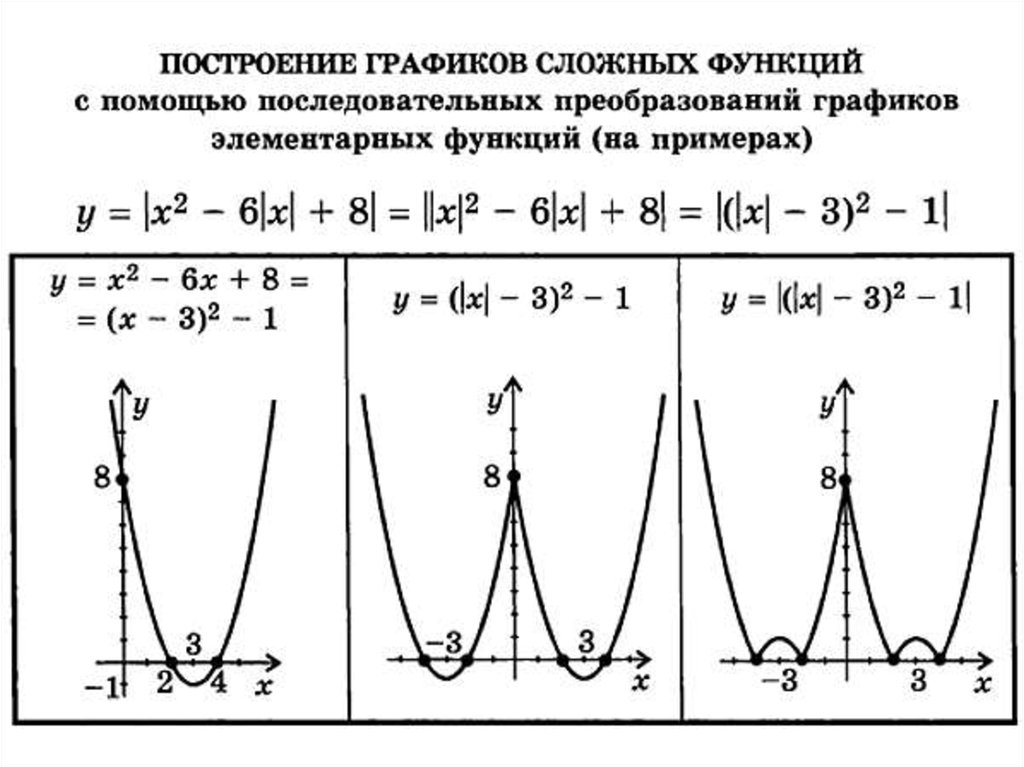
15. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

y=|x²-6|x|+8|=||x|²-6|x|+8|=|(|x|-3) ²-1|

16. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

17. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

18.

Применение правил преобразования графиков при решении заданий ЕГЭ (части C).

19. Решить систему уравнений:

5 x 1 y 0
y 5 x 1
| x 4| 3 y
y | x 4| 3
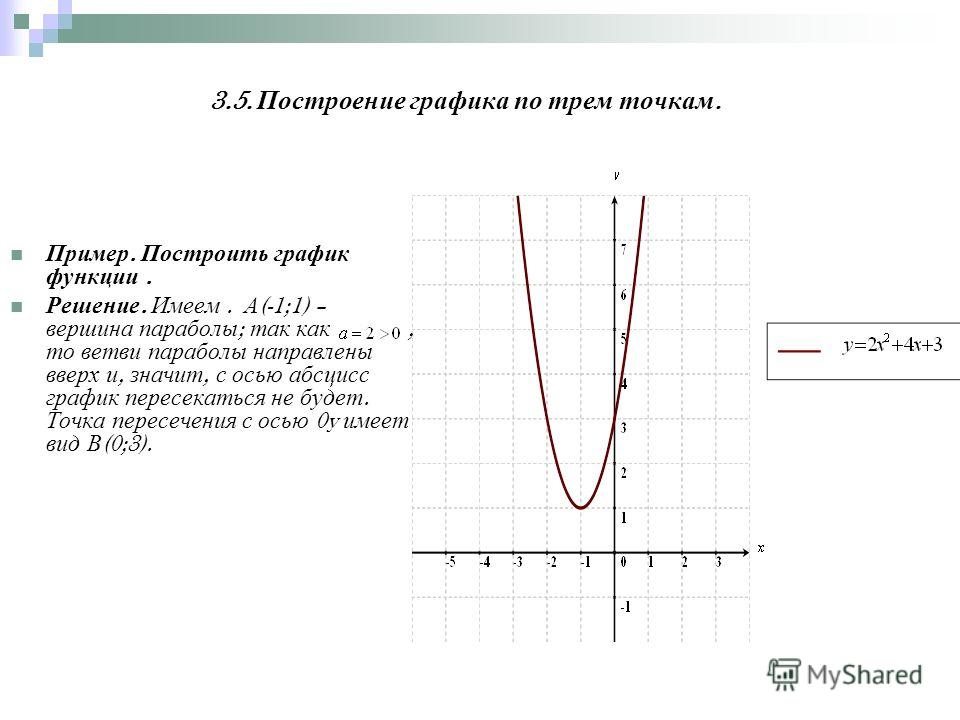
В одной системе координат, построим графики функций: а)
y 5x 1
График этой функции получается в результате построения
графика y 5 x
y 5x
в новой системе координат x’o’y’, где O’(1;0)
б) y | x 4 | 3
В системе x”o”y”, где o”(4;3) построим график y=|x|.
Решением системы являются
координаты точки
пересечения графиков
и
y | x 4 | 3,
y 5x 1
Пара чисел:
x y
Проверка:
5 2 1 5 0
|2 4| 3 5
Ответ: (2;5).
(2; 5) .
(верно)
(верно)

20. Решить уравнение: f(g(x))+g(f(x))=32, если известно, что и

Решить уравнение:
f(g(x))+g(f(x))=32, если известно, что
f ( x ) 0,5 x 2 2 x 12
Решение: Преобразуем функцию f(x).
f ( x) 0,5( x 2) 10
2
Так как 0,5( x 2) 0 , то
20, при x 5
g ( x)
8
0 , 5 2 x
ï при
6 x
2
и
x 5.

f ( x) 0,5( x 4 x 4) 10
2
f ( x) 10
Тогда g(f(x))=20.
Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;
f(g(x))=12
Пусть g(x)=t, тогда f(t)=12 или
0,5t 2 2t 12 12
0,5t 2 2t 0
t 2 4t 0
t (t 4) 0
t 0 или t 4
Имеем: g(x)=0 или g(x)=4
Так как при x≥5 g(x)=20, то решения уравнений: g(x)=0 и g(x)=4 будем искать среди x<5.
Тогда: а) Уравнение g(x)=0 примет вид:
0,5 2 x
Так как x<5, то 6-x>0
8
16
0 | 2 2 x
0
6 x
6 x
16
16
0 2x
0
6 x
6 x
Вывод: уравнение g(x)=0 не имеет корней.
б) уравнение g(x)=4 примет вид:
0,5 2 x
8
1
8
8
4 2x 4
2 x 1
4
6 x
2
6 x
x 6
В одной системе координат построим графики функций
y и2
x 1
8
y
4
x 6
а)y 2 x 1
x
График данной функции получается построением графика y 2
В системе x’o’y’, где o’(1;0).
8
4
б)y
x 6
8
y
В системе x”o”y”, где o”(6;4), построим график функции
x
( x 0)
Условию x<5 удовлетворяет
абсцисса общей точки
графиков x=2.

Ответ: 2.

22. Вывод:

Мы видим, что правила преобразования
графиков существенно упрощают
построение графиков сложных
функций.
Помогают найти нетрадиционное
решение сложных задач.

23. Тема: «Преобразование графиков функции»

English Русский Правила

Исследовательская работа по теме: Построение графиков сложных функций на основе свойства монотонности

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1.

Исследовательская работа по теме:ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА ПО ТЕМЕ:

2. Актуальность выбранной темы

АКТУАЛЬНОСТЬ ВЫБРАННОЙ ТЕМЫ
Умение читать графики функций, т.е. по графику
описывать
свойства
функции
(промежутки
монотонности, экстремальные значения, интервалы
знакопостоянства и т.д.), необходимо и врачу
(кардиограмма),
и
экономисту
(график
производительности труда, курсы валют), метеорологу
(суточное изменение температуры) и другим
специалистам.
Поэтому
в
огромном
море
зависимостей величин необходимо
хорошо
ориентироваться.
Проблема:
Зачастую методами математического анализа в курсе школы
невозможно исследовать функцию и построить график.
Цель:
познакомиться с другими методами исследования функций и
построения графика с тем, чтобы применить их при решении
задач с параметрами;
научиться моделировать условия нахождения значения параметра
для различных математических моделей.

Объект исследования:
Многообразие задач, содержащих параметр.
Предмет исследования:
Сложные функции.
Задачи исследования:
Изучить метод построения графиков сложных функций на основе
свойства монотонности функций.
Применить данный метод при моделировании задач с
параметрами.
Научиться ставить вопросы, имея построенный график сложной
функции (картинку, рисунок).
В курсе алгебры 7-9 классов мы изучали
алгебраические
функции,
т.е.
функции,
заданные аналитическими выражениями, в
записи
которых
использовались
алгебраические операции над числами и
переменной
(сложение,
вычитание,
умножение, возведение в степень, извлечение
квадратного корня). К концу 9 класса у нас
формируется
цепочка
следующих
представлений:
При этом десятиклассник
оказывается
в
двусмысленной ситуации:
в 9 классе он научился
строить график функции и по
графику
перечислять
её
свойства; теперь же от него
требуется
исследовать
функцию и затем строить
график.

А
в
старшей
школе
при
изучении
тригонометрических функций, логарифмических
функций,
показательных и алгебраических
функций высших степеней
формулировка
«исследуйте функцию и постройте её график»
предполагает несколько другой подход:
Сложные функции можно исследовать
разными методами.
Один из методов: построение графиков
сложных
функций
на
основе
монотонности. Математические модели
реальных ситуаций часто бывают
связаны с функциями других классов,
которые
называют
сложными.
Рассмотрим сложную функцию y = f(v(x)).
Напомним, что если внутренняя функция
v(x) и внешняя функция f(v) – монотонны,
то сложная функция y = f(v(x)) также
монотонна.
Пусть, например, v(x) и f(x) – убывают.
Тогда при x1 < x2
v1 = f(x1) > v2 = f(x2).
Неравенство v1 > v2 влечёт за собой неравенство
f(v1) < f(v2), т.е.
f(v(x1)) < f(v(x2)).
Итак, большему значению аргумента (x1 < x2)
соответствует большее значение сложной
функции.

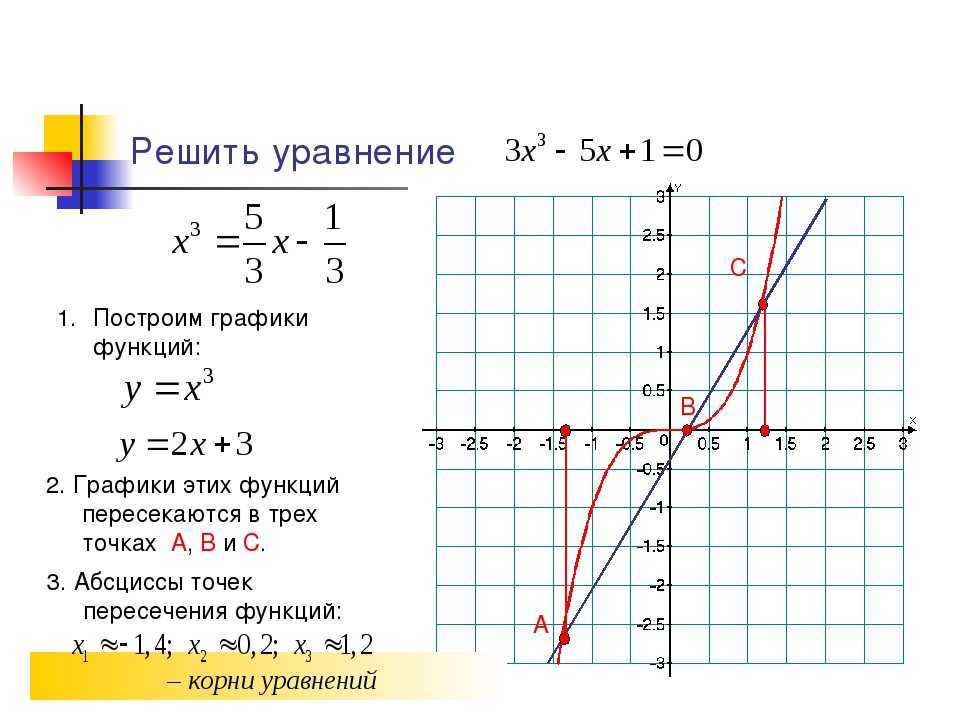
Следовательно, по определению, она является
возрастающей.
Конечно, говоря о монотонности функции, всегда
надо указывать соответствующее множество из
области определения.
АНАЛИТИЧЕСКИЙ АППАРАТ:
найдём производную.
НА ОСНОВЕ МЕТОДА МОНОТОННОСТИ:
D(y):R
Чётная
– внутренняя функция,
— внешняя.
при
Знак y`
Поведение y
+
0
Рассматривается только
,
т.к. функция
чётная, и,
следовательно, её график
симметричен относительно
оси Оy.

12. МОДЕЛИРОВАНИЕ

1)
:
a) При каких значениях a данное уравнение имеет один корень, т.е. горизонтальная
прямая пересекает график 1 раз?
Ответ: a = 1.
a) При каких значениях параметра a данное уравнение не имеет решение, т.е.
горизонтальные прямые не пересекают график?
Ответ: (-∞;0]∩(1;∞).

13. МОДЕЛИРОВАНИЕ

a) При каких значениях параметра a данное уравнение имеет решение, т.е.
горизонтальные прямые пересекают график?
Ответ: (0;1].

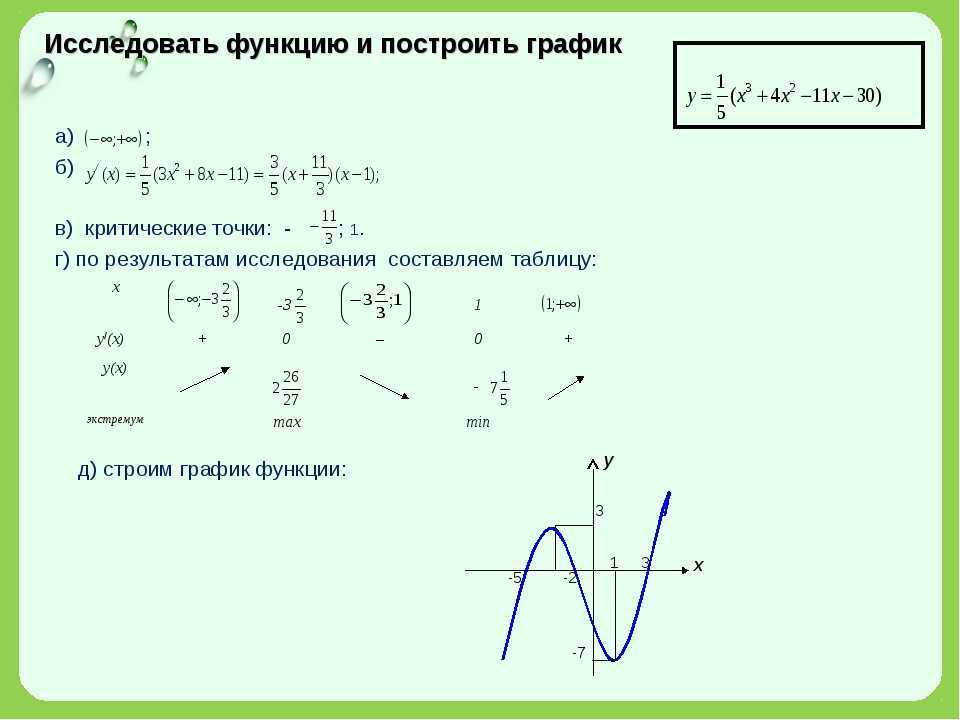
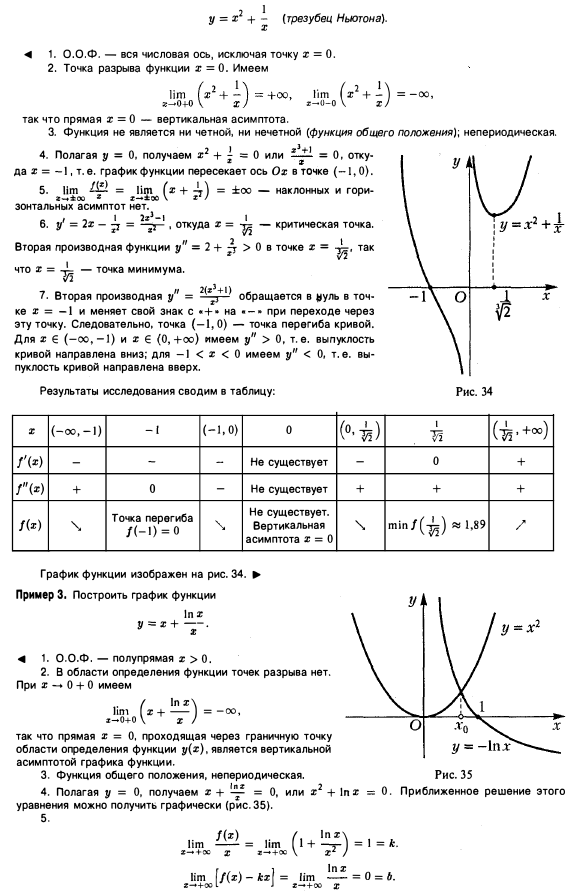
Пример 2: Исследовать функцию
и
построить её график.
Можно исследовать функцию методами
математического анализа. Большой сложности
нет. Но объём исследования достаточно
большой: нахождение нулей функции ;
нахождение промежутков возрастания и
убывания…
А можно применить метод на основе свойства
монотонности функций.
А можно применить метод на основе свойства монотонности функций.

2008 г., С3: при каких значениях a неравенство не имеет
решений?
На промежутке (-5;-2] неравенство не
выполняется, т.е. горизонтальные линии не
пересекают полученные области.

English Русский Правила

Сложный функциональный плоттер

Вы можете использовать этот инструмент для построения графиков функций комплексных, расщепленно-комплексных и двойных чисел, а также их инверсий в 2D и 3D.
Основная цветовая схема и идея были полностью вдохновлены плоттером сложных функций Дэвида Бау, но моя цель состояла в том, чтобы моя версия работала быстрее (используя webgl) и имела больше функций (разделенные комплексные числа, двойные числа, трехмерное построение, инверсии) и была более настраиваемый.

Основное использование

Чтобы ввести функцию, наведите указатель мыши на нижнюю часть окна (или коснитесь на мобильном телефоне) и щелкните 3 горизонтальные полосы, которые отобразят интерфейс для ввода функций и настройки инструмента.
В порядке чтения значки в нижней части экрана: справка, меню (три горизонтальные полосы, упомянутые выше), загрузка фонового изображения (это позволяет вам управлять изображением по вашему выбору с помощью введенной вами функции), загрузка и полноэкранный режим.
Переменная z предоставляет координаты x и y каждого пикселя в форме x + iy.
Любые другие переменные станут переключаемыми значениями в меню, которые вы можете использовать для управления программой.
Когда пользователь входит в функцию, каждая точка (x,y) окрашивается в соответствии с тем, где они находятся под f(x+iy). Если вы хотите, чтобы точки окрашивались в зависимости от того, где они возникли, а не где они закончились, включите «инвертировать» в настройках, чтобы численно инвертировать функцию.

Это довольно дорого, поэтому подумайте об отключении AA или уменьшении окна, если у вас возникнут проблемы (вы также можете настроить параметры инверсии в меню).

Константы

пи или π
i

Операторы и функции

Примечание: ниже u и v используются для представления любого выражения
Группировка (u)
Величина |u| или ‖u‖
Conjuagte u*
Основная арифметика : u+v,u-v,u*v или u⋅v,u/v или u÷v
Для умножения вы также можете просто написать переменные рядом друг с другом, то есть uv или 2uv или 2 u v или ipiuv или i pi u v все действительны и будут вести себя так же, как если бы использовалось *. Обратите внимание, что 2(u) будет работать нормально, но v(u) — это функция, а не умножение (также обратите внимание, что (v)u или (v)(u) будут работать нормально). 9v, ln(u), log(u), log(u,b) (Аргумент b в log может использоваться для указания базы, по умолчанию e)
Факториал : u! (действительно gamma(u+1))

Триггерные функции : sin(u), cos(u), tan(u)

Обратные триггерные функции : asin(u), acos(u), atan(u)
Гиперболические триггерные функции : sinh(u), ch(u), tanh(u)

Угол : arg(u)
Получить действительные/мнимые компоненты : re(u), im(u)
Знак : sgn(u)
Шаг : шаг(u)
Квадратный корень : sqrt(z) или √(z) (или просто возведение в степень)
Гамма-функция : gamma(u) или Γ(u)
Дзета-функция 90 018 : zeta(u) или ζ(z)

Итерируемая функция {var=update, var=initial, iterations} (Думайте о var=update как о теле цикла for, например, {z’ = z’ +1 , z’ = 0, 5} будет инициализировать z’ значением 0, а затем добавлять к нему единицу в каждой из 5 итераций).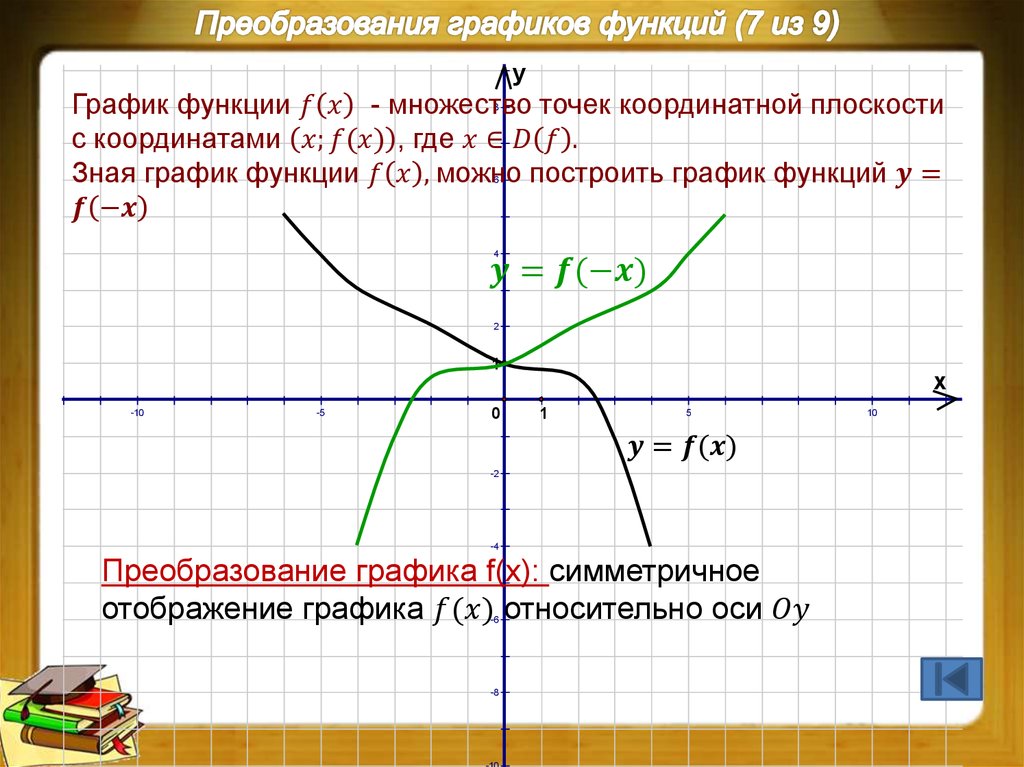 Значение по умолчанию var равно z’, вам не нужно указывать «z’=», если вы планируете использовать z’ (поэтому {z’ +1, 0, 5} также работает), но если вы хотите использовать другую переменную, такую как «y», вам нужно будет указать ее ({y = y +1, y = 0, 5}). Итерации должны быть целым числом

Производная w.r.t z (u)’ (Вы можете вкладывать производные так глубоко, как хотите, но из-за ограничений арифметических операций с плавающей запятой результаты ухудшаются довольно быстро) Обратите внимание на круглые скобки, z’ в итерируемой функции не является производной из з.
Интеграл w.r.t z $(u) или $[нижний](u) или $[нижний, верхний](u). Когда параметры нижней и верхней границы опущены, используются значения по умолчанию 0 и z соответственно. Интегрируется по прямой от нижней до верхней границы. Вы также можете использовать $[lower, upper, variable](u), чтобы указать переменную для интегрирования по отношению к z по умолчанию. Используйте $[lower,upper,variable,iter](u), чтобы указать количество шагов, которые необходимо выполнить при интеграции.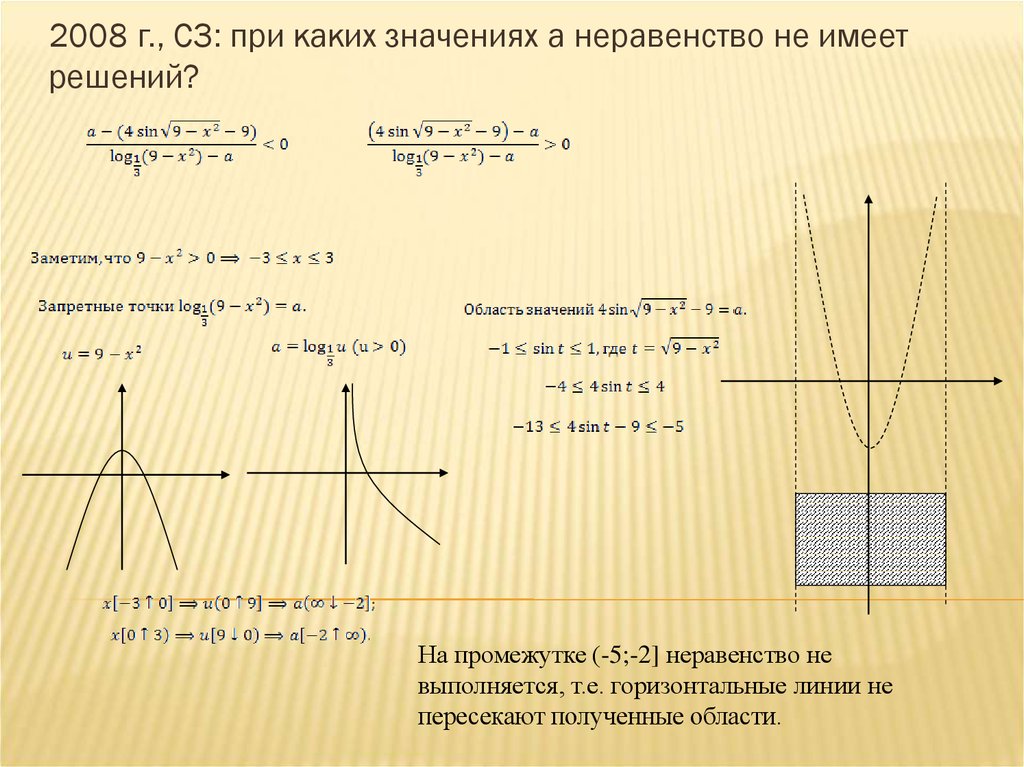

Вы можете использовать ∫ вместо $. 9я, 100н).
Прочее
Чтобы сгенерировать парсер для пользовательского ввода, я использовал peg.js. Сгенерированный файл синтаксического анализатора включен вместе с файлом грамматики, который я написал и использовал для создания синтаксического анализатора.
Wolfram|Альфа-примеры: комплексный анализ
Wolfram|Альфа-примеры: комплексный анализ
О-о! Wolfram|Alpha не работает без JavaScript.
Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.
Примеры для
Комплексный анализ — это область математики, занимающаяся изучением комплексных чисел и функций комплексной переменной. Авторитетные вычислительные возможности Wolfram|Alpha позволяют выполнять сложные арифметические действия, анализировать и вычислять свойства сложных функций, а также применять методы комплексного анализа для решения связанных математических запросов.
Комплексные числа
Анализ свойств функций комплексной переменной или выполнение основных арифметических операций, поиск корней или применение функций к комплексным числам. 9(2z)+1) с |z| < 3pi
СВЯЗАННЫЕ ПРИМЕРЫ
Исчисление и анализ
Дифференциальные уравнения
Кватернионы
СВЯЗАННЫЕ РЕСУРСЫ WOLFRAM
Изучение комплексного анализа в Wolfram MathWorld
90 137 Руководство по комплексным числам Wolfram Страница
Руководство по функциям комплексных переменных Wolfram Страница
Учебное пособие по Wolfram о выражениях, включающих комплексные переменные
Римановы поверхности
Вычисление и визуализация римановых поверхностей для сложных функций. 9(1/3)
Pro
Мобильные приложения
Продукты
Бизнес
API и решения для разработчиков
Решения LLM
Ресурсы и инструменты 9 0138
О
Контакты
Связь
© ООО «Вольфрам Альфа», 2023 г.
No related posts.