Построение графиков функций по уравнению онлайн: Построение графика функции онлайн

Содержание

Построить график функции y 3 в степени. Калькуляторы для построения графика функции

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.

На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

Введите ваше уравнение в поле после знака «=».
Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.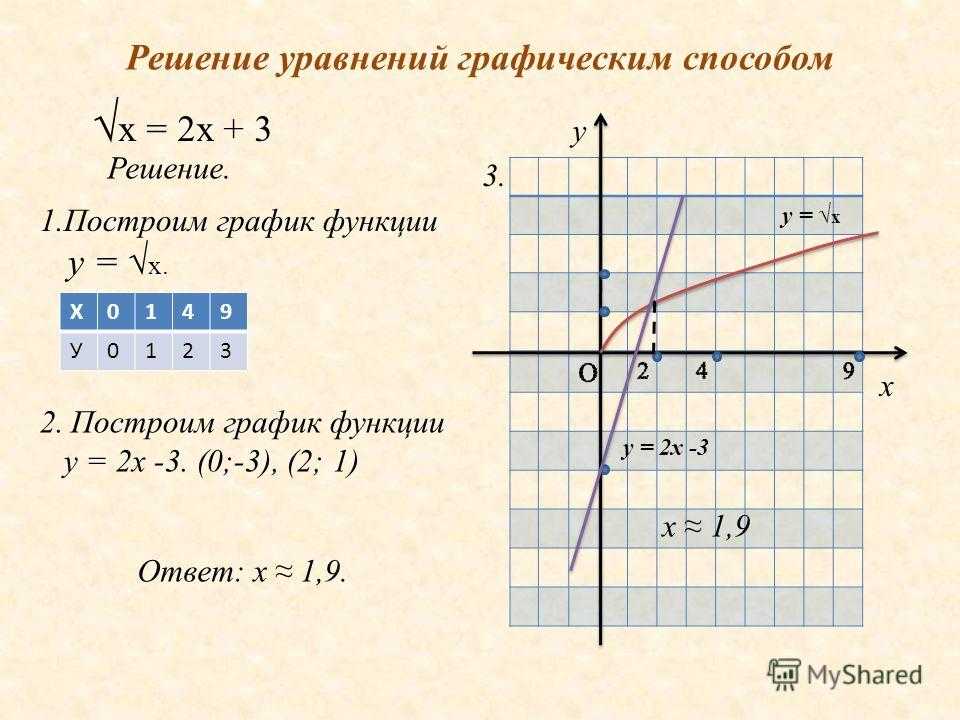

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

Выберите необходимый способ задания графика.

Введите уравнение.
Задайте интервал.
Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

Найдите в списке необходимую вам функцию.
Щелкните на нее левой кнопкой мыши
При необходимости введите коэффициенты в поле «Функция:» .
Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

В левом столбце кликните правой кнопкой мыши по свободной строке.
В нижнем левом углу нажмите на значок клавиатуры.
На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений.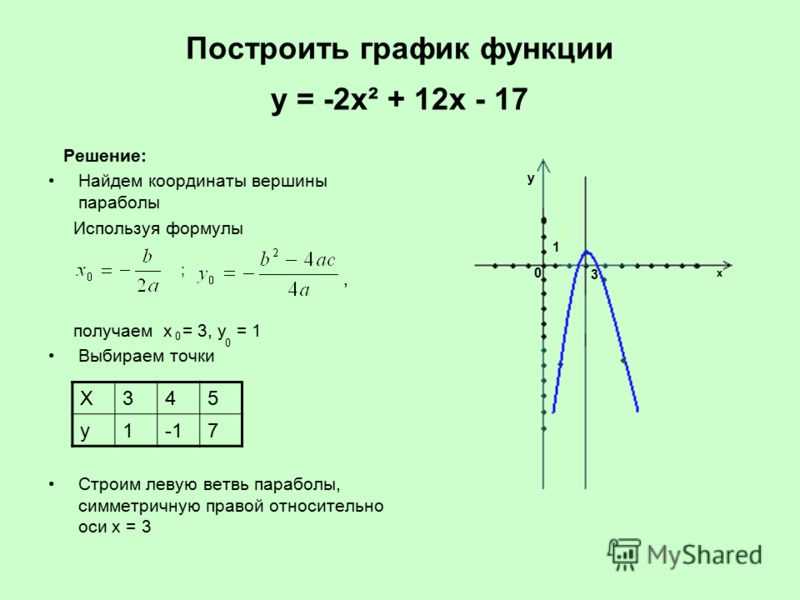

3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).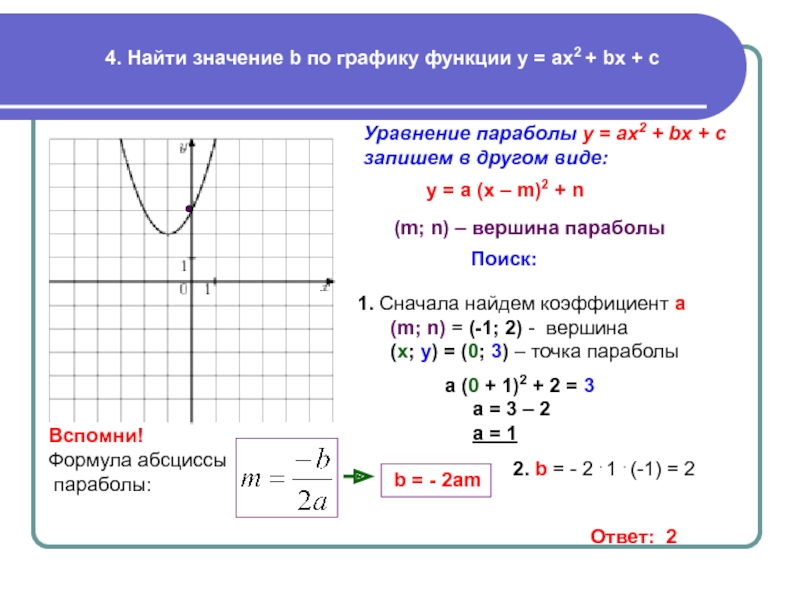

В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция

у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т.

е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции

у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Построение графиков функций содержащих знак модуля

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Построение графиков функций содержащих знак модуля для учащихся гуманитарного класса.

Учитель математики
Восточной гимназии
Дудрова И. А.
График функции у = |х|
а) Если х≥0, то |х| = х функция у = х, т.е. график
совпадает с биссектрисой первого координатного угла.
б) Если х<0, то |х| = — х и у = — х. При отрицательных
значениях аргумента х график данной функции – прямая
у = -х, т.е. биссектриса второго координатного угла.
у = |х|
График функции у = — |х|
Получается симметричным отображением графика у = |х|
относительно оси х.

у = — |х|
График функции у = |х| + а
График функции у=|х|+а получается параллельным
переносом графика у=|х| в положительном направлении
оси у на а единиц отрезка при а>0 и в отрицательном
направлении на а единиц при а<0.
у = |х| + а
у = |х|
у = |х| — а
График функции у = а|х|
График функции у=а|х| получается
растяжением графика у=|х| вдоль оси у в а раз при а>1 и
сжатием вдоль этой оси в 1\а раз при 0<a<1.
у = а|х|
у = |х|
у = а|х|
График функции у = |х+а|
График функции у = |x+a| получается параллельным
переносом графика y=|x|
в отрицательном направлении от оси х на |а| при а>0 и
в положительном направлении на |a| при a<0.
у = |х+а|
у = |х — а|
у = |х|
-а
а
Построить график функции у = х² — 4|х| + 3.
1 способ.
Раскрываем |х| = х при х≥0, получаем график у = х² — 4х + 3.
При х<0, |х|= — х, получаем график у = х² + 4х + 3.
2
х 4 х 3, если х 0,
у 2
х 4 х 3, если х 0.

Строим кусочно – заданную функцию по алгоритму:
1. Находим вершину параболы для каждой функции.
2. Находим точки пересечения каждой параболы с осью х.
3. Строим параболы по заданным условиям.
х 4 х 3, если х 0,
у 2
х 4 х 3, если х 0.
2
2 способ.
Если рассмотрим график у = х² — 4х + 3 при х≥0 и
отобразить его относительно оси ОУ мы получим тот же
самый график.
Для построения графика функции у = |f(х) | достаточно:
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где
f(х) <0, симметрично отражаем относительно оси абсцисс.
Построить график функции у = |х² — х -6|
1.Построим график функции
у =х² — х -6
2. Участки графика, расположенные в нижней
полуплоскости, отображаем симметрично
относительно оси ОХ.
Построить график функции у = |х + 3| + |2x + 1| — x
Строить график будем с помощью раскрытия модуля.
1.
2.
3.
4.
Алгоритм построения:
Приравняем каждое подмодульное выражение к
нулю и находим точки, в которых подмодульные
выражения, входящие в уравнение функции
меняют знак.

Наносим эти точки на ось х и выделяем
промежутки, в которых подмодульные выражения
сохраняют знак.
Раскрываем модуль на каждом промежутке и
получаем соответствующие уравнения функции.
Строим график на каждом промежутке.
у = |х + 3| + |2x + 1| — x
1. Приравниваем каждое подмодульное выражение к нулю и
находим точки, в которых происходит смена знака:
х 3 0; х 3
2 х 1 0; х 0,5
2. Наносим точки на ось х:
3. При
x 3
y x 3 2 x 1 x x 3 2 x 1 x 4 x 4
3 x 0,5
y x 3 2 x 1 x x 3 2 x 1 x 2 x 2
x 0,5
y x 3 2 x 1 x 2 x 4
4 x 4, если х 3
y 2 х 2, если 3 x 0,5
2 x 4, если x 0,5

16. у = |х + 3| + |2x + 1| — x

Построить график функции у = | 2|х | — 3|
1. Построить у = 2|х | — 3 , для 2 |х| — 3 > 0 , |х |>1,5 т.е. х< -1,5 и х>1,5
а) у = 2х — 3 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
2. Построить у = -2 |х| + 3 , для 2|х | — 3 < 0.

т.е. -1,5<х<1,5
а)у = -2х + 3 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
у = | 2|х | — 3|
1) Построить у = 2х-3, для х>0.
2) Построить прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаем
симметрично относительно оси ОХ.
Сравнивая оба графика, видим что они одинаковые.
у = | х² – 5|х| |
Построим у = х² – 5 х, для х>0. Вершина параболы в (2,5; -6,25)
Участки графика, расположенные в нижней полуплоскости, отображаем
симметрично относительно оси ОХ.
3. Для х<0, симметрично отражаем построенную часть относительно оси
ОУ.
1.
2.

20. Найти корни уравнения ||x-2|-5| = 3.

Найти корни уравнения ||x-2|-5| = 3.
• Выполняем построение первого
(внутреннего) модуля y = |x-2|
• Параллельно переносим линии вниз на 5,
чтобы получить график функции y = |x-2|- 5
• Отражаем все что находится ниже оси
абсцисс.

Это и будет искомая
функция y=||x-2|-5|. Также выполняем
построение прямой у=3

21. Найти корни уравнения ||x-2|-5|=3.

Найти корни уравнения ||x-2|-5|=3.
Нетрудно определить по графику, что решениями уравнения с
модулями будут значения x = — 6; x = 0; x = 4; x = 10.

22. Построить график функции у = | (|х| — 2) 2 – 3 |

• Строим график функции у = (х — 2) 2 – 3
• Совершаем преобразование: для этого часть графика,
расположенную левее оси оу стираем.

23. Построить график функции у = | (|х| — 2) 2 – 3 |

• Часть графика, расположенную правее оси оу
достраиваем симметрично относительно этой оси.
Получаем график функции у = (|х| — 2) 2 – 3

24. Построить график функции у = | (|х| — 2) 2 – 3 |

• Часть графика, расположенную ниже оси ох
отображаем симметрично относительно этой оси.

25. График неравенства | у — 2х -1| + 2|х| ≤ 3

• Задача. Изобразите на координатной
плоскости множество решений неравенства.

• Раскроем модули. Для этого каждое
подмодульное выражение приравняем к
нулю: у – 2х – 1 = 0; у = 2х + 1
х=0
Подмодульные выражения меняют знак при
переходе через прямые у = 2х + 1 и х = 0.

26. Выводы:

Для построения графика функции у = f |(х)|:
1.Построить график функции у = f(х) для х>0;
2.Построить для х<0 часть графика, симметричную
построенной относительно оси ОУ.
Для построения графика функции у = | f(х) |
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней
полуплоскости, т.е., где f(х) <0, строить кривые, симметричные
построенным графикам относительно оси абсцисс.
Для построения графика функции у = | f |(х)| |
1. Построить график функции у = f(х) для х>0.
2. Строим вторую часть графика, т. е. построенный график
симметрично отражаем относительно ОУ
3. Участки получившегося графика, расположенные в нижней
полуплоскости, преобразовываем на верхнюю полуплоскость
симметрично оси ОХ.

у = f |(х)|
у = |f |(х)||
у =| f (х)|
у = f(х), х>0
у = f(х), х>0
Построить часть для х<0,
симметричную
относительно
оси ОУ
у = f(х)
Построить для х<0 часть
графика, симметричную
построенной относительно
оси ОУ
Часть графика, расположенного
в нижней полуплоскости
симметрично отобразить
относительно оси ОХ

English Русский Правила

Как построить график функций на TI-84 Plus

Авторы: Джефф МакКалла и К.С. Эдвардс и

Обновлено: 19 октября 2022 г.

Из книги: 900 04 Графический калькулятор TI-84 Plus CE для Для чайников

Графический калькулятор TI-84 Plus CE для чайников

Изучите книгу Купить на Amazon

После того, как вы ввели функции в калькулятор TI-84 Plus и отформатировали график, вы почти готовы приступить к рисованию графиков. Как только вы освоите построение графиков, вам не нужно будет выполнять все эти шаги.
Отключение графиков статистики (при необходимости)
Верхняя строка в редакторе Y= сообщает вам о графическом статусе графиков статистики. Если Plot1 , Plot2 или Plot3 выделены, то этот график статистики будет отображаться вместе с графиком ваших функций. Если он не выделен, он не будет отображаться на графике. На первом экране выделено Plot1 , и оно будет отображаться вместе с функциями в редакторе Y=.
Чтобы отключить выделенный график статистики в редакторе Y=, используйте кнопку 9.0005
клавиш, чтобы поместить курсор на выделенный график статистики, а затем нажать [ENTER]. Смотрите второй экран. Тот же самый процесс используется для повторного выделения графика статистики, чтобы позднее отобразить его в виде графика.
Когда вы строите графики функций, графики статистики могут доставлять неудобства, если они включены, когда вы на самом деле не хотите, чтобы они отображались на графике. Наиболее распространенным симптомом этой проблемы является сообщение об ошибке ОШИБКА: НЕДОПУСТИМОЕ ИЗМЕРЕНИЕ, которое само по себе почти не дает вам понимания того, что вызывает проблему. Поэтому, если вы не планируете строить график статистики вместе со своими функциями, убедитесь, что все графики статистики отключены!
Выбор и отмена функции на TI-84 Plus
Отмените выбор (выключите) Y ₁ и Y ₂, удалив выделение их знаков равенства. Это делается в редакторе Y= с помощью клавиш
, чтобы поместить курсор на знак равенства, а затем нажать [ENTER], чтобы переключить знак равенства между выделенным и невыделенным. Калькулятор отображает функцию только тогда, когда выделен ее знак равенства!
Вы видите разницу между двумя экранами?
Настройка окна графика TI-84 Plus
Когда вы рисуете функцию, вы обычно не можете видеть весь график. Вы ограничены просмотром графического окна, которое обычно показывает только небольшую часть функции. Есть четыре значения, определяющие видимую часть координатной плоскости: Xmin, Xmax, Ymin и Ymax. Нажмите [WINDOW] для отображения текущих переменных окна.
Требуется практика, чтобы найти хорошее окно просмотра функции, которую вы строите. Вот шаги, необходимые для установки окна вашего графика:
Нажмите [WINDOW] для доступа к оконному редактору.
После каждой переменной окна введите числовое значение, подходящее для отображаемых функций. Нажимайте e после ввода каждого числа.
При вводе нового значения окна старое значение автоматически очищается.
Убедитесь, что (Xmin < Xmax) и (Ymin < Ymax), иначе вы получите сообщение об ошибке ERROR: WINDOW RANGE.
Редактирование переменных окна — это хорошее место для начала поиска хорошего окна просмотра. Кроме того, использование функций масштабирования может быть необходимо для улучшения графического окна. Ниже приводится объяснение переменных, которые необходимо установить для настройки окна графика:
Xmin и Xmax: Это, соответственно, наименьшее и наибольшее значения x на оси x .
Если вы не знаете, какие значения потребуются вашему графику для Xmin и Xmax , нажмите [ZOOM][6], чтобы вызвать команду ZStandard . Эта команда автоматически отображает ваши функции в стандартном окне просмотра.
Xscl: Это расстояние между делениями на x — ось. (Полегче с делениями; слишком большое их количество делает ось похожей на железнодорожный путь. Двадцать или меньше делений делают ось x красивой.)
Если вы хотите полностью отключить деления, установите Xscl=0 и Yscl=0 .
Ymin и Ymax: Это, соответственно, наименьшее и наибольшее значения y , которые будут размещены на оси y .
Если вы присвоили значения Xmin и Xmax , но не знаете, какие значения присвоить Ymin и Ymax , нажмите [ZOOM][0], чтобы вызвать команду ZoomFit . Эта команда использует настройки Xmin и Xmax , чтобы определить соответствующие настройки для Ymin и Ymax , а затем автоматически строит график.
Yscl: Это расстояние между делениями на оси y . (как и x — ось, слишком много засечек делают ось похожей на железнодорожный путь. Пятнадцать или меньше делений — хорошее число для оси y .)
Xres: Этот параметр определяет разрешение графика. Можно задать любое из целых чисел от 1 до 8. Когда Xres установлено равным 1, калькулятор вычисляет функцию для каждого из 133 пикселей по оси x и отображает результат в виде графика. Если Xres установлено равным 8, функция оценивается и отображается на каждом восьмом пикселе.
Xres обычно устанавливается равным 1. Если вы строите график большого количества функций, калькулятору может потребоваться некоторое время, чтобы построить их график с таким разрешением. Если вы измените Xres на более высокое число, ваша функция будет строиться быстрее, но вы можете получить не такой точный график.
TraceStep и
Эти две переменные связаны друг с другом, и TraceStep всегда в два раза больше, чем
, которое определяет, как ваш курсор перемещается на экране графика в режиме «свободной трассировки». TraceStep управляет скачком значения X при отслеживании функции на экране графика.
Нажмите [GRAPH], чтобы построить график функций.
Остановка или приостановка графика TI-84 Plus
После нажатия [GRAPH] обычно возникает небольшая задержка перед тем, как вы начнете видеть свою функцию на графике слева направо. Если калькулятору требуется много времени, чтобы построить график ваших функций (возможно, настройка Xres слишком мала), нажмите [ON], чтобы завершить процесс построения графика.
Просто нажмите [ENTER], чтобы приостановить построение графика, а затем снова нажмите [ENTER], чтобы возобновить построение графика. См. следующие два экрана. Обратите внимание на эллиптический индикатор занятости в правом верхнем углу экрана, указывающий на то, что ваш калькулятор активно работает.
Об этой статье
Эта статья из книги:
Графический калькулятор TI-84 Plus CE для чайников,
Об авторах книги:
Джеффалла 9002 Мак 1 — учитель математики в Епископальной церкви Святой Марии. Школа в Мемфисе, Теннесси. Он стал соучредителем группы суперпользователей TI-Nspire и получил Президентскую премию за выдающиеся достижения в области преподавания естественных наук и математики.
К.К. Эдвардс — преподаватель, который провел множество семинаров по использованию калькуляторов TI.
Джефф МакКалла — учитель математики в Епископальной школе Святой Марии в Мемфисе, Теннесси. Он стал соучредителем группы суперпользователей TI-Nspire и получил Президентскую премию за выдающиеся достижения в области преподавания естественных наук и математики.
К.К. Эдвардс — преподаватель, который провел множество семинаров по использованию калькуляторов TI.
Этот артикул находится в категории:
Графические калькуляторы ,
10 лучших графических калькуляторов (физических и онлайн)

Графический калькулятор — это уникальный инструмент в математике и естественных науках. Графические калькуляторы выполняют те же функции, что и обычные калькуляторы, но имеют более сложные функции, такие как возможность вычисления дробей, логарифмов и квадратных корней. Есть несколько громких имен в области графических калькуляторов, которым доверяют и которые существуют уже давно — вы можете узнать классический TI-84 на одном из ваших уроков математики. Графические онлайн-калькуляторы появились относительно недавно и часто бесплатны. Мы рассмотрим лучшие физические и графические онлайн-калькуляторы, чтобы помочь вам решить, какой из них подходит именно вам.

Что такое графический калькулятор?
Графические калькуляторы имеют более мощные и сложные компьютеры, чем стандартные калькуляторы, и названы так потому, что они имеют графические возможности. Они могут решать сложные уравнения и строить графики . Они также программируются и являются полезным инструментом, если вы работаете над долгосрочным проектом и нуждаетесь в нем для хранения информации или решения математических задач более высокого уровня.
Некоторые графические калькуляторы также имеют цифру 9.0226 CAS, или система компьютерной алгебры, что означает, что она также может решать алгебраические уравнения . Графические калькуляторы — это, по сути, карманные компьютеры, поэтому важно выбрать подходящий именно вам.

Что делает графический калькулятор?
Графические калькуляторы позволяют рассчитывать статистику и легко преобразовывать результаты в графики. Конечно, построение графиков — очень важная часть графического калькулятора. Это позволяет вам работать над самой проблемой, а не тратить время на математические расчеты. Это может показаться нелогичным. Разве изучение математики не является целью? Да, но даже если вы овладели навыками, для решения некоторых уравнений может потребоваться много времени.
Графические функции и статистика — две основные функции, которыми вы будете пользоваться будучи студентом. Вы также можете использовать их для исчисления и тригонометрии, и в этом случае может помочь CAS. Не все графические калькуляторы оснащены CAS. Убедитесь, что вы знаете, для чего вы будете использовать свой калькулятор и нужен ли он вам с CAS.
Я упомянул, что графические калькуляторы являются программируемыми, поэтому их также можно использовать для хранения данных на случай, если они потребуются позже для уравнения или графика. Некоторые исследователи используют графические калькуляторы вместе с другим оборудованием. Они подключаются к компьютерам или другим машинам и собирают информацию, которая впоследствии может быть доступна и учтена в уравнениях. Помните, графические калькуляторы могут решать несколько уравнений одновременно, поэтому это может помочь сэкономить много времени и труда.

Лучшие физические графические калькуляторы
Физические графические калькуляторы — это крупная инвестиция, и часто действительно хорошая. Если вы серьезно относитесь к своему графическому калькулятору и знаете, что вам нужно мощное устройство, чтобы брать его с собой на занятия, экзамены или на работу, этот мини-компьютер станет важной частью вашей жизни.

TI-84 Plus
TI-84 Plus представляет собой традиционный графический калькулятор и представляет собой простое устройство, на котором можно изучить основы работы с графическим калькулятором. Это отличный инструмент для учащихся средних и старших классов , которые начинают более углубленное изучение математики, поскольку дизайн и 10 предварительно загруженных приложений могут помочь вам одновременно освоить математические навыки и научиться пользоваться графическим калькулятором. Этот калькулятор одобрен для экзаменов SAT, PSAT, ACT, IB и AP.

TI-Nspire CX CAS
Этот сверхмощный графический калькулятор отлично подходит для учащихся средних школ и колледжей, изучающих математику и естественные науки более высокого уровня . Экран с диагональю 3,2 дюйма — отличная возможность для студентов, изучающих инженерное дело, физику и математический анализ. CAS сохраняет и хранит информацию, поэтому вы можете редактировать уравнения и манипулировать ими, что помогает вам эффективно использовать свое время при решении сложных задач. Этот калькулятор одобрен для экзаменов SAT, PSAT и AP.

Casio FX-9860 GII
Casio FX-9860 GII идеально подходит для младших школьников, которые только изучают графические калькуляторы, а также для тех, кто ограничен в средствах. Сверхширокий дисплей и удобный интерфейс облегчают навигацию по этому калькулятору, хотя он менее эффективен, чем некоторые другие варианты. Он также поставляется с предварительно загруженными приложениями, такими как приложение для работы с электронными таблицами, приложение для геометрии и приложение для конусов, , а также справочное руководство пользователя и 200 часов автономной работы. Этот калькулятор одобрен для тестов SAT, PSAT, ACT и AP.

TI-84 Plus CE
TI-84 Plus CE — это калькулятор высокого разрешения с полноцветным дисплеем с подсветкой. У него стильный дизайн и большой объем памяти. По сравнению с другими моделями это реальное обновление как по мощности, так и по удобству использования, особенно с точки зрения отображения и скорости. Он также поставляется с перезаряжаемой батареей и доступен в различных цветах. Этот калькулятор одобрен для экзаменов SAT, PSAT, ACT, AP и IB.

HP Prime
Удивительно маленький и тонкий графический калькулятор CAS, HP Prime имеет огромный экран, что делает его отличным выбором как для студентов, так и для профессионалов, которым нужен мощный инструмент. Этот калькулятор был создан по образцу смартфонов, и это видно. Он имеет сенсорный дисплей, геометрию, электронные таблицы и расширенные графические приложения, а также другие приложения, доступные для загрузки . Интерфейс похож на смартфон и имеет дополнительные функции, такие как режим экзамена. Этот калькулятор одобрен для SAT.

Лучшие графические онлайн-калькуляторы
Онлайн-калькуляторы — отличный ресурс для тех, кто очень мобилен. Вы можете опробовать разные калькуляторы без каких-либо финансовых вложений, а также создать учетную запись, чтобы сохранить свою работу и вернуться к ней в любое время и с любого устройства. Ваш предпочтительный графический онлайн-калькулятор будет зависеть от ваших потребностей и того, какой интерфейс вы предпочитаете.

GraphCalc
Этот загружаемый графический калькулятор отлично подходит для тех, кто использовал или учился на TI-84, поскольку в нем перечислены функции и примеры по сравнению с TI-84 . GraphCalc также предоставляет инструкции по использованию калькулятора и всех его инструментов и утверждает, что он «почти полностью заменяет калькуляторы TI83 и TI84 Plus». Он также имеет раздел часто задаваемых вопросов и предлагает ресурсы для других графических онлайн-калькуляторов.

Desmos
У Desmos есть длинный список примеров в каждой категории, что делает этот графический калькулятор простым в использовании и понимании. Он работает в полноэкранном режиме, поэтому вы можете легко просматривать и редактировать свою работу. Он имеет всплывающую клавиатуру, позволяющую вводить уравнения в диалоговом окне с левой стороны и просматривать их, одновременно позволяя просматривать график справа. Вы также можете создать учетную запись и сохранить свои графики.

Mathway
Mathway имеет раскладку, аналогичную Demos, и включает в себя всплывающую клавиатуру, диалоговое окно, а также отображение уравнений и графиков. Различные функции находятся в раскрывающемся меню, что очень удобно для навигации по калькулятору. У него нет примеров, но у него есть обучающая функция, похожая на чат, которая помогает вам изучать калькулятор и решать уравнения . Он также имеет возможность создать учетную запись.

Метакалькулятор
Метакалькулятор фактически разделяет функции традиционного «графического калькулятора» на четыре разных калькулятора. На главной странице вы выбираете графический калькулятор, научный калькулятор, матричный калькулятор и калькулятор статистики. Это упрощает использование, поскольку вам не нужно играть и искать различные функции, если вы не знакомы со стандартным графическим калькулятором. Вы можете переключаться между калькуляторами с помощью вкладок вверху, и каждый калькулятор также разделяет функции с помощью вкладок. Так, например, графический калькулятор переключается между уравнениями, таблицами, пересечениями и точками графика. Это позволяет легко организовать и отслеживать вашу работу.

Geogebra
Калькулятор Geogebra имеет самую удобную систему. Меню инструментов и функций представлено с помощью удобной графики, которая поможет вам быстро перемещаться по калькулятору и легко находить то, что вы ищете. Функция калькулятора позволяет вводить и просматривать уравнения в диалоговом окне слева и просматривать график справа. В нем также есть раскрывающееся меню со знакомыми параметрами, которые вы найдете в большинстве программ (сохранение, экспорт и т. д.), и вы можете создать учетную запись для сохранения своей работы.

Как выбрать калькулятор
Вам нужно знать больше, чем просто пользоваться графическим калькулятором; надо уметь выбирать! Важно помнить, что графические онлайн-калькуляторы не разрешены для использования в SAT, ACT и других стандартизированных тестах. Многие физические калькуляторы одобрены для тестирования, поэтому, если вы покупаете физический калькулятор, убедитесь, что он одобрен для использования. Если вы не покупаете физический калькулятор, убедитесь, что у вас есть план, когда вы будете проходить стандартизированные тесты, например, 9.0226 аренда или одолжение калькулятора .
Если вы не являетесь специалистом по математике или естественным наукам, вы можете использовать графический калькулятор только в качестве домашнего задания в одном или двух курсах, чтобы помочь вам с уравнениями или задачами. В этом случае можно воспользоваться онлайн-калькулятором. Для этих курсов проконсультируйтесь со своим учителем или профессором, чтобы узнать, можете ли вы использовать онлайн-курс в классе.
Вы также можете найти интерфейс графического онлайн-калькулятора более простым в использовании. Онлайн-калькуляторы также позволяют сохранять вашу работу и получать к ней доступ с любого устройства через вашу учетную запись. Если вам удобнее быть мобильным, а не носить с собой графический калькулятор на всякий случай, вам может подойти онлайн.
Для специалистов по математике и естественным наукам, которые планируют сделать карьеру в STEM , инвестирование в хороший физический графический калькулятор может быть правильным решением. Поскольку вы будете использовать его часто, вы окупите свои деньги и вам не придется беспокоиться о таких вещах, как доступ к Wi-Fi, если вы хотите использовать графический калькулятор.
При покупке графического калькулятора важно учитывать, как вы собираетесь его использовать. Если вам нужно что-то взять с собой на длительные экзамены в колледже, такие факторы, как дисплей, скорость обработки и время автономной работы, также являются важными факторами. Кроме того, убедитесь, что вы знаете, нужен ли вам калькулятор с CAS или нет.
Если вы ищете калькулятор для использования только в течение одного или двух семестров, вы можете взять его напрокат или купить в Интернете, в дополнение к перечисленным выше отличным бесплатным онлайн-калькуляторам. Вы также можете искать скидки для студентов, доступные в вашей школе или у продавца.
Графические калькуляторы — невероятно полезный инструмент. Они позволяют учащимся получить визуальный доступ к математике высокого уровня и сократить множество трудоемких уравнений. Существует множество вариантов этих калькуляторов, и многое следует учитывать при принятии решения о том, какой из них приобрести, или если вам вообще нужен такой калькулятор. В конце концов, приоритетом является то, что вы получите все инструменты, необходимые для обучения и достижения успеха.

Что дальше?
Ищете дополнительную информацию об использовании графических калькуляторов на вступительных экзаменах в колледж? Руководство по калькуляторам ACT и калькуляторам SAT: советы экспертов могут помочь!
Усердно готовишься к предстоящим экзаменам? Ознакомьтесь с Руководством для экспертов по экзамену AP Calculus AB и Полным руководством по экзамену AP Statistics.

Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша база данных проверенных преподавателей включает в себя ряд опытных преподавателей, которые могут помочь вам отполировать эссе по английскому языку или объяснить, как производные работают для исчисления.
No related posts.