9 корней из 512: Mathway | Популярные задачи — Таловская средняя школа

Содержание

Извлечение корней: определение, методы извлечения, примеры

Из этой статьи вы узнаете:

что такое «извлечение корня»;
в каких случаях он извлекается;
принципы нахождения значения корня;
основные способы извлечения корня из натуральных и дробных чисел.

Что такое «извлечение корня»

Для начала введем определение «извлечение корня».

Определение 1

Извлечение корня — процесс нахождения значения корня.

При извлечении корня n-ной степени из числа a, мы находим число b, n-ная степень которого равняется a. Если мы нашли такое число b, можно утверждать, что корень извлечен.

Замечание 1

Выражения «извлечение корня» и «нахождение значения корня» равнозначны.

В каких случаях извлекается корень?

Определение 2

Корень n-ной степени можно извлечь из числа a точно в случае, если a можно представить в виде n-ной степени некоторого числа b.

Пример 1

4=2×2, следовательно, из числа 4 можно точно извлечь квадратный корень, который равен 2

Определение 3

Когда корень n-ной степени из числа a невозможно представить в виде n-ной степени числа b, то такой корень

не извлекается, либо извлекается только приближенное значение корня с точностью до любого десятичного разряда.

Пример 2

2≈1,4142.

Принципы нахождения значения корня и способы их извлечения

Использование таблицы квадратов, таблицы кубов и т.д.
Разложение подкоренного выражения (числа) на простые множители
Извлечение корней из дробных чисел
Извлечение корня из отрицательного числа
Поразрядное нахождение значения корня

Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.

Определение 4

Главный принцип нахождения значения корней — основываться на свойствах корней, в том числе на равенстве: bnn=b, которое является справедливым для любого неотрицательного числа b.

Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.

Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).

Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.

Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.

И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.

Использование таблицы квадратов, кубов и т.д.

Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.

Таблица квадратов

Таблица квадратов		единицы
Таблица квадратов		0	1	2	3	4	5	6	7	8	9
десятки	0	0	1	4	9	16	25	36	49	64	81
	1	100	121	144	169	196	225	256	289	324	361
	2	400	441	484	529	576	625	676	729	784	841
	3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
	4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2041
	5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
	6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
	7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
	8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
	9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Существуют также таблицы кубов, четвертой степени и т. д., которые созданы по принципу, аналогичному таблице квадратов.

Таблица кубов

Таблица кубов			единицы
Таблица кубов		0	1	2	3	4	5	6	7	8	9
десятки	0	0	1	8	27	64	125	216	343	512	729
	1	1000	1 331	1 728	2 197	2 744	3 375	4 096	4 913	5 832	6 859
	2	8000	9 261	10 648	12 167	13 824	15 625	17 576	19 683	21 952	24 389
	3	27000	29 791	32 768	35 937	39 304	42 875	46 656	50 653	54 872	59 319
	4	64000	68 921	74 088	79 507	85 184	91 125	97 336	103 823	110 592	117 649
	5	125000	132 651	140 608	148 877	157 464	166 375	175 616	185 193	195 112	205 379
	6	216000	226 981	238 328	250 047	262 144	274 625	287 496	300 763	314 432	328 509
	7	343000	357 911	373 248	389 017	405 224	421 875	438 976	456 533	474 552	493 039
	8	512000	531 441	551 368	571 787	592 704	614 125	636 056	658 503	681 472	704 969
		729000	753 571	778 688	804 357	830 584	857 375	884 736	912 673	941 192	970 299

Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.

Разложение подкоренного числа на простые множители

Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.

Определение 5

Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.

Пример 3

Извлечем квадратный корень из 144.

Разложим 144 на простые множители:

Таким образом: 144=2×2×2×2×3×3=(2×2)2×32=(2×2×3)2=122. Следовательно, 144=122=12.

Также при использовании свойств степени и корней можно записать преобразование немного по-другому:

144=2×2×2×2×3×3=24×32=24×32=22×3=12

144=12 — окончательный ответ.

Извлечение корней из дробных чисел

Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.

Определение 6

Следуя свойству корня из частного, справедливым является следующее равенство:

pqn=pnqn. Исходя из этого равенства, необходимо воспользоваться правилом извлечения корня из дроби: корень из дроби равен от деления корня числителя на корень знаменателя.

Пример 4

Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.

Необходимо извлечь кубический корень из 474,552. Первым делом, представим десятичную дробь в виде обыкновенной: 474,552 = 474552/1000. Из этого следует: 47455210003=474552310003. Затем можно приступить к процессу извлечения кубических корней в числителе и знаменателе:

474552=2×2×2×3×3×3×13×13×13=(2×3×13)3=783 и 1000=103, то

4745523=7833=78 и 10003=1033=10.

Завершаем вычисления: 474552310003=7810=7,8.

Извлечение корня из отрицательных чисел

Если знаменатель является нечетным числом, то число под знаком корня может оказаться отрицательным. Из этого следует: для отрицательного числа -a и нечетного показателя корня 2n-1 справедливо равенство:

-a2×n-1=-a2×n-1

Определение 7

Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.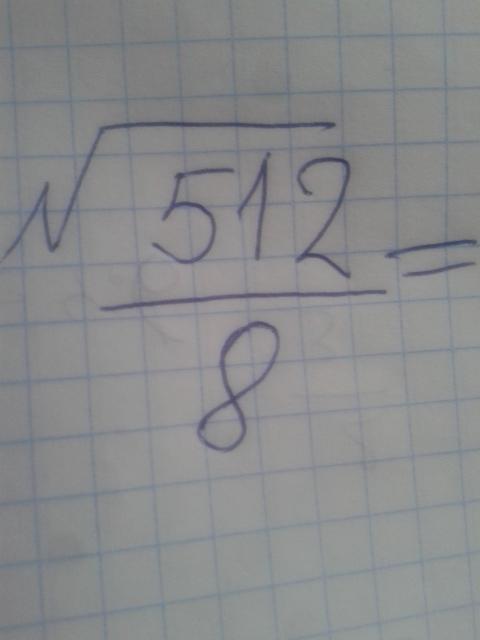

Пример 5

-122092435. Для начала необходимо преобразовать выражение, чтобы под знаком корня оказалось положительно число:

-122092435=12209243-5

Затем следует заменить смешанное число обыкновенной дробью:

12209243-5=3125243-5

Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:

3125243-5=-312552435

Вычисляем корни в числителе и знаменателе:

-312552435=-555355=-53=-123

Краткая запись решения:

-122092435=12209243-5=3125243-5=-312552435=-555355=-53=-123.

Ответ: -122092435=-123.

Поразрядное нахождение значения корня

Бывают случаи, когда под корнем находится число, которое не получается представить в виде n-ной степени некоторого числа. Но необходимо знать значение корня с точностью до некоторого знака.

В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.

Пример 6

Как это происходит, разберем на примере извлечения квадратного корня из 5.

Сперва необходимо найти значение разряда единиц. Для этого начнем перебирать значения 0,1,2,…,9, вычисляя при этом 02, 12, …, 92 до необходимого значения, которое больше, чем подкоренное число 5. Все это удобно представить в виде таблицы:

Возможное значение корня	0	1	2	3
Это значение в степени	0	1	4	9

Значение ряда единиц равняется 2 (так как 22<5, а 23>5). Переходим в разряду десятых — будем возводить в квадрат числа 2,0, 2,1, 2,2,…,2,9, , сравнивая полученные значения с числом 5.

Возможное значение корня	2,0	2,1	2,2	2,3
Это значение в степени	4	4,41	4,84	5,29

Поскольку 2,22<5, а 2,32>5, то значение десятых равняется 2. Переходим к нахождению значения сотых:

Возможное значение корня	2.20	2,21	2,22	2,23	2,24
Это значение в степени	4,84	4,8841	4,8294	4,9729	5,0176

Таким образом, найдено значение корня из пяти — 2,23. Можно находить значения корня дальше:

2,236, 2,2360, 2, 23606, 2,236067,…

Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Квадратный корень из 512 — Как найти квадратный корень из 512?

LearnPracticeDownload

Квадратный корень обозначается символом √. Если n — целое число, квадрат n равен m, который также является целым числом. Если n² = m, то n=√m. Квадратный корень из 512 записывается как √512. Давайте подробно рассмотрим квадратный корень из 512 в этом уроке. 512 — это составное число, так как оно имеет более двух делителей. √ 512 иррациональное число. В этом уроке мы вычислим квадратный корень из 512 методом деления в большую сторону и поймем, почему 512 — иррациональное число. Теперь найдем квадратный корень из 512.

Квадратный корень из 512 : √ 512 = 22,62741
Квадрат 512: 512 ² = 262 144

1.	Какой квадратный корень из 512?
2.	Является ли квадратный корень из 512 рациональным или иррациональным?
3.	Как найти квадратный корень из 512?
4.	Нестандартное мышление!
5.	Часто задаваемые вопросы о квадратном корне из 512

Что такое квадратный корень из 512?

Квадратный корень — это просто операция, обратная квадрату. Число, квадрат которого дает 512 – это квадратный корень из 512. Квадратный корень из 512 в радикальной форме представляется как √512. Он выражается как (512) ^½ в форме экспоненты. Неквадратные числа также имеют квадратный корень, но они не являются целыми числами. Квадратный корень из 512, округленный до 5 знаков после запятой, равен 22,62741.

Является ли квадратный корень из 512 рациональным или иррациональным?

Рациональное число — это число, которое выражается в форме p/q, где p и q — целые числа, а q не равно 0. Число, которое нельзя выразить как отношение двух целых чисел, является иррациональным числом. Неконечные десятичные числа с повторяющимися числами после запятой являются рациональными числами. √512 = 22,62741. Квадратный корень из 512 нельзя записать в виде p/q, где p, q — целые числа, а q не равно 0. Значение √ 512 – это 22,62741. Следовательно, √ 512 не является рациональным числом.

Как найти квадратный корень из 512?

Существуют разные способы извлечения квадратного корня из любого числа. Нажмите здесь, чтобы узнать больше о различных методах.

Упрощенная подкоренная форма квадратного корня из 512

512 — составное число, полученное произведением простого числа 2. Следовательно, упрощенная подкоренная форма √ 512 равна 16√2.

Мы можем найти квадратный корень из 512 следующими двумя способами:

Метод простой факторизации
Метод длинного деления

Квадратный корень из 512 методом простой факторизации

Чтобы найти квадратный корень из 512 методом простой факторизации, нам нужно найти простые множители числа 512.
512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2 ⁹
512 = 16√2

Квадратный корень из 512 методом деления в длину

Значение квадратного корня из 512 методом деления в длину состоит из следующих шагов:

Шаг 1: Поместите черту над каждой парой цифр числа, начиная с разряда единицы (крайняя правая сторона). У нас будет две пары, т.е. 5 и 12.
Шаг 2: Мы делим самое левое число на наибольшее число, квадрат которого меньше или равен числу в самой левой паре. (2 × 2 = 4)
Шаг 3: Опустите число под следующей чертой справа от остатка. Прибавьте к делителю последнюю цифру частного (2 + 2 = 4). Справа от полученной суммы найти подходящее число, которое вместе с результатом суммы образует новый делитель (42) для нового делимого (112), переносимого вниз.
Шаг 4: Новое число в частном будет иметь то же число, что и в делителе (42 × 2 = 84). Условие такое же, как если бы оно было меньше или равно делимому (84 < 112).
Шаг 5: Теперь мы продолжим этот процесс дальше, используя десятичную точку и добавляя нули попарно к остатку.
Шаг 6: Полученное частное будет квадратным корнем числа.

Повторяя вышеуказанные шаги, мы получим значение квадратного корня из 512, которое равно √512 = 22,62741 с точностью до 5 знаков после запятой.

Изучите квадратные корни с помощью иллюстраций и интерактивных примеров

Квадратный корень из 121
Квадратный корень из 576
Квадратный корень из 125
Квадратный корень из 500
Квадратный корень из 625

Аналитический центр:

Можете ли вы найти квадратное уравнение с корнем √ 512?
Поскольку (- √ 512) ² = 512, можем ли мы сказать, что — √ 512 также является квадратным корнем из 512?

Пример 1: Помогите Рону найти квадратный корень из 512 с точностью до 3 знаков после запятой.
Решение
Следуя тем же шагам, что и выше, мы найдем квадратный корень из 512 с точностью до 3 знаков после запятой.
- Шаг 1: Поместите черту над каждой парой цифр числа, начиная с разряда единицы (крайняя правая сторона). У нас будет две пары, т. е. 5 и 12.
- Шаг 2: Мы делим самое левое число на наибольшее число, квадрат которого меньше или равен числу в самой левой паре. (2 × 2 = 4)
- Шаг 3: Опустите число под следующей чертой справа от остатка. Прибавьте к делителю последнюю цифру частного (2 + 2 = 4). Справа от полученной суммы найти подходящее число, которое вместе с результатом суммы образует новый делитель (42) для нового делимого (112), переносимого вниз.
- Шаг 4: Новое число в частном будет иметь то же число, что и в делителе (42 × 2 = 84). Условие такое же, как если бы оно было меньше или равно делимому (84 < 112).
- Шаг 5: Теперь мы продолжим этот процесс дальше, используя десятичную точку и добавляя нули попарно к остатку.
- Шаг 6: Полученное частное будет квадратным корнем числа.
- Шаг 7: Повторите процесс до 3 знаков после запятой.
Пример 2 : Какова разница между длинами радиусов кругов с площадями 512π и 100π квадратных дюймов?
Решение
Необходимо вычислить длину радиуса круга площадью 512π.
Площадь = πr ² = 512π
Здесь r = √512 = 22,62 дюйма 91 001 Далее необходимо вычислить длину радиуса круга площадью 100π.
Площадь = πr ² = 100π
Здесь r = √100 = 10 дюймов 91 001 Следовательно, разница между длинами радиусов кругов с площадями 512π и 100π квадратных дюймов составляет (22,62 — 10) = 12,62 дюйма.

перейти к слайдуперейти к слайду

Хотите создать прочную основу для изучения математики?

Выйдите за рамки заучивания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Записаться на бесплатный пробный урок

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о квадратном корне из 512

Как вычислить квадратный корень из 512?

Чтобы вычислить квадратный корень из совершенных квадратных чисел, мы можем использовать простые факторизации и метод повторного вычитания.