Тригонометрические функции: онлайн калькулятор, формулы, графики, значения
Функция {$ main.types[data.type] $}
Введите угол α{$ main.angles[data.angle1] $}
Результат расчёта
{$ data.type $}(α) = {$ result[0]|number:data.round $}
Введите {$ data.type $}(α){$ main.angles[data.angle2] $}
Результаты расчёта
- {$ result[1] $}
- {$ result[2] $}
Округлять до {$ data.round $} {$ Plural(data.round, [‘знака’, ‘знаков’, ‘знаков’]) $} после запятой
Тригонометрия – наука, изучающая свойства тригонометрических функций и их практическое применение. Наука берет начало в древности: с изучения свойств сторон прямоугольного треугольника.
История вопроса
Термин «тригонометрия» впервые встречается в работе немецкого математика Питискуса в далеком 1505 году. Сам термин обозначает «измерение треугольников», так как тригонометрические функции были выведены на основании соотношений катетов и гипотенузы для разных углов. И хотя различные свойства прямоугольного треугольника были известны еще в Древнем Вавилоне, расцвет геометрии пришелся на античные времена.
Сам термин обозначает «измерение треугольников», так как тригонометрические функции были выведены на основании соотношений катетов и гипотенузы для разных углов. И хотя различные свойства прямоугольного треугольника были известны еще в Древнем Вавилоне, расцвет геометрии пришелся на античные времена.
Интересно, но в Древней Греции рассматривали не сколько прямоугольный треугольник, катеты и гипотенузы, а окружность. Круг и прямая – идеальные геометрические фигуры по мнению античных математиков, поэтому построения производились при помощи циркуля и линейки. Соответственно, для измерения углов и их характеристик древнегреческие геометры использовали технику хорд. Перпендикуляр к хорде, проведенный из центра окружности, делит пополам дугу и опирающуюся хорду. Половина от этой хорды численно представляет собой синус половинного угла.
Позднее индийские учены пришли к выводу, что хорды – ни что иное, как соотношение катетов и гипотенуз для построенного на хорде и радиусе прямоугольного треугольника.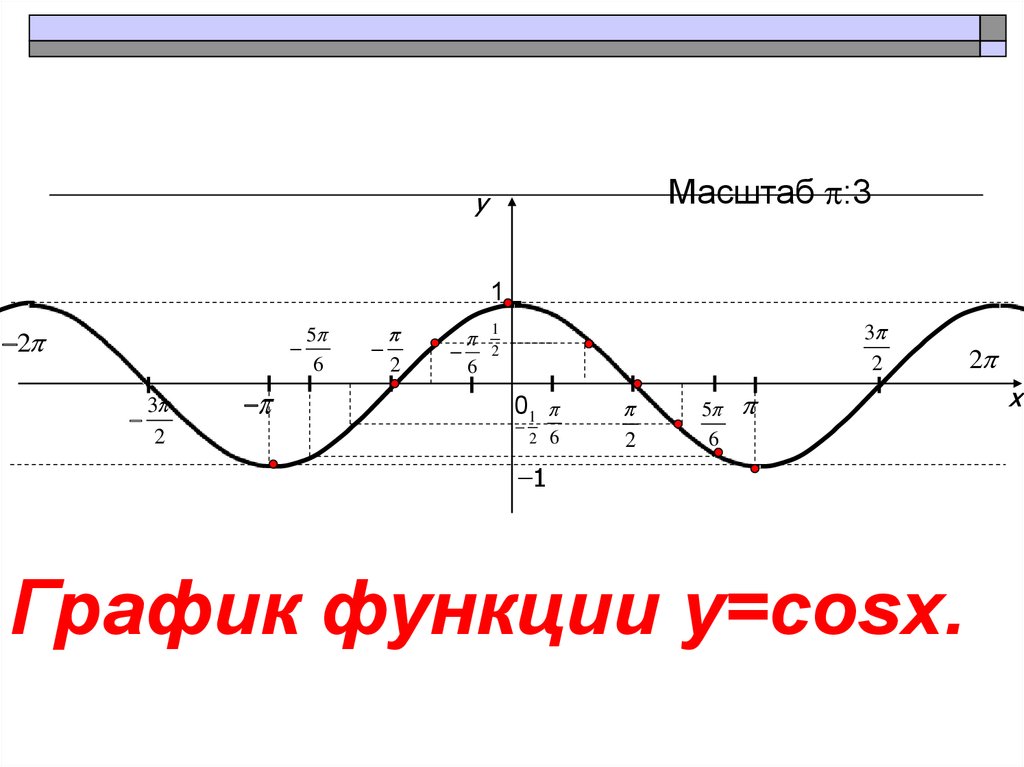 Замена хорд значениями синусов позволила математикам использовать в вычислениях функции, связанные со свойствами катетов и гипотенузы. Такой ход считается одной из величайших математических хитростей Средневекового мира. Позднее эта «фишка» попала в руки арабских ученых, после чего тригонометрические функции вошли в мир европейской математики. В последствии, благодаря зависимости хорд и радиусов окружности, были выведены и доказаны не только синус, но и основные тригонометрические функции.
Замена хорд значениями синусов позволила математикам использовать в вычислениях функции, связанные со свойствами катетов и гипотенузы. Такой ход считается одной из величайших математических хитростей Средневекового мира. Позднее эта «фишка» попала в руки арабских ученых, после чего тригонометрические функции вошли в мир европейской математики. В последствии, благодаря зависимости хорд и радиусов окружности, были выведены и доказаны не только синус, но и основные тригонометрические функции.
Основные функции
Все тригонометрические функции рассчитываются для определенного угла и представляют собой соотношение сторон. Катеты – это стороны треугольника, которые образуют прямой угол. Катет и гипотенуза образуют произвольный угол, для которого образующий катет является прилежащим. Второй катет для этого угла называют противолежащим. Функция угла – это соотношение длин определенных сторон треугольника. Такое соотношение представляет собой дробь и выражается численно, например, 1/2. Таким образом, основные тригонометрические функции приобретают следующие формулы:
Таким образом, основные тригонометрические функции приобретают следующие формулы:
- Синус = противолежащий катет / гипотенуза;
- Косинус = прилежащий катет / гипотенуза;
- Тангенс = противолежащий катет / прилежащий катет;
- Котангенс = прилежащий катет / противолежащий катет.
Кроме того, существуют функции секанса (гипотенуза/противолежащий катет) и косеканса (гипотенуза/прилежащий катет), однако они не получили широкого распространения в прикладных науках.
Интересно, что косинус – основная тригонометрическая функция, однако этот термин появился гораздо позднее синуса. Допустим, что в прямоугольном треугольнике непрямой угол обозначен как a. Косинус или complementry sinus угла a – это дополнительный синус для угла (90 – a). Именно поэтому долгое время ученые не вводили дополнительную функцию, а просто пересчитывали угол. Из-за постоянной работы с углами известный ученый Клейн даже предложил переименовать тригонометрию в гониометрию или «измерение углов».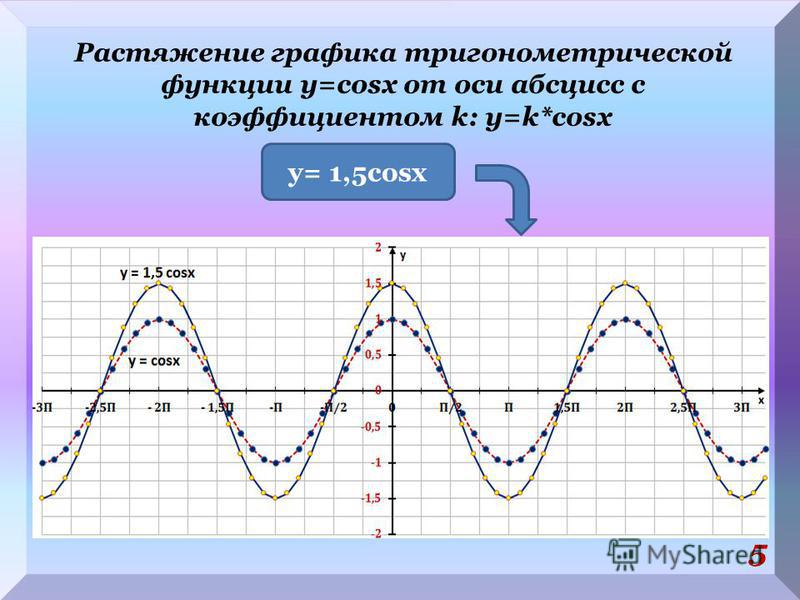 Однако такое название не прижилось.
Однако такое название не прижилось.
Применение тригонометрии
Невозможно представить область науки, которая обошлась бы без применения тригонометрических функций. Еще в Древнем мире астрономы использовали метод триангуляции для определения приблизительного расстояния до небесных тел. Сегодня этот метод улучшен и автоматизирован и используется во многих прикладных приложениях. Сами же функции синуса, косинуса, тангенса и котангенса применяются для описания волновых, циклических или нарастающих процессов. Если перед ученым стоит задача описать банальное движение маятника, ускорение вала асинхронного двигателя или экономическое процветание государства, то ему на помощь приходят тригонометрические функции.
Наша программа позволяет вычислить значения основных тригонометрических функций для любых углов с точностью до четырех знаков после запятой. Для определения численного значения выбранной в меню функции вам потребуется задать угол в градусах или радианах и сделать один клик мышью.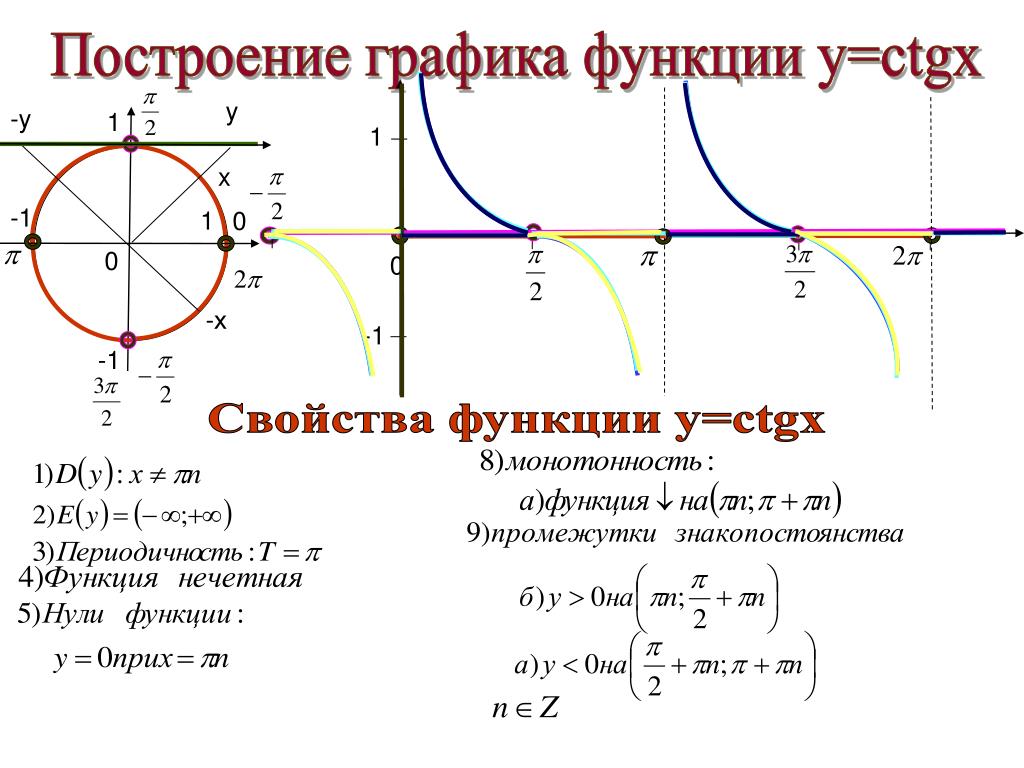 Если вы хотите произвести обратную операцию и узнать угол по численному значению синуса или тангенса, то введите число от 0 до 1 в ячейку функции, после чего программа вернет величину соответствующего угла.
Если вы хотите произвести обратную операцию и узнать угол по численному значению синуса или тангенса, то введите число от 0 до 1 в ячейку функции, после чего программа вернет величину соответствующего угла.
Пример из жизни
Школьная задача
Благодаря тригонометрическим функциям мы можем без проблем определять длины сторон треугольника. Пусть в школьной задаче задан прямоугольный треугольник, у которого известен угол А, равный 50 градусов. Один из катетов «а» имеет длину 15 см. Требуется найти длину гипотенузы. Это простая задача, которую легко решить при помощи теоремы синусов.
Известно, что стороны любого треугольника соотносятся как a / sinA = b / sinB = c / sinC. Мы знаем угол А и длину катета «а», а требуется найти длину гипотенузы с. Известно, что противолежащий гипотенузе угол С – это всегда прямой угол, а синус прямого угла всегда равен 1. Таким образом, мы получаем соотношение:
a / sinA = c / 1 или c = a / sinA
Нам осталось подсчитать синус угла величиной 50 градусов и выразить гипотенузу. Для этого выберите в меню калькулятора функцию синуса и выберите градусы для ячейки угла. В итоге мы получим:
Для этого выберите в меню калькулятора функцию синуса и выберите градусы для ячейки угла. В итоге мы получим:
с = 15 / sin50 = 15/0,766 = 15,55
Заключение
Тригонометрия – раздел математики, важность которого сложно переоценить. Функции синуса и тангенса используются как в физике и механике, так и в биологии, экономике, геодезии и криптографии. Наши онлайн-калькуляторы пригодятся вам при расчете любых тригонометрических функций.
Тригонометрические функции
В школьной программе изучаются четыре тригонометрических функции — синус, косинус, тангенс и котангенс. В этой статье мы рассмотрим графики и основные свойства этих функций.
1. Начнем с построения графика функции y = sin x.
Выберем подходящий масштаб. По оси X: три клетки примем за (это примерно полтора). Тогда — одна клеточка, — две клетки.
По оси Y: две клетки примем за единицу.
Область определения функции y = sin x — все действительные числа, поскольку значение sin α можно посчитать для любого угла α.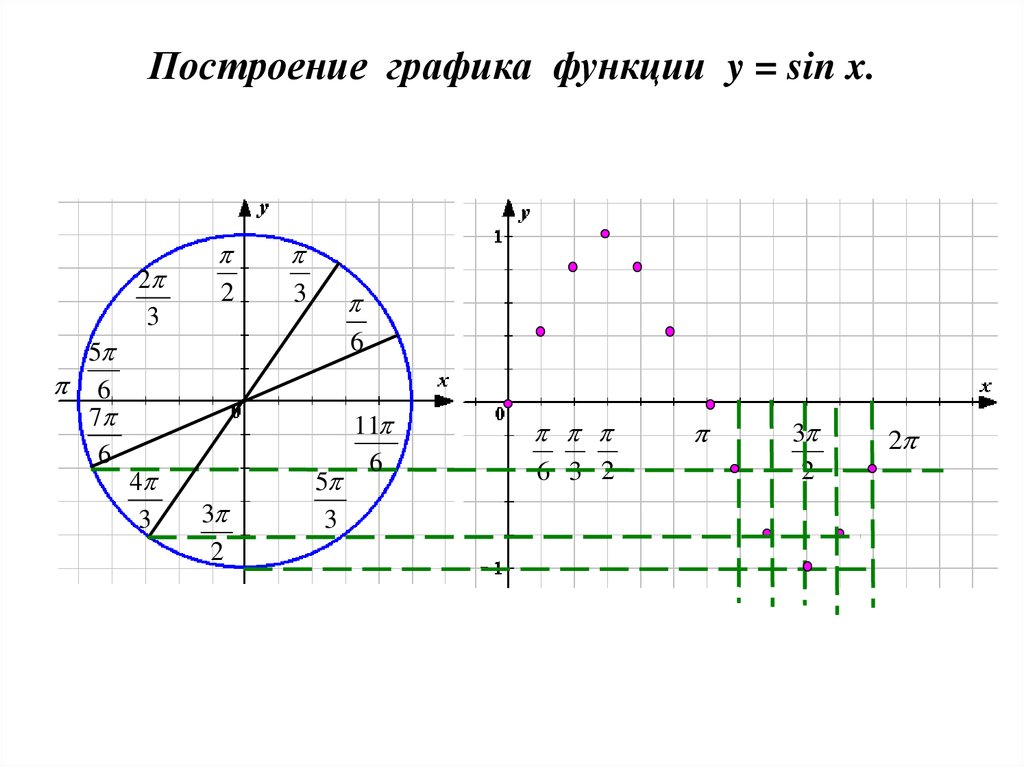
Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.
| x | 0 | ||||
| sin x | 0 |
Можем добавить, для большей плавности графика, точки и В них значение синуса равно
Мы помним, что . Это значит, что
Получается часть графика, симметричная той, которую нарисовали раньше.
Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть
Это значит, что функция y = sin x является периодической. Мы уже построили участок графика длиной 2π. А теперь мы как будто «копируем» этот участок и повторяем его с периодом 2π:
Синусоида построена.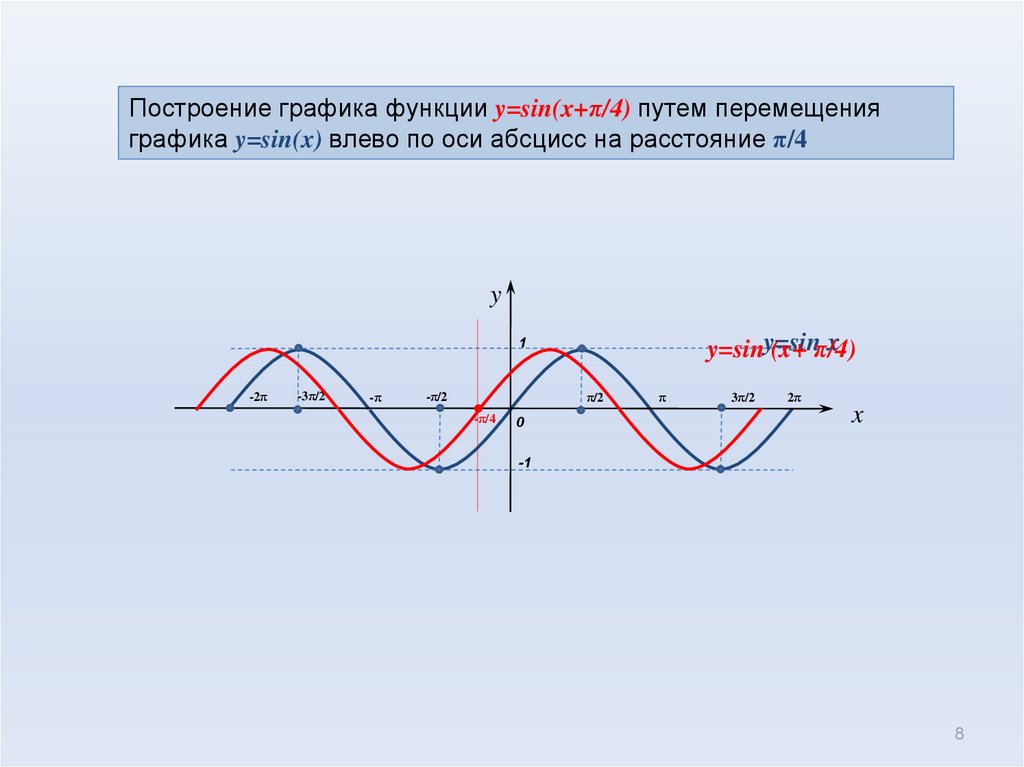
Перечислим основные свойства функции y = sin x.
1) D(y): x ∈ R, то есть область определения — все действительные числа.
2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = sin x равно единице, а наименьшее — минус единице.
3) Функция y = sin x — нечетная. Ее график симметричен относительно нуля.
4) Функция y = sin x — периодическая. Ее наименьший положительный период равен 2π.
2. Следующий график: y = cos x. Масштаб — тот же. Отметим на графике точки, в которых косинус является рациональным числом:
| x | 0 | ||||
| cos x | 1 | 0 |
Поскольку cos (−x) = cos x, график будет симметричен относительно оси Y , то есть левая его часть будет зеркальным отражением правой.
Функция y = cos x — тоже периодическая. Так же, как и для синуса, ее значения повторяются через 2πn. «Копируем» участок графика, который уже построили, и повторяем периодически.
«Копируем» участок графика, который уже построили, и повторяем периодически.
Перечислим основные свойства функции y = cos x.
1) D(y): x ∈ R, то есть область определения — все действительные числа.
2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = cos x равно единице, а наименьшее — минус единице.
3) Функция y = cos x — четная. Ее график симметричен относительно оси Y.
4) Функция y = cos x — периодическая. Ее наименьший положительный период равен 2π.
Отметим еще одно свойство. Графики функций y = sin x и y = cos x весьма похожи друг на друга. Можно даже сказать, что график косинуса получится, если график синуса сдвинуть на влево. Так оно и есть — по одной из формул приведения,.
Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!
Функции синус и косинус идеально подходят для описания колебаний и волн — то есть процессов, повторяющихся во времени.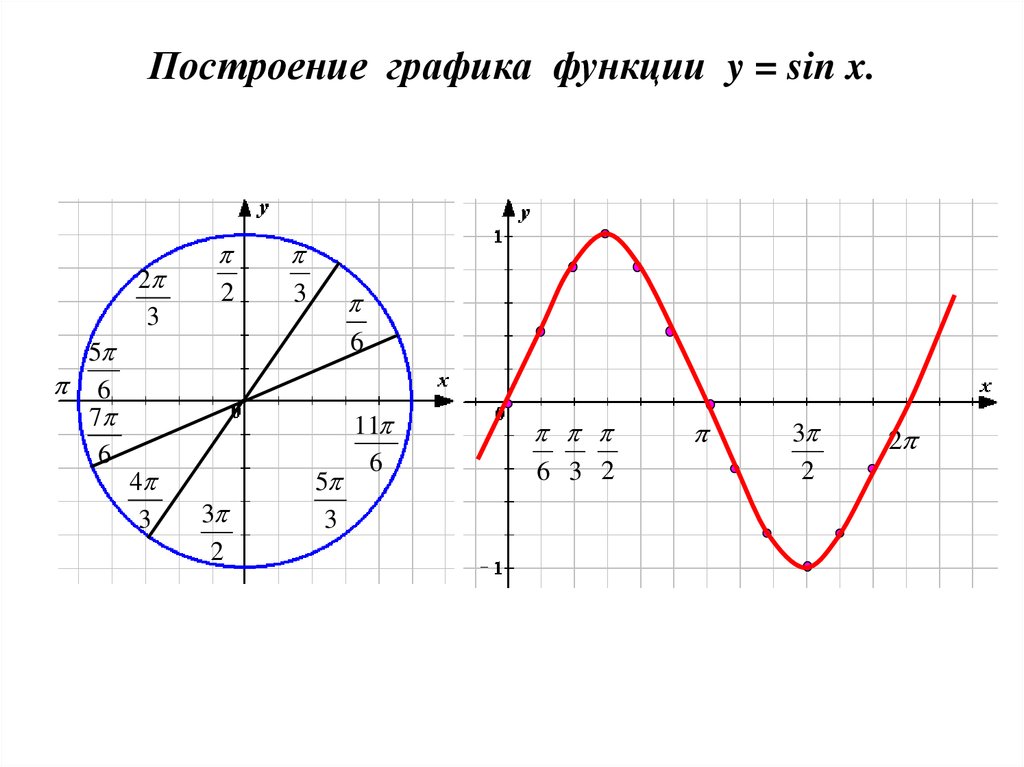
По закону синуса (или косинуса) происходят колебания маятника или груза на пружине. Переменный ток (тот, который в розетке) выражается формулой I(t) = I cos(ωt+α). Но и это не все. Функции синус и косинус описывают звуковые, инфра– и ультразвуковые волны, а также весь спектр электромагнитных колебаний. Ведь то, что наш глаз воспринимает как свет и цвет, на самом деле представляет собой электромагнитные колебания. Разные длины волн света воспринимается нами как разные цвета. Наши глаза видят лишь небольшую часть спектра электромагнитных волн. Кроме видимого цвета, в нем присутствуют радиоволны, тепловое (инфракрасное) излучение, ультрафиолетовое, рентгеновское и гамма–излучение. Более того — объекты микромира (например, электрон) проявляют волновые свойства.
3. Перейдем к графику функции y = tg x.
Чтобы построить его, воспользуемся таблицей значений тангенса. Масштаб возьмем тот же — три клетки по оси X соответствуют , две клетки по Y — единице. График будем строить на отрезке от 0 до π.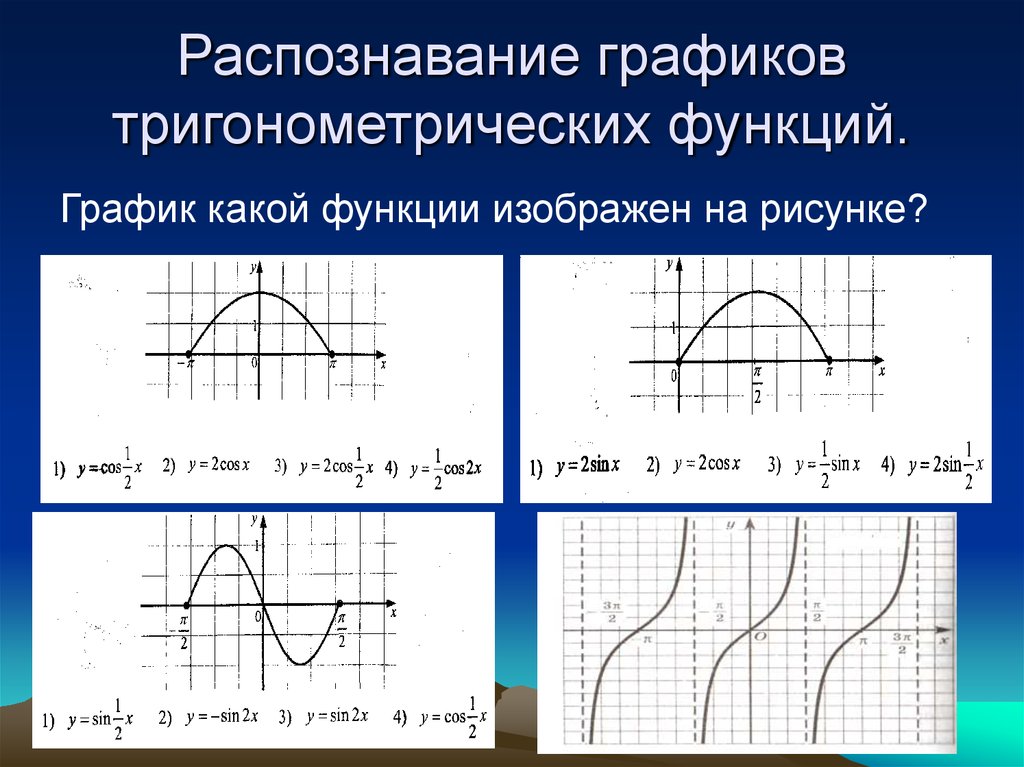
Непонятно только, как быть с точкой Ведь в этой точке значение тангенса не определено. А как же будет вести себя график функции y = tg x при x, близких к то есть к 90 градусам?
Чтобы ответить на этот вопрос, возьмем значение x, близкое к , и посчитаем на калькуляторе значения синуса и косинуса этого угла. Пусть .
Синус угла — это почти 1. Точнее, sin = 0,9998. Косинус этого угла близок к нулю. Точнее, cos = 0,0175.
Тогда
график уйдет на 59 единиц (то есть на 118 клеток) вверх. Можно сказать, что если x стремится к (то есть к ), значение функции y = tg x стремится к бесконечности.
Аналогично, при x, близких к , график тангенса уходит вниз, то есть
Осталось только «скопировать» этот участок графика и повторить его с периодом π.
Перечислим свойства функции y = tg x.
1) .
Другими словами, тангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.
3) Функция y = tg x — нечетная. Ее график симметричен относительно начала координат.
4) Функция y = tg x — периодическая. Ее наименьший положительный период равен π.
5) Функция y = tg x возрастает при , то есть на каждом участке, на котором она непрерывна.
4. График функции y = ctg x строится аналогично. Вот он:
1) .
Другими словами, котангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.
3) Функция y = сtg x — нечетная. Ее график симметричен относительно начала координат.
4) Функция y = сtg x — периодическая. Ее наименьший положительный период равен π.
5) Функция y = сtg x убывает при , то есть на каждом участке, на котором она непрерывна.
Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Тригонометрические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Информация на странице «Тригонометрические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 07.04.2023
Тригонометрические функции
М. Борна
Зачем изучать тригонометрические функции…?
Как высоко над уровнем моря находится крыша Сиднейского оперного театра? Посмотрите, как это сделать, в книге «Правильный треугольник и его применение».
Триггерные функции очень важны в технических предметах, таких как наука, инженерия, архитектура и даже медицина. Вы будете сталкиваться с ними все время, так что стоит хорошенько их выучить!
Съемка — одно из многих приложений. Строители дорог, строители мостов и те, чья работа заключается в том, чтобы возводить здания в нужном месте, — все используют тригонометрию в своей повседневной работе.
Строители дорог, строители мостов и те, чья работа заключается в том, чтобы возводить здания в нужном месте, — все используют тригонометрию в своей повседневной работе.
Чтобы узнать больше о приложениях и примерах тригонометрии в интерактивной математике, ознакомьтесь со многими вариантами использования тригонометрии. См. также: Математические советы — Тригонометрия.
В этой главе мы начнем с объяснения основных тригонометрических функций с использованием градусов (°), а в последней части главы мы узнаем о радианах и о том, как они используются в тригонометрии.Связанные разделы в «Интерактивной математике»
Графики тригонометрических функций, которые действительно помогают понять, что происходит в тригонометрии.
Аналитическая тригонометрия, включающая формулы двойного угла, тригонометрические соотношения суммы двух углов, тригонометрические уравнения и обратные тригонометрические уравнения.
Полярные координаты, которые работают так же, как темы в этой главе.
Производные трансцендентных функций, в котором показано, как различать функции sin, cos, tan, csc, sec и cot.
Интеграция с использованием тригонометрических форм, где мы видим, как наши знания тригонометрии могут упростить исчисление.
Линейный спектр в рядах Фурье, который является расширенным приложением тригонометрии.
И, конечно же, не пропустите сводку «Использование тригонометрии».
В этой главе
1. Углы — строительные блоки тригонометрии. В градусов .
2. Синус, косинус, тангенс и обратные числа — эти дроби являются ключом для всех будущих исследований по тригонометрии.
3. Значения тригонометрических функций. Почему sin 30° = 0,5?
4. Прямоугольный треугольник и приложения — включает угол наклона n и угол подъема .
5. Знаки тригонометрических функций — в этом нет ничего страшного, если вспомнить, как мы определяем основные соотношения. Включает интерактивный документ , в котором показано, как работают отношения углов больше 90 градусов.
Включает интерактивный документ , в котором показано, как работают отношения углов больше 90 градусов.
6. Тригонометрические функции любого угла — не сдавайтесь в этом разделе!
7. Радианы — альтернатива градусам — и многое другое.
8. Применение радианной меры — включает длину дуги, площадь сектора , угловую скорость , игру и шкивы.
9. Радианы и тригонометрические отношения — как работает тригонометрия, когда мера угла составляет радиан .
Эта глава начинается с некоторых напоминаний об Углах.
реальный анализ — Аксиоматическое построение тригонометрических функций
Позвольте мне сделать вступительное замечание, что, как указано в комментариях, просто алгебраические тождества и указанные значения при $x=0$ включают дикие примеры.
Однако, как написано, ваше требование монотонности подразумевает, что желаемый предел эквивалентен непрерывности при $x=0$. В самом деле, искомый предел естественным образом влечет за собой топологическое требование, чтобы его можно было вывести. Давайте сначала введем более слабое понятие, чем ваше требование монотонности (доказательство включения см. в конце).
В самом деле, искомый предел естественным образом влечет за собой топологическое требование, чтобы его можно было вывести. Давайте сначала введем более слабое понятие, чем ваше требование монотонности (доказательство включения см. в конце).
Определение: Скажем, что функция $f$ свободно разделяет точку $x_0$, если существует окрестность $\mathcal{U}$ точки $x_0$ такая, что $f(\mathcal{U})\cap\mathcal{U} =\пустой набор$.
Чтобы быть педантичным, давайте также используем $S(x)$ и $C(x)$ для ваших предполагаемых функций синуса и косинуса соответственно. Тогда у нас есть
Теорема: Если для некоторого $\varepsilon_0\in(-1,1]$ мы имеем, что $C(x)+\varepsilon_0$ свободно разделяет $x=0$, то в дополнение к вашим алгебраическим тождествам и указанным значениям в $x= 0$ следующие эквивалентны
- $\lim_{x\to0}\frac{S(x)}{x}$ существует.
- $S$ (равномерно) непрерывна в окрестности $0$.

- $S$ непрерывна при $x=0$.
Примечание: обратите внимание, что вам нужна непрерывность только одного из $S$ или $C$, а непрерывность другого следует из этого.
Доказательство теоремы . Для начала обратите внимание, что из ваших аксиоматических алгебраических тождеств выполняется следующее тождество: $$(S(x)-S(y))(1+C(x-y))=S(x-y)(C(x)+C(y))\,.$$ Теперь заметим, что $C(x)+\varepsilon$ свободно разделяет $0$ для любого $\varepsilon\in(\varepsilon_0,1]$, как только $C(x)+\varepsilon_0$ свободно разделяет $0$. Следовательно, пусть $ \mathcal{U}\ni0$ открыт так, что $\{C(\mathcal{U})+1\}\cap \mathcal{U}=\emptyset$. Тогда рассмотрим любой отрезок $\mathcal{L} $ с центром в $0$, такое что $2 \mathcal{L}\subset\mathcal{U}$. В частности, отсюда следует, что $M:=\inf_{z\in2\mathcal{L}}|C(z)+ 1|>0$.9{-1}|S(x-y)|\, $$ и (равномерная) непрерывность $S$ на $\mathcal{L}$ следует из непрерывности в точке $0$. КЭД.
Приложение: Чтобы увидеть, что ваше требование монотонности подразумевает, что $C(x)+\varepsilon_0$ свободно разделяет $x=0$ для некоторого $\varepsilon_0$, предположим обратное (фактически, любая строгая монотонность относительно начала координат достаточна).