Другие функции: floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция — округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция — Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа
Неопределенный интеграл онлайн
В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!
Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?
Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!
Вводная к интегралам
В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел.
Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
В этом заключается один из физических смыслов интеграла.
Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.
Решение интегралов
Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.
Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.
Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
Калькулятор решения интегралов
Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.
И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.
Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн .
Решить неопределенный интеграл
Онлайн сервис на сайт позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте.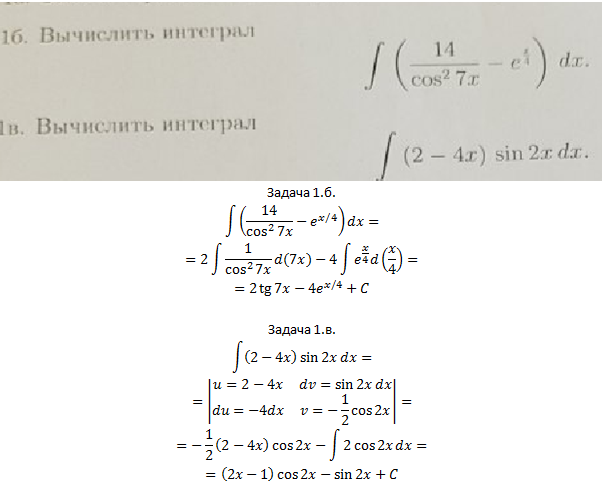
Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт сайт поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте сайт, вы всегда получите точный ответ.
Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу.
Решение высшей математики онлайн
‹— Назад
Для вычисления интегралов вида
потребуются более сложные преобразования, нежели в предыдущем разделе.
Заметим, что при и получаются табличные интегралы:
Выведем формулы, позволяющие свести вычисление и к и соответственно.
Применяя эти формулы к исходным интегралам несколько раз, при чётном мы сведём дело к вычислению табличного интеграла или , а при нечётном — к вычислению табличного интеграла или .
Итак, получим формулу, выражающую через ; эта формула называется формулой понижения степени. Преобразуем интеграл следующим образом:
Последний интеграл вычислим, применив формулу интегрирования по частям:
(В комментарии, между вертикальными чёрточками, мы не вполне корректно обозначили через не полный набор первообразных для , а какую-либо, произвольную, первообразную, одну из которых и нашли.
Только эта первообразная нам и нужна для дальнейшего. Поэтому произвольную постоянную добавлять не стали.) После этого получаем
| (2.2) |
Мы получили выражение интеграла через интеграл и известную функцию.
С помощью аналогичных преобразований, для интеграла получаем такое выражение через интеграл и известную функцию:
| (2.3) |
Как упражнение, выполните эти преобразования и получите приведённую здесь формулу (2.3).
Замечание 2.1 В промежуточных вычислениях мы получили также способ нахождения интегралов вида
и
которые сводятся, после интегрирования по частям, к интегралам и .
Пример 2.7 Вычислим интеграл
Здесь . После однократного применения формулы понижения степени (2.2), дело сведётся к нахождению интеграла . Итак,
Замечание 2.2 Приведённый в этом примере способ вычисления интеграла и подобных ему — не единственно возможный. Если записать подынтегральное выражение в виде
и заметить, что и , то получим равенство
где . Первообразные в этих двух ответах тождественно равны друг другу:
Пример 2.8 Для вычисления интеграла
формулу (2.
3) нужно будет применить два раза подряд:
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Исчисление— Два разных решения интеграла
спросил
Изменено 2 года, 7 месяцев назад
Просмотрено 4к раз
$\begingroup$
Учитывая очень простой интеграл
\begin{equation} \int -\frac{1}{2x} дх \end{уравнение}
Очевидное решение:
\begin{equation} \int -\frac{1}{2x} dx = -\frac{1}{2} \int \frac{1}{x} dx = -\frac{1}{2} \ln{|x|} + С \end{equation}
Однако по следующему правилу интегрирования \begin{уравнение} \int \frac{1}{ax + b} dx = \frac{1}{a} \ln{|ax + b|} + C \end{equation}
получается следующее решение \begin{уравнение} \int -\frac{1}{2x} dx = -\frac{1}{2}\ln{|-2x|} + C \end{equation}
Почему эти решения разные? Что правильно?
Второе решение можно упростить
\begin{уравнение}
-\frac{1}{2}\ln{|-2x|} + C = -\frac{1}{2}\ln{|-2|} -\frac{1}{2}\ln{| x|} + C= -\ln{\frac{1}{\sqrt{2}}} — \frac{1}{2}\ln{|x|} + C
\end{уравнение}
но они все же отличаются.
- вычисления
- интеграция
$\endgroup$
2
$\begingroup$
Они оба верны: они отличаются только с точки зрения их константы интегрирования .
$$\begin{выравнивание} -\frac{1}{2}\ln|-2x| + \color{red}{C} &= -\frac{1}{2}(\ln 2 + \ln |x|) + \color{red}{C} \\&= -\frac{1} {2}\ln |х| + \color{red}{(C — \frac{1}{2} \ln 2)}\\ &= -\frac{1}{2}\ln |x| + \цвет{красный}{К} \end{выравнивание} $$
$C \neq K\;$ но тем не менее $\;C, K\;$ константы!
СОВЕТ
РЕДАКТИРОВАТЬ: Вы почти у цели (при получении скорректированной константы интегрирования), но: $$-\frac{1}{2}\ln{|-2|} + C\; \ne \;-\ln{\frac{1}{\sqrt{2}}} + C$$ Скорее, поскольку $\;|-2| \;= \;2,\;$ имеем $$-\frac{1}{2}\ln{|-2|}+C \; знак равно -\frac{1}{2}\ln 2 + C\;=\; +\ln{\frac{1}{\sqrt{2}}} + C = K$$
Важно отметить, что все $K$ являются постоянными членами.
$\endgroup$
2
$\begingroup$
Они оба верны!
$$ -\frac{1}{2}\ln|-2x| + C = -\frac{1}{2}(\ln 2 + \ln |x|) + C = -\frac{1}{2}\ln |x| + (C — \frac{1}{2} \ln 2) $$
Здесь «отличается» постоянная интегрирования.
$\endgroup$
$\begingroup$
Оба результата в норме. Обратите внимание, что нет необходимости, чтобы две константы $C$ в первом результате и $C$ во втором были одинаковыми.
Здесь у нас есть $C_1=C_2\times0.5\ln|2|$.
$\endgroup$
0
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через FacebookЗарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Калькулятор несобственных интегралов — онлайн Калькулятор несобственных интегралов
Несобственный интеграл — это обратный процесс дифференцирования. Несобственный интеграл — это интеграл, имеющий верхний предел и нижний предел. Несобственный интеграл также находит площадь под кривой от нижнего предела до верхнего предела. Несобственный интеграл также известен как определенный интеграл.
Что такое неправильный калькулятор интегралов?
«Калькулятор несобственных интегралов » — это бесплатный онлайн-инструмент, который помогает вычислить значение несобственного интеграла для заданной функции. В этом калькуляторе вы можете ввести функцию, верхний и нижний пределы, и значение несобственного интеграла отобразится в течение нескольких секунд.
Неправильный интегральный калькулятор
Как использовать неправильный интегральный калькулятор?
- Шаг 1: Введите функцию, верхний и нижний предел в соответствующем поле.
