Онлайн решение уравнений с параметрами: Решение уравнений с параметром онлайн · Как пользоваться Контрольная Работа РУ

Содержание

Решение уравнений с параметром модулем онлайн. §6

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.

Задачи:

Образовательные : научить решать некоторые виды уравнений уравнений модулями и параметрами;
Развивающие : развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.
Воспитательные : воспитывать самостоятельность и умение преодолевать трудности.

Оборудование: наглядный материал для устного счёта и объяснения новой темы.

Интерактивная доска, мультимедийное оборудование урока.

Структура урока:

Повторение изученного материала (устный счёт).
Изучение нового материала.
Закрепление изученного материала.
Итог урока.
Домашнее задание.

ХОД УРОКА

1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»

1) «Уравнения, содержащие модуль»

Абсолютной величиной или модулем числа a называется число a , если a > 0, число – a , если a a = 0. Или

Из определения следует, что | a | > 0 и | a | > a для всех a € R .
Неравенство | x | a , (если a > 0) равносильно двойному неравенству – a х a .
Неравенство | x | a , (если a 0.
Неравенство | x | > a , (если a > 0) равносильно двум неравенствам

Неравенство | x | > a , (если a х € R.

2) «Решение уравнений с параметрами»

Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.

а) определить множество допустимых значений неизвестного и параметров;

б) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнения.

2. Устные упражнения

1. Решить уравнение | x – 2 | = 5; Ответ : 7; – 3

| x – 2 | = – 5; Ответ : решения нет

| x – 2 | = х + 5; Ответ : решения нет; 1,5

| x – 2 | = | x + 5 |; Ответ : решения нет; – 1,5; решения нет; – 1,5;

2. Решить уравнение: | x + 3 | + | y – 2 | = 4;

Расcмотрим четыре случая

{	x + 3 > 0	{	x > – 3
	y – 2 > 0		y > 2
	x + 3 + y – 2 = 4		y = – x + 3

{	x + 3 > 0	{	x > – 3
	y – 2		y
	x + 3 – y + 2 = 4		y = x + 1

{	x + 3	{	x
	y + 2 > 0		y > – 2
	– x – 3 – y – 2 = 4		y = x + 9

{	x + 3	{	x
	y + 2		y
	– x – 3 – y – 2 = 4		y = – x – 9

В результате мы получаем квадрат, центр которого (–3; 2), а длина диагонали равна 8, причем диагонали параллельны осям координат.

Из наглядных соображений можно сделать вывод: что уравнение вида | х + a | + | у + b | = с ; задает на плоскости квадрат с центром в точке (– а ; – b ), диагоналями параллельными осям OX и ОУ, и длина каждой диагонали равна 2с . Ответ : (– 3; 2).

2. Решить уравнение aх = 1

Ответ : если a = 0, то нет решения; если a = 0, то х = 1/ a

3. Решить уравнение (а 2 – 1) х = а + 1.

Решение .

Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи:

1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения

2) а = – 1; получаем ОX = О, и очевидно х – любое.

1
3) если а = + 1, то х = –––
а – 1

Ответ:
если а = – 1, то х – любое;
если а = 1, то нет решения;

1
если а = + 1 , то х = –––
а – 1

3. Решения примеров (из вариантов С)

1. При каком значении параметра р уравнение | х 2 – 5х

+ 6 | + | х 2 – 5х + 4 | = р имеет четыре корня.

Рассмотрим функцию у = | х 2 – 5х + 6 | + | х 2 – 5х + 4 |

Так как х 2 – 5х + 6 = (х – 2)(х – 3) и х 2 – 5х + 4 = (х – 1)(х – 4), то y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |, корни квадратных трехчленов отметим на числовой прямой

1 2 3 4 х

Числовая прямая при этом разбивает на 5 промежутков

{	x	{	x
	y = x 2 – 5x + 6 + x 2 – 5x + 4		y = 2x 2 – 10x + 10

{	1 x	{	1 x
	y = x 2 – 5x + 6 – x 2 + 5x – 4		y = 2

{	2 x	{	2 x
	y = – 2x 2 + 10x – 10		y = – x 2 + 5x – 6 – x 2 + 5x – 4

{	3 x	{	3 x
	y = 2		y = x 2 – 5x + 6 – x 2 + 5x – 4

{	x > 4	{	x > 4
	y = 2x 2 – 10x + 10		y = x 2 – 5x + 6 + x 2 –5x + 4

Для случая 3) х 0 = – b | 2a = 2, y 0 = 25: 2 + 25 – 10 = 2,5

Итак, (2,5; 2,5) – координаты вершины параболы y = – 2x 2 + 10x – 10.

Построим график функции, заданной равенством

Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 а

Ответ : при 2 а

4. Самостоятельная работа по уровням

1 уровень

1. Решить уравнение х 2 – | x | = 6
2. При каких целых значениях а имеет единственное решение уравнение ах 2 – (а + 1) + а 2 + а = 0?

2 уровень

1. Решить уравнение: | x – 5 | – | 2x + 3 | = 10

а –12) х 2 + 2 = 2(12 – а ) имеет два различных корня?

3 уровень

1. Решить уравнение | x – 5 | – | 2x + 3| = 10
2. Найти все значениях параметра а, при которых уравнение (а – 12) х 2 + 2 = 2(12 – а ) имеет два различных корня?

5. Итог урока

1. Определение модуля.
2. Что значит решить уравнение с параметром?

6. Задание на дом. C5 варианта №11 Ф.Ф. Лысенко. Математика, 2012

Слайд 2

.

Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения Цель урока.

Слайд 3

Абсолютной величиной или модулем числа a называется число a, если a>0, число -a, если a 0 ׀ a ׀={ 0, если a=0 -a, если a 0) равносильно двойному неравенству -a 0. Неравенство ׀ х׀>a, (если a>0) равносильно двум неравенствам — Неравенство׀ х׀>a, (если a

Слайд 4

Решить уравнение с параметрами — значит указать, при каких значениях параметров существуют решения и каковы они. а) определить множество допустимых значений неизвестного и параметров; б) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнения. Повторение важнейшего теоретического материала по темам «Решение уравнений с параметрами»

Слайд 5

1. Решить уравнение׀ х-2 ׀ =5; Ответ 7;-3 ׀ х-2 ׀ =-5; Ответ решения нет ׀ х-2 ׀ =х+5; ; Ответ решения нет; 1,5 ׀ х-2 ׀ = ׀ х+5 ׀ ; Ответ решения нет; -1,5; решения нет; -1,5; Устные упражнения.

Слайд 6

2. Решить уравнениеах=1; Ответ. Если a=0, то нет решения;если a=0, тох=1/ a 1.3. Решить уравнение (а²-1) х = а+ 1. 1) а = 1; тогда уравнение принимает вид Ох = 2 и не имеет решения 2) а = 1; получаем Ох = О, и очевидно х — любое. 1 3) если а =± 1 ,то х = — а-1 Ответ. Если а=-1 , то х- любое; если а=1, то нет решения 1 если а =± 1 ,то х= — а-1

Слайд 7

2.Решить уравнение׀ х+3 ׀ + ׀ у -2 ׀= 4; . 2 3. 4. 1

Слайд 8

3 3 2 x y 0 1 Ответ: (-3; 2).

Слайд 9

2. Решить уравнениеaх=1;

Ответ. Если a=0, то нет решения; если a=0, то х=1/ a 1.3. Решить уравнение (а²-1) х = а+ 1. 1) а = 1; тогда уравнение принимает вид Ох = 2 и не имеет решения 2) а = 1; получаем Ох = О, и очевидно х — любое. 1 3) если а =± 1 ,то х = — а-1 Ответ. Если а=-1 , то х- любое; если а=1, то нет решения 1 если а =± 1 ,то х= — а-1

Слайд 10

3 Построить график функции у= ׀х׀, у= ׀х-2 ׀, у = ׀ х+5I , у = ׀х-2 ׀+3, у = ׀ х+3 ׀-2

y x У=IxI 1 2 -3 -4 -1 1 -2 2 3 0 -5 4 5 6 -1 -2 Y=Ix+3I-2 Y=Ix-2I Y=Ix+5I Y=Ix-2I +3

Алгебра.

Задачи с параметрами. 9–11 классы. 3-е издание

Образовательный комплекс «1С:Школа. Алгебраические задачи с параметрами, 9–11 кл.» посвящен одной из наиболее трудных тем школьного курса алгебры. Уравнения и неравенства с параметрами вошли в школьную алгебру «извне»: несколько десятилетий назад такие задачи появились на вступительных экзаменах в вузы, причем сначала – в наиболее престижные, затем область распространения задач этого типа постепенно расширялась, им стали уделять все большее внимание составители программ и авторы учебников, и наконец они заняли постоянное место среди заданий типа «C» единого государственного экзамена по математике. Сегодня невозможно рассчитывать на высокую оценку по ЕГЭ, не зная основных методов и приемов решения таких задач.

Данный диск содержит оригинальный авторский курс из 36 уроков по методам решения задач с параметрами, представляющий теоретические и практические материалы в наглядной и лаконичной мультимедийной форме, которая поможет лучше их понять и усвоить, быстрее и эффективнее повторить. Поддерживаются все виды учебной деятельности – как самостоятельная работа дома, так и использование в классе под руководством учителя. Содержание диска соответствует требованиям ЕГЭ по математике и может использоваться при подготовке к выполнению заданий типа «C».

В состав электронного пособия входят обучающие, справочные, иллюстративные и контролирующие материалы по следующим темам:

Элементарные функции в уравнениях с параметрами
Решение неравенств с параметрами
Некоторые особые приемы решения задач с параметрами

Особенностями изложения материала являются:

модульный принцип построения, при котором каждый последующий модуль содержит более сложные задачи по сравнению с предыдущим;
объяснение нового материала в форме разбора типовых задач с разной степенью подробности изложения;
иллюстрирование материалов интерактивными моделями, созданными в среде «1С:Математический конструктор»;
наличие в каждом уроке контрольных тестов, позволяющих проверить усвоение материала.

ученику –

понять методы решения уравнений и неравенств с параметрами с помощью множества примеров и интерактивных тренажеров;
проверить полученные знания с помощью тестовых вопросов;
подготовиться к решению задач типа С;

учителю –

повысить заинтересованность учащихся в предмете;
подобрать интерактивный материал к уроку;
проверить знания учащихся, используя подборки тестовых заданий.

Авторы курса: Голубев В.И., Дубровский В.Н., Кравцев С.В., Шавгулидзе Е.Т.

Тема 1. Решение уравнений с параметрами для элементарных функций

Тема 1.1 Линейная функция в уравнениях с параметро

Тема 1. 2. Квадратичная функция в уравнениях с параметром

Тема 1.3 Квадратичная функция в уравнениях с параметром

Тема 1.4 Модуль в уравнениях с параметром

Тема 1.5 Рациональные уравнения с параметром

Тема 1.6 Квадратный корень в уравнениях с параметром

Тема 1.7 Иррациональные уравнения с параметром

Тема 1.8 Показательные уравнения с параметром

Тема 1.9 Логарифмические уравнения с параметром

Тема 1.10 Тригонометрические уравнения с параметром

Тема 1.11 Тригонометрические уравнения с параметром

Тема 1.12 Обратные тригонометрические функции в уравнениях с параметром

Тема 2. Решение неравенств с параметрами

Тема 2.1 Линейные и квадратные неравенства с параметром

Тема 2.2 Модуль в неравенствах с параметром

Тема 2.3 Рациональные неравенства с параметром

Тема 2. 4 Иррациональные неравенства с параметром

Тема 2.5 Логарифмические неравенства с параметром

Тема 2.6 Тригонометрические неравенства с параметром

Тема 2.7 Тригонометрические неравенства с параметром

Тема 3. Некоторые особые приемы решения задач с параметром

Тема 3.1 Особенности использования теоремы Виета в задачах с параметром

Тема 3.2 Особенности использования теоремы Виета в задачах с параметром

Тема 3.3 Особенности использования теоремы Виета в задачах с параметром

Тема 3.4 Метод трех точек

Тема 3.5 Использование алгебраической симметрии в решении задач с параметрами

Тема 3.6 Использование алгебраической симметрии в решении задач с параметрами

Тема 3.7 Решение уравнений и неравенств относительно параметра

Тема 3.8 Решение уравнений и неравенств относительно параметра

Тема 3. 9 Решение уравнений и неравенств относительно параметра

Тема 3.10 Решение задач с параметром с использованием графиков входящих в условие задачи функций

Тема 3.11 Решение задач с параметром с использованием графиков входящих в условие задачи функций

Тема 3.12 Использование области определения и множества значений ходящих в условие функций для решения задач с параметрами

Тема 3.13 Задачи со свободным параметром

Тема 3.14 Метод введения параметра в задачу, изначально параметр не содержащую

Тема 3.15 Использование свойства монотонности функции

Тема 3.16 Использование свойства монотонности функции

Тема 3.17 Метод областей

Графопостроитель

Операционная система Microsoft Windows 2000/XP/7;
Требует наличие Flash-плеер! (см. https://obr.1c.ru/read/info/rabota-adobe-flash-v-2021-godu/)
Pentium III 700 МГц;
память 256 Мб;
Видеокарта, поддерживающая разрешение 1024х768, true color;
устройство воспроизведения DVD/CD-ROM;
да 2 Гб на выбранном для установки диске
не менее 400 Мб на системном диске
звуковая карта;
колонки или наушники;
мышь.

Дата выхода продукта: 30.09.2016
Разработчик: ООО «1C-Паблишинг»
Адрес техподдержки: [email protected]
Штрих-код: 4601546119438
ISBN: 978-5-9677-2406-0
Серии: 1С:Школа, Учебное пособие
Возрастная категория: 12+

Уравнения с параметрами.

— Математика

Файл к уроку

Решение уравнений с параметрами.

Не так давно 8 класс познакомился с квадратными уравнениями и алгоритмами их решения. Сегодня мы рассмотрим еще один вид уравнений, который часто встречается на олимпиадах и турнирах, и включен в ЕГЭ по профильной математике – это уравнения с параметром. Что такое параметр? Обычно это число, в зависимости от значения которого уравнение, будь оно линейным или квадратным, может иметь корни, а может их не иметь.

Задачи с параметрами считаются сложными ,однако если разобраться досконально, из каких шагов состоит путь к решению уравнения, то параметр уже не кажется такой злобной величиной.

Линейные уравнения с параметрами.

Уравнение вида

ax + b = 0,

(1)

где a, b из R, x — переменная, называется уравнением первой степени (линейным уравнением).

Уравнение равносильно уравнению

ax = – b

откуда следует следующее утверждение.

Если a ≠ 0, то уравнение имеет единственное решение x = – ^b/_a;
Если a = 0, b ≠ 0, то множество решений уравнения пусто;
Если a = 0, b = 0, то любое действительное число является решением уравнения.

Решить уравнение с параметром – значит указать решение при всех значениях параметра, то есть фактически решить бесконечное множество уравнений, объединив их в одно по неким схожим зависимостям от параметра.

Пример 1. Решить уравнение: a²x – 1 = x + a.

Пример 2. Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.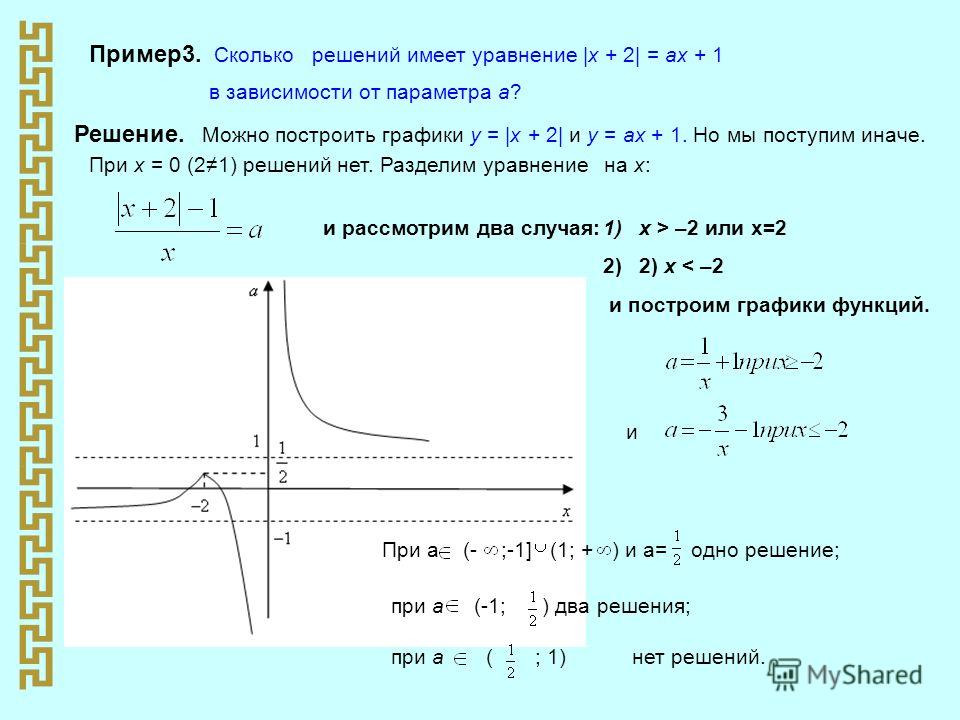

По правилу модуля 6 – x = ±a, выразим х:

x = 6 ± a.

Ответ: х = 6 ± a, где a ≥ 0.

Пример 3. Решить уравнение x/a + 1 = а + х относительно переменной х.

Решение.

Если а = 0, то преобразуем уравнение к виду а + х = а² + ах или (а – 1)х = —а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.

Если а ≠ 1, то последнее уравнение примет вид х = —а.

Данное решение можно проиллюстрировать на координатной прямой (рис. 1)

Ответ: нет решений при а = 0; х – любое число при а = 1; х = —а при а ≠ 0 и а ≠ 1.

Пример 4. При каких значениях параметра b уравнение не имеет корней:

Графический метод

Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.

Пример 5. Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?

Решение. Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2).

На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.

Ответ: корней у уравнения не будет, если а a 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0 a

Пример 6. При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?

Решение.

Изобразим графики функций y = 2|x| + |x – 1| и y = a. Для y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:

{-3x + 1, при x

y = {x + 1, при 0 ≤ x ≤ 1,

{3x – 1, при x 1.

На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.

Ответ: а = 1.

Пример 7. При каких значениях параметра а неравенство имеет решением все действительные числа:

Системы линейных уравнений с параметрами.

– Система имеет единственное решение.

– Система имеет бесконечное множество решений.

– Система не имеет решений.

Пример 8. Для всех значений параметра а решить систему уравнений

Квадратичные уравнения с параметрами.

Решение уравнений второй степени сводится к исследованию поведения квадратного трехчлена, исследованию знака дискриминанта при различных значениях параметра. Часто при решении нам может помочь теорема Виета, когда вопрос стоит о корнях разных знаков, о корнях одного знака.

Квадратное уравнение может не иметь решений (Da=0 или D=0), два решения (D0) или бесконечное множество решений (когда при каком-то значении параметра получаем 0=0).

Пример 9. Решить уравнение в зависимости от параметра а:

Пример 10. При каких значениях корни уравнения положительны?

Пример 11. Найти значения параметра а, при которых среди корней уравнения имеется ровно один отрицательный:

Пример 12. Найти все значения параметра а, при которых уравнение имеет два различных отрицательных корня:

Пример 13. При каких значениях m корни уравнения 4x² – (3m + 1) x – m – 2 = 0 лежат в промежутке между –1 и 2?

Пример 14: Найти все значения параметра а, при которых меньший корень уравнения x² + (a + 1) x + 3 = 0 лежал в интервале (–1; 3)

Калькулятор параметрических уравнений

+ онлайн-решатель со свободными шагами

Калькулятор параметрических уравнений используется для расчета результатов параметрических уравнений, соответствующих параметру . Этот калькулятор, в частности, работает, решая пару параметрических уравнений, которые соответствуют единственному параметру , вводя различные значения параметра и вычисляя результаты для основных переменных.

Калькулятор очень прост в использовании и работает путем ввода ваших данных в поля ввода калькулятора. Он также предназначен для демонстрации того, как Параметрические уравнения формируют геометрию в результате двух измерений.

Что такое калькулятор параметрических уравнений?

Калькулятор параметрических уравнений — это онлайн-калькулятор, который может решить ваши задачи параметрических уравнений в браузере без каких-либо предварительных условий.

Этот калькулятор представляет собой стандартный калькулятор, в котором не требуется много сложной обработки. Этот калькулятор может решить набор двумерных параметрических уравнений для нескольких различных входов общей независимой переменной, также называемой 9.0003 Параметр .

Значение параметра выбирается произвольно для решения этих уравнений, так как оно записывает отклик, генерируемый выходными переменными. Этот ответ — это то, что описывают эти переменные и формы, которые они рисуют.

Как пользоваться калькулятором параметрических уравнений?

Для использования Калькулятора параметрических уравнений необходимо настроить два параметрических уравнения, одно для x, а другое для y. Эти уравнения должны иметь одинаковые Параметр в них обычно используется как $t$ для времени.

Наконец, вы можете получить результаты одним нажатием кнопки. Теперь, чтобы получить наилучшие результаты от этого калькулятора, вы можете следовать пошаговому руководству, приведенному ниже:

Шаг 1

Во-первых, правильно настройте входные параметрические уравнения, что означает, что параметр останется прежним.

Шаг 2

Теперь вы можете ввести уравнения в соответствующие поля ввода, которые помечены как: решить y = и х = .

Шаг 3

После того, как вы ввели данные в соответствующие поля ввода, вы можете продолжить, нажав кнопку «Отправить» . Это даст желаемые результаты.

Шаг 4

Наконец, если вы собираетесь повторно использовать этот калькулятор, вы можете просто ввести новые задачи, следуя каждому шагу, описанному выше, чтобы получить столько решений, сколько захотите.

Важно отметить, что этот калькулятор оснащен только 2-мерный параметрический решатель уравнений, что означает, что он может решать 3-мерные или более высокие задачи. Количество параметрических уравнений, соответствующих выходным переменным, связано с количеством измерений, с которыми имеет дело Параметризация .

Как работает калькулятор параметрических уравнений?

A Калькулятор параметрических уравнений работает путем решения алгебры параметрического уравнения с использованием произвольных значений параметра, выступающего в качестве независимой переменной во всем этом. Таким образом, мы можем построить небольшой информационный набор табличного типа, который в дальнейшем можно использовать для построения кривых, созданных указанными параметрическими уравнениями.

Параметрические уравнения

Это группа уравнений, представленных общей независимой переменной , которая позволяет им соответствовать друг другу. Эта специальная независимая переменная чаще называется параметром этих параметрических уравнений .

Параметрические уравнения обычно используются для демонстрации геометрических данных, следовательно, для рисования поверхностей и кривых Геометрия , которые определяются этими уравнениями.

Этот процесс обычно называется Параметризация , в то время как параметрические уравнения могут быть известны как Параметрические представления указанных геометрий. Параметрические уравнения обычно имеют вид:

x = f1(t)

y = f2(t)

случай представляет «время» как независимую переменную.

Пример параметрических уравнений

Как мы уже говорили выше, Параметрические уравнения в основном используются для описания и рисования геометрических фигур. Они могут включать в себя кривые и поверхности и даже основные геометрические формы, такие как Круг . Круг является одной из базовых фигур, существующих в геометрии, и параметрически описывается следующим образом: точка на декартовой плоскости. Эта точка лежит на окружности окружности, координаты этой точки можно увидеть следующим образом, выраженные в виде вектора:

(x, y) = (cost t, sin t)

Параметрические уравнения в геометрии

Теперь, Параметрические уравнения также способны выражать алгебраические ориентации высших измерений вместе с описаниями многообразий, тогда как другой важный факт В отношении этих параметрических уравнений следует отметить, что количество этих уравнений соответствует количеству задействованных измерений. Таким образом, для 2 измерений количество уравнений будет равно 2, и наоборот.

Аналогичные параметрические представления можно также наблюдать в области кинематики, где используется параметр $t$, который соответствует времени как независимой переменной . Таким образом, изменения состояний объектов, соответствующие их траекторным траекториям, представлены относительно времени .

Важным фактом для наблюдения будут те параметрических уравнений , и процесс описания этих событий с точки зрения параметра не уникален. Таким образом, может быть много разных представлений одной и той же формы или траектории в Параметризация .

Параметрические уравнения кинематики

Кинематика — это раздел физики, изучающий движущиеся или покоящиеся объекты, и Параметрические уравнения играют важную роль в описании траекторий движения этих объектов. Здесь пути этих объектов называются параметрическими кривыми , и каждый специальный объект описывается независимой переменной, которая в основном является временем.

Такие Параметрические представления 9Затем 0004 можно легко подвергнуть дифференциации и интеграции для дальнейшего физического анализа . Поскольку положение объекта в пространстве можно рассчитать с помощью:

r(t) = (x(t), y(t), z(t))

При этом первая производная этой величины приводит к значению следующим образом:

v(t) = r'(t) = (x'(t), y'(t), z'(t))

a(t) = v'(t) = r»(t) = (x»(t), y»(t), z»(t))

Решение для параметрических уравнений

Теперь предположим, что у нас есть набор двумерных параметрических уравнений, представленных в виде: задачу, взяв произвольные значения для $t$ из строки целых чисел, мы получим следующий результат:

\[\begin{matrix}t & x & y \\ -2 & x_{-2} & y_{-2 }\\ -1 & x_{-1} & y_{-1}\\ 0 & x_{0} & y_{0}\\ 1 & x_{1} & y_{1} \\ 2 & x_{2 } & y_{2} \end{matrix}\] 92 + 1\]

y = 2t – 1

Решите эти параметрические уравнения для параметра t.

Решение

Итак, мы начнем с того, что сначала возьмем Произвольный набор данных параметров, исходя из его природы. Таким образом, если бы мы использовали Angular Data , мы бы полагались на углы как на параметрическую основу, но в этом случае мы используем целые числа. Для целочисленного случая , мы используем значения числовой строки в качестве параметров.

Это показано здесь:

\[\begin{matrix}t & x & y \\ -2 & 2 & -5\\ -1 & 0 & -3\\ 0 & \frac{-1}{4} & -2\\ 1 & 0 & -1 \\ 2 & 2 & 1 \end{matrix}\]

График, созданный этими параметрическими уравнениями, имеет вид:

Рисунок 1

Пример 2

Учтите, что существуют следующие параметрические уравнения :

\[\begin{matrix} x = 5 \cos t & y = 2 \sin t & 0 \leq t \leq 2 \pi \end{matrix} \]

Найдите решение этих параметрических уравнений, соответствующих к параметру $t$ в заданном диапазоне.

Решение

В этом примере мы аналогичным образом начинаем с Произвольного набора данных параметров в зависимости от его природы. Если Integer Data соответствует целочисленным значениям, которые должны быть введены в систему, при использовании Angular Data мы должны полагаться на углы как на параметрическую основу. Таким образом, углы должны быть в диапазоне и на небольшом расстоянии друг от друга, поскольку эти данные являются угловыми.

Это делается следующим образом:

\[\begin{matrix}t & x & y \\ 0 & 5 & 0\\ \frac{\pi}{2} & 0 & 2\\ \pi & — 5 & 0\\ \frac{3\pi}{2} & 0 & -2 \\ 2\pi & 5 & 0 \end{matrix}\] 92 t & y = 2 \cos t & 0 \leq t \leq 2 \pi \end{matrix} \]

Найдите решение указанных уравнений, связанных с параметром $t$, представляющим собой угол.

Решение

Это еще один пример, когда произвольный набор данных параметров создается на основе его природы. Мы знаем, что в данном примере рассматриваемый параметр $t$ соответствует углу, поэтому мы используем угловые данные в диапазоне $0 – 2\pi$. Теперь мы решаем это дальше, используя эти точки данных.

Это происходит следующим образом:

\[\begin{matrix}t & x & y \\ 0 & 0 & 2\\ \frac{\pi}{2} & 1 & 0\\ \pi & 0 & -2\\ \frac{ 3\pi}{2} & 1 & 0 \\ 2\pi & 0 & 2 \end{matrix}\]

Параметрическая кривая для этого может быть построена следующим образом:

Рисунок 3

Все изображения /графики создаются с помощью GeoGebra.

Список математических калькуляторов

Параметрические системы уравнений

Этот сайт является частью JavaScript E-labs обучающих объектов для принятия решений. Другие сценарии JavaScript из этой серии относятся к разным областям применения в разделе МЕНЮ на этой странице.
Профессор Хоссейн Аршам
Во многих прикладных задачах принятия решений, таких как анализ чувствительности линейной оптимизации, необходимо решить линейно-параметрическую правостороннюю (ПСР) систему уравнений. Часто разновидности параметрических систем уравнений РГО можно привести к следующему стандартному виду:
АХ = б + Др, где A — невырожденная матрица размера n на n, матрица-столбец b — числовое значение RHS, а диагональная матрица D содержит коэффициенты при параметрах r = [r1, r2, rn]T соответственно.
Следующий JavaScript решает параметрические системы до 7 уравнений. Начиная с верхней левой таблицы, введите матрицу A, а затем столбец RHS, за которым следует диагональная матрица n на n D, затем нажмите кнопку «Рассчитать». JavaScript возвращает постоянный член решения в виде элементов столбца (n+1), за которым следует коэффициент r в виде квадратной матрицы.
Приложение 1: Предположим, мы хотим решить следующие параметрические системы RHD из 2 уравнений с 2 неизвестными:
2 Х1 + Х2 = 40 + г1
Х1 + 2 Х2 = 50 + г2 Введя матрицу [A, b, D]: 2    1    40    1    0
1    2    50    0    1 и после нажатия на кнопку Calculate получаем следующее параметрическое решение: X1 = 10 + 2/3r1 — 1/3 r2
Х2 = 20 — 1/3r1 + 2/3r2 Приложение 2: При каких условиях на значения r1 и r2 решение следующей параметрической системы уравнений остается неотрицательным? 2 Х1 + Х2 = 40 + . 4r1
Х1 + 2 Х2 = 50 + 0,5r2 Следуя приведенной выше инструкции по вводу данных, таблица ввода будет [A, b, D]: 2    1    40    0,4    0
1    2    50    0    0,5
Параметрическое решение: Х1 = 10 + 4/15р1 — 1/6р2
Х2 = 20 — 2/15р1 + 1/3р2 Поэтому, чтобы иметь неотрицательное решение, допустимая область для r1 и r2 представляет собой набор: S = {r1, r2 | 10 + 4/15р1 -1/6р2 ³ 0, 20 -2/15р1 + 1/3р2 ³ 0}.
Приложение 3: Обратите внимание, что этот JavaScript можно использовать для решения обычного, т.е. непараметрическая система уравнений, установив матрицу D в нулевую матрицу, и тем более не запись матрицы D в матрицу данных.
Простой JavaScript для решения систем уравнений до 10 уравнения и быть найдены в Решение системы линейных уравнений .
Приложение 4: Чтобы найти обратную квадратную матрицу A, введите матрицу A, а затем единичную матрицу того же размера, затем нажмите кнопку «Рассчитать». Следующее числовой пример иллюстрирует процесс:
Предположим, мы хотим найти обратную (A ^-1 ) следующей матрицы (если она существует) A:
2 1
А =
1 -1
Введя матрицу A, а затем единичную матрицу 2 на 2, результат будет следующим: Это дает X1 = 1/3, X2 = -2/3. Следовательно, А ^-1 является:
1/3 1/3
А ^-1 =
1/3 -2/3
Для альтернативного подхода используйте Решение системы линейных уравнений который вычисляет обратную матрицу до 10 на 10.
Предупреждение: Во всех приложениях и случаях после нажатия кнопки «Рассчитать» выходные данные должны содержать единичную матрицу, отображаемую в левой части таблицы. В противном случае входящая матрица могла бы быть сингулярной матрицей.
EES: Решатель инженерных уравнений | Программное обеспечение F-Chart: Инженерное программное обеспечение
Исходная информация
EES начинается с отображения диалогового окна, в котором отображается регистрационная информация, номер версии и другая информация. Номер версии и регистрационная информация потребуются, если вы запросите техническую поддержку. Нажмите кнопку OK, чтобы закрыть диалоговое окно.
Подробная помощь доступна в любой точке EES. Нажатие клавиши F1 вызовет окно справки, относящееся к первому окну. При нажатии на кнопку «Содержание» отображается указатель справки, показанный ниже. Щелкнув по подчеркнутому слову (отображаемому зеленым на цветных мониторах), вы получите справку по этому вопросу.
Команды EES распределены по девяти выпадающим меню. (Десятое определяемое пользователем меню может быть размещено справа от меню «Справка». Далее следует краткое описание их функций. Подробное описание команд приведено в главе 3 руководства EES.
Обратите внимание, что панель инструментов находится под строкой меню. Панель инструментов содержит небольшие кнопки, обеспечивающие быстрый доступ ко многим наиболее часто используемым командам меню EES. Если вы наведете курсор на кнопку и подождите несколько секунд, появится несколько слов, объясняющих функцию этой кнопки. При желании панель инструментов можно скрыть с помощью элемента управления в диалоговом окне «Настройки» (меню «Параметры»). Системное меню, представленное значком EES, появляется над меню файлов. Системное меню не является частью EES, а является функцией операционной системы Windows. Он содержит команды, которые позволяют перемещать окно, изменять его размер и переключаться на другие приложения.
Меню «Файл» содержит команды для загрузки, объединения и сохранения рабочих файлов и библиотек, а также для печати.
Меню «Правка» содержит команды редактирования для вырезания, копирования и вставки информации.
В меню «Поиск» представлены команды «Найти» и «Заменить» для использования в окне «Уравнения».
Меню «Параметры» содержит команды для установки предполагаемых значений и границ переменных, системы единиц, информации по умолчанию и программных предпочтений. Также предусмотрена команда для вывода информации о встроенных и пользовательских функциях.
Меню «Расчет» содержит команды для проверки, форматирования и решения набора уравнений.
Меню «Таблицы» содержит команды для настройки и изменения содержимого параметрических таблиц и таблиц поиска, а также для выполнения линейной регрессии данных в этих таблицах. Параметрическая таблица, похожая на электронную таблицу, позволяет многократно решать набор уравнений, изменяя значения одной или нескольких переменных. (или **) используется для обозначения возведения в степень.
При желании вы можете просмотреть уравнения в математической записи, выбрав команду Formatted Equations в меню Windows.
Выберите команду «Решить» в меню «Расчет». Появится диалоговое окно, показывающее ход решения. Когда расчеты завершены, кнопка изменится с Прервать на Продолжить.
Нажмите кнопку «Продолжить». Затем будет отображено решение этого набора уравнений.
Пример задачи термодинамики
В этом разделе будет поставлена и решена простая задача термодинамики, чтобы проиллюстрировать доступ к функциям свойств и возможности EES решать уравнения. Проблема, типичная для тех, с которыми можно столкнуться в курсе термодинамики бакалавриата, состоит в следующем.
Хладагент-134а поступает в клапан при 700 кПа, 50°C со скоростью 15 м/с. На выходе из клапана давление 300 кПа. Площадь входа и выхода жидкости составляет 0,0110 м2. Определить температуру, массовый расход и скорость на выходе из клапана.
Для решения этой задачи необходимо выбрать систему, а затем применить баланс массы и энергии. Система — клапан. Массовый расход постоянный, так что массовый баланс равен:
где

м = массовый расход [кг/с]
A = площадь поперечного сечения [м2] Vel
92 9 = скорость [м/с]
v = удельный объем [м3/кг]
Мы знаем, что
Предполагается, что клапан хорошо изолирован и не имеет движущихся частей. Эффекты тепла и работы равны нулю. Установившийся баланс энергии на клапане:
, где h — удельная энтальпия, а Vel2/2 — удельная кинетическая энергия. В единицах СИ удельная энтальпия обычно выражается в единицах [кДж/кг], поэтому могут потребоваться некоторые преобразования единиц измерения. EES предоставляет возможности преобразования единиц измерения с помощью функции CONVERT.
Из соотношений между свойствами R134a:

Обычно членами, содержащими скорость, пренебрегают, прежде всего потому, что эффекты кинетической энергии обычно малы, а также потому, что эти члены затрудняют решение задачи. Однако с EES вычислительная сложность не имеет значения. Пользователь может решить задачу с терминами кинетической энергии и оценить их важность.
Известны значения T 1, P 1, A 1, Vel 1 и P2. Есть девять неизвестных: A 2, m ₁ , m ₂ , Vel 2, h 1, v 1, h 2, v 2, T 2. Since имеется 9 уравнений, решение задачи определено. Теперь осталось решить уравнения. В этом может помочь EES.
Запустите EES и выберите команду «Создать» в меню «Файл». Появится пустое окно уравнений. Однако прежде чем вводить уравнения, установите систему единиц для встроенных функций теплофизических свойств. Чтобы просмотреть или изменить систему единиц, выберите Система единиц в меню «Параметры».
EES изначально настроен на единицы СИ с T в °C, P в кПа и значениями конкретных свойств в их обычных единицах на основе массы. Эти значения по умолчанию могли быть изменены во время предыдущего использования. Нажмите на элементы управления, чтобы установить единицы измерения, как показано выше. Нажмите кнопку OK (или нажмите клавишу возврата), чтобы принять системные настройки единиц измерения.
Уравнения теперь можно вводить в окно Уравнения. Текст вводится так же, как и для любого текстового процессора. Правила форматирования следующие:
Буквы верхнего и нижнего регистра не различаются. EES (опционально) изменит регистр всех переменных, чтобы они соответствовали тому, как они появляются в первый раз.
Пустые строки и пробелы можно вводить по желанию, поскольку они игнорируются.
Комментарии должны быть заключены в фигурные скобки { } или в кавычки » «. Комментарии могут занимать столько строк, сколько необходимо. Комментарии внутри фигурных скобок могут быть вложенными, и в этом случае распознается только самый внешний набор { }. Комментарии в кавычках также будут отображаться в окне Форматированные уравнения. 9или ** используется для обозначения возведения в степень.
Порядок ввода уравнений не имеет значения.
Положение известных и неизвестных в уравнении не имеет значения.
После ввода уравнений для этой задачи и (необязательно) проверки синтаксиса с помощью команды «Проверить/Формат» в меню «Расчет» появится окно «Уравнения», как показано на рисунке. Комментарии обычно отображаются синим цветом на цветном мониторе. Другие параметры форматирования задаются с помощью команды «Настройки» в меню «Параметры». 92] к единицам удельной энтальпии [кДж/кг]. Функция Convert наиболее полезна в этих задачах.
Функции термодинамических свойств, такие как энтальпия и объем, требуют специального формата. Первым аргументом функции является название вещества, в данном случае R134a. Следующие аргументы представляют собой независимые переменные, которым предшествует одна буква идентификации и знак равенства. Допустимые буквы: T, P, H, U, S, V и X, соответствующие температуре, давлению, удельной энтальпии, удельной внутренней энергии, удельной энтропии, удельному объему и качеству. (Для психрометрических функций допустимы дополнительные буквы W, R, D и B, соответствующие коэффициенту влажности, относительной влажности, температуре точки росы и температуре по влажному термометру.)
Простым способом ввода функций без необходимости вспоминать формат является использование команды «Информация о функциях» в меню «Параметры». Эта команда вызовет диалоговое окно, показанное ниже. Нажмите на переключатель «Теплофизические опоры». Список встроенных функций теплофизических свойств появится слева, а список веществ справа. Выберите функцию свойств, щелкнув ее имя, используя, если необходимо, полосу прокрутки, чтобы отобразить ее. Таким же образом выберите вещество. Пример функции, показывающей формат, появится в прямоугольнике примера внизу. При необходимости информацию в прямоугольнике можно изменить. Нажатие кнопки «Вставить» скопирует пример в окно уравнений в позиции курсора. Дополнительную информацию можно получить, нажав кнопку «Информация».
Обычно перед решением уравнений рекомендуется установить предполагаемые значения и (возможно) нижнюю и верхнюю границы для переменных. Это делается с помощью команды «Переменная информация» в меню «Параметры». Перед отображением диалогового окна «Информация о переменной» EES проверяет синтаксис и компилирует вновь введенные и/или измененные уравнения, а затем решает все уравнения с одним неизвестным. Появится диалоговое окно Информация о переменной.
Диалоговое окно «Информация о переменной» содержит строку для каждой переменной, отображаемой в окне «Уравнения». По умолчанию каждая переменная имеет предполагаемое значение 1,0 с нижними и верхними границами отрицательной и положительной бесконечности. (Если EES ранее вычислила значение переменной, в столбце Предполагаемое значение вычисленное значение будет выделено жирным шрифтом. Эти предполагаемые значения все еще можно отредактировать, что заставит EES пересчитать значение этой переменной.)
Буква A в столбце «Параметры отображения» указывает на то, что EES автоматически определяет формат отображения числового значения переменной, когда оно отображается в окне «Решение». В этом случае EES выберет соответствующее количество цифр, поэтому столбец цифр справа от буквы A будет отключен. Автоматическое форматирование по умолчанию. Альтернативными вариантами отображения являются F (для фиксированного количества цифр справа от десятичной точки) и E (для экспоненциального формата). Отображение и другие значения по умолчанию можно легко изменить с помощью команды «Информация по умолчанию» в меню «Параметры», описанной в главе 3. Третий столбец «Параметры отображения» управляет эффектами выделения, такими как обычный (по умолчанию), полужирный, в рамках. При желании можно указать единицы измерения переменных. Единицы будут отображаться вместе с переменной в окне решения и/или в параметрической таблице. EES не выполняет преобразование единиц измерения автоматически, но может обеспечить преобразование единиц с помощью функции преобразования. Введенная здесь информация о единицах измерения предназначена только для отображения.
При работе с нелинейными уравнениями иногда необходимо указать разумные предполагаемые значения и границы, чтобы определить желаемое решение. (Для этой задачи это не обязательно.) Границы некоторых переменных известны из физики задачи. В примере задачи энтальпия на выходе h_2 должна быть достаточно близкой к значению h_1. Установите его предполагаемое значение на 100 и его нижнюю границу на 0. Установите предполагаемое значение объема выхода, v_2, на 0,1, а его нижнюю границу на 0. Прокрутите список информации о переменных, чтобы отобразить Vel2. Нижняя граница Vel2 также должна быть равна нулю.
Чтобы решить набор уравнений, выберите команду «Решить» в меню «Расчет». Появится информационное диалоговое окно с указанием прошедшего времени, максимального остатка (т. е. разницы между левой и правой частями уравнения) и максимального изменения значений переменных с момента последней итерации. Когда расчеты завершены, EES отображает общее количество уравнений в задаче и количество блоков. Блок представляет собой подмножество уравнений, которые можно решить независимо. EES автоматически блокирует набор уравнений, когда это возможно, для повышения эффективности расчетов, как описано в Приложении B. Когда расчеты завершены, кнопка изменится с Прервать на Продолжить.
По умолчанию вычисления останавливаются, когда произошло 100 итераций, истекшее время превышает 60 секунд, максимальная невязка меньше 10-6 или максимальное изменение переменной меньше 10-9. Эти значения по умолчанию можно изменить с помощью команды Stop Criteria в меню Options. Если максимальная невязка больше, чем значение, установленное для критериев остановки, уравнения не были правильно решены, возможно, из-за того, что ограничения на одну или несколько переменных ограничивали решение. Нажатие кнопки «Продолжить» удалит информационное диалоговое окно и отобразит окно «Решение», показанное на следующей странице. Теперь задача решена, поскольку определены значения T_2, m_2 и Vel_2.
Одной из самых полезных функций EES является возможность проводить параметрические исследования. Например, в этой задаче может быть интересно посмотреть, как температура и скорость на выходе из дросселя изменяются в зависимости от давления на выходе. Ряд расчетов можно автоматизировать и нанести на график с помощью команд в меню «Таблицы».
Выберите команду «Новая таблица». Появится диалоговое окно со списком переменных, появляющихся в окне уравнений. В этом случае мы построим таблицу, содержащую переменные P_2, T_2, Vel_2 и h_2. Щелкните P_2 в списке переменных слева. Это приведет к тому, что P_2 будет выделен, а кнопка «Добавить» станет активной.
Теперь нажмите кнопку «Добавить», чтобы переместить P_2 в список переменных справа. Повторите для T_2, h_2 и Vel_2, используя полосу прокрутки, чтобы при необходимости отобразить переменную. (В качестве короткого пути вы можете дважды щелкнуть имя переменной в списке слева, чтобы переместить ее в список справа.). Теперь должно появиться диалоговое окно настройки таблицы, как показано выше. Нажмите кнопку ОК, чтобы создать таблицу.
Параметрическая таблица во многом похожа на электронную таблицу. Вы можете вводить числа прямо в ячейки. Числа, которые вы вводите, отображаются черным цветом и производят такой же эффект, как если бы вы установили переменную в это значение с помощью уравнения в окне уравнений. Удалите уравнение P_2 =300 [kPa], которое сейчас находится в окне Equations, или заключите его в квадратные скобки комментария { }. Это уравнение не понадобится, поскольку значение P_2 будет установлено в таблице. Теперь введите значения P_2, для которых определяется T_2. Для этого примера были выбраны значения от 100 до 550. (Значения также могут быть автоматически введены с помощью команды «Изменить значения» в меню «Таблицы» или с помощью элемента управления «Изменить значения» в правом верхнем углу заголовка каждого столбца таблицы, как описано в главе 2.) Теперь параметрическая таблица должна выглядеть, как показано ниже.
Теперь выберите «Решить таблицу» в меню «Расчет». Появится диалоговое окно «Таблица решения», позволяющее выбрать прогоны, для которых будут выполняться расчеты.
Когда выбран элемент управления Обновить предполагаемые значения, как показано, решение для последнего запуска предоставит предполагаемые значения для следующего запуска. Нажмите кнопку ОК. Появится окно состояния, показывающее ход решения. Когда расчеты будут завершены, значения T_2, Vel_2 и h_2 будут введены в таблицу. Значения, рассчитанные EES, будут отображаться синим цветом, жирным шрифтом или курсивом в зависимости от настройки, сделанной на вкладке «Экран» диалогового окна «Настройки» в меню «Параметры».
Связь между такими переменными, как P_2 и T_2, теперь очевидна, но ее можно более четко увидеть на графике. Выберите «Новое окно графика» в меню «График». Появится диалоговое окно New Plot Window, показанное ниже. Выберите P_2 в качестве оси x, щелкнув P_2 в списке осей x. Нажмите на T2 в списке оси Y. Выберите пределы шкалы для P_2 и T_2 и установите количество делений шкалы, как показано. Линии сетки облегчают чтение сюжета. Нажмите на элемент управления Grid Lines для обеих осей x и y. Когда вы нажмете кнопку OK, график будет построен, и окно графика появится, как показано.
После создания существует множество способов изменить внешний вид графика, как описано в разделе «Окна графика» главы 2 и в разделе меню «График» главы 3 руководства EES.
No related posts.