Виджет Координаты—ArcGIS Web AppBuilder | Документация
Виджет Координаты отображает значения координат x,y, высоты и высоты камеры в 3D приложении. При использовании системы координат веб-сцены по умолчанию, эти значения динамически меняются при перемещении курсора по сцене. Можно настроить несколько пространственных привязок, при этом значения координат будут показаны в соответствии с выбранной привязкой.
Настройка Виджета Координаты
По умолчанию виджет Координаты отображает координаты в проекции WGS_1984_Web_Mercator_Auxiliary_Sphere (WKID 3857). Для показа координат в других проекциях или датумах добавьте пространственные привязки во время настройки.
- Наведите курсор на виджет Координаты и щелкните маленькую кнопку , чтобы отобразить или скрыть этот виджет в приложении.
- Наведите курсор на виджет и щелкните кнопку Настроить этот виджет , чтобы открыть диалоговое окно параметров настройки.
- Дополнительно, щелкните Добавить выходную систему координат, чтобы отобразить другие проекции.
- Укажите корректный WKID в поле Выходная система координат WKID, выберите отображаемые единицы и введите корректный WKID в поле Трансформация датума WKID, если датум выходной системы координат отличается от используемого по умолчанию.
- Установите высоту рельефа и взгляда в метрических или британских единицах.
- Щёлкните OK.
Заданная вами пространственная привязка будет добавлена в список. Повторите шаги с 1 по 5, чтобы добавить еще одну пространственную привязку, если необходимо.
- Кроме того, можно щелкнуть значок редактирования под пунктом Действия и изменить систему координат и единицы отображения. Щёлкните OK.
- Под таблицей выходной системы координат выберите десятичные разряды для округления координат.
- Выберите число десятичных знаков для округления высоты наблюдения.
- Уберите отметку, если вы не хотите отображать разделители тысячных долей.
- Выберите порядок отображения координат.
- Щёлкните OK.
Использование виджета Координаты
После запуска приложения будет отображена система координат, находящаяся вверху списка Имя выходной системы координат. При использовании системы координат веб-сцены по умолчанию, значения координат, высоты и высоты камеры при перемещении курсора мыши по сцене будут изменяться автоматически.
Щелкните кнопку системы координат , чтобы включить опцию щелчка на сцене для получения координат и высот. Таким образом вы можете добавить точку в сцену, выделить все значения и скопировать их.
Щелкните стрелку виджета для показа списка пространственных привязок, заданных в конфигурации. Когда вы выбираете одну из них из списка, она становится активной.
Для большинства пространственных привязок, кроме WKID 3857 и 4326, необходимо снова щелкнуть кнопку системы координат , чтобы отобразить координаты и высоту путем добавления точки на карте.
Вы также можете выделить все значения и копировать их.
Отзыв по этому разделу?
Пространственная привязка и системы координат
Пространственная привязка — это использование координат карты для присвоения пространственных местоположений векторным объектам карты. У всех элементов слоя карты есть определенное географическое положение и экстент, которые позволяют находить их местоположения на земной поверхности. Возможность точного определения местоположений географических объектов очень важна при картографировании и в ГИС.
Для описания корректного местоположения и формы пространственных объектов реального мира требуется координатная сетка. Для определения географических положений объектов используется географическая система координат. Глобальная система координат из параллелей и меридианов — одна из таких систем отсчёта. Другая — плоская или Декартова система координат.
Карты представляют местоположения на земной поверхности с помощью сеток и меток (тиков), надписанных с различными местоположениями на земной поверхности — как в измерениях широты-долготы, так и в системах координат проекции, например метрах UTM.
Географические элементы, содержащиеся в различных слоях карты, отображаются в определенном порядке (поверх друг друга) для заданного экстента карты.
Наборы данных ГИС содержат местоположения в глобальной или декартовой системе координат. Таким образом, множество слоев данных ГИС могут накладываться на земную поверхность.
Широта и долгота
Один из методов описания географических местоположений на земной поверхности использует сферические измерения широты и долготы. Измерения осуществляются в углах (градусах) от центра Земли до точки на земной поверхности. Такой тип системы привязки координат называется географической системой координат.
Долгота измеряется в градусах (восточная и западная долгота). Измерения долготы традиционно выполняются относительно начального меридиана — воображаемой линии, проходящей от Северного до Южного полюса через Гринвич (Великобритания). Угол на этом меридиане равен 0. Обычно к западу от него значения меридианов отрицательные, а к востоку — положительные.
Например, координаты Лос-Анджелеса (Калифорния) приблизительно 33 градуса, 56 минут широты и минус 118 градусов, 24 минуты долготы.
Хотя широта и долгота определяет точное местоположение на поверхности глобуса, такие данные не дают точных сведений об измерениях расстояний. Только на экваторе расстояние, соответствующее одному градусу долготы примерно равно расстоянию, соответствующему одному градусу широты. Это происходит из-за того, что экватор — это единственная параллель, чья длина соответствует длине меридиана. (Окружности, у которых тот же радиус, что и у сфероида Земли, носят название больших окружностей. Таковыми являются экватор и все меридианы).
Выше и ниже экватора, окружности, которые определяют параллели, становятся постепенно все короче и короче, пока не превратятся в точку на Северном и Южном полюсах, в которой сходятся меридианы. По мере того, как меридианы сходятся к полюсам, расстояние, соответствующее одному градусу широты уменьшается до нуля. На сфероиде Кларка 1866г.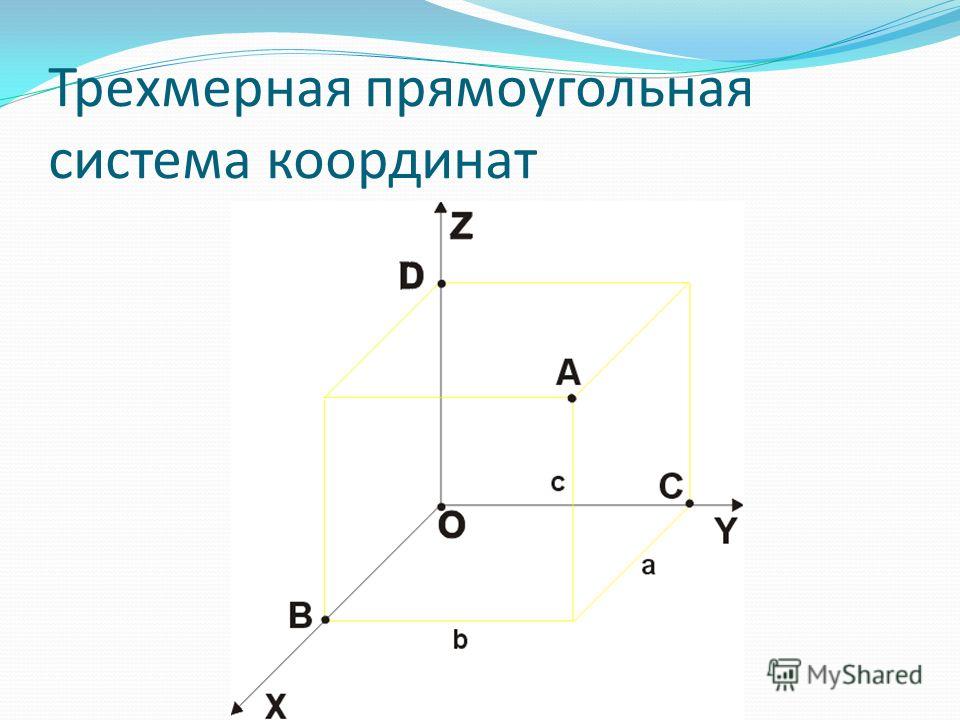
один градус широты на экваторе равен 111,321 км, в то время как на широте 60° — только 55,802 км. Так как у градусов широты и долготы нет стандартной длины, с помощью них невозможно корректно мерить длины и площади на плоских картах или компьютерных мониторах. Для многих (но не всех) функций ГИС-анализа и картографических приложений нередко требуется более постоянная плоская система координат, которую обеспечивают системы координат проекции. В качестве альтернативы, некоторые используемые пространственными операторами алгоритмы учитывают геометрическое поведение сферических (географических) систем координат.
Картографические проекции с декартовой системой координат
Системы координат проекции специально разработаны для плоских поверхностей — бумажных карт или компьютерных мониторов.
Как 2D, так и 3D декартова система координат предоставляет механизм для описания географических положений и форм пространственных объектов с помощью x- и y-значений (и, как описано далее, столбцов и строк для растров).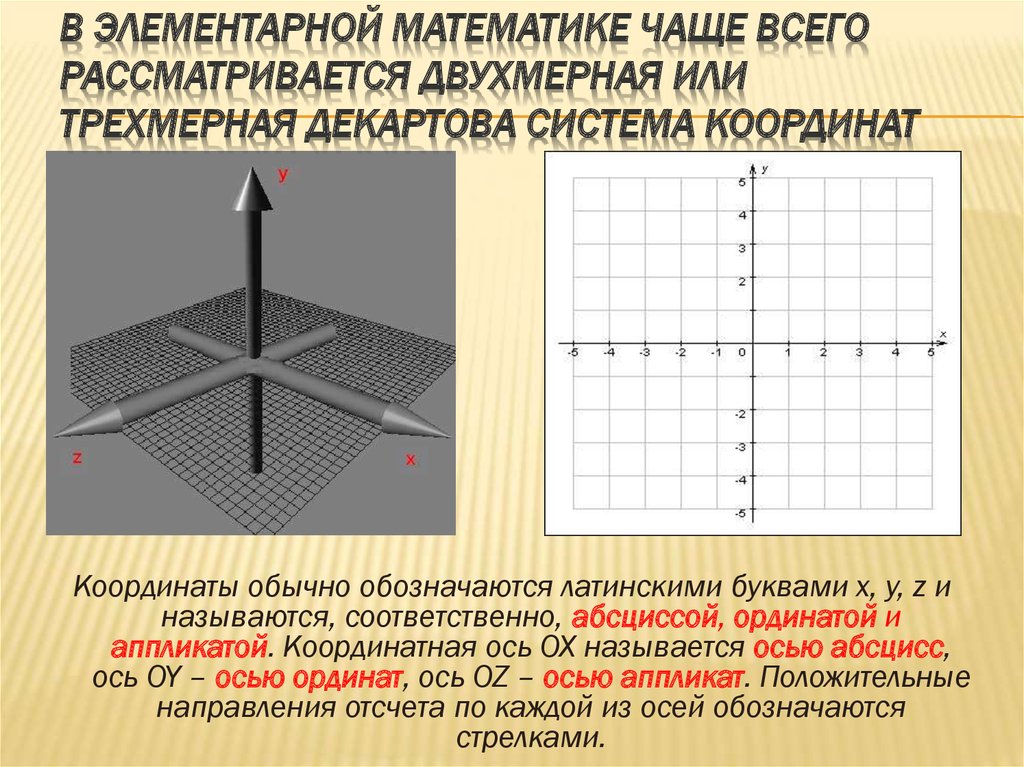
В декартовой системе координат используются две оси: одна горизонтальная (x), представляющая направление с востока на запад, и одна вертикальная (y), представляющая направление с севера на юг. Точка пересечения этих осей называется началом координат. Местоположения географических объектов задаются относительно начала отсчёта в координатах (x,y), где x описывает расстояние вдоль горизонтальной оси, а y — вдоль вертикальной. Начальная точка описывается как (0,0).
На рисунке ниже координаты (4,3) описывают точку, находящуюся в четырех единицах правее и трех единицах выше начала отсчета.
Трехмерные системы координат
Системы координат проекции используют ещё и значение z для измерения высоты выше или ниже уровня моря.
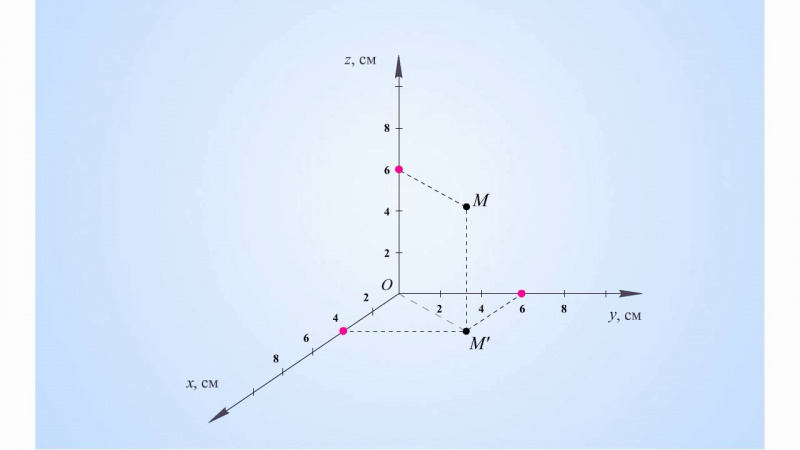
На рисунке ниже координаты (2,3,4) описывают точку, находящуюся в двух единицах по оси х, трех единицах по оси y и на 4 единицы выше начала отсчета (например, 4 м над уровнем моря).
Свойства и их искажение картографическими проекциями
Поверхность Земли имеет сферическую форму, поэтому картографам и ГИС-специалистам приходится каким-то образом изображать реальный мир в плоской, или планарной системе координат.
Чтобы глубже понять дилемму, представьте, как бы вы сделали плоским половину баскетбольного мяча. Объемную форму невозможно превратить в плоскую без искажений или разрывов. Процесс перемещения информации с объемной поверхности Земли на плоскость называется проецированием, отсюда и берется термин »картографическая проекция».
Система координат проекции определяется на плоской, двухмерной поверхности. Координаты проекции могут быть определены как двухмерные (x,y) и трехмерные (x,y,z), где измерения х,у представляют местоположение на земной поверхности, а z — высоту относительно среднего уровня моря.
В отличие от географической системы координат, система координат проекции имеет постоянную длину, углы и области в двух измерениях. Но все картографические проекции, преобразующие поверхность Земли на плоскую карту, в некоторой степени искажают расстояния, площади, формы и направления.
Пользователи обходят эти ограничения, используя проекции, применимые для их целей, географического положения и экстента.
Программное обеспечение ГИС также может трансформировать информацию между системами координат в целях поддержания целостности данных и рабочих процессов.
Многие картографические проекции были разработаны для определенных целей. Некоторые проекции не искажают формы, иные сохраняют площади (равноугольные и равноплощадные проекции).
Эти свойства — картографическая проекция вместе со сфероидом и датумом — стали важными параметрами при определении системы координат для каждого набора данных ГИС и каждой карты. При помощи подробных описаний этих свойств, записываемых для каждого набора данных ГИС, компьютеры могут перепроецировать и трансформировать географические положения элементов наборов данных «на лету» в любую подходящую систему координат. В результате стало возможно интегрировать и комбинировать информацию из разных слоёв ГИС. Это очень важная возможность ГИС. Точная информация о местоположениях является основой практически для всех операций ГИС.
Более подробно о проекциях карты
Геообработка — Вычисления с геоданными
Онлайн-калькулятор: Трехмерные системы координат
Исследование Математика Геометрия
Преобразование трехмерных координат из/в декартову, цилиндрическую и сферическую системы координат.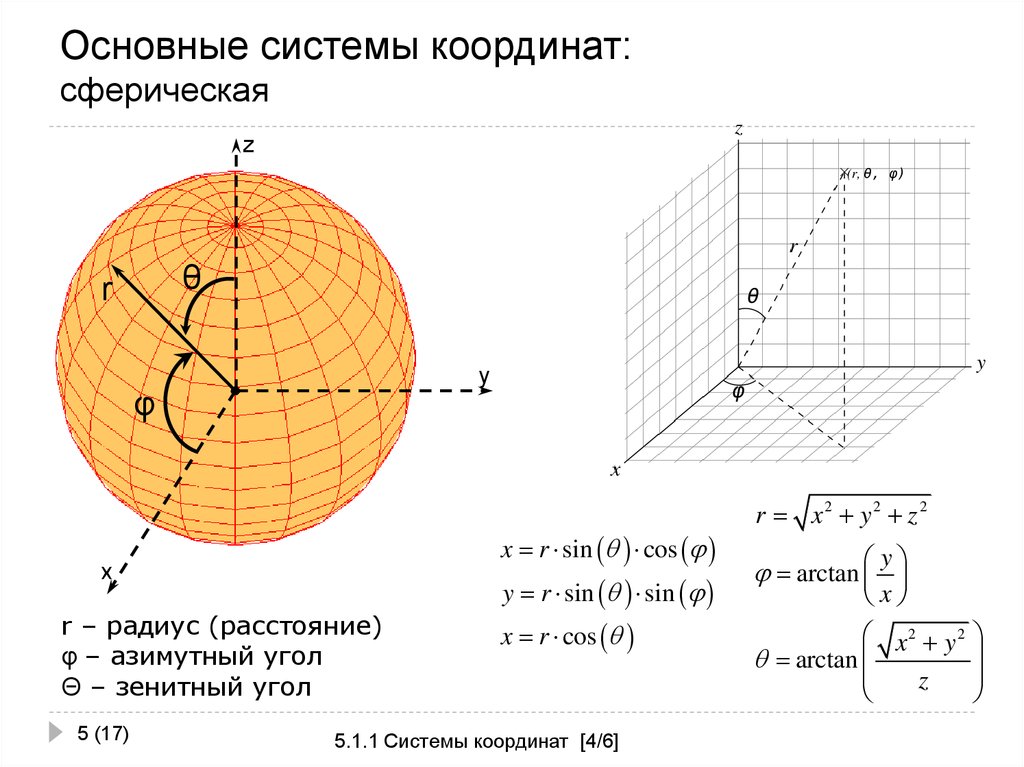
Калькулятор предназначен для преобразования координат из/в следующие трехмерные системы координат:
- Декартова
- Цилиндрический
- Сферическая
Декартова, цилиндрическая и сферическая системы координат
Декартова система координат
Точка может быть определена в декартовой системе координат тремя действительными числами: x, y, z. Каждое число соответствует минимальному расстоянию со знаком по одной из осей (x, y или z) между точкой и плоскостью, образованной оставшимися двумя осями. Координата отрицательна, если точка находится за началом системы координат.
Цилиндрическая система координат
Эта система координат определяет точку в трехмерном пространстве с радиусом r, азимутальным углом φ и высотой z. Высота z напрямую соответствует координате z в декартовой системе координат. Радиус r — положительное число, кратчайшее расстояние между точкой и осью z. Азимутальный угол φ представляет собой значение угла в диапазоне 0.
.360. Это угол между положительной полуосью x и радиусом от начала координат до перпендикуляра из точки к плоскости XY.
Сферическая система координат
Эта система определяет точку в трехмерном пространстве с 3 действительными значениями — радиусом ρ, азимутальным углом φ и полярным углом θ. Азимутальный угол φ совпадает с азимутальным углом в цилиндрической системе координат. Радиус ρ — расстояние между началом системы координат и точкой. Положительная полуось z и радиус от начала координат до точки образуют полярный угол θ.
Трехмерная пространственная декартова система координат
Точность расчета
Цифры после запятой: 2
Цилиндрические координаты
Радиус (r)
Азимут (φ), градусы
Высота (z )
Сферические координаты
Радиус (ρ)
Азимут (φ), град
Полярный угол (θ), град
Формулы преобразования декартовых координат:
Радиус в цилиндрической системе:
Радиус в сферической системе:
Азимутальный угол:
, см.
Два аргумента арктангенс
Полярный угол:
Цилиндрические координаты
Радиус (r)
Азимут (φ), градусы
Высота (z)
Точность вычислений
Цифры после десятичная точка: 2
Декартовы координаты
Сферические координаты
Радиус (ρ)
Азимут (φ), градусы
Полярный угол (θ), градусы
Формулы преобразования цилиндрических координат:
В декартовы координаты:
,
Радиус в сферической системе координат:
Полярный угол:
, см. Два аргумента арктангенс
Радиус (ρ)
Азимут ( φ), градусы
Полярный угол (θ), градусы
Точность расчета
Знаки после запятой: 2
Декартовы координаты
Цилиндрические координаты
Радиус (r)
Азимут (φ), градусы
Высота (z)
Формулы преобразования сферических координат
Декартовы координаты:
,
,
Радиус в цилиндрической системе:
URL скопирован в буфер обмена
Похожие калькуляторы
- • Декартова и полярная двумерные системы координат
- • Площадь треугольника по координатам
- • Площадь прямоугольника по координатам
- • Расстояние между двумя городами
- • Азимут и угол места Солнца
- • Раздел геометрии ( 84 калькулятора )
#координаты #геометрия 3d декартовы координаты преобразователи система координат цилиндрические координаты Геометрия Математические сферические координаты
PLANETCALC, 3d системы координат
Антон 13.
02.2021 11:39:00
3D-координаты Калькулятор Декартова↔Сферическая↔Цилиндрическая — Онлайн
Поиск инструмента
Поиск инструмента в dCode по ключевым словам:Просмотреть полный список инструментов dCode
3D Coordinates Systems
Инструмент для создания системы изменения координат в 3d-пространстве (декартовы, сферические, цилиндрические и т.д.), геометрических операций для представления элементов по разным ссылкам.
Результаты
Системы трехмерных координат — dCode
Теги: Геометрия
Поделиться
dCode и многое другое Цзин, головоломки и задачи для решения каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Изменение 3D-координат (пробел)
Из декартовых координат
Координата X $ x $Координата Y $ y $
Координата Z $ z $
От декартовых до сферических координат
От декартовых до цилиндрических координат
Из сферических координат
Расстояние $ \rho $ (rho)Полярный угол $ \theta $ (Theta)
Азимутальный угол $ \varphi $ (Phi)
От сферических до декартовых координат
От сферических до цилиндрических координат
Из цилиндрических координат
Расстояние $ r $ (r)Полярный угол $ \theta $ (Theta)
Z-координата $ z $ (высота)
От цилиндрических до декартовых координат
От цилиндрических до сферических координат
Изменение 2D координат (плоскость)
⮞ Перейти к: Система 2D координат
Ответы на вопросы (FAQ)
2}} \right) = \arccos \left( \frac{z}{\rho} \right) \\ \varphi = \arctan \left( \frac{y}{x} \right) $$Пример: Le точка в пространстве в положении $ (0,\sqrt{2},\sqrt{2}) $ из декартовых координат определяется сферическими координатами $ \rho = 1 $, $ \theta = \pi/ 4 $ и $ \varphi = \pi/2 $
Преобразование можно рассматривать как два последовательных преобразования декартовых координат в полярные, первое в плоскости $ xy $ для преобразования $ (x, y) $ в $ (R, \varphi)$ (с $R$ проекцией $\rho$ на плоскость $xy$, затем второе преобразование, но уже в плоскости $zR$ для замены $(z,R)$ на $(\rho,\ тета) $
NB: по соглашению значение $ \rho $ положительно, значение $ \theta $ включено в интервал $ ] 0, \pi [ $ и значение $ \varphi $ включено в интервал $ ] -\pi, \pi [ $
Если $\rho = 0 $, то углы можно определить любыми действительными числами интервала
Как перевести декартовы координаты в цилиндрические?
Из декартовых координат $(x, y, z)$ базовая/относительная замена на цилиндрических координат $(r,\theta,z)$ следует уравнениям: $$ r = \sqrt{x^2 + y ^2} \\ \theta = \arctan \left( \frac {y}{x} \right) \\ z = z $$
NB: по соглашению значение $ \rho $ положительно, значение $ \theta $ включено в интервал $ ] -\pi, \pi [ $ и $ \varphi $ является действительным числом
Как преобразовать сферические координаты в декартовы?
Из сферических координат $ (\rho,\theta,\varphi) $ базовая/относительная замена декартовых координат $(x,y,z)$ следует уравнениям: $$ x = \rho \sin\theta \cos\varphi \\ y = \rho \sin\theta \sin\varphi \\ z = \rho \cos\theta $$ 9* $$
Исходный код
dCode сохраняет за собой право собственности на исходный код «3D Coordinates Systems».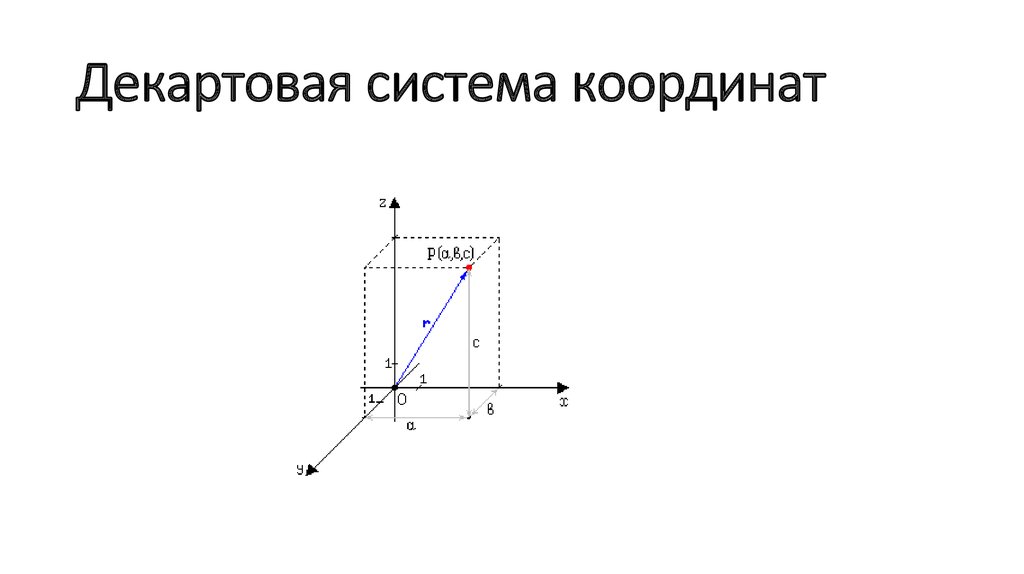
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Системы 3D-координат» или любых ее результатов разрешено, если вы цитируете dCode!
Бесплатный экспорт результатов в виде файла .csv или .