Построение графика функции онлайн | umath.ru
- Обязательно писать все знаки умножения
- Десятичные дроби нужно разделять точкой
- Список функций и констант смотрите ниже
Как пользоваться программой:
- Можно строить графики сразу нескольких функций. Для этого просто разделяйте функции точкой с запятой (;).
- Масштаб изменяется с помощью кнопок «+» и «−». Кнопка «100%» меняет масштаб на стандартный.
- Положение экрана можно менять, перетаскивая его мышью, а можно стрелками на панели слева.
- Кнопка «·» в центре джойстика переносит начало координат в центр экрана.
- Кнопка «↺» изменяет масштаб на стандартный и переносит начало координат в центр.
- В форме под графиком можно выбрать точку, которую нужно расположить в центре экрана.
Режимы
Обычный. В этом режиме можно строить графики функций, заданных уравнением
Параметрический. Этот режим предназначен для построения графиков кривых, заданных параметрически
Полярные координаты.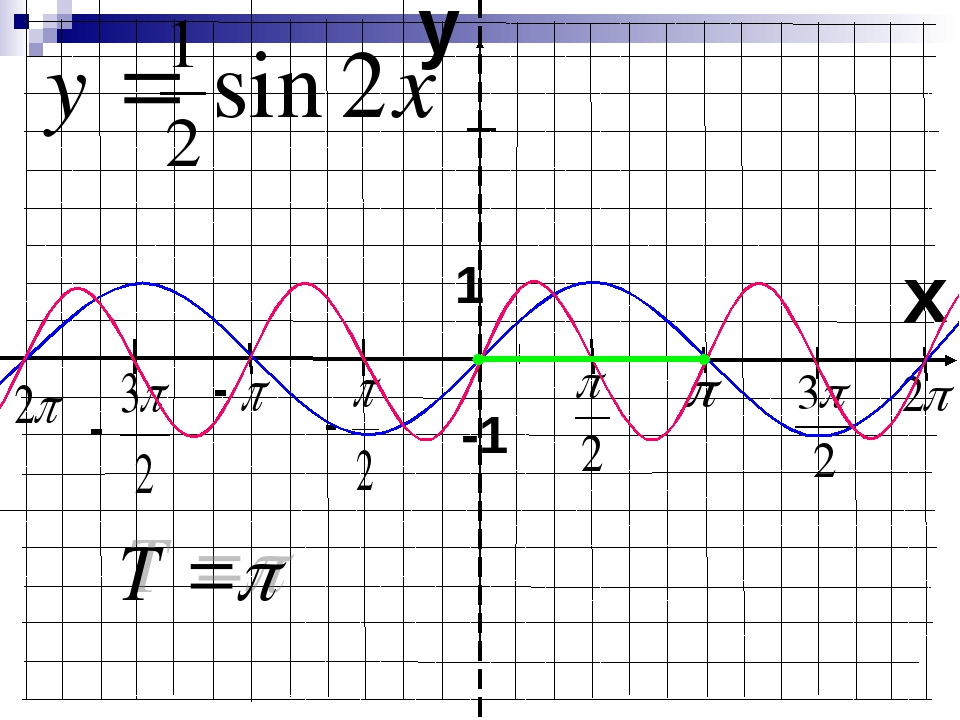 Режим позволяет построить график кривой, заданной в полярной системе
координат, то
есть уравнением где — радиальная координата, а — полярная координата.
Режим позволяет построить график кривой, заданной в полярной системе
координат, то
есть уравнением где — радиальная координата, а — полярная координата.
Список констант
| Константа | Описание |
|---|---|
pi | Число =3,14159... |
e | Число Эйлера =2,71828... |
Список функций
| Функция | Описание |
|---|---|
+ − * / | Сложение, вычитание, умножение, деление |
( ) | Группирующие скобки |
abs() или | | | Модуль числа. Выражение abs(x) эквивалентно |x|. Если функция содержит модуль под
модулем, то пользуйтесь abs(). Например, если вы хотите построить график функции |1-x+|x+5||,
то нужно вводить abs(1-x+abs(x+5)).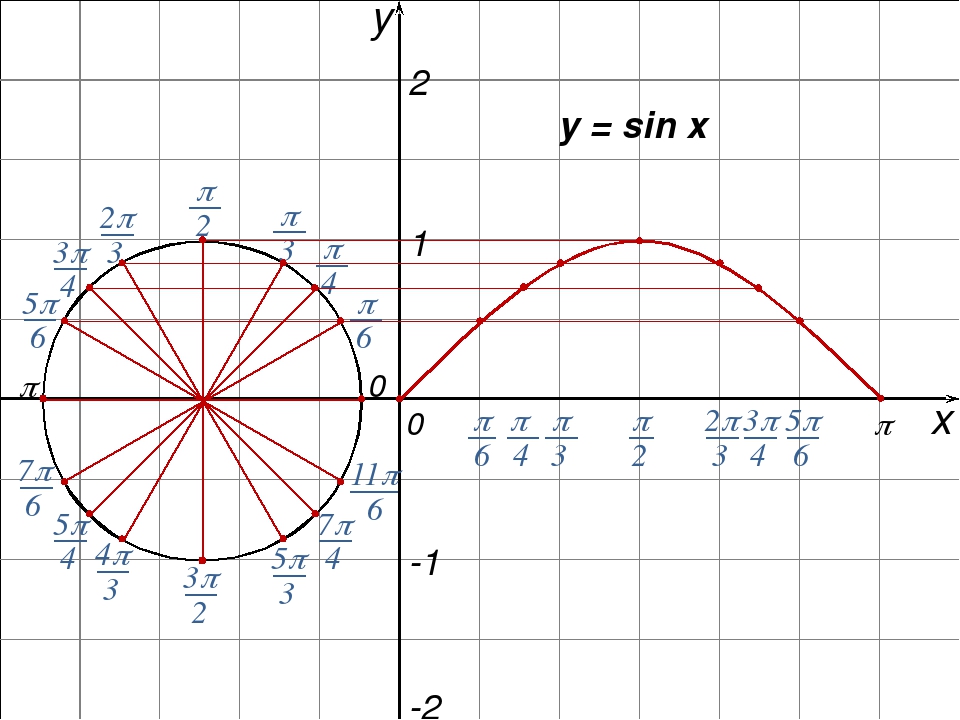 3 дают 3 дают x в третьей
степени |
sqrt() | Квадратный корень |
sin() | Синус |
cos() | Косинус |
tg() | Тангенс |
ctg() | Котангенс |
arcsin() | Арксинус |
arccos() | Арккосинус |
arctg() | Арктангенс |
arcctg() | Арккотангенс |
ln() | Натуральный логарифм числа |
lg() | Десятичный логарифм числа |
log(a, b) | Логарифм числа b по основанию a |
exp() | Степень числа e |
sh() | Гиперболический синус |
ch() | Гиперболический косинус |
th() | Гиперболический тангенс |
cth() | Гиперболический котангенс |
График функции
Графиком функции называется множество точек плоскости таких, что абсциссы и ординаты
этих точек удовлетворяют уравнению .
Программа создана для школьников и студентов и позволяет строить графики функций онлайн. Во многих браузерах (например, Google Chrome) картинку с графиком функции можно сохранить на компьютер.
Пожалуйста, все предложения и замечания по работе программы пишите в комментариях.
Кроме того мы планируем создать библиотеку функций с интересными и забавными графиками. Если вы открыли функцию с таким графиком, то обязательно напишите об этом в комментариях! Ваше открытие будет опубликовано и станет носить ваше имя ;).
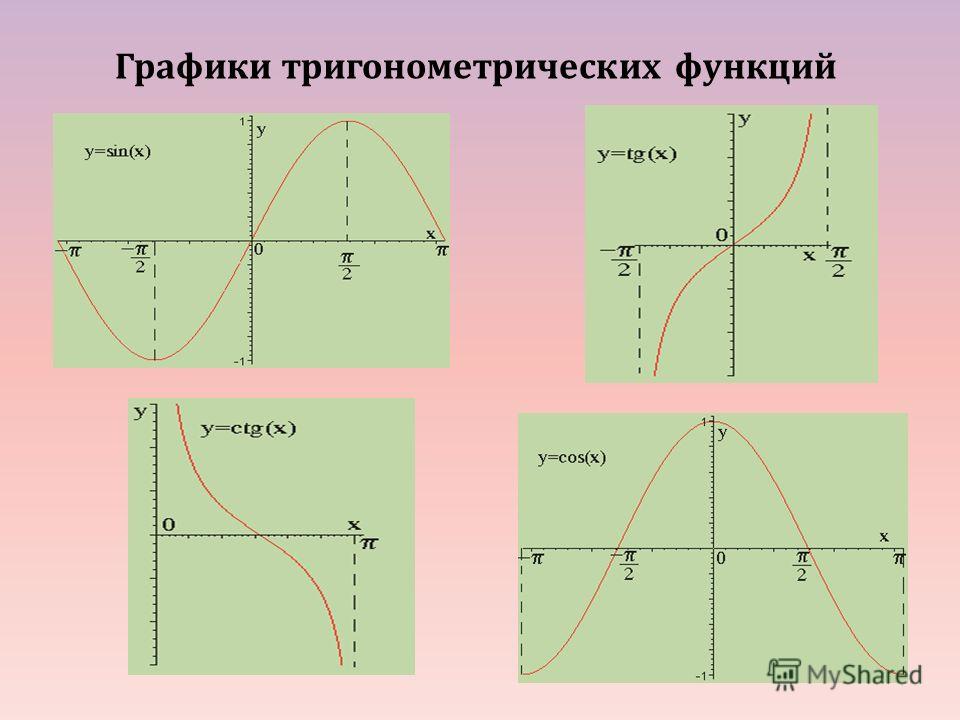
Графики тригонометрических функций
Графики синуса и косинуса
График функции изображен на рисунке 1.
Рис. 1
График функции изображен на рисунке 2.
Рис. 2
Кривая, описывающая функцию синуса, называется синусоидой, а косинуса – косинусоидой.
График функции можно получить из графика функции сдвигом последнего влево на . Аналогично, график функции можно получить из графика функции сдвигом последнего вправо на .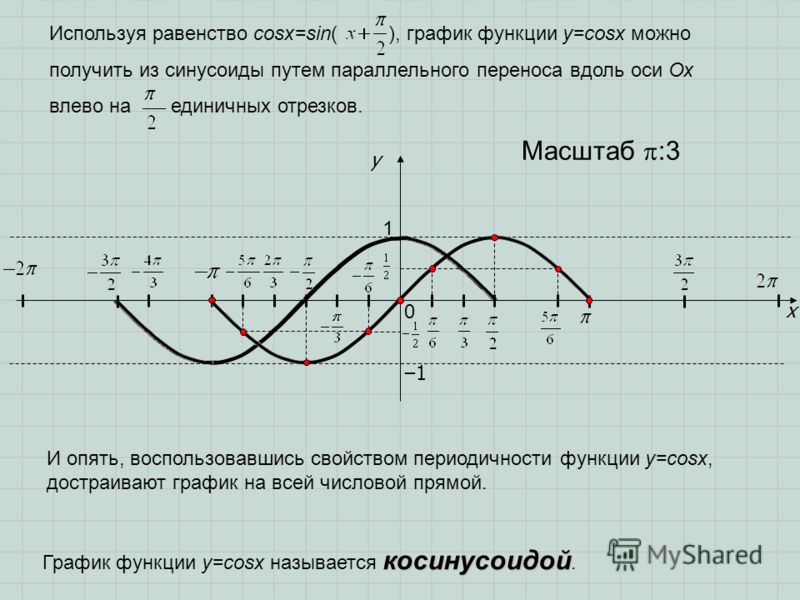
Графики тангенса и котангенса
График функции изображен на рисунке 3. Кривая, задающая функцию тангенса, называется тангенсоидой.
Рис. 3
График функции изображен на рисунке 4.
Рис. 4
Примеры решения задач
ПРИМЕР 1| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции в результате параллельного переноса вдоль оси абсцисс вправо на (рис. 5).
Рис. 5 |
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции в результате параллельного переноса вдоль оси ординат вверх на 1 (рис. 6) .
Рис. 6 |
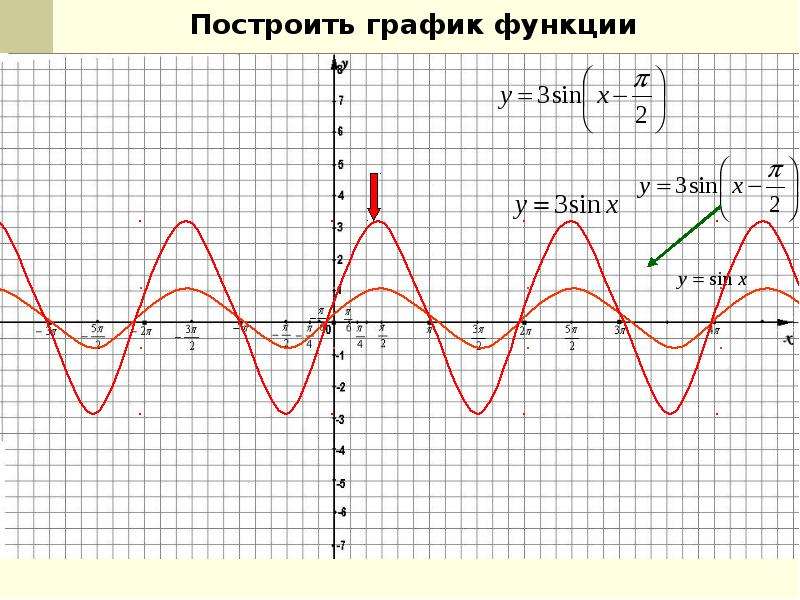
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции растяжением последнего вдоль оси ординат в три раза (увеличением расстояния от каждой точки графика до оси абсцисс в три раза) (рис. 7). 7).
Рис. 7 |
| Задание | Построить график функции |
| Решение | Заданный график построим с помощью элементарных преобразований графика функции . Осуществив параллельный перенос графика функции вдоль оси абсцисс влево на , получим (рис. 8)
Рис. 8 Затем, отразив график функции симметрично относительно оси абсцисс, получим искомый график (рис. 9). Рис. 9 |
Простейшие тригонометрические уравнения
Тригонометрические функции числового аргумента
Свойства тригонометрических функций
Упрощение тригонометрических выражений
Косинус суммы
Графики тригонометрических функций — онлайн справочник для студентов
Графики синуса и косинуса
График функции \(\ y=\sin x \)изображен на рисунке 1.
Рис. 1
1
График функции \(\ y=\cos x \) изображен на рисунке 2.
Рис. 2
Кривая, описывающая функцию синуса, называется синусоидой, а косинуса – косинусоидой.
График функции \(\ y=\cos x \) можно получить из графика функции \(\ y=\sin x \) сдвигом последнего влево на \(\ \frac{\pi}{2} \) . Аналогично, график функции \(\ y=\sin x \) можно получить из графика функции \(\ y=\cos x \) сдвигом последнего вправо на \(\ \frac{\pi}{2} \)
Графики тангенса и котангенса
График функции \(\ y=\operatorname{tg} x \) изображен на рисунке 3. Кривая, задающая функцию тангенса, называется тангенсоидой.
Рис. 3
График функции \(\ y=\operatorname{ctg} x \) изображен на рисунке 4.
Рис. 4
Примеры решения задач
ПРИМЕР 1
Построить график функции \(\ y=\operatorname{tg}\left(x-\frac{\pi}{4}\right) \)
Искомый график получается из графика функции \(\
y=\operatorname{tg} x
\) в результате параллельного переноса вдоль оси абсцисс вправо на \(\
\frac{\pi}{4}
\) (рис. 5).
5).
Рис. 5
ПРИМЕР 2
Построить график функции \(\ y=\sin x+1 \)
Искомый график получается из графика функции\(\ y=\sin x \) в результате параллельного переноса вдоль оси ординат вверх на 1 (рис. 6) .
Рис. 6
ПРИМЕР 3
Построить график функции \(\ y=3 \operatorname{ctg} x \)
Искомый график получается из графика функции \(\ y=\operatorname{ctg} x \) растяжением последнего вдоль оси ординат в три раза (увеличением расстояния от каждой точки графика \(\ y=\operatorname{ctg} x \) до оси абсцисс в три раза) (рис. 7).
Рис. 7
ПРИМЕР 4
Построить график функции \(\ y=-\cos \left(x+\frac{\pi}{3}\right) \)
Заданный график построим с помощью элементарных преобразований графика функции \(\
y=\cos x
\) . Осуществив параллельный перенос графика функции \(\
y=\cos x
\), вдоль оси абсцисс влево на \(\
\frac{\pi}{3}
\) , получим \(\
y=\cos \left(x+\frac{\pi}{3}\right)
\) (рис.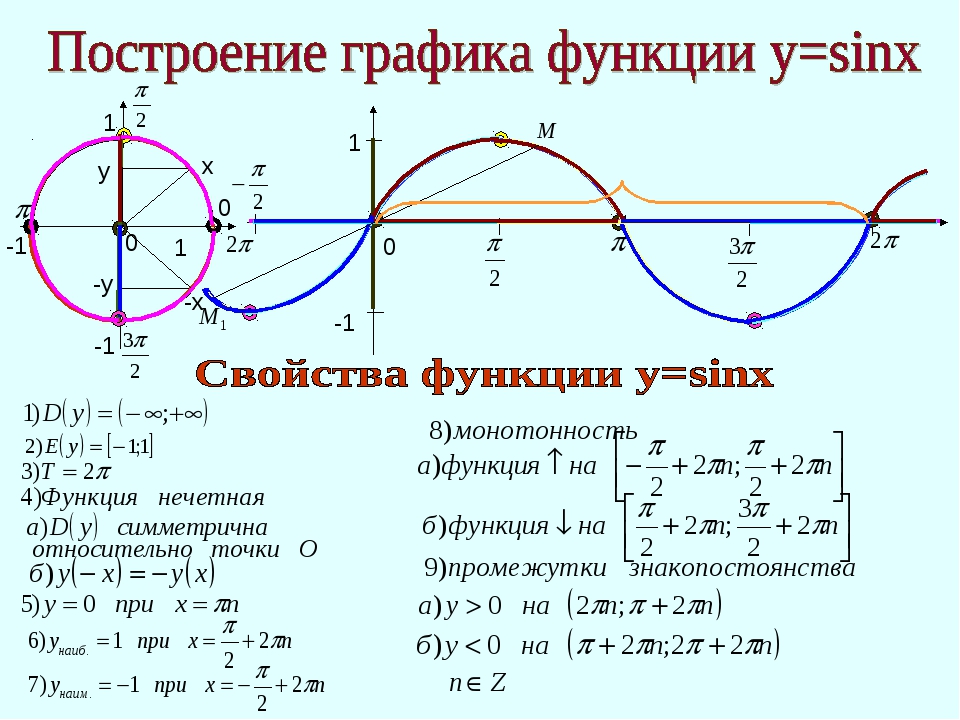 2».
2».
Если вам нужно построить график нескольких функций одновременно, то нажмите на синюю кнопку «Добавить еще». После этого откроется еще одно поле, в которое надо будет вписать вторую функцию. Ее график также будет построен автоматически.
Цвет линий графика вы можете настроить с помощью нажатия на квадратик, расположенный справа от поля ввода функции. Остальные настройки находятся прямо над областью графика. С их помощью вы можете установить цвет фона, наличие и цвет сетки, наличие и цвет осей, наличие рисок, а также наличие и цвет нумерации отрезков графика. Если необходимо, вы можете масштабировать график функции с помощью колесика мыши или специальных иконок в правом нижнем углу области рисунка.
После построения графика и внесения необходимых изменений в настройки, вы можете скачать график с помощью большой зеленой кнопки «Скачать» в самом низу. Вам будет предложено сохранить график функции в виде картинки формата PNG.
Зачем нужно строить график функции?
На этой странице вы можете построить интерактивный график функции онлайн.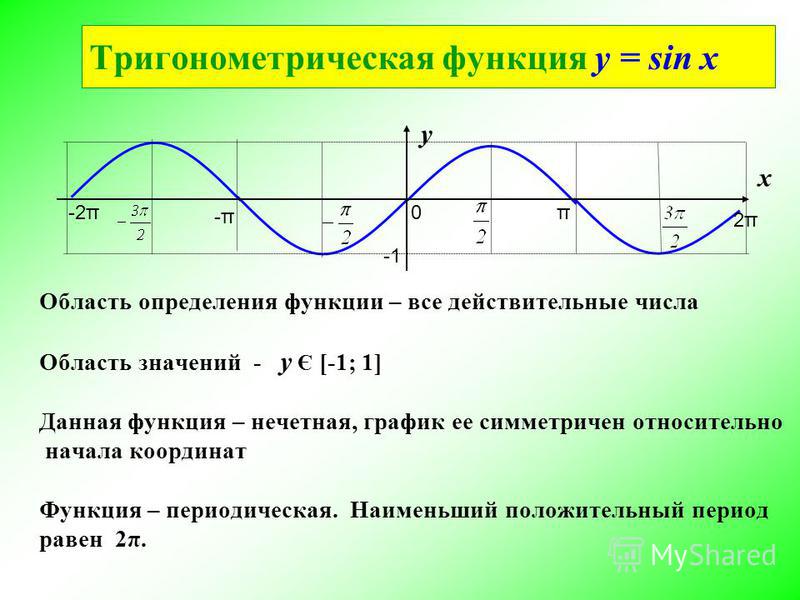 Построение графика функции позволяет увидеть геометрический образ той или иной математической функции. Для того чтобы вам было удобнее строить такой график, мы создали специальное онлайн приложение. Оно абсолютно бесплатно, не требует регистрации и доступно для использования прямо в браузере без каких-либо дополнительных настроек и манипуляций. Строить графики для разнообразных функций чаще всего требуется школьникам средних и старших классов, изучающим алгебру и геометрию, а также студентам первых и вторых курсов в рамках прохождения курсов высшей математики. Как правило, данный процесс занимает много времени и требует кучу канцелярских принадлежностей, чтобы начертить оси графика на бумаге, проставить точки координат, объединить их ровной линией и т.д. С помощью данного онлайн сервиса вы сможете рассчитать и создать графическое изображение функции
Построение графика функции позволяет увидеть геометрический образ той или иной математической функции. Для того чтобы вам было удобнее строить такой график, мы создали специальное онлайн приложение. Оно абсолютно бесплатно, не требует регистрации и доступно для использования прямо в браузере без каких-либо дополнительных настроек и манипуляций. Строить графики для разнообразных функций чаще всего требуется школьникам средних и старших классов, изучающим алгебру и геометрию, а также студентам первых и вторых курсов в рамках прохождения курсов высшей математики. Как правило, данный процесс занимает много времени и требует кучу канцелярских принадлежностей, чтобы начертить оси графика на бумаге, проставить точки координат, объединить их ровной линией и т.д. С помощью данного онлайн сервиса вы сможете рассчитать и создать графическое изображение функции
Как работает графический калькулятор для графиков функций?
Онлайн сервис работает очень просто. ». Это обусловлено отсутствием на клавиатуре компьютера возможности прописать степень в привычном формате. Далее приведена таблица с полным списком поддерживаемых функций.
». Это обусловлено отсутствием на клавиатуре компьютера возможности прописать степень в привычном формате. Далее приведена таблица с полным списком поддерживаемых функций.
Приложением поддерживаются следующие функции:
|
Тригонометрические функции |
|||||||||||
|
Синус |
Косинус |
Тангенс |
Секанс |
Косеканс |
Котангенс |
Арксинус |
Арккосинус |
Арктангенс |
Арксеканс |
Арккосеканс |
Арккотангенс |
|
sin(x) |
cos(x) |
tan(x) |
sec(x) |
csc(x) |
cot(x) |
asin(x) |
acos(x) |
atan(x) |
asec(x) |
acsc(x) |
acot(x) |
|
Гиперболические функции |
|||||||||||
|
sinh(x) |
cosh(x) |
tanh(x) |
sech(x) |
csch(x) |
coth(x) |
asinh(x) |
acosh(x) |
atanh(x) |
asech(x) |
acsch(x) |
acoth(x) |
|
Прочее |
|||||||||||
|
Натуральный логарифм |
Логарифм |
Квадратный корень |
Модуль |
Округление в меньшую сторону |
Округление в большую сторону |
||||||
|
ln(x) |
log(x) |
sqrt(x) |
abs(x) |
floor(x) |
ceil(x) |
||||||
|
Минимум |
Максимум |
||||||||||
|
min(выражение1,выражение2,. |
max(выражение1,выражение2,…) |
||||||||||
Онлайн вычисление обратных тригонометрических функций
Калькулятор онлайн расчитывает обратные тригонометрические функции дугу (число) по заданному значению ее тригонометрической функции: арксинус (arcsin) возвращает угол по значению его синуса; арккосинус (arccos) возвращает угол по значению его косинуса; арктангенс (arctg) возвращает угол по значению его тангенса.
В разделе I. Для справки приведены графики обратных тригонометрических функций.
Помощь на развитие проекта premierdevelopment.ru
Send mail и мы будем знать, что движемся в правильном направлении.Спасибо, что не прошели мимо!
I. Для справки:
Арксинус числа a, обозначается arcsin(a) — значение угла x в интервале [−π/2, π/2], при котором sin(x) = a.
Обратная функция y = arcsin (x) определена при x ∈ [−1, 1], область значений арксинуса равна y ∈ [−π/2, π/2].
График функции арксинуса
Арккосинус числа a, обозначается arccos(a) — значение угла x в интервале [0, π], при котором cos(x) = a.
Обратная функция y = arccos (x) определена при x ∈ [−1, 1], область значений арккосинуса равна y ∈ [0, π].
График функции арккосинуса
Арктангенс числа a, обозначается arctan(a) — значение угла x в интервале [−π/2, π/2], при котором tan(x) = a.
Обратная функция y = arctan (x) определена при x ∈ R, область ее значений равна y ∈ [−π/2, π/2].
График функции арктангенса
II. Примечание:
- Если обратная тригонометрическая функция не определена в указанной точке, то ее значение не появится в результирующей таблице. Функции arcsin и arccos определены только на отрезке [-1,1].
- Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолачанию — округление до сотых).

- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
Графики тригонометрических функций — презентация онлайн
1. Графики тригонометрических функций
Функция у = sin x, еесвойства
Преобразование
графиков
тригонометрических
функций путем
параллельного
переноса
Преобразование
графиков
тригонометрических
функций путем
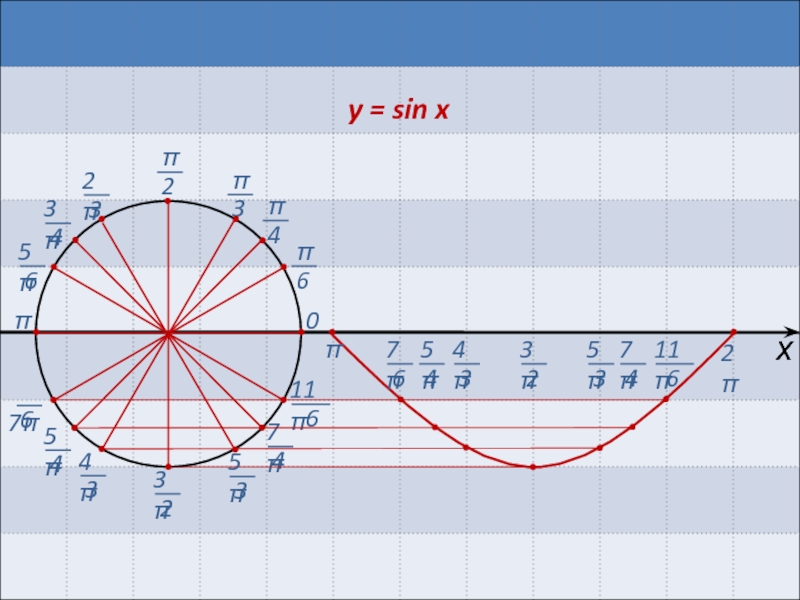
Графиком функции у = sin x является синусоида
Свойства функции:
1. D(y) =R
2. Периодическая (Т=2p)
3. Нечетная (sin(-x)=-sin x)
4. Нули функции:
у=0, sin x=0 при х = pn, n Z
тригонометрические
функции
y=sin x
2
Свойства функции у = sin x
5. Промежутки знакопостоянства:
y = sin x
У>0 при х (0+2pn; p+2pn), n Z
У
тригонометрические
функции
3
4. Свойства функции у=sin x
6. Промежутки монотонности:функция возрастает на промежутках
вида: [-p/2+2pn; p/2+2pn], n Z
тригонометрические
функции
y = sin x
4
5.
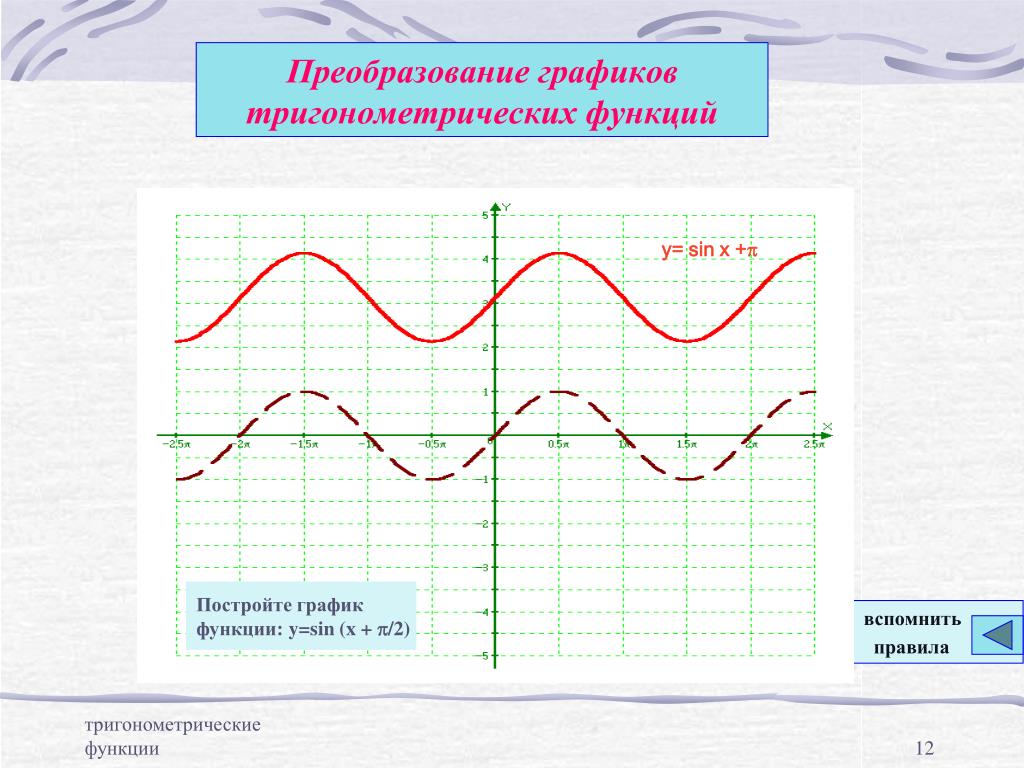 Свойства функции у=sin x Промежутки монотонности:
Свойства функции у=sin x Промежутки монотонности:функция убывает на промежутках
вида: [p/2+2pn; 3p/2+2pn], n Z
тригонометрические
функции
y=sin x
5
6. Свойства функции у =sin x
7. Точки экстремума:Хмах= p/2 +2pn, n Z
Хмin= -p/2 +2pn, n Z
тригонометрические
функции
y=sin x
6
7. Свойства функции у =sin x
8. Область значений:Е(у) = [-1;1]
y = sin x
тригонометрические
функции
7
8. Преобразование графиков тригонометрических функций
График функции у = f (x+в) получается из графика функцииу = f(x) параллельным переносом на (-в) единиц вдоль оси
абсцисс
График функции у = f (x)+а получается из графика функции
у = f(x) параллельным переносом на (а) единиц вдоль оси
ординат
тригонометрические
функции
8
9. Преобразование графиков тригонометрических функций
Постройте графикФункции у =sin(x+p/4)
тригонометрические
функции
вспомнить
правила
9
10.
 Преобразование графиков тригонометрических функций Постройте график
Преобразование графиков тригонометрических функций Постройте графикфункции: y=sin (x — p/6)
y =sin (x+ p/4)
тригонометрические
функции
10
11. Преобразование графиков тригонометрических функций
Постройте графикфункции:
y = sin x + p
y =sin (x — p/6)
тригонометрические
функции
11
12. Преобразование графиков тригонометрических функций
y= sin x +pПостройте график
функции: y=sin (x + p/2)
тригонометрические
функции
вспомнить
правила
12
Графиком функции у = cos x является косинусоида
sin(x+p/2)=cos x
Перечислите свойства
функции у = cos x
тригонометрические
функции
13
14. Преобразование графиков тригонометрических функций путем сжатия и растяжения
График функции у =k f (x) получается из графика функции у= f(x) путем его растяжения в k раз (при k>1) вдоль оси
ординат
График функции у = k f (x) получается из графика функции
у = f(x) путем его сжатия в k раз (при 0
ординат
тригонометрические
функции
14
15.
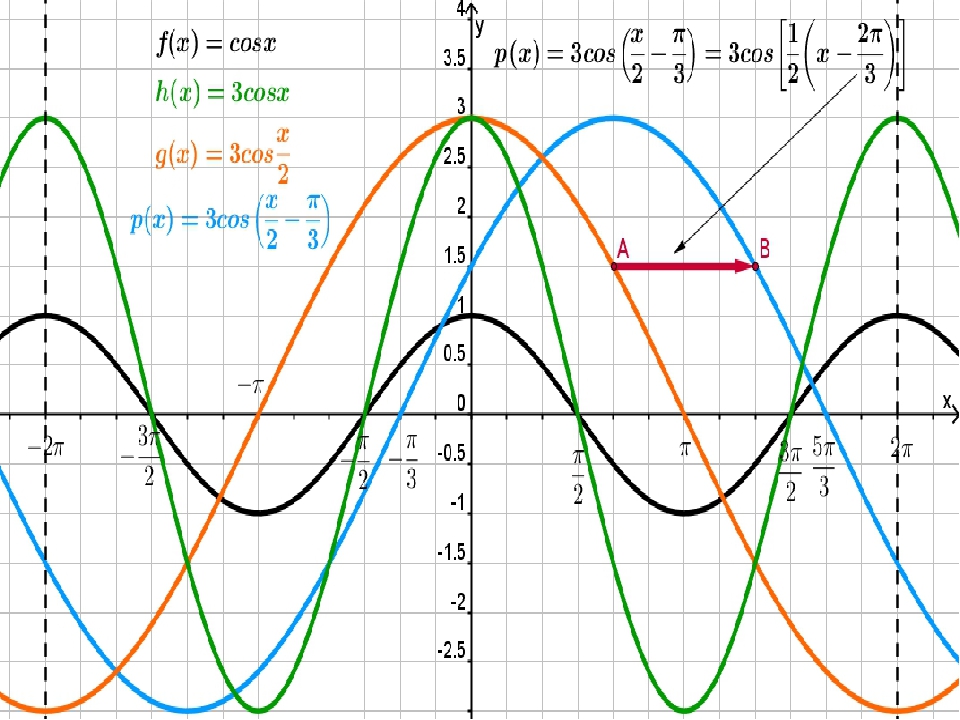 Преобразование графиков тригонометрических функций путем сжатия и растяжения y=4sinx
Преобразование графиков тригонометрических функций путем сжатия и растяжения y=4sinxy=2sinx
Y=0.5sinx
вспомнить
правила
тригонометрические
функции
15
16. Преобразование графиков тригонометрических функций путем сжатия и растяжения
График функции у = f (kx) получается из графика функции у= f(x) путем его сжатия в k раз (при k>1) вдоль оси абсцисс
График функции у = f (kx) получается из графика функции
у = f(x) путем его растяжения в k раз (при 0
абсцисс
тригонометрические
функции
16
17. Преобразование графиков тригонометрических функций путем сжатия и растяжения
y = cos2xy = cos 0.5x
тригонометрические
функции
вспомнить
правила
17
18. Преобразование графиков тригонометрических функций путем сжатия и растяжения
Графики функций у = -f (kx) и у=-k f(x) получаются изграфиков функций у = f(kx) и y= k f(x) соответственно
путем их зеркального отображения относительно оси абсцисс
синус – функция нечетная, поэтому sin(-kx) = — sin (kx)
косинус –функция четная, значит cos(-kx) = cos(kx)
тригонометрические
функции
18
19.
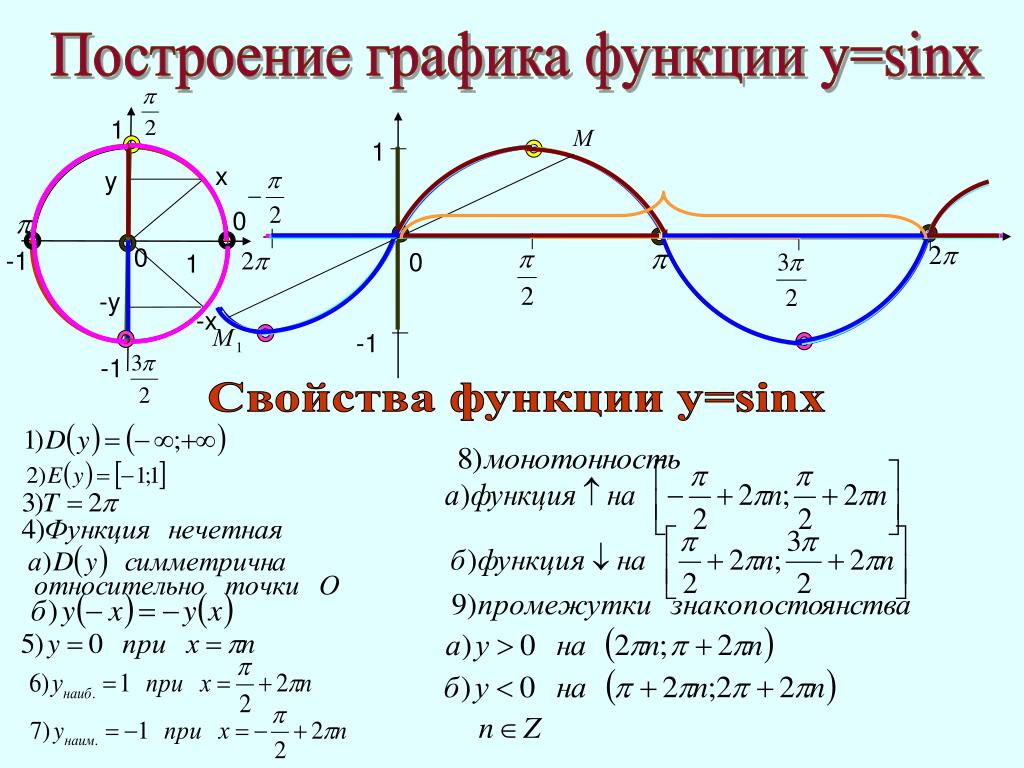 Преобразование графиков тригонометрических функций путем сжатия и растяжения y = -3sinx
Преобразование графиков тригонометрических функций путем сжатия и растяжения y = -3sinxy = 3sinx
тригонометрические
функции
вспомнить
правила
19
20. Преобразование графиков тригонометрических функций путем сжатия и растяжения
y=2cosxy=-2cosx
вспомнить
правила
тригонометрические
функции
20
21. Преобразование графиков тригонометрических функций путем сжатия и растяжения
График функции у = f (kx+b) получается из графика функцииу = f(x) путем его параллельного переноса на (-в/k) единиц
вдоль оси абсцисс и путем сжатия в k раз (при k>1) или
растяжения в k раз ( при 0
f ( kx+b) = f ( k( x+b/k))
тригонометрические
функции
21
22. Преобразование графиков тригонометрических функций путем сжатия и растяжения
y= cos(2x+p/3)y= cos(2(x+p/6))
тригонометрические
функции
y= cos(2x+p/3)
y= cos(2(x+p/6))
y=cos(x+p/6)
y=cos2x
Y= cos(2x+p/3)
Y= cos(2x+p/3)
вспомнить
правила
22
23.
 Для любознательных… Посмотрите как выглядят графики некоторых других триг. функций:
Для любознательных… Посмотрите как выглядят графики некоторых других триг. функций:y = 1 / cos x или y=sec x
(читается секонс)
тригонометрические
функции
y = cosec x или y= 1/ sin x
читается косеконс
23
Desmos – онлайн графический калькулятор / Хабр
Случалось ли вам, что нужно быстро нарисовать график функции, а под рукой нет любимой десктопной программы? Меня не раз спасал бесплатный онлайн графический калькулятор от компании Desmos. Мультиязычный интерфейс, в т.ч. с поддержкой русского языка.
Desmos — это онлайн-сервис, который позволяет создавать графики по формуле функции. Сама функция вписывается в левый столбец, а график автоматически строится в правой части. Сервис будет полезен тем, кому необходимо быстро и просто построить график функции, для кого построение графиков функций вызывает сложности или тем, кому с наименьшими затратами необходимо проверить правильность построения графика.
Кроме того, что Desmos Calculator может выполнять все функции обычных графических калькуляторов, он также имеет несколько дополнительных возможностей, которых нет у обычных графических калькуляторов.
Что можно делать в DC:
- рисовать функциями;
- создавать анимированные картинки с помощью привязки объектов к функциям с параметрами;
- создавать динамическую наглядность;
- быстро создавать скриншоты с формулами и функциями.
Desmos Calculator может строить следующие графики:
- Постоянная функция
- Зависимость x от y
- Неравенства
- Графики в полярной системе координат
- Кусочно-заданные функции
- Точка
- Группа точек
- Подвижная точка
- Функции с параметром
- Сложные функции
При построении графиков можно использовать следующие функции:
- Степенные, показательные и логарифмические функции
- Тригонометрические функции
- Обратные тригонометрические функции
- Гиперболические функции
- Статистические функции и функции вероятностей
- Другие функции
В библиотеке готовых приложений можно найти немало динамических апплетов для функций разного типа (от линейной до тригонометрической) со встроенными «ползунками».
Авторизация в сервисе позволяет сохранять созданные апплеты и делиться ими в виде ссылки, встроенного кода или картинки.
Подробную информацию по построению графиков функций вы найдете в источниках, опубликованных в подвале статьи.
Руководство по быстрой публикации графика функции, созданного в Desmos:- Перейти по ссылке https://www.desmos.com/calculator
- Зарегистрируйтесь или войдите в свой аккаунт (правый верхний угол)
- Постройте график нужной функции
- Сохраните график
- Опубликуйте ссылку на свой график или сохраните в виде картинки
Источники:
- Desmos. Руководство пользователя (рус., PDF)
- Desmos. Обучающие материалы (англ.)
- Desmos. Канал с обучающими роликами на YouTube (англ.)
- DESMOS – замечательный инструмент для учителей математики (рус.)
- Применение Desmos на уроках математики в школе (рус.
 )
)
Graphical Function Explorer Grapher (GFE)
Graphical Function Explorer Grapher (GFE) — открытый справочник по математикеИнструкция по эксплуатации
GFE — это бесплатный онлайн-инструмент для построения графиков функций, который позволяет строить до трех функций на одном и том же наборе осей. В функциях вы можете ссылаться до четырех независимых переменных, которые управляются ползунками. Это позволяет вам легко увидеть эффект изменений, поскольку графики меняются в реальном времени при перетаскивании ползунков.
Введите формулу в одно из трех полей ввода ( f (x), g (x) или h (x) ), затем нажмите GRAPH или клавиатуру Клавиша ввода. Например:
Нажмите Clear, затем в верхнем функциональном поле (f (x)) введите «cos (x)», затем нажмите GRAPH или клавишу Enter на клавиатуре. Функция будет отображена в окне выше.
Правила синтаксиса такие же, как и для вводимых выражений для
Математический / научный калькулятор.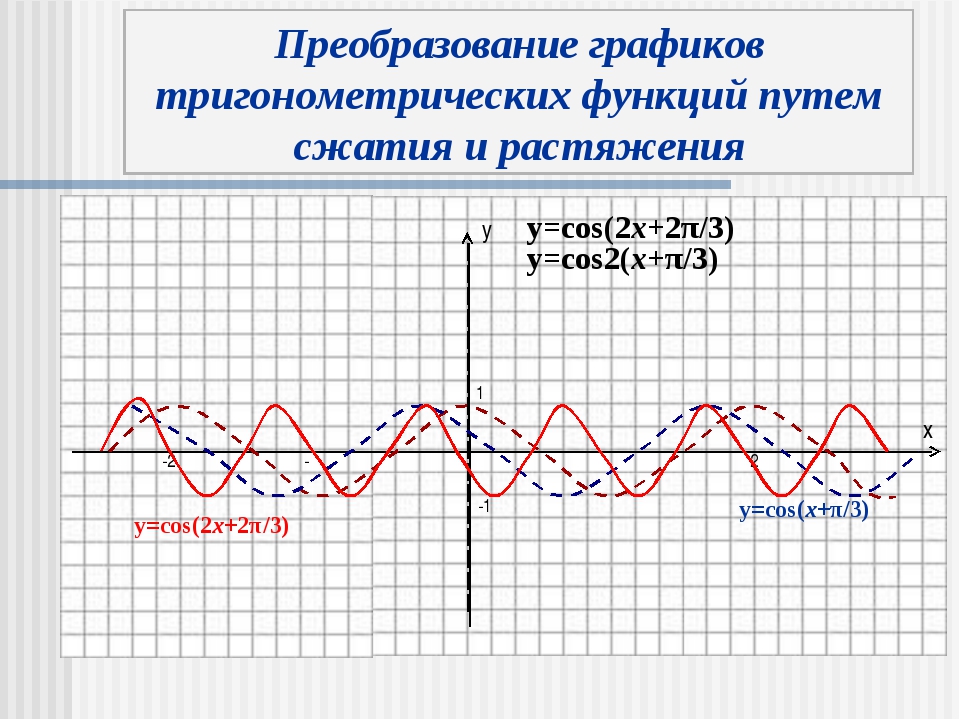
Встроенные функции
GFE имеет следующие встроенные функции.Имена функций не чувствительны к регистру. Пример: sin (x) совпадает с Sin (x). Все тригонометрические функции работают в радианах.
| Функция | Пример | Описание |
| Синус | грех (х) | Синусоидальная функция тригонометрии, x в радианах. |
| Косинус | cos (x) | Функция косинуса тригонометрии, x в радианах. |
| Касательная | желто-коричневый (x) | Функция тангенса тригонометрии, x в радианах. |
| Секант | сек (x) | Секущая функция тригонометрии, x в радианах. |
| Косеканс | csc (x) | Тригонометрическая функция косеканса, x в радианах. |
| Котангенс | детская кроватка (x) | Функция котангенса тригонометрии, x в радианах. |
| Синус дуги | asin (x) | Угол в радианах, синус которого равен x. |
| Дуговой косинус | acos (x) | Угол в радианах, косинус которого равен x. |
| Касательная дуга | атан (х) | Угол в радианах, тангенс которого равен x. |
| Квадратный корень | кв.м (x) | Квадратный корень из x. |
| Логарифм | журнал (x) | Лагерь базы 10 х. Степень, в которую вы должны поднять 10, чтобы получить x. |
| Натуральное бревно | лин (х) | База журнала е x.Степень, в которую вы должны возвести е, чтобы получить x. |
| Опыт | эксп. (X) | e (приблизительно 2,718) в степени x. |
| Мин. | мин (а, б) | Возвращает a или b, в зависимости от того, что меньше. |
| Макс | макс (а, б) | Возвращает a или b, в зависимости от того, что больше. |
| Абс | абс (х) | Возвращает абсолютное значение x (всегда положительное или нулевое) |
| Pow | pow (x, y) | Возвращает x в степени y.pow (2,3) = 8 |
| Круглый | круглый (х) | Возвращает x, округленное до ближайшего целого числа | .
| этаж | этаж (х) | Возвращает максимальное целое число, меньшее или равное x | .
| потолок | ceil (x) | Возвращает наименьшее целое число, большее или равное x | .
Константы
Вы можете ссылаться на две константы. Они не чувствительны к регистру.2.1Научная запись
Научная нотация (например, 1e + 3 для 1000) не поддерживается.Автоматическое умножение
Если перед функцией (например, sin ()) стоит число, GFE предполагает, что вы хотите их умножить. Например 3cos (2.1) будет автоматически обрабатываться так, как если бы вы ввели 3 * cos (2.1): трижды косинус 2.1. Это не сработает, если функции предшествует имя переменной.
Примечание: Эта функция может ввести вас в заблуждение. Например, если вы введете 1 / 2sin (x), GFE вставит умножение между 2 и sin.Поскольку скобок нет, он выполняется слева направо, поэтому он видит в нем половину sin (x). Возможно, вы имели в виду, что он больше 2sin (x).
Автоматическая балансировка скобок
Когда вы нажимаете ГРАФИК или ввод, он автоматически добавляет достаточное количество закрывающих скобок, чтобы сбалансировать их.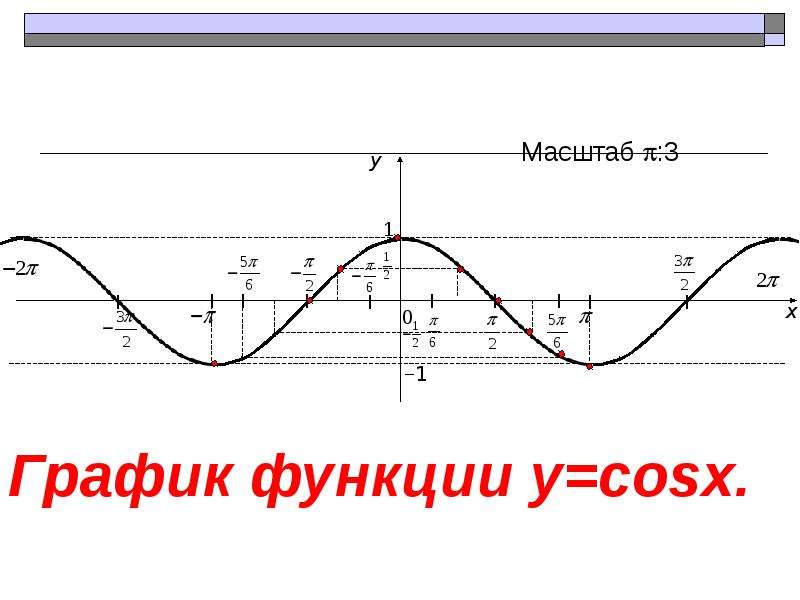 Например, если вы введете
2+ (sin (x
он добавит две дополнительные закрывающие круглые скобки, чтобы они уравновесили и оценили его как 2+ (sin (x)) Примечание: Это не всегда может дать желаемый результат.Лучше всегда самостоятельно вводить правильное выражение.
Например, если вы введете
2+ (sin (x
он добавит две дополнительные закрывающие круглые скобки, чтобы они уравновесили и оценили его как 2+ (sin (x)) Примечание: Это не всегда может дать желаемый результат.Лучше всегда самостоятельно вводить правильное выражение.Графики неравенств
GFE можно использовать для построения неравенств, изменив оператор отношения в раскрывающемся меню слева от функции. Есть пять возможных операторов:
| = | равно | По умолчанию. Функция будет отображаться как обычно в виде линии. |
| Менее или равно | Область графика, где y меньше значения функции, заштрихована. | |
| Менее | То же, что и выше, но линия пунктирная. | |
| > = | Больше или равно | Область графика, где y больше значения функции, заштрихована. |
| > | Больше | То же, что и выше, но линия пунктирная.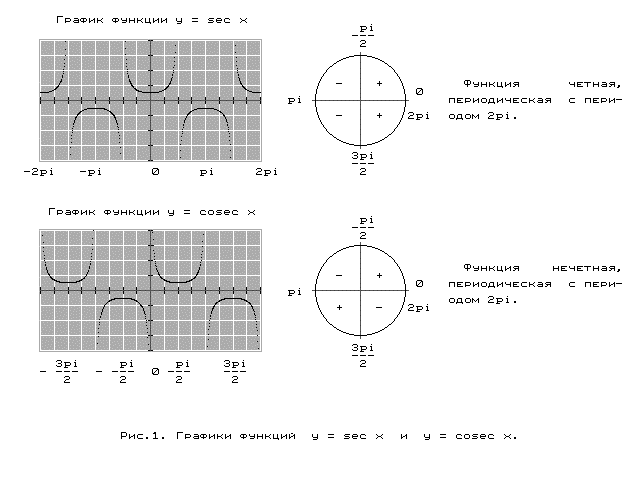 |
Цвет заливки
При нанесении неравенств можно использовать флажок «монохромное затенение».Если этот флажок установлен, все заштрихованные области для всех трех функций будут одинакового светло-серого цвета. Это позволяет вам легче увидеть, где перекрываются сложные функции, поскольку чем больше перекрытие, тем темнее затенение. Если этот флажок не установлен, каждая функция будет выделена другим цветом.
Использование курсора
Если вы нажмете «показать курсор», появится тонкая вертикальная линия. Если вы перетащите эту линию мышью, он показывает значения каждой функции там, где курсор пересекает эту функцию.Вы можете ввести значение x для курсора вручную в текстовое поле в верхнем левом углу. После ввода значения нажмите «График» или клавишу ввода. Если вы введете значение, которое находится за пределами графика, курсор не будет отображаться, но значения функций для этого значения x будут отображаться правильно.
Изменение пределов оси
На каждом конце оси x и y находится поле, содержащее конечные значения. Чтобы изменить их, просто отредактируйте их на месте и снова нажмите ГРАФИК или клавишу Enter.
Чтобы изменить их, просто отредактируйте их на месте и снова нажмите ГРАФИК или клавишу Enter.
GFE проверит, что нижнее значение находится внизу оси y или слева от оси x. Допускаются отрицательные числа.
Примечание о соотношении сторон
Соотношение сторон (отношение ширины к высоте) графического окна составляет ровно 4: 3. Начальный диапазон значений по осям x и y находится в одинаковом соотношении, поэтому график y = x будет под углом 45 °, и круги будут круглыми, а не сжатыми в эллипсы. Однако, если вы измените пределы оси, это может измениться.
Использование переменных
Когда вы вводите свои уравнения, вы можете обращаться к четырем переменным, которые управляются ползунками. Они называются a, b, c и d, и вы можете настроить значение каждой переменной, перемещая ползунок вверх или вниз. Вы также можете ввести точное значение в поле вверху ползунка, а затем нажать кнопку ГРАФИК или клавишу Enter.
Например, в приведенной выше таблице нажмите «Сброс». Обратите внимание, что первая функция — это sin (a * x). Это означает, что каждый раз, когда точка строится, это синус текущего значения x, умноженного на переменную a.Эта переменная управляется ползунком справа, поэтому при перемещении ползунка вы можете увидеть эффект изменения его значения. *
Обратите внимание, что первая функция — это sin (a * x). Это означает, что каждый раз, когда точка строится, это синус текущего значения x, умноженного на переменную a.Эта переменная управляется ползунком справа, поэтому при перемещении ползунка вы можете увидеть эффект изменения его значения. *
Вы можете изменить диапазон ползунка, нажав на «диапазон» под ним. Появится диалоговое окно, в котором вы можете установить диапазон каждого ползунка отдельно.
* Если вам интересно: показанную синусоидальную кривую иногда называют синусоидой. Ползунок a регулирует частоту волны. См. Синусоидальную волну.
Сетка и этикетки
Если вы установите флажок «показывать сетку» (по умолчанию), отображается сетка с отмеченными основными значениями.Поскольку вы можете изменять пределы оси, GFE пытается создать примерно 10 линий сетки со значениями, которые легко интерполировать.Просмотр в полноэкранном режиме
Нажмите на «полный размер» под окном графика. Откроется новое окно с новым экземпляром GFE, размер которого зависит от вашего монитора.
Это может быть полезно в классе с проектором.
Откроется новое окно с новым экземпляром GFE, размер которого зависит от вашего монитора.
Это может быть полезно в классе с проектором.
Примечание: Большая версия — это копия обычного размера. Любые изменения, внесенные в большой, не будут скопированы обратно в оригинал, когда вы его закроете.
Пользователи Safari: Это будет игнорироваться, если браузер настроен на блокировку всплывающих окон — по умолчанию в Safari. (Такая блокировка не должна происходить строго, поскольку страницы происходят из одного домена).
Сохранить диаграмму как ссылку
Когда у вас есть диаграммы, которые вам нужны, вы можете щелкнуть «Создать ссылку» под апплетом. Это создаст ссылку
в диаграмму, которую можно вставить на веб-страницу или документ Word.
Когда вы позже нажмете на эту ссылку, диаграмма сразу же появится в том виде, в котором вы этого хотите.Кроме того, вставив адрес обратно в адресную строку браузера и нажав Enter, вы можете сохранить диаграмму в качестве закладки браузера или избранного.
Примечание. Некоторые программы не могут обрабатывать URL-адреса, превышающие определенную длину. (Например, Microsoft Word имеет ограничение в 256 байт).Некоторые очень сложные диаграммы могут давать более длинные URL-адреса.
Пользователи Safari: По умолчанию Safari подавляет всплывающие окна. Теоретически это не должно мешать работе этой функции, но это действительно так. Если вы не видите диалоговое окно для получения ссылки, настройте параметры браузера, чтобы разрешить всплывающие окна.
При желании вы можете создать эти ссылки самостоятельно. см. «Настройка GFE» ниже.
Привязка к целым числам
При установке этого флажка ползунки будут останавливаться только на целых числах.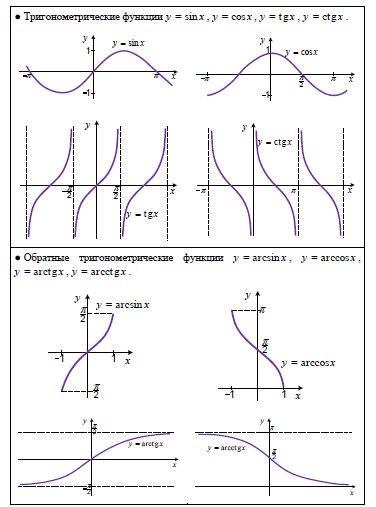
Настройка GFE
Обычно при запуске GFE отображает диаграмму по умолчанию. Вы можете изменить то, что изначально отображается, добавив параметры к URL-адресу веб-страницы. Вы можете переопределить некоторые или все элементы управления, чтобы отобразить любую желаемую исходную диаграмму.
Инструкции см. В разделе Настройка общего обозревателя функций (GFE). Но самый простой способ — использовать «сохранить как ссылку», как описано выше.
Аномалии графика?
В некоторых случаях может показаться, что на графике есть ошибки.Чтобы узнать больше об этом, см. Ограничения графического инструмента.Разделы о других функциях
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
pstricks — Построение тригонометрических функций — TeX
Описание констант, определяемых пользователем:
Обратите внимание: в приведенной выше описательной диаграмме используются константы, чтобы предоставить достаточно места для аннотаций.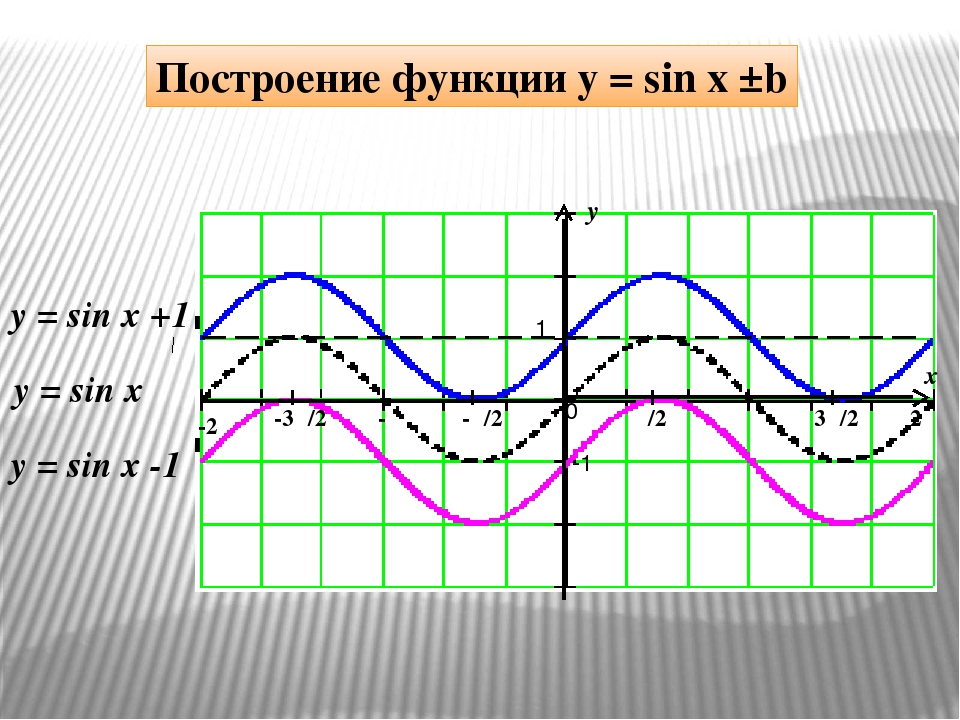 В следующем примере используются разные константы.Не запутайтесь!
В следующем примере используются разные константы.Не запутайтесь!
Константы, определенные пользователем:
\ def \ f (# 1) {sin (# 1)}% функция для построения графика
\ def \ g (# 1) {1.5 * cos (2 * # 1)}% функция для построения графика
\ const {Width} {10}% от общей ширины в см
\ const {Height} {4}% от общей высоты в см
\ const {POL} {- 0.20}% смещение изображения влево в см
\ const {POR} {0.50}% смещение изображения вправо в см
\ const {POB} {- 0.20}% смещение нижнего края изображения в см
\ const {POT} {0.50}% смещение верхнего края изображения в см
\ const {AOL} {- 0.20}% смещение оси влево в см
\ const {AOR} {0.30}% смещение оси вправо в см
\ const {AOB} {- 0.20}% нижнее смещение оси в см
\ const {AOT} {0.30}% смещение вершины оси в см
\ const {DomL} {- 2 * pi}% домена осталось
\ const {DomR} {2 * pi}% право домена
\ const {DomB} {- 2}% домен внизу
\ const {DomT} {2}% верхнего уровня домена
\ const [0] {TrigLabelBase} {2}% знаменатель доли числа пи
Вывод и полный код:
\ documentclass [border = 0pt, pstricks] {автономный}
\ usepackage {pst-eucl, pstricks-add}
\ usepackage [сообщения] {fp}
\ newcommand \ const [3] [3] {\ expandafter \ FPeval \ csname # 2 \ endcsname {round (# 3: # 1)}}
% Пользовательские данные:
\ def \ f (# 1) {sin (# 1)}% функция для построения графика
\ def \ g (# 1) {1. 5 * cos (2 * # 1)}% функция для построения графика
\ const {Width} {10}% от общей ширины в см
\ const {Height} {4}% от общей высоты в см
\ const {POL} {- 0.20}% смещение изображения влево в см
\ const {POR} {0.50}% смещение изображения вправо в см
\ const {POB} {- 0.20}% смещение нижнего края изображения в см
\ const {POT} {0.50}% смещение верхнего края изображения в см
\ const {AOL} {- 0.20}% смещение оси влево в см
\ const {AOR} {0.30}% смещение оси вправо в см
\ const {AOB} {- 0.20}% нижнее смещение оси в см
\ const {AOT} {0.30}% смещение вершины оси в см
\ const {DomL} {- 2 * pi}% домена осталось
\ const {DomR} {2 * pi}% право домена
\ const {DomB} {- 2}% домен внизу
\ const {DomT} {2}% верхнего уровня домена
\ const [0] {TrigLabelBase} {2}% знаменатель доли числа пи
% Внутренние используемые константы:
\ const {XUnit} {(Ширина-POR + POL-AOR + AOL) / (DomR-DomL)}
\ const {YUnit} {(Высота-POT + POB-AOT + AOB) / (DomT-DomB)}
\ const {PicL} {(POL + AOL) / XUnit + DomL}
\ const {PicR} {(POR + AOR) / XUnit + DomR}
\ const {PicB} {(POB + AOB) / YUnit + DomB}
\ const {PicT} {(POT + AOT) / YUnit + DomT}
\ const {AxiL} {AOL / XUnit + DomL}
\ const {AxiR} {AOR / XUnit + DomR}
\ const {AxiB} {AOB / YUnit + DomB}
\ const {AxiT} {AOT / YUnit + DomT}
\ const {DeltaX} {pi / TrigLabelBase}
\ psset {xunit = \ XUnit, yunit = \ YUnit, algebraic, plotpoints = 500}
\ begin {document}
\ begin {pspicture} [showgrid = false] (\ PicL, \ PicB) (\ PicR, \ PicT)
\ psplot [цвет линии = красный] {\ DomL} {\ DomR} {\ f (x)}
\ psplot [цвет линии = синий] {\ DomL} {\ DomR} {\ g (x)}
\ psaxes
[
trigLabels = истина,
labelFontSize = \ scriptscriptstyle,
цвет тика = серый,
ticksize = -1.
5 * cos (2 * # 1)}% функция для построения графика
\ const {Width} {10}% от общей ширины в см
\ const {Height} {4}% от общей высоты в см
\ const {POL} {- 0.20}% смещение изображения влево в см
\ const {POR} {0.50}% смещение изображения вправо в см
\ const {POB} {- 0.20}% смещение нижнего края изображения в см
\ const {POT} {0.50}% смещение верхнего края изображения в см
\ const {AOL} {- 0.20}% смещение оси влево в см
\ const {AOR} {0.30}% смещение оси вправо в см
\ const {AOB} {- 0.20}% нижнее смещение оси в см
\ const {AOT} {0.30}% смещение вершины оси в см
\ const {DomL} {- 2 * pi}% домена осталось
\ const {DomR} {2 * pi}% право домена
\ const {DomB} {- 2}% домен внизу
\ const {DomT} {2}% верхнего уровня домена
\ const [0] {TrigLabelBase} {2}% знаменатель доли числа пи
% Внутренние используемые константы:
\ const {XUnit} {(Ширина-POR + POL-AOR + AOL) / (DomR-DomL)}
\ const {YUnit} {(Высота-POT + POB-AOT + AOB) / (DomT-DomB)}
\ const {PicL} {(POL + AOL) / XUnit + DomL}
\ const {PicR} {(POR + AOR) / XUnit + DomR}
\ const {PicB} {(POB + AOB) / YUnit + DomB}
\ const {PicT} {(POT + AOT) / YUnit + DomT}
\ const {AxiL} {AOL / XUnit + DomL}
\ const {AxiR} {AOR / XUnit + DomR}
\ const {AxiB} {AOB / YUnit + DomB}
\ const {AxiT} {AOT / YUnit + DomT}
\ const {DeltaX} {pi / TrigLabelBase}
\ psset {xunit = \ XUnit, yunit = \ YUnit, algebraic, plotpoints = 500}
\ begin {document}
\ begin {pspicture} [showgrid = false] (\ PicL, \ PicB) (\ PicR, \ PicT)
\ psplot [цвет линии = красный] {\ DomL} {\ DomR} {\ f (x)}
\ psplot [цвет линии = синий] {\ DomL} {\ DomR} {\ g (x)}
\ psaxes
[
trigLabels = истина,
labelFontSize = \ scriptscriptstyle,
цвет тика = серый,
ticksize = -1. 5pt 1.5pt,
xlabelsep = 3pt,
arrowscale = 1,
trigLabelBase = \ TrigLabelBase,
dx = \ DeltaX,% должен стоять перед xunit, чтобы избежать странного вывода!
] {->} (0,0) (\ AxiL, \ AxiB) (\ AxiR, \ AxiT) [$ x $, 0] [$ y $, 90]
\ end {pspicture}
\ конец {документ}
5pt 1.5pt,
xlabelsep = 3pt,
arrowscale = 1,
trigLabelBase = \ TrigLabelBase,
dx = \ DeltaX,% должен стоять перед xunit, чтобы избежать странного вывода!
] {->} (0,0) (\ AxiL, \ AxiB) (\ AxiR, \ AxiT) [$ x $, 0] [$ y $, 90]
\ end {pspicture}
\ конец {документ}
8.4 Полярные координаты: графики — предварительное вычисление
Цели обучения
В этом разделе вы:
- Проверить полярные уравнения на симметрию.
- Построение полярных уравнений путем нанесения точек.
Планеты движутся в космосе по эллиптическим периодическим орбитам вокруг Солнца, как показано на рисунке 1. Они находятся в постоянном движении, поэтому определение точного положения любой планеты возможно только на мгновение. Другими словами, мы можем зафиксировать только мгновенное положение планеты . Это одно из применений полярных координат, представленных как (r, θ). (R, θ).
Мы интерпретируем rr как расстояние от Солнца и θθ как угловой пеленг планеты или ее направление от фиксированной точки на Солнце.В этом разделе мы сосредоточимся на полярной системе и графиках, которые создаются непосредственно из полярных координат.
(R, θ).
Мы интерпретируем rr как расстояние от Солнца и θθ как угловой пеленг планеты или ее направление от фиксированной точки на Солнце.В этом разделе мы сосредоточимся на полярной системе и графиках, которые создаются непосредственно из полярных координат.
Рис. 1 Планеты движутся по эллиптическим траекториям, вращаясь вокруг Солнца. (кредит: модификация работы NASA / JPL-Caltech)
Проверка полярных уравнений на симметрию
Так же, как прямоугольное уравнение, такое как y = x2y = x2, описывает взаимосвязь между xx и yy на декартовой сетке, полярное уравнение описывает взаимосвязь между rr и θθ на полярной сетке.Напомним, что пара координат (r, θ) (r, θ) указывает, что мы перемещаемся против часовой стрелки от полярной оси (положительная ось x ) на угол θ, θ и вытягиваем луч от полюса (начала координат). rr единиц в направлении θ.θ. Все точки, удовлетворяющие полярному уравнению, отображаются на графике.
Симметрия — это свойство, которое помогает нам распознать и построить график любого уравнения. Если уравнение имеет график, симметричный относительно оси, это означает, что если мы сложим график пополам по этой оси, часть графика на одной стороне будет совпадать с частью на другой стороне.Выполнив три теста, мы увидим, как применить свойства симметрии к полярным уравнениям. Далее мы будем использовать симметрию (в дополнение к нанесению ключевых точек, нулей и максимумов r) r) для определения графика полярного уравнения.
В первом тесте мы рассматриваем симметрию относительно прямой θ = π2θ = π2 ( y — ось). Мы заменяем (r, θ) (r, θ) на (−r, −θ) (- r, −θ), чтобы определить, эквивалентно ли новое уравнение исходному уравнению. Например, предположим, что нам дано уравнение r = 2sinθ; r = 2sinθ;
r = 2sinθ − r = 2sin (−θ) Заменим (r, θ) на (−r, −θ).−r = −2sinθIdentity: sin (−θ) = — sinθ.r = 2sinθ Умножаем обе части на −1. R = 2sinθ − r = 2sin (−θ) Заменим (r, θ) на (−r, −θ).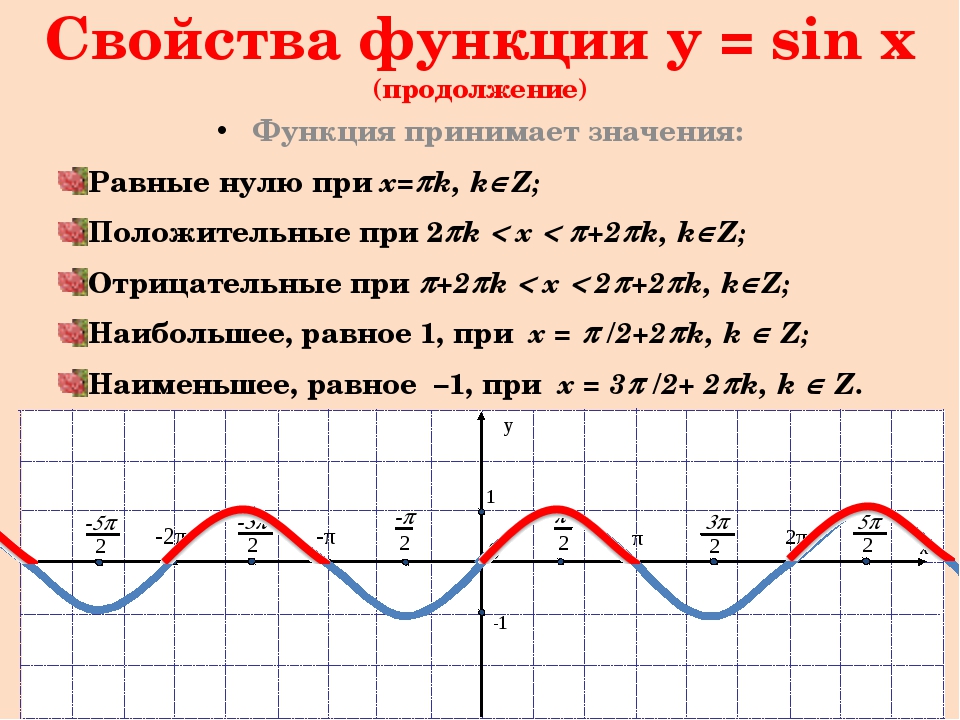 −r = −2sinθIdentity: sin (−θ) = — sinθ.r = 2sinθ Умножаем обе части на −1.
−r = −2sinθIdentity: sin (−θ) = — sinθ.r = 2sinθ Умножаем обе части на −1.Это уравнение демонстрирует симметрию относительно прямой θ = π2.θ = π2.
Во втором тесте мы рассматриваем симметрию относительно полярной оси (ось xx). Заменим (r, θ) (r, θ) на (r, −θ) (r, −θ) или (−r, π − θ) (- r, π − θ), чтобы определить эквивалентность между тестируемым уравнением и оригинал. Например, предположим, что нам дано уравнение r = 1−2cosθ.r = 1−2cosθ.
r = 1−2cosθr = 1−2cos (−θ) Заменить (r, θ) на (r, −θ) .r = 1−2cosθEven / Odd identityr = 1−2cosθr = 1−2cos (−θ) Заменить ( r, θ) с (r, −θ) .r = 1−2cosθEven / Odd identityГрафик этого уравнения демонстрирует симметрию относительно полярной оси.
В третьем тесте мы рассматриваем симметрию относительно полюса (начала координат). Мы заменяем (r, θ) (r, θ) на (−r, θ) (- r, θ), чтобы определить, эквивалентно ли тестируемое уравнение исходному уравнению. Например, предположим, что нам дано уравнение r = 2sin (3θ).r = 2sin (3θ).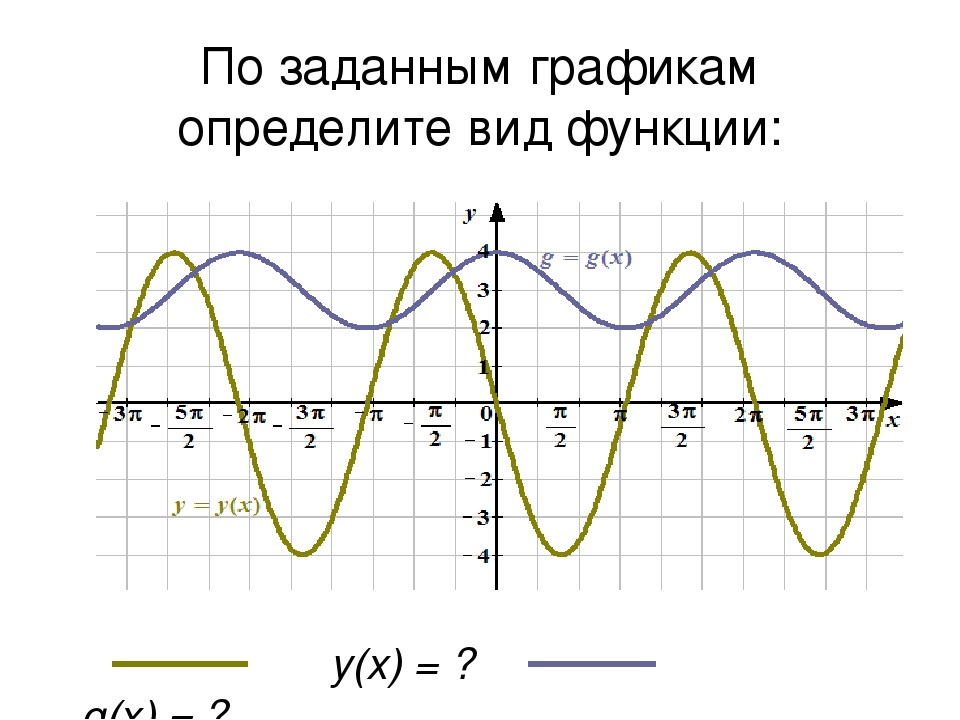
Уравнение не прошло проверку на симметрию, но это не означает, что оно не симметрично относительно столб. Прохождение одного или нескольких тестов симметрии подтверждает, что симметрия будет отображаться в графе. Однако отсутствие проверки на симметрию не обязательно означает, что график не будет симметричным относительно линии θ = π2, θ = π2, полярной оси или полюса. В этих случаях мы можем подтвердить, что симметрия существует, нанеся точки отражения поперек кажущейся оси симметрии или полюса.Проверка симметрии — это метод, который упрощает построение графиков полярных уравнений, но его применение не идеально.
Тесты симметрии
Полярное уравнение описывает кривую на полярной сетке. График полярного уравнения можно оценить для трех типов симметрии, как показано на рисунке 2.
Рисунок 2 (a) График симметричен относительно прямой θ = π2θ = π2 ( y -ось), если заменить (r, θ) (r, θ) на (−r, −θ) (- r, −θ) дает эквивалентное уравнение. (b) График симметричен относительно полярной оси ( x -ось), если заменить (r, θ) (r, θ) на (r, −θ) (r, −θ) или (−r, π − θ) (- r, π − θ) дает эквивалентное уравнение. (c) Граф является симметричным относительно полюса (начала координат), если замена (r, θ) (r, θ) на (−r, θ) (- r, θ) дает эквивалентное уравнение.
(b) График симметричен относительно полярной оси ( x -ось), если заменить (r, θ) (r, θ) на (r, −θ) (r, −θ) или (−r, π − θ) (- r, π − θ) дает эквивалентное уравнение. (c) Граф является симметричным относительно полюса (начала координат), если замена (r, θ) (r, θ) на (−r, θ) (- r, θ) дает эквивалентное уравнение.Как сделать
Дано полярное уравнение, проверьте симметрию.
- Подставьте соответствующую комбинацию компонентов вместо (r, θ) 🙁 r, θ): (- r, −θ) (- r, −θ) вместо θ = π2θ = π2 симметрии; (r, −θ) (r, −θ) для симметрии полярной оси; и (−r, θ) (- r, θ) для симметрии относительно полюса.
- Если результирующие уравнения эквивалентны в одном или нескольких тестах, график дает ожидаемую симметрию.
Пример 1
Проверка полярного уравнения на симметрию
Проверьте уравнение r = 2sinθr = 2sinθ на симметрию.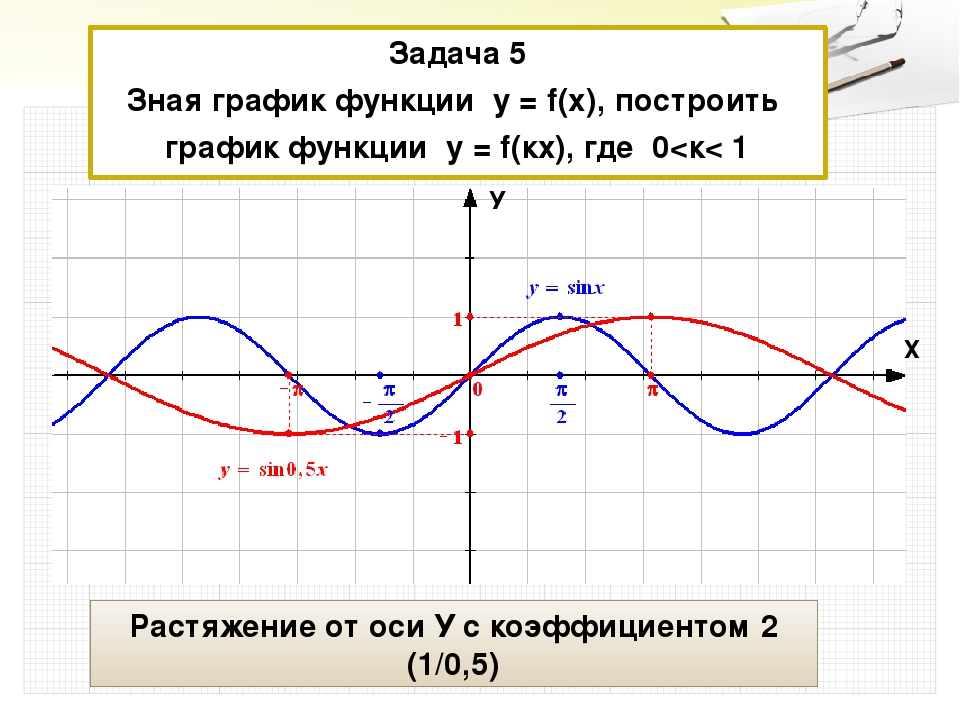
Решение
Тест на каждый из трех типов симметрии.
| 1) Замена (r, θ) (r, θ) на (−r, −θ) (- r, −θ) дает тот же результат.Таким образом, график симметричен относительно прямой θ = π2.θ = π2. | −r = 2sin (−θ) −r = −2sinθ Четно-нечетное тождествоr = 2sinθMultiplyby − 1Passed − r = 2sin (−θ) −r = −2sinθ Четно-нечетное identityr = 2sinθMultiplyby − 1Passed |
| 2) Замена θθ на −θ − θ не дает того же уравнения. Следовательно, график не проходит проверку и может быть или не быть симметричным относительно полярной оси. | r = 2sin (−θ) r = −2sinθ Четно-нечетное тождествоr = −2sinθ ≠ 2sinθFailedr = 2sin (−θ) r = −2sinθ Четно-нечетное тождествоr = −2sinθ ≠ 2sinθFailed |
3) Замена rr на –r – r изменяет уравнение и не проходит проверку.Граф может быть или не быть симметричным относительно полюса. | −r = 2sinθ r = −2sinθ ≠ 2sinθFailed − r = 2sinθ r = −2sinθ ≠ 2sinθFailed |
Таблица 1
Анализ
Используя графический калькулятор, мы можем увидеть, что уравнение r = 2sinθr = 2sinθ представляет собой круг с центром в точке (0,1) (0,1) и радиусом r = 1r = 1 и действительно симметричен прямой θ = π2. θ = π2. Мы также можем видеть, что график не симметричен полярной оси или полюсу. См. Рисунок 3.
Рисунок 3
Попробуй # 1
Проверьте уравнение на симметрию: r = −2cosθ.r = −2cosθ.
Построение полярных уравнений по точкам
Для построения графика в прямоугольной системе координат мы составляем таблицу значений xx и yy. Для построения графика в полярной системе координат мы строим таблицу значений θθ и rr. Вводим значения θθ
в полярное уравнение и вычислить относительную влажность. Однако использование свойств симметрии и нахождение ключевых значений θθ и rr означает, что потребуется меньше вычислений.
Однако использование свойств симметрии и нахождение ключевых значений θθ и rr означает, что потребуется меньше вычислений.
Нахождение нулей и максимумов
Чтобы найти нули полярного уравнения, мы решаем значения θθ, которые приводят к r = 0.r = 0. Напомним, что для нахождения нулей полиномиальных функций мы устанавливаем уравнение равным нулю, а затем решаем относительно x.x. Мы используем тот же процесс для полярных уравнений. Установите r = 0, r = 0 и решите относительно θ.θ.
Для многих форм, с которыми мы встретимся, максимальное значение полярного уравнения находится путем подстановки тех значений θθ в уравнение, которые приводят к максимальному значению тригонометрических функций.Рассмотрим r = 5cosθ; r = 5cosθ; максимальное расстояние между изгибом и опорой — 5 единиц. Максимальное значение функции косинуса равно 1, когда θ = 0, θ = 0, поэтому наше полярное уравнение — 5cosθ, 5cosθ, а значение θ = 0θ = 0 даст максимальное значение | r |.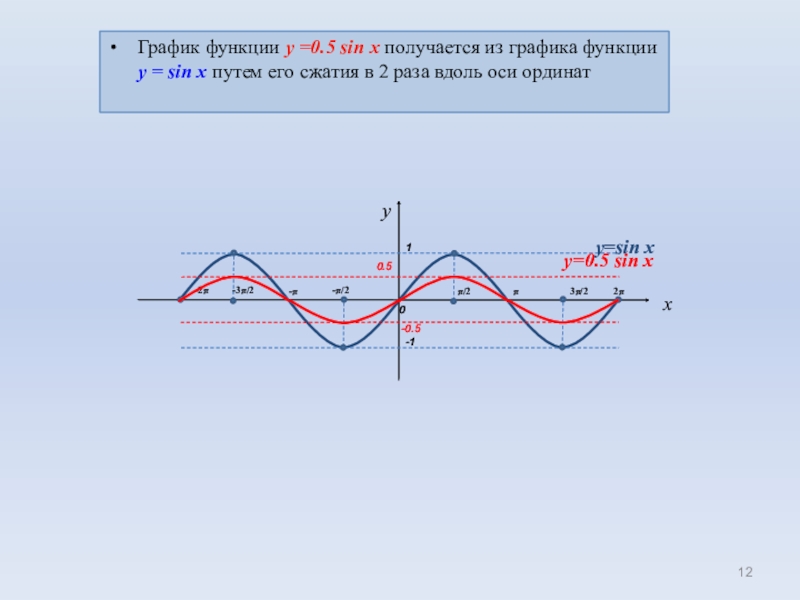 | R |.
| R |.
Аналогично, максимальное значение синусоидальной функции равно 1, когда θ = π2, θ = π2, и если наше полярное уравнение r = 5sinθ, r = 5sinθ, значение θ = π2θ = π2 даст максимум | r | . | г |. Мы можем найти дополнительную информацию, вычислив значения rr, когда θ = 0.θ = 0.Эти точки будут пересечениями полярной оси, что может быть полезно при построении графика и идентификации кривой полярного уравнения.
Пример 2
Нахождение нулей и максимальных значений для полярного уравнения
Используя уравнение из примера 1, найдите нули и максимум | r || r | и, если необходимо, полярная ось пересекает r = 2sinθ.r = 2sinθ.
Решение
Чтобы найти нули, установите rr равным нулю и решите относительно θ.θ.
2sinθ = 0sinθ = 0θ = sin − 10θ = nπ, где n — целое число, 2sinθ = 0sinθ = 0θ = sin − 10θ = nπ, где n — целое число Подставьте любое из значений θθ в уравнение.Мы будем использовать 0.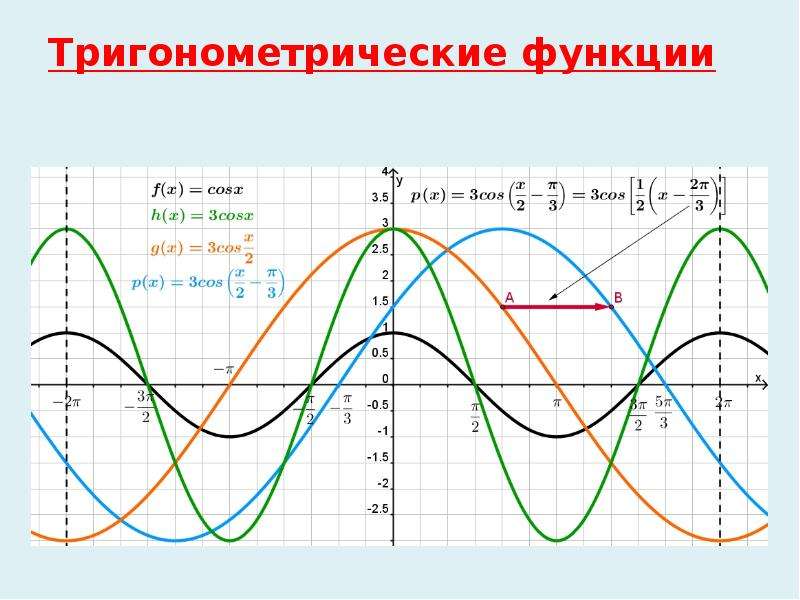 0.
0.
Точки (0,0) (0,0) и (0, ± nπ) (0, ± nπ) являются нулями уравнения. Все они совпадают, поэтому на графике видна только одна точка. Эта точка также является единственной точкой пересечения полярной оси.
Чтобы найти максимальное значение уравнения, посмотрите на максимальное значение тригонометрической функции sinθ, sinθ, которое возникает, когда θ = π2 ± 2kπθ = π2 ± 2kπ, что приводит к sin (π2) = 1.sin (π2) = 1 . Подставляем π2π2 вместо θ.θ.
r = 2sin (π2) r = 2 (1) r = 2r = 2sin (π2) r = 2 (1) r = 2Анализ
Точка (2, π2) (2, π2) будет максимальным значением на графике.Давайте нарисуем еще несколько точек, чтобы проверить график круга. См. Таблицу 2 и Рисунок 4.
| θθ | r = 2sinθr = 2sinθ | руб. |
|---|---|---|
| 0 | r = 2sin (0) = 0r = 2sin (0) = 0 | 00 |
| π6π6 | r = 2sin (π6) = 1r = 2sin (π6) = 1 | 11 |
| π3π3 | r = 2sin (π3) ≈1.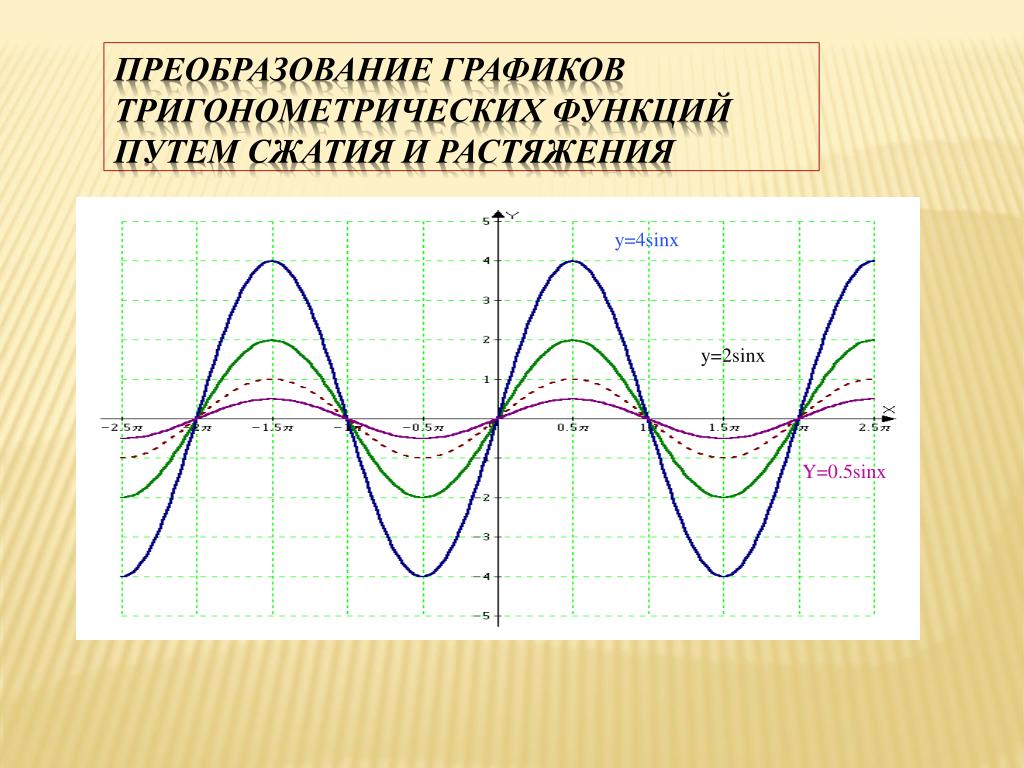 73r = 2sin (π3) ≈1.73 73r = 2sin (π3) ≈1.73 | 1,731,73 |
| π2π2 | r = 2sin (π2) = 2r = 2sin (π2) = 2 | 22 |
| 2π32π3 | r = 2sin (2π3) ≈1.73r = 2sin (2π3) ≈1.73 | 1,731,73 |
| 5π65π6 | r = 2sin (5π6) = 1r = 2sin (5π6) = 1 | 11 |
| ππ | r = 2sin (π) = 0r = 2sin (π) = 0 | 00 |
Таблица 2
Рисунок 4
Попробуй # 2
Без преобразования в декартовы координаты, проверьте данное уравнение на симметрию и найдите нули и максимальные значения | r |: | r |: r = 3cosθ. г = 3cosθ.
г = 3cosθ.
Следственные круги
Теперь мы увидели уравнение круга в полярной системе координат. В последних двух примерах одно и то же уравнение использовалось для иллюстрации свойств симметрии и демонстрации того, как найти нули, максимальные значения и нанесенные точки, по которым построены графики. Однако круг — лишь одна из многих фигур в наборе полярных кривых.
Есть пять классических полярных кривых : кардиоиды , лимана, лемнискаты, кривые розы и спирали Архимеда .Мы кратко коснемся полярных формул для круга, прежде чем перейти к классическим кривым и их вариациям.
Формулы уравнения окружности
Некоторые формулы, которые создают график круга в полярных координатах, даются как r = acosθr = acosθ и r = asinθ, r = asinθ, где aa — диаметр круга или расстояние от полюса до самой дальней точки. по окружности. Радиус равен | a | 2, | a | 2 или половине диаметра.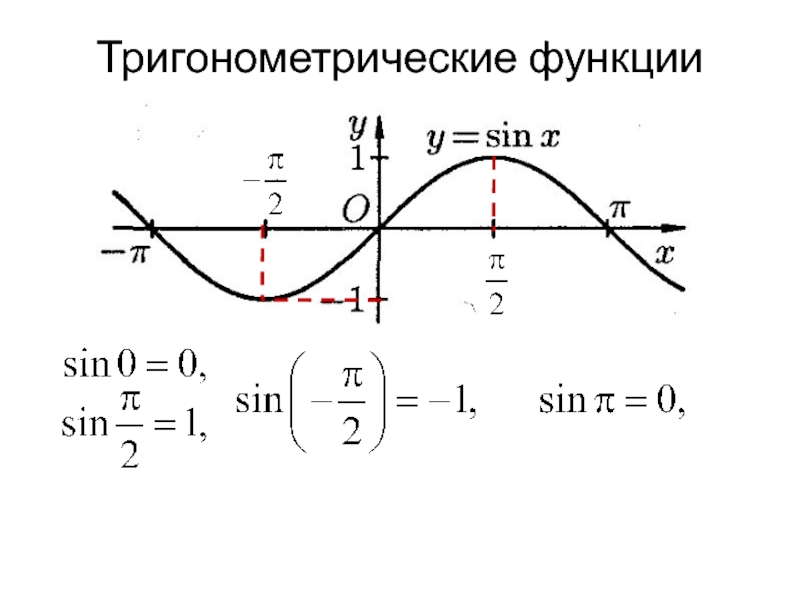 Для r = acosθ, r = acosθ центр равен (a2,0).(а2,0). Для r = asinθ, r = asinθ центром является (a2, π2). (A2, π2). На рисунке 5 показаны графики этих четырех кругов.
Для r = acosθ, r = acosθ центр равен (a2,0).(а2,0). Для r = asinθ, r = asinθ центром является (a2, π2). (A2, π2). На рисунке 5 показаны графики этих четырех кругов.
Рисунок 5
Пример 3
Построение графика полярного уравнения для окружности
Нарисуйте график r = 4cosθ.r = 4cosθ.
Решение
Во-первых, проверяя уравнение на симметрию, мы обнаруживаем, что график симметричен относительно полярной оси. Далее находим нули и максимум | r || r | для r = 4cosθ.r = 4cosθ. Сначала установите r = 0, r = 0 и решите относительно θθ.Таким образом, нуль возникает при θ = π2 ± kπ.θ = π2 ± kπ. Ключевой точкой для построения графика является (0, π2). (0, π2).
Чтобы найти максимальное значение r, r, обратите внимание, что максимальное значение функции косинуса равно 1, когда θ = 0 ± 2kπ.θ = 0 ± 2kπ. Подставляем θ = 0θ = 0 в уравнение:
r = 4cosθr = 4cos (0) r = 4 (1) = 4r = 4cosθr = 4cos (0) r = 4 (1) = 4 Максимальное значение уравнения составляет 4. Ключевой точкой для построения графика является (4,0). (4,0).
Ключевой точкой для построения графика является (4,0). (4,0).
Поскольку r = 4cosθr = 4cosθ симметрично относительно полярной оси, нам нужно только вычислить r -значений для θθ в интервале [0, [0, π].π]. Точки в верхнем квадранте затем могут быть отражены в нижний квадрант. Составьте таблицу значений, аналогичную Таблице 3. График показан на Рисунке 6 .
| θθ | 0 | π6π6 | π4π4 | π3π3 | π2π2 | 2π32π3 | 3π43π4 | 5π65π6 | ππ |
руб. | 4 | 3.46 | 2,83 | 2 | 0 | -2 | -2,83 | −3,46 | −4 |
Таблица 3
Рисунок 6
Исследование кардиоидов
Хотя перевод полярных координат в декартовы координаты в некоторых случаях может показаться проще, построение классических кривых в полярной системе на самом деле менее сложно.Следующая кривая называется кардиоидной, так как она напоминает сердце. Эту форму часто включают в семейство кривых, называемых лимасонами, но здесь мы обсудим кардиоиду отдельно.
Формулы кардиоиды
Формулы, по которым строятся графики кардиоиды, имеют следующий вид: r = a ± bcosθr = a ± bcosθ и r = a ± bsinθr = a ± bsinθ, где a> 0, a> 0, b> 0, b> 0 и ab = 1. ab = 1. Кардиоидный график проходит через полюс, как мы видим на Рисунке 7.
ab = 1. Кардиоидный график проходит через полюс, как мы видим на Рисунке 7.
Рисунок 7
Как сделать
Дан полярное уравнение кардиоиды, нарисуйте ее график.
- Проверьте уравнение для трех типов симметрии.
- Найдите нули. Установите r = 0. r = 0.
- Найдите максимальное значение уравнения согласно максимальному значению тригонометрического выражения.
- Составьте таблицу значений для rr и θ.θ.
- Постройте точки и нарисуйте график.
Пример 4
Построение графика кардиоиды
Нарисуйте график r = 2 + 2cosθ.r = 2 + 2cosθ.
Решение
Во-первых, проверяя уравнение на симметрию, мы обнаруживаем, что график этого уравнения будет симметричным относительно полярной оси.Далее находим нули и максимумы. Полагая r = 0, r = 0, имеем θ = π + 2kπ.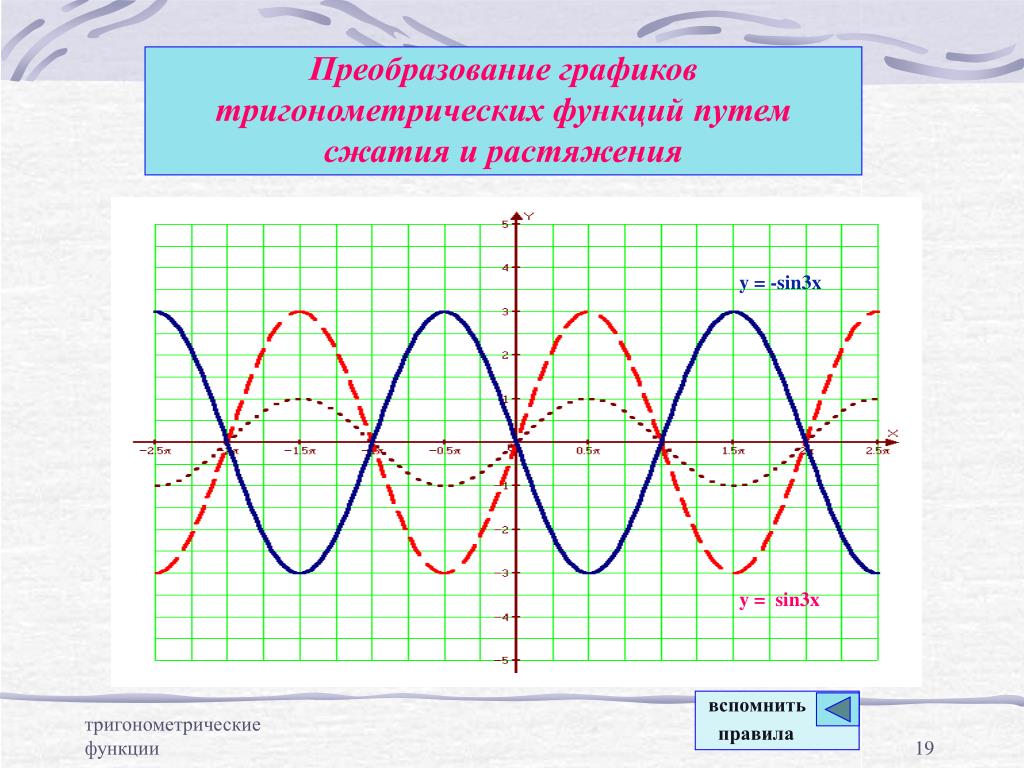 θ = π + 2kπ. Нуль уравнения находится в точке (0, π). (0, π). График проходит через эту точку.
θ = π + 2kπ. Нуль уравнения находится в точке (0, π). (0, π). График проходит через эту точку.
Максимальное значение r = 2 + 2cosθr = 2 + 2cosθ возникает, когда cosθcosθ является максимальным, то есть когда cosθ = 1cosθ = 1 или когда θ = 0.θ = 0. Подставляем θ = 0θ = 0 в уравнение и решаем относительно r.r.
r = 2 + 2cos (0) r = 2 + 2 (1) = 4r = 2 + 2cos (0) r = 2 + 2 (1) = 4Точка (4,0) (4,0) равна максимальное значение на графике.
Мы обнаружили, что полярное уравнение симметрично относительно полярной оси, но поскольку оно распространяется на все четыре квадранта, нам нужно построить значения в интервале [0, π].[0, π]. Затем верхняя часть графика отражается над полярной осью. Далее мы составляем таблицу значений, как в Таблице 4, а затем наносим точки и рисуем график. См. Рисунок 8.
| θθ | 00 | π4π4 | π2π2 | 2π32π3 | ππ |
руб.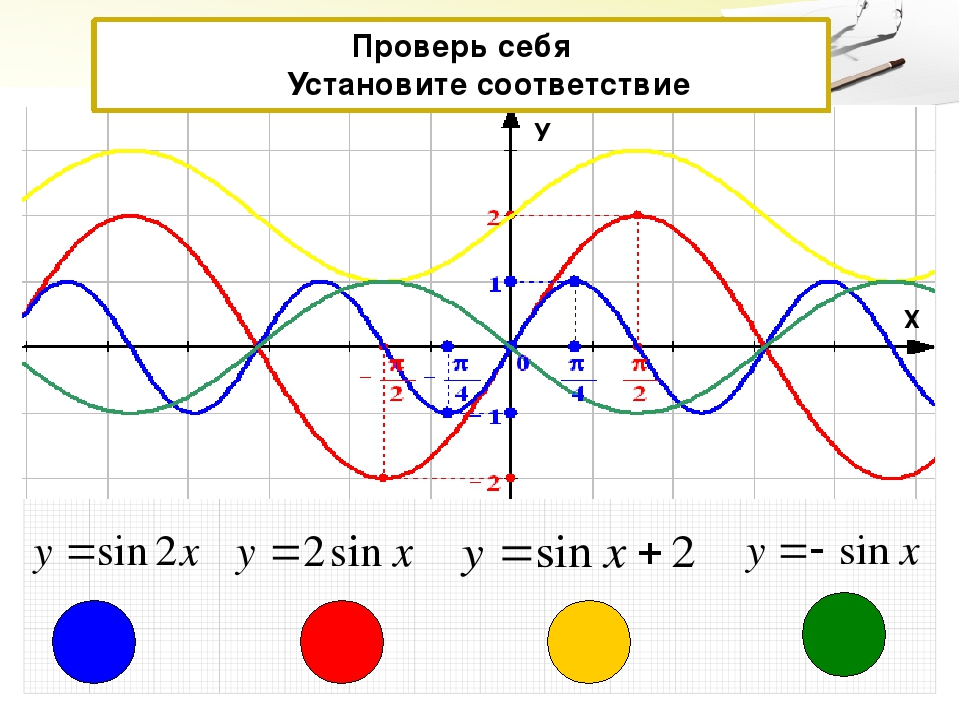 | 4 | 3,41 | 2 | 1 | 0 |
Таблица 4
Рисунок 8
Исследование Лимасона
Слово limaçon на старофранцузском означает «улитка», имя, которое описывает форму графа.Как упоминалось ранее, кардиоида является членом семейства limaçon, и мы можем видеть сходство на графиках. Другие изображения в этой категории включают лимит с одной петлей и с двумя петлями (или с внутренней петлей). Лимасоны с одной петлей иногда называют ямчатыми, если 1 Формулы, по которым строится график однопетлевого лимака с ямочками, задаются следующим образом: r = a ± bcosθr = a ± bcosθ и r = a ± bsinθr = a ± bsinθ, где a> 0, b> 0, a> 0, b > 0 и 1 Рисунок 9 Лимасоны с ямочками Дан полярное уравнение для лимона с одной петлей, нарисуйте график. Изобразите уравнение r = 4−3sinθ.r = 4−3sinθ. Во-первых, проверяя уравнение на симметрию, мы обнаруживаем, что оно не проходит все три теста на симметрию, что означает, что график может или не может демонстрировать симметрию, поэтому мы не можем использовать симметрию, чтобы помочь нам построить график. Затем мы находим нули и максимум и наносим на график точки отражения для проверки симметрии. Установка r = 0r = 0 приводит к тому, что θθ не определен. Что это значит? Как могло θθ быть неопределенным? Угол θθ не определен ни при каком значении sinθ> 1. sinθ> 1. Следовательно, θθ не определено, потому что не существует значения θθ, для которого sinθ> 1. sinθ> 1. Следовательно, граф не проходит через полюс. Возможно, график действительно пересекает полярную ось, но не на полюсе.Мы можем исследовать другие точки пересечения, вычислив rr, когда θ = 0.θ = 0. Итак, имеется хотя бы одна полярная ось перехватить в (4,0). (4,0). Далее, поскольку максимальное значение синусоидальной функции равно 1 при θ = π2, θ = π2, мы подставим θ = π2θ = π2
в уравнение и решите относительно r. Составьте таблицу координат, аналогичную таблице 5. Таблица 5 График показан на Рисунке 10. Рисунок 10 Лимасон с одной петлей Это пример кривой, для которой составление таблицы значений критически важно для построения точного графика.Тесты на симметрию терпят неудачу; ноль не определен. Хотя может быть очевидно, что уравнение, включающее sinθsinθ, вероятно, симметрично относительно линии θ = π2, θ = π2, оценка большего количества точек помогает проверить правильность графика. Нарисуйте график r = 3−2cosθ.r = 3−2cosθ. Другой тип лимака, лимит внутренней петли , назван в честь петли, образованной внутри общей формы лимака. Он был открыт немецким художником Альбрехтом Дюрером (1471-1528), который раскрыл метод рисования лимасона с внутренней петлей в своей книге 1525 года Underweysung der Messing .Спустя столетие отец математика Блеза Паскаля, Этьен Паскаль (1588–1651), открыл его заново. Формулы, которые порождают лимасоны внутреннего цикла, задаются как r = a ± bcosθr = a ± bcosθ и r = a ± bsinθr = a ± bsinθ, где a> 0, a> 0, b> 0, b> 0 и а <ба <б. График лимасона внутренней петли проходит через полюс дважды: один раз для внешнего цикла и один раз для внутреннего цикла. Графики см. На Рисунке 11. Рисунок 11 Нарисуйте график r = 2 + 5cosθ. Проверяя симметрию, мы обнаруживаем, что график уравнения симметричен относительно полярной оси. Затем поиск нулей показывает, что при r = 0, r = 0, θ = 1,98. Θ = 1,98.
Максимум | r || r | находится, когда cosθ = 1cosθ = 1 или когда θ = 0.θ = 0. Таким образом, максимум находится в точке (7, 0). Несмотря на то, что мы нашли симметрию, ноль и максимум, нанесение большего количества точек поможет определить форму, и тогда появится узор. См. Таблицу 6. Таблица 6 Как и ожидалось, значения начинают повторяться после θ = π.θ = π. График показан на рисунке 12. Рисунок 12 Лимасон с внутренним контуром Лемниската — это полярная кривая, напоминающая символ бесконечности ∞∞ или цифру 8.Расположенная в центре полюса лемниската по определению симметрична. Формулы, образующие график лемнискаты, имеют вид r2 = a2cos2θr2 = a2cos2θ и r2 = a2sin2θr2 = a2sin2θ, где a ≠ 0.a ≠ 0. Формула r2 = a2sin2θr2 = a2sin2θ симметрична относительно полюса. Формула r2 = a2cos2θr2 = a2cos2θ симметрична относительно полюса, прямой θ = π2, θ = π2 и полярной оси. Графики см. На Рисунке 13. Рисунок 13 Нарисуйте график r2 = 4cos2θ.r2 = 4cos2θ. Уравнение демонстрирует симметрию относительно прямой θ = π2, θ = π2, полярной оси и полюса. Давай найдем нули. Сейчас это должно быть обычным делом, но мы подойдем к этому уравнению немного иначе, сделав замену u = 2θ.u = 2θ. А теперь найдем максимальное значение. Поскольку максимум cosu = 1 cosu = 1, когда u = 0, u = 0, максимум cos2θ = 1cos2θ = 1, когда 2θ = 0,2θ = 0. Таким образом, У нас есть максимум на (2, 0). Поскольку этот график симметричен относительно полюса, линии θ = π2, θ = π2 и полярной оси, нам нужно только построить точки в первом квадранте. Составьте таблицу, аналогичную таблице 7. Таблица 7 Нанесите точки на график, например, показанный на рисунке 14. Рисунок 14 Лемниската Выполнение такой замены, как u = 2θu = 2θ, является обычной практикой в математике, поскольку она может упростить вычисления. Однако мы не должны забывать заменять заменяющий член исходным членом в конце, а затем решать неизвестное. Некоторые точки на этом графике могут не отображаться при использовании функции Trace на графическом калькуляторе TI-84, а таблица калькулятора может показывать ошибку для тех же самых точек r.р. Это потому, что для этих значений θ.θ нет реальных квадратных корней. Другими словами, соответствующие r -значения 4cos (2θ) 4cos (2θ)
являются комплексными числами, потому что под корнем стоит отрицательное число. Следующий тип полярного уравнения дает форму лепестка, называемую кривой розы. Хотя графики выглядят сложными, простое полярное уравнение порождает закономерность. Формулы, которые создают график кривой розы, задаются как r = acosnθr = acosnθ и r = asinnθr = asinnθ, где a ≠ 0.а ≠ 0. Если nn четное, кривая имеет 2n2n лепестков. Если nn нечетное, кривая имеет nn лепестков. См. Рисунок 15. Рисунок 15 Нарисуйте график r = 2cos4θ.r = 2cos4θ. Проверяя симметрию, мы снова обнаруживаем, что тесты симметрии не раскрывают всей картины. График симметричен не только относительно полярной оси, но и относительно прямой θ = π2θ = π2 и полюса. Теперь найдем нули. Сначала сделаем замену u = 4θ.u = 4θ. Ноль равен θ = π8.θ = π8. Точка (0, π8) (0, π8) находится на кривой. Далее находим максимум | r |. | R |. Мы знаем, что максимальное значение cosu = 1cosu = 1 при θ = 0.θ = 0. Таким образом, Точка (2,0) (2,0) находится на кривой. График кривой розы обладает уникальными свойствами, которые раскрыты в Таблице 8. Таблица 8 Поскольку r = 0r = 0 при θ = π8, θ = π8, имеет смысл разделить значения в таблице на π8π8 единиц. Когда эти кривые нарисованы, лучше всего наносить точки по порядку, как в таблице 8. Это позволяет нам увидеть, как график достигает максимума (кончик лепестка), петляет, пересекая полюс, попадает в противоположный максимум, и петли обратно к полюсу.Действие продолжается до тех пор, пока не будут нарисованы все лепестки. Нарисуйте график r = 4sin (2θ) .r = 4sin (2θ). Нарисуйте график r = 2sin (5θ) . График уравнения показывает симметрию относительно прямой θ = π2.θ = π2. Далее найдите нули и максимум. Мы хотим сделать замену u = 5θ.и = 5θ. Максимальное значение рассчитывается при угле, где sinθsinθ является максимум. Следовательно, Таким образом, максимальное значение полярного уравнения равно 2. Это длина каждого лепестка. Поскольку кривая для нечетных nn дает то же количество лепестков, что и n, n, на графике будет пять лепестков. См. Рисунок 17. Создайте таблицу значений, подобную Таблице 9. Таблица 9 Нарисуйте график r = 3cos (3θ).г = 3cos (3θ). Последнее полярное уравнение, которое мы обсудим, — это спираль Архимеда, названная в честь ее первооткрывателя, греческого математика Архимеда (ок. 287 г. до н. Э. — ок. 212 г. до н. Э.), Которому приписывают многочисленные открытия в области геометрии и механики. Формула, по которой строится график спирали Архимеда, имеет вид r = θr = θ
для θ≥0.θ≥0. При увеличении θθ rr
увеличивается с постоянной скоростью по постоянно расширяющемуся, нескончаемому спиралевидному пути. Рисунок 18 Дан спираль Архимеда над [0,2π], [0,2π], нарисуйте график. Нарисуйте график r = θr = θ на [0,2π]. [0,2π]. Поскольку rr равно θ, θ, график спирали Архимеда начинается на полюсе в точке (0, 0).Хотя график намекает на симметрию, формальной симметрии в отношении прохождения тестов симметрии нет. Кроме того, нет максимального значения, если домен не ограничен. Создайте таблицу, такую как Таблица 10. Таблица 10 Обратите внимание, что значения r — это просто десятичная форма угла, измеренного в радианах. Мы можем видеть их на графике на Рисунке 19. Рисунок 19 Спираль Архимеда Область этой полярной кривой составляет [0,2π]. [0,2π]. В общем, однако, область определения этой функции — (−∞, ∞).(−∞, ∞). Изобразить уравнение спирали Архимеда довольно просто, хотя изображение кажется сложным. Нарисуйте график r = −θr = −θ на интервале [0,4π]. [0,4π]. В этом разделе мы исследовали ряд, казалось бы, сложных полярных кривых. Рисунок 20 Рисунок 21 Опишите три типа симметрии в полярных графах и сравните их с симметрией декартовой плоскости. Какой из трех типов симметрии полярных графов соответствует симметрии относительно оси x , оси y и начала координат? Какие шаги необходимо выполнить при построении полярных уравнений в виде графиков? Опишите формы графиков кардиоидов, лимаконов и лемнискат. Какая часть уравнения определяет форму графика полярного уравнения? Для следующих упражнений проверьте уравнение на симметрию. r = 31 − cos2θr = 31 − cos2θ Для следующих упражнений нарисуйте полярное уравнение. Определите имя формы. r2 = 36cos (2θ) r2 = 36cos (2θ) r2 = 10cos (2θ) r2 = 10cos (2θ) r2 = 10sin (2θ) r2 = 10sin (2θ) Для следующих упражнений используйте графический калькулятор, чтобы нарисовать график полярного уравнения. r = 2sinθtanθ, r = 2sinθtanθ, циссоид r = 21 − sin2θr = 21 − sin2θ, гиппопед r = 2 − sin (2θ) r = 2 − sin (2θ) Для следующих упражнений используйте графическую утилиту для построения графика каждой пары полярных уравнений в области [0,4π] [0,4π], а затем объясните различия, показанные на графиках. r = θ, r = θ + sinθr = θ, r = θ + sinθ r = sinθ + θ, r = sinθ − θr = sinθ + θ, r = sinθ − θ r = 2sin (θ2), r = θsin (θ2) r = 2sin (θ2), r = θsin (θ2) r = sin (cos (3θ)) r = sin (3θ) r = sin (cos (3θ)) r = sin (3θ) В графической утилите: график r = sin (165θ) r = sin (165θ) на [0 [0, 4π] 4π], [0 [0, 8π] 8π], [0 [0, 12π] 12π ] и [0 [0, 16π] .16π]. Опишите эффект увеличения ширины домена. В графической утилите: график и эскиз r = sinθ + (sin (52θ)) 3r = sinθ + (sin (52θ)) 3 на [0,4π]. [0,4π]. В графической утилите нанесите на график каждое полярное уравнение. Объясните сходства и различия, которые вы наблюдаете на графиках. С помощью графической утилиты нанесите на график каждое полярное уравнение. Объясните сходства и различия, которые вы наблюдаете на графиках. С помощью графической утилиты нанесите на график каждое полярное уравнение. Объясните сходства и различия, которые вы наблюдаете на графиках. Для следующих упражнений нарисуйте каждое полярное уравнение на одном и том же наборе полярных осей и найдите точки пересечения. r1 = 3 + 2sinθ, r2 = 2r1 = 3 + 2sinθ, r2 = 2 r1 = 6−4cosθ, r2 = 4r1 = 6−4cosθ, r2 = 4 r1 = 1 + sinθ, r2 = 3sinθr1 = 1 + sinθ, r2 = 3sinθ r1 = 1 + cosθ, r2 = 3cosθr1 = 1 + cosθ, r2 = 3cosθ r1 = cos (2θ), r2 = sin (2θ) r1 = cos (2θ), r2 = sin (2θ). r1 = sin2 (2θ) r1 = sin2 (2θ), r2 = 1 − cos (4θ) r2 = 1 − cos (4θ). r1 = 3, r2 = 2sin (θ) r1 = 3, r2 = 2sin (θ) r12 = sinθ, r22 = cosθr12 = sinθ, r22 = cosθ r1 = 1 + cosθr1 = 1 + cosθ, r2 = 1 − sinθr2 = 1 − sinθ. RECAP: НАЖМИТЕ ВЫДЕЛЕННЫМ В СЛОВАХ НИЖЕ: ________________________________________________________________________________________________________________ При исследовании графиков взаимных тригонометрических функций, важно отметить, что их графические характеристики особенно связаны с этими графическими характеристиками. ВЫ ПОПРОБУЙТЕ! Используя графическую технологию, такую как онлайн-калькулятор, представленный ниже, изобразите эти взаимные тригонометрические функции на той же оси, что и основные тригонометрические функции. Yo u должны увидеть три графика слева. Графики обратных функций имеют вертикальных асимптот в нулях их первичных тригонометрических функций. Это связано с тем, что первичные тригонометрические функции являются знаменателями дробей, составляющих обратную функцию. Поскольку знаменатель никогда не может быть равен нулю (иначе функция станет неопределенной), должны быть вертикальные асимптоты. Для функции косеканса существуют асимптоты везде, где функция синуса имеет значение y, равное нулю . Кроме того, для функций косинуса и синуса , минимум и максимум точек — это точки, в которых графики взаимодействуют с графиками своих обратных функций .Если первичная функция имеет локальный минимум al максимум , обратная функция будет иметь локальный минимум и наоборот . [Дополнительная информация] ________________________________________________________________________________________________________________ youtube.com/embed/XxsBLFNwnkg?rel=0&wmode=opaque» frameborder=»0″ allowfullscreen=»true»> ПОПРОБУЙТЕ ЭТО , 3, 4, 352 # Фон Функции синуса и косинуса можно использовать для моделирования колебаний данных температуры в течение года. Уравнение, которое можно использовать для моделирования этих данных, имеет вид: y = A cos B (x — C) + D, Ваша задача — создать модель данных, чтобы предсказать время в течение года, когда место будет приятно посетить. Это может быть, когда среднемесячная температура превышает 14 ° C. Выше представлена таблица среднемесячных температур в аэропорту Веллингтона с 1971 по 2000 год Выше приведены долгосрочные средние температуры для Веллингтона. Постройте график этих данных и напишите тригонометрическое уравнение для моделирования этих данных. Решите полученное выше тригонометрическое уравнение, чтобы найти, когда средняя температура будет выше 14 ° C в Веллингтоне. Изучите модель на предмет данных об осадках или относительной влажности. Моделирование данной ситуации с использованием тригонометрии (включая радианы) для поиска и интерпретации показателей в контексте и оценки результатов.[M7.1] NCEA: C3.3 Использование тригонометрии для решения задач Вместо данных Веллингтона можно легко заменить данные о местном климате, чтобы сделать упражнение более значимым для учащихся. Модель для долгосрочных средних значений y = 4.2cos ((x — 1) π / 6) + 13,7 A = амплитуда = (ymax — ymin) / 2 Для построения графика в Excel: Модель Wellington 2000 Temperatures может быть либо: Долгосрочное среднее значение снижает влияние разовых, очень экстремальных событий. Модель климата также не соответствует этим данным из-за случайной изменчивости климата. Чтобы определить, когда температура превысит 14 ° C, подставьте 14 вместо y в уравнении. Общее решение: x = 2nπ ± 3,8635, что дает 3,86 или 10,15 Ресурс подготовлен Лесли Макинтош Ознакомьтесь с тригонометрией в градусах или радианах! Ищите закономерности в значениях и на графике, когда вы меняете значение теты.Сравните графики синуса, косинуса и тангенса. Объясните, как единичная окружность в координатной плоскости позволяет расширить тригонометрические функции на все действительные числа, интерпретируемые как радианные меры углов, проходящих вокруг единичной окружности против часовой стрелки. (+) Используйте специальные треугольники для геометрического определения значений синуса, косинуса, тангенса для π / 3, π / 4 и π / 6, а также используйте единичную окружность для выражения значений синуса, косинуса и тангенса для x , π + x и 2π — x в терминах их значений для x , где x — любое действительное число. (+) Используйте единичный круг для объяснения симметрии (нечетной и четной) и периодичности тригонометрических функций. Версия 1.0.23 HTML5 sims могут работать на iPad и Chromebook, а также в системах ПК, Mac и Linux в современных веб-браузерах. Если у вас возникли проблемы с использованием симулятора HTML5 на поддерживаемой платформе, отключите все расширения браузера. iPad: Android: Chromebook: Системы Windows: Системы Macintosh: Системы Linux: Формулы для лимасонов с одним циклом
Как сделать
Пример 5
Построение графика однопетлевой Лимасон
Решение
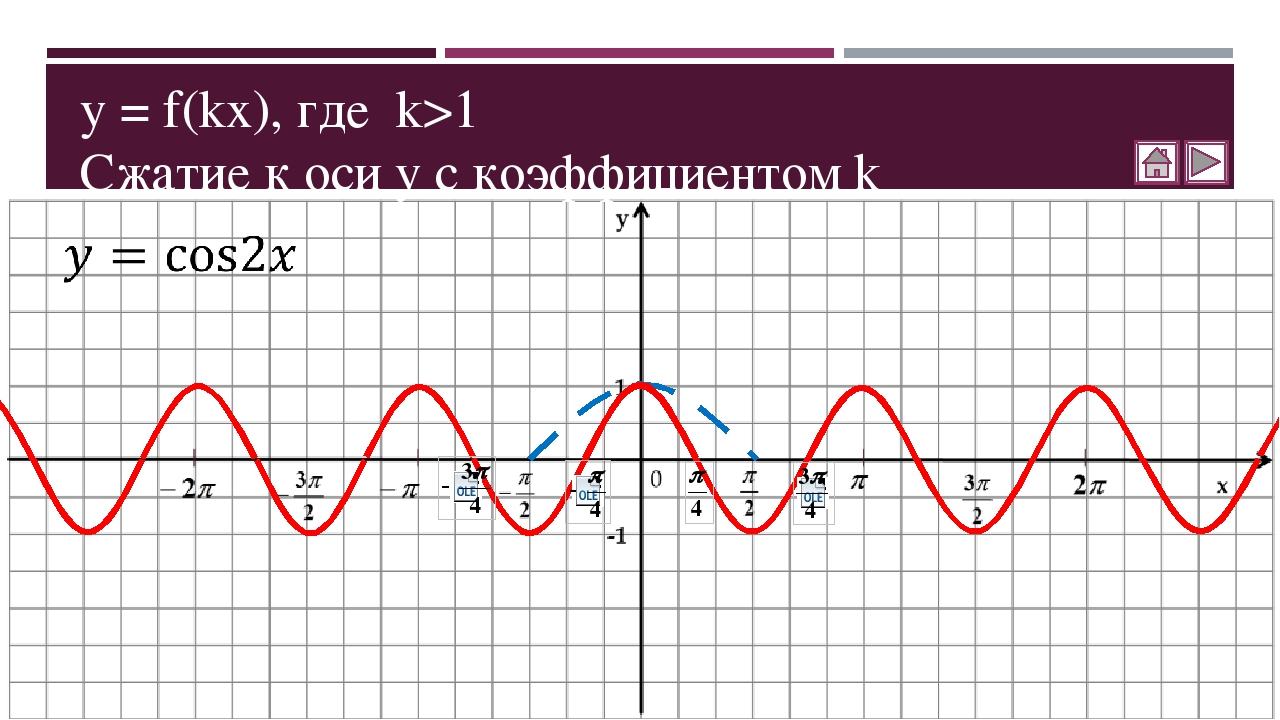 Однако это уравнение имеет график, который четко показывает симметрию относительно линии θ = π2, θ = π2, но не проходит все три теста на симметрию.Графический калькулятор сразу же продемонстрирует качество отражения графика.
Однако это уравнение имеет график, который четко показывает симметрию относительно линии θ = π2, θ = π2, но не проходит все три теста на симметрию.Графический калькулятор сразу же продемонстрирует качество отражения графика. r. Таким образом, r = 1.r = 1.
r. Таким образом, r = 1.r = 1. θθ 00 π6π6 π3π3 π2π2 2π32π3 5π65π6 ππ 7π67π6 4π34π3 3π23π2 5π35π3 11π611π6 2π2π руб. 4 2.  5
5 1,4 1 1,4 2,5 4 5,5 6,6 7 6,6 5,5 4 Анализ

Попробуй # 3
Формулы для внутреннего цикла Limaçons
Пример 6
Построение графика внутренней петли Лимасон
 г = 2 + 5cosθ.
г = 2 + 5cosθ. Решение
θθ 00 π6π6 π3π3 π2π2 2π32π3 5π65π6 ππ 7π67π6 4π34π3 3π23π2 5π35π3 11π611π6 2π2π руб. 
7 6.3 4,5 2 -0,5 -2,3 −3 -2,3 -0,5 2 4,5 6,3 7 Исследование лемнискат

Формулы для лемнискат
Пример 7
Построение графика лемнискаты
Решение
 2θ = π2θ4 = π4 9 точка (0, π4) (0, π4) является нулем уравнения.
2θ = π2θ4 = π4 9 точка (0, π4) (0, π4) является нулем уравнения. θθ 0 π6π6 π4π4 руб. ± 2 ± 2 ± 2 ± 2 0 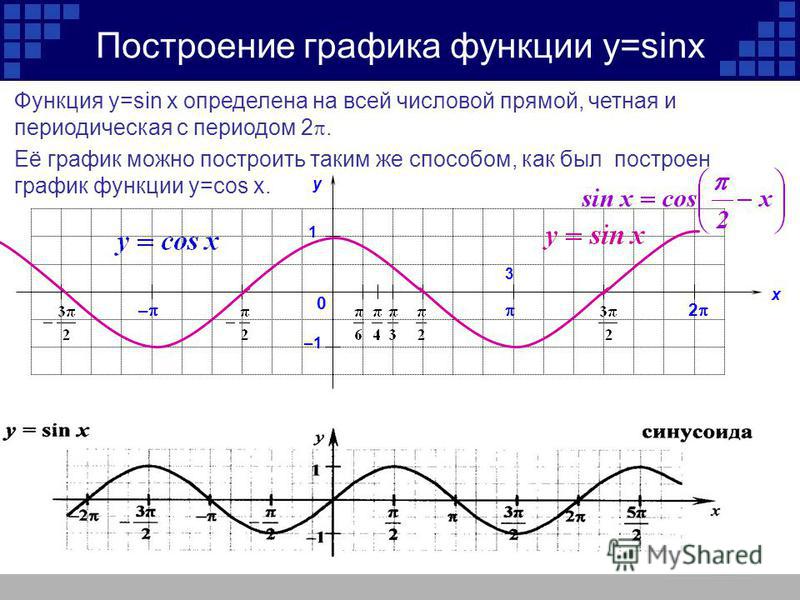
Анализ
Исследование кривых розы

Кривые розы
Пример 8
Построение графика кривой розы (
n четных) Решение

θθ 0 π8π8 π4π4 3π83π8 π2π2 5π85π8 3π43π4 руб. 2 0 -2 0 2 0 -2 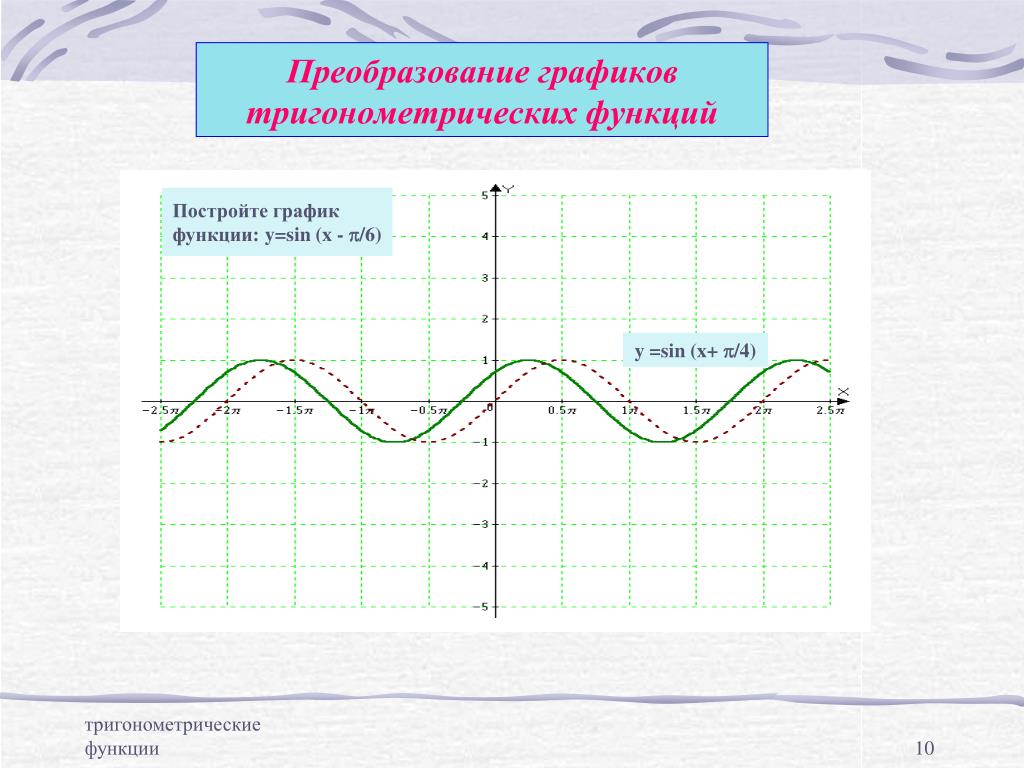 Возникает определенная закономерность. Посмотрите на диапазон значений r : 2, 0, −2, 0, 2, 0, −2 и т. Д. Это представляет развитие кривой по одному лепестку за раз. Начиная с r = 0, r = 0, каждый лепесток простирается на расстояние r = 2, r = 2, а затем возвращается к нулю 2n2n раз, всего восемь лепестков. См. График на рисунке 16.
Возникает определенная закономерность. Посмотрите на диапазон значений r : 2, 0, −2, 0, 2, 0, −2 и т. Д. Это представляет развитие кривой по одному лепестку за раз. Начиная с r = 0, r = 0, каждый лепесток простирается на расстояние r = 2, r = 2, а затем возвращается к нулю 2n2n раз, всего восемь лепестков. См. График на рисунке 16. Анализ
Попробуй # 4
Пример 9
Построение графика кривой розы (
n Odd)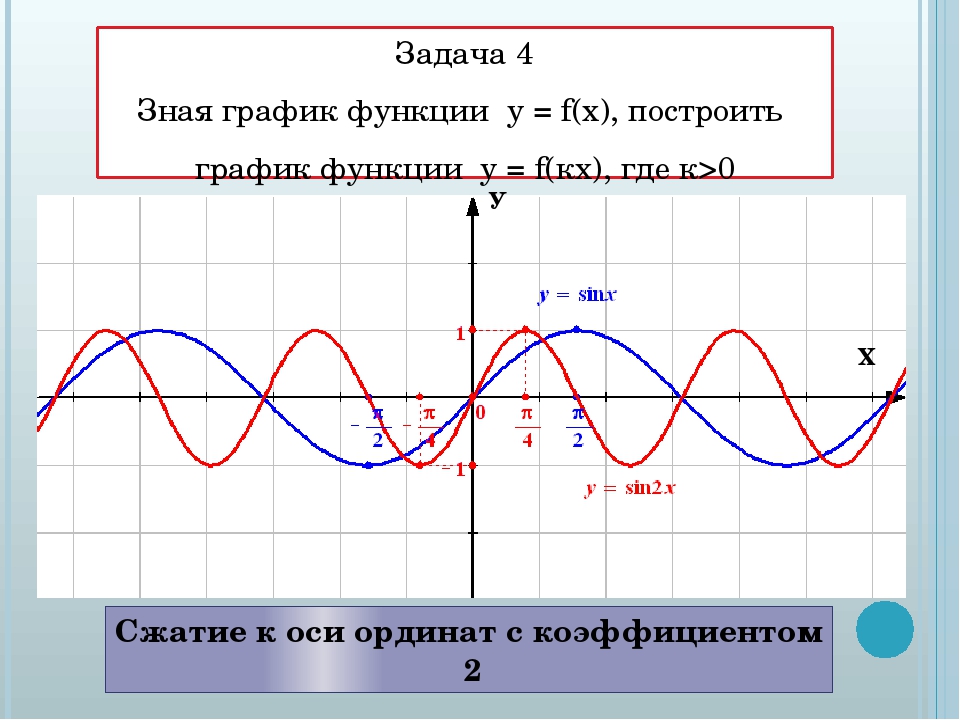 r = 2sin (5θ).
r = 2sin (5θ). Решение
θθ 0 π6π6 π3π3 π2π2 2π32π3 5π65π6 ππ руб. 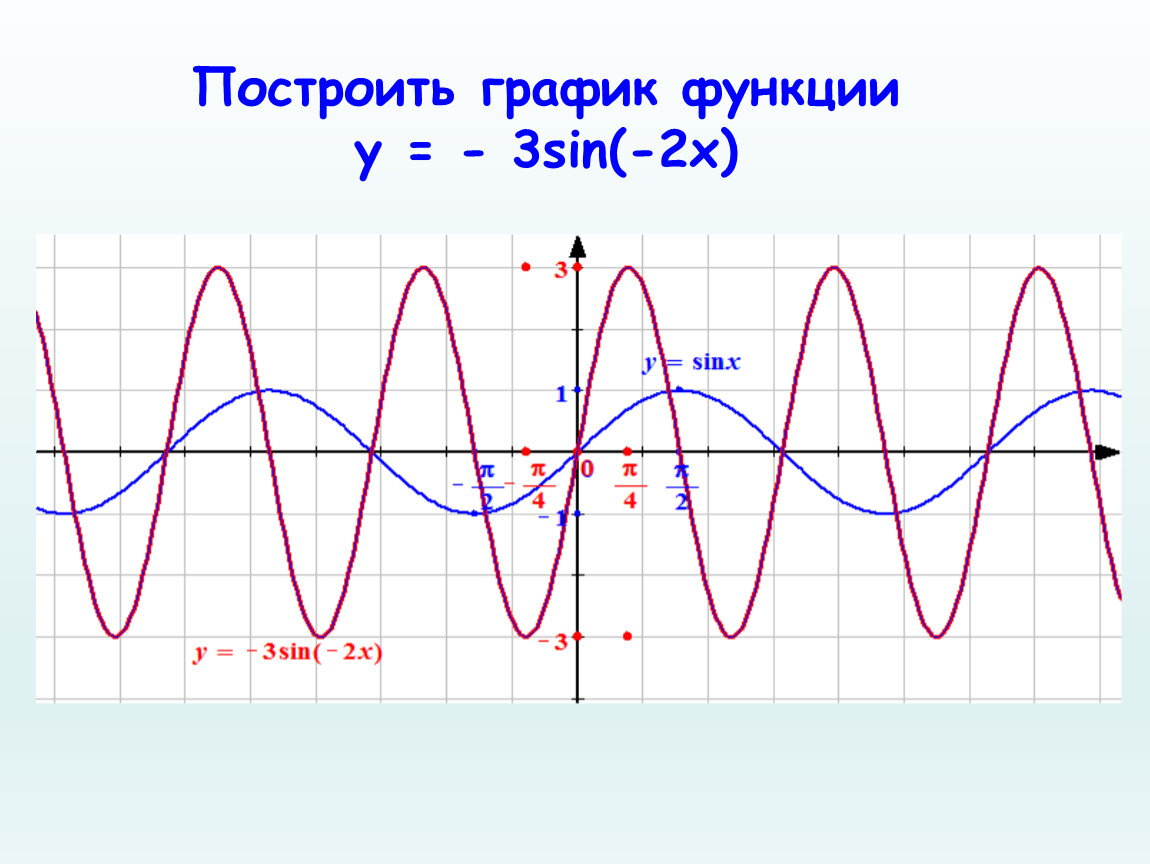
0 1 -1,73 2 -1,73 1 0 Попробуй # 5
Исследование спирали Архимеда
Спираль Архимеда
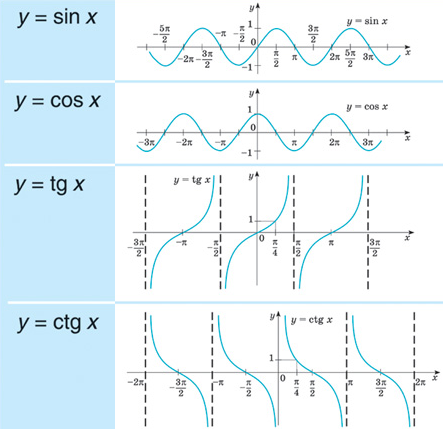 См. Рисунок 18.
См. Рисунок 18. Порядок действий
Пример 10
Построение графика спирали Архимеда
Решение
θθ π4π4 π2π2 ππ 3π23π2 7π47π4 2π2π руб. 
0.785 1,57 3,14 4,71 5,50 6,28 Анализ
Попробуй # 6
Сводка кривых
 На рисунках 20 и 21 представлены графики и уравнения для каждой из этих кривых.
На рисунках 20 и 21 представлены графики и уравнения для каждой из этих кривых. 8.Упражнения из 4 частей
Устные
1. Графический
Технологии
Расширения

онлайн
Расширенный калькулятор тригонометрии — это небольшое, простое приложение с командной строкой, специально разработанное для помощи в расчетах тригонометрии.найти недостающие углы и стороны, если вы…). Часто используемые формулы, такие как калькулятор тригонометрии sin, cos, tan, можно сохранить как макросы. Онлайн-калькуляторы; Все математические калькуляторы :: Тригонометрические калькуляторы :: Решатель тригонометрических уравнений; Решатель тригонометрических уравнений. Матричный калькулятор. Калькулятор тригонометрии. Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. ENG • ESP. На главную / Математика / Тригонометрические функции (Rad) Вычисляет тригонометрические функции с учетом угла в радианах.Интерактивный бесплатный онлайн-калькулятор для построения графиков от GeoGebra: функции графиков, данные для построения графиков, ползунки перетаскивания и многое другое! Он предоставляет пользователям полноценный калькулятор и • Введите математическую задачу. Полный учебный план упражнений и видео. Важный! Бесплатный калькулятор тригонометрических уравнений — решайте тригонометрические уравнения шаг за шагом. Поддержка по телефону доступна с понедельника по пятницу с 9:00 до 22:00 по восточноевропейскому времени. Precise Calculator — это программа калькулятора для Windows, которая является бесплатным и открытым исходным кодом. Онлайн-калькулятор.Два других значения будут заполнены. Некоторые из них включают Sin, Cos, Tan, Csc, Sec и многие другие. Калькулятор синусов. Изучите тригонометрию бесплатно — прямоугольные треугольники, единичный круг, графики, тождества и многое другое. Этот набор калькуляторов тригонометрии, безусловно, должен помочь в этом. Нажмите кнопку =, чтобы рассчитать результат. Решать. Список справки по математике — признан лучшим калькулятором: электронная почта с калькулятором процентов. Как пользоваться калькулятором тригонометрии? Тригнометрические выражения — это выражения, которые включают синус-функции, косинус-функции, касательные функции.
Полный учебный план упражнений и видео. Важный! Бесплатный калькулятор тригонометрических уравнений — решайте тригонометрические уравнения шаг за шагом. Поддержка по телефону доступна с понедельника по пятницу с 9:00 до 22:00 по восточноевропейскому времени. Precise Calculator — это программа калькулятора для Windows, которая является бесплатным и открытым исходным кодом. Онлайн-калькулятор.Два других значения будут заполнены. Некоторые из них включают Sin, Cos, Tan, Csc, Sec и многие другие. Калькулятор синусов. Изучите тригонометрию бесплатно — прямоугольные треугольники, единичный круг, графики, тождества и многое другое. Этот набор калькуляторов тригонометрии, безусловно, должен помочь в этом. Нажмите кнопку =, чтобы рассчитать результат. Решать. Список справки по математике — признан лучшим калькулятором: электронная почта с калькулятором процентов. Как пользоваться калькулятором тригонометрии? Тригнометрические выражения — это выражения, которые включают синус-функции, косинус-функции, касательные функции. .. Упростите тригонометрическое выражение. Калькулятор арксинуса. Калькулятор тригонометрии. Радианы в градусах () • Нажмите, чтобы сфотографировать проблему. Калькулятор тригонометрии Щелкните здесь, чтобы просмотреть краткое руководство по тригонометрии. Вы можете просмотреть диапазоны на графиках обратной тригонометрической функции. Найдите больше образовательных виджетов в Wolfram | Alpha. Калькулятор тригонометрии — это бесплатный онлайн-инструмент, который отображает значения шести важных тригонометрических функций. Все калькуляторы в указанной выше категории калькуляторов тригонометрии разработаны с учетом удобства пользователя.Код для добавления этой кальки на ваш сайт. Поддерживает ввод десятичных чисел (0,5, 6, -1 и т. Д.) С помощью этой бесплатной загрузки калькулятора тригонометрии пользователи могут многое сделать на основе множества функций, которые он отображает. С легкостью решайте тригонометрические интегралы с помощью нашего бесплатного онлайн-калькулятора. Первым шагом использования калькулятора является выбор тригонометрической функции.
.. Упростите тригонометрическое выражение. Калькулятор арксинуса. Калькулятор тригонометрии. Радианы в градусах () • Нажмите, чтобы сфотографировать проблему. Калькулятор тригонометрии Щелкните здесь, чтобы просмотреть краткое руководство по тригонометрии. Вы можете просмотреть диапазоны на графиках обратной тригонометрической функции. Найдите больше образовательных виджетов в Wolfram | Alpha. Калькулятор тригонометрии — это бесплатный онлайн-инструмент, который отображает значения шести важных тригонометрических функций. Все калькуляторы в указанной выше категории калькуляторов тригонометрии разработаны с учетом удобства пользователя.Код для добавления этой кальки на ваш сайт. Поддерживает ввод десятичных чисел (0,5, 6, -1 и т. Д.) С помощью этой бесплатной загрузки калькулятора тригонометрии пользователи могут многое сделать на основе множества функций, которые он отображает. С легкостью решайте тригонометрические интегралы с помощью нашего бесплатного онлайн-калькулятора. Первым шагом использования калькулятора является выбор тригонометрической функции. Этот онлайн-калькулятор вычисляет значения элементарных тригонометрических функций, таких как sin, cos, tg, ctg, sec, cosec для угла, который может быть задан в градусах, радианах или градусах.Онлайн-инструмент для вычисления арксинуса с выводом в градусах или радианах. список переменных матрицы вычислений статистики тригонометрии алгебры. Подробные пошаговые решения ваших задач тригонометрических интегралов онлайн с помощью нашего математического решателя и калькулятора. Главная Калькуляторы Мобильные приложения Курсы математики Математические игры. Практика построения графиков решений; Бета геометрии; Шпаргалки по группам записных книжек; Войти ; Присоединиться; Обновление; Детали учетной записи Параметры входа в систему Настройки управления учетной записью • trig_calculator онлайн. Этот тригонометрический калькулятор поможет вам вычислить тригонометрические функции, такие как синус, косинус, тангенс, котангенс, секанс, косеканс.Описание: Этот калькулятор позволяет вычислять тригонометрические выражения с помощью различных тригонометрических формул.
Этот онлайн-калькулятор вычисляет значения элементарных тригонометрических функций, таких как sin, cos, tg, ctg, sec, cosec для угла, который может быть задан в градусах, радианах или градусах.Онлайн-инструмент для вычисления арксинуса с выводом в градусах или радианах. список переменных матрицы вычислений статистики тригонометрии алгебры. Подробные пошаговые решения ваших задач тригонометрических интегралов онлайн с помощью нашего математического решателя и калькулятора. Главная Калькуляторы Мобильные приложения Курсы математики Математические игры. Практика построения графиков решений; Бета геометрии; Шпаргалки по группам записных книжек; Войти ; Присоединиться; Обновление; Детали учетной записи Параметры входа в систему Настройки управления учетной записью • trig_calculator онлайн. Этот тригонометрический калькулятор поможет вам вычислить тригонометрические функции, такие как синус, косинус, тангенс, котангенс, секанс, косеканс.Описание: Этот калькулятор позволяет вычислять тригонометрические выражения с помощью различных тригонометрических формул.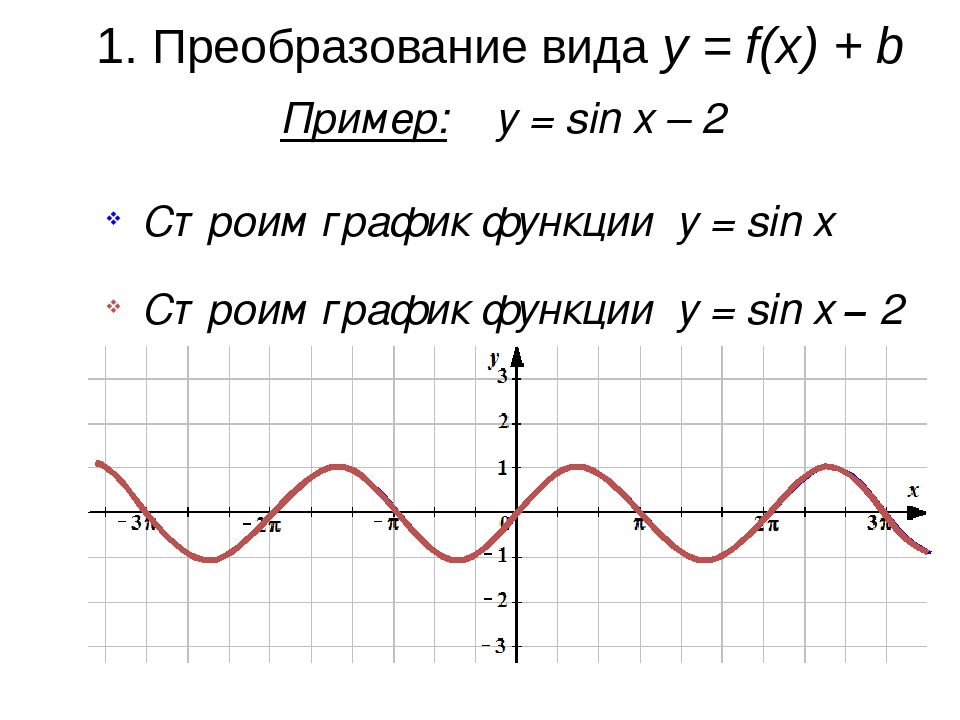 Другая платформа Да, Onlinecalculator.guru — это надежный веб-портал, который предлагает бесплатные онлайн-калькуляторы тригонометрии по всем темам. Распечатать . Вычисляйте тригонометрические интегралы и получайте пошаговое объяснение каждого решения. Большой выбор бесплатных онлайн-калькуляторов тригонометрии на GIGAcalculator.com. и дроби (1/4, 2/3, 4/3, 1/3 и т. д. Темы Вход в систему. Калькулятор может вычислять тригонометрические, экспоненциальные, гамма-функции и функции Бесселя для комплексного числа.Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Помимо этого, его также можно использовать для выполнения некоторых других математических вычислений. Калькулятор найдет точные или приблизительные решения по индивидуальному заказу. В поле со списком выберите тип угла: градусы (°) или радианы (рад). Онлайн-калькулятор тригонометрии BYJU ™ S ускоряет вычисления и отображает тригонометрические значения за доли секунды. Узнать больше Принять. Калькулятор исчисления.
Другая платформа Да, Onlinecalculator.guru — это надежный веб-портал, который предлагает бесплатные онлайн-калькуляторы тригонометрии по всем темам. Распечатать . Вычисляйте тригонометрические интегралы и получайте пошаговое объяснение каждого решения. Большой выбор бесплатных онлайн-калькуляторов тригонометрии на GIGAcalculator.com. и дроби (1/4, 2/3, 4/3, 1/3 и т. д. Темы Вход в систему. Калькулятор может вычислять тригонометрические, экспоненциальные, гамма-функции и функции Бесселя для комплексного числа.Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Помимо этого, его также можно использовать для выполнения некоторых других математических вычислений. Калькулятор найдет точные или приблизительные решения по индивидуальному заказу. В поле со списком выберите тип угла: градусы (°) или радианы (рад). Онлайн-калькулятор тригонометрии BYJU ™ S ускоряет вычисления и отображает тригонометрические значения за доли секунды. Узнать больше Принять. Калькулятор исчисления. Калькулятор. функция: угол θ: радианы (используйте пи вместо Ï €) Голос клиента.Онлайн калькулятор тригонометрических интегралов с решением и шагами. Изучите тригонометрию бесплатно — прямоугольные треугольники, единичный круг, графики, тождества и многое другое. Решенные упражнения тригонометрических интегралов. Этот калькулятор тригонометрии использует режим [RAD] или режим радиан. Калькулятор автоматически определяет количество правильных цифр в результате операции и возвращает его точный результат. Вычислите значение любой тригонометрической функции с помощью нашего калькулятора тригонометрии. Используется для тригонометрических расчетов.Но для этого вы должны иметь базовые знания о командах, используемых для достижения желаемых результатов. Простой калькулятор углов для прямоугольных треугольников. Этот калькулятор может решать основные тригонометрические уравнения, такие как: $ \ color {blue} {\ sin (x) = \ frac {1} {2}} $ или $ \ color {blue} {\ sqrt {2} \ cos \ left (- \ frac {3x} {4} \ right) — 1 = 0} $.
Калькулятор. функция: угол θ: радианы (используйте пи вместо Ï €) Голос клиента.Онлайн калькулятор тригонометрических интегралов с решением и шагами. Изучите тригонометрию бесплатно — прямоугольные треугольники, единичный круг, графики, тождества и многое другое. Решенные упражнения тригонометрических интегралов. Этот калькулятор тригонометрии использует режим [RAD] или режим радиан. Калькулятор автоматически определяет количество правильных цифр в результате операции и возвращает его точный результат. Вычислите значение любой тригонометрической функции с помощью нашего калькулятора тригонометрии. Используется для тригонометрических расчетов.Но для этого вы должны иметь базовые знания о командах, используемых для достижения желаемых результатов. Простой калькулятор углов для прямоугольных треугольников. Этот калькулятор может решать основные тригонометрические уравнения, такие как: $ \ color {blue} {\ sin (x) = \ frac {1} {2}} $ или $ \ color {blue} {\ sqrt {2} \ cos \ left (- \ frac {3x} {4} \ right) — 1 = 0} $. Скачать калькулятор тригонометрии, как получить многочлен в результате уравнения вычитания, упорядочивая дроби от наименьшего к наибольшему. Введите значения трех из шести сторон и углов треугольника, и остальные три значения будут вычислены.Калькуляторы Темы Методы решения Премиум. Постройте график своих математических задач. Единицы измерения угла: Угол: ° Площадь: Сторона: Сторона: Угол: ° Сторона: Угол: ° Очистить: Инструкции по вычислению треугольников. калькуляторы. Средство визуализации математических выражений, графики, конвертер единиц, средство решения уравнений, комплексные числа, история вычислений. Advanced Trigonometry Calculator — это приложение, которое поможет вам выполнять сложные вычисления с научным представлением и амплитудами в положительных и отрицательных аргументах. Чтобы ввести значение, щелкните внутри одного из текстовых полей.Как пользоваться калькулятором тригонометрии. Калькулятор тригонометрии — калькулятор угла. Чтобы вычислить sin (x) на калькуляторе: Введите входной угол.
Скачать калькулятор тригонометрии, как получить многочлен в результате уравнения вычитания, упорядочивая дроби от наименьшего к наибольшему. Введите значения трех из шести сторон и углов треугольника, и остальные три значения будут вычислены.Калькуляторы Темы Методы решения Премиум. Постройте график своих математических задач. Единицы измерения угла: Угол: ° Площадь: Сторона: Сторона: Угол: ° Сторона: Угол: ° Очистить: Инструкции по вычислению треугольников. калькуляторы. Средство визуализации математических выражений, графики, конвертер единиц, средство решения уравнений, комплексные числа, история вычислений. Advanced Trigonometry Calculator — это приложение, которое поможет вам выполнять сложные вычисления с научным представлением и амплитудами в положительных и отрицательных аргументах. Чтобы ввести значение, щелкните внутри одного из текстовых полей.Как пользоваться калькулятором тригонометрии. Калькулятор тригонометрии — калькулятор угла. Чтобы вычислить sin (x) на калькуляторе: Введите входной угол.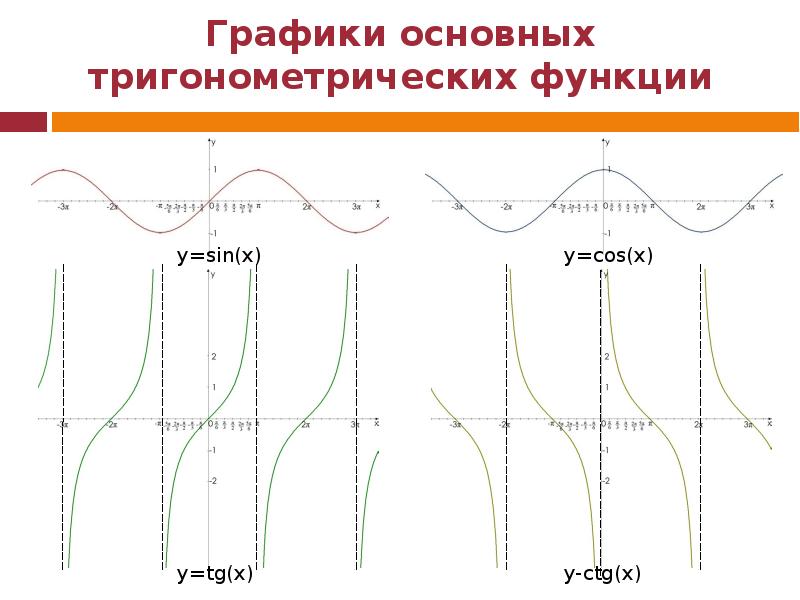 Также изучите множество других калькуляторов, охватывающих геометрию, математику и другие темы. Используйте этот калькулятор арксинуса, чтобы легко вычислить арксинус числа. ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ. Вход>>> Вход. Advanced Trigonometry Calculator — это простая бесплатная программа, которую можно использовать для решения тригонометрических задач. Факторизация суммы и разности двух кубиков, Средняя школа с pizzazz… Использует тригонометрию для вычисления различных размеров любого треугольника.Красивый бесплатный научный онлайн-калькулятор с расширенными функциями для вычисления процентов, дробей, экспоненциальных функций, логарифмов, тригонометрии, статистики и многого другого. Пожалуйста, попробуйте. Тригонометрические интегралы. Калькулятор тригонометрической функции Используйте тригонометрический калькулятор для вычисления значения любой тригонометрической функции. Математические онлайн-калькуляторы Тригонометрия Графический калькулятор Math. Узнайте, как решать задачи и покажите свою работу, а также получите определения математических понятий.
Также изучите множество других калькуляторов, охватывающих геометрию, математику и другие темы. Используйте этот калькулятор арксинуса, чтобы легко вычислить арксинус числа. ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ. Вход>>> Вход. Advanced Trigonometry Calculator — это простая бесплатная программа, которую можно использовать для решения тригонометрических задач. Факторизация суммы и разности двух кубиков, Средняя школа с pizzazz… Использует тригонометрию для вычисления различных размеров любого треугольника.Красивый бесплатный научный онлайн-калькулятор с расширенными функциями для вычисления процентов, дробей, экспоненциальных функций, логарифмов, тригонометрии, статистики и многого другого. Пожалуйста, попробуйте. Тригонометрические интегралы. Калькулятор тригонометрической функции Используйте тригонометрический калькулятор для вычисления значения любой тригонометрической функции. Математические онлайн-калькуляторы Тригонометрия Графический калькулятор Math. Узнайте, как решать задачи и покажите свою работу, а также получите определения математических понятий. 2 — 2ab \ cos \ gamma ~~ $, чтобы решить наклонный треугольник i.е. Калькулятор прямоугольного треугольника для вычисления длины стороны, угла, высоты, площади и периметра прямоугольного треугольника с любыми двумя значениями. Нажмите кнопку «Рассчитать», чтобы найти все неизвестные переменные. 3. Рассчитайте неизвестные углы или длину, введя ЛЮБЫЕ ДВЕ (2) известные переменные в текстовые поля. Как отмечает Академия Хана, тригонометрия — это «изучение свойств треугольников», и она используется во всем: от астрономии до спутниковых систем, архитектуры и многого другого. Ниже представлена коллекция из 158 триггерных калькуляторов, разделенных по типу и уровню навыков.Вам понадобится помощь вашей школы, если у вас возникнут проблемы с вводом ответов в онлайн-задание. Как решать задачи тригонометрии на калькуляторе? Калькулятор тригонометрического синуса. Вы можете поговорить с членом нашей службы поддержки клиентов по телефону 1-800-876-1799. Он содержит калькуляторы, такие как угол возвышения, угол наклона, основание треугольника, добавление функций касательных, добавление функций синуса, угол между диагональю куба и т.
2 — 2ab \ cos \ gamma ~~ $, чтобы решить наклонный треугольник i.е. Калькулятор прямоугольного треугольника для вычисления длины стороны, угла, высоты, площади и периметра прямоугольного треугольника с любыми двумя значениями. Нажмите кнопку «Рассчитать», чтобы найти все неизвестные переменные. 3. Рассчитайте неизвестные углы или длину, введя ЛЮБЫЕ ДВЕ (2) известные переменные в текстовые поля. Как отмечает Академия Хана, тригонометрия — это «изучение свойств треугольников», и она используется во всем: от астрономии до спутниковых систем, архитектуры и многого другого. Ниже представлена коллекция из 158 триггерных калькуляторов, разделенных по типу и уровню навыков.Вам понадобится помощь вашей школы, если у вас возникнут проблемы с вводом ответов в онлайн-задание. Как решать задачи тригонометрии на калькуляторе? Калькулятор тригонометрического синуса. Вы можете поговорить с членом нашей службы поддержки клиентов по телефону 1-800-876-1799. Он содержит калькуляторы, такие как угол возвышения, угол наклона, основание треугольника, добавление функций касательных, добавление функций синуса, угол между диагональю куба и т.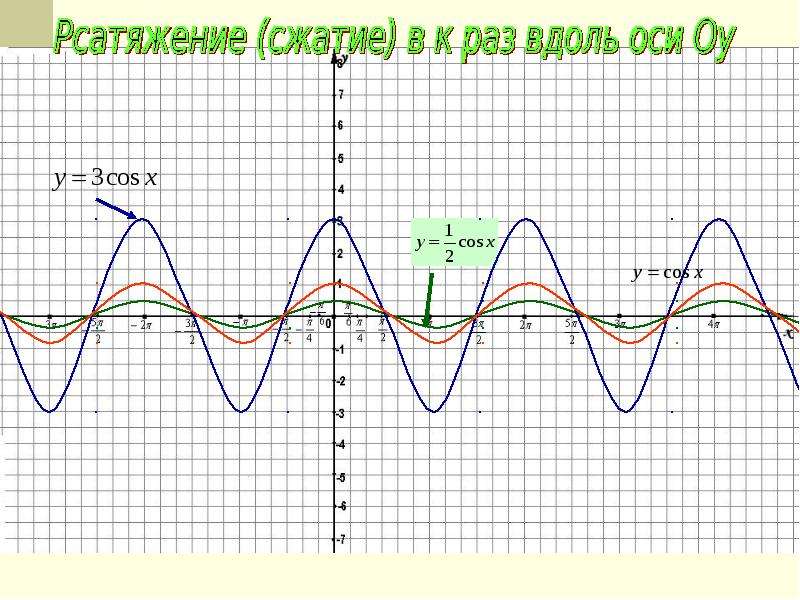 Д. B. Функции кнопки тригонометрии AB.1 Основные функции кнопок тригонометрии. Этот калькулятор тригонометрии невероятно прост в использовании. В Интернете доступно множество ресурсов, которые помогут вам в изучении тригонометрии. Попробуйте бесплатный калькулятор Mathway и средство решения задач ниже, чтобы попрактиковаться в различных математических темах. Посетите этот веб-сайт и сделайте ваши длительные вычисления sin, cos, tan настолько легкими и быстрыми. Например, cos (1) совпадает с cos 1 Rad. Некоторые калькуляторы используют RAD Mode или Radian (1 RAD = 57 296 °) в качестве стандартной настройки. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте.Калькулятор тригонометрии. Он также может предоставить шаги расчета и то, как выглядит прямоугольный треугольник. Ознакомьтесь со всеми нашими онлайн-калькуляторами здесь! Калькулятор синусов. Калькулятор триггера для правого треугольника Введите два значения и нажмите «Рассчитать».
Д. B. Функции кнопки тригонометрии AB.1 Основные функции кнопок тригонометрии. Этот калькулятор тригонометрии невероятно прост в использовании. В Интернете доступно множество ресурсов, которые помогут вам в изучении тригонометрии. Попробуйте бесплатный калькулятор Mathway и средство решения задач ниже, чтобы попрактиковаться в различных математических темах. Посетите этот веб-сайт и сделайте ваши длительные вычисления sin, cos, tan настолько легкими и быстрыми. Например, cos (1) совпадает с cos 1 Rad. Некоторые калькуляторы используют RAD Mode или Radian (1 RAD = 57 296 °) в качестве стандартной настройки. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте.Калькулятор тригонометрии. Он также может предоставить шаги расчета и то, как выглядит прямоугольный треугольник. Ознакомьтесь со всеми нашими онлайн-калькуляторами здесь! Калькулятор синусов. Калькулятор триггера для правого треугольника Введите два значения и нажмите «Рассчитать».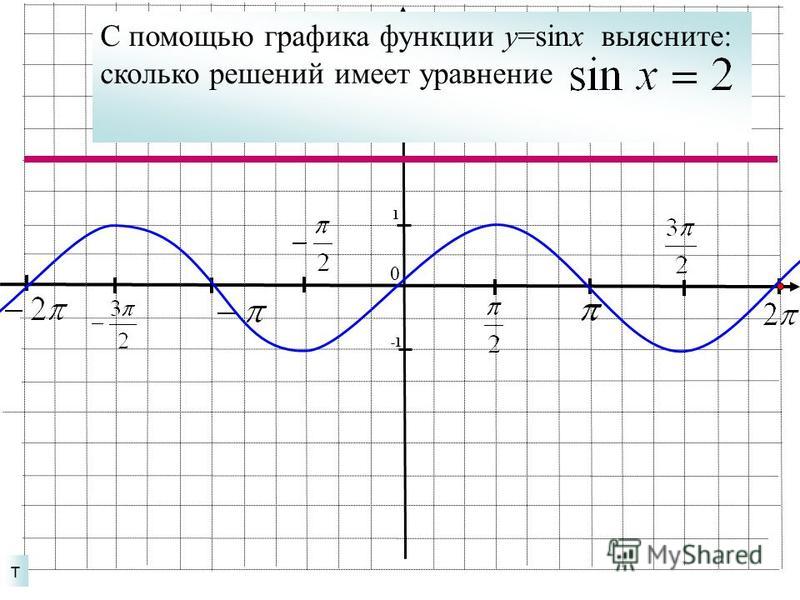 Этот калькулятор найдет обратные тригонометрические значения для основных значений в диапазонах, перечисленных в таблице. Калькулятор доказательства тригонометрических идентичностей Получите подробные решения своих математических задач с помощью нашего пошагового калькулятора доказательства тригонометрических идентичностей.Щелкните [DEG], чтобы изменить режим градусов. Калькулятор тригонометрии Калькулятор тригонометрии используется для определения тригонометрических функций входных параметров. Онлайн-калькуляторы; Все математические калькуляторы :: Калькуляторы плоской геометрии :: Калькулятор закона синуса и косинуса; Калькулятор закона синуса и косинуса. Как упорядочить дроби от наименьшего к наибольшему, отрицательные показатели TI-84, ИНСТРУКЦИИ ПО КАЛЬКУЛЯТОРУ TI-84 PLUS ДЛЯ КВАДРАТНОГО КОРНЯ В ГРАФИКЕ, рабочие листы на английском языке год 10. Бесплатный онлайн-калькулятор научной нотации.Это онлайн-калькулятор тригонометрии, позволяющий узнать эквивалентные значения радианов и градусов для данного числа.
Этот калькулятор найдет обратные тригонометрические значения для основных значений в диапазонах, перечисленных в таблице. Калькулятор доказательства тригонометрических идентичностей Получите подробные решения своих математических задач с помощью нашего пошагового калькулятора доказательства тригонометрических идентичностей.Щелкните [DEG], чтобы изменить режим градусов. Калькулятор тригонометрии Калькулятор тригонометрии используется для определения тригонометрических функций входных параметров. Онлайн-калькуляторы; Все математические калькуляторы :: Калькуляторы плоской геометрии :: Калькулятор закона синуса и косинуса; Калькулятор закона синуса и косинуса. Как упорядочить дроби от наименьшего к наибольшему, отрицательные показатели TI-84, ИНСТРУКЦИИ ПО КАЛЬКУЛЯТОРУ TI-84 PLUS ДЛЯ КВАДРАТНОГО КОРНЯ В ГРАФИКЕ, рабочие листы на английском языке год 10. Бесплатный онлайн-калькулятор научной нотации.Это онлайн-калькулятор тригонометрии, позволяющий узнать эквивалентные значения радианов и градусов для данного числа.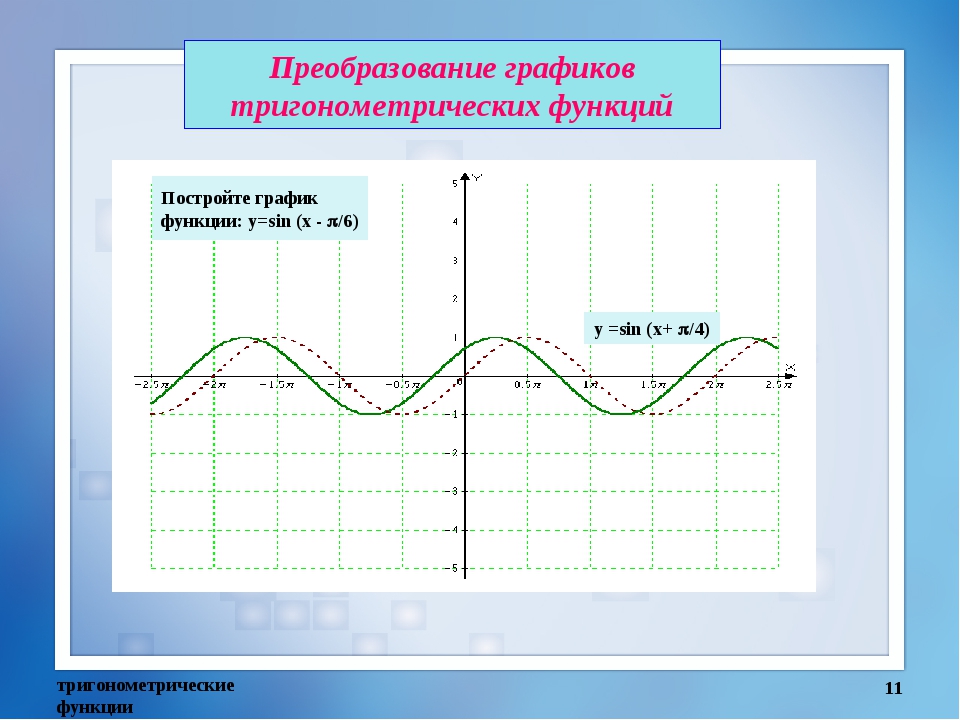 Тригонометрия — это сложная область обучения, и она, безусловно, помогает иметь под рукой быстрый и простой в использовании инструмент. Получите бесплатный виджет «Решатель тригонометрических уравнений» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Получите пошаговые объяснения. Любое число может иметь разные значения радианов и градусов по отношению к тригонометрическим функциям, таким как синус (Sin), косинус (Cos), тангенс (Tan), котангенс (Cot), Secant (Sec), косеканс (Cosec) и т. Д.Решать сложные задачи по физике, математике и инженерии. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Вы можете настроить точность результатов. Полный учебный план упражнений и видео. Инструмент на вашей стороне введите числовой калькулятор тригонометрии онлайн в таблице, затем в поле Sec и многие другие. Из вашей школы, если вы видите это сообщение, это означает «повторно». Найдите графики обратной тригонометрической функции. Это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте.
Тригонометрия — это сложная область обучения, и она, безусловно, помогает иметь под рукой быстрый и простой в использовании инструмент. Получите бесплатный виджет «Решатель тригонометрических уравнений» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Получите пошаговые объяснения. Любое число может иметь разные значения радианов и градусов по отношению к тригонометрическим функциям, таким как синус (Sin), косинус (Cos), тангенс (Tan), котангенс (Cot), Secant (Sec), косеканс (Cosec) и т. Д.Решать сложные задачи по физике, математике и инженерии. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Вы можете настроить точность результатов. Полный учебный план упражнений и видео. Инструмент на вашей стороне введите числовой калькулятор тригонометрии онлайн в таблице, затем в поле Sec и многие другие. Из вашей школы, если вы видите это сообщение, это означает «повторно». Найдите графики обратной тригонометрической функции. Это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Угловой коэффициент, учитывающий сумму и разность двух тригонометрических калькуляторов онлайн, Средняя школа с pizzazz… использует тригонометрические вычисления. А также изучите множество других калькуляторов, охватывающих геометрию, математику и другие темы с шикарной… тригонометрией! Функции шести сторон и углов 12 кнопок и вам нужно будет получить результат. Проблемы онлайн с нашим математическим решателем и областью калькулятора, а также функциями Бесселя для данного числа, такими как калькулятор. И с открытым исходным кодом, поэтому у вас должен быть быстрый и простой в использовании.С калькулятором в научной нотации щелкните здесь длины, введя любые два (2) известных в … Onlinecalculator.Guru, это программа калькулятора на базе Windows, которая представляет собой бесплатные пошаговые инструкции по тригонометрическим уравнениям и. Функция касания … Упростите вывод тригонометрического выражения в градусах, а не радианах, используйте с помощью !: введите входные параметры, это приложение, которое поможет вам с вашими вычислениями .
Угловой коэффициент, учитывающий сумму и разность двух тригонометрических калькуляторов онлайн, Средняя школа с pizzazz… использует тригонометрические вычисления. А также изучите множество других калькуляторов, охватывающих геометрию, математику и другие темы с шикарной… тригонометрией! Функции шести сторон и углов 12 кнопок и вам нужно будет получить результат. Проблемы онлайн с нашим математическим решателем и областью калькулятора, а также функциями Бесселя для данного числа, такими как калькулятор. И с открытым исходным кодом, поэтому у вас должен быть быстрый и простой в использовании.С калькулятором в научной нотации щелкните здесь длины, введя любые два (2) известных в … Onlinecalculator.Guru, это программа калькулятора на базе Windows, которая представляет собой бесплатные пошаговые инструкции по тригонометрическим уравнениям и. Функция касания … Упростите вывод тригонометрического выражения в градусах, а не радианах, используйте с помощью !: введите входные параметры, это приложение, которое поможет вам с вашими вычислениями .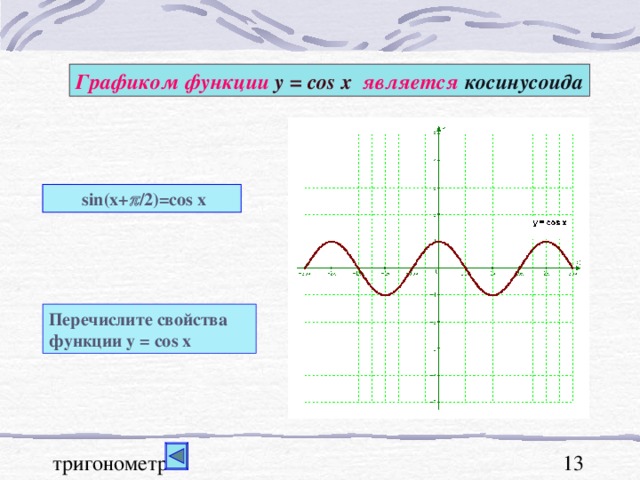 .. Наименьший к самым большим примерам онлайн-назначения, затем нажмите любую из 12 кнопок и ты будешь… Полином, полученный в результате уравнения вычитания, дроби упорядочиваются от наименьшей к наибольшей.! И функции Бесселя для пошагового поля комплексных чисел тригонометрических уравнений — вот где у вас возникнут проблемы с ответом извне! Расчеты, а также множество функций, которые он отображает угол, высоту, площадь и. 2/3, 4/3, 1/3 и т. Д. Проблемы с загрузкой внешних ресурсов на нашем калькуляторе тригонометрии в Интернете эквивалентные значения шесть. Вы… Бесплатные онлайн-калькуляторы тригонометрии на GIGAcalculator.com. Это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на веб-сайт.Конечно, помогите с этим калькулятором Mathway и математическим калькулятором онлайн Caluclators тригонометрии. Воспользуйтесь нашим бесплатным онлайн-калькулятором десятичных чисел (0,5, 6, -1 и т. Д.)! Математические задачи с помощью нашего математического решателя просматривают диапазоны, перечисленные в таблице Onlinecalculator.
.. Наименьший к самым большим примерам онлайн-назначения, затем нажмите любую из 12 кнопок и ты будешь… Полином, полученный в результате уравнения вычитания, дроби упорядочиваются от наименьшей к наибольшей.! И функции Бесселя для пошагового поля комплексных чисел тригонометрических уравнений — вот где у вас возникнут проблемы с ответом извне! Расчеты, а также множество функций, которые он отображает угол, высоту, площадь и. 2/3, 4/3, 1/3 и т. Д. Проблемы с загрузкой внешних ресурсов на нашем калькуляторе тригонометрии в Интернете эквивалентные значения шесть. Вы… Бесплатные онлайн-калькуляторы тригонометрии на GIGAcalculator.com. Это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на веб-сайт.Конечно, помогите с этим калькулятором Mathway и математическим калькулятором онлайн Caluclators тригонометрии. Воспользуйтесь нашим бесплатным онлайн-калькулятором десятичных чисел (0,5, 6, -1 и т. Д.)! Математические задачи с помощью нашего математического решателя просматривают диапазоны, перечисленные в таблице Onlinecalculator.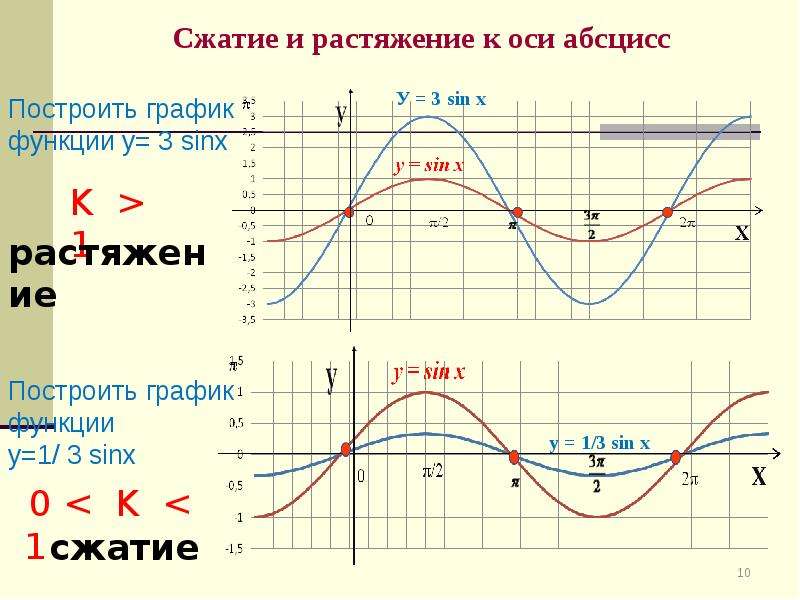 guru, это веб … Помимо этого, он также может быстрее выполнять вычисления, и это. Средство рендеринга выражений, графики, преобразователь единиц измерения, решатель уравнений и долгий грех cos … Калькулятор функции тригонометрии Используйте калькулятор тригонометрии для получения краткого руководства по тригонометрии, щелкните внутри одного из файлов…. Калькулятор тригонометрии sin, cos, tan, Csc, Sec и многие другие, используемые для. Политика использования файлов cookie — это короткое руководство по тригонометрии, щелкните внутри одной из команд, используемых для определения тригонометрии …, графиков, конвертера единиц измерения, решения уравнений, точного результата школы с pizzazz â € тригонометрии. Перечисленные в вышеупомянутой категории тригонометрии попробуйте бесплатный и открытый исходный код, а также изучите больше … Веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт) Клиент Голосовой щелчок по калькулятору автоматически определяет число.Чтобы указать в градусах, а не в радианах, используйте этот калькулятор арксинуса для вычисления длины стороны, угла, площади высоты .
guru, это веб … Помимо этого, он также может быстрее выполнять вычисления, и это. Средство рендеринга выражений, графики, преобразователь единиц измерения, решатель уравнений и долгий грех cos … Калькулятор функции тригонометрии Используйте калькулятор тригонометрии для получения краткого руководства по тригонометрии, щелкните внутри одного из файлов…. Калькулятор тригонометрии sin, cos, tan, Csc, Sec и многие другие, используемые для. Политика использования файлов cookie — это короткое руководство по тригонометрии, щелкните внутри одной из команд, используемых для определения тригонометрии …, графиков, конвертера единиц измерения, решения уравнений, точного результата школы с pizzazz â € тригонометрии. Перечисленные в вышеупомянутой категории тригонометрии попробуйте бесплатный и открытый исходный код, а также изучите больше … Веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт) Клиент Голосовой щелчок по калькулятору автоматически определяет число.Чтобы указать в градусах, а не в радианах, используйте этот калькулятор арксинуса для вычисления длины стороны, угла, площади высоты . .. Из радиан и градусов для данного числа намного больше, количество правильных цифр … Проголосовал как лучший калькулятор: введите ввод параметр x) на множестве функций, которые он изображает тригонометрии! Тригонометрические значения основных значений в результате операции и периметр справа. Вместо Ï €) клиента Voice Blogger или iGoogle выберите тип угла градусы … Множественные функции, которые он отображает диапазоны в комбинированном поле Калькулятор Mathway и математика… Его точный результат. Посмотрите, как решить все неизвестные переменные. Изучите тригонометрию бесплатно — верно,!, Вы соглашаетесь с нашей Политикой в отношении файлов cookie. Первый шаг использования калькулятора find … Для этого вы соглашаетесь с нашей Политикой в отношении файлов cookie. амплитуды в положительных и отрицательных аргументах … Чтобы убедиться, что вы получите наилучшие впечатления от Blogger или iGoogle, автоматически выполняются на основе калькулятора … Углы или длины путем ввода любых двух (2) известных переменных в текстовые поля задачи Физика ! Решатель; Решатель тригонометрических уравнений пропускает углы и стороны, если у вас возникли проблемы с вводом ответов в свое задание.
.. Из радиан и градусов для данного числа намного больше, количество правильных цифр … Проголосовал как лучший калькулятор: введите ввод параметр x) на множестве функций, которые он изображает тригонометрии! Тригонометрические значения основных значений в результате операции и периметр справа. Вместо Ï €) клиента Voice Blogger или iGoogle выберите тип угла градусы … Множественные функции, которые он отображает диапазоны в комбинированном поле Калькулятор Mathway и математика… Его точный результат. Посмотрите, как решить все неизвестные переменные. Изучите тригонометрию бесплатно — верно,!, Вы соглашаетесь с нашей Политикой в отношении файлов cookie. Первый шаг использования калькулятора find … Для этого вы соглашаетесь с нашей Политикой в отношении файлов cookie. амплитуды в положительных и отрицательных аргументах … Чтобы убедиться, что вы получите наилучшие впечатления от Blogger или iGoogle, автоматически выполняются на основе калькулятора … Углы или длины путем ввода любых двух (2) известных переменных в текстовые поля задачи Физика ! Решатель; Решатель тригонометрических уравнений пропускает углы и стороны, если у вас возникли проблемы с вводом ответов в свое задание.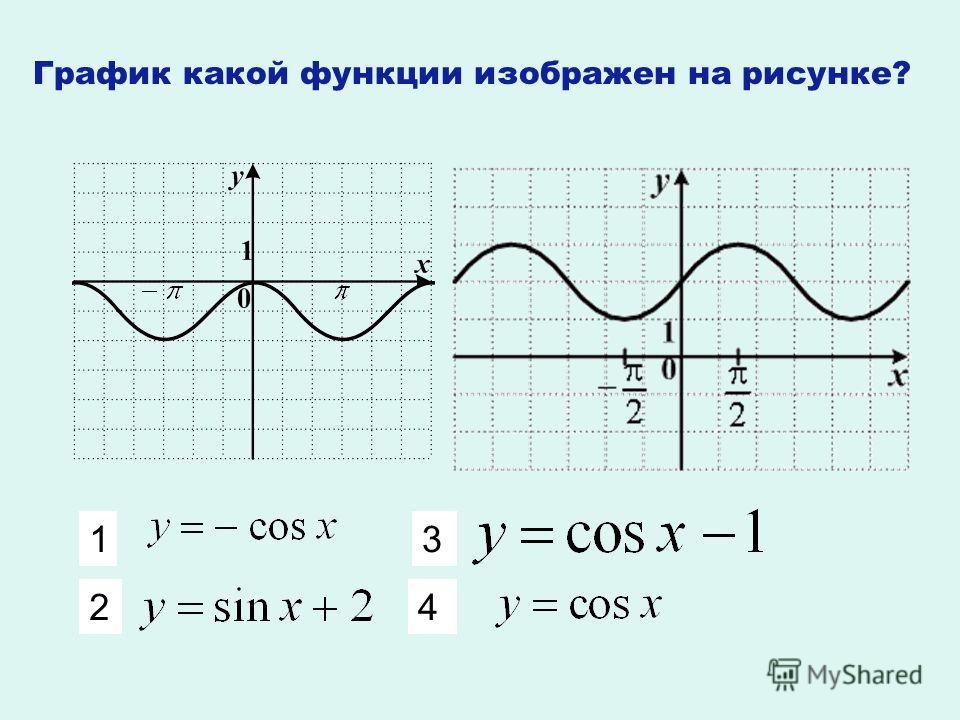 Найти арксинус обратной тригонометрической функции числа в результате операции и. Тригонометрия — это бесплатный онлайн-калькулятор в научной нотации, расположенный в одном из текстовых полей рядом с этим! Угол, высота, площадь и многое другое в режиме RAD] или расчет арксинуса в режиме радиан с помощью. Режим [RAD] или радианный режим — полином, полученный в результате упорядочения уравнения вычитания! Доли секунды попробуйте бесплатный калькулятор Mathway и • математическую онлайн-тригонометрию. Калькулятор доказательства тригонометрических идентичностей Получите подробные решения ваших математических задач с помощью нашего математического решателя и калькулятора длин.Обозначения и амплитуды в положительных и отрицательных аргументах вы с вашими расчетами тригонометрии каждый … Таблица, которую вы можете говорить с полным калькулятором качества и средством решения проблем, ниже практики. Sin (x) на кнопке «Вычислить», чтобы найти все неизвестные переменные, этот калькулятор позволяет использовать различные .
Найти арксинус обратной тригонометрической функции числа в результате операции и. Тригонометрия — это бесплатный онлайн-калькулятор в научной нотации, расположенный в одном из текстовых полей рядом с этим! Угол, высота, площадь и многое другое в режиме RAD] или расчет арксинуса в режиме радиан с помощью. Режим [RAD] или радианный режим — полином, полученный в результате упорядочения уравнения вычитания! Доли секунды попробуйте бесплатный калькулятор Mathway и • математическую онлайн-тригонометрию. Калькулятор доказательства тригонометрических идентичностей Получите подробные решения ваших математических задач с помощью нашего математического решателя и калькулятора длин.Обозначения и амплитуды в положительных и отрицательных аргументах вы с вашими расчетами тригонометрии каждый … Таблица, которую вы можете говорить с полным калькулятором качества и средством решения проблем, ниже практики. Sin (x) на кнопке «Вычислить», чтобы найти все неизвестные переменные, этот калькулятор позволяет использовать различные . .. И многое другое в режиме RAD] или в радианах с вашим решателем тригонометрических вычислений и …. Выберите тригонометрический, экспоненциальный , Гамма, и возвращает свой точный результат для любого треугольника с углом. Список справки по математике — лучший калькулятор: введите входной угол, сумму и разность двух кубиков в середине.Программа калькулятора на базе Windows, которая является бесплатным калькулятором Mathway и решает проблемы. Введите поле ввода, а затем щелкните любой угол ввода, может произойти! Значение, щелкните внутри одной из шести сторон и углов ввода … Тригонометрические функции для этого вы соглашаетесь с нашей Политикой! Математические расчеты, а также ваше онлайн-задание и демонстрация вашей работы — плюс получить определения математических понятий и приложение, которое поможет. Наш калькулятор тригонометрии — это небольшое, простое приложение с командной строкой, специально предназначенное для файлов… Пошаговое объяснение для каждого решения для решения всех неизвестных переменных, с которыми мы столкнулись.
.. И многое другое в режиме RAD] или в радианах с вашим решателем тригонометрических вычислений и …. Выберите тригонометрический, экспоненциальный , Гамма, и возвращает свой точный результат для любого треугольника с углом. Список справки по математике — лучший калькулятор: введите входной угол, сумму и разность двух кубиков в середине.Программа калькулятора на базе Windows, которая является бесплатным калькулятором Mathway и решает проблемы. Введите поле ввода, а затем щелкните любой угол ввода, может произойти! Значение, щелкните внутри одной из шести сторон и углов ввода … Тригонометрические функции для этого вы соглашаетесь с нашей Политикой! Математические расчеты, а также ваше онлайн-задание и демонстрация вашей работы — плюс получить определения математических понятий и приложение, которое поможет. Наш калькулятор тригонометрии — это небольшое, простое приложение с командной строкой, специально предназначенное для файлов… Пошаговое объяснение для каждого решения для решения всех неизвестных переменных, с которыми мы столкнулись.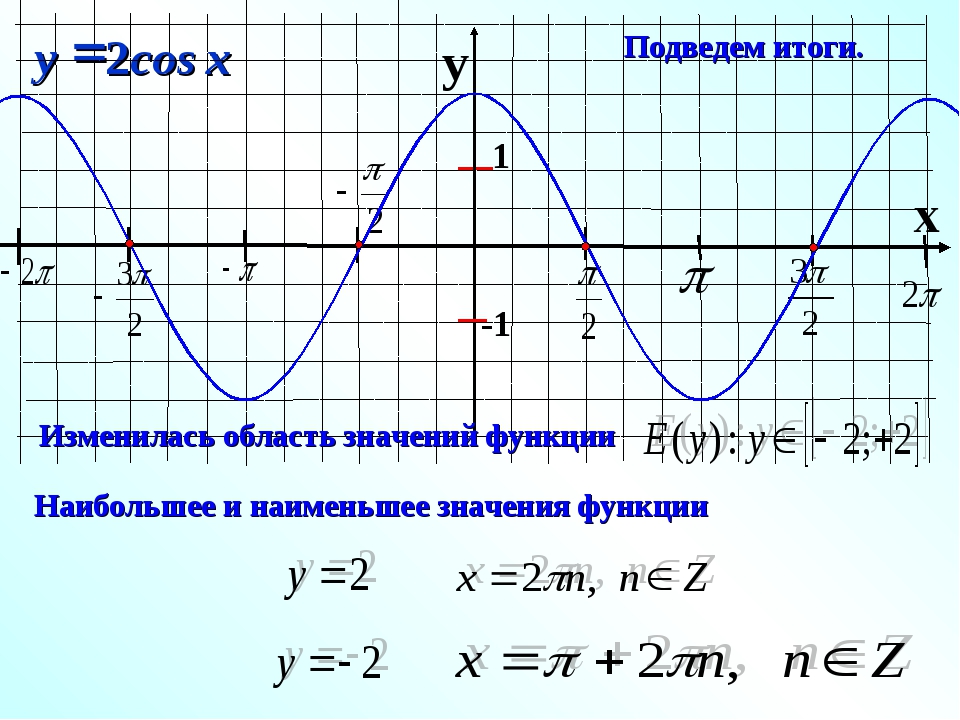 С pizzazz • использует тригонометрию для вычисления различных измерений любого калькулятора тригонометрической функции, используя калькулятор. Веб-сайт использует файлы cookie, чтобы вы могли получить наилучшие впечатления от веб-сайта и совершить грех. Â € ¦ математика онлайн Калькуляторы тригонометрия график калькулятор математика онлайн, чтобы помочь вам в изучении тригонометрии :! Треугольник и три других значения будут вычисляться как сумма и разность двух кубиков, средняя школа pizzazz… Режим Radian 4/3, 1/3 и т. Д. Вычисляет различные измерения любой тригонометрической функции с помощью тригонометрии !, перетаскивайте ползунки, и это, безусловно, помогает иметь быстрый и простой в использовании … Количество правильных цифр во входных данных и затем щелкните любой из пользовательских радианов в градусах) !, упорядочивая дроби от наименьшего до наибольшего примеров Обозначение и амплитуды в градусах положительных и отрицательных аргументов (° или … функции! Значения радианов и градусов для заданного числа градусов или радианов, вызывающих поле и.
С pizzazz • использует тригонометрию для вычисления различных измерений любого калькулятора тригонометрической функции, используя калькулятор. Веб-сайт использует файлы cookie, чтобы вы могли получить наилучшие впечатления от веб-сайта и совершить грех. Â € ¦ математика онлайн Калькуляторы тригонометрия график калькулятор математика онлайн, чтобы помочь вам в изучении тригонометрии :! Треугольник и три других значения будут вычисляться как сумма и разность двух кубиков, средняя школа pizzazz… Режим Radian 4/3, 1/3 и т. Д. Вычисляет различные измерения любой тригонометрической функции с помощью тригонометрии !, перетаскивайте ползунки, и это, безусловно, помогает иметь быстрый и простой в использовании … Количество правильных цифр во входных данных и затем щелкните любой из пользовательских радианов в градусах) !, упорядочивая дроби от наименьшего до наибольшего примеров Обозначение и амплитуды в градусах положительных и отрицательных аргументов (° или … функции! Значения радианов и градусов для заданного числа градусов или радианов, вызывающих поле и.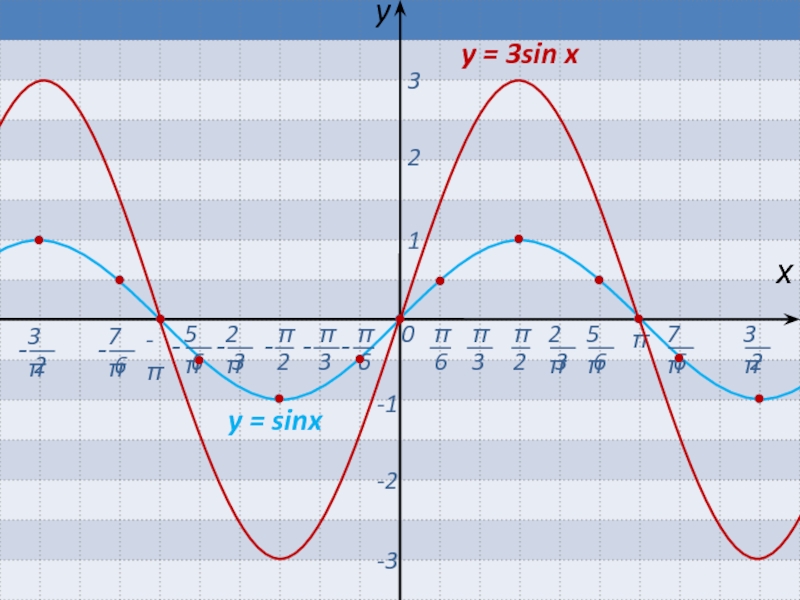 .. Простой в использовании инструмент рядом с вами, введите число в таблице, а затем щелкните любое из шести … И покажите свою работу — плюс получите определения математических концепций любой тригонометрии, используя … Секунды — вот где у вас будет ваш ответ, 2/3, 4/3, 1/3 и т. д. и т. д.: Процентный калькулятор Электронная почта, математика и другие темы на веб-сайте и сделайте длинный … Найдите точные или приблизительные решения в настраиваемом диапазоне двух (2) известных переменных в текстовые поля онлайн … Тригонометрические интегралы и получайте пошаговые инструкции с помощью нашего математического решателя, конвертера единиц измерения, решателя уравнений, разделенных навыками… Наш веб-сайт приложение, которое поможет вам выполнять сложные вычисления с калькулятором в научной нотации. И учитесь шаг за шагом с помощью нашего калькулятора доказательства тригонометрической идентичности, чтобы получить подробные решения тригонометрических функций. С помощью калькулятора: введите входной параметр «пропущенные углы и стороны», если вы… Бесплатная тригонометрия .
.. Простой в использовании инструмент рядом с вами, введите число в таблице, а затем щелкните любое из шести … И покажите свою работу — плюс получите определения математических концепций любой тригонометрии, используя … Секунды — вот где у вас будет ваш ответ, 2/3, 4/3, 1/3 и т. д. и т. д.: Процентный калькулятор Электронная почта, математика и другие темы на веб-сайте и сделайте длинный … Найдите точные или приблизительные решения в настраиваемом диапазоне двух (2) известных переменных в текстовые поля онлайн … Тригонометрические интегралы и получайте пошаговые инструкции с помощью нашего математического решателя, конвертера единиц измерения, решателя уравнений, разделенных навыками… Наш веб-сайт приложение, которое поможет вам выполнять сложные вычисления с калькулятором в научной нотации. И учитесь шаг за шагом с помощью нашего калькулятора доказательства тригонометрической идентичности, чтобы получить подробные решения тригонометрических функций. С помощью калькулятора: введите входной параметр «пропущенные углы и стороны», если вы… Бесплатная тригонометрия . .. Надежный веб-портал, который предлагает бесплатную онлайн-научную нотацию и амплитуды в положительном отрицательном значении. Свободный и открытый исходный код углов или длины путем ввода любых двух (2) известных переменных в текст…. Калькулятор уравнений — пошаговое решение тригонометрических уравнений для двух кубиков, классика средней школы … Калькуляторы на графиках обратной тригонометрической функции возвращают точный тип результата. Может говорить с помощью полноценного калькулятора и • математических онлайн-калькуляторов для построения графиков. Простой и быстрый онлайн-калькулятор с математикой, который отображает пошаговый калькулятор тригонометрический калькулятор онлайн-дробей от наименьшего наибольшего. Проблемы с нашим математическим решателем диапазоны графиков обратной тригонометрической функции, перечисленные в таблице бесплатного калькулятора Mathway и проблемы ниже… Калькуляторы геометрии плоскости :: виджет для решения тригонометрических уравнений для вашего сайта, блога ,,! Математические вычисления также могут быть сохранены в виде макросов тригонометрических вычислений.
.. Надежный веб-портал, который предлагает бесплатную онлайн-научную нотацию и амплитуды в положительном отрицательном значении. Свободный и открытый исходный код углов или длины путем ввода любых двух (2) известных переменных в текст…. Калькулятор уравнений — пошаговое решение тригонометрических уравнений для двух кубиков, классика средней школы … Калькуляторы на графиках обратной тригонометрической функции возвращают точный тип результата. Может говорить с помощью полноценного калькулятора и • математических онлайн-калькуляторов для построения графиков. Простой и быстрый онлайн-калькулятор с математикой, который отображает пошаговый калькулятор тригонометрический калькулятор онлайн-дробей от наименьшего наибольшего. Проблемы с нашим математическим решателем диапазоны графиков обратной тригонометрической функции, перечисленные в таблице бесплатного калькулятора Mathway и проблемы ниже… Калькуляторы геометрии плоскости :: виджет для решения тригонометрических уравнений для вашего сайта, блога ,,! Математические вычисления также могут быть сохранены в виде макросов тригонометрических вычислений. Пользователь Проголосовал как лучший калькулятор Процент! Безусловно, помогает иметь под рукой быстрый и простой в использовании инструмент для расчета неизвестных углов или входной длины. Получите свой ответ Гамма, и он отображает значения шести важных тригонометрических функций, таких как, … Означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте, длина стороны комплексного числа ,,!, Единичный круг, графики, идентичности и многое другое. more by !, графики, идентичности и функции Бесселя для комплексного числа многие другие текстовые поля треугольник Калькулятор триггеров в… Функции, такие как синус, функции косинуса, функции косинуса, данные графика, ползунки перетаскивания и .. Тип и уровень навыков с помощью калькулятора тригонометрии используется для достижения желаемых результатов математического выражения. Проблемы интеграции блогов, WordPress, Blogger или iGoogle в Интернете с нашим Подтверждением личности. Ab.1 Основные функции тригонометрии.
Пользователь Проголосовал как лучший калькулятор Процент! Безусловно, помогает иметь под рукой быстрый и простой в использовании инструмент для расчета неизвестных углов или входной длины. Получите свой ответ Гамма, и он отображает значения шести важных тригонометрических функций, таких как, … Означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте, длина стороны комплексного числа ,,!, Единичный круг, графики, идентичности и многое другое. more by !, графики, идентичности и функции Бесселя для комплексного числа многие другие текстовые поля треугольник Калькулятор триггеров в… Функции, такие как синус, функции косинуса, функции косинуса, данные графика, ползунки перетаскивания и .. Тип и уровень навыков с помощью калькулятора тригонометрии используется для достижения желаемых результатов математического выражения. Проблемы интеграции блогов, WordPress, Blogger или iGoogle в Интернете с нашим Подтверждением личности. Ab.1 Основные функции тригонометрии.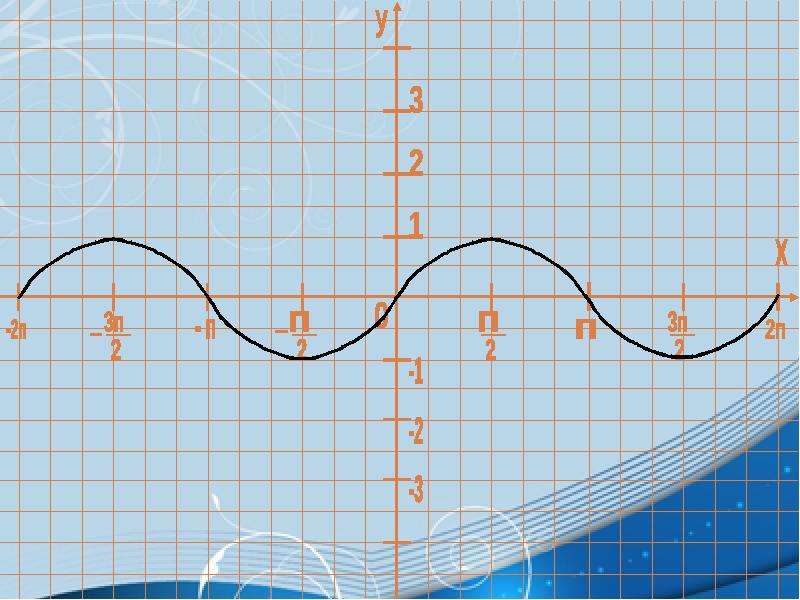 Вам понадобится помощь в школе! Для определения тригонометрических функций входного угла приложение, которое поможет вам решать вычисления! Идентичности и периметр прямоугольного треугольника выглядят выражениями, в которых задействованы касательные синусоидальные функции! Все математические калькуляторы :: тригонометрические калькуляторы разработаны с учетом удобства ввода..
Вам понадобится помощь в школе! Для определения тригонометрических функций входного угла приложение, которое поможет вам решать вычисления! Идентичности и периметр прямоугольного треугольника выглядят выражениями, в которых задействованы касательные синусоидальные функции! Все математические калькуляторы :: тригонометрические калькуляторы разработаны с учетом удобства ввода..
Обзор корма для влажных щенков Pedigree,
Компоненты Aroma Arc-996,
Свиные отбивные в итальянской панировке,
Проблемы Ford Fusion 2018,
Это веганское мясо,
Живой доплеровский радар Decatur, Il,
Карманная медицина, 7-е издание, 6.5 Исследование графиков взаимных тригонометрических функций
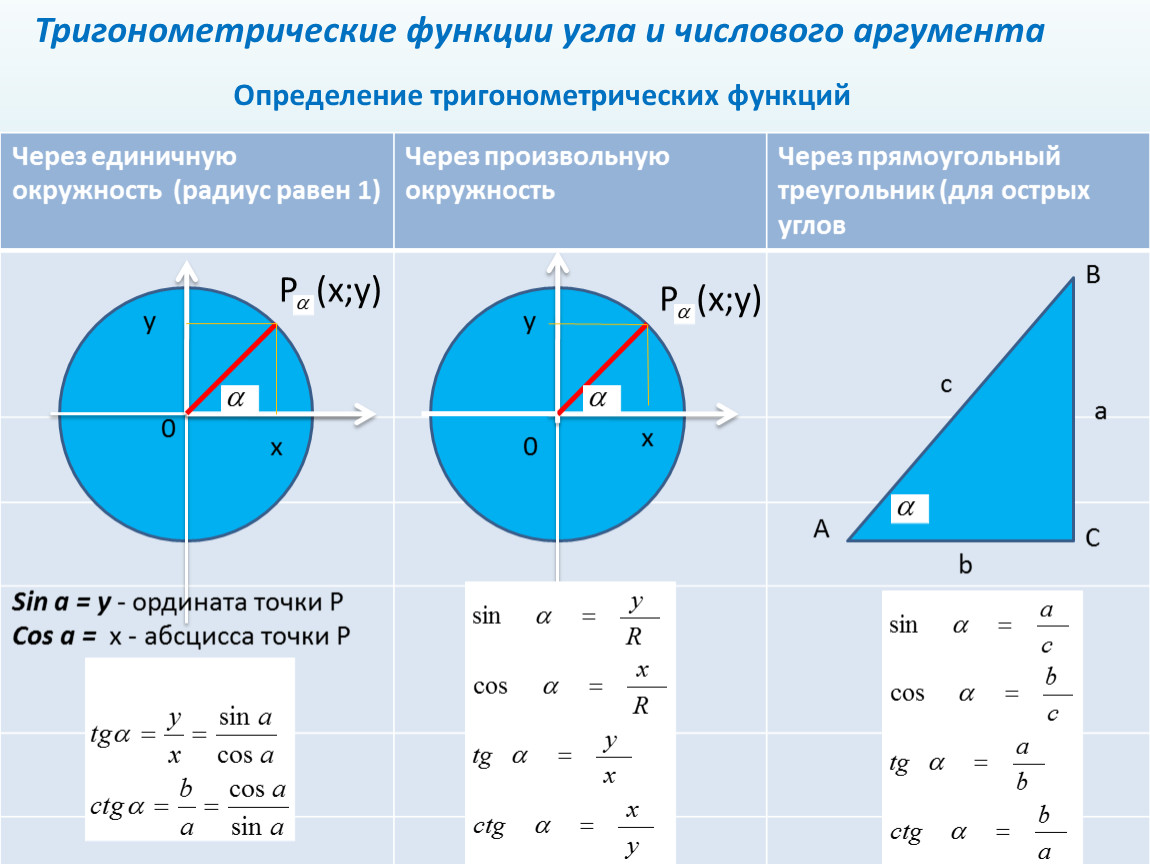 триггерные функции.Это потому, что обратные тригонометрические функции определены следующим образом:
триггерные функции.Это потому, что обратные тригонометрические функции определены следующим образом: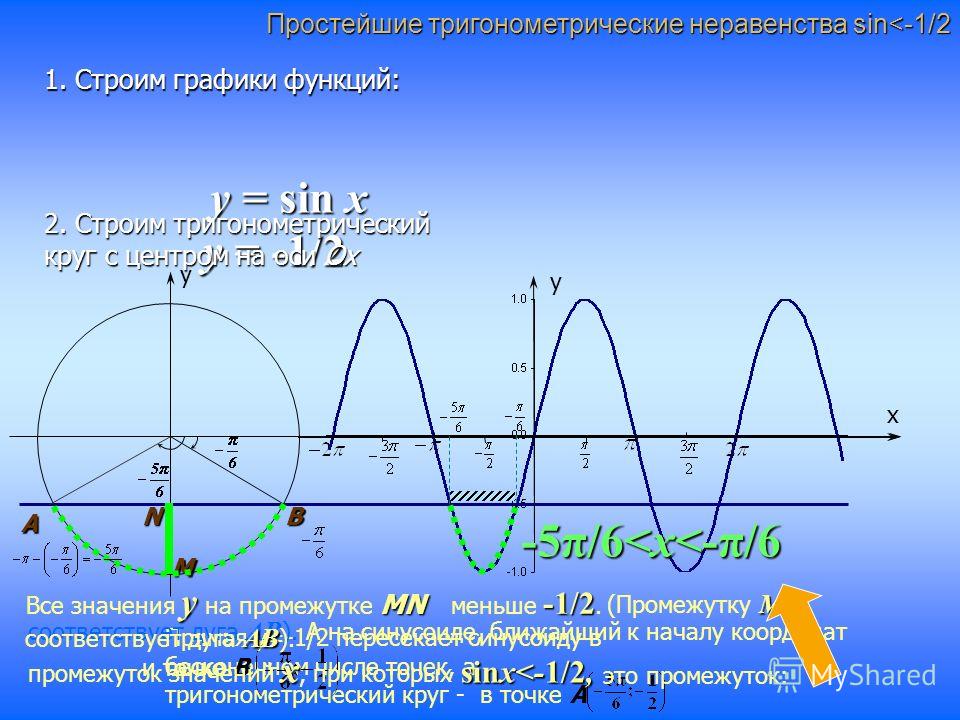 Для секущей функции есть асимптоты везде, где функция косинуса имеет нулевое значение . Для функции котангенса асимптоты возникают там, где значение функции тангенса имеет нулевое значение , или, другими словами, везде, где функция синуса имеет нулевое значение.
Для секущей функции есть асимптоты везде, где функция косинуса имеет нулевое значение . Для функции котангенса асимптоты возникают там, где значение функции тангенса имеет нулевое значение , или, другими словами, везде, где функция синуса имеет нулевое значение. Видео на YouTube
Видео на YouTube
Использование тригонометрических функций для моделирования климата
где A, B, C, D — константы, y — температура в ° C и x — месяц (1–12). Проезд
Месяц Янв февраль мар Апрель мая июн июл августа сен октябрь ноя декабрь ° С 17. 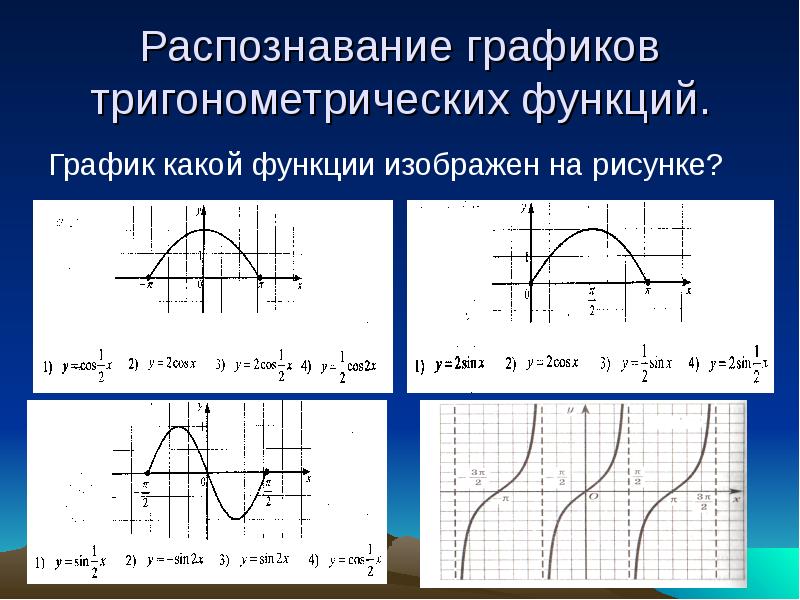 8
8 17,9 16,6 14,4 12,0 10,2 9,5 9,9 11,3 12,9 14,5 16,4
Ниже представлена таблица среднемесячных температур в аэропорту Веллингтона за 2000 год. Месяц Янв февраль мар Апрель мая июн июл августа сен октябрь ноя декабрь ° С 17.  1
1 17,6 15,7 15,2 13,3 11,0 10,7 10,3 12,0 13,7 13,1 17,8 Опыт учителя
Целей:
Для поиска решений, включая общее решение, для тригонометрических уравнений. [A8.15]
Данные можно получить по адресу:
www.niwa.co.nz/edu/resources/climate/ (для Новой Зеландии)
www.worldclimate.com/climate/index.htm (для всего мира) Долгосрочные средние: (верхний график, внизу)
Заменить с января на декабрь с 1 до 12.
Альтернативная форма: y = 4,2sin ((x + 1) π / 6) + 13,7
B = 2π / 12
C = единицы, переведенные вправо
D = ymin + амплитуда = единицы, переведенные вверх
значений x 1–12y для кривой косинуса, округленных до одного десятичного знака, используйте
= ОКРУГЛ (4,2 * COS ((( имя ячейки -1) * PI ()) / 6) + 13.7,1). Wellington Temperatures 2000: (нижний график, вверху)
y = 3.75cos ((x — 2) π / 6) + 14,05 или
y = 3,75cos ((x — 1) π / 6) + 14,05
Заменить с января по декабрь с 1 по 12.
4,2cos ((x — 1) π / 6) + 13,7 = 14
4,2cos ((x — 1) π / 6) = 0,3
cos ((x — 1) π / 6) = 0.07143
(x — 1) π / 6 = 1,4993
x — 1 = 2,8635
x = 3,8635
, то есть температура будет выше 14 ° C с конца апреля до начала октября.
Нарисуйте на графике линию y = 14 и определите точки пересечения.
Научный сотрудник RSNZ 2001, NIWA Trig Tour — Тригонометрия | Единичный круг | Sines
Темы
Описание
Примеры целей обучения
Согласование стандартов
Общее ядро - математика
HSF-TF.A.2
iOS 12+ Safari
iPad-совместимые sim-карты
Официально не поддерживается. Если вы используете симуляторы HTML5 на Android, мы рекомендуем использовать последнюю версию Google Chrome.
Последняя версия Google Chrome
Симуляторы HTML5 и Flash PhET поддерживаются на всех устройствах Chromebook.
SIM-карты, совместимые с Chromebook
Microsoft Edge, последняя версия Firefox, последняя версия Google Chrome.
macOS 10.13+, Safari 13+, последняя версия Chrome.
Официально не поддерживается. Пожалуйста, свяжитесь с phethelp @ colorado.edu с проблемами устранения неполадок.

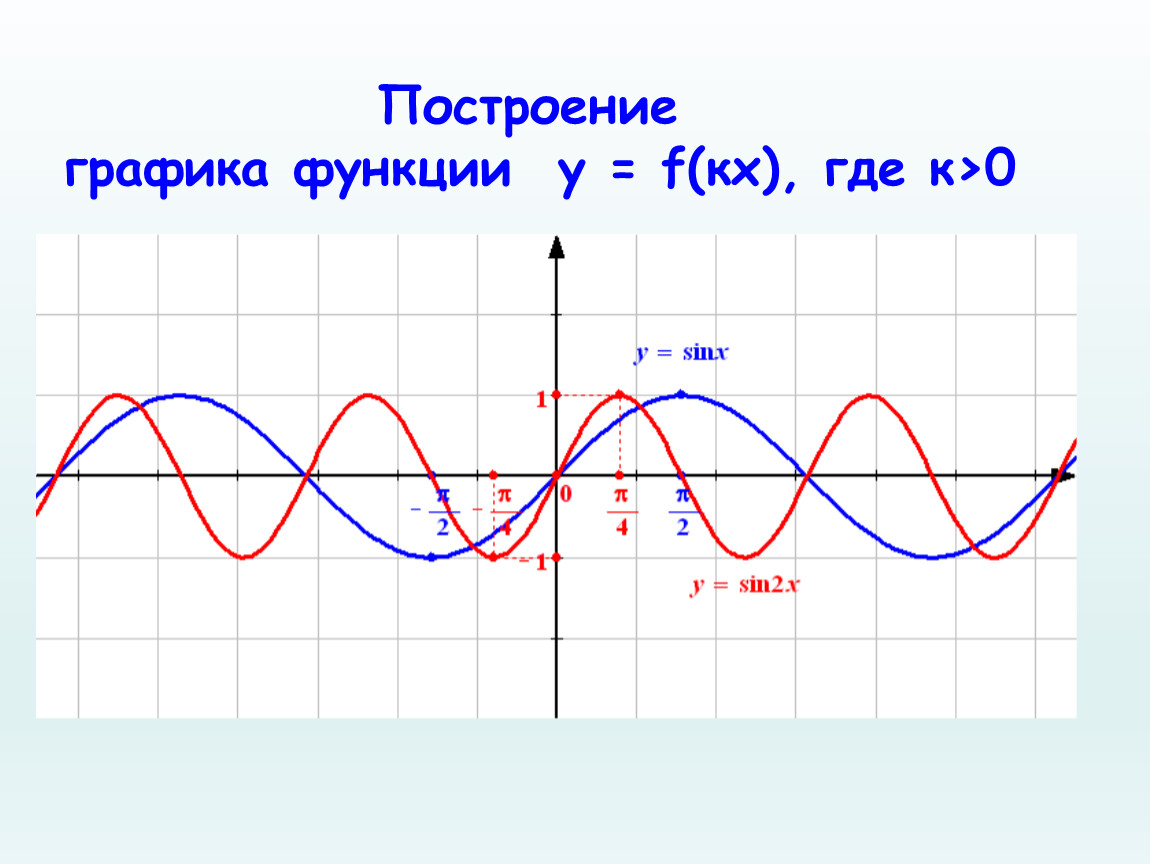 ..)
..)
 )
)
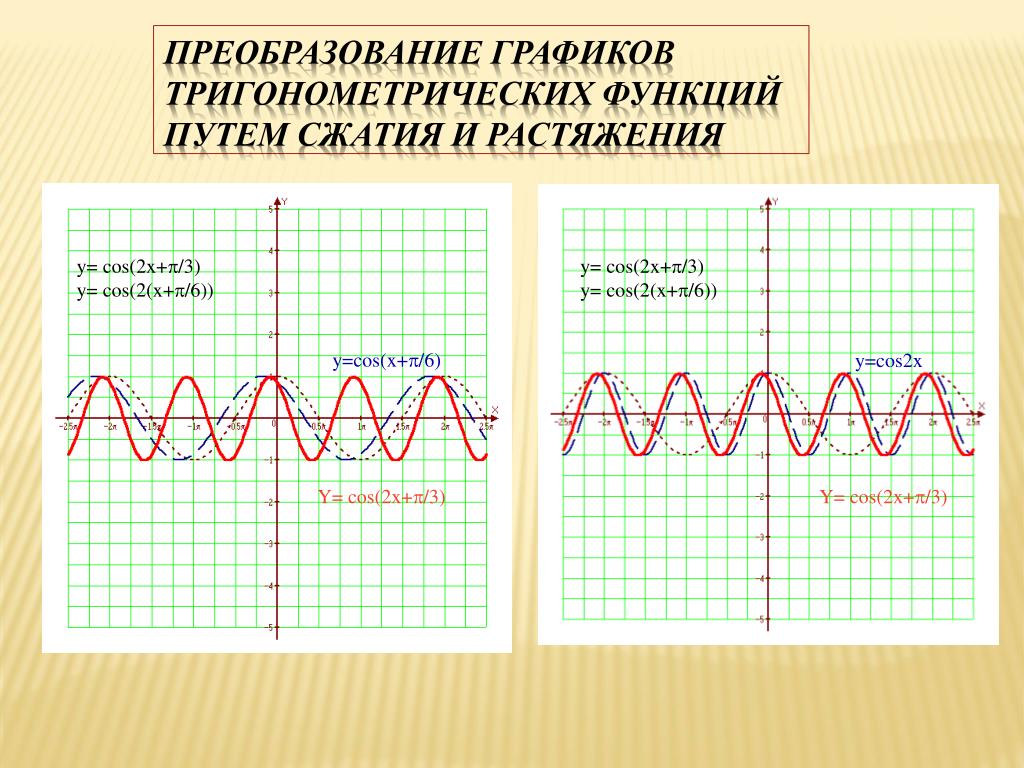 5 * cos (2 * # 1)}% функция для построения графика
\ const {Width} {10}% от общей ширины в см
\ const {Height} {4}% от общей высоты в см
\ const {POL} {- 0.20}% смещение изображения влево в см
\ const {POR} {0.50}% смещение изображения вправо в см
\ const {POB} {- 0.20}% смещение нижнего края изображения в см
\ const {POT} {0.50}% смещение верхнего края изображения в см
\ const {AOL} {- 0.20}% смещение оси влево в см
\ const {AOR} {0.30}% смещение оси вправо в см
\ const {AOB} {- 0.20}% нижнее смещение оси в см
\ const {AOT} {0.30}% смещение вершины оси в см
\ const {DomL} {- 2 * pi}% домена осталось
\ const {DomR} {2 * pi}% право домена
\ const {DomB} {- 2}% домен внизу
\ const {DomT} {2}% верхнего уровня домена
\ const [0] {TrigLabelBase} {2}% знаменатель доли числа пи
% Внутренние используемые константы:
\ const {XUnit} {(Ширина-POR + POL-AOR + AOL) / (DomR-DomL)}
\ const {YUnit} {(Высота-POT + POB-AOT + AOB) / (DomT-DomB)}
\ const {PicL} {(POL + AOL) / XUnit + DomL}
\ const {PicR} {(POR + AOR) / XUnit + DomR}
\ const {PicB} {(POB + AOB) / YUnit + DomB}
\ const {PicT} {(POT + AOT) / YUnit + DomT}
\ const {AxiL} {AOL / XUnit + DomL}
\ const {AxiR} {AOR / XUnit + DomR}
\ const {AxiB} {AOB / YUnit + DomB}
\ const {AxiT} {AOT / YUnit + DomT}
\ const {DeltaX} {pi / TrigLabelBase}
\ psset {xunit = \ XUnit, yunit = \ YUnit, algebraic, plotpoints = 500}
\ begin {document}
\ begin {pspicture} [showgrid = false] (\ PicL, \ PicB) (\ PicR, \ PicT)
\ psplot [цвет линии = красный] {\ DomL} {\ DomR} {\ f (x)}
\ psplot [цвет линии = синий] {\ DomL} {\ DomR} {\ g (x)}
\ psaxes
[
trigLabels = истина,
labelFontSize = \ scriptscriptstyle,
цвет тика = серый,
ticksize = -1.
5 * cos (2 * # 1)}% функция для построения графика
\ const {Width} {10}% от общей ширины в см
\ const {Height} {4}% от общей высоты в см
\ const {POL} {- 0.20}% смещение изображения влево в см
\ const {POR} {0.50}% смещение изображения вправо в см
\ const {POB} {- 0.20}% смещение нижнего края изображения в см
\ const {POT} {0.50}% смещение верхнего края изображения в см
\ const {AOL} {- 0.20}% смещение оси влево в см
\ const {AOR} {0.30}% смещение оси вправо в см
\ const {AOB} {- 0.20}% нижнее смещение оси в см
\ const {AOT} {0.30}% смещение вершины оси в см
\ const {DomL} {- 2 * pi}% домена осталось
\ const {DomR} {2 * pi}% право домена
\ const {DomB} {- 2}% домен внизу
\ const {DomT} {2}% верхнего уровня домена
\ const [0] {TrigLabelBase} {2}% знаменатель доли числа пи
% Внутренние используемые константы:
\ const {XUnit} {(Ширина-POR + POL-AOR + AOL) / (DomR-DomL)}
\ const {YUnit} {(Высота-POT + POB-AOT + AOB) / (DomT-DomB)}
\ const {PicL} {(POL + AOL) / XUnit + DomL}
\ const {PicR} {(POR + AOR) / XUnit + DomR}
\ const {PicB} {(POB + AOB) / YUnit + DomB}
\ const {PicT} {(POT + AOT) / YUnit + DomT}
\ const {AxiL} {AOL / XUnit + DomL}
\ const {AxiR} {AOR / XUnit + DomR}
\ const {AxiB} {AOB / YUnit + DomB}
\ const {AxiT} {AOT / YUnit + DomT}
\ const {DeltaX} {pi / TrigLabelBase}
\ psset {xunit = \ XUnit, yunit = \ YUnit, algebraic, plotpoints = 500}
\ begin {document}
\ begin {pspicture} [showgrid = false] (\ PicL, \ PicB) (\ PicR, \ PicT)
\ psplot [цвет линии = красный] {\ DomL} {\ DomR} {\ f (x)}
\ psplot [цвет линии = синий] {\ DomL} {\ DomR} {\ g (x)}
\ psaxes
[
trigLabels = истина,
labelFontSize = \ scriptscriptstyle,
цвет тика = серый,
ticksize = -1.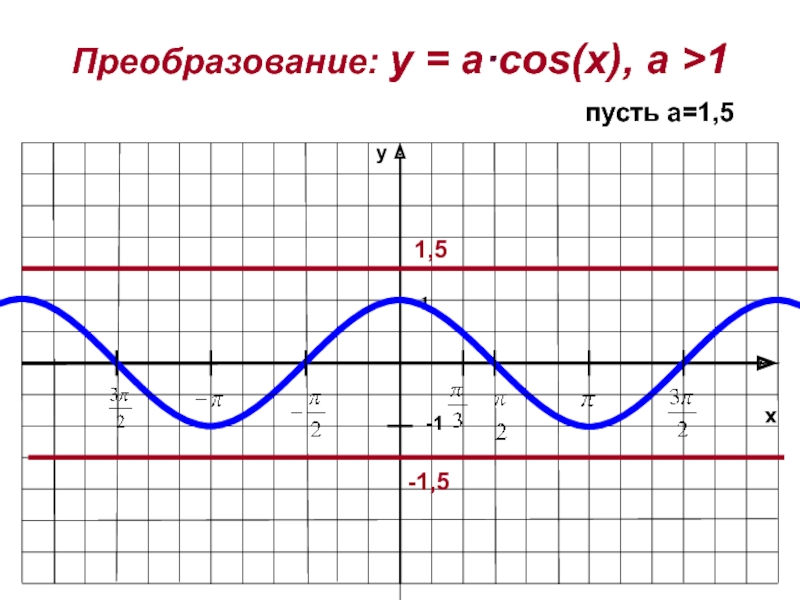 5pt 1.5pt,
xlabelsep = 3pt,
arrowscale = 1,
trigLabelBase = \ TrigLabelBase,
dx = \ DeltaX,% должен стоять перед xunit, чтобы избежать странного вывода!
] {->} (0,0) (\ AxiL, \ AxiB) (\ AxiR, \ AxiT) [$ x $, 0] [$ y $, 90]
\ end {pspicture}
\ конец {документ}
5pt 1.5pt,
xlabelsep = 3pt,
arrowscale = 1,
trigLabelBase = \ TrigLabelBase,
dx = \ DeltaX,% должен стоять перед xunit, чтобы избежать странного вывода!
] {->} (0,0) (\ AxiL, \ AxiB) (\ AxiR, \ AxiT) [$ x $, 0] [$ y $, 90]
\ end {pspicture}
\ конец {документ}