Определение синуса, косинуса и тангенса угла
Вспомним, как в курсе геометрии были введены синус, косинус и тангенс угла из промежутка от до . На координатной плоскости построим полуокружность с центром в начале координат и единичным радиусом, расположенную в первой и второй четвертях. Такую полуокружность называют единичной полуокружностью.
Затем из точки проведём луч , который пересекает нашу полуокружность в точке . Угол между лучом и положительным направлением оси обозначим . При этом, если луч совпадает с положительным направлением оси , то считают, что угол .
Пусть
угол острый.
Опустим из точки перпендикуляр
на
ось и
получим прямоугольный треугольник .
Тогда из этого треугольника имеем: ;
.
– это радиус единичной полуокружности, а значит, равняется . равняется абсциссе точки , то есть . равняется ординате точки , то есть . Подставим эти значения в выражения синуса и косинуса и получим,
что , .
А если угол не является острым, то как определяются синус и косинус этого угла?
Если угол альфа прямой, тупой, развёрнутый или равен нулю, то синус и косинус также определяются по формулам: , .
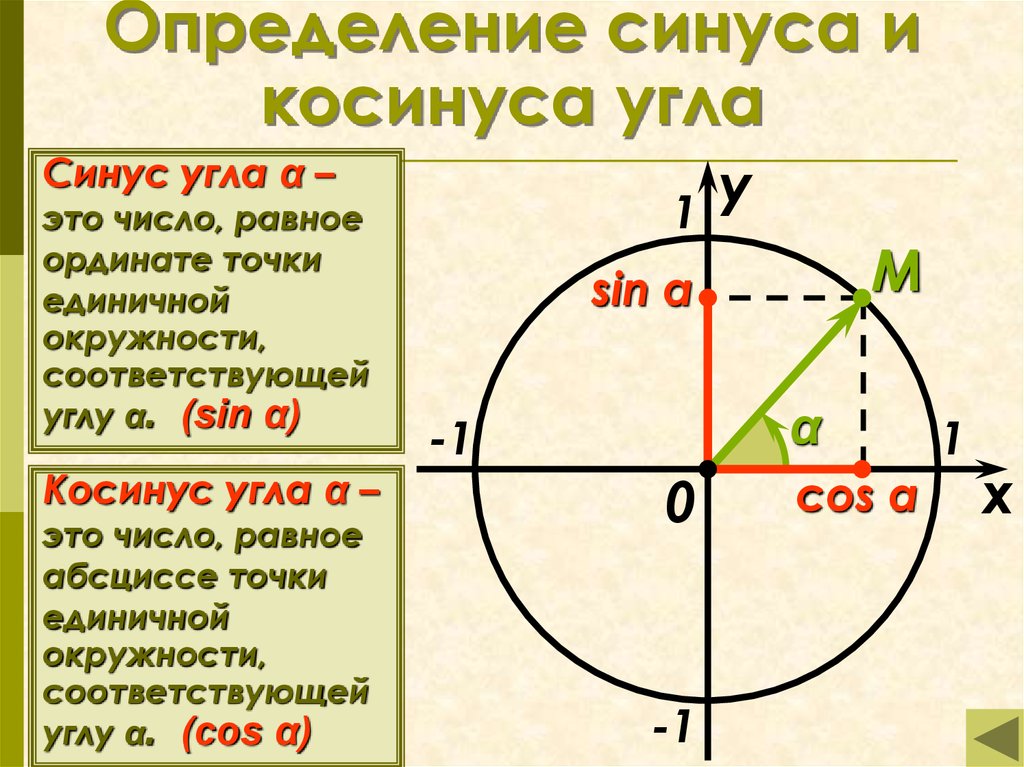
Таким образом, для любого угла альфа из промежутка от до синусом угла называется ордината точки , а косинусом угла – абсцисса точки .
При этом не забудем отметить, что так как координаты и точек единичной полуокружности удовлетворяют неравенствам , а , то для из промежутка от до справедливы неравенства ; .
Тангенсом угла , причём , называется отношение к : . Отметим, что , так как , а в формуле знаменатель не должен обращаться в нуль.
Так как же определяются синус, косинус и тангенс произвольного угла?
Запомните! Синусом угла называется ордината точки , полученной поворотом точки вокруг начала координат на угол . Обозначают: .
Косинусом угла
называется абсцисса точки , полученной поворотом точки вокруг начала координат на угол .
Обозначают: .Причём угол может выражаться и в градусах, и в радианах.
Давайте найдём значения синуса и косинуса угла , то есть угла . При повороте точки на угол получаем точку . Ордината полученной точки равна , а, следовательно, . Абсцисса полученной точки равна , а, следовательно, .
Отметим, что приведённые выше определения синуса и косинуса произвольного угла в случае, если угол принадлежит промежутку от до , совпадают с определениями синуса и косинуса из курса геометрии, которые мы с вами повторили в начале урока. Так, например, , .
А давайте найдём значения синуса и косинуса угла не из промежутка от до .
Найдём и . Итак, при повороте точки на угол мы осуществим поворот по часовой стрелке и окажемся в точке . Ордината полученной точки равна , следовательно, с. Абсцисса полученной точки равна , следовательно, .
Сейчас давайте решим уравнение . Решить это уравнение означает найти все углы, синус которых
равен .
Ординату, равную , имеет точка единичной окружности . Эта точка получается из точки поворотом на угол , на угол , на угол и так далее. А также на угол , на угол и так далее.
При этом , , ,
, .
Следовательно, при , где – это любое целое число.
Вы знаете, что множество целых чисел обозначается буквой . Обозначить то, что число принадлежит целым числам можно вот таким образом: . Читают: принадлежит . Тогда ответ к нашей задаче можно записать так: , .
Решим уравнение . Абсциссу, равную , имеет точка . Эта точка получается из точки поворотом на рад, то есть точка остаётся на своём месте; на угол , на угол и так далее. А также на угол , и так далее.
При этом рад мы можем записать как , , , , .
Следовательно, при , .
А что называют тангенсом произвольного угла?
Запомните! Тангенсом угла называется отношение синуса угла к его косинусу. Обозначают: .
Таким образом, можем записать, что .
Иногда используют котангенс угла , который равен отношению косинуса угла к синусу угла : . При этом .
Давайте найдём и .
. Подставим значения синуса и косинуса: . Выполним вычисления и в результате получим .
. Подставим значения косинуса и синуса: . Выполним вычисления и получим .
Также . , а, следовательно, .
Важно помнить, что и определены для любого угла , а их значения заключены в промежутках от до , так как координаты точек единичной окружности заключены в промежутках от до .
А вот определён только для тех углов, для которых , так как делить на нуль нельзя. Найдём углы, косинус которых равен нулю. Итак, абсциссу, равную , имеет точка и . Эти точки получаются поворотом точки на углы , , и так далее. А также на углы , и так далее.
Следовательно, при , .
определён для любых углов, кроме , .
А для каких углов определён ? определён только для тех углов, для
которых . Найдём углы, синус которых равен нулю.
Итак, ординату, равную нулю,
имеет точка и точка . Эти точки получаются поворотом точки на углы , , , и так далее. А также на углы , , и так далее.
Следовательно, при , .
Тогда определён для любых углов, кроме , .
На следующем слайде приведена таблица значений синуса, косинуса, тангенса и котангенса, с которыми вы будете встречаться чаще всего:
Найдём значение выражения .
Воспользуемся только что приведённой таблицей. Подставим значения в наше выражения: . Теперь выполним вычисления и в результате получим .
Отметим, что значения синуса, косинуса, тангенса и котангенса для углов, которых нет в этой таблице, можно найти с помощью инженерного микрокалькулятора или по четырёхзначным математическим таблицам Брадиса.
Синус, косинус, тангенс и котангенс на единичной окружности. Шпаргалка по тригонометрии
12+
6 месяцев назад
Математика от Баканчиковой299 подписчиков
Алгебра 10 класс.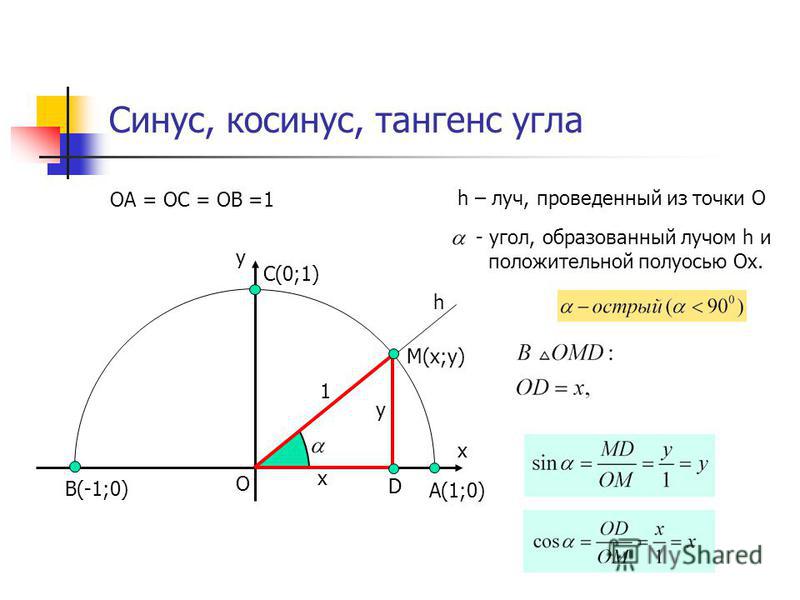
Как определить тригонометрические функции синус и косинус на единичной окружности? Как определить и запомнить значения синуса и косинуса 0°, 90°, 180°, 270°, 360°, -90° и т.д.? Сегодня мы ответим на эти вопросы. Если Вы не видели наш первый урок по теме: «Что такое единичная окружность и зачем она нужна. Тригонометрические функции», то обязательно посмотрите его, тогда этот урок будет Вам очень понятен. Мы объясним Вам, что такое синус и косинус на единичной окружности. Научим Вас видеть синус и косинус на единичной окружности. Дадим Вам шпагалку, которая позволит Вам в любой момент вспомнить значения синуса и косинуса 0°, 90°, 180°, 270°, 360°, -90° и т.д. Обратим Ваше внимание на то, что даёт нам рассмотрение тригонометрических функций на единичной окружности и в треугольнике. Поясним, почему тригонометрические функции называют круговыми. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:43 Итак начинаем.
06:14 Что такое sin α на единичной окружности?
08:27 Что такое cos α на единичной окружности?
09:38 Учимся видеть sin α и cos α на рисунке.
Примеры. https://rutube.ru/video/be19beb2a973ffbad226194f7e36e0f8/
#синуснаединичнойокружности #косинуснаединичнойокружности #определениесинусаикосинуса10класс #определениесинуса10класс #определениекосинуса10класс #определениесинусаикосинусаугла10класс #алгебратригонометрическиефункции #тригонометрическиефункцииалгебра10 #уголповоротаединичнойокружности #шпаргалкапотригонометрии #МатематикаОтБаканчиковой
алгебра 10 класс, синус на единичной окружности, косинус на единичной окружности, определение синуса и косинуса 10 класс, определение синуса 10 класс, определение косинуса 10 класс, определение синуса и косинуса угла 10 класс, алгебра тригонометрические функции, тригонометрические функции алгебра 10, угол поворота единичной окружности, шпаргалка по тригонометрииОпределения синуса и косинуса — Концепция
Определения синуса и косинуса прямоугольного треугольника применимы только к острым углам, поэтому необходимо более полное определение. Точка, в которой крайняя сторона пересекает единичную окружность (x, y), является основой для этого определения.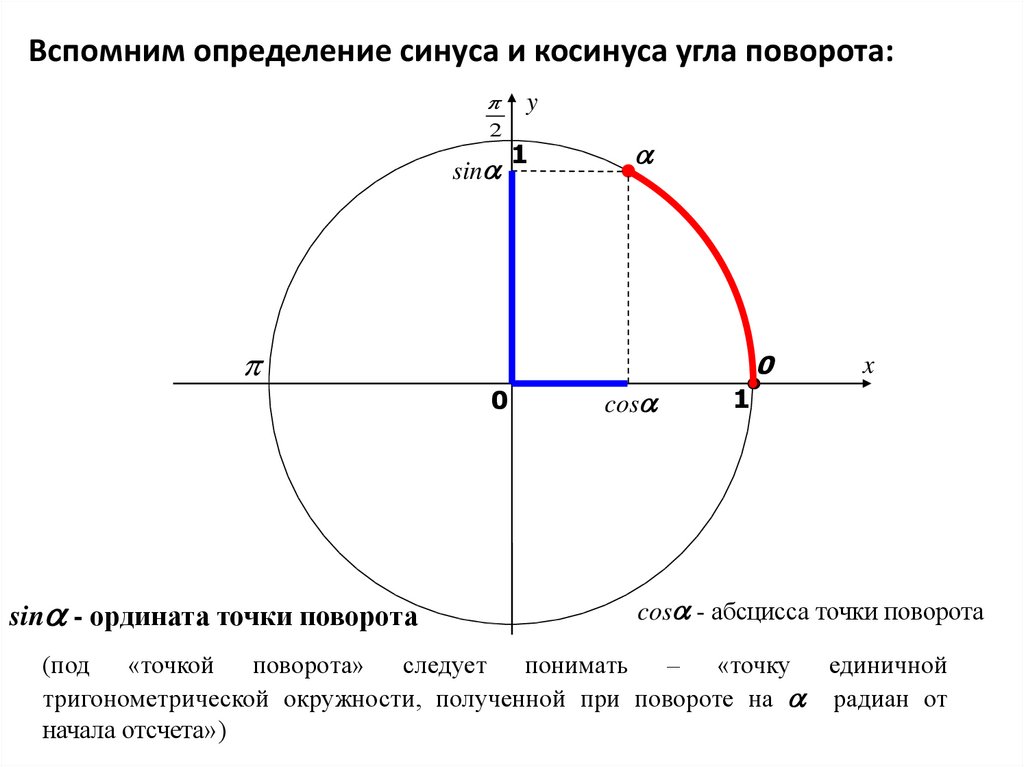
синус косинус определение синуса и косинуса прямоугольного треугольника углы в стандартном положении единица круг определения синуса и косинуса
Я хочу поговорить о чем-то действительно важном определении синуса и косинуса. Теперь вы, возможно, помните из геометрии определение синуса и косинуса прямоугольного треугольника, которое начинается с прямоугольного треугольника, и мы обозначим 3 стороны x, y и z, острый угол здесь — тета, а это прямой угол. Мы определили косинус теты как сторону, примыкающую к тете, деленную на гипотенузу.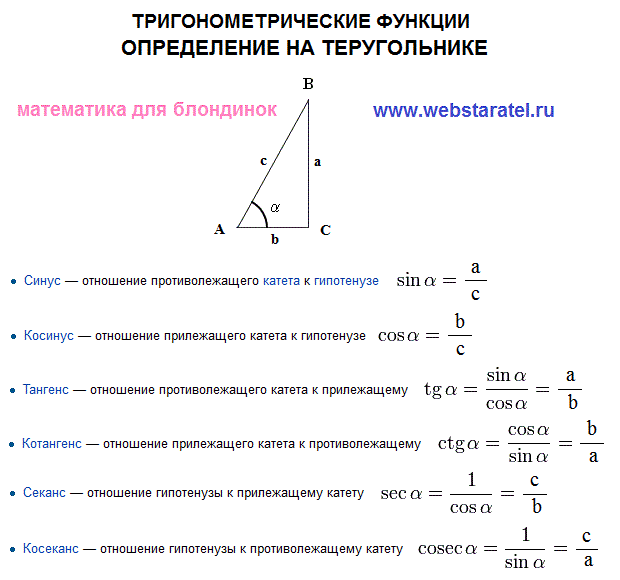
И под соседним мы подразумеваем сторону, которая находится рядом с тета, это гипотенуза, длинная сторона прямоугольного треугольника, и поэтому это означает, что x больше z. Синус определяется как сторона, противоположная тете y относительно гипотенузы, поэтому y больше z.
Проблема с этим определением в том, что оно работает только для острых углов. Это означает, что тета должна быть между 0 и 90 градусами вправо, иначе этот треугольник не будет иметь смысла, поэтому одна из вещей, которую мы делаем в предварительном исчислении, — расширяем это определение, чтобы оно включало все углы. Хорошо, вот как выглядит угол в стандартном положении. В стандартном положении вы рисуете угол так, чтобы его вершина находилась в начале координат на плоскости координат. Это начальная сторона, это конечная сторона, и вы можете думать об угле как о вращении, как если бы конечная сторона начиналась здесь и вращалась на угол тета, заканчивающийся здесь.
Теперь прибавьте к этому углу в стандартном положении единичную окружность, окружность с радиусом 1 x в квадрате плюс у в квадрате равно 1, здесь это окружность.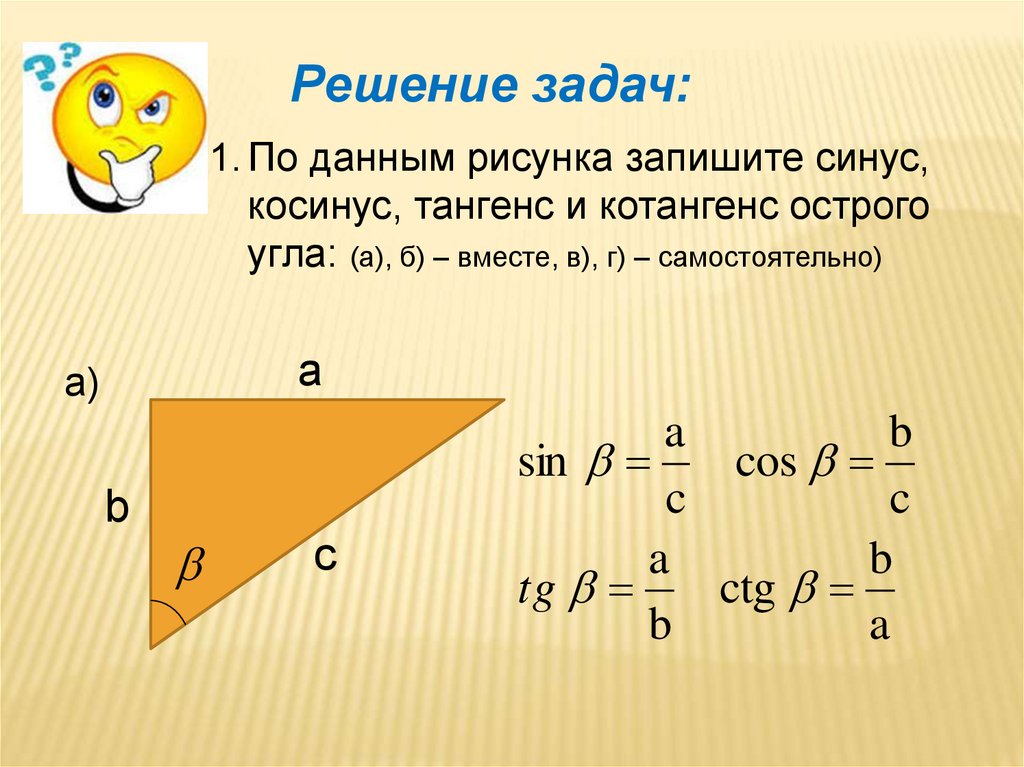
Теперь, чтобы сориентироваться, когда у вас есть радиус окружности 1, он пройдет через точку 1, 0 пройдет через точку 0, 1 минус 1, 0 и 0 минус 1. Тот же угол, который мы хотим отметить точка, в которой крайняя сторона пересекает единичную окружность. Эта точка будет иметь координаты x, y, мы определяем косинус как значение x и синус как значение y. Эта точка, конечно, будет уникальной, она будет однозначно зависеть от тета угла, поэтому для разных тета углов вы получите разные значения синуса и косинуса, но эта идея здесь позволит нам измерить синус и косинус для любого угла вообще. . Это сработает для острых углов, когда тета находится здесь в первом квадранте.
Это будет работать для 0 градусов, 90 градусов и любого другого угла, так что сила определений единичного круга заключается в том, что они работают для всех углов, которые мы будем использовать для остальной части курса тригонометрии.
Определение и значение косинуса — Merriam-Webster
косинус ˈkō-ˌsīn 98}{8!} — \dots{/latex}, что в точности равно косинусу угла измерения θ в радианах
Примеры предложений
Недавние примеры в Интернете
Эти функции, такие как синус и косинус , определяются с помощью прямоугольных треугольников.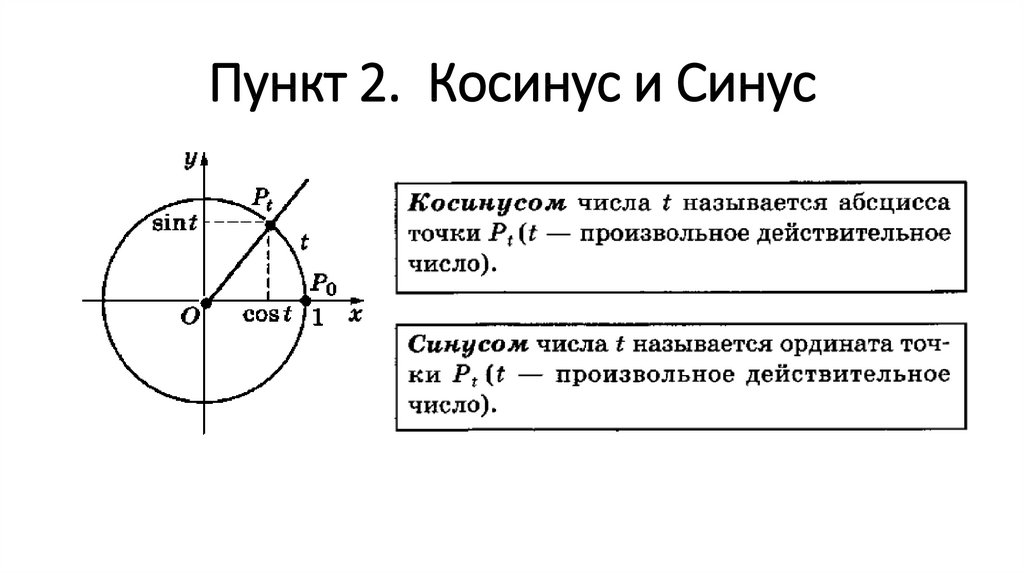
— Лейла Сломан, 9 лет.0033 Scientific American , 10 апреля 2023 г.
Хотя доказательство представляет собой впечатляющую часть математики, другие математики использовали аналогичные подходы раньше, используя синус и косинус , чтобы независимо доказать теорему Пифагора, не полагаясь на sin²α + cos²α = 1.
— Даррен Орф, Popular Mechanics , 31 марта 2023 г.
Иллюстрация: Ретт Аллен Это решение включает тригонометрическую функцию косинус .
— Ретт Аллен, WIRED , 14 марта 2023 г.
Ответ: ничего. Помните, что основные тригонометрические функции (синус, , косинус , тангенс) — это просто отношения сторон прямоугольных треугольников.
— Ретт Аллен, Wired , 14 марта 2022 г.
Среди вещей, которым обычно учат студентов в старшей школе: как найти косинус угла, с чего началась война 1812 года, и химический состав соли.
— BostonGlobe.com , 29 октября 2021 г.
В 1807 году Жозеф Фурье обнаружил, что любая периодическая функция — уравнение, значения которого циклически повторяются, — может быть выражена в виде суммы тригонометрических функций, таких как синус и косинус .
— Журнал Quanta , 13 октября 2021 г.
Рынки движутся как бы по синусоиде, 9Модель 0033 косинус от рынка продавца к рынку покупателя и обратно.
— Дэвид Фридман, Forbes , 24 мая 2021 г.
В качестве примера рассмотрим оператор, преобразующий функцию в ее производную (превращающий синус x в косинус x , например, или x3 в 3×2 и т. д.).
— Журнал Quanta , 19 апреля 2021 г.
Узнать больше
Эти примеры программно скомпилированы из различных онлайн-источников, чтобы проиллюстрировать текущее использование слова «косинус».
Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
История слов
Этимология
Новая латиница cosinus , из co- + средневековая латиница sinus sine
Первое известное использование
1635, в значении, определенном в смысле 1
Путешественник во времени
Первое известное использование косинуса было в 1635 г.
Посмотреть другие слова того же года
Словарные статьи Рядом с
косинускосинаж
косинус
косинусная кривая
Посмотреть другие записи поблизости
Процитировать эту запись «Косинус.
