§4. Подобие треугольников. Признаки подобия треугольников. Методические особенности изучения темы «Подобные треугольники» в средней общеобразовательной школе
Влияние коллектива на формирование личности младшего школьника
1.2 Признаки коллектива
коллектив школьник воспитание психологический Коллектив рассматривается как качественно высокая ступень развития контактной группы, как чрезвычайно сложная динамическая система…
Изучение темы «Многоугольники» в школьном курсе геометрии
3.1 Определения равных треугольников
Треугольник — самый «экономный» вид многоугольника. Для его задания достаточно указать его вершины — три точки, не лежащие на одной прямой, или три попарно пересекающиеся прямые…
Изучение темы «Многоугольники» в школьном курсе геометрии
3.2 Признаки равенства треугольников
Основная идея доказательства I и II признаков равенства треугольников в учебнике Атанасяна (4) и др. Атанасян Л.С…
Изучение темы «Треугольники» в курсе геометрии 7-9 классов средней школы
п.
 п. 3 Признаки равенства треугольников
п. 3 Признаки равенства треугольниковВо всех четырёх учебниках применяется один и тот же подход с использованием аксиомы существования треугольника равного данному. Но нигде ссылок на эту аксиому нет…
Изучение темы «Треугольники» в курсе геометрии 7-9 классов средней школы
п. п. 4 Признаки подобия треугольников
Определение подобных треугольников даётся как треугольники, у которых соответственные углы равны, а соответственные стороны пропорциональны. Атанасян вводит понятие пропорциональных сходственных сторон…
Изучение темы «Треугольники» в курсе геометрии 7-9 классов средней школы
п. 1 Обобщающий урок по теме «Признаки равенства треугольников»
(По учебнику Погорелова А.В. Геометрия 7-11) Цель: повторить и систематизировать знания учащихся по данной теме; применить полученные знания для решения задач связанных с треугольниками; осуществить проверку полученных знаний…
Методика обучения школьников применению теории к решению задач на вычисление и доказательство по теме «Многоугольники»
3.
 1 Определения равных треугольников
1 Определения равных треугольниковТреугольник — самый «экономный» вид многоугольника. Для его задания достаточно указать его вершины — три точки, не лежащие на одной прямой, или три попарно пересекающиеся прямые…
Методика обучения школьников применению теории к решению задач на вычисление и доказательство по теме «Многоугольники»
3.2 Признаки равенства треугольников
Основная идея доказательства I и II признаков равенства треугольников в учебнике Атанасяна (4) и др. Атанасян Л.С…
Методические особенности изучения темы «Подобные треугольники» в средней общеобразовательной школе
1.1 История возникновения преобразований, преобразования подобия
Искусство изображать предметы на плоскости с древних времен привлекало к себе внимание человека. Попытки таких изображений появились значительно раньше, чем возникла письменность. Ещё в глубокой древности люди рисовали на скалах, стенах…
Методические особенности изучения темы «Подобные треугольники» в средней общеобразовательной школе
1.
 4 Преобразование подобия плоскости. Гомотетия плоскости
4 Преобразование подобия плоскости. Гомотетия плоскостиОпределение. Пусть имеются две прямоугольные декартовые системы координат Oij и O/i/j/, при этом |i/|=|j/|=k|i|=k|j|=k (k>0). Тогда преобразование плоскости, которое каждой точки М с координатами (x…
Методические особенности изучения темы «Подобные треугольники» в средней общеобразовательной школе
1.5 Группа преобразований подобия и её подгруппы
Теорема 1. Множество всех преобразований подобия плоскости есть группа преобразований, называемая группой подобий. Доказательство. Если и — преобразования подобия с коэффициентами и , то — преобразования подобия с коэффициентом…
Начала систематического курса планиметрии в средней школе
3. Методическая схема изучения признаков равенства треугольников
Систематический курс геометрии начнем изучать в 7 классе со знакомства с основными свойствами простейших геометрических фигур, которые сформулированы в виде аксиом.
№ 47, стр.23
АС и ВС пересекаются, т.
Решение треугольников в 9 классе
2. Анализ методических особенностей изложения темы: «Решение треугольников в 9 классе» в различных действующих учебниках по геометрии
В процессе обучения геометрии используются разнообразные методы обучения. Они должны составлять единый комплекс, основой которого являются учебники по геометрии. Все остальные средства обучения…
Решение треугольников в 9 классе
4.5 Решение треугольников
обучение треугольник синус учебный На уроках по теме: «Решение треугольников», ставится вопрос о том, как, зная один из основных элементов треугольника, найти другие. Очень важно, чтобы учащиеся поняли, что теоремы синусов, косинусов…
Решение треугольников в 9 классе
4.6 Решение треугольников по двум сторонам и углу, лежащему против одной из них
При изучении темы «Решение треугольников» нам поставили дополнительный урок, или осталось время, то с учащимися можно разобрать четвертый случай решения треугольников, но рекомендуется его провести как урок — факультатив. ..
..
Решение:
B A C D F E Получили: ∠A=∠E; ∠B=∠D; ∠C=∠F
, то ΔABC∾ΔEDF (по определению) Вывод: ΔABC∾ΔEDF. | Решение:
АВ и КМ – сходственные, значит ∠С=∠N. ВС и МN – сходственные, значит ∠А=∠К. 2)Получаем следующий чертеж М К N В А С 3) (так как ΔMNK∾ΔBCA) и . Тогда . |
ПОДОБНЫЕ ТРЕУГОЛЬНИКИ презентация, доклад, проект
ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
ПЛАН
Пропорциональные отрезки.
Свойство биссектрисы треугольника.
Определение подобных треугольников.
Отношение периметров подобных фигур.
Отношение площадей подобных фигур.
Признаки подобия треугольников.
Пропорциональные отрезки
Отношением отрезков называется отношение их длин.
Отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1,, если
ПРИМЕР
ПРИМЕР
Даны два прямоугольных треугольника
Стороны ΒC и CA пропорциональны MN и MK, так как
т.е.
и
НАЙДИТЕ ГИПОТЕНУЗУ БОЛЬШЕГО ТРЕУГОЛЬНИКА.
Пропорциональность отрезков
Понятие пропорциональности вводится для любого числа отрезков.
например
Подобные фигуры
Предметы одинаковой формы, но разных размеров
Фотографии, отпечатанные с одного негатива, но с разными увеличениями;
Здание и его макет
Планы, географические карты одного и того же района, выполненные в разных масштабах.
Подобные фигуры
В геометрии фигуры одинаковой формы называют подобными фигурами
Подобными являются любые два квадрата
Подобными являются любые два круга
два куба
два шара
Подобные треугольники
Даны два треугольника AΒC и A1Β1C1,
у которых A = A1, Β = Β1, C = C1.
Стороны AΒ и A1Β1 , AC и A1C1 , ΒC и Β1C1, лежащие против равных углов, называют сходственными
Определение
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
A = A1, Β = Β1, C = C1.
ΔAΒC ~ ΔA1Β1C1
Коэффициент подобия
Число k , равное отношению сходственных сторон, называется коэффициентом подобия.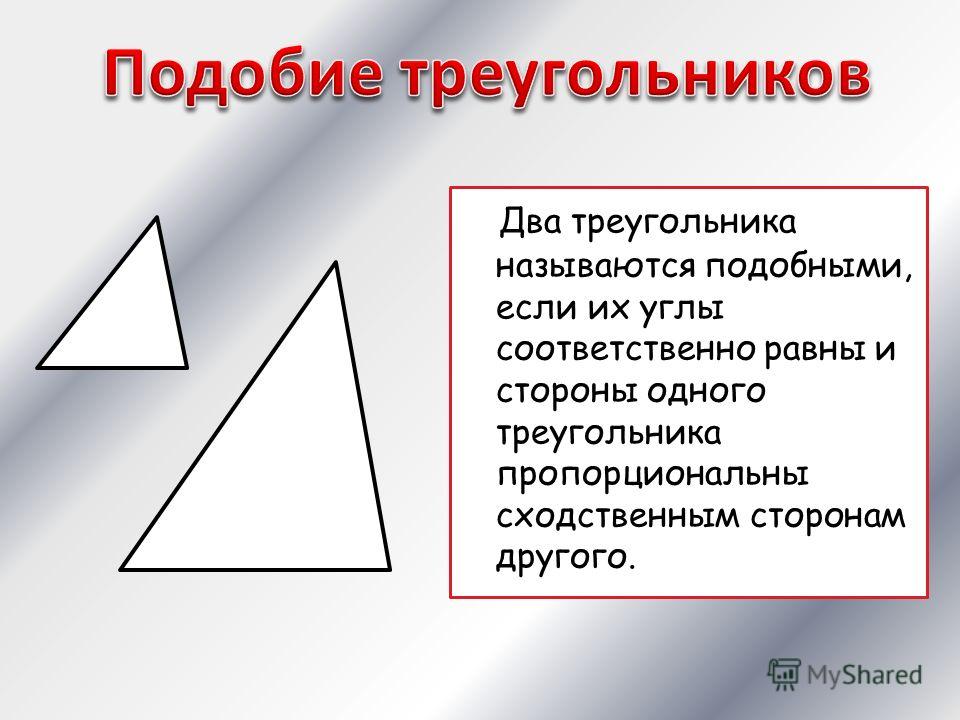
ΔAΒC ∞ ΔA1Β1C1
k – коэффициент подобия.
Дополнительные свойства
Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия.
Отношение медиан подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия.
Отношение биссектрис подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия.
Отношение периметров
Отношение периметров подобных треугольников равно
коэффициенту подобия.
ΔAΒC ~ ΔA1Β1C1
ДОКАЗАТЕЛЬСТВО
Отношение периметров
Выносим общий множитель за скобку и сокращаем дробь.
Отношение площадей
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.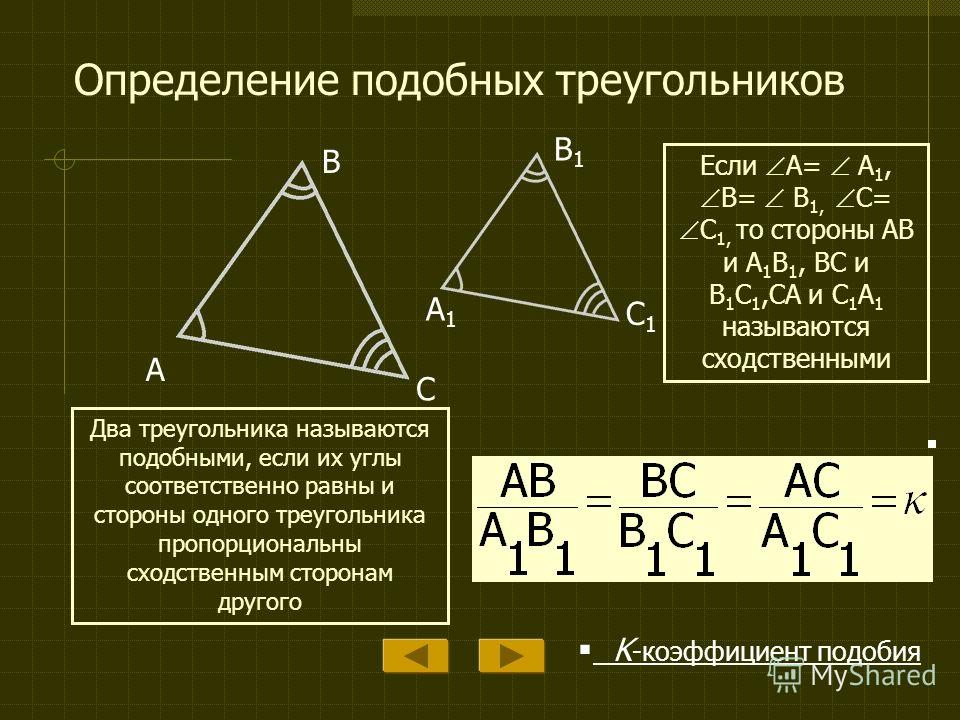
ΔAΒC ~ ΔA1Β1C1
ДОКАЗАТЕЛЬСТВО
Отношение площадей
Пусть ΔAΒC ~ ΔA1Β1C1,
коэффициент подобия k
A = A1, по теореме об отношении площадей треугольников, имеющих по равному углу, имеем
Свойство биссектрисы треугольника
C
B
A
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
D
или
ДОКАЗАТЕЛЬСТВО
ПРИМЕР
Свойство биссектрисы треугольника
ΔABD и ΔACD имеют общую высоту AH
ΔABD и ΔACD имеют равные углы 1 = 2
ИМЕЕМ
Свойство биссектрисы треугольника
Дано: ΔABC
AD – биссектриса
AB = 14 см
BC = 20 см
AC = 21 см
Найти: BD,CD.
Решение:
Свойство биссектрисы треугольника
Решение:
Пусть BD = x см,
тогда CD = (20 – x) см.
По свойству биссектрисы треугольника
имеем
Решая уравнение, получим х = 8
BD = 8 см, CD = 12 см.
Признаки подобия треугольников
Первый признак подобия треугольников.
(по двум углам)
Второй признак подобия треугольников.
(по углу и двум пропорциональным сторонам)
Третий признак подобия треугольников.
(по трем пропорциональным сторонам)
Первый признак подобия треугольников.
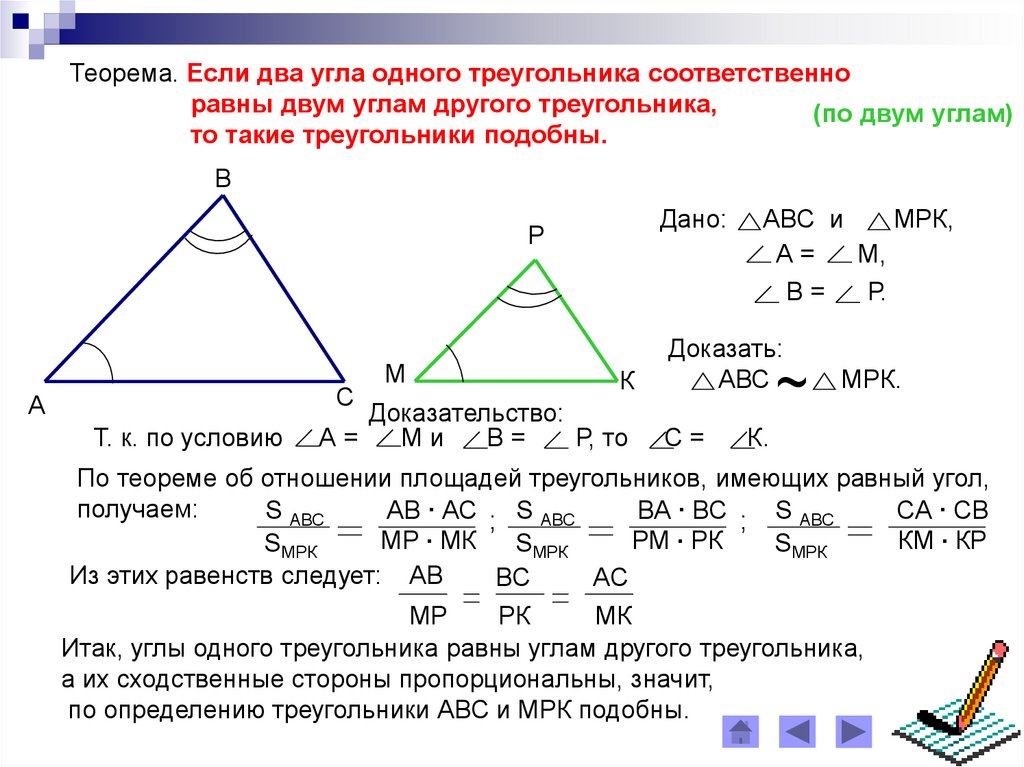
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Первый признак подобия треугольников.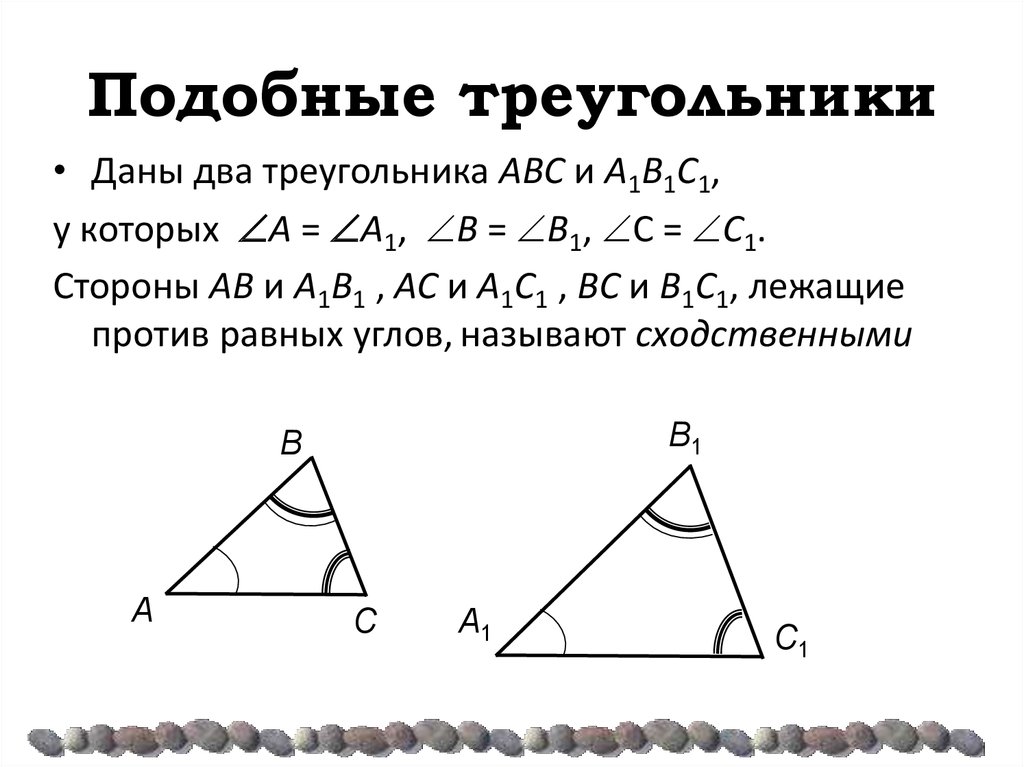
Дано:
ΔABC и ΔA1B1C1, A =A1,
B = B.
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
Первый признак подобия треугольников.
Доказательство:
A = A1, B = B1.
C = 180º – A – B,
C1 = 180º – A1 – B1.
C = C1
Таким образом углы треугольников соответственно равны.
Первый признак подобия треугольников.
Доказательство:
A = A1,
B = B1.
Имеем
Аналогично, рассматривая равенство углов C=C1, A=A1, получим
Итак, сходственные стороны пропорциональны.
Второй признак подобия треугольников.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Второй признак подобия треугольников.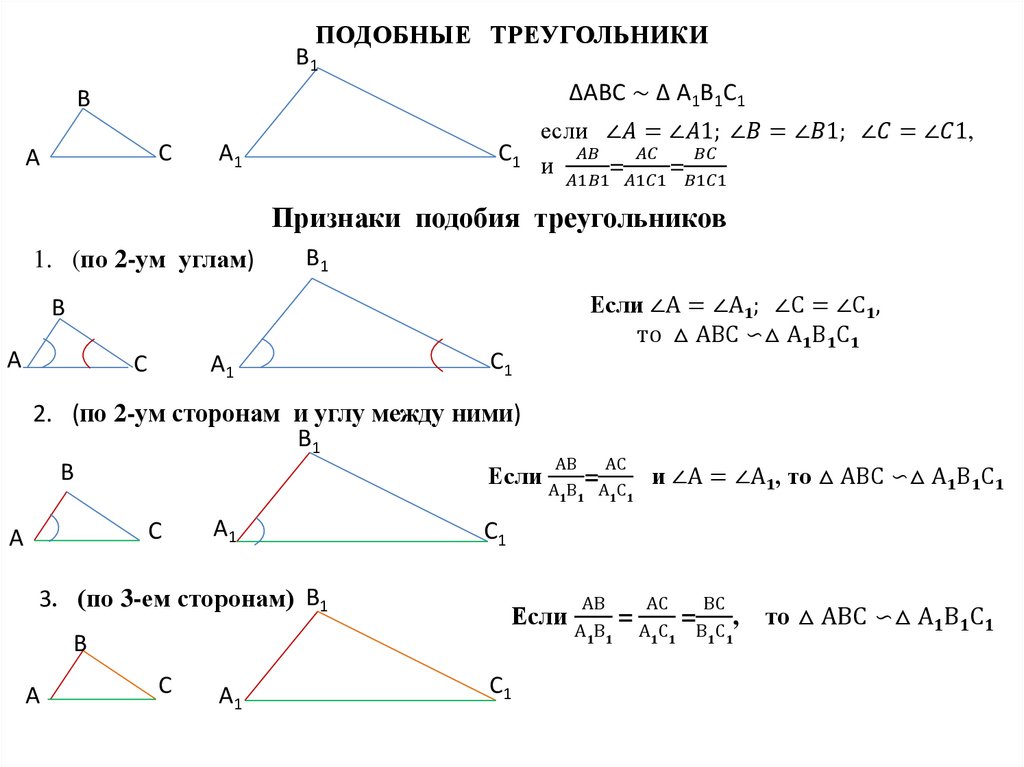
Дано:
ΔABC и ΔA1B1C1,
A =A1,
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
Второй признак подобия треугольников.
Доказательство:
Достаточно доказать, что B = B1.
ΔABC2, 1=A1, 2=B1,
ΔABC2 ~ ΔA1B1C1 по двум углам.
(из подобия).
По условию
AC=AC2.
ΔABC=ΔABC2, т.е. B = B1.
Третий признак подобия треугольников.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Третий признак подобия треугольников.
Дано:
ΔABC и ΔA1B1C1,
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
Третий признак подобия треугольников.
Доказательство:
Достаточно доказать, что A=A1
ΔABC2, 1=A1, 2=B1,
ΔABC2 ~ ΔA1B1C1 по двум углам.
Отсюда
По условию
ΔABC=ΔABC2 по трем сторонам, т.е. A = A1
ТЕСТ
1. По данным рисунка х равен
А) 7
Б) 14
В) 3,5
Г) 14/3
ТЕСТ
2) По данным рисунка периметр ΔABC равен
А) 9
Б) 27
В) 36
Г) 18
ТЕСТ
3) По данным рисунка отрезок BC равен
А) 3,75
Б) 7,5
В) 5
Г) 4,5
А
В
С
3
3
4
0,5
2,5
ТЕСТ
4) По данным рисунка площади данных треугольников относятся
А) 3 : 1
Б) 9 : 1
В) 6 : 1
Г) 9 : 4
ТЕСТ
5) По данным рисунка прямые AB и DE
А) нельзя ответить
Б) пересекаются
В) параллельны
Конспект урока «Определение подобных треугольников» | План-конспект урока по геометрии (8 класс):
Ход урока
I. Вступительное слово учителя.
Вступительное слово учителя.
Здравствуйте, ребята! Закройте пожалуйста глаза,и покрутитесь на месте.скажите не открыва глаз,легко определит где вы находитесь?Закройте уши руками и скажите легко ли понять что я говорю?
Это сделать затруднительно.Поэтому мне бы хотелось чтобы на нашем уроке вы вниметель смотрель ,слушали и мыслили.
Девизом к сегодняшнему уроку будут слова гениального ученого Альберта Эйнштейна:
«Есть только два способа прожить жизнь.
Первый — будто чудес не существует.
Второй — будто кругом одни чудеса!»
Учитель: Я желаю всем вам сегодня, чтобы знания, полученные на нашем уроке, были очередным чудом. Итак, начинаем урок!
(слайд № 1)
В Атлантическом океане есть место, по форме напоминающее геометрическую фигуру, о которой мы сегодня будем говорить.
Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида. Его ещё называют “дьявольским”, “проклятым”. Загадочность его заключается в том, что в нем бесследно исчезают самолеты и корабли. Природа этого места остается, тайной и по сей день
Природа этого места остается, тайной и по сей день
(Слайд №2,3,4).
Учитель: Как вы думаете, что это за место?
(Слайд № 5)
Обучающиеся: Бермудский треугольник.
II. Мотивация и актуализация знаний.
Учитель: Какой же геометрической фигуре мы посвятим сегодняшний урок?
Обучающиеся: Треугольнику.
Учитель: У вас на рабочих столах лежат оценочные листы, в которых по мере прохождения заданий на уроке вы будите выставлять сами себе оценку по пяти бальной шкале. Затем, в конце урока, найдя среднее арифметическое ваших оценок, вы оцените себя, прокомментируя свою деятельность.
Учитель: Давайте вспомним все, что нам известно о треугольнике.
(Слайд № 6)
Вопросы:
- Какая фигура называется треугольником?
- Какие элементы треугольника вы знаете?
- Какими могут быть треугольники в зависимости от величины углов, длин сторон?
- Расскажите о равнобедренном треугольнике
(Слайд № 7)
о равностороннем треугольнике
(Слайд № 8)
о прямоугольном треугольнике
(Слайд № 9)
- Чему равна сумма углов треугольника?
(Слайд № 10)
- Признаки равенства треугольников.

(Слайд № 11)
Учитель: Оцените себя в оценочном листе.
Ребята, это еще маленькая часть того, что мы должны знать и узнаем в будущем.
III. Изложение нового материала.
Показываю два равных треугольника.
Учитель: Что вы можете сказать об этих треугольниках?
Обучающиеся: Равные.
Учитель: Как проверить, что они равны?
Обучающиеся: Треугольники должны совместиться наложением.
Учитель: А что вы можете сказать о предметах которые вы видите?(матрешки, елочные шары, формочки для выпекания) ?
Обучающиеся: …?(они одинаковые по форме ,но разного размера)
Учитель: Называются эти фигуры подобными . Какова же будет тема нашего урока?
Обучающиеся: Подобные треугольники.
Учитель: Тема нашего урока: “Определение подобных треугольников”
(слайд № 14).
Учитель: Какие цели вы поставите перед собой?
Обучающиеся:
- Сформулировать определение подобных треугольников;
- Изучить характеристики подобных треугольников и их свойства;
- Узнать, где применяется подобие треугольников.

(слайд № 15)
Учитель: Приглашаю вас в геометрическую лабораторию. Как и при любом исследовании, результаты будут зависеть от того, насколько точно и аккуратно будет сделана работа. Перед вами на столах наборы для исследования, рассмотрев несколько примеров, ваша задача ввести понятие подобных треугольников и сформулировать их основные свойства.
Учитель: Для того чтобы начать работу, давайте, вспомним понятия:
— Что называется отношением двух отрезков?
— Когда отрезки являются пропорциональными отрезками?
1этап. Для каждого из рисунков, заполните таблицу 1 и таблицу 2 по рядам соответственно, результаты внесите в рабочую карту:
(слайд № 16)
На выполнение этого этапа исследования отводится 6-7 минут, затем выполняем самопроверку с плаката
(слайд № 17)
2 этап. Ответьте на вопросы:
- Что можно сказать про углы каждой пары треугольников? (соответственные углы каждой пары треугольников равны).
- Что можно сказать про стороны каждой пары треугольников? (соответственные стороны каждой пары треугольников пропорциональны).

— Сформулировать определение подобных треугольников, вписав необходимые пропущенные слова:
Если углы двух треугольников РАВНЫ и стороны одного треугольника ПРОПОРЦИОНАЛЬНЫ сходственным сторонам другого, то такие треугольники называются ПОДОБНЫМИ.
(слайд № 18)
Число равное отношению сходственных сторон подобных треугольников называется КОЭФФИЦИЕНТОМ ПОДОБИЯ.
Физкультминутка:
3 этап. Определите, чему равны коэффициенты подобия каждой пары треугольников из 1 этапа исследования. Ответы запишите в рабочую карту. Выполняем самопроверку со слайда..
(слайд № 19,20)
4 этап. Сравните данные коэффициенты подобия треугольников с соответствующими им отношениями периметров и площадей. Результаты запишите в рабочую карту.
Ответьте на вопросы:
- Чему равно отношение периметров подобных треугольников? (отношение периметров подобных треугольников равно коэффициенту подобия)
- Чему равно отношение площадей подобных треугольников? (отношение площадей подобных треугольников равно квадрату коэффициента подобия)
Ответы запишите в рабочую карту. Выполняем самопроверку с плаката.
Выполняем самопроверку с плаката.
Учитель: Оцените себя в оценочном листе.
IV. Решение задач.
Учитель:прежде чем приступить к решению задач мне бы хотелось рассказать вам об открытии Фалеса
Теперь рассмотрим, где же на практике применяется подобие треугольников. Ребята, уже совсем немного времени вам остаётся до ОГЭ в 9 классе, поэтому мы решим задачу из раздела реальная математика:
(Слайд № 23)
Один ученик решает задачу у доски, остальные в рабочих тетрадях.
Учитель: Оцените себя в оценочном листе.
VI.. Подведение итогов урока (рефлексия), выставление оценок.
Возвращаемся к слайду, содержащему цели урока, дети отвечают, что узнали, чему научились.
(слайд № 24)
Вычислите в оценочном листе средний бал и прокомментируйте свою деятельность на уроке, поставив себе оценку.
Выставляю оценки за урок.
VI I.. Домашнее задание (слайд № 25)
п. 56-58, из рабочей карты выучить определения и свойства, №533, 536 для всех
№1 На рисунке изображён колодец с «журавлём». опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м? |
3. подготовить рисунки или макеты подобных фигур.
4. подготовить историческую справку о Фалесе Милетском.
VII. Заключительное слово учителя.
Ребята, сегодня на уроке все хорошо постарались для того, чтобы достигнуть поставленных вами целей. В ходе проведения исследования были открыты новые для нас понятия и сформулированы свойства. В дальнейшем мы с вами узнаем как подобие можно применить в жизненных ситуациях. На сегодня все молодцы и спасибо за урок!
Презентация к уроку «Определение подобных треугольников» | Презентация к уроку геометрии (8 класс) по теме:
Слайд 1
Подобные треугольники
Слайд 2
Подобные фигуры Фигуры принято называть подобными, если они имеют одинаковую форму (похожи по виду).
Слайд 3
Подобие в жизни( карты местности )
Слайд 4
Пропорциональные отрезки Определение: отрезки называются пропорциональными, если пропорциональны их длины. 12 6 8 4 А 1 В 1 АВ С 1 К 1 СК Говорят, что отрезки А 1 В 1 и С 1 К 1 пропорциональны отрезкам АВ и СК . Пропорциональны ли отрезки АВ и СК отрезкам ЕР и НТ, если: а) АВ = 15 см, СК = 2,5 см, ЕР = 3 см, НТ = 0,5 см ? б) АВ = 12 см, СК = 2,5 см, ЕР = 36 см, НТ = 5 см ? в) АВ = 24см, СК = 2,5 см, ЕР = 12 см, НТ = 5 см ? да нет нет А В 6 см С К 4 см А 1 В 1 12 см С 1 8 см К 1
12 6 8 4 А 1 В 1 АВ С 1 К 1 СК Говорят, что отрезки А 1 В 1 и С 1 К 1 пропорциональны отрезкам АВ и СК . Пропорциональны ли отрезки АВ и СК отрезкам ЕР и НТ, если: а) АВ = 15 см, СК = 2,5 см, ЕР = 3 см, НТ = 0,5 см ? б) АВ = 12 см, СК = 2,5 см, ЕР = 36 см, НТ = 5 см ? в) АВ = 24см, СК = 2,5 см, ЕР = 12 см, НТ = 5 см ? да нет нет А В 6 см С К 4 см А 1 В 1 12 см С 1 8 см К 1
Слайд 5
б Пропорциональные отрезки Тест 1. Указать верное утверждение: а) отрезки АВ и РН пропорциональны отрезкам СК и МЕ; б) отрезки МЕ и АВ пропорциональны отрезкам РН и СК; в) отрезки АВ и МЕ пропорциональны отрезкам РН и СК. А В 3 см С К 2см М Е 9 см Р Н 6 см Приложение: равенство МЕ АВ РН СК можно записать ещё тремя равенствами: РН СК МЕ АВ ; МЕ РН АВ СК ; АВ СК МЕ РН .
Слайд 6
Пропорциональные отрезки 2 . Тест F Y Z R L S N 1 c м 2 см 4 см 2 см 3 см Какой отрезок нужно вписать , чтобы было верным утверждение: отрезки FY и YZ пропорциональны отрезкам LS и ……. а) RL ; б) RS ; в) SN а) RL
Слайд 7
Пропорциональные отрезки ( нужное свойство ) Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Н Дано: АВС, АК – биссектриса. Доказательство: 1 А В К С 2 Т. к. АК – биссектриса, то 1 = 2, значит, АВК и АСК имеют по равному углу, поэтому Доказать: ВК АВ КС АС S АВК S АСК АВ ∙ АК АС ∙ АК AB AC АВК и АСК имеют общую высоту АН, значит, S АВК S АСК ВК К C AB А C BK K С ВК АВ КС АС Следовательно, Проведём АН ВС.
Н Дано: АВС, АК – биссектриса. Доказательство: 1 А В К С 2 Т. к. АК – биссектриса, то 1 = 2, значит, АВК и АСК имеют по равному углу, поэтому Доказать: ВК АВ КС АС S АВК S АСК АВ ∙ АК АС ∙ АК AB AC АВК и АСК имеют общую высоту АН, значит, S АВК S АСК ВК К C AB А C BK K С ВК АВ КС АС Следовательно, Проведём АН ВС.
Слайд 8
Подобные треугольники Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональны сходственным сторонам другого. А 1 В 1 С 1 А В С Сходственными сторонами в подобных треугольниках называются стороны, лежащие против равных углов. А 1 = А, В 1 = В, С 1 = С А 1 В 1 В 1 С 1 А 1 С 1 АВ ВС АС k A 1 B 1 C 1 ABC K – коэффициент подобия ~
Слайд 9
Подобные треугольники А 1 В 1 С 1 А В С Нужное свойство: А 1 = А, В 1 = В, С 1 = С, АВ ВС АС А 1 В 1 В 1 С 1 А 1 С 1 1 k ABC ~ A 1 B 1 C 1 , – коэффициент подобия 1 k A 1 B 1 C 1 ABC , K – коэффициент подобия ~
Слайд 10
Реши задачи 3.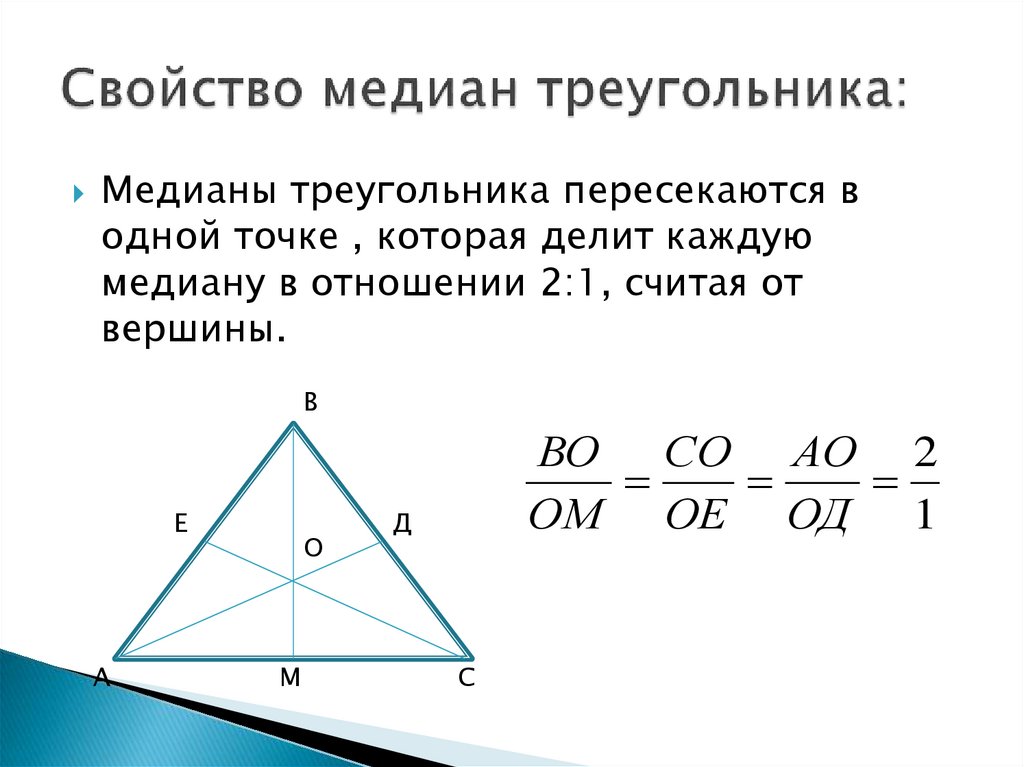 По данным на чертеже найти стороны АВ и В 1 С 1 подобных треугольников АВС и А 1 В 1 С 1 : А В С А 1 С 1 В 1 6 3 4 2,5 ? ? Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 3 . 2. Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 1/3.
По данным на чертеже найти стороны АВ и В 1 С 1 подобных треугольников АВС и А 1 В 1 С 1 : А В С А 1 С 1 В 1 6 3 4 2,5 ? ? Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 3 . 2. Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 1/3.
Слайд 11
Теорема 1. Отношение периметров подобных треугольников равно коэффициенту подобия. М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: Р МКЕ : Р АВС = k Доказательство: K , МК АВ КЕ ВС МЕ АС Значит, МК = k ∙ АВ, КЕ = k ∙ ВС, МЕ = k ∙ АС. Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то Р МКЕ = МК + КЕ + МЕ = k ∙ АВ + k ∙ ВС + k ∙ АС = k ∙ (АВ + ВС + АС) = k ∙ Р АВС . Значит, Р МКЕ : Р АВС = k .
Слайд 12
Теорема 2. Отношение площадей подобных треугольников равно квадрату коэффициент a подобия. М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: S МКЕ : S АВС = k 2 Доказательство: Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то M = A, k, MK AB ME AC значит, МК = k ∙ АВ, МЕ = k ∙ АС. S MKE S ABC MK ∙ ME AB ∙ AC k ∙ АВ ∙ k ∙ АС АВ ∙ АС k 2
S MKE S ABC MK ∙ ME AB ∙ AC k ∙ АВ ∙ k ∙ АС АВ ∙ АС k 2
Слайд 13
Реши задачи Две сходственные стороны подобных треугольников равны 8 см и 4 см. Периметр второго треугольника равен 12 см. Чему равен периметр первого треугольника ? 24 см 2. Две сходственные стороны подобных треугольников равны 9 см и 3 см. Площадь второго треугольника равна 9 см 2 . Чему равна площадь первого треугольника ? 81 см 2 3. Две сходственные стороны подобных треугольников равны 5 см и 10 см. Площадь второго треугольника равна 32 см 2 . Чему равна площадь первого треугольника ? 8 см 2 4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 . Одна из сторон первого треугольника равна 4 см. Чему равна сходственная сторона второго треугольника ? 8 см
Слайд 14
Решение задачи Площади двух подобных треугольников равны 50 дм 2 и 32 дм 2 , сумма их периметров равна 117 дм. Найдите периметр каждого треугольника. Найти: Р АВС , Р РЕК Решение: Т. к. по условию треугольники АВС и РЕК подобны, то: Дано: АВС , РЕК подобны, S АВС = 50 дм 2 , S РЕК = 32 дм 2 , Р АВС + Р РЕК = 117дм.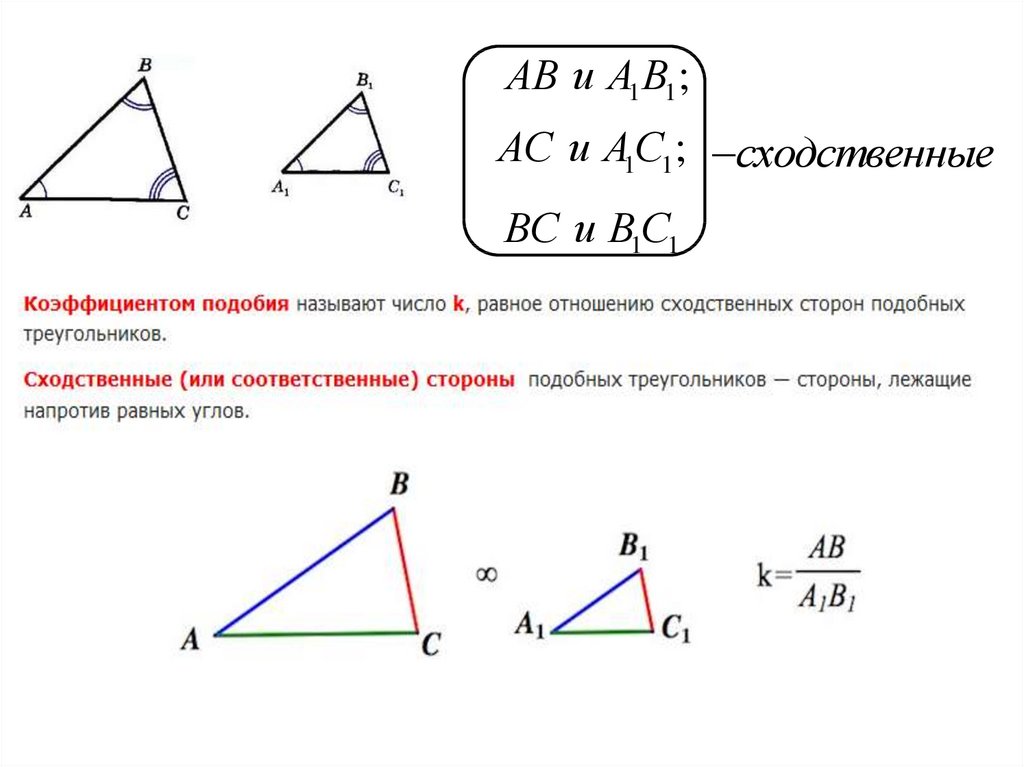 S АВС S РЕК 50 32 25 16 K 2 . Значит, k = 5 4 K , Р АВС Р РЕК Р АВС Р РЕК 5 4 1,25 Значит, Р АВС = 1,25 Р РЕК Пусть Р РЕК = х дм, тогда Р АВС = 1,25 х дм Т. к. по условию Р АВС + Р РЕК = 117дм, то 1,25 х + х = 117, х = 52. Значит, Р РЕК = 52 дм, Р АВС = 117 – 52 = 65 (дм). Ответ: 65 дм, 52 дм.
S АВС S РЕК 50 32 25 16 K 2 . Значит, k = 5 4 K , Р АВС Р РЕК Р АВС Р РЕК 5 4 1,25 Значит, Р АВС = 1,25 Р РЕК Пусть Р РЕК = х дм, тогда Р АВС = 1,25 х дм Т. к. по условию Р АВС + Р РЕК = 117дм, то 1,25 х + х = 117, х = 52. Значит, Р РЕК = 52 дм, Р АВС = 117 – 52 = 65 (дм). Ответ: 65 дм, 52 дм.
Слайд 15
« Математику уже затем учить следует, что она ум в порядок приводит» М. В. Ломоносов Желаю успехов в учёбе! Михайлова Л. П. ГОУ ЦО № 173.
Урок по геометрии 8 класс » Определение подобных треугольников»
Развивать исследовательские навыки, способствовать осознанию изучаемого материала
Предметные: определять пропорциональные отрезки, подобные треугольники, применять свойства биссектрисы при решении задач.
Познавательные: активизация познавательной деятельности учащихся через решение практических задач;
Регулятивные: умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы;
Коммуникативные: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей;
Личностные: проявляют способность к эмоциональному восприятию математических рассуждений.
Задачи: создать условия для определения отношения отрезков, пропорциональных отрезков, подобных треугольников, применения этого свойства при решении задач.
Пропорциональные отрезки, пропорции, сходственные стороны, подобные фигуры, коэффициент подобия
Этапы урока | Деятельность учителя | Деятельность обучающихся | ||
Актуализация знаний | 1.Предлагаю проблемную задачу классу: Человек может прожить без пищи несколько недель, без воды несколько дней, а без кислорода не больше 3-4 минут. Почему? 2. Поговорка “Это нам нужно как воздух!” выражает особую потребность организма в воздухе. Сопоставить с данной поговоркой и выразить значение понятия подобия для планиметрии. 3. Давайте выясним, почему и установим его отношения с другими понятиями? | Ответы -Из внешней среды поступает постоянно кислород. -“Понятие подобия нужно как воздух планиметрии!” | ||
2.Подготовка к изучению новой темы | — Что называют отношением двух чисел? — Что показывает отношение? — Отношение АВ и СD равно 2 : 7. О чем это говорит? — Найдите отношение СD к АВ. — В треугольнике АВС АВ : ВС : АС = 2 : 4 : 3, РАВС = 45 дм. Найдите стороны треугольника АВС. — Что называют пропорцией? Верны ли пропорции 1,5 : 1,8 = 25 : 30; 18 : 3 = 5 : 30? — В пропорции a : b = с : d укажите крайние и средние члены. Сформулируйте основное свойство пропорции. — Переставив средние и крайние члены пропорции, составьте три верные пропорции: а) 12 : 0,2 = 30 : 0,5 б) АВ : МN = СD : КР — Найдите неизвестный член пропорции а) 7х : 4,2 = 12,3 : 6; б) х : АВ = MN : KP. | Отвечают на вопросы | ||
Изучение новой темы | 1. Нам, ребята, необходимо вывести понятие отношения отрезков. Давайте проведем исследования и установим связь между отношением чисел и отрезков. Существует ли она? Перед уроком было опрошено 76 учащихся 8 – х классов. 80 % учащихся считают, что связь между отношением чисел и отрезков существует. Почему? 2. Могут ли отношения длин отрезков быть равными? Приведите пример 3. Отрезки АВ, СD, MN пропорциональны отрезкам А1В1, С1D1 и M1N1. Найдите С1D1 и MN, если АВ = 5 см, А1В1 = 20 см, СD = 6 см, M1N1 = 8 см. 4. . Попробуем вывести главное понятие урока – понятие подобных фигур. К моменту изучения темы вы знакомы с реальными предметами, дающими наглядное представление о подобных фигурах: географические карты, модели автомобилей, два круга, два квадрата, два мяча разных размеров, изображения на кинопленке и на экране, на фотопленке и т.д. Введем понятие подобных треугольников: Определение: два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого. Записывают: , если = А1, В = В1, С = С1, k, k – коэффициент подобия. Стороны АВ и А1В1, ВС и В1С1, АС и А1С1 называют сходственными. Из книги рекордов Гиннеса: Самое большое расстояние. При тихой погоде вне помещения обычный человеческий голос слышен на расстоянии 180 м. Зарегистрирован случай, когда человеческий голос можно различить на расстоянии 8 км при особых условиях ночью над тихой водой на расстоянии 17 км. Найти отношение обычного человеческого голоса к зарегистрированному случаю? | — Любой отрезок имеет длину. Длина выражается положительным числом. Отношение отрезков это отношение их длин, т.е. отношение чисел. — могут — Если АВ = 5 см, СD = 7см; А1В1 = 7,5 см, С1D1 = 10,5 см, то АВ : А1В1 = СD : C1D1, т.е. отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1. Чему равно отношение отрезков? — решают задачу — работают в тетради, выполняют записи | ||
5.Закрепление | 1. Работа в рабочих тетрадях: решить задачи № 51, 52. 2. Решение задачи № 535. Вопросы, контролирующие глубину усвоения доказательства: — Почему ? — Сформулируйте теорему, на основании которой если 1 = 2, то . — Поясните, на каком основании из равенства следует равенство . 3. Решить на доске и в тетрадях учащихся задачи № 536 (б), 541. 4. Задача № 536 (б).
Ответ: 10 . Наводящие вопросы: К задаче 536 (б) — Как биссектриса треугольника делит противолежащую сторону? — Длину какого отрезка необходимо найти для нахождения отрезка СD — Как можно вычислить длину отрезка ВС? Решение. №541 В треугольнике А = 1060, В = 34 0, значит С = 1800 — ( А + В) = 1800 – 1400 = 400. В треугольнике DEF E = 1060, F = 400. По определению подобных треугольников в треугольниках АВС и DEF: А = Е = 1060, В = D = 340. C = F = 400, ВС : DF = 7,6 : 22,8 = 1 : 3. АС : ЕF = 4,4 : 13,2 = 1 : 3; АВ : DE = 5,2 : 15,6 = 1 : 3, значит треугольники АВС и DEF подобны. Ответ: АВС подобен DEF. Наводящие вопросы: к № 541 — Когда два треугольника подобны? — Равны ли углы этих треугольников? — пропорциональны ли сходственные стороны данных треугольников? — Подобны ли АВС и EDF? | Задание учащимся: заполнить пропуски в тетради. Учащиеся по указанию учителя читают по одному предложению, исправляя имеющиеся ошибки. Если кто – то допустил ошибку, то другие ее исправляют. Таким же образом решают задачу № 52. Прочитать самостоятельно задачу и ее решение. Вызывается к доске один из наиболее подготовленных учащихся и решает задачу самостоятельно (без помощи учебника, выполнив рисунок и записывая краткое решение). — Один из учащихся решает задачу № 536 (б) на доске, остальные в тетрадях. Отвечать на наводящие вопросы имеет право любой ученик. Таким же образом решается задача № 541. | ||
Проверка усвоение знаний | Самостоятельная работа. Решить самостоятельно задачи № 534(в), 537 по выбору. | Взаимопроверка | ||
Итог урока Рефлексия | Итак, нужно ли понятие подобия планиметрии? Применяется для решения многих задач, имеет большое применение в геометрии. Учитель: Да, это понятие имеет большое применение в планиметрии и в этом вы убедитесь на последующих уроках. Выбрать карточку по цвету и оценить свою работу на уроке: Карточка красного цвета – заслуживаю высокой оценки; Карточка желтого цвета – заслуживаю хорошей оценки; Карточка зеленого цвета – заслуживаю удовлетворительной оценки Карточка черного цвета – заслуживаю неудовлетворительной оценки. VII. Домашнее задание. П. 56, 57, вопросы 1,2,3. Решить задачи № 534 (а,б), 536 (а), Решить задачи по желанию и выбору: №538, 542. | Ответ: да. Оно связано с понятиями пропорциональность отрезков, отношение отрезков, отношение чисел, пропорцией. |
Подобие треугольников. Определение, свойства и теоремы
Треугольники, имеющие одинаковую форму, но разные размеры, называются подобными треугольниками. Два конгруэнтных треугольника всегда подобны, но подобные треугольники не обязательно должны быть конгруэнтны. Две геометрические фигуры, имеющие одинаковые форму и размеры, называются конгруэнтными фигурами. О конгруэнтных фигурах мы узнали и ранее. Конгруэнтные фигуры одинаковы во всех отношениях. Два треугольника называются равными, если стороны и углы одного треугольника в точности равны соответствующим сторонам и углам другого треугольника. В этой статье мы будем изучать подобие треугольников.
Изучим подобие треугольников, свойства подобных треугольников, примеры треугольников подобия, теорему о треугольнике подобия и доказательство теоремы о треугольнике подобия.
Определение подобных треугольников
Подобные треугольники — это треугольники, которые выглядят похожими друг на друга, но они могут не быть точно такими же по своим размерам. Два объекта (или треугольники в данном случае) можно назвать подобными по геометрии, только если они имеют одинаковую форму, но могут различаться по размеру.
Два треугольника называются подобными, если
(i) их соответствующие углы равны и
(ii) их соответствующие стороны пропорциональны.
т.е. Два треугольника ABC и DEF подобны, если
∠ A = ∠ D; ∠ В = ∠ Е; ∠ С = ∠ F; и
\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}\]
Символ для обозначения подобия треугольников ‘~ ‘. Мы можем записать подобные треугольники как
△ABC ∼ △DEF
Свойства подобных треугольников
Подобные треугольники обладают следующими свойствами:
Подобные треугольники имеют одинаковую форму, но разные размеры.

Каждая соответствующая пара углов двух подобных треугольников равна.
Отношение любой пары соответствующих сторон подобных треугольников одинаково.
Отношение площадей пары треугольников равно отношению квадратов измерений любой пары соответствующих сторон.
Теоремы о треугольниках подобия
Два треугольника называются подобными, если доказана любая из теорем о треугольниках подобия. Эти теоремы в основном подобны критерию для пары треугольников, чтобы считаться парой подобных треугольников. Эти теоремы позволяют учащемуся быстро определить, подобна ли пара треугольников с точки зрения геометрии.
ААА Критерий подобия: Если два треугольника равноугольные, то они подобны.
 Равноугольный означает, что измерения соответствующих углов двух треугольников равны. Ее также называют теоремой подобия углов и углов.
Равноугольный означает, что измерения соответствующих углов двух треугольников равны. Ее также называют теоремой подобия углов и углов.SAS Критерий подобия: Если в двух треугольниках две пары соответствующих сторон пропорциональны и углы между ними равны, то эти два треугольника подобны. Ее также называют теоремой подобия бокового угла стороне.
SSS Критерий подобия: Если соответствующие стороны двух треугольников пропорциональны, то они подобны. Ее также называют теоремой подобия стороны, стороны, стороны.
AA Сходство (угол-угол-сторона) Критерий
Критерий подобия АА утверждает, что если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.
Это также иногда называют правилом ААА, потому что равенство двух соответствующих пар углов означает, что третья соответствующая пара углов также равна.
На приведенном выше рисунке
∠ A = ∠ D
∠ C = ∠ F
Затем △ABC ∼ △DEF …….по правилу АА0007
Критерий подобия SAS гласит, что если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а также один угол между сторонами равен углу другого треугольника, то эти два треугольника подобны.
На приведенном выше рисунке
\[\frac{LM}{QR} = \frac{LN}{QS}\]
И углы между сторонами равны
, т.е. ∠ L = ∠Q, поэтому , △MLN ∼ △RQS …….по правилу SAS
Сходство SSS (сторона-сторона-сторона) Критерий
SSS Критерий подобия утверждает, что если стороны одного треугольника пропорциональны сторонам другого треугольника или находятся в том же отношении, то эти два треугольника подобны.
На приведенном выше рисунке
\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}\]
, поэтому △ABC ∼ △DEF ……. по правилу SSS
по правилу SSS
ПРИМЕЧАНИЕ: Следует отметить, что подобие двух треугольников также следует выражать символически, используя правильное соответствие их вершин. Например, для △ABC и △DEF мы не можем писать Δ ABC ∼ Δ EDF или Δ ABC ∼ Δ FED. Но мы можем написать ∆ BAC ∼ ∆ EDF.
Основная теорема о пропорциональности (Теорема Фалеса)
Основная теорема о пропорциональности была сформулирована Фалесом, греческим математиком. Поэтому она также известна как теорема Фалеса. Сокращенно БПТ.
Основная теорема о пропорциональности утверждает, что:
Если прямая параллельна стороне треугольника, которая пересекает другие стороны в двух различных точках, то прямая делит эти стороны пропорционально.
На приведенном выше рисунке, если мы считаем, что DE параллелен BC, то согласно теореме,
\[\frac{AD}{DB} = \frac{AE}{EC}\]
Дано: В ΔABC DE параллельна BC
DE пересекает стороны AB и AC в точках D и E соответственно.
Чтобы доказать \[\frac{AD}{DB} = \frac{AE}{EC}\]
Построение: Проведите EG ⟂ AB и DF⟂ AC и соедините отрезки BE и CD.
Доказательство:
Так как EG ⟂ AB. EG – высота ADE и DBE.
Теперь у нас есть
Площадь треугольника =\[ \frac{1}{2} \умножить на основание \умножить на высоту \]
Следовательно, площадь (ΔADE) = \[ \frac{1}{2} (AD \times EG) \]
и площадь (ΔDBE) = \[ \frac{1}{2} (DB \times EG) ) \]
Теперь примем пропорции
\[\frac{Площадь \Delta ADE}{Площадь \Delta DBE } = \frac{\frac{1}{2}(AD \times EG)}{\ frac{1}{2}(DB \times EG)} = \frac{AD}{DB}….(1)\]
аналогично имеем
\[\frac{Площадь \Delta ADE }{Площадь \Delta DEC} = \frac{\frac{1}{2}(AE \times DF)}{\frac{1}{2}(EC \times DF)} = \frac{AE}{ ЕС}….(2)\]
Но ΔDBE и ΔDEC находятся на одном основании DE и между одними и теми же параллелями DE и BC
Следовательно,
Площадь(ΔDBE) = Площадь(ΔDEC) 1}{Площадь \Delta DBE} = \frac{1}{Площадь \Delta DEC}\]
Умножение обеих сторон на Area(ΔADE)
\[\frac{Площадь \Delta ADE}{Площадь \Delta DBE} = \frac{Площадь \Delta ADE}{Площадь \Delta DEC}\]
Используя уравнения 1 и 2, мы получаем
\[ \frac{AD}{DB} = \frac{AE} {ЕС}\]
Отсюда доказано
Обратная теорема о пропорциональности
Если прямая делит любые две стороны треугольника в одном и том же отношении, то эта прямая параллельна третьей стороне, т. е. если \[ \frac{AD}{DB} = \frac{AE}{EC}\], то DE параллелен BC
е. если \[ \frac{AD}{DB} = \frac{AE}{EC}\], то DE параллелен BC
Мы будем использовать это доказательство теоремы о треугольнике подобия для решения примеров треугольников подобия.
Подобие решенных треугольников Примеры
Пример 1. Даны два треугольника. Докажите, что они подобны.
Решение:
Поскольку оба треугольника имеют два угла равных, т.е. 170 и 1140
Таким образом, по теореме подобия AA мы можем сказать, что два треугольника подобны.
Пример 2. Докажите, что ABC и DEF подобны.
Решение:
В ΔABC и ΔXYZ
∠ A = ∠ X = 750
И \[ \frac{AB}{XY} = \frac{15}{10} = \frac{3}{2} \]
\[ \frac{AC}{XZ} = \frac{21}{14} = \frac{3}{2}\]
Следовательно, \[ \frac{AB}{XY} = \ frac{AC}{XZ}\]
Следовательно, по сходству SAS мы получаем ΔABC ∼ ΔXYZ
Попробуйте еще несколько примеров треугольников подобия самостоятельно.
Время викторины
Учитывая, что два треугольника подобны. Найдите значение с.
Докажите, что эти треугольники подобны.
Заключение
Это все о теоремах, объяснениях и решенных примерах подобия треугольников. Поймите причины, по которым два треугольника похожи друг на друга, чтобы легко решать проблемы.
Свойства подобных треугольников — обзор по алгебре (видео)
Привет! Добро пожаловать в этот обзор подобных треугольников! Сегодня мы собираемся изучить, как идентифицировать подобные треугольники и как мы можем использовать эти знания для решения очень популярной задачи геометрии.
Определение подобных треугольников
Начнем с простого определения. Подобные треугольники – это треугольники, имеющие одинаковую форму. Это означает, что они будут иметь те же самые три угла . Но вот в чем загвоздка — похожие треугольники не обязательно должны быть одинакового размера! Поэтому, если вы возьмете копию треугольника и увеличите ее в два раза, она все равно будет похожа на исходный треугольник.
Но вот в чем загвоздка — похожие треугольники не обязательно должны быть одинакового размера! Поэтому, если вы возьмете копию треугольника и увеличите ее в два раза, она все равно будет похожа на исходный треугольник.
Метод «угол-угол-угол»
Обратите внимание, что два треугольника имеют одинаковую форму и пропорции. Это потому, что у них одинаковые углы, что делает их похожими треугольниками. Это Angle-Angle-Angle , или AAA, метод определения сходства. Следует отметить, что каждый раз, когда вы расширяете треугольник, вы получаете два подобных треугольника.
Поскольку мы знаем, что эти два треугольника подобны треугольникам, мы можем выразить это в математической записи следующим образом: \(△ABC\) ~ \(△A’B’C’\)
Хорошо, но что, если мы не начали с расширения и не знаем всех углов? Есть ли другой способ определить, подобны ли два треугольника?
Метод стороны-стороны-стороны
Давайте рассмотрим пример, где мы знаем только длины сторон двух треугольников:
Эти два треугольника кажутся одной и той же формы, но помните, что в геометрии мы не всегда можем доверяйте нашим глазам. Нам нужно доказать, что они имеют одинаковую форму, и мы можем сделать это, проверив, пропорциональны ли их стороны друг другу. Мы настраиваем наши пропорции, устанавливая отношения или дроби соответствующих сторон и устанавливая их равными друг другу, например: (△DEF\) — знаменатели. Это сработало бы так же хорошо, если бы мы поменяли его местами.
Нам нужно доказать, что они имеют одинаковую форму, и мы можем сделать это, проверив, пропорциональны ли их стороны друг другу. Мы настраиваем наши пропорции, устанавливая отношения или дроби соответствующих сторон и устанавливая их равными друг другу, например: (△DEF\) — знаменатели. Это сработало бы так же хорошо, если бы мы поменяли его местами.
Очень важно обозначить пропорции, чтобы убедиться, что мы поместили все числа на свои места.
Итак, что нам дает эта пропорция? Что ж, нам нужно проверить, правда ли это. В данном случае мы можем сделать это, приведя каждую из этих дробей к простейшей форме. Мы видим, что 3 идет вверху и внизу \(\frac{6}{9}\), поэтому мы можем уменьшить его до 2 вместо 3. Четыре входит в \(\frac{8}{12}\) и 5 переходит в \(\frac{10}{15}\). Когда мы уменьшаем эти две дроби, мы также получаем \(\frac{2}{3}\). В сокращенном виде наша пропорция выглядит так:
Это доказательство того, что все наши стороны пропорциональны. Если все стороны пропорциональны, то мы знаем, что наши треугольники пропорциональны. Это Side-Side-Side , или SSS, метод доказательства сходства. Итак, теперь мы можем сказать, что \(△ABC\) ~ \(△DEF\).
Если все стороны пропорциональны, то мы знаем, что наши треугольники пропорциональны. Это Side-Side-Side , или SSS, метод доказательства сходства. Итак, теперь мы можем сказать, что \(△ABC\) ~ \(△DEF\).
Вместо уменьшения мы могли бы также проверить, пропорциональны ли отношения, преобразовав каждое отношение в десятичное число, разделив верхнее значение каждого из них на нижнее. В этом случае \(\frac{6}{9}\), \(\frac{8}{12}\) и \(\frac{10}{15}\) дали бы нам одно и то же десятичное число значение, которое составляет 0,66666666.
Итак, теперь мы знаем, что если все углы равны или если все стороны пропорциональны, то наши треугольники подобны.
Метод сторона-угол-сторона
Существует еще один метод доказательства сходства, который называется Сторона-угол-сторона или SAS. Здесь мы знаем, что два треугольника имеют один угол, который имеет одинаковую меру, и что две стороны, исходящие из этого угла, пропорциональны.
Давайте посмотрим на наши последние два треугольника, но вместо того, чтобы знать все три стороны, мы знаем только два набора соответствующих сторон вместе с углом между ними, например:
Мы видим, что угол между двумя измеренными сторонами помечен квадратом, что, как мы знаем, означает, что это прямой угол и, следовательно, 90 градусов. Поскольку этот угол одинаков в обоих треугольниках, нам просто нужно проверить, пропорциональны ли две соседние стороны, например:
Поскольку этот угол одинаков в обоих треугольниках, нам просто нужно проверить, пропорциональны ли две соседние стороны, например:
Повторное сокращение дробей дает 2 на 3, поэтому стороны пропорциональны. Поскольку угол между этими сторонами одинаков или конгруэнтен , этот треугольник подобен.
Задача о высоте дерева
Итак, что мы можем сделать с этой способностью распознавать похожие треугольники? Возможно, вы уже видели это раньше, но вот классическая задача о высоте дерева:
Вот что мы знаем. Дерево и флагшток стоят прямо перпендикулярно земле. Каждый из них отбрасывает тень от одного и того же источника света — солнца. Лучи, исходящие от солнца, представляют собой прямые линии, падающие на предметы под углом. Земля плоская и может считаться плоской, а это значит, что любые две точки на ней можно соединить прямой линией. Это означает, что я могу нарисовать два треугольника поверх этого рисунка, например:
Теперь давайте сохраним наши треугольники, но избавимся от красивого пейзажа.
Далее давайте пометим все точки, чтобы мы могли ссылаться на них. Неважно, какую букву мы используем для каждой точки.
Мы также знаем, что угол B и угол D являются прямыми углами, так как флагшток и дерево направлены вертикально вверх, перпендикулярно земле, поэтому мы также пометим это:
Поскольку мы знаем, что угол A одинаков для обоих треугольников и что углы B и D являются прямыми углами и, следовательно, конгруэнтны, это означает, что углы C и E также конгруэнтны. Почему? Потому что сумма внутренних углов треугольника должна составлять 180°. Итак, если A равно 30°, а B и D равны 90°, то C и E будут равны 60°.
Теперь мы знаем, что это подобные треугольники, используя метод доказательства сходства ААА.
Теперь мы можем перейти к самой интересной части и использовать эти треугольники, чтобы найти высоту дерева. Во-первых, нам нужно провести некоторые измерения. Нам нужно измерить флагшток, длину тени флагштока и длину тени дерева. К счастью, все это легко сделать. Стандартный флажок для гольфа имеет высоту 7 футов. Очевидно, что тени лежат на земле, поэтому мы можем измерить их длинной рулеткой. Затем мы можем добавить их к нашим треугольникам.
Стандартный флажок для гольфа имеет высоту 7 футов. Очевидно, что тени лежат на земле, поэтому мы можем измерить их длинной рулеткой. Затем мы можем добавить их к нашим треугольникам.
Так как стороны подобных треугольников всегда пропорциональны, мы можем установить пропорцию со всеми строками и столбцами, помеченными:
Мы не знаем ни одной из диагональных сторон, но они нам не нужны для этого типа задач. . Мы знаем наземные стороны обоих треугольников и знаем высоту \(△ABC\). Мы можем поместить переменную для высоты дерева, которая равна \(\overline{DE}\) в нашем треугольнике. Теперь мы просто используем перекрестные произведения для решения:
Взятие перекрестных произведений приводит к уравнению \(9x=45\cdot 7\) или \(9x=315\) после умножения 45 и 7. Разделив обе части на 9, мы получим \(x=35\). Итак, наше дерево 35 футов в высоту!
Обзор
Хорошо, теперь, когда мы все рассмотрели, давайте кратко подытожим:
Подобные треугольники — это треугольники, имеющие одинаковую форму. Есть три способа доказать, что два треугольника подобны. Метод подобия ААА – это когда пропорции всех трех углов треугольников одинаковы. Метод SSS – это когда все три стороны треугольников имеют одинаковую длину. И, наконец, метод SAS заключается в том, что два треугольника имеют один угол одинаковой меры, а две стороны, выходящие из этого угла, пропорциональны.
Есть три способа доказать, что два треугольника подобны. Метод подобия ААА – это когда пропорции всех трех углов треугольников одинаковы. Метод SSS – это когда все три стороны треугольников имеют одинаковую длину. И, наконец, метод SAS заключается в том, что два треугольника имеют один угол одинаковой меры, а две стороны, выходящие из этого угла, пропорциональны.
Надеюсь, отзыв был полезен! Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Что такое подобные треугольники?
A
Подобные треугольники — это треугольники, соответствующие углы которых равны, а соответствующие стороны пропорциональны, но не обязательно равны.
Пример.
Q
Все ли прямоугольные треугольники подобны?
A
Нет, не все прямоугольные треугольники подобны. Чтобы треугольники были подобны, они должны иметь одинаковые величины углов. Все прямоугольные треугольники имеют один прямой угол, но два других угла могут быть любой комбинацией мер, которые в сумме дают 9. 0°.
0°.
Пример. ⊿ABC не похож на ⊿DEF.
Q
Все равносторонние треугольники подобны?
A
Да, все равносторонние треугольники подобны, потому что все они имеют одинаковые углы.
Q
Все равнобедренные треугольники подобны?
A
Нет, не все равнобедренные треугольники подобны. Чтобы треугольники были подобны, они должны иметь одинаковые величины углов. Не все равнобедренные треугольники имеют одинаковые величины углов.
пр. ⊿ABC не похож на ⊿DEF
Практические вопросы
Вопрос № 1:
Какое из следующих утверждений неверно относительно подобных треугольников?
У них одинаковая форма
У них одинаковые углы
У них одинаковый размер
У них одинаковые пропорции
Показать ответ
Ответ:
. Подобные треугольники — это треугольники, которые имеют одинаковую форму, одинаковые величины углов и пропорциональны друг другу. Подобные треугольники не имеют одинакового размера. Если треугольники одинакового размера, то они равны.
Подобные треугольники — это треугольники, которые имеют одинаковую форму, одинаковые величины углов и пропорциональны друг другу. Подобные треугольники не имеют одинакового размера. Если треугольники одинакового размера, то они равны.
Скрыть ответ
Вопрос №2:
△ ABC похож на △ DEF . Найдите х.
12
18
3
6
Показать ответ
Ответ:
Правильный ответ равен 12, поэтому их треугольники пропорциональны. \(\overline{BC}\) пропорционально \(\overline{EF}\) и \(\overline{AC}\) пропорционально \(\overline{DF}\). Составьте пропорцию.
\(\frac{6}{x}=\frac{7}{14}\)
Крест умножить и найти x.
\(6\times14=7x\)
\(84=7x\)
\(12=x\)
Скрыть ответ
Вопрос №3:
△ ABC 903 903 ДЕФ . Найдите х.
Найдите х.
81°
31°
46°
56°
Показать ответ
Ответ:
° Правильный ответ:
°. Подобные треугольники имеют конгруэнтные меры углов. Поскольку ∠B = 46°, ∠E также должно быть 46°.
Скрыть ответ
Вопрос №4:
Эти два треугольника подобны?
Да
Нет
Иногда
Невозможно определить по данной информации
Показать ответ
Ответ:
Правильный ответ — да. Подобные треугольники должны иметь конгруэнтные меры углов. Поскольку в каждом треугольнике известны два угла, и они одинаковы, их можно определить как подобные треугольники, поскольку третьи углы также должны быть одинаковыми. У всех треугольников внутренние углы в сумме составляют 180°, поэтому третий угол в обоих этих треугольниках должен быть равен \(180°-93°-47°=30°\).
Скрыть ответ
Вопрос №5:
△ ABC похож на △ DEF . Найдите х.
58,53
52,27
47,19
43,62
Показать ответ
Ответ:
3 90 Поскольку треугольники подобны, их стороны пропорциональны. \(\overline{AB}\) пропорционально \(\overline{DE}\) и \(\overline{BC}\) пропорционально \(\overline{EF}\). Составьте пропорцию.
\(\frac{13}{27}=\frac{21}{x}\)
Крест умножить и найти x.
\(13x=21\times27\)
\(13x=567\)
\(x≈43,62\)
Скрыть ответ
Подобные треугольники: определение, формула и тип
Вы когда-нибудь задумывались, как можно измерить что-то выше вас, может быть, дом или даже самое высокое здание? На этот вопрос часто можно ответить с помощью свойств подобных форм. В этой статье мы узнаем об одной из похожих фигур под названием 9.0237 подобных треугольников .
В этой статье мы узнаем об одной из похожих фигур под названием 9.0237 подобных треугольников .
Определение похожих треугольников
Похожая фигура может быть описана как две фигуры одинаковой формы, но разных размеров.
Подобные треугольники — это тип одинаковой формы, где два треугольника — это треугольники одного типа, но разных размеров.
Правила для подобных треугольников
Два треугольника считаются подобными, если они соблюдают следующие два правила:
- У них одинаковые соответствующие углы.
- Все соответствующие длины сторон имеют одинаковое соотношение.
Доказательство подобных треугольников
Идея подобных треугольников может быть показана и объяснена на следующей диаграмме:
Пример подобных треугольников, StudySmarter Originals
Выше вы можете видеть, что два треугольника имеют соответствующий угол. Кроме того, оба треугольника имеют равные отношения сторон. Это означает, что длины сторон треугольника пропорциональны друг другу, больший треугольник справа в 2 раза больше меньшего треугольника слева. Это соотношение также известно как масштабный коэффициент .
Это соотношение также известно как масштабный коэффициент .
Соответствующий угол описывает угол, который одинаков в обоих треугольниках.
Существуют различные теоремы, которые могут дополнительно доказать идею аналогичных треугольников:
Теорема сходства SSS
AA Теорема
SAS сходства. предполагает, что когда три стороны одного треугольника пропорциональны соответствующему треугольнику, треугольник подобен.
Пример теоремы подобия SSS, StudySmarter Originals
Эта теорема может быть представлена в виде следующей формулы:
Теорема подобия AA
два угла в другом треугольнике, оба треугольника подобны.
Пример теоремы подобия AA, StudySmarter Originals
Эта теорема может быть представлена следующей формулой:
Теорема подобия SAS
Теорема подобия SAS предполагает, что когда внутренний угол одного треугольника равен внутреннему углу другого треугольника, а длины сторон обоих треугольников пропорциональны, треугольник будет подобен.

Пример теоремы подобия SAS, StudySmarter Originals
Эту теорему можно представить в виде следующей формулы:
и
Формулы для подобных треугольников
Когда мы рассматриваем подобные треугольники, мы часто видим их с помощью символа. Формулы можно использовать, чтобы показать каждую из подобных теорем треугольника:
- Когда,
- Когда ,
- Когда ,
Типы примеров подобных треугольников
Укажите, подобны ли два приведенных ниже треугольника и почему.
Пример подобных треугольников, StudySmarter Originals
Решение:
Вы можете видеть, что соответствующие длины сторон треугольника пропорциональны друг другу, больший треугольник справа в два раза больше другого треугольника, а это означает, что это подобные треугольники. Чтобы доказать это, мы можем взглянуть на теорему подобия SSS, которая предполагает, что если вы разделите длины сторон на соответствующие им длины, вы получите тот же ответ.
 Затем это дает вам масштабный коэффициент. Давайте проверим:
Затем это дает вам масштабный коэффициент. Давайте проверим:Это доказывает теорему сходства SSS, что означает, что масштабный коэффициент составляет 2.
Найти недостающие углы в этих аналогичных треугольниках:
Пример. Поскольку вам сказали, что это подобные треугольники, вы знаете, что углы соответствуют каждому треугольнику. Следовательно, вы знаете, что угол B равен 60°, а угол X равен 45°, вам просто нужно вычислить третий угол в треугольниках:
Это означает, что угол C и угол Z равны 75°.
Подобные треугольники — ключевые выводы
- Подобные треугольники имеют одинаковую форму, но могут быть разных размеров, чтобы считаться подобными, они должны иметь одинаковые соответствующие углы или пропорциональные длины сторон.
- Существуют различные теоремы для доказательства подобия треугольника:
- Теорема подобия SSS
- Теорема подобия AA
- Теорема подобия SAS
- Вы можете использовать информацию из подобных треугольников, чтобы найти недостающие углы или длины сторон.

Часто задаваемые вопросы о подобных треугольниках
Подобные треугольники — это два треугольника, которые имеют равные углы или пропорциональные длины сторон.
Существуют три теоремы, доказывающие, подобны ли треугольники:
- Теорема подобия SSS
- Теорема подобия AA
- Теорема подобия SAS
Вы можете рассчитать отношение длин сторон подобных треугольников, разделив длину одной стороны на соответствующую длину стороны.
Треугольники считаются подобными, если они обладают следующими характеристиками:
- У них одинаковые размеры соответствующих углов.
- Все соответствующие длины сторон имеют одинаковое соотношение.
Чтобы вычислить, есть ли у вас подобные треугольники, вы можете найти соответствующие углы и длины сторон. Это скажет вам, соответствуют ли они каким-либо характеристикам подобных треугольников.
org/Thing» data-name=»flashcards-dot»> Финальная викторина о подобных треугольникахВопрос
Что такое подобный треугольник?
Показать ответ
Ответ
Подобные треугольники — это треугольники, которые:
- Имеют соответствующие углы одинаковой величины
- Все соответствующие длины сторон имеют одинаковое соотношение
Показать вопрос
Вопрос
Какие три теоремы можно использовать для доказательства подобных треугольников?
Показать ответ
Ответ
- Теорема подобия SSS
- Теорема подобия AA
- Теорема подобия SAS
Показать вопрос
Вопрос
Что такое теорема подобия SSS?
Показать ответ
Ответ
Теорема подобия SSS предполагает, что треугольники подобны, когда три стороны одного треугольника пропорциональны соответствующему треугольнику.

Показать вопрос
Вопрос
Что такое теорема подобия AA?
Показать ответ
Ответ
Теорема подобия AA предполагает, что когда два угла в одном треугольнике равны двум углам в другом треугольнике, оба треугольника подобны.
Показать вопрос
Вопрос
Что такое теорема подобия SAS?
Показать ответ
Ответ
Теорема подобия SAS предполагает, что когда внутренний угол одного треугольника равен внутреннему углу другого треугольника, а длины сторон обоих треугольников пропорциональны, треугольник будет подобен.
Показать вопрос
Вопрос
На что похожа форма?
Показать ответ
Ответ
Похожая фигура может быть описана как две фигуры одинаковой формы, но разных размеров.

Показать вопрос
Подобные треугольники – определение, свойства, формулы, примеры
Что такое подобные треугольники
Два треугольника подобны, если они имеют одинаковую форму, но разные размеры. Таким образом, математически, если два треугольника подобны, то их соответствующие стороны пропорциональны, а их соответствующие углы равны. Например, все равносторонние треугольники всегда подобны.
Ниже показаны два подобных треугольника, ΔABC и ΔPQR, которые математически представлены символом ~. Здесь ΔABC ~ ΔPQR.
Подобные треугольникиКроме того, при повороте или отражении треугольника и его переименовании будут образовываться подобные треугольники.
Подобные перевернутые треугольникиСвойства
Свойства подобных треугольников Формулы- Имеет одинаковую форму, но размер может отличаться; в ΔZYX и ΔPQR, ΔZYX > ΔPQR размера
- Каждая пара соответствующих углов конгруэнтна; здесь ∠Z ≅ ∠P, ∠Y ≅∠Q и ∠X ≅ ∠R
- Имеет одинаковое отношение соответствующих сторон: здесь x/r = z/p = y/q
Доказательство подобных треугольников: Правила
Есть три способа определить, подобны ли треугольники, условия приведены ниже:
Правила подобных треугольников 1) Правило угла-угла (AA)Оно утверждает, что если два угла в одном треугольнике равны двум углов другого треугольника, то эти треугольники подобны.

Из приведенного выше рисунка с помощью правила AA мы можем написать
AB/EF = BC/FG = AC/EG и ∠B ≅ ∠F
Таким образом, чтобы доказать, что два треугольника подобны, достаточно показать, что два углы одного треугольника соответственно равны двум соответствующим углам другого треугольника.
2) Правило стороны-угла-стороны (SAS)Оно гласит, что если отношение их двух соответствующих сторон пропорционально, а также угол, образованный двумя сторонами, равен, то два треугольника подобны.
Из приведенного выше рисунка с правилом SAS мы можем написать
AB/EF = BC/FG = AC/EG и ∠B ≅ ∠F, ∠C ≅ ∠G
Таким образом, чтобы доказать треугольники, подобные SAS, нужно достаточно, чтобы показать, что наборы соответствующих сторон пропорциональны, а прилежащий угол равен.
3) Правило стороны-стороны-стороны (SSS)Оно гласит, что если все три соответствующие стороны одного треугольника пропорциональны трем соответствующим сторонам другого треугольника, то эти два треугольника подобны.

Из приведенного выше рисунка с помощью правила SSS мы можем написать
∠A ≅ ∠E ∠B ≅ ∠F и ∠C ≅ ∠G
Таким образом, для доказательства треугольников, подобных по SSS, достаточно показать, что три набора соответствующих сторон пропорциональны.
Как решать задачи на подобные треугольники
Есть два типа подобных задач на треугольник. Один набор требует доказательства того, подобны ли данный набор треугольников, а другой требует вычисления недостающих углов и длин сторон подобных треугольников.
Давайте решим несколько задач, чтобы понять концепцию.
Какие из данных пар треугольников подобны? Напишите правило сходства, определяющее их отношения.
Решение:
а) ΔABC ~ ΔPQR по правилу подобия SSS, б) Не похоже, в) ΔSTU ~ ΔSVW по правилу подобия SAS, г) ΔKLM ~ ΔHIJ по правилу подобия AA
Ниже приведены два треугольника. Они похожи?
Решение:
В ΔEFG, по свойству суммы углов
∠E + ∠F + ∠G = 180°
80° + ∠F + 30° = 180° 30°)
∠F = 70°
Аналогично, в ΔLMN, по свойству суммы углов
∠L + ∠M + ∠N = 180°
80° + 70° + ∠N = 180°
∠N = 180° – (80° + 70°)
∠N = 30°
Так как
∠F = ∠M = 70° и ∠N = ∠G = 30°
Таким образом, по правилу АА,
ΔEFG ~ ΔLMNВ данном треугольнике ΔABC со сторонами AE = 2 см, EB = 4 см и BC = 9 см.
 Также ЭФ || ДО Н.Э. Рассчитать ЭФ.
Также ЭФ || ДО Н.Э. Рассчитать ЭФ. Решение:
В ΔABC и ΔAEF
∠EAF является общим и ∠AEF = ∠ABC (соответствующие углы)
Таким образом,
ΔABC ~ ΔAEF (правило AA)
0 Теперь мы можем написать8 EF/BC
AE/AE + EB = EF/BC, здесь AE = 2 см, EB = 4 см, BC = 9см
2/(2 + 4) = EF/9
EF = 3 смНайдите подобные треугольники и напишите утверждение о сходстве, описывающее их взаимосвязь.
Решение:
в ΔXAB и ΔXDC,
ϩABX ≅ ϩdcx (Альтернативные внутренние углы)
ϩcaxb ≅ ϩdxc (вертикально противоположные углы)
Таким Найдите значение x в заданной паре подобных треугольников.Решение:
Данная пара треугольников подобна по правилу АА
Таким образом, можно записать
FG/QR = EF/PQ, здесь FG = x, QR = 15, EF = 4, PQ = 5
x/ 15 = 4/5
x = 12Определите, подобны ли данные пары треугольников.

Решение:
Данные пары треугольников подобны по правилу SSS.
Чтобы треугольники были подобны, отношение их соответствующих сторон должно быть равно
Если ΔCDE ~ ΔSRQ
SR/CE = RQ/DE = SQ/CD
Теперь
SR/CE = 4/10 = 2/5
RQ/DE = 6/15 = 2/5
SQ/CD = 8 /20 = 2/5
Следовательно,
ΔCDE ~ ΔSRQНайдите x на данном рисунке.
Решение:
На приведенном рисунке
ΔPQT ≅ ΔRST (все прямоугольные треугольники конгруэнтны)
Кроме того, ∠S ≅ ∠S (рефлексивное свойство) /ST = PQ/RS (соответствующие стороны подобных треугольников пропорциональны)
=> x/12 = 5/3
=> x = (12 x 5)/3 = 20Подобные треугольники и масштабный коэффициент
Когда два треугольника подобны, минимальное отношение любых двух соответствующих сторон называется масштаб.
Подобные треугольники с масштабным коэффициентомВ ΔEFG и ΔPQR отношение длин соответствующих сторон составляет 2/1.
 Таким образом, можно сказать, что масштабный коэффициент ΔEFG к ΔPQR равен 2.
Таким образом, можно сказать, что масштабный коэффициент ΔEFG к ΔPQR равен 2.Давайте рассмотрим пример, чтобы лучше понять концепцию.
Как найти масштабный коэффициент двух подобных треугольников
Найдите масштабный коэффициент в заданной паре подобных треугольников.
Решение:
Как мы знаем, соответствующие стороны подобных треугольников пропорциональны по правилу SSS,
Таким образом,
Коэффициент масштабирования = 5/15 = 1/3
9 = 1/3
Таким образом, масштабный коэффициент между двумя заданными треугольниками равен 1:3Реальные приложения
Подобные треугольники можно найти повсюду вокруг нас и даже где-то, чего мы не можем заметить. Их значение особенно важно там, где мы не можем физически измерить расстояния и высоты с помощью простых измерительных инструментов. Многочисленные приложения в основном в области машиностроения, архитектуры и строительства.
 Они приведены ниже:
Они приведены ниже:- Определение высоты высоких объектов, таких как деревья, здания и башни, на которые слишком сложно взобраться, и измерение с помощью рулетки.
- Анализ теней, помогающий определить реальную высоту объектов.
- Определение расстояний от неба до определенной точки на земле при аэрофотосъемке.
- Анализ устойчивости мостов во время строительства, а также измерение размеров помещений в зданиях.
Часто задаваемые вопросы
Q1. Все ли равносторонние треугольники подобны?
Ответ . Да, все равноугольные треугольники подобны.
Q2. Все ли равнобедренные треугольники подобны?
Ответ . Нет, все равнобедренные треугольники не подобны.
Q3. Все ли прямоугольные треугольники подобны?
Ответ .
 Нет, прямоугольные треугольники не всегда подобны.
Нет, прямоугольные треугольники не всегда подобны.Q4. Подобны ли равные треугольники?
Ответ . Да, равные треугольники всегда подобны.
Q5. Все ли равноугольные треугольники подобны?
Ответ . Да, все равноугольные треугольники подобны.
Пропорциональность в подобных треугольниках: межкультурное сравнение. Введение
Автор(ы):
Джерри Лоддер (Университет штата Нью-Мексико) отношений соответствующих сторон подобных треугольников. Это понятие ожидается от студентов, изучающих физику, технику и естественные науки, поскольку его простая формулировка весьма полезна при нахождении неизвестных длин элементарных фигур в планиметрии. Почему этот геометрический результат верен? Чему мы учим наших студентов об этой связи и, что более важно, как этот результат преподносится специалистам среднего образования, которые будут обучать будущих студентов? Оправдан ли результат обращением к разуму, или подобные треугольники определяются как те треугольники, у которых соответствующие стороны имеют равные отношения? Оба эти подхода встречаются в сегодняшней учебной программе, хотя ни один из них не является особенно показательным.

В этой статье предлагаются учебные материалы для доказательства теорем подобия, основанных на древнекитайском принципе площади, известном как принцип «внутри-из» или «включение-исключение». Применительно к прямоугольнику принцип определяет определенные (неконгруэнтные) подпрямоугольники равной площади, которые остаются после исключения конгруэнтных треугольников. Этот принцип легко применить, когда исключенные треугольники являются прямоугольными, а для учета всех возможных пар соответствующих сторон в прямоугольном треугольнике дальнейшее применение гоу-гу (пифагорейская) теорема используется. Еще одним интересным применением принципа включения-исключения является доказательство самой теоремы гоу-гу , заимствующее идею из текста Zhou bi suan jing ( Mathematical Classic of the Zhou Gnomon ) [5], составленного между 100 г. до н.э. и 100 г. н.э. Строго говоря, гу относится к основанию или тени, а гу относится к высоте или гномону, хотя, по-видимому, в древнем Китае не существовало слова per se для понятия треугольника [5, с.
 215]. Дополнительную информацию об История китайской математики.
215]. Дополнительную информацию об История китайской математики.Поскольку преподавание сходства, вытекающего из древнекитайских принципов рассуждения, может быть новым для многих преподавателей, статья начинается с классического подхода Евклида к предмету. Хотя идеи рассуждений и концепция строгости различаются между китайской и греческой школами математической мысли, сходство результатов для обеих культур в конечном итоге основывается на аргументах двумерной области. Скрытой математической аксиомой, стоящей за любым результатом подобия, является постулат о параллельности, тонкая аксиома, последствия которой затрагивают многие построения и теоремы геометрии. Существование самого прямоугольника, не говоря уже о формуле его площади, логически эквивалентно постулату евклидовой параллельности [2]. Точно так же выражение площади треугольника как произведение половины основания на высоту является евклидовой формулой, поскольку оно основано на результате площади огибающего прямоугольника или параллелограмма.
 Евклидово доказательство сходства результатов основано на предложении 38 из книги I из 9.0397 Элементы [1]:
Евклидово доказательство сходства результатов основано на предложении 38 из книги I из 9.0397 Элементы [1]:
I.38. Треугольники, имеющие одинаковые основания и проходящие через одни и те же параллели, равны друг другу.
Дан треугольник ABC со стороной AB , определенной как основание, через C проходит только одна линия, параллельная AB , что определяет высоту треугольника. Предложение I.38 утверждает, что два треугольника с одинаковыми основаниями и одинаковыми высотами на самом деле будут иметь одинаковую площадь. Другим результатом, эквивалентным постулату евклидовой параллельности, является теорема, утверждающая, что любой треугольник имеет сумму углов 180 ° [2], что в свою очередь эквивалентно прямоугольнику с суммой углов 360°. Веб-ресурс Non-Euclidean Geometry http://www-history.mcs.st-and.ac.uk/HistTopics/Non-Euclidean_geometry.html> в MacTutor History of Mathematics Archive http://www-history. mcs. st-and.ac.uk> предлагает дальнейшую историю постулата параллельности.
mcs. st-and.ac.uk> предлагает дальнейшую историю постулата параллельности.В то время как Евклид следует пошаговой модели дедуктивных рассуждений, где каждое утверждение обосновывается предыдущим предложением, определением или постулатом, китайский метод немного более интуитивен, особенно при определении того, что сегодня назвали бы конгруэнтными треугольниками. Легкость, с которой затем доказываются результаты подобия (как современное упражнение), привлекательна. Более того, аргумент, основанный на китайских принципах, не требует сравнения, возможно, двух несоизмеримых длин оснований в подобных треугольниках, как это должен учитывать Евклид. Две длины L 1 , L 2 соизмеримы, если целое число, кратное L 1 , может быть построено на целом числе, кратном L 2 , или на современном языке, 3, с. 30], if there are positive integers n 1 , n 2 with n 1 L 1 = n 2 L 2 , or equivalently , [( L 1 )/( L 2 )] — рациональное число.
 См. веб-ресурс Греческая математика http://www-history.mcs.st-and.ac.uk/Indexes/Greeks.html> в MacTutor History of Mathematics Archive http://www-history.mcs.st-and .ac.uk> для получения подробной информации об истории греческой математики.
См. веб-ресурс Греческая математика http://www-history.mcs.st-and.ac.uk/Indexes/Greeks.html> в MacTutor History of Mathematics Archive http://www-history.mcs.st-and .ac.uk> для получения подробной информации об истории греческой математики.Материалы, представленные в разделе 4, идеально подходят для курса геометрии, который преподается в колледже или средней школе, или для курса, который привлекает будущих учителей математики средней школы. Для использования в классе инструктор должен представить результаты Раздела 3, хотя Раздел 2 может быть исключен из обсуждения в классе, в зависимости от направления курса и временных ограничений. При назначении материала в классе преподаватель может удалить или изменить порядок определенных частей учебного модуля в соответствии с курсом.
Джерри Лоддер (Университет штата Нью-Мексико), «Пропорциональность в подобных треугольниках: межкультурное сравнение — введение», Convergence (июль 2010 г.)
Площадь подобных треугольников: теоремы, формулы, примеры
- Автор Гурудат
- Последнее изменение 20-09-2022
- Автор Гурудат
- Последнее изменение 20-09-2022
Геометрические фигуры имеют одинаковую форму, но разные размеры называются подобными фигурами.
 Два треугольника называются подобными, если их соответствующие углы равны, а соответствующие стороны пропорциональны. Два условия, данные в приведенном выше определении, независимы. Если выполняется одно из двух условий, то автоматически выполняется и второе. Таким образом, любое из двух условий может быть использовано для определения подобных треугольников. Для подобных треугольников не только их углы и стороны имеют отношение, но и отношения их периметра, площадей и других аспектов пропорциональны. В этой статье мы узнаем об отношениях между
Два треугольника называются подобными, если их соответствующие углы равны, а соответствующие стороны пропорциональны. Два условия, данные в приведенном выше определении, независимы. Если выполняется одно из двух условий, то автоматически выполняется и второе. Таким образом, любое из двух условий может быть использовано для определения подобных треугольников. Для подобных треугольников не только их углы и стороны имеют отношение, но и отношения их периметра, площадей и других аспектов пропорциональны. В этой статье мы узнаем об отношениях между Два треугольника называются подобными, если
- их соответствующие углы равны
- соответствующие стороны пропорциональны.

Если два треугольника \(A B C\) и \(D E F\) подобны, то \(\угол A=\угол D, \угол B=\угол E, \угол C=\угол F\) и \(\ frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F}\).
Два условия, данные в приведенном выше определении, независимы. Если выполняется одно из двух условий, то автоматически выполняется и второе. Таким образом, любое из двух условий может быть использовано для определения подобных треугольников.
Если соответствующие углы двух треугольников равны, то они известны как равноугольные треугольники.
Площадь подобных треугольников
В двух подобных треугольниках отношение их соответствующих сторон одинаково. Однако, чтобы убедиться, что два треугольника подобны, нам не обязательно нужна информация обо всех сторонах и всех углах. Для подобных треугольников не только их углы и стороны имеют отношение, но и отношения их периметра, площадей и других аспектов пропорциональны. 9{\sim} \треугольник D M E\)
\(\Стрелка вправо \frac{A L}{D M}=\frac{A B}{D E} \quad \ldots \ldots(ii)\)Из \((i)\) и \((ii)\) получаем
\(\frac{A B}{DE}=\frac{B C}{FE}=\frac{A C}{D F}= \frac{A L}{D M} \quad \ldots \ldots(iii)\)Теперь: {\ frac {1} {2} (E F \ times D M)} \)
\ (\ Rightarrow \ frac {\ operatorname {Area} (\ треугольник A B C)} {\ operatorname {Area} (\ треугольник D E F)} = \frac{B C}{E F} \times \frac{A L}{D M}\) 9{2}}\)Теорема 4
Теорема: Площади двух подобных треугольников находятся в отношении квадратов отрезков биссектрисы соответствующих углов.
 {2 }}\справа]\) 9{2}\)
{2 }}\справа]\) 9{2}\)
\(\Стрелка вправо A B=DE, B C=E F\) и \(A C=D F\)Следовательно, \(\треугольник A B C \cong \треугольник D E F\)
Решенные примеры – площадь подобных треугольников
Q.1. На данном рисунке отрезок \(X Y\) параллелен стороне \(A C\) стороны \(\треугольник A B C\), и делит треугольник на две части равной площади. Найдите соотношение \(\frac{A X}{A B}\). 9{2}=\frac{2}{1} \Rightarrow \frac{A B}{X B}=\frac{\sqrt{2}}{1}\)
\(\Rightarrow \frac{A X}{A B}=\frac{ \sqrt{2}-1}{\sqrt{2}}=\frac{2-\sqrt{2}}{2}\)
\(\Rightarrow \frac{X B}{A B} =\frac{1}{\sqrt{2}}\)
\(\Rightarrow 1-\frac{X B}{A B}=1-\frac{1}{\sqrt{2}}\)
\( \Rightarrow \frac{A B-X B}{A B}=\frac{\sqrt{2}-1}{\sqrt{2}}\)
Следовательно, \(\frac{A X}{A B}=\frac{2 -\sqrt{2}}{2}\)Q.2. Докажите, что площадь равностороннего треугольника, описанного на стороне квадрата, равна половине площади равностороннего треугольника, описанного на его диагонали.
 9{2}}\)
9{2}}\)
\(\Стрелка вправо \frac{\operatorname{Area}(\Delta B C E)}{\operatorname{Area}(\triangle A C F)}=\frac{1}{2}\)Q.3. \(D, E, F\) — середины сторон \(BC, C A\), и \(AB\), соответственно, \(\треугольник А В С\). Определите отношение площадей \(\треугольник D E F\) и \(\треугольник A B C\).
Ответ: Так как \(D\) и \(E\) являются серединами сторон \(BC, C A\) и \(AB\) соответственно треугольника A B C\.Так как \(D\) и \(F\) являются серединами сторон \(BC\) и \(AB\) соответственно \(\треугольника ABC\). Следовательно,
\(D F||C A \Rightarrow D F|| A E\)
Из \((i)\) и \((ii)\) мы заключаем, что \(AF D E\) является параллелограммом.
Аналогично, \(B D E F\) — параллелограмм. 9{\sim} \треугольник D E F\) такой, что \(A B=1,2 \mathrm{~см}\) и \(D E=1,4 \mathrm{~см}\). {2}}\) 9{2}=\frac{36}{49}\)
{2}}\) 9{2}=\frac{36}{49}\)
Следовательно, \(\frac{\text {Площадь} \треугольника A B C}{\text {Площадь } \triangle D E F}=\frac{36}{ 49}\)Q.5. В двух подобных треугольниках \(A B C\) и \(P Q R\), , если их соответствующие высоты \(A D\) и \(PS\) отношение \(4:9\), найти отношение площадей \(\треугольник A B C\) 9{2}\)
Получите решения NCERT для класса 10 по математике, глава 6
Резюме
В вышеуказанной статье мы изучили значение подобия треугольников и понятие площади подобных треугольников. Также мы доказали некоторые теоремы о площади подобных треугольников и решили несколько примеров задач на площади подобных треугольников.
Часто задаваемые вопросы (FAQ) – Площадь подобных треугольников
Q.1. Имеют ли подобные треугольники равные площади?
Ответ : Нет, у подобных треугольников отношение площадей будет равно квадрату отношения их пары соответствующих сторон.

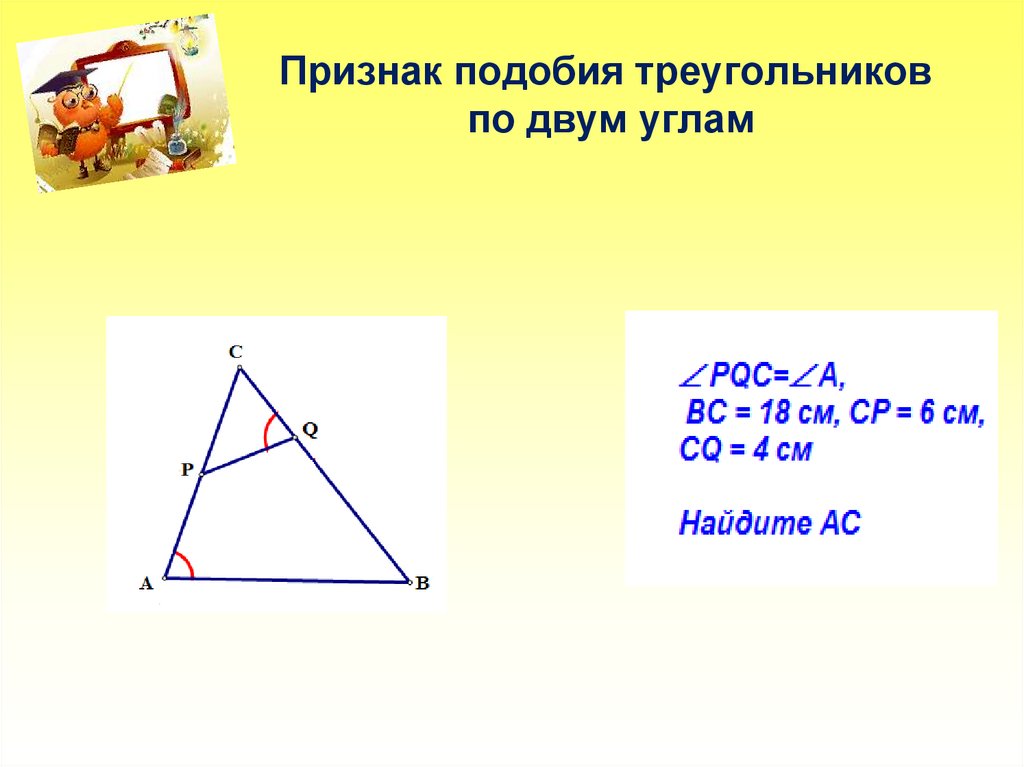 (Задачи были заданы на дом)
(Задачи были заданы на дом)

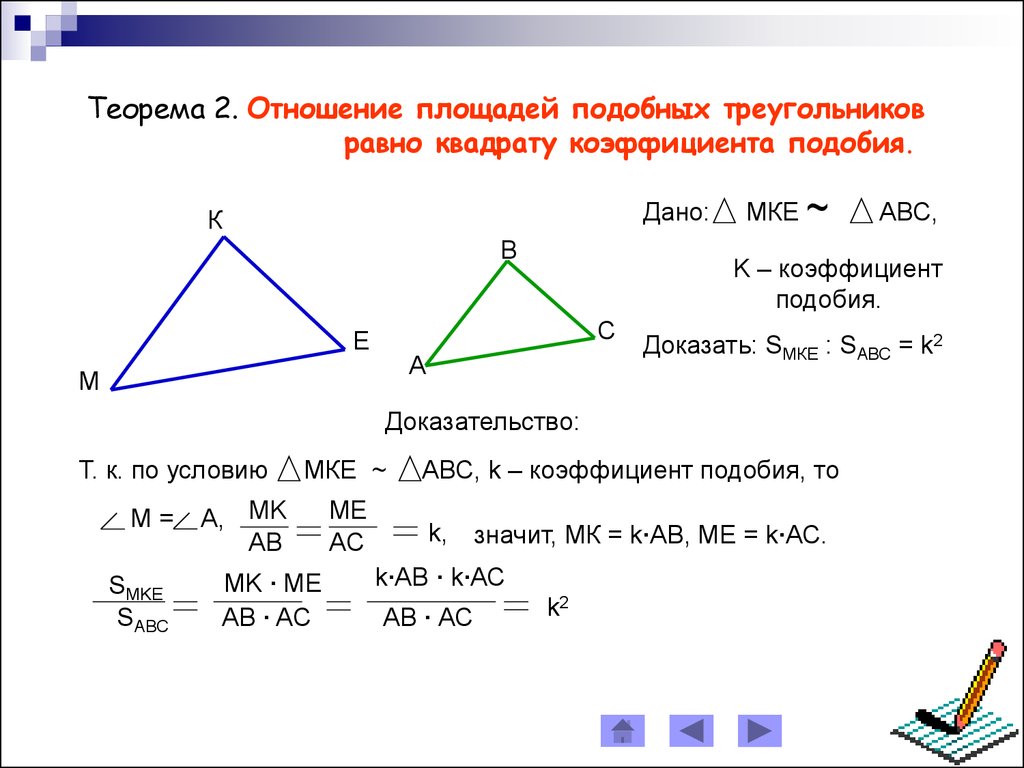 »
»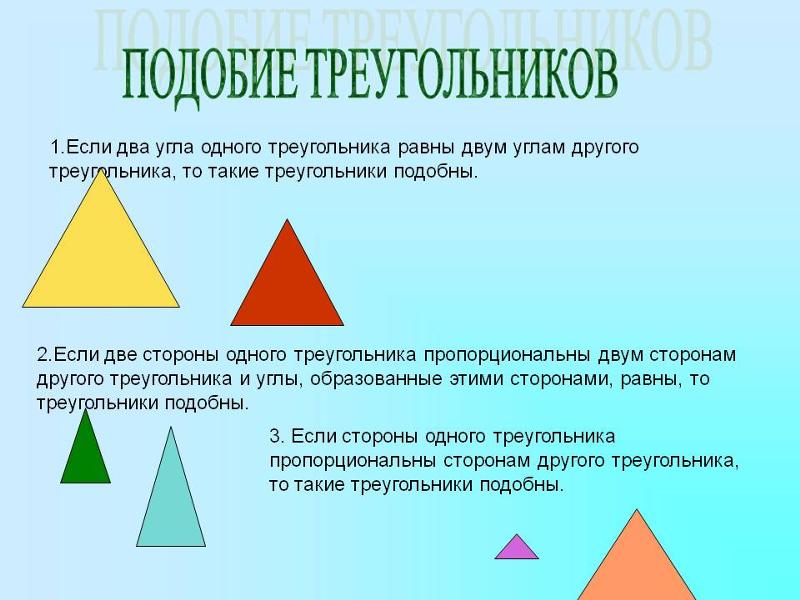
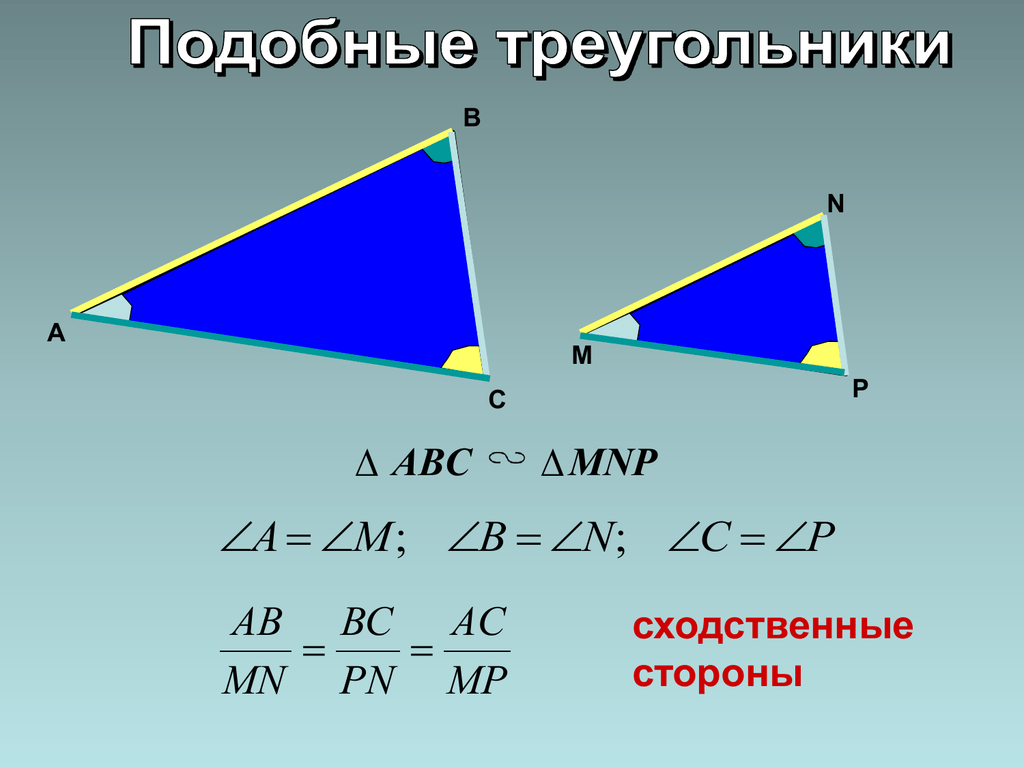
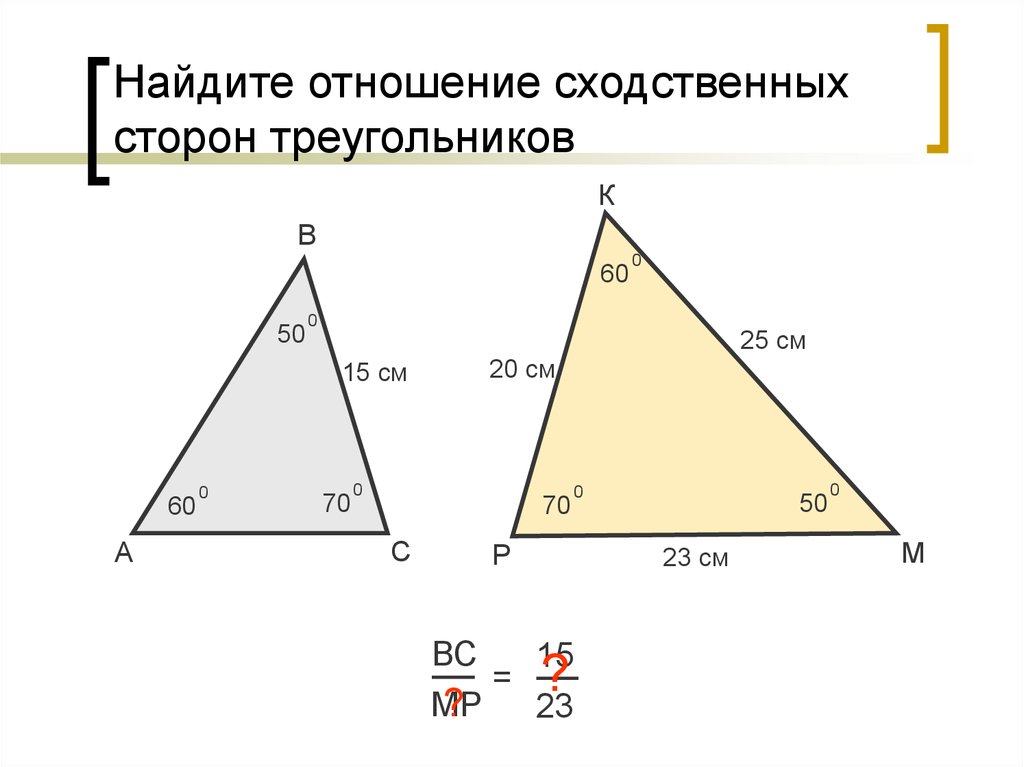
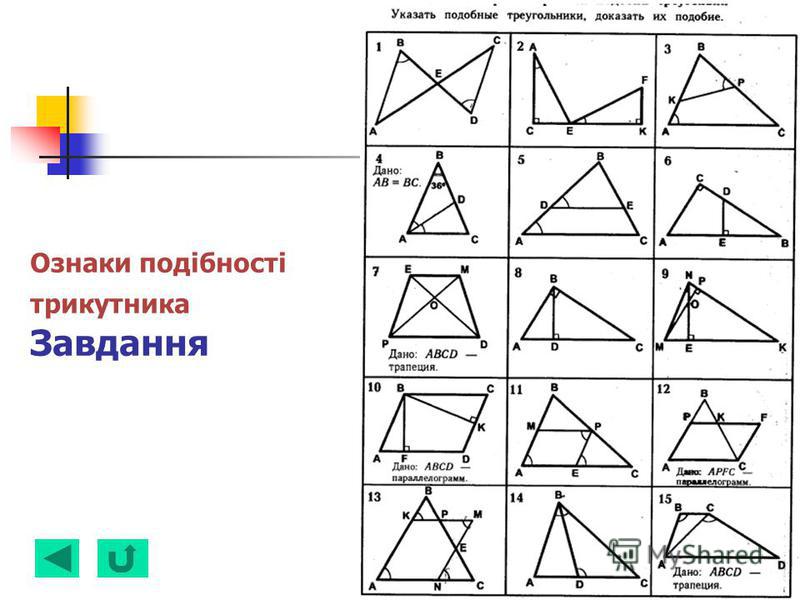

 Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров
Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров 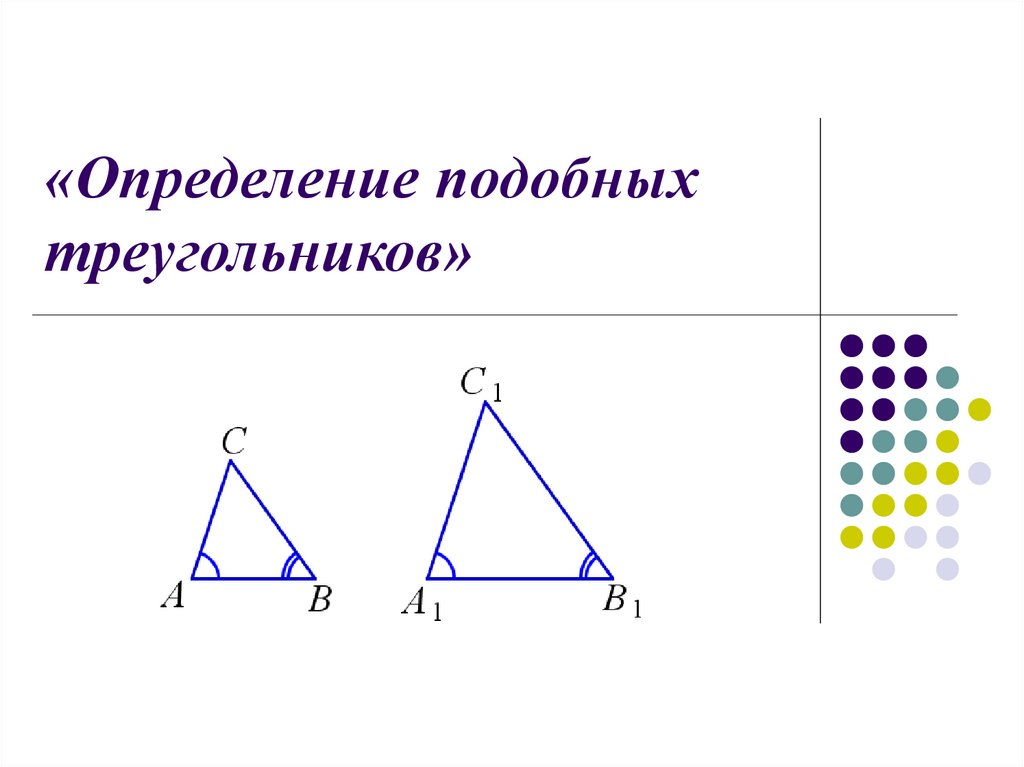
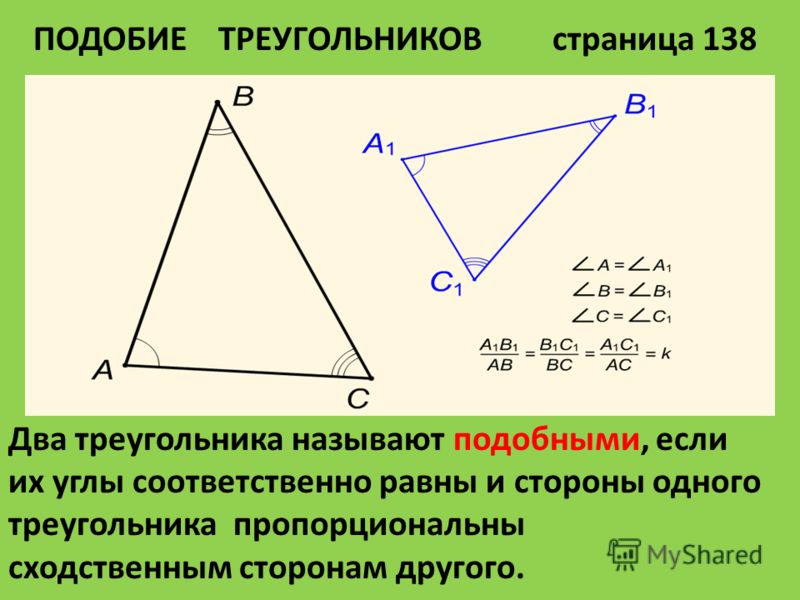

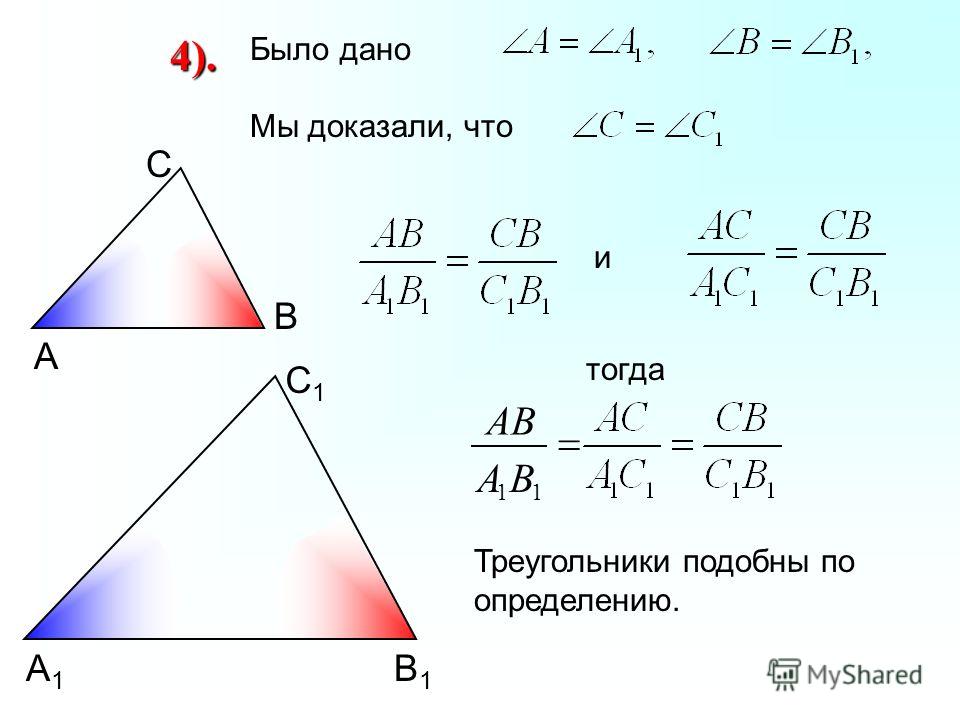
 Отсюда D = 1800 – ( Е + F) = 1800 – 1460 = 340.
Отсюда D = 1800 – ( Е + F) = 1800 – 1460 = 340.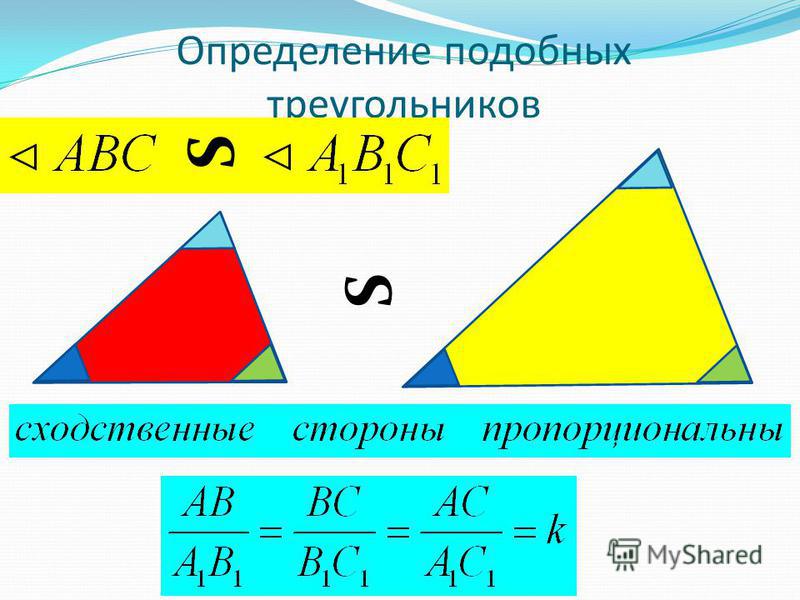 Остальные учащиеся работают в тетрадях.
Остальные учащиеся работают в тетрадях.
