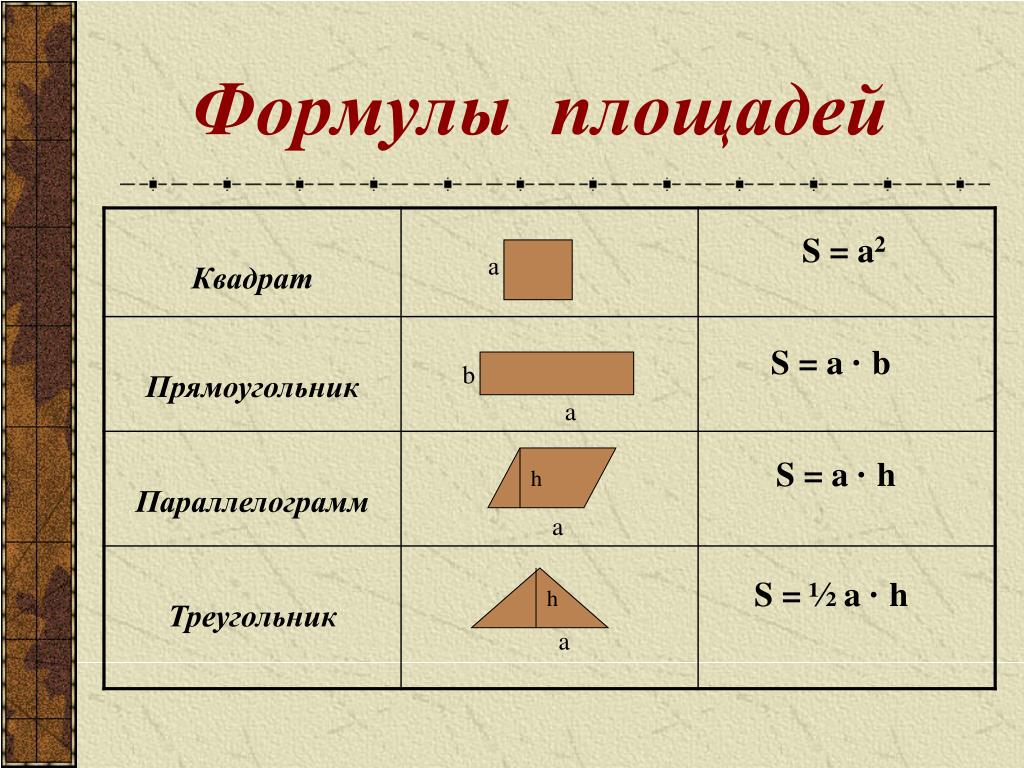
Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц. Формулы площади плоских фигур: Формулы площади треугольника Формулы площади квадрата Формула площади прямоугольника Формулы площади параллелограмма Формулы площади ромба Формула площади трапеции Формула площади выпуклого четырехугольника Формулы площади круга Формулы площади эллипса Онлайн калькуляторы для вычисления площадей плоских фигур Формулы площади треугольника
Вы можете воспользоваться онлайн калькулятором для расчета площади треугольника. Формулы площади квадрата
Вы можете воспользоваться онлайн калькулятором для расчета площади квадрата. Формула площади прямоугольникаПлощадь прямоугольника равна произведению длин двух его смежных сторон S = a · b где S — Площадь прямоугольника, Вы можете воспользоваться онлайн калькулятором для расчета площади прямоугольника. Формулы площади параллелограмма
Вы можете воспользоваться онлайн калькулятором для расчета площади параллелограмма. Формулы площади ромба
Вы можете воспользоваться онлайн калькулятором для расчета площади ромба. Формулы площади трапеции
Вы можете воспользоваться онлайн калькулятором для расчета площади трапеции. Формулы площади выпуклого четырехугольника
Вы можете воспользоваться онлайн калькулятором для расчета площади четырехугольника. Формулы площади круга
Вы можете воспользоваться онлайн калькулятором для расчета площади круга. Формулы площади эллипсаПлощадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи. S = π · a · b где S — Площадь эллипса, Вы можете воспользоваться онлайн калькулятором для расчета площади эллипса. Формулы по геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур Все таблицы и формулы Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! |
Площадь. Формула площади прямоугольника
- Кутузова Светлана Николаевна, учитель математики
org/BreadcrumbList»> Разделы: Математика
Цели урока:
- Образовательные: формирование понятие площади фигур, вывод формул площади прямоугольника и квадрата, понятия равных фигур и изучение их свойств, совершенствование вычислительных и графических навыков;
- Развивающие: развитие логического и творческого мышления, пространственного воображения, доказательной математической речи;
- Воспитательные: воспитание целеустремленности, самостоятельности, культуры речи воспитание доброжелательных отношений друг к другу, выслушивать мнения других и высказывать свою точку зрения.
Тип урока: Изучение нового материала (с применением информационных технологий).
Методы:
- частично-поисковый;
- объяснительно-иллюстративный;
- репродуктивный.
1. Структура урока:
- Организационный момент (1-2 мин.
 ).
). - Устный счет (3 мин.)
- Сообщение темы урока, постановка цели урока и его задач. (1-2 мин.)
- Ознакомление с новым материалом.
- Первичное осмысление и закрепление изученного.
- Домашнее задание (3 мин.)
- Итог урока. (5 мин.)
2. Устный счет проводится на компьютере с использованием программы Excel (правильность вычислений данных примеров проверяется компьютером и выставляется оценка).
3. Тему урока сообщает учитель, а цели и задачи урока учащиеся формулируют самостоятельно.
4. Ознакомление с новым материалом. (Приложение 1)
Учитель: Каким способами можно найти площадь фигуры представленной на экране прямоугольника (Слайд 1)?
Пусть дан прямоугольник со сторонами а и b, S – площадь прямоугольника,
требуется записать формулу, по которой можно вычислить площадь любого
прямоугольника (+ проговорить словами). (Слайд 3)
(Слайд 3)
5. Первичное осмысление и закрепление изученного.
1) Найдите площадь закрашенных фигур (рисунок 1). (Слайд 4)
Рисунок 1
2) Нарисуйте три разные фигуры площадью 8 кв. единиц (учащиеся выполняют задание на компьютере в программе Paint на ранее заготовленной учителем сетке).
3) Работа с раздаточным материалом.
Заранее учителем готовятся конверты с различными геометрическими фигурами (равными среди них должны быть прямоугольники и квадраты).
Найти среди них равные фигуры.
Учитель: А теперь назовите равные фигуры среди предложенных на экране. (Слайд 5)
Учитель:
- Каким образом вы определили равенство данных фигур? А теперь давайте откроем учебник и прочитаем, как в нем дается определение равных фигур.
- Учащимся предлагается одним найти периметр равных фигур, а другим площадь.
Учитель: Ребята, а что можно сказать о периметре и площади равных фигур?
Далее учащимся предлагается: (Слайд 6)
- Выбрать многоугольники.

- Выбрать четырехугольники.
- Выбрать прямоугольники и квадраты.
- Найти площадь прямоугольников и квадрата.
Учитель: Пусть дан квадрат со стороной а. Как найти площадь квадрата? Записать формулу для вычисления площади квадрата. (Слайд 7)
Нарисуйте фигуру той же площади, что и фигура на рисунке 2, но другой формы (учащиеся выполняют задание на компьютере в программе Paint на ранее заготовленной учителем сетке). (Слайд 9)
Рисунок 2
Найдите площади нарисованных прямоугольников. (Слайд 8)
Физминутка (игра «истинно — ложно»).
Если высказывание верно, то учащиеся встают со своих мест и хлопают в ладоши.
- Делить на нуль нельзя.
- 32 = 6.
- Квадрат — это прямоугольник.
- 5 «В» — самый дружный в школе! (Речь идет о классе, в котором проводится этот
урок).

- Всякий прямоугольник — квадрат.
- У любого треугольника 3 вершины, 3 угла, 2 стороны.
- Математика — царица наук.
Составьте задачу и решите ее. (Слайд 11)
Найдите площадь участка, план которого изображен на рисунке (размеры указаны в метрах). (Слайд 12)
Решение задач № 730, 731 из учебника.
6. Домашнее задание.
- Измерить площадь пола комнаты, выразить ее в м, см.
- № 716, 724.
7. Итог урока.
- О каких геометрических фигурах шел разговор на уроке?
- Что нужно знать, чтобы найти площади прямоугольника, квадрата?
- Пригодятся ли вам в жизни полученные знания? Где?
- Что на уроке было самым сложным, простым?
- Анализ урока.
- Выставление оценок.
Использованная литература и статьи:
- Губич Е.Н. статья «Урок математики в 5-м классе по теме «Прямоугольник,
квадрат.
 Их площади».
Их площади». - Котельникова Л.В. статья «Практические работы по математике: «Площади фигур».Объем параллелепипеда «5 класс».
- Учебник. Виленкин Н.Я., Жохов В.И. и др. Математика, 5, 2000 г.
Как мы находим площадь. Как найти площадь прямоугольника
Прямоугольник – это частный случай четырехугольника. Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Как узнать площадь прямоугольника по двум сторонам
Для того чтобы найти площадь прямоугольника, надо умножить его длину на ширину: Площадь = Длина × Ширина. 2 × sin(острого угла между диагоналями)/2.
2 × sin(острого угла между диагоналями)/2.
Одна из первых формул, которая изучается в математике, связана с тем, прямоугольника. Она же является и самой часто используемой. Прямоугольные поверхности окружают нас повсюду, поэтому часто требуется знать их площади. Хотя бы для того, чтобы узнать, хватит ли имеющейся в наличии краски для покраски полов.
Какие единицы измерения площади существуют?
Если говорить о той, которая принята за международную, то это будет квадратный метр. Его удобно использовать при расчете площадей стен, потолка или пола. В них указывается площадь жилья.
Когда речь идет о меньших предметах, то вводят квадратные дециметры, сантиметры или миллиметры. Последние нужны, если фигура не больше ногтя.
При измерении площади города или страны самыми подходящими оказываются квадратные километры. Но есть еще и единицы, которые используют для того, чтобы указать размер площади: ар и гектар. Первая из них еще называется соткой.
Как быть, если заданы стороны прямоугольника?
Подобным образом рассчитывается который является частным случаем прямоугольника. Так как у него все стороны равны, то произведение становится квадратом буквы а .
Так как у него все стороны равны, то произведение становится квадратом буквы а .
Как быть, если фигура изображена на клетчатой бумаге?
В этой ситуации нужно полагаться на количество клеточек внутри фигуры. По их числу бывает просто посчитать площадь прямоугольника. Но это можно сделать тогда, когда стороны прямоугольника совпадают с линиями клеток.
Часто имеет место такое положение прямоугольника, при котором его стороны наклонены по отношению к разлиновке бумаги. Тогда количество клеток определить сложно, поэтому расчет площади прямоугольника усложняется.
Потребуется сначала узнать площадь прямоугольника, который можно прочертить по клеточкам точно вокруг данного. Это просто: перемножить высоту и ширину. Потом вычесть из получившегося значения площади всех А их четыре. К слову, их рассчитывают как половину произведения катетов.
Итоговый результат даст значение площади данного прямоугольника.
Как поступить, если стороны неизвестны, зато даны его диагональ и угол между диагоналями?
До того в этой ситуации нужно вычислить его стороны, чтобы воспользоваться уже знакомой формулой. Поначалу потребуется вспомнить свойство его диагоналей. Они равны и делятся точкой пересечения пополам. Можно увидеть на чертеже, что диагонали делят прямоугольник на четыре равнобедренных треугольника, которые попарно равны друг другу.
Поначалу потребуется вспомнить свойство его диагоналей. Они равны и делятся точкой пересечения пополам. Можно увидеть на чертеже, что диагонали делят прямоугольник на четыре равнобедренных треугольника, которые попарно равны друг другу.
Равные стороны этих треугольников определяются как половины диагонали, которая известна. То есть в каждом треугольнике есть две стороны и угол между ними, которые даны в задаче. Можно воспользоваться
Одна сторона прямоугольника будет вычислена по формуле, в которой фигурируют равные стороны треугольника и косинус заданного угла. Для вычисления второй значение косинуса придется брать от угла, равного разности 180 и известного угла.
Что делать, если в задаче дан периметр?
Обычно в условии указывается еще и соотношение длины и ширины. Вопрос о том, как посчитать площадь прямоугольника, в этом случае проще на конкретном примере.
Допустим, что в задаче периметр некоторого прямоугольника равен 40 см. Известно также, что его длина в полтора раза больше ширины. Необходимо узнать его площадь.
Необходимо узнать его площадь.
Решение задачи начинается с записи формулы периметра. Его удобнее расписать как сумму длины и ширины, каждую из которых умножить на два по отдельности. Это будет первым уравнением в системе, которую потребуется решить.
Второе связано с известным по условию соотношением сторон. Первая сторона, то есть длина, равна произведению второй (ширины) и числа 1,5. Это равенство нужно подставить в формулу для периметра.
Получится, что он равен сумме двух одночленов. Первый — произведение 2 и неизвестной ширины, второй — произведение чисел 2 и 1,5 и той же ширины. В этом уравнении всего одна неизвестная — это ширина. Нужно ее сосчитать, а потом воспользоваться вторым равенством, чтобы сосчитать длину. Останется только перемножить эти два числа, чтобы узнать площадь прямоугольника.
Расчеты дают такие величины: ширина — 8 см, длина — 12 см, а площадь — 96 см 2 . Последнее число — ответ рассмотренной задачи.
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину.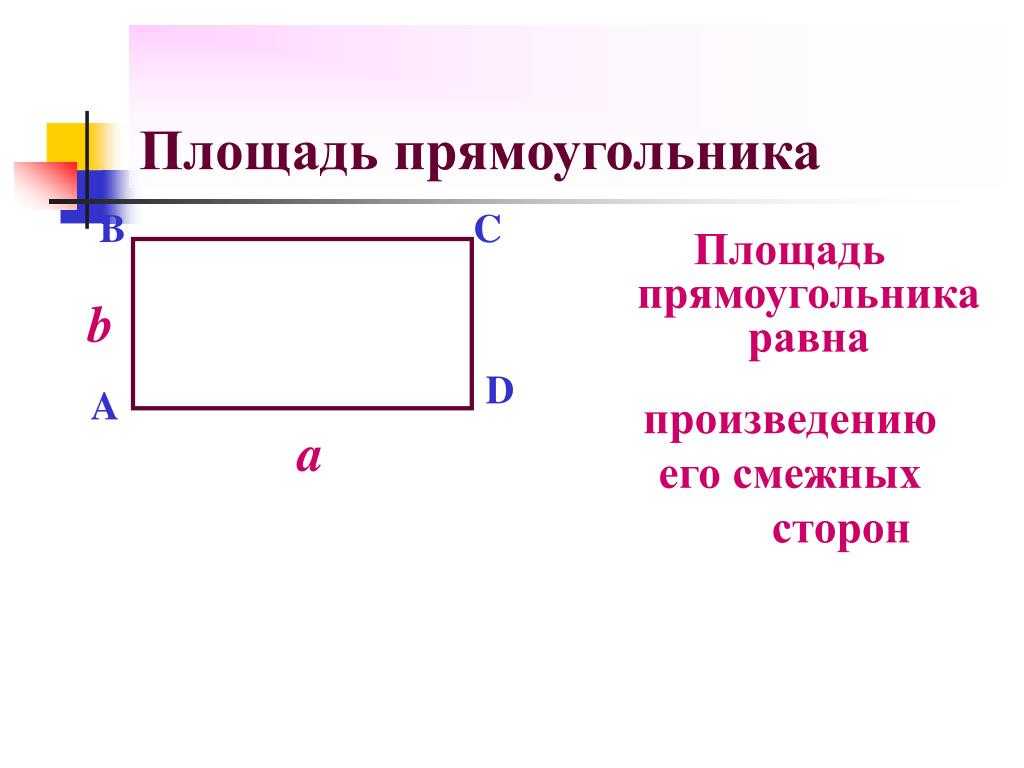 Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны.
 А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два.
 Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Инструкция
Например, вам , что длина одной из сторон (а) равна 7 см, а периметр прямоугольника (P) равен 20 см. Так как периметр любой фигуры равен сумме длин ее сторон, а у прямоугольника противоположные стороны равны, то его периметр а будет выглядеть следующим образом: P = 2 x (a + b), или P = 2a + 2b. Из этой формулы следует, что найти длину второй стороны (b) можно с помощью несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.
Теперь, зная длины обеих смежных сторон (a и b), вы сможете подставить их в формулу площади S = ab. В данном случае прямоугольника будет равна 7х3 = 21. Обратите на то, что единицами измерения будут уже не , а сантиметры квадратные, так как длин двух сторон единицы их измерения (сантиметры) вы тоже умножали друг на друга.
Обратите на то, что единицами измерения будут уже не , а сантиметры квадратные, так как длин двух сторон единицы их измерения (сантиметры) вы тоже умножали друг на друга.
Источники:
- как находится периметр прямоугольника
Плоская фигура, состоящая из четырех сторон и четырех прямых углов. Из всех фигур площадь прямоугольника приходится вычислять чаще других. Это и площадь квартиры, и площадь садового участка, и площадь поверхности стола или полки. Например, чтобы просто оклеить комнату обоями, вычисляют площадь ее прямоугольных стен.
Инструкция
Кстати, из прямоугольника можно легко вычислить площадь . Достаточно достроить прямоугольный до прямоугольника так, чтобы гипотенуза стала диагональю прямоугольника . Тогда будет очевидно, что площадь такого прямоугольника равна произведению катетов треугольника, а площадь самого треугольника, соответственно, равна половине произведения катетов.
Видео по теме
Частный случай параллелограмма — прямоугольник – известен только в геометрии Евклида. У прямоугольника равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.
Инструкция
Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями EFА. Согласно свойству прямоугольника его диагонали равны и пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.
Далее вычислите первую EF прямоугольника . Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.
Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.
Найдите вторую сторону прямоугольника FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.
Относится к простейшим плоским геометрическим фигурам и является одним из частных случаев параллелограмма. Отличительная черта такого параллелограмма — прямые углы во всех четырех вершинах. Ограниченную сторонами прямоугольника площадь можно вычислить несколькими способами, используя размеры его сторон, диагонали и углы между ними, радиус вписанной окружности и т.д.
Инструкция
Если известна величина угла (α), который составляет диагональ прямоугольника с одной из его сторон, а также длина (С) этой диагонали, то для вычисления площади можно задействовать определения тригонометрических в прямоугольном . Прямоугольный треугольник здесь образуют две стороны четырехугольника и его диагональ. Из определения косинуса вытекает, что длина одной из сторон будет равна произведению длины диагонали на угла, величина известна. Из определения синуса можно вывести формулу длины другой стороны — она равна произведению длины диагонали на синус все того же угла. Подставьте эти тождества в формулу из предыдущего шага, и получится, что для нахождения площади надо перемножить синус и косинус известного угла, а также длины диагонали прямоугольника : S=sin(α)*cos(α)*С².
Прямоугольный треугольник здесь образуют две стороны четырехугольника и его диагональ. Из определения косинуса вытекает, что длина одной из сторон будет равна произведению длины диагонали на угла, величина известна. Из определения синуса можно вывести формулу длины другой стороны — она равна произведению длины диагонали на синус все того же угла. Подставьте эти тождества в формулу из предыдущего шага, и получится, что для нахождения площади надо перемножить синус и косинус известного угла, а также длины диагонали прямоугольника : S=sin(α)*cos(α)*С².
Если кроме длины диагонали (С) прямоугольника известна величина угла (β), который образуют диагонали, то для вычисления площади фигуры можно тоже задействовать одну из тригонометрических функций — синус. Возведите в квадрат длину диагонали и умножьте полученный результат на половину синуса известного угла: S=С²*sin(β)/2.
Если известен (r) вписанной в прямоугольник окружности, то для вычисления площади возведите эту величину во вторую степень и увеличьте результат в четыре раза: S=4*r². Четырехугольник, в который можно , будет являться квадратом, а длина его стороны равна диаметру вписанной окружности, то есть удвоенному радиусу. Формула получена подстановкой длин сторон, выраженных через радиус в тождество из первого шага.
Четырехугольник, в который можно , будет являться квадратом, а длина его стороны равна диаметру вписанной окружности, то есть удвоенному радиусу. Формула получена подстановкой длин сторон, выраженных через радиус в тождество из первого шага.
Если известны длины (P) и одной из сторон (A) прямоугольника , то для нахождения площади внутри этого периметра вычислите половину произведения длины стороны на разницу между длиной периметра и двумя длинами этой стороны: S=A*(P-2*A)/2.
Видео по теме
С задачей найти периметр или площадь многоугольника сталкиваются не только ученики на уроках геометрии. Порой ее случается решать и взрослому человеку. Приходилось ли вам рассчитывать необходимое количество обоев для комнаты? Или, может быть, вы измеряли протяженность дачного участка, чтобы огородить его забором? Так знания основ геометрии иногда незаменимы для осуществления важных проектов.
Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма.
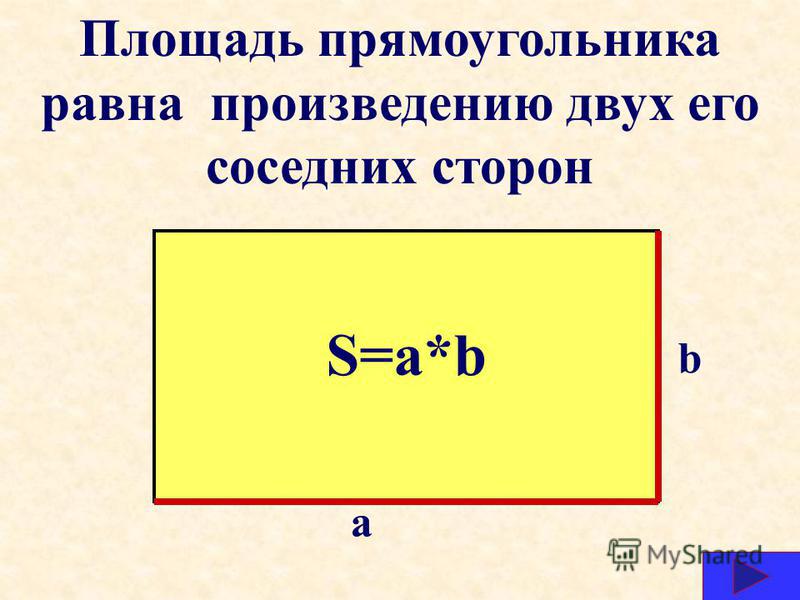 Площади плоских фигур. Формулы площади.
Площади плоских фигур. Формулы площади.Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы./ / Плоские фигуры. Поделиться:
| ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||
Формулы площадей фигур для школьников и студентов
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
- формулы площади треугольника
- формулы площади квадрата
- формула площади прямоугольника
- формулы площади параллелограмма
- формулы площади ромба
- формулы площади трапеции
- формулы площади дельтоида
- формулы площади произвольного выпуклого четырехугольника
- формулы площади круга
- формула площади эллипса
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
S=12a·h ,
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.
S=pp-ap-bp-c,
где p — полупериметр треугольника: p=a+b+c2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S=12a·b·sinγ ,
где a, b — стороны треугольника,
γ — угол между сторонами a и b.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S=a·b·c4R ,
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
S=p·r ,
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p=a+b+c2
Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
S=a2 ,
где S — площадь квадрата,
a — длина стороны квадрата.
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
S=d22 ,
где S — площадь квадрата,
d — длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон.
S=a·b ,
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S=a·h ,
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
S=a·b·sinα ,
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S=d1 ·d2 · sinβ2=d1·d2 · sinγ2 ,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β, γ — угол между диагоналями параллелограмма.
Формулы площади ромба
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S=a·h ,
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
S=a2·sinα ,
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.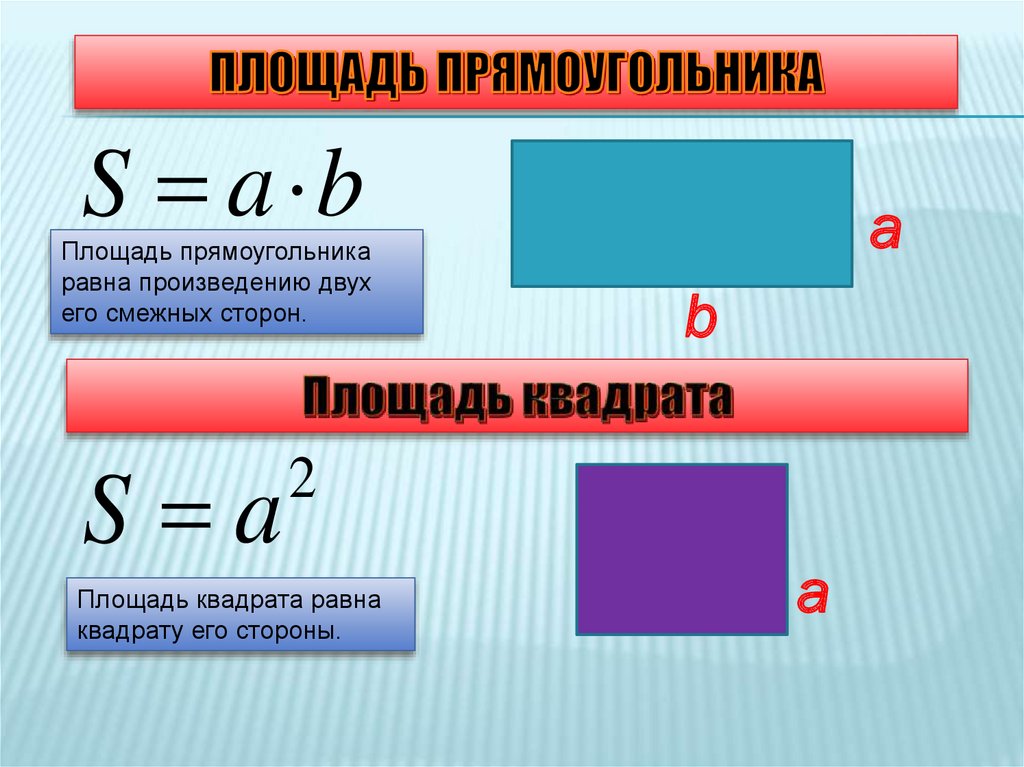
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
S=d1·d22 ,
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
Формулы площади трапеции
Трапеция — это четырёхугольник, у которого две (a, b) стороны параллельны (основания), а две другие (c, d) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
S=a+b|a-b|p-ap-bp-a-cp-a-d ,
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p=a+b+c+d2 — полупериметр трапеции.
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы её оснований на высоту.
S=a+b·h3 ,
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
S=a·bsinβ ,
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S=a2sinγ+b2sinα2 ,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b,
γ — угол между равными сторонами a.
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
S=a+br ,
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
Формула площади дельтоида по двум диагоналям
Площадь дельтоида равна половине произведения длин двух диагоналей.
S=d1·d22 ,
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
Формулы площади произвольного выпуклого четырехугольника
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S=d1·d2·sinγ2 ,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.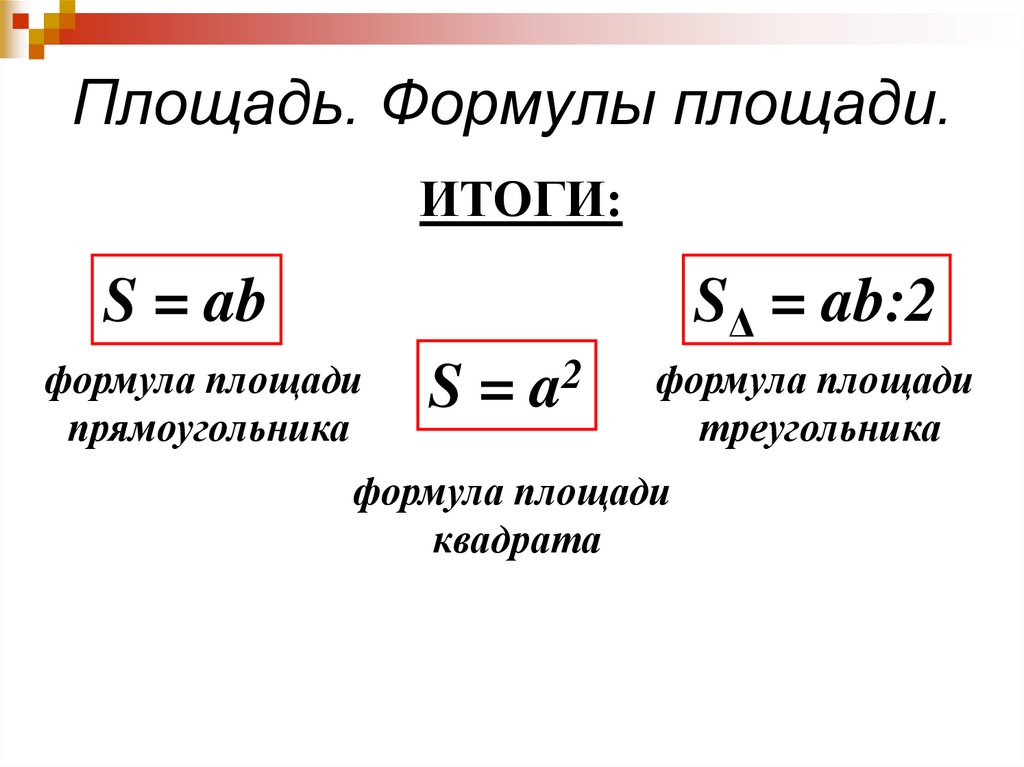
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
S=p-ap-bp-cp-d-a·b·c·d·cos2θ ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p=a+b+c+d2 — полупериметр четырехугольника,
θ=α+β2 — полусумма двух противоположных углов четырехугольника.
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S=p-ap-bp-cp-d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p=a+b+c+d2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной окружностью
Если в четырехугольник можно вписать окружность, то его площадь равна:
S=p·r ,
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p=a+b+c+d2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной и описанной окружностями
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
S=a·b·c·d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
S=πr2 ,
где S — площадь круга,
r — радиус круга.
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
S=πd24 ,
где S — площадь круга,
d — диаметр круга.
Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
S=R22·π·α°180°-sinα ,
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
S=R22·αрад.-sinα ,
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
Формула площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S=π·a·b ,
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
Формулы площади треугольника — Студопедия
Поделись
1-ая формула
S — площадь треугольника
a, b — длины 2-х сторон треугольника
С — угол между сторонами a и b
2-ая формула
S — площадь треугольника
a — длина стороны треугольника
h — длина высоты, опущенной на сторону a
3-ья формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
p — полупериметр треугольника
4-ая формула
S — площадь треугольника
r — радиус вписанной окружности
p — полупериметр треугольника
5-ая формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
R — радиус описанной окружности
См.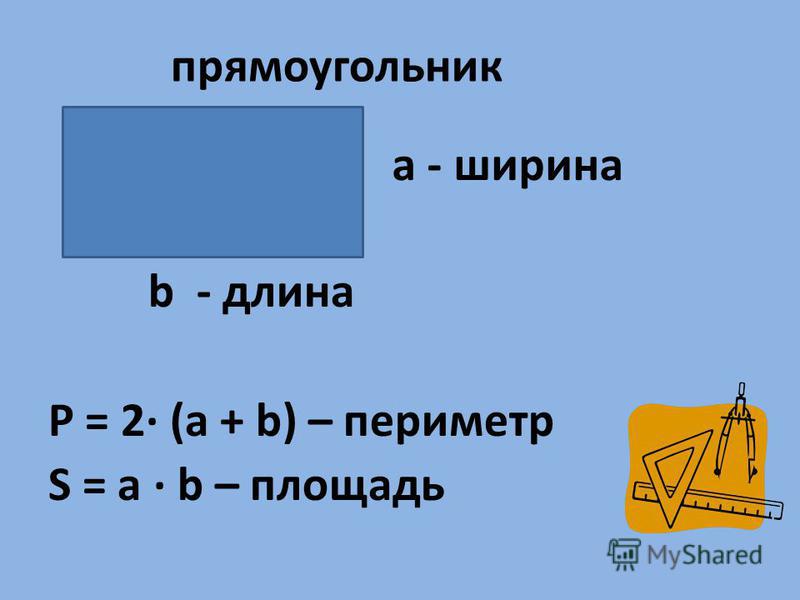 также: Программа для расчета площади треугольника.
также: Программа для расчета площади треугольника.
Формулы площади квадрата:
1) Площадь квадрата равна квадрату длины его стороны (a).
2) Площадь квадрата равна половине квадрата длины его диагонали (d).
S — площадь квадрата
a — длина стороны квадрата
d — длина диагонали квадрата
См. также: Программа для расчета площади квадрата.
Формула площади прямоугольника:
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
S — площадь прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
См. также: Программа для расчета площади прямоугольника.
Формула площади параллелограмма:
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).
S — площадь параллелограмма
a — длина основания
h — длина высоты
См. также: Программа для расчета площади параллелограмма.
также: Программа для расчета площади параллелограмма.
Формула площади трапеции:
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
S — площадь трапеции
a — длина 1-ого основания
b — длина 2-ого основания
h — длина высоты трапеции
См. также: Программа для расчета площади трапеции.
Формулы площади ромба:
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
S — площадь ромба
a — длина основания ромба
h — длина высоты ромба
d1 — длина 1-ой диагонали
d2 — длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула площади круга:
1) Площадь круга равна произведению квадрата радиуса на число пи (3. 1415).
1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
S — площадь круга
π — число пи (3.1415)
r — радиус круга
См. также: Программа для расчета площади круга.
Формула площади эллипса:
1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).
S — площадь эллипса
π — число пи (3.1415)
a — длина большой полуоси
b — длина малой полуоси
Формулы периметра
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
Формула периметра круга (длины окружности):
1) Периметр круга равен произведению радиуса на два пи (3.1415).
P — Периметр круга (длина окружности)
π — число пи (3. 1415)
1415)
r — радиус круга (окружности)
См. также: Программа для расчета периметра круга (длины окружности).
Формула периметра треугольника:
1) Периметр треугольника равен сумме 3-ех его сторон (a, b, c).
P — периметр треугольника
a, b, c — длины сторон треугольника
См. также: Программа для расчета периметра треугольника.
Формула периметра прямоугольника:
1) Периметр прямоугольника равен удвоенной сумме 2-х его смежных сторон (a, b).
P — периметр прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
См. также: Программа для расчета периметра прямоугольника.
Формулы периметра квадрата:
1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).
2) Периметр квадрата равен произведению длины его диагонали на два корня из двух.
P — периметр квадрата
a — длина стороны квадрата
d — длина диагонали квадрата
См. также: Программа для расчета периметра квадрата.
Формула периметра трапеции:
1) Периметр трапеции равен сумме 4-х её сторон (a, b, c, d).
P — периметр трапеции
a, c — длины оснований трапеции
b, d — длины боковых сторон трапеции
См. также: Программа для расчета периметра трапеции.
Формула периметра параллелограмма:
1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).
P — периметр параллелограмма
a — длина 1-ой стороны параллелограмма
b — длина 2-ой стороны параллелограмма
См. также: Программа для расчета периметра параллелограмма.
также: Программа для расчета периметра параллелограмма.
Формула периметра ромба:
1) Периметр ромба равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
P — периметр ромба
a — длина стороны ромба
Формулы треугольника
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Площадь прямоугольников: формулы, уравнения и примеры
Прямоугольник — это частный случай четырехугольника, представляющего собой четырехстороннюю плоскую фигуру. Все 4 внутренних угла прямоугольника прямые. Книга, футбольное поле, окно, дорожный чемодан — все это примеры прямоугольников.
Теперь предположим, что вы хотите вычислить общую площадь футбольного поля. Затем вам нужно знать, как вычислить площадь прямоугольника.
Затем вам нужно знать, как вычислить площадь прямоугольника.
Прямоугольник – это четырехугольник, все внутренние углы которого прямые. Двумерное пространство, занимаемое прямоугольником, называется площадью прямоугольника.
Четырехугольник с двумя парами параллельных противоположных сторон называется параллелограммом. Так как все углы прямоугольника прямые, то и противоположные пары сторон прямоугольника всегда параллельны. Это делает каждый прямоугольник параллелограммом. На самом деле прямоугольник считается особым типом параллелограмма.
Площадь прямоугольников: Формула
Рассмотрим следующий прямоугольник.
Иллюстрация прямоугольника, Нилабхро Датта – StudySmarter Originals
Площадь прямоугольника определяется по формуле:
Площадь = b × h
где b = длина основания, h = длина высоты
Теперь значение b равно длине стороны AB, который здесь считается базовым. Условно одну из длинных сторон прямоугольника принимают за основание, а одну из сторон, перпендикулярных основанию, считают высотой. В этом прямоугольнике высота равна длине AD.
В этом прямоугольнике высота равна длине AD.
В некоторых соглашениях основание и высота называются длиной и шириной прямоугольника.
Частный случай: Формула площади квадрата
Квадрат — это частный случай прямоугольника. Кроме того, что все 4 внутренних угла прямые, все 4 стороны квадрата равны.
Квадратная иллюстрация, Нилабхро Датта, StudySmarter Originals
Посмотрите на приведенный выше квадрат и вспомните формулу площади прямоугольника: Площадь = основание × высота.
Так как все 4 стороны квадрата равны, то основание и высота равны. Достаточно знать длину стороны квадрата, чтобы вычислить его площадь. Таким образом, в случае квадрата формулу можно сократить до:
Площадь=длинастороны×длинастороны=(длинастороны)2
Площадь прямоугольников: Квадратные единицы
Рассматривая площадь фигуры, помните, что площадь измеряется в квадратных единицах , таких как квадратные сантиметры (см 2 ), квадратные футы (ft 2 ), квадратные дюймы (в 2 ) и т. д. ниже. Подумайте, сколько квадратных единиц необходимо, чтобы точно и исчерпывающе покрыть всю поверхность замкнутой фигуры. Эта сумма и есть площадь фигуры.
д. ниже. Подумайте, сколько квадратных единиц необходимо, чтобы точно и исчерпывающе покрыть всю поверхность замкнутой фигуры. Эта сумма и есть площадь фигуры.
Квадратные единицы, Юргенсен и Браун– Геометрия
Площадь прямоугольников: примеры задач
Прямоугольник площадью 60 м 2 имеет основание длиной 20 м. Какова высота прямоугольника?
Решение
Площадь = B × H
⇒60 M 2 = 20 м × H
⇒ H = 60 M 2 ÷ 20 M
⇒ H = 3 M
Если вы зная длину 1 из сторон (основание или высоту) прямоугольника и длину диагонали, вы можете вычислить неизвестную длину стороны (высоту или основание), используя теорему Пифагора. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон.
На следующем рисунке показано, как диагональ прямоугольника делит его на 2 прямоугольных треугольника, что позволяет нам использовать теорему Пифагора.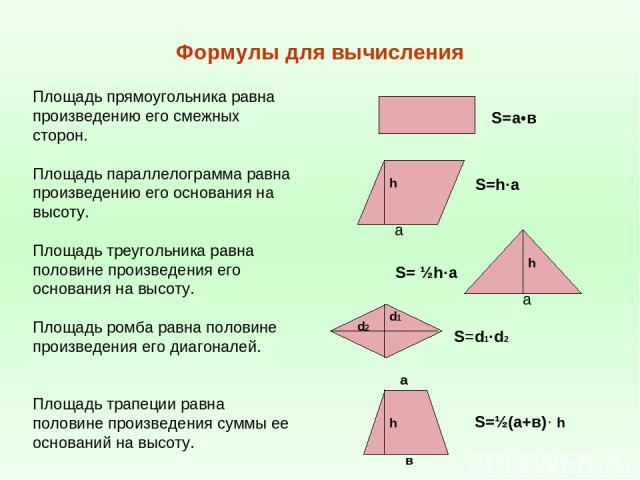 Затем, когда известны и основание, и высота прямоугольника, можно вычислить площадь.
Затем, когда известны и основание, и высота прямоугольника, можно вычислить площадь.
Диагональ прямоугольника делит его на 2 прямоугольных треугольника, Nilabhro Datta — StudySmarter Originals
В следующем прямоугольнике ABCD, AB = 9, BD = 15. Найдите площадь прямоугольника.
Решение
Поскольку внутренние углы прямоугольника прямые, BD — это гипотенуза прямоугольного треугольника, ΔABD.
Итак,
Согласно теореме Пифагора,
AD2+AB2=BD2⇒AD2+92=152⇒AD2=152-92⇒AD2=144⇒AD=12
Площадь прямоугольника = b × h
= 12 футов × 9 футов
= 108 футов 2
Длина стороны квадрата 10 футов. Какова площадь квадрата?
Решение
Площадь = сторона × сторона
= 10 футов × 10 футов
= 100 футов 2
Площадь прямоугольников. .
Площадь = b × h
где b = основание, h = высота.
Квадрат — это частный случай прямоугольника. Кроме того, что все 4 внутренних угла прямые, все 4 стороны квадрата равны.
Площадь квадрата определяется по формуле: Площадь = сторона × сторона
Площадь прямоугольника: формула, как рассчитать, примеры
- Автор Keerthi Kulkarni
- Последнее изменение 19-07-2022
- Автор Кирти Кулкарни
- Последнее изменение 19-07-2022
Площадь прямоугольника: Площадь прямоугольника является одним из основных понятий, связанных с математикой. Площадью называется общее пространство, ограниченное двумерной фигурой. Принимая во внимание, что площадь прямоугольника — это площадь, заключенная в прямоугольник. Другими словами, пространство, занимаемое в пределах периметра (границы) прямоугольника, называется площадью прямоугольника. Основное свойство прямоугольника состоит в том, что у него четыре стороны и каждый угол равен 90 градусов.
Существует много интересных применений площади прямоугольника, таких как определение площади прямоугольного пола, вычисление высоты здания и т. д. Кроме того, когда дело доходит до решения задач измерения или геометрии, формула площади прямоугольника Формула играет важную роль. В этой статье давайте подробно разберемся с понятием площади прямоугольника. Продолжайте читать, чтобы узнать больше.
Площадь прямоугольника определяется его сторонами. В общем случае площадь прямоугольника равна произведению его длины на ширину. С другой стороны, периметр прямоугольника равен сумме всех его четырех сторон. В результате площадь прямоугольника определяется как область, ограниченная его периметром.
Прямоугольник – это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. Поскольку у прямоугольника четыре стороны, у него четыре угла. Все углы прямоугольника равны \(90\) градусов; таким образом, все углы прямоугольника прямые.
Определение: Площадь, занимаемая прямоугольником внутри его границ, называется площадью прямоугольника.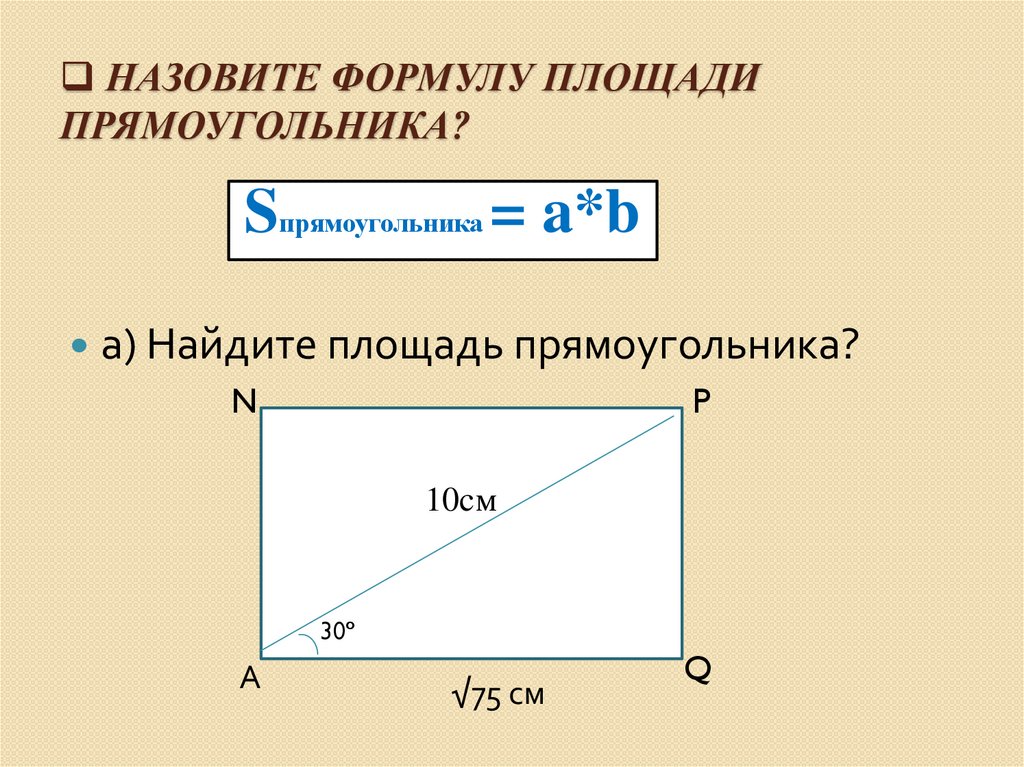
Мы привели несколько примеров прямоугольников, с которыми мы сталкиваемся в повседневной жизни, таких как двери комнаты, экран компьютера, книги, весы и т. д.
Какова площадь прямоугольника?
Площадь прямоугольника в основном зависит от его сторон. Например, площадь прямоугольника школьной доски зависит от меры длины и ширины (или ширины).
В основном формула площади прямоугольника равна произведению длины и ширины (или ширины) прямоугольника. Тогда как, когда мы говорим о периметре прямоугольника, он равен сумме всех его четырех сторон.
Следовательно, область, ограниченная периметром прямоугольника, является его площадью.
Формула площади прямоугольника:
Площадь прямоугольника \(= {\text{Длина}} \times {\text{Ширина}}\)
Какова единица измерения прямоугольника?
Площадь любого многоугольника — это количество пространства, которое он занимает или заключает в себе на плоскости. Площадь обычно измеряется в квадратных единицах, таких как квадратные метры, квадратные футы, квадратные дюймы и т. д. Площадь более крупных фигур, таких как поля или города, измеряется в квадратных километрах, гектарах или акрах.
Площадь обычно измеряется в квадратных единицах, таких как квадратные метры, квадратные футы, квадратные дюймы и т. д. Площадь более крупных фигур, таких как поля или города, измеряется в квадратных километрах, гектарах или акрах.
Практические экзаменационные вопросы
Формула площади прямоугольника и периметра прямоугольника
Периметр прямоугольника — это длина границы прямоугольника, которая определяется как сумма всех сторон прямоугольника.
Площадь прямоугольника вычисляется в единицах путем умножения ширины (или ширины) на длину прямоугольника.
Таким образом, периметр и площадь прямоугольника определяются как:
92}.\)Основное различие между квадратом и прямоугольником состоит в том, что длина и ширина квадрата равны, тогда как длина и ширина прямоугольника различны.
Площадь прямоугольника методом квадрата
Самый простой способ найти площадь прямоугольника — подсчитать количество квадратных единиц в нем.
Площадь прямоугольника = количество квадратных единиц, образующих прямоугольник
Пример 1. Сначала вычислим площадь прямоугольника методом квадратов. Рассмотрим прямоугольник \(ABCD\) длины \({\text{5 см}}\) и ширины \({\text{4 см}}\). 9{\текст{2}}}\).
Попытка пробных тестов
Как найти площадь прямоугольника?
Выполните следующие действия, чтобы найти площадь прямоугольника:
- Отметьте размеры длины и ширины (или ширины) по заданным данным.
- Умножение значений длины и ширины (или ширины).
- Запишите ответ в квадратных единицах.
Площадь прямоугольника: вывод
Во-первых, диагонали прямоугольника делят его на два равных прямоугольных треугольника. Следовательно, площадь прямоугольника будет в два раза больше площади прямоугольного треугольника.
Предположим, \(ABCD\) — прямоугольник.
Теперь пусть диагональ \(AC\) делит прямоугольник на два конгруэнтных прямоугольных треугольника, т.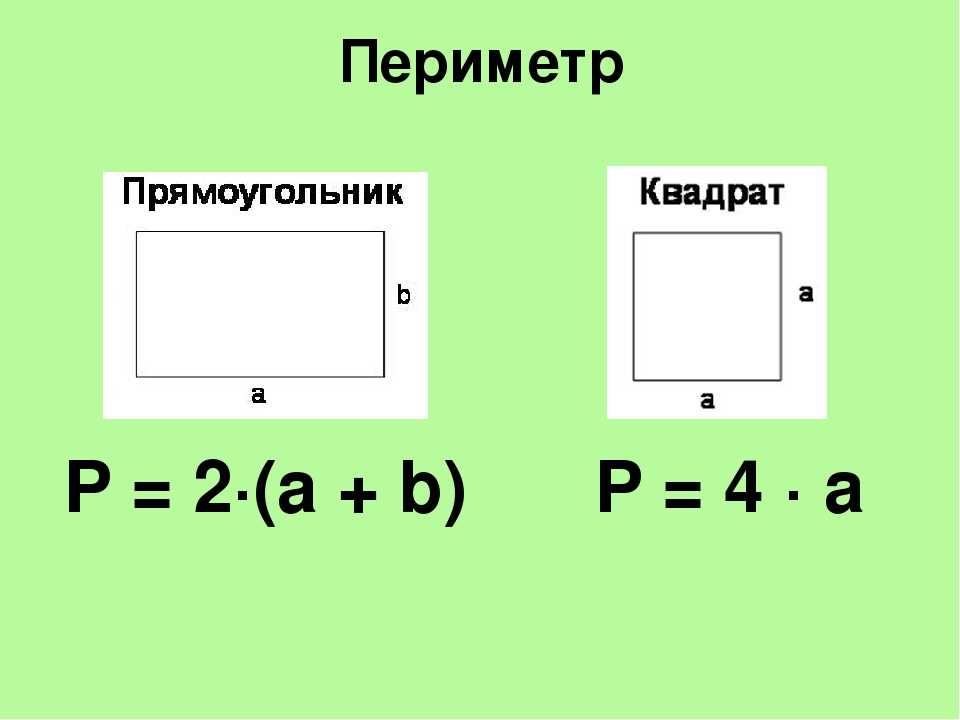 е. \(\Delta ABC\) и \(\Delta ADC.\). Таким образом, площадь обоих прямоугольных треугольников будет быть равным.
е. \(\Delta ABC\) и \(\Delta ADC.\). Таким образом, площадь обоих прямоугольных треугольников будет быть равным.
Следовательно, площадь прямоугольника \(ABCD\; = \) \(2 \times \) Площадь \(\Delta ABC\).
Мы знаем, что площадь треугольника \(= \frac{1}{2} \times {\text{основание}} \times {\text{высота}}\)
Площадь прямоугольника \( = 2 \times \frac{1}{2} \times AB \times BC\)
\(= 2 \times \left( {\frac{1}{2} \times l \times b} \ right) = l \times b\)
Таким образом, площадь прямоугольника \(= {\text{Длина}} \times {\text{Ширина}}\)
Площадь прямоугольника по диагоналям
Мы знаем, что диагональ делит прямоугольник на два равных прямоугольных треугольника. Таким образом, диагональ становится гипотенузой соответствующего прямоугольного треугольника.
Мы знаем, что диагональ прямоугольника вычисляется с помощью теоремы Пифагора следующим образом: 92}} \)
Важная область формул прямоугольника
Пусть длина прямоугольника равна \(«l»,\), ширина прямоугольника равна \(«b»,\), периметр прямоугольника равен \(«P»\), а площадь прямоугольника равна \(«A «»,\), затем
1. Площадь прямоугольника \(= l \times b\)
Площадь прямоугольника \(= l \times b\)
2. Периметр прямоугольника \(= 2\left( {l + b} \right)\)
3. Длина прямоугольника \( = \frac{A}{b}\)
4. Длина прямоугольника \( = \frac{P}{2} – b\)
5. Ширина прямоугольника \( = \frac{A}{l}\) 92}\)
\( = \frac{{26,400}}{{10,000}} = 2,64\) га.
2) Длина прямоугольного экрана \({\text{15}}\,{\text{см}}\) Его площадь \({\text{180}}\,{\ text{sq}}{\text{.}}\,{\text{см}}\). Найдите его ширину.
Решение: Площадь экрана \(= 180\,{\text{кв}}.{\text{см}}\)
Длина экрана \({\text{15}}\,{\ text{cm}}\)
Площадь прямоугольника = \(l \times b\)
Итак, \({\text{Ширина=}}\frac{{{\text{Площадь}}}}{{{ \text{Длина}}}}\)
\( = \frac{{180}}{{15}} = 12~{\text{см}}\)
3) Найдите периметр и площадь прямоугольника длиной \({\text{17}}\,{\text{см}}\) и шириной \({\text{13} }\,{\text{см}}\) .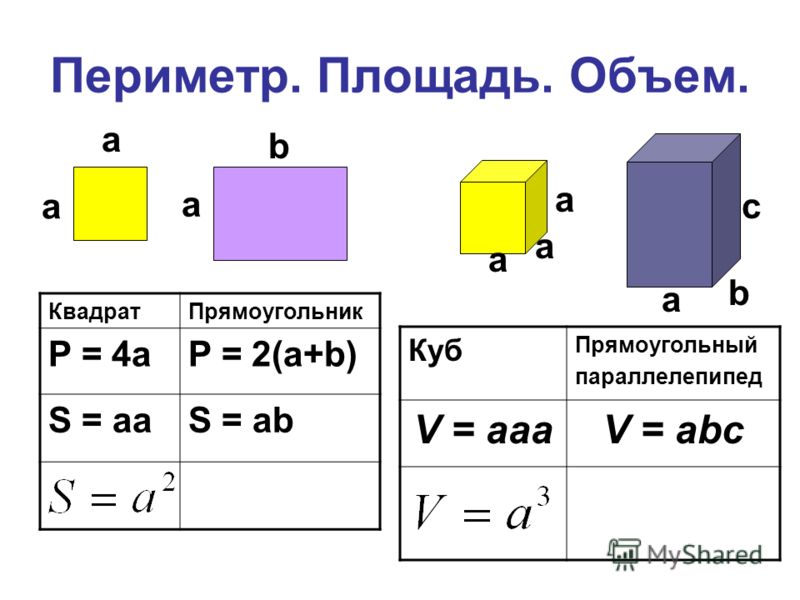
Решение:
Дано: длина \((l) = 17~{\text{см}}\) и ширина \((b) = 13~{\text{см}}\)
Периметр прямоугольника \ ( = 2\влево( {l + b} \вправо)\)
\( = 2\влево( {17 + 13} \вправо) = 2\влево( {30} \вправо)\)
\(=60 \mathrm{~см}\)
Мы знаем, что площадь прямоугольника .см}}\)
4) Найдите площадь прямоугольника длины \({\text{43}}\,{\text{m}}\) и ширины \({\text{13}}\, {\ текст {см}} \).
Решение:
Дано: длина прямоугольника \((l) = 43\,{\text{m}}\).
Ширина прямоугольника \((b) = 13~{\text{m}}\)
Мы знаем, что площадь прямоугольника \(= l \times b.\) 92}\).
5) Длина и ширина прямоугольной фермы составляют \(80\) ярдов и \(60\) ярдов. Найдите площадь фермы.
Решение:
Дано: Длина прямоугольника \((l) = 80\,{\text{ярд}}\)
Ширина фермы \((b) = 60\,{\text{ярд} }\)
Мы знаем, что площадь прямоугольника равна длине \( \×\) ширине. 2}\) 92}\)
2}\) 92}\)
Количество конвертов, которые можно сделать \({\text{=}}\frac{{{\text{Площадь листа}}}}{{{\text{площадь конверта}}} }\)
\( = \frac{{7500}}{{100}}\)
\( = 75\) конвертов
8) Длина и ширина прямоугольной стены равны \({\text{75}}\,{\text{m}}\) и \({\text{32}}\,{\ text{m}}\), соответственно. Найдите стоимость покраски стены, если стоимость покраски равна \text{.}}\,{\text{м}}\)
Решение:
Дано: Длина стены \({\text{=75}}\,{\text{м}}\)
Ширина стены \({\text{=32}}\ ,{\text{м}}\)
Площадь стены \(= {\text{длина}} \times {\text{ширина}}\)
\(= 75{\text{~м}} \ раз 32 {\ text {~ m}} \)
\ ({\ text {= 2400}} \, {\ text {sq}} {\ text {.m}} \)
Для \ ({\ text { =1}}\,{\text{кв}}{\text{.м}}\) стоимости покраски \({\text{Rs}}.\,3\)
Таким образом, для \({\text {2400}}\,{\text{кв}}{\text{.м}}\) стоимость покраски стены составит \(= 3 \times 2400\)
\(= 7200 рупий\)
9) Длина и ширина прямоугольной стены равны \( {\text{70}}\,{\text{м}}\) и \({\text{30}}\ {\text {m}}\), соответственно. Найдите стоимость покраски стены, если стоимость покраски \({\text{3 рупии за кв}}{\text{. м}}\)
Найдите стоимость покраски стены, если стоимость покраски \({\text{3 рупии за кв}}{\text{. м}}\)
Ответ:
Длина стены \({\text{=70}}\,{\text{м}}\)
Ширина стены \({\text{=30}}\,{ \text{м}}\)
Площадь стены \( = {\text{длина}} \times {\text{ширина}} = 70~{\text{м}} \times 30~{\text{ м}} = 2100\,{\text{кв}}.{\text{м}}\)
За \({\text{1}}\,{\text{кв}}{\text{.}}\,{\text{м}}\) расходов на покраску \({\text{Rs}} {\text{.3}}\)
Таким образом, для \({\text{2100}}\,{\text{sq}}{\text{.}}\,{\text{m}}\) стоимость покраски стены составит \( = 3 \times 2100 = {\text{Rs}}\,6300\).
10) Этаж, длина и ширина которого равны \({\text{50}}\,{\text{м}}\) и \({\text{40}}\,{\text{ m}}\), соответственно, должны быть покрыты прямоугольными плитками. Размер каждой плитки равен \({\text{1}}\,{\text{m}} \times 2\,{\text{m}}\). Найдите общее количество плиток, которые потребуются, чтобы полностью покрыть пол.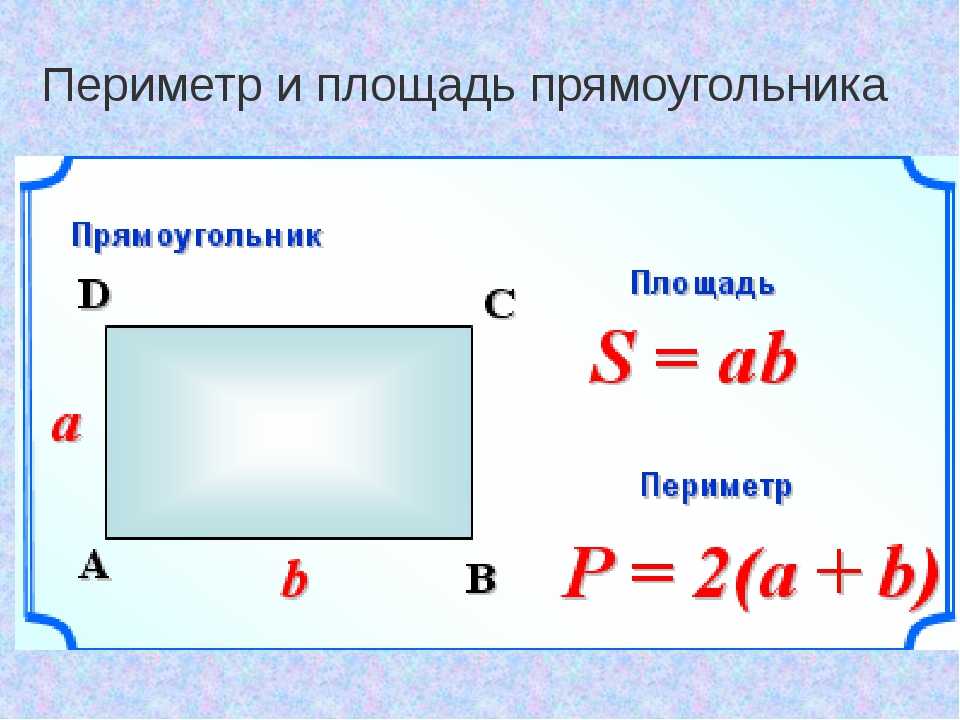
Ответ:
Длина пола \(= 50\,{\text{м}}\)
Ширина пола \(= 40\,{\text{м}}\)
Площадь пола \(={\text{длина}} \times {\text{ширина}} = 50\,{\text{m}} \times 40\,{\text{m}} = 2000\,{\text{ sq}}{\text{.}}\,{\text{m}}\)
Длина одной плитки \(= 2\,{\text{m}}\)
Ширина одной плитки \(= 1 \,{\text{m}}\)
Площадь одной плитки \(={\text{длина}} \times {\text{ширина}} = 2\,{\text{m}} \times 1\ , {\ text {м}} = 2 \, {\ text {кв}} {\ text {.}} \, {\ text {м}} \)
Требуемое количество плиток \( = \) площадь пола/площадь плитки \( = \frac{{2000}}{2}\;= \;1000\) плиток
Часто задаваемые вопросы о площади прямоугольника
Проверить свойства прямоугольника здесь
Часто задаваемые вопросы, связанные с площадью прямоугольника, приведены ниже:
Q.1. По какой формуле находится площадь прямоугольника?
Ответ: Формула площади прямоугольника:
\({\text{Площадь}} = {\text{Длина}} \times {\text{Ширина}}\)
Q.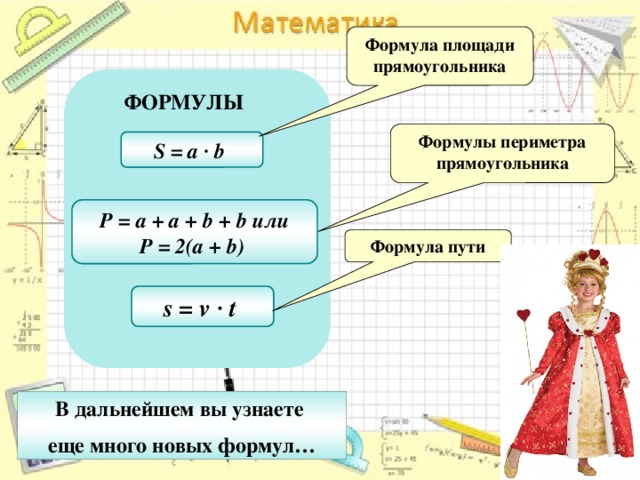 2. Чему равен периметр прямоугольника?
2. Чему равен периметр прямоугольника?
Ответ: Периметр прямоугольника равен сумме всех его четырех сторон.,
Следовательно, \({\text{Периметр}}\left({{\text{прямоугольник}}} \right) = 2\влево({{\текст{Длина}} + {\текст{Ширина}}}\вправо)\)
Q.3. Какова площадь прямоугольника?
Ответ: Площадь прямоугольника – это площадь, занимаемая сторонами прямоугольника. 9{\text{2}}}\) и т. д.
Q.5. Как найти длину, зная площадь и ширину прямоугольника?
Ответ: Когда площадь и ширина прямоугольника известны, длину можно вычислить, используя:
\({\text{Длина=}}\frac{{{\text{Площадь}}}} {{{\text{Ширина}}}}\)
Q.6. Как найти ширину, зная площадь и длину?
Ответ: Когда площадь прямоугольника и длина прямоугольника известны, ширину можно вычислить, используя:
\({\text{Ширина=}}\frac{{{\text{Площадь}}}}{{{\text{Длина}}}}\)
В. 2}\).
2}\).
В Embibe мы предоставляем бесплатные вопросы по математике для классов \(8,9,10,11,\) и \(12\) вместе с подробными решениями:
Итак, используйте эти ресурсы наилучшим образом и овладейте предметом.
Мы обсудили все, что касается площади прямоугольника. Мы надеемся, что эта подробная статья о площади прямоугольника будет вам полезна. Если у вас есть какие-либо вопросы об этой странице, напишите нам через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.
Сокращение глупых ошибок; Пройдите бесплатные пробные тесты, связанные с прямоугольниками
Формула площади прямоугольника — как она представлена в вашей учебной программе?
Стратегии работы в классе, информация о согласовании стандартов
Соавтор стандартаДжейсон Зимба распаковывает формулу площади прямоугольника и указывает на проблемы, связанные с тем, как учебники иногда знакомят учащихся с этой формулой.
Автор: Джейсон Зимба
Размещено:
Поделиться
Распечатать
Примечание редактора. Этот пост впервые появился в личном блоге Джейсона Зимбы 10 августа 2016 г. В этом сообщении в блоге соавтор стандартов Джейсон Зимба описывает формулу площади на концептуальном уровне и выделяет некоторые недостатки в том, как формула представлена в учебниках.
В формуле площади прямоугольника A = L × W ,
- A – количество единичных квадратов, необходимое для замостивания прямоугольника
- L число единиц длины при измерении одной стороны прямоугольника
- W — количество единиц длины при измерении смежной стороны прямоугольника.
Формула работает благодаря тому, что означает символ ×.
Сегодня давайте ограничим наш анализ формулы целыми числами, потому что сегодня я думаю о формуле с точки зрения молодого студента, который еще не усвоил дробные величины или операции с дробями. Для целых чисел простая интерпретация 90 650 м 90 651 × 90 650 n 90 651 состоит в том, что это означает количество вещей в 90 650 м 90 651 групп из 90 650 n 90 651 вещей в каждой.
Для целых чисел простая интерпретация 90 650 м 90 651 × 90 650 n 90 651 состоит в том, что это означает количество вещей в 90 650 м 90 651 групп из 90 650 n 90 651 вещей в каждой.
В контексте прямоугольника, скажем, длиной 7 единиц и шириной 5 единиц, что такое группы и что такое вещи?
Если одна сторона прямоугольника состоит из 7 единиц длины, то мы можем провести линии, чтобы разделить прямоугольник поровну на 7 полос. В прямоугольнике столько полос, сколько единиц длины стороны.
Мы могли бы сделать то же самое с любой из двух соседних сторон, в результате чего число полосок равнялось бы 5.
делится на квадраты (вопрос: почему идеальные квадраты?). Например, 7 полос превратятся в 7 групп по 5 квадратов в каждой. Если вспомнить, что означает ×, то общее количество квадратов должно быть равно 7 × 5,9.0003
Этот аргумент вполне очевиден для любого прямоугольника с целым числом сторон, поэтому мы можем сказать, что для любого такого прямоугольника: по одной стороне, умноженной на количество единиц длины, которые подходят по соседней стороне.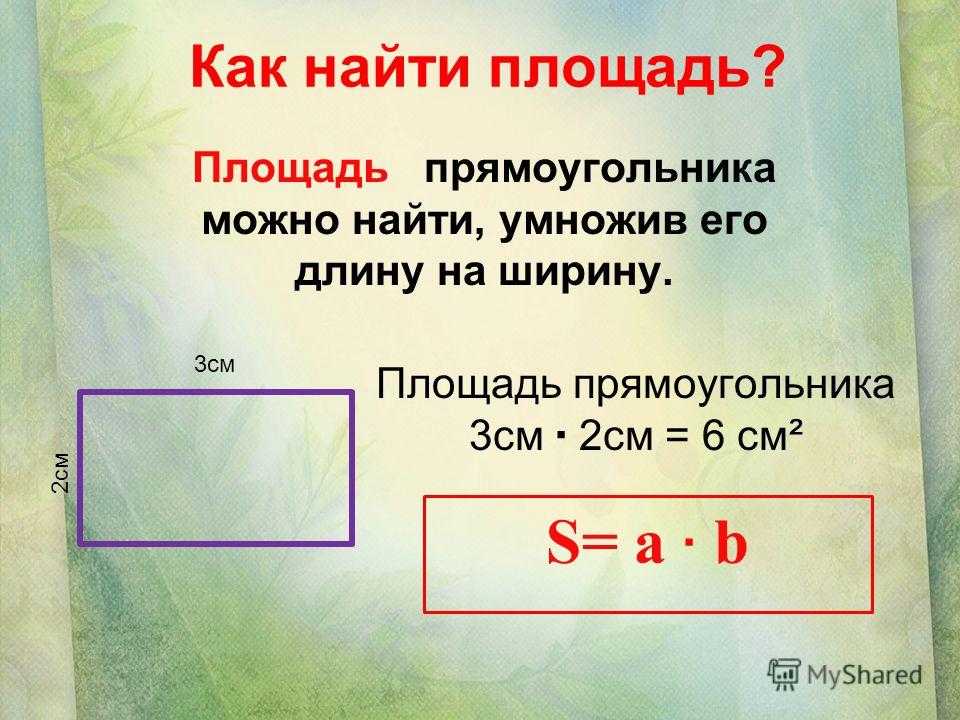
Вот что означает выражение «Площадь равна длине, умноженной на ширину».
Некоторые недостатки, которые я заметил в том, как преподаются некоторые учебники по математике A = L × W :
- Плохая работа по установлению того, что вообще означает m × n. Тогда книга не сможет нормально работать с площадью или с чем-либо еще, зависящим от умножения.
- Плохая работа с основными принципами измерения. Тогда непонятно, что означает измерение длины или что означает измерение площади. Вы не можете связать две идеи, которые не понимаете по отдельности.
- Непонятная разница между площадью и длиной. Примером этого может быть стирание различия между повторениями единиц длины вдоль границы и повторениями единиц площади непосредственно внутри границы. В одной книге говорится: «Количество квадратов в одном ряду равно длине прямоугольника в единичных квадратах». Что такое «длина объекта в единичных квадратах»? Квадраты — это единицы площади, а не длины.
 Правильно было бы сказать: «Количество квадратов в одном ряду равно количеству единиц длины на краю прямоугольника». Может быть, это звучит запутанно, но в математике слова означают вещи; вы должны объединить слова в утверждения, которые верны или, по крайней мере, не противоречат существующему различию.
Правильно было бы сказать: «Количество квадратов в одном ряду равно количеству единиц длины на краю прямоугольника». Может быть, это звучит запутанно, но в математике слова означают вещи; вы должны объединить слова в утверждения, которые верны или, по крайней мере, не противоречат существующему различию. - Слишком много времени уходит на то, чтобы обдумать соответствующие рассуждения.
Теги:
- Развитие концептуального понимания математики
- Начальная школа
- Математика
Об авторе: Джейсон Зимба был ведущим автором Common Core State Standards for Mathematics и партнером-основателем Student Achievement Partners. Он имеет степень бакалавра гуманитарных наук. из Уильямс-колледжа по двойной специализации по математике и астрофизике; степень магистра наук исследованиями в области математики Оксфордского университета; и доктор философии. по математической физике Калифорнийского университета в Беркли. Работа доктора Зимбы как исследователя охватывала целый ряд областей, включая астрономию, астрофизику, теоретическую физику, философию науки и чистую математику. Его академические награды включают стипендию Родса и премию Майораны в области теоретической физики. В качестве педагога он преподавал физику, математику и другие предметы студентам колледжей, специалистам университетов по физике и инженерии, взрослым заключенным, старшеклассникам из неблагополучных семей и детям иммигрантов, не говорящих по-английски.
Его академические награды включают стипендию Родса и премию Майораны в области теоретической физики. В качестве педагога он преподавал физику, математику и другие предметы студентам колледжей, специалистам университетов по физике и инженерии, взрослым заключенным, старшеклассникам из неблагополучных семей и детям иммигрантов, не говорящих по-английски.
Формулы площади
| Формула периметра прямоугольника |
| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
( пи = = 3,141592. Район ФормулыПримечание: «аб» означает «а» умножить на «б». «а2 » означает «а в квадрате», что то же самое, что «а» умножить на «а».Будьте осторожны!! Считаются единицы. Используйте тот же единицы для всех измерений. Примерыsquare = a 2 rectangle = ab parallelogram = bh trapezoid = h/2 (b 1 + b 2 ) circle = пи r 2 эллипс = пи r 1 r 2
треугольник с заданным SAS (две стороны и противолежащий угол) треугольник, заданный a,b,c = [s(s-a)(s-b)(s-c)] когда s = (a+b+c)/2 (формула Герона) правильный многоугольник = (1/2) n sin(360°/n) S 2 Единиц Площадь измеряется в квадратных единицах. Площадь квадрата = сторона умноженная на сторону. Так как каждая сторона квадрата равна то же самое, это может быть просто длина одной стороны в квадрате. Если у квадрата одна сторона равна 4 дюймам, площадь будет равна 4 дюймам, умноженным на 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также могут быть записаны в 2 .) Обязательно используйте одни и те же единицы измерения для всех измерений. Нельзя умножать футы на дюймы, это не дает квадрат измерение. Площадь прямоугольника равна длине стороны раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, то что это площадь? НЕПРАВИЛЬНО …. 4 раза по 6 = 24 ПРАВИЛЬНО …. 4 дюйма равно 1/3 фута. Площадь 1/3 фута
умножить на 6 футов = 2 квадратных фута. | ||||||||||||||||||||||
© 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика. |
Площадь прямоугольника — определение, формулы и примеры
Прямоугольник — это двумерная фигура, имеющая четыре стороны. В этой статье мы обсудим площадь прямоугольника и способы ее вычисления.
Какова площадь прямоугольника
Площадь прямоугольника определяется как общая область, покрытая им. Это произведение двух смежных сторон, т. е. длины и ширины. Мы измеряем его в квадратных единицах.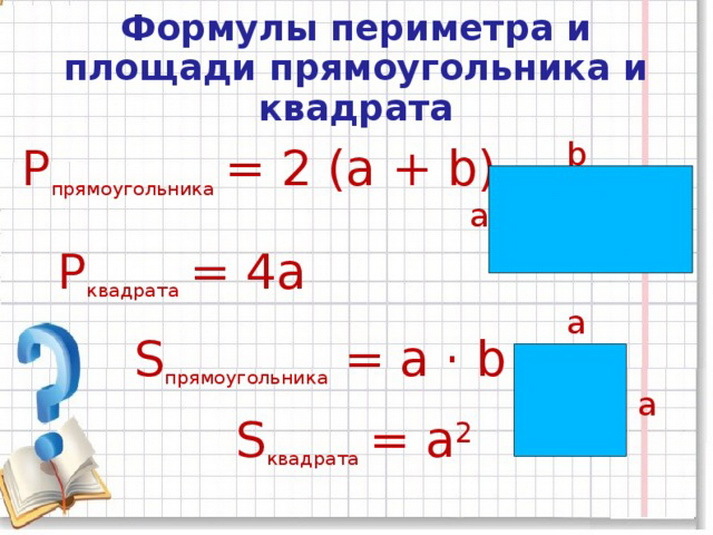
Формулы
Формула для нахождения площади прямоугольника приведена ниже:
Площадь прямоугольникаКак найти площадь прямоугольника
Существует 3 стандартных шага для вычисления площади прямоугольника, учитывая его длину и ширина.
Шаг 1 : Обратите внимание на значение и единицы длины и ширины из заданного вопроса или примера
Шаг 2 : Умножьте длину на ширину
Шаг 3 : Запишите ответ в квадратных единицах
Теперь выведем стандартную формулу площади прямоугольника.
Вывод: почему площадь прямоугольника равна ширине × длине
Возьмем ▭ ABCD и проведем диагональ BD.
Четко делит прямоугольник на 2 равноправных прямоугольных треугольника ∆BAD и ∆BCD.
Следовательно, площадь прямоугольника будет равна сумме площадей этих двух треугольников.
Вывод формулы площади прямоугольникаПоскольку мы знаем, что ∆BAD и ∆BCD являются конгруэнтными прямоугольными треугольниками
Площадь ▭ ABCD = площадь ∆BAD + площадь ∆BCD
= 2 × площадь ∆BCD
= 2 × (1/2 × основание × высота ∆BCD)
= (CD × BC)
Когда CD = w, BC = l
Площадь ▭ ABCD = w × l = ширина × длина
Таким образом получаем стандартную формулу площади прямоугольника по его длине и ширине.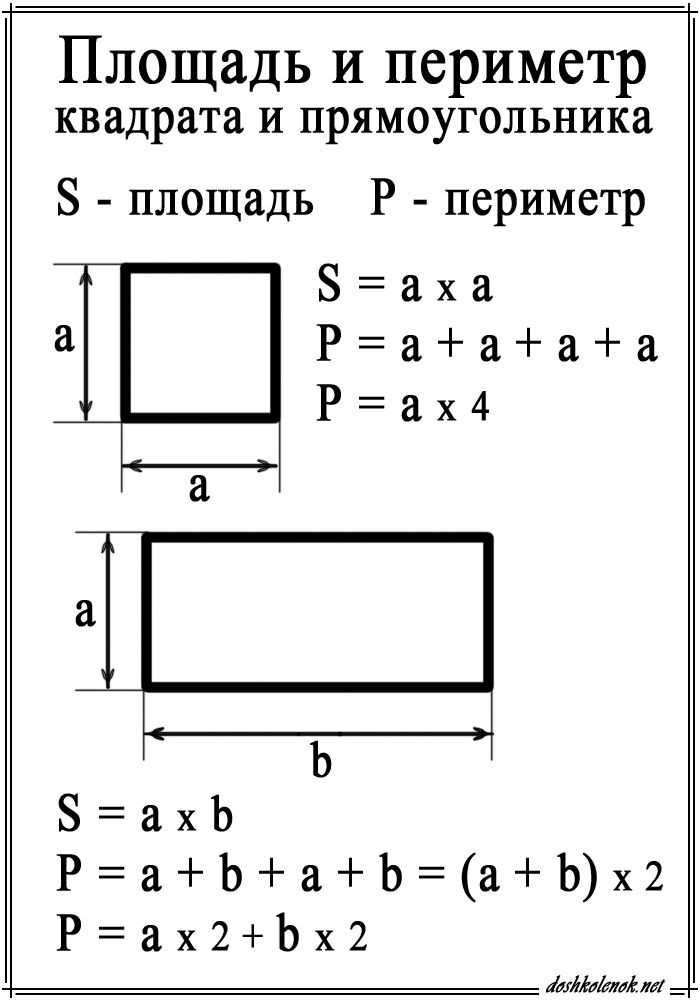
Теперь давайте решим несколько примеров, используя приведенную выше формулу для вычисления площади прямоугольника.
Найдите площадь прямоугольного бассейна длиной 45 футов и шириной 25 футов.
Решение:
Как известно,
Площадь (A) = w × l, здесь w = 25 футов, а l = 45 футов
= (25 × 45) кв. футов
= 1125 кв. футов
Деление прямоугольника на квадраты
Почему площадь выражается в квадратных единицах?
Возьмем прямоугольник длиной 3 дюйма и шириной 2 дюйма.
Теперь мы рисуем единичные квадраты внутри прямоугольника.
Каждый единичный квадрат имеет длину 1 дюйм.
Площадь прямоугольника Единица измерения квадратовТеперь подсчитайте количество квадратов в прямоугольном блоке.
Внутри 6 квадратов.
Мы всегда измеряем площадь в квадратных единицах.
Поскольку единицей измерения этого прямоугольника являются дюймы, площадь измеряется и выражается в квадратных дюймах.
Таким образом, площадь указанного выше прямоугольника составляет 6 квадратных дюймов.
Найдите количество плиток, необходимых для покрытия прямоугольной стены шириной 20 дюймов и длиной 80 дюймов. Каждая плитка имеет длину 8 дюймов и ширину 5 дюймов.
Решение:
Как мы знаем,
Площадь стены = w × l, здесь w = 20 дюймов, а l = 80 дюймов
= (20 × 80) кв. дюймов
= 1600 кв. дюймов
Площадь плитки = w × l, здесь w = 5 дюймов, а l = 8 дюймов 91 104 = (5 × 8) кв. дюймов 91 104 = 40 кв. дюймов.
Следовательно, количество плиток, необходимых для покрытия стены = площадь прямоугольной стены ÷ площадь прямоугольной плитки
= 1600 ÷ 40 = 40
Таким образом, нам понадобится 40 плиток, чтобы покрыть стену.
Найдите количество плиток, необходимых для покрытия пола площадью 3630 кв. дюймов квадратными плитками со стороной 11 дюймов .
Решение:
Как мы знаем,
Площадь квадратной плитки = a 2 , здесь a = 11 дюймов
= 11 × 11
= 121 кв. дюйм.
Требуемое количество плиток = площадь пола ÷ площадь плитки, здесь площадь пола = 3630 квадратных дюймов
3630 ÷ 121 = 30
Итак, чтобы покрыть пол, нужно 30 плиток.
Помимо стандартного способа нахождения площади прямоугольника, вычислим площадь по диагонали и любой из его сторон, т. е. длине или ширине.
Площадь прямоугольника, если даны диагональ и любая сторона
Ниже приведена формула для вычисления площади прямоугольника.
Вывод
Площадь прямоугольника с диагональюКак мы знаем из теоремы Пифагора,
(Диагональ) 2 = (Длина) 2 + (Ширина) 2 ,
диагональ = d, длина = l, ширина = w
Следовательно, l 2 = d 2 – w 2 ,
или, l = √(d 2 – w 2 ) ………. (1)
(1)
Альтернативно, w 2 = d 2 – l 2 (d 2 – l 2 ) ……….(2)
Мы знаем, что площадь прямоугольника (A) = w × l
Возможны два варианта:
1. Диагональ и ширина известны
Подставив значение l из (1) в стандартную формулу, получим,
A = w × √(d 2 – w 2 )
2. Диагональ и длина известны
(d 2 – l 2 )
Теперь решим несколько примеров, использующих приведенные выше формулы диагонали и стороны.
Нахождение площади прямоугольника, когда известны ДИАГОНАЛЬ и ОДНА СТОРОНА
Найдите площадь прямоугольника с диагональю 15 см и длиной 12 см.
Решение:
Как известно,
Площадь прямоугольника A = l × √(d 2 – l 2 ), здесь d = 15 см, l = 12 см
= 12 × √(225 – 144) см²
= (12 × 9) см² = 108 см²
Найдите площадь прямоугольника, диагональ которого равна 19 см, а ширина 9 см.
Решение:
Как известно,
Площадь прямоугольника A = w × √(d 2 – w 2 ), здесь d = 19 см, w = 9 см
= 9 × √(19 2 – 9 2 ) кв. см
≈ 150,6 кв. см
Найдите площадь заштрихованной области.
Решение:
Как мы знаем,
Площадь (A) = w × l, здесь w = 18 м, а l = 25 м для большего прямоугольника
= (18 × 25) кв. м
= 450 кв. м
А,
Площадь (А) = w × l, здесь w = 12 м, а l = 20 м для меньшего прямоугольника
= (12 × 20) кв.м
= 240 кв.м
Теперь
Площадь заштрихованной области = Площадь большего прямоугольника – Площадь меньшего прямоугольника
= (450 – 240) кв.м
= 210 м2
Найдите площадь заштрихованной области.
Решение:
Как мы знаем,
Площадь (A) = w × l, здесь w = 16 м, а l = 24 м для большего прямоугольника
= (16 × 24) кв. м
м
= 384 кв. м
Аналогично,
Площадь (A) = w × l, здесь w = 6 м, а l = 9м для меньшего прямоугольника
= (6 × 9) кв. м
= 54 кв. м
Теперь
Площадь заштрихованной области = Площадь большего прямоугольника – Площадь меньшего прямоугольника
= (384 – 54) кв.м
= 330 кв.м
Найдите площадь прямоугольника с дробными длинами сторон 7/9 и 5/8 фута.
Решение:
Как мы знаем,
Площадь (A) = w × l, здесь w = 5/8 фута, а l = 7/9 фута
= 5/8 × 7/9 кв. фута
= 35/72 кв. футов
Таким образом, мы получаем площадь прямоугольника в дробной форме, когда длины сторон даны в дробной форме.
Найдите площадь прямоугольника со сторонами 1 и 1 ярда.
Решение:
Как мы знаем,
Площадь (A) = w × l, здесь w = 1 ярд и l = 1 ярд
= 1 × 1
= × 1 кв. ≈ 2,058 кв. ярда
Найдите максимальную площадь прямоугольника с фиксированным периметром? Имеет длину 120 см и ширину 40 см.
Решение:
Как известно,
Площадь (A) прямоугольника = w × l, здесь w = 40 см, l = 120 см
= 40 × 120
= 4800 кв. см.
Периметр (P) прямоугольника = 2 (ш + л),
= 2 × (120 + 40)
= 320 см.
Теперь возьмем квадрат с периметром (P), таким же, как у прямоугольника, т. е. 320 см.
Как известно,
а = Р/4, здесь Р = 320 см, а = каждая сторона квадрата
= 320/4
= 80 см
А, площадь (А) квадрата = а 2
= 80 × 80
= 6400 кв.см
Таким образом, если мы хотим получить максимальную площадь прямоугольника с фиксированным периметром, мы должны преобразовать его в квадрат.
Часто задаваемые вопросы
Q1. Как найти максимальную площадь прямоугольника с фиксированным периметром
Ответ. Чтобы получить максимальную площадь прямоугольника, нужно, чтобы все его стороны были равны. Другими словами, чтобы оптимизировать площадь прямоугольника с фиксированным периметром, нужно преобразовать его в квадрат.
Другими словами, чтобы оптимизировать площадь прямоугольника с фиксированным периметром, нужно преобразовать его в квадрат.
Площадь прямоугольника — ChiliMath
Площадь прямоугольника равна количеству пространства внутри прямоугольника. Мы можем найти площадь прямоугольника как , умножив длину прямоугольника на его ширину .
Но прежде чем мы углубимся в формулу, давайте быстро коснемся того, что такое площадь прямоугольника. Площадь, как известно, измеряется в квадратных единицах. Поэтому, когда мы говорим о площади, мы также имеем в виду количество квадратных единиц одинакового размера, которые охватывает прямоугольник, или количество квадратных единиц одинакового размера, необходимых для заполнения плоской поверхности прямоугольника или любой двумерной формы. Запишем площадь в единиц в квадрате или единиц 2 .
На приведенном выше рисунке мы можем разместить 24 квадратных элемента внутри прямоугольника.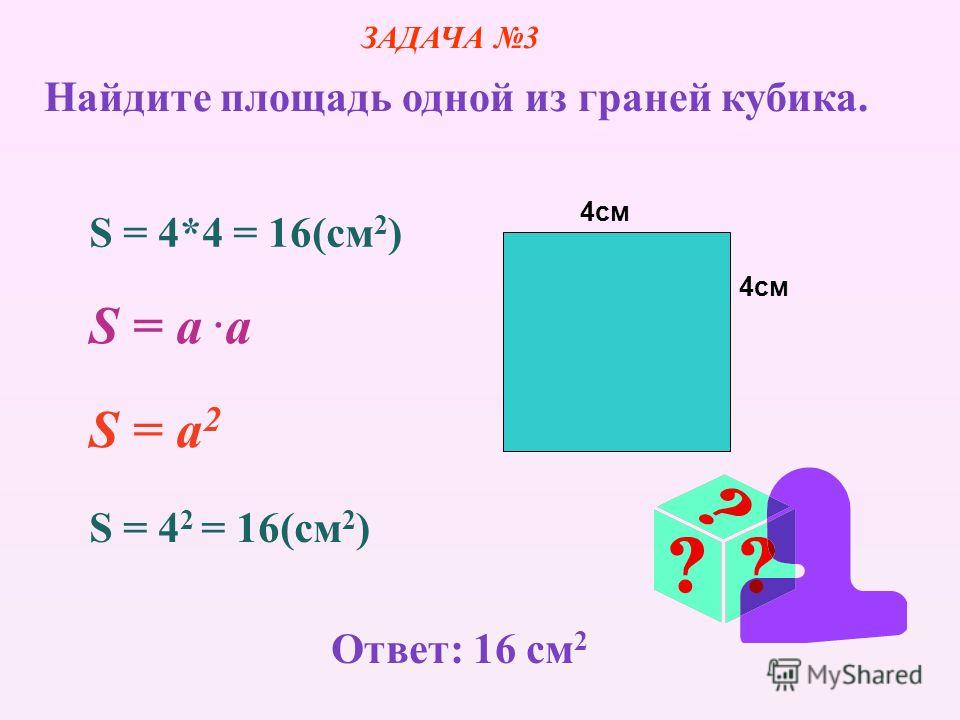 Таким образом, если площадь каждого единичного квадрата составляет 1 фут 2 , то мы можем сказать, что площадь прямоугольника составляет 24 квадратных фута 2 .
Таким образом, если площадь каждого единичного квадрата составляет 1 фут 2 , то мы можем сказать, что площадь прямоугольника составляет 24 квадратных фута 2 .
Допустим, у вас есть прямоугольная кухня, и вы хотите заменить напольную плитку. Разве не было бы полезно узнать, сколько квадратных плиток вам нужно, чтобы покрыть всю площадь вашей кухни, прежде чем вы начнете делать покупку? Однако попытки измерить пол по одной плитке за раз отнимают много времени и просто непрактичны. Вот где формула для нахождения площади становится очень полезной. 92}
Мы получаем ответ 24 фута 2 , что также означает, что 24 квадратных единицы, каждая площадью 1 фут 2 , могут поместиться внутри прямоугольника.
Примеры нахождения площади прямоугольника
Давайте теперь решим некоторые задачи, связанные с нахождением площади прямоугольника.
Пример 1 : Найдите площадь прямоугольника.
Давайте начнем с определения фрагментов информации, которые нам доступны. Здесь нам даны измерения длины прямоугольника (L) и ширины (W). 92}
Площадь прямоугольника 464 в 2 .
Пример 2 : Если площадь прямоугольника ниже 187 м 2 , какова мера его длины ?
В этой задаче вместо площади прямоугольника нас просят найти длину. Мы по-прежнему можем использовать формулу площади прямоугольника, чтобы определить длину прямоугольника.
\textbf{\textit{A = LW}}
187 = L(11) 92}
Так и есть! Следовательно, длина прямоугольника равна 17 метрам или 17 м .
Пример 3 : Мистер Джонсон решает огородить участок земли на своем ранчо. Земельный участок имеет площадь 414 м 2 . Какова ширина земельного участка, если его длина 23 метра ?
Чтобы лучше представить себе участок земли, который мистер Джонсон хочет огородить забором, давайте нарисуем его с помощью предоставленной нам информации.
Как и в нашем предыдущем примере, мы найдем измерение ширины прямоугольника, подставив заданное значение площади и длины в формулу площади прямоугольника, а затем найдем ширину (W).
A = LW
414 = 23W
\Large{{414} \over {23}} = {{23W} \over {23}}
18 = W или W = 18 \,m
И чему равно 23 м умножить на 18 м? Да, вы правильно поняли! Оба измерения, если их перемножить, дадут нам площадь 414 м 9 .0047 2 .
Итак, Земельный участок мистера Джонсона имеет ширину 18 метров или 18 метров .
Пример 4 : Элайджа хочет покрасить стену в своей спальне. Стена 18 футов в длину и 15 футов в ширину . Если он может покрасить 90 футов 2 стены одной банкой, сколько банок краски ему понадобится, чтобы покрасить всю стену?
Давайте снова начнем с рисования стены, используя размеры, данные нам в словесной задаче.
92} Теперь, когда мы знаем площадь прямоугольной стены, мы можем перейти к делению общей площади стены на 90 футов 2 , что является площадью, которую покрыла бы одна банка краски.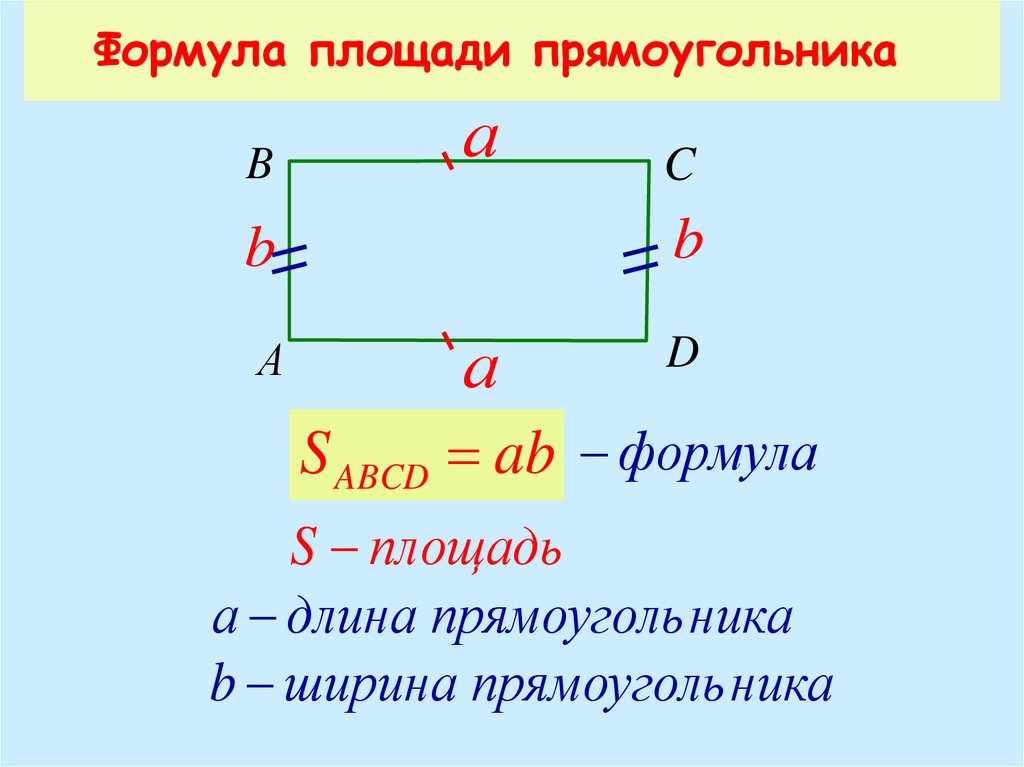 При этом мы сможем определить, сколько банок нужно Элайдже, чтобы покрасить всю стену.
При этом мы сможем определить, сколько банок нужно Элайдже, чтобы покрасить всю стену.
Элайдже нужны три (3) банки краски, чтобы покрасить стену в его спальне.
Пример 5 : Синди и ее друзья покрасили лист фанеры длиной 95 дюймов и шириной 48 дюймов для фестивального парада. Одна банка краски покрыта 1140 2 фанерой. Если одна банка краски стоит $15,25 , сколько денег Синди и ее друзья потратили, чтобы покрасить весь лист фанеры?
Эта задача со словами чем-то похожа на наш предыдущий пример. Здесь нам также даны измерения длины и ширины, которые помогут нам легко найти площадь. Но имейте в виду, что потребуются дополнительные шаги, прежде чем мы получим точный ответ, который ищем. Нам нужно сначала найти площадь, а затем сделать еще один расчет, прежде чем мы сможем узнать, какова общая стоимость покраски всего листа фанеры. 92}
Теперь, когда мы знаем площадь листа фанеры, давайте посмотрим, какие еще данные нам даются в задаче. В нем говорится, что одна (1) банка краски покрыла 1140 дюймов 2 фанеры.
В нем говорится, что одна (1) банка краски покрыла 1140 дюймов 2 фанеры.
Шаг 2 : Таким образом, наш следующий шаг должен состоять в том, чтобы разделить общую площадь фанеры на площадь, которую покрывает банка с краской. При этом мы сможем узнать, сколько банок краски ушло на покраску всего листа.
Отлично, мы на верном пути! Итак, Синди и ее друзья использовали четыре (4) банки с краской, чтобы покрасить весь лист фанеры. Сколько это стоило в общей сложности? Ну, мы знаем, что одна банка краски стоит 15,25 доллара, поэтому
Шаг 3 :
Стоимость одной банки краски x Использованные банки краски = \$ 15,25\,(4)
Общая стоимость краски = \$ 61,00
Синди и ее друзья целый лист фанеры для фестивального парада.
Пример 6 : Какова площадь составной фигуры?
Определение общей площади составной фигуры на первый взгляд может показаться пугающим. Однако составная фигура — это не что иное, как две фигуры или формы, объединенные или соединенные вместе. Поэтому их также иногда называют «комбинированными фигурами». Чтобы найти его общую площадь, нам просто нужно разделить две фигуры, просто нарисовав линию и вычислив площадь каждой из них. 92}
Однако составная фигура — это не что иное, как две фигуры или формы, объединенные или соединенные вместе. Поэтому их также иногда называют «комбинированными фигурами». Чтобы найти его общую площадь, нам просто нужно разделить две фигуры, просто нарисовав линию и вычислив площадь каждой из них. 92}
Общая площадь составной фигуры 520 см 2 .
Пример 7 : Площадь прямоугольного бассейна составляет 392 фута 2 . Если его длина вдвое больше его ширины , каковы размеры прямоугольного бассейна?
Эта задача совершенно уникальна, потому что нам дана площадь прямоугольного бассейна, но измерение его длины выражается математической фразой, а это значит, что ее нужно сначала перевести в алгебраическое выражение, прежде чем мы сможем начать находить размеры бассейна. 92}}
14 = W или W = 14 м
- Шаг 2 : Теперь, когда мы знаем ширину бассейна или значение переменной W, мы можем легко найти длину.







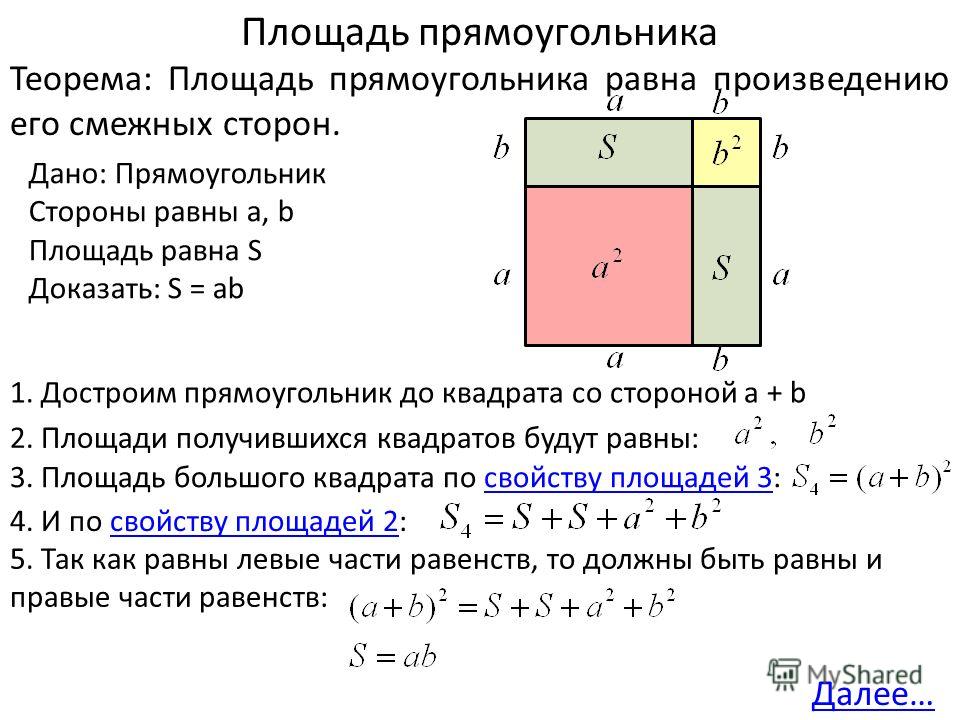

 ).
).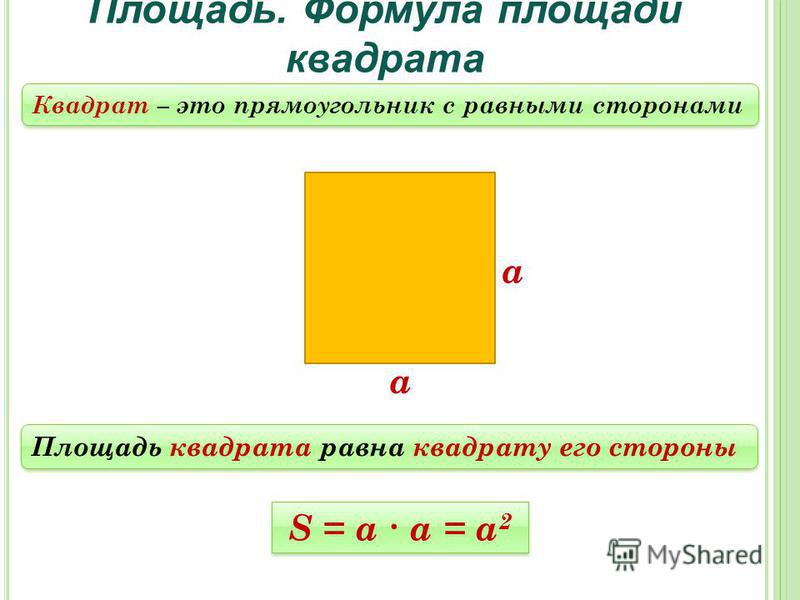

 Их площади».
Их площади».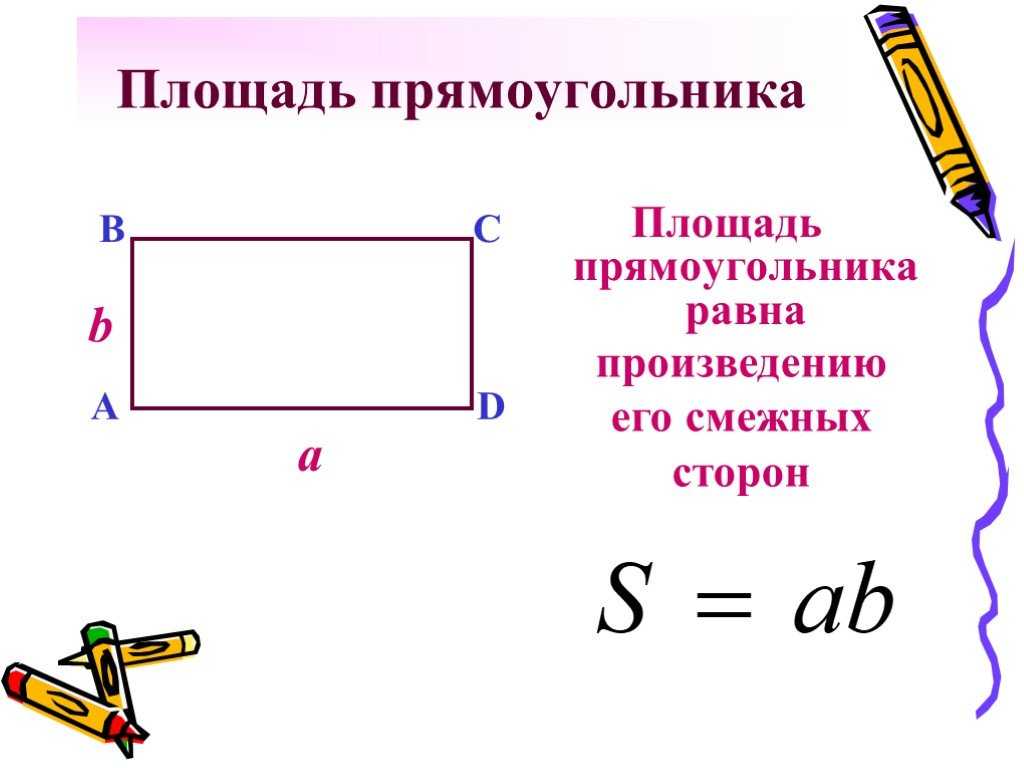 А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так: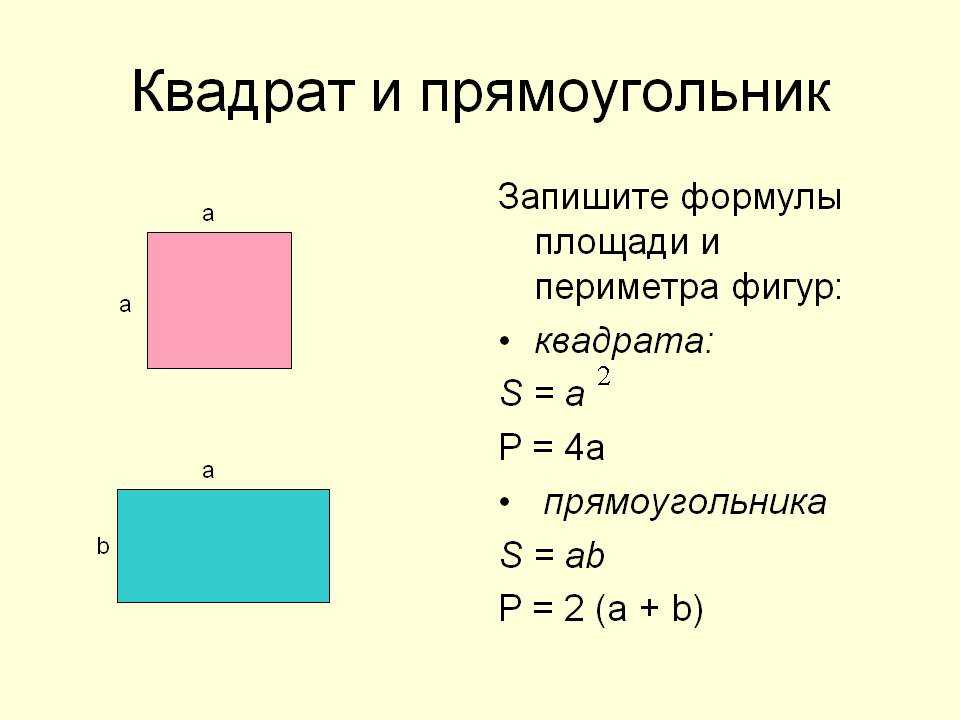

 Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма. Площади плоских фигур. Формулы площади.
Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма. Площади плоских фигур. Формулы площади. 315 м2
315 м2 3=429 мм2
3=429 мм2 62 мм2
62 мм2 =1/2*основание*высота
=1/2*основание*высота Правильно было бы сказать: «Количество квадратов в одном ряду равно количеству единиц длины на краю прямоугольника». Может быть, это звучит запутанно, но в математике слова означают вещи; вы должны объединить слова в утверждения, которые верны или, по крайней мере, не противоречат существующему различию.
Правильно было бы сказать: «Количество квадратов в одном ряду равно количеству единиц длины на краю прямоугольника». Может быть, это звучит запутанно, но в математике слова означают вещи; вы должны объединить слова в утверждения, которые верны или, по крайней мере, не противоречат существующему различию.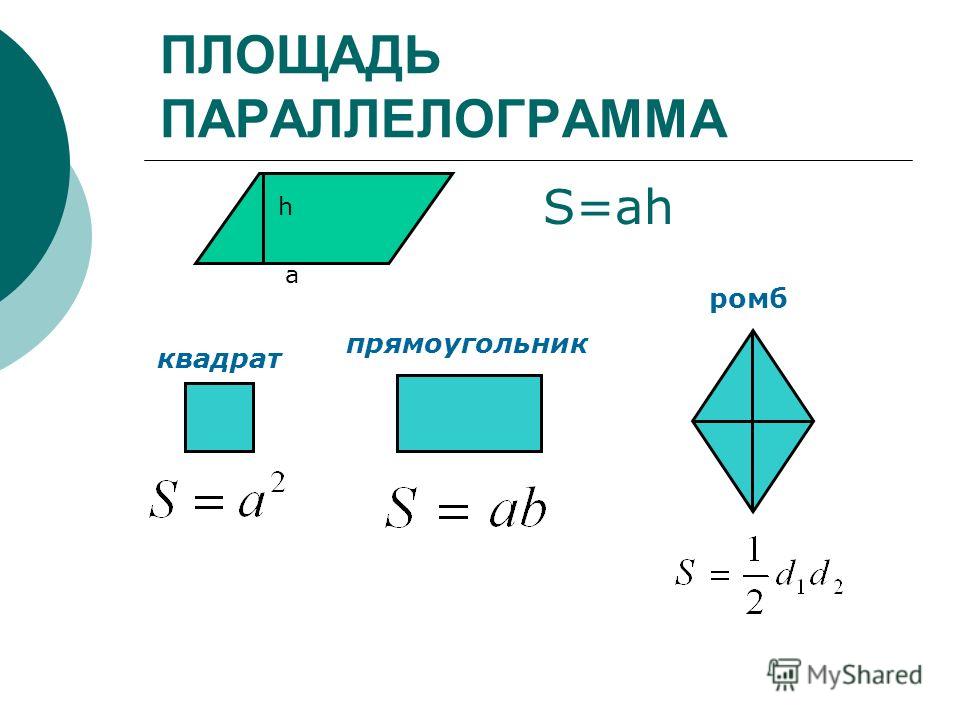 ..)
..)  Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол.
Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол. (или 2 кв. фута, или 2 фута 2 ).
(или 2 кв. фута, или 2 фута 2 ).