Определение свойства и признаки параллелограмма: Признаки параллелограмма — урок. Геометрия, 8 класс.

Параллелограмм. Признаки параллелограмма 8 класс онлайн-подготовка на Ростелеком Лицей

Тема 1: Четырехугольники

• Видео
• Тренажер
• Теория

Заметили ошибку?

Параллелограмм. Признаки параллелограмма.

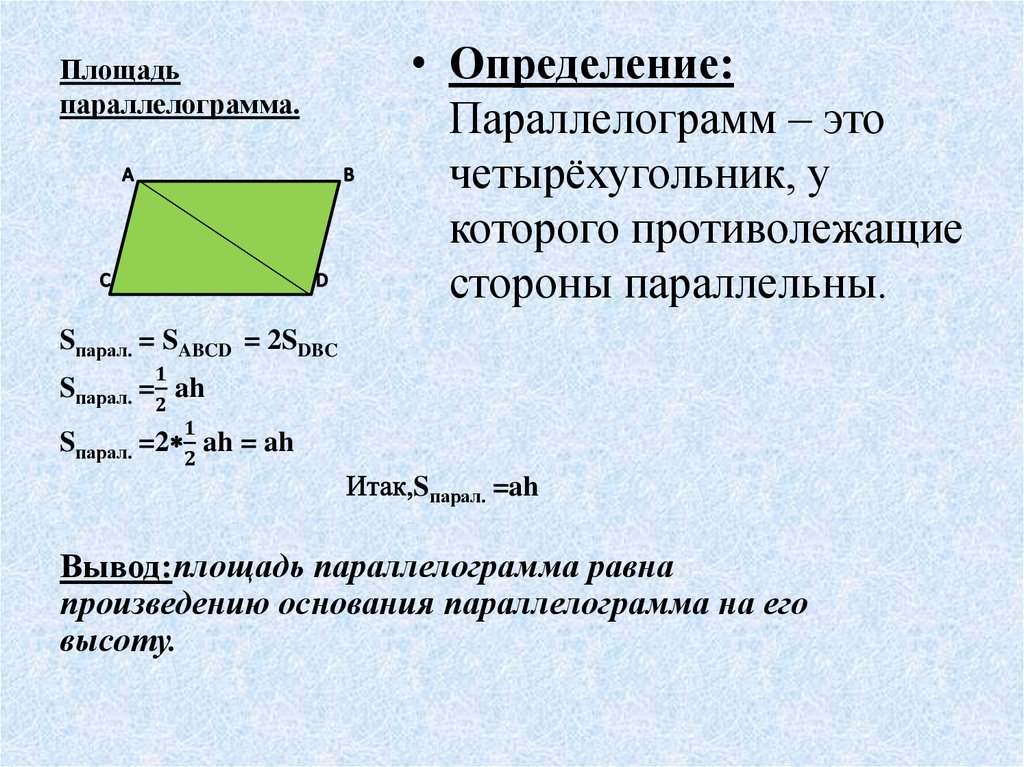
Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны.

 

 

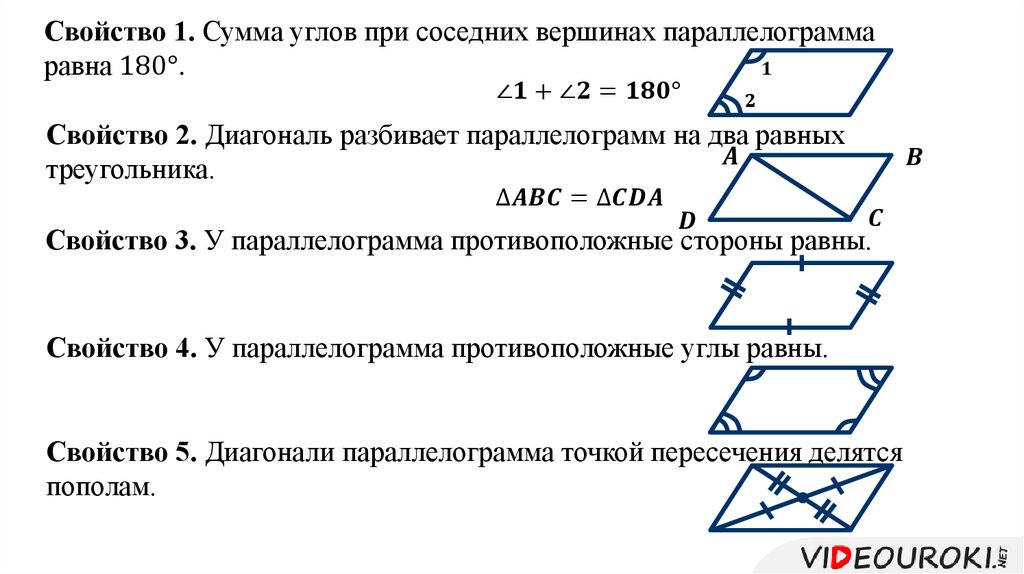
Основные свойства параллелограмма:

1. ∠ВАD = ∠BCD, ∠ABC = ∠CDA (противоположные углы равны).

2. AB = DC, BC = AD (противоположные стороны равны).

   Первые два свойства следуют из равенства треугольников ABC и ACD, а также треугольников ABD и BCD.

3. AO = OC, BO = OD (диагонали точкой пересечения делятся пополам).

   Третье свойство следует из равенства треугольников BOC и AOD.

4. ∠BAD + ∠ABC = 180° (сумма углов, прилежащих к одной стороне, равна 180°).

   Четвертое свойство следует из параллельности прямых BC и AD, а также AB и CD.

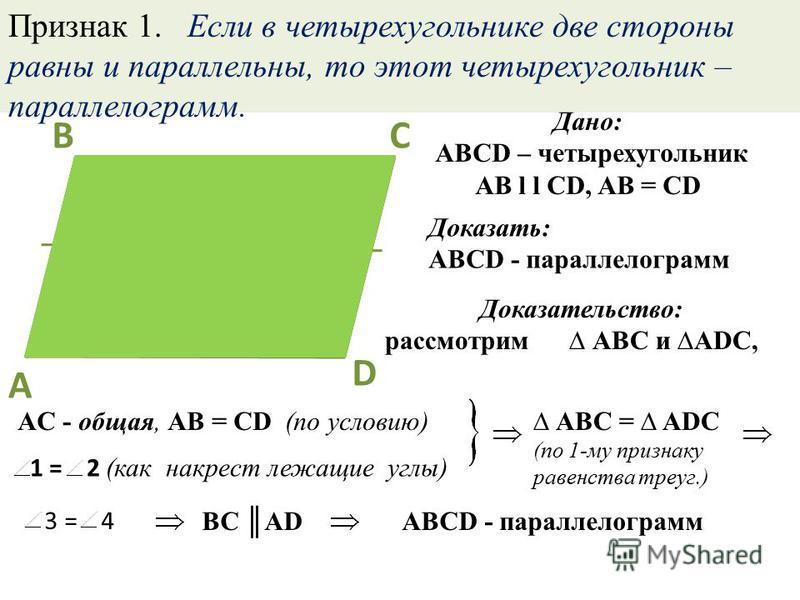
Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник – параллелограмм.

 

 

Дано: АВ||CD, AB = CD.

Доказать: ABCD – параллелограмм.

Доказательство: проведем в четырехугольнике диагональ, она разобьет его на два треугольника. Запишем, что мы знаем об этих треугольниках:

AB = CD по условию.

BD – диагональ параллелограмма, является общей стороной для треугольников АВD и BCD.

∠АВD = ∠ВDС как накрест лежащие.

Значит, треугольник АВD равен треугольнику BCD по первому признаку равенства треугольников.

Из равенства указанных треугольников следует, что ∠СВD = ∠АDB, а значит, АD||BC по признаку параллельности прямых при пересечении их секущей. Имеем, что AB||CD и AD||BC, значит АВСD – параллелограмм по определению.

Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны, то этот четырехугольник – параллелограмм.

 

 

Дано: АВ = СD, AD = BC.

Доказать: ABCD – параллелограмм.

Доказательство: проведем в четырехугольнике диагональ BD, она разобьет его на два треугольника. Запишем, что мы знаем об этих треугольниках:

АВ = СD по условию.

AD = BC по условию.

BD – общая сторона.

Значит, треугольник АВD равен треугольнику CBD по третьему признаку равенства треугольников.

Из равенства треугольников следует, что ∠СВD = ∠АDB, ∠АВD = ∠ВDС, а значит, АD||BC и AB||DC по признаку параллельности прямых при пересечении их секущей. Получаем AD||BC и AB||DC, значит АВСD – параллелограмм по определению.

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Параллелограмм. Свойства и признаки параллелограмма

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Параллелограмм. Свойства и признаки параллелограмма

Геометрия 8 класс
Параллелограмм. Свойства и
признаки параллелограмма

2. Задачи урока:

Повторить
Узнать
Научиться
• Определение и свойства
параллелограмма
• Понятие прямой и обратной
теоремы
• признаки параллелограмма
• применять признаки
параллелограмма при
решении задач

3. Четырехугольники

параллелограмм
трапеция
Нет параллельных сторон
2 пары параллельных
сторон
1 пара параллельных сторон
Определение
Четырехугольник, у которого
противоположные стороны попарно
параллельны, называется параллелограммом
А
C
AB CD, AC BD
B
D
Определение

6.

Свойство равнобедренного треугольникаВ равнобедренном
треугольнике углы при
основании равны.
Если в треугольнике углы
при основании равны, то
треугольникравнобедренный.

7. Свойство 1. В параллелограмме противоположные стороны равны и противоположные углы равны.

В
С
3
2
1
4
А
Дано: ABCD — параллелограмм
Доказать: 1) АВ = СD, BC = AD;
2) A = C, B = D
Доказательство: рассмотрим
∆ ABCи ∆ADC,
AC — общая,
1 = 2 и 3 = 4 (как
D накрест лежащие углы)
∆ АВС = ∆ ADC (по 2-му признаку
равенства треугольников)
Следовательно: АВ = СD, BC = AD;
1 + 4= 2 + 3 , т.е.
A = C, B = D.

8. Решите задачи

N
P
7 см
1
2
4 см
70
M
K
Найдите периметр параллелограмма MNPK
Найдите все углы параллелограмма MNPK

9. Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.

В
А
3
2
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
АВ = СD (противоположные
стороны параллелограмма,
O
АВ СD, ВD, AC – секущие
1= 2 и 3= 4 (как
С накрест лежащие углы)
∆ АОВ = ∆СОD (по 2-му признаку равенства
треугольников)
Следовательно: АО = ОС, ВО = ОD
1
D
Дано: АВСD — параллелограмм
ВD AC = O
Доказать: ВО = ОD, АО = ОС
4

10.

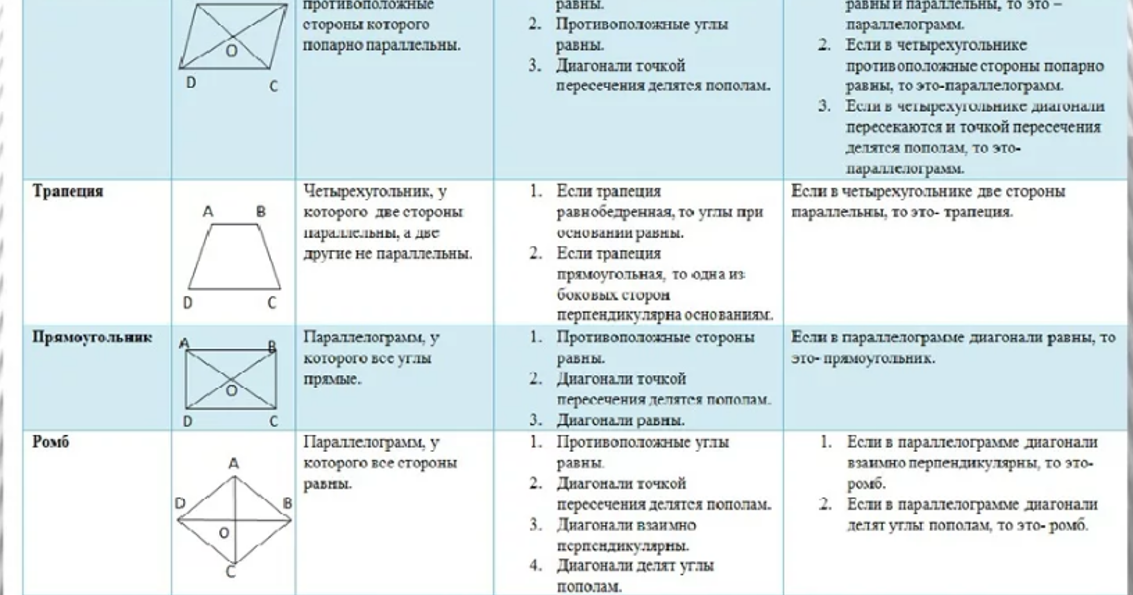Решите задачу. В параллелограмме ABCD: О – точка пересечения диагоналей, отрезок MK проходит через эту точку.M
B
C
1
O
2
A
K
Докажите, что ∆ OMB = ∆ OKD
D

11. Признак 1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

В
Признак 1. Если в четырехугольнике две стороны равны
и параллельны, то этот четырехугольник –
параллелограмм.
Дано:
С АВСD – четырехугольник
4
AB l l CD, AB = CD
2
1
3
A
D
Доказать:
АВСD — параллелограмм
Доказательство:
рассмотрим ∆ АВС и ∆ADC,
AC — общая, AB = CD (по условию)
1 = 2 (как накрест лежащие углы)
3 = 4
BC l l AD
= ∆ ADC
∆(поАВС
1-му признаку
равенства треуг.)
АВСD — параллелограмм

12. Решите задачу. В параллелограмме ABCD точки A₁, B₁, C₁, D₁ — середины отрезков OA, OB, OC, OD

B
C
B₁
A₁
A
O
C₁
D₁
D
Докажите, что четырехугольник A₁B₁C₁D₁ параллелограмм

13.

Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.Дано:
С АВСD – четырехугольник
В
2
1
AB = CD, BC = AD
Доказать:
АВСD — параллелограмм
Доказательство:
рассмотрим ∆ АВС и ∆ADC,
D
А
AC — общая, AB = CD, BC = AD (по условию)
1 = 2
∆ АВС = ∆ ADC
(по 3-му признаку
равенства треуг.)
AB l l CD и AB = CD АВСD — параллелограмм
(по 1-му признаку параллелогр.)

14. Решите задачу. В четырехугольнике ABCD  1=  2, ВС = АD. Докажите, что ABCD – параллелограмм.

Решите задачу. В четырехугольнике ABCD 1= 2,
ВС = АD. Докажите, что ABCD – параллелограмм.
B
C
1
2
A
D

15. Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник –

В
Признак 3. Если в четырехугольнике диагонали
пересекаются и точкой пересечения делятся пополам,
то этот четырехугольник – параллелограмм.
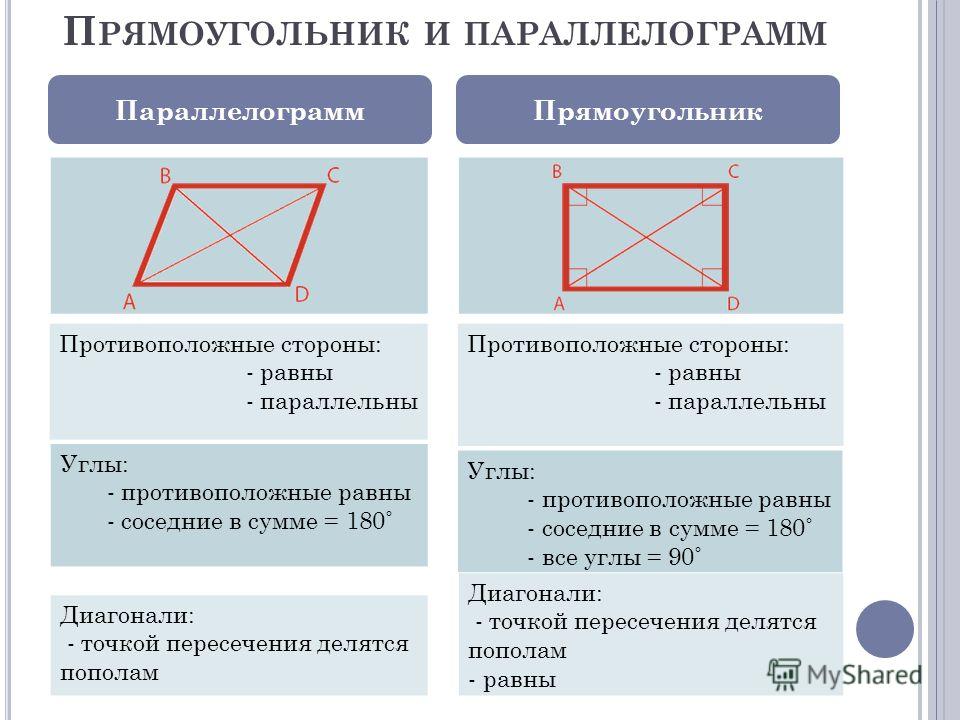
Дано: АВСD — четырехугольник
ВD AC = O, АО = ОС и ВО = ОD
С
3
O
1
Доказать:
ABCD — параллелограмм
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
2
4
А
D
АО = ОС и ВО = ОD (по условию)
1= 2 (как вертикальные)
(по 1-му признаку рав. треуг.)
∆ АОВ = ∆СОD
АВ = СD и 3 = 4
АВ l l СD( по призн. парал. прямых)
Итак, АВ = СD и АВ l l СD ABCD – параллелограмм
(по 1 призн. параллелогр.)

16. Решите задачу. В четырехугольнике ABCD  1=  2, ОА =ОС. Докажите, что ABCD – параллелограмм.

Решите задачу. В четырехугольнике ABCD 1= 2,
ОА =ОС. Докажите, что ABCD – параллелограмм.
B
C
1
2
A
D

17. Домашнее задание

Свойства, признаки выучить п. 42, 43
№ 372(б), № 376(в,г)

English     Русский Правила

Свойства параллелограммов — макеты

Авторы:

Марк Райан и

Обновлено: 26 марта 2016 г.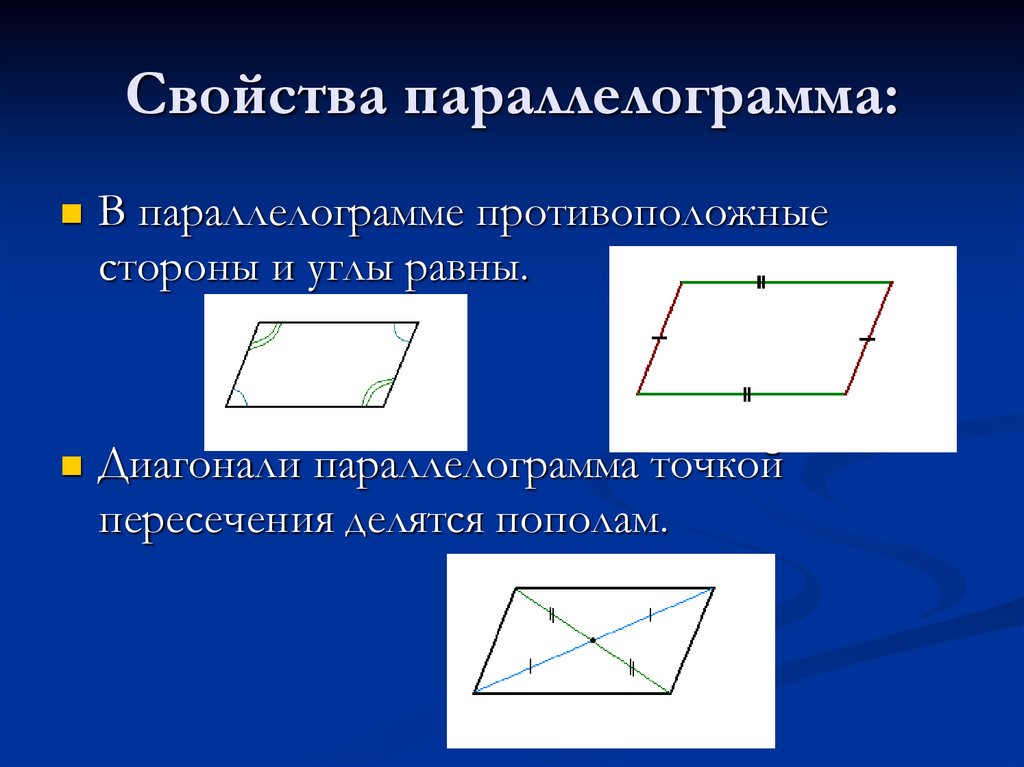 это правда об этом. Эти свойства касаются его сторон, углов и диагоналей.

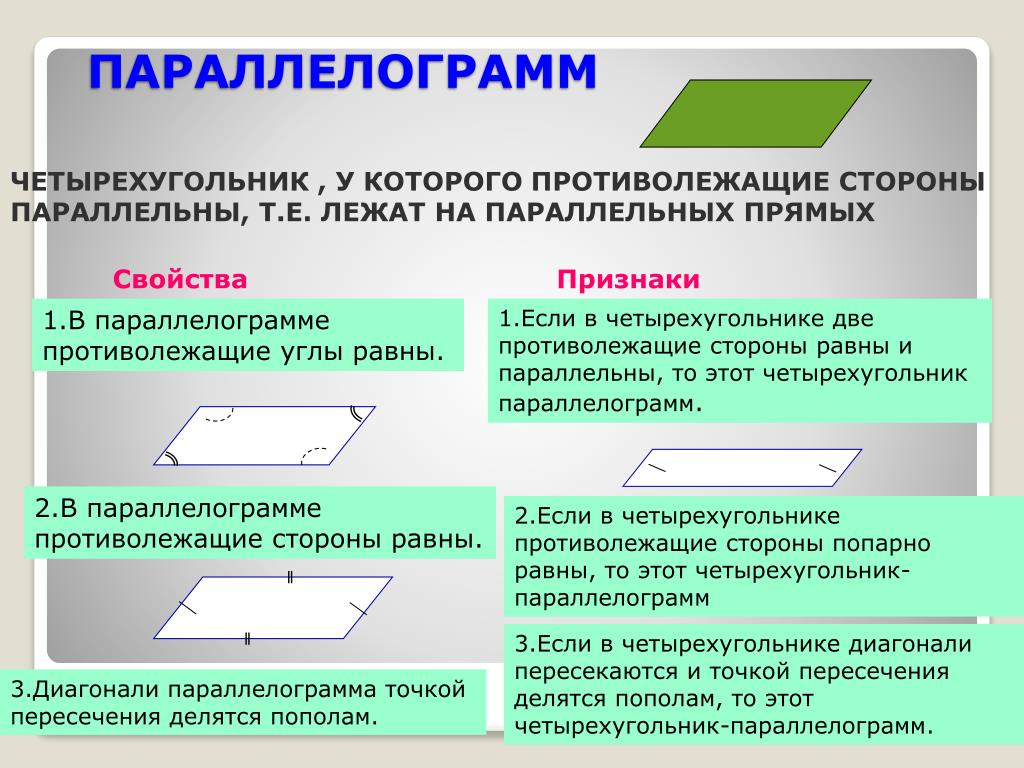
Параллелограмм обладает следующими свойствами:

• Противоположные стороны параллельны по определению.

• Противоположные стороны равны.

• Противоположные углы равны.

• Смежные углы являются дополнительными.

• Диагонали делят друг друга пополам.

Если вы просто посмотрите на параллелограмм, то вещи, которые кажутся истинными (а именно, вещи в этом списке), истинны и, следовательно, являются свойствами, а вещи, которые не выглядят так, как будто они истинны, свойствами не являются.

Если вы рисуете рисунок, который поможет вам разобраться в свойствах четырехугольника, сделайте свой набросок как можно более общим. Например, когда вы рисуете свой параллелограмм, убедитесь, что он не является почти ромбом (с четырьмя почти конгруэнтными сторонами) или почти прямоугольником (с четырьмя углами, близкими к прямым).

Если ваш набросок параллелограмма близок, скажем, к прямоугольнику, то что-то, что верно для прямоугольников, но не верно для всех параллелограммов (например, конгруэнтность диагоналей), может выглядеть правдой и, таким образом, привести к ошибочному выводу, что это свойство параллелограммов. Капиш?

Представьте, что вы не можете вспомнить свойства параллелограмма. Вы можете просто набросать один (как на рисунке выше) и просмотреть все, что может быть свойствами. (Обратите внимание, что этот параллелограмм не похож на прямоугольник или ромб.)

Следующие вопросы касаются сторон параллелограмма (см. предыдущий рисунок).

• Стороны кажутся конгруэнтными?

  Да, противоположные стороны выглядят конгруэнтными, и это свойство. Но соседние стороны не выглядят конгруэнтными, и это , а не свойство.

• Стороны кажутся параллельными?

  Да, противоположные стороны выглядят параллельными (и, конечно, вы знаете это свойство, если знаете определение параллелограмма).

Следующие вопросы исследуют углы параллелограмма (снова обратитесь к рисунку).

• Какие углы кажутся равными?

  Да, противоположные углы выглядят конгруэнтными, и это свойство. (Углы A и C кажутся равными примерно 45°, а углы B и D выглядят примерно как 135°).

• Какие углы кажутся дополнительными?

  Да, последовательные углы (например, углы

  A и B ) выглядят как дополнительные, и это свойство. (Используя параллельные линии
  Уголки

  A и B являются односторонними внутренними углами и поэтому являются дополнительными.)

• Какие углы кажутся прямыми?

  Очевидно, что нет, и это не свойство.

Следующие вопросы касаются утверждений о диагоналях параллелограмма

.

• Диагонали кажутся конгруэнтными?

  Даже не близко (на приведенном выше рисунке один примерно в два раза длиннее другого, что удивляет большинство людей) — не свойство.

• Диагонали кажутся перпендикулярными?

  Даже не близко; не собственность.

• Кажется, что диагонали делят друг друга пополам?

  Да, каждый как бы разрезает другой пополам, и это свойство.

• Кажется, что диагонали делят пополам углы, вершины которых пересекаются?

  №

  Не собственность.

Эту статью можно найти в категории:

• Геометрия,

Свойства параллелограммов — Уроки Византа

Самый широкий термин, который мы использовали для описания любой формы, — «многоугольник». Когда мы
обсуждали четырехугольники
в предыдущем разделе, мы, по сути, только что указали, что это многоугольники с четырьмя
вершинами и четырьмя сторонами. Тем не менее, в этом разделе мы подробнее рассмотрим
и обсудим особый тип четырехугольника: параллелограмм . Однако прежде чем мы это сделаем, давайте рассмотрим некоторые определения, которые помогут нам описать различные части четырехугольников.

Четырехсторонняя терминология

Поскольку весь этот раздел посвящен изучению четырехугольников, мы воспользуемся

некоторой терминологией, которая поможет нам описать определенные пары прямых, углов и
вершин четырехугольников. Давайте сейчас изучим эти термины.

Последовательные углы

Два угла, вершины которых являются концами одной и той же стороны, называются последовательными
углами .

?Q и ?R являются последовательными углами, поскольку Q и R являются конечными точками одной и той же стороны.

Противоположные углы

Два противоположных угла называются противоположными углами .

?Q и ?S — противоположные углы, потому что они не являются концами общей стороны.

Последовательные стороны

Две стороны четырехугольника, которые пересекаются, называются последовательными сторонами .

QR и RS являются последовательными сторонами, поскольку они пересекаются в точке R.

Противоположные стороны

Две непоследовательные стороны называются противоположными сторонами .

QR и TS являются противоположными сторонами четырехугольника, потому что они не пересекаются.

Теперь, когда мы понимаем, что означают эти термины, мы готовы начать наш урок
о параллелограммах.

Свойства параллелограммов: стороны и углы

Параллелограмм — это тип четырехугольника, у которого пары противоположных сторон параллельны.

Четырехугольник ABCD является параллелограммом, потому что AB ? DC и AD ? г. до н.э.

Хотя определяющими характеристиками параллелограмма являются пары параллельных
противоположных сторон, есть и другие способы определить, является ли четырехугольник
параллелограммом.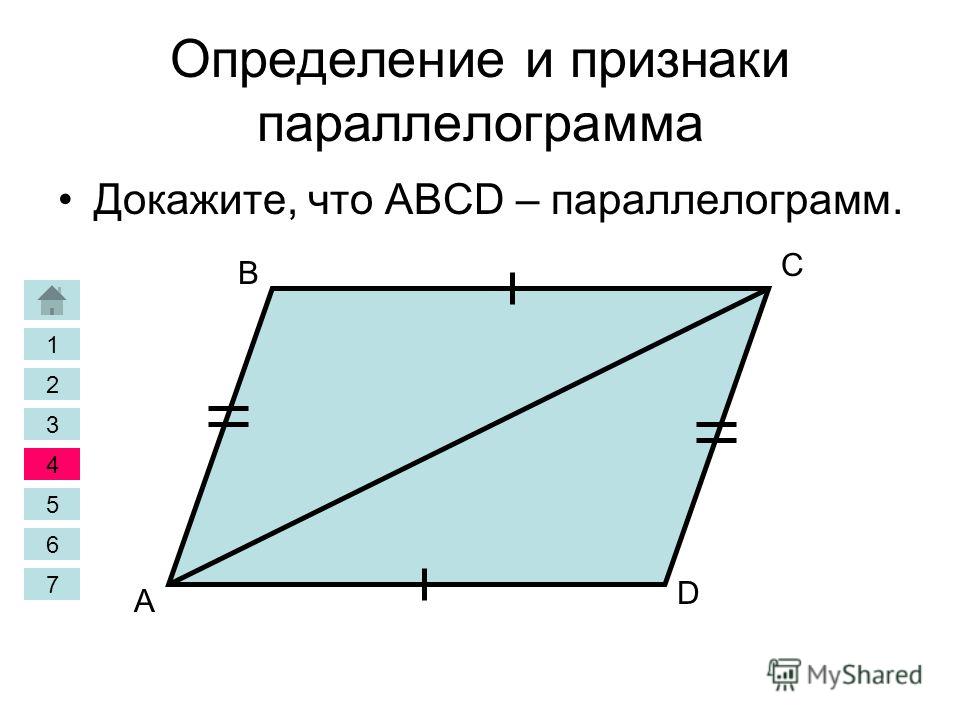

Мы будем использовать эти свойства в наших двухколоночных геометрических доказательствах
, чтобы получить полезную информацию.

Если четырехугольник является параллелограммом, то.

(1) его противоположные стороны конгруэнтны,

(2) его противоположные углы равны, и

(2) его последовательные углы являются дополнительными.

Еще одно важное свойство параллелограмма, на которое стоит обратить внимание, заключается в том, что если один угол
параллелограмма является прямым, то и все они прямые. Почему это свойство
верно? Давайте внимательно разберем эту ситуацию. Рассмотрим рисунок ниже.

Учитывая, что ?J — прямой угол, мы также можем определить, что ?L
— прямой угол, поскольку противоположные стороны параллелограмма конгруэнтны. Вместе
сумма этих углов равна 180 , потому что

Мы также знаем, что остальные углы должны быть равны, потому что они также являются противоположными углами
. К Сумма внутренних углов многоугольника Теорема , мы знаем, что все четырехугольники
имеют меры углов, которые в сумме дают 360 . С ? J и
? L Сумма до 180 , мы знаем, что сумма ? K
и ? K
и ? K
и ? ? K
и ? ? K
и ? ? K
и ? ? K
и ? :

С ?K и ?M конгруэнтны, мы можем определить их меры
с одной и той же переменной, x . Итак, у нас есть

Следовательно, мы знаем, что ?K и ?M являются прямыми углами.
Наша последняя иллюстрация показана ниже.

Давайте поработаем над парой упражнений, чтобы попрактиковаться в использовании свойств стороны и угла 9. 0143 параллелограммов.

Упражнение 1

Учитывая, что QRST является параллелограммом, найдите значения x и y
на диаграмме ниже.

Решение:

Изучив диаграмму, мы понимаем, что сначала будет проще решить для x
, потому что y используется в том же выражении, что и x 9.0054
(в ?R ), но x сам по себе находится в сегменте QR .
Поскольку противоположные стороны параллелограмма конгруэнтны, мы можем положить величины
равными друг другу и найти x:

Теперь, когда мы определили, что значение x равно 7 ,
, мы можем использовать это, чтобы подставить выражение, данное в 9.0147 ?R . Мы знаем, что
?R и ?T конгруэнтны, поэтому имеем

Подставляем х на 7 и получаем

Итак, мы определили, что x=7 и y=8 .

Упражнение 2

Учитывая, что EDYF является параллелограммом, определите значения x и y .

Решение:

Для решения этой задачи нам потребуется использовать тот факт, что последовательные углы
параллелограмма являются дополнительными. Единственный угол, который мы можем вычислить изначально
, — это угол в вершине Y , поскольку все, что для этого требуется, — это сложение
углов. У нас есть

Знание, что ? Y имеет меру 115 позволит нам решить
x и y С тех пор, как они обнаруживаются в Angles. . Давайте сначала найдем и . У нас есть

Осталось решить x сейчас. Мы будем использовать тот же метод
, который мы использовали при решении y :

Итак, у нас есть x=10 и y=13 .

Стороны и углы параллелограмма — не единственные их уникальные характеристики.
Давайте узнаем еще некоторые определяющие свойства параллелограммов.

Свойства параллелограммов: диагонали

Когда мы ссылаемся на диагоналей параллелограмма, мы говорим о прямых
, которые можно провести из вершин, не соединенных отрезками. Каждый параллелограмм
будет иметь только две диагонали. Иллюстрация диагоналей параллелограмма
показана ниже.

У нас есть два важных свойства, которые касаются диагоналей параллелограмма.

Если четырехугольник является параллелограммом, то.

(1) его диагонали делят друг друга пополам, и

(2) Каждая диагональ делит параллелограмм на два равных треугольника.

Отрезки AE и CE конгруэнтны друг другу, потому что диагонали пересекаются в точке
E, которая делит их пополам. Отрезки BE и DE также конгруэнтны.

Две диагонали делят параллелограмм на конгруэнтные треугольники.

Воспользуемся этими свойствами для решения следующих упражнений.

Упражнение 3

Зная, что ABCD — параллелограмм, найдите значение x .

Решение:

Мы знаем, что диагонали параллелограмма делят друг друга пополам. Это означает, что
точка E разбивает каждую биссектрису на два эквивалентных сегмента.
Таким образом, мы знаем, что DE и BE конгруэнтны, поэтому мы имеем

Итак, значение x равно 3 .

Упражнение 4

Зная, что FGHI является параллелограммом, найдите значения x и y .

Попробуем решить на x первый. Нам дано, что ?FHI
— прямой угол, поэтому его мера равна 90° . Мы можем сделать вывод, что ?HFG также является прямым углом по Теореме о альтернативных внутренних углах.

Если мы посмотрим на ?HIJ , мы заметим, что два его угла конгруэнтны,
так что это равнобедренный треугольник. Это означает, что ?HIJ имеет меру
из 9x с ?IJH имеет эту меру.

Мы можем использовать тот факт, что треугольник имеет прямой угол и что в нем два конгруэнтных угла
, чтобы найти x . Мы будем использовать теорему о сумме углов треугольника , угол
, чтобы показать, что сумма углов должна составлять 180° .

Теперь давайте найдем y .