Искусство решения проблем
Функция — это правило, которое отображает один набор значений в другой набор значений, присваивая каждому значению в первом наборе ровно одно значение во втором. Например, одна функция может отображать 1 в 1, 2 в 4, 3 в 9, 4 в 16 и так далее. У этой функции есть правило, согласно которому она берет входное значение и возводит его в квадрат, чтобы получить выходное значение. Эту функцию можно вызвать.
Содержание
- 1 Строгое определение
- 2 Вводные темы
- 2.1 Домен и диапазон
- 2.2 Реальные функции
- 2.3 Графики
- 2.4 Инверсия
- 3 промежуточные темы
- 3.1 Инъекции, сюръекции, биекции
- 3.1.1 Примеры
- 3.2 Монотонные функции
- 3.1 Инъекции, сюръекции, биекции
- 4 Дополнительные темы
- 4.1 Функции действительных переменных
- 4.2 Непрерывность
- 4.2.1 Эпсилон-Дельта Определение
- 4.
- 4.2.3 Свойства непрерывных функций
- 4.3 Дифференцируемость
- 4.4 Интегрируемость
- 4.5 Выпуклость
- 5 Обозначение
- 6 История функций
- 7 Проблемы
- 7.1 Введение
- 7.2 Промежуточный уровень
- 7.3 Олимпиада
- 7.4 Расширенный
- 8 См. также
Строгое определение
Позвольте , быть множествами и пусть быть подмножеством , которое обозначает декартово произведение и . (То есть это отношение ben и .) Мы говорим, что это функция от до (записано ) тогда и только тогда, когда
- Для каждого есть такое, что , и
- если и то . (Здесь упорядоченная пара.)
Вводные темы
Домен и диапазон
Домен функции — это набор входных значений для аргумента функции. диапазон функции — это набор выходных значений для этой функции.
Вещественные функции
Вещественная функция — это функция, диапазон значений которой находится в действительных числах. Обычно говорят о функциях, область определения которых также является подмножеством действительных чисел.
Графики
Функции часто отображаются в виде графиков. График соответствует функции только в том случае, если он выдерживает проверку вертикальной линией.
Инверсия
Инверсия функции — это функция, которая «отменяет» функцию. Например, рассмотрим функцию: . Функция обладает тем свойством, что . Поэтому называется (справа) обратной функцией . (Аналогично функция, которая удовлетворяет
Обычно правая и левая обратные функции совпадают в подходящей области, и в этом случае мы просто называем правую и левую обратную функцию .0003 обратная функция .) Часто обратная функция обозначается .Промежуточные темы
Инъекции, сюръекции, биекции
- Инъекция (или функция «один к одному») — это функция, которая всегда дает разные значения для разных аргументов в заданной области.
- По определению является инъективным, если , или эквивалентно,
- Из инъективности функции следует, что она имеет обратную. Кроме того, если и конечные множества, инъективность влечет .
- Сюръекция (или на функцию) отображает по крайней мере один элемент из своего домена на каждый элемент своего диапазона,
- Биекция (или взаимно однозначное соответствие, которое должно быть взаимно однозначным и на) — это функция, одновременно инъективная и сюръективная.
- Если инъекция из и инъекция из то существует биекция между и . Это теорема Шредера-Бернштейна.
- Если инъекция из и инъекция из то существует биекция между и .
Это теорема Шредера-Бернштейна.Примеры
- является инъективным и сюръективным (и, следовательно, биективным) из .
- является инъективным от .
- является сюръективным от .
- не является ни инъективным из (поскольку ), ни сюръективным из (поскольку не отображает никакого значения в , который является элементом ).
Монотонные функции
Функция называется монотонно возрастающей, если выполняется всякий раз, когда . Если неравенство выполняется строго , то функция называется строго возрастающей.
Аналогично, функция называется монотонно убывающей, если выполняется всякий раз, когда . Если неравенство выполняется строго , то функция называется строго убывающей.
Расширенные темы
Функции вещественных переменных
Вещественная функция — это функция, диапазон значений которой находится в действительных числах. Обычно говорят о функции, область определения которой также является подмножеством действительных чисел.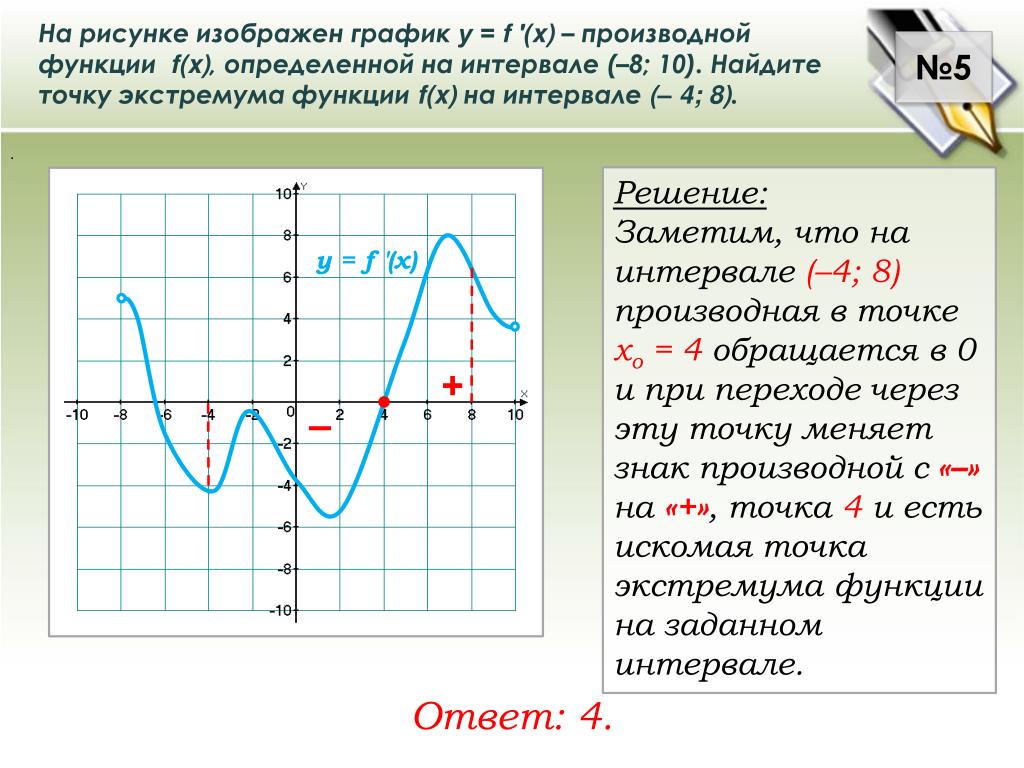
Непрерывность
Интуитивно непрерывная функция обладает тем свойством, что ее график можно нарисовать, не отрывая карандаша от бумаги. Чтобы строго определить непрерывные функции, необходима более сложная математика.
Эпсилон-Дельта Определение
Функция называется непрерывной в некоторой точке своей области определения, если для всех существует такое, что для любого из условия следует, что .
Определение Гейне
Предыдущее определение непрерывности at эквивалентно следующему: для каждой последовательности такой, что мы имеем, что .
Легко видеть, что функция непрерывна в изолированных точках и непрерывна в больших группах точек, если предел функции в этих точках равен значению функции.
Функция непрерывна на множестве, если она непрерывна в каждой точке множества.
Свойства непрерывных функций
- Сумма и произведение двух непрерывных функций являются непрерывными функциями.
- Композиция двух непрерывных функций является непрерывной функцией.
- В любом замкнутом интервале существуют действительные числа и такие, которые имеют максимальное значение при и минимальное значение при .
- Если функция непрерывна, то она имеет теорему о промежуточном значении. Обратное не всегда верно.
Дифференцируемость
Дифференцируемость — это условие гладкости функций. Для функций одной переменной дифференцируемость — это просто вопрос о том, существует ли производная. Для функций более чем одной переменной понятие дифференцируемости существенно усложняется. В случае функций как одной, так и многих переменных из дифференцируемости следует непрерывность.
Функция одной переменной дифференцируема в точке if . Производная является значением этого предела.
Интегрируемость
Все непрерывные функции интегрируемы, как и многие не непрерывные функции.
Выпуклость
Дважды дифференцируемая функция является вогнутой вверх (или выпуклой ) в интервале, если в интервале, и вогнутой вниз (или вогнутой ), если .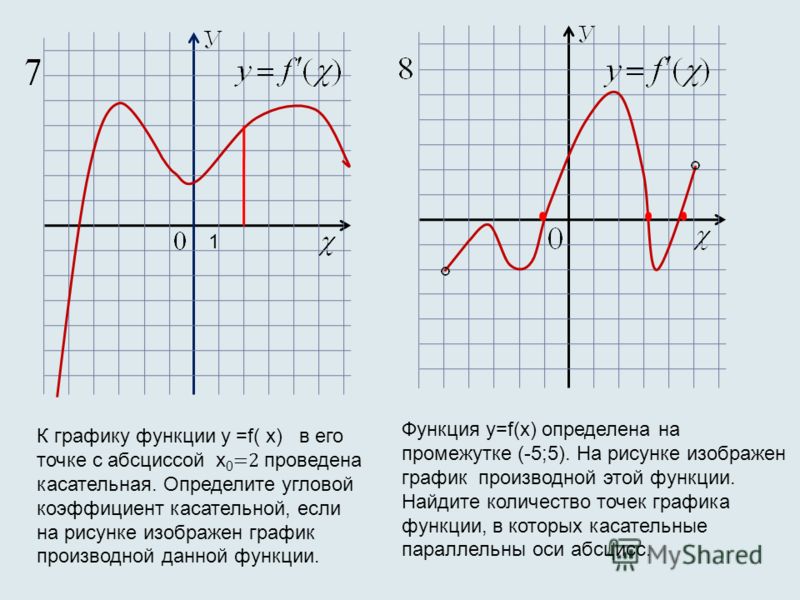
Точки перегиба при переключении вогнутости функции находятся в корнях .
Обозначение
Обычная нотация для определения: (где , конечно, является просто примером). Это говорит нам о том, что это функция, которая возводит в квадрат свой аргумент (свое входное значение). Обратите внимание, что это «правило» может быть сколь угодно сложным, и его не обязательно задавать простой формулой или описанием. Единственное требование состоит в том, что оно должно однозначно определяться . Ниже приведены примеры функций:
- для, в противном случае
История функций
без использования Explicitly, и Motion Of Pronceient с Antisient, и с Emply -Grycients, и Explicient Grycients. Сначала появляется функция, и в Emod grycient нет.
Строгое определение было сформулировано в 19 веке и является результатом работ некоторых известных математиков: А.Л. Коши, Леонарда Эйлера и Бернхарда Римана.
С развитием теории множеств появился новый раздел математики — математический анализ, в котором понятие функции играет центральную роль.
Текущая система обозначений принадлежит Леонарду Эйлеру.
Проблемы
Введение
- Определить . Что ?
(Источник)
Промежуточный
- Функция f определена на множестве целых чисел и удовлетворяет
Находить . (Источник)
Олимпиада
- Пусть функция со следующими свойствами:
- определена для каждого положительного целого числа ;
- — целое число;
- ;
- для всех и ;
- всякий раз, когда .
Докажите, что . (Источник)
Расширенный
- Опишите все многочлены такие, что для всех .
(
См. также
- Нечетная функция
- Четная функция
- Алгебра
- Функциональное уравнение
- Многочлены
- Исчисление
- Предел
- Производная
- Интеграл
Отношения, функции и обозначения функций
Отношения, функции и обозначения функций
Определение отношения, домена и диапазона
Примеры
-
Рассмотрим отношение, которое отправляет ученика к возрасту этого ученика.
Рассмотрим отношение, которое посылает студента к курсам, которые студент принимает.
Рассмотрим отношение, которое отправляет родителя к дочернему родителю.
Рассмотрим отношение, которое отправляет ключевое слово либо его совпадениям из Yahoo поисковой системе или к заявлению «Совпадений не найдено».
Каждое из этих отношений является примером. определение ниже формализует эту идею.
Определение: А связь является соответствием между двумя множествами (называемыми домен и диапазон |
Примечание.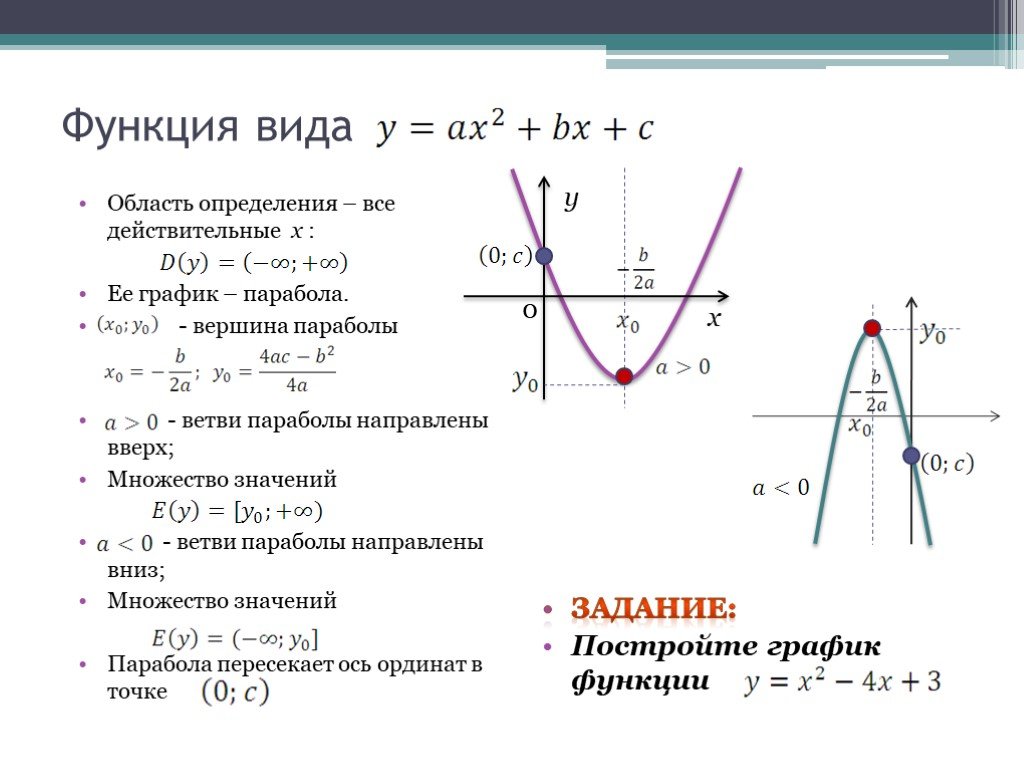
Чтобы определить отношение, необходимо три вещи.
должны быть указаны: набор диапазонов, набор доменов и правило
назначение.
Non-Example
Пусть домен будет набором всех студентов LTCC и диапазон будет набором всех предложений математических курсов в LTCC. Затем карта, которая берет студента и отправляет студента на курс математики он или она берет, это не отношения, так как есть студенты, которые не берут математические курсы.
Пример
(2,3), (2,4), (3,7) и (5,2)
определяет отношения с
Домен: {2,3,5}
Диапазон: {2,3,4,7}
Пример
Круг представляет собой график отношения с доменом, состоящим из значений x.
от левой стороны круга к правой стороне. Диапазон состоит из значений y
снизу вверх.
Функции
Функция — это особый тип отношения, в котором каждый вход имеет уникальный выход.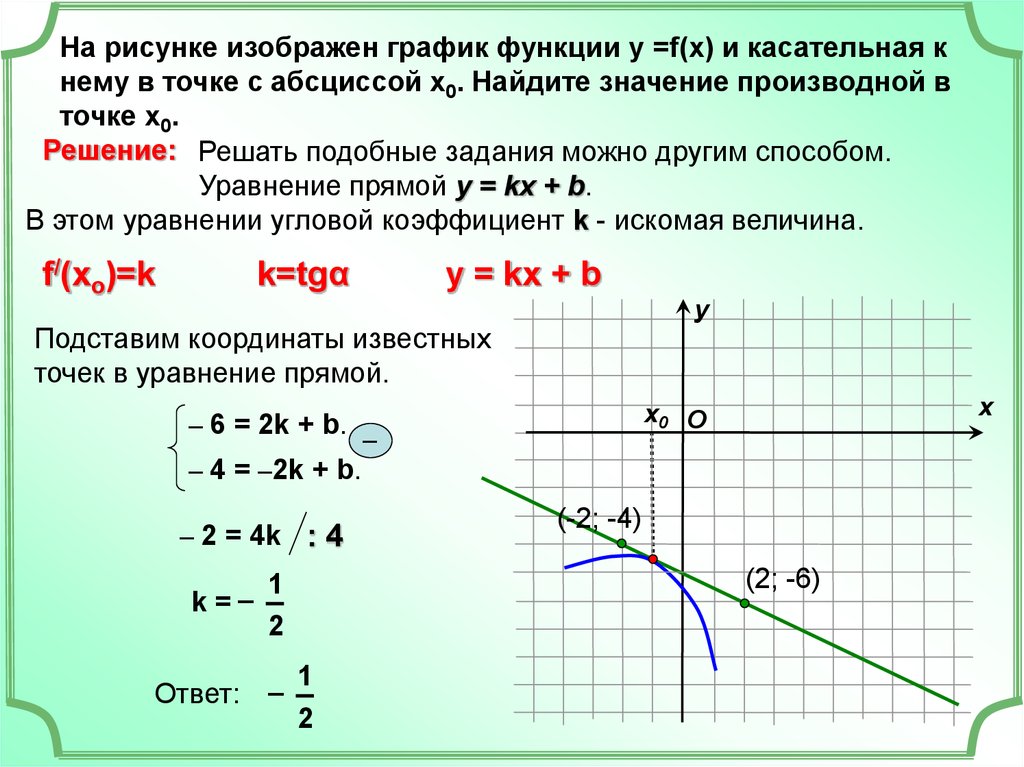
Определение: А функция есть соответствие между двумя множествами (называемыми домен и диапазон ) таким образом, что для каждого элемента домена существует назначается ровно один элемент диапазона.
|
Пример
(3,3), (4,3), (2,1), (6,5)
это функция с
Домен: {2,3,4,6}
Диапазон: {1,3,5}
Непример:
(2,1), (5,6), (2,3), (6,7)
не является функцией, так как 2 отправляется более чем
одно значение.
Тест вертикальной линии
Чтобы определить, является ли график графиком функции, мы используем следующий критерий.
Тест вертикальной линии Если любой вертикальная линия проходит через график более чем в одной точке, то
график не является графиком функции. |
В противном случае это график
функции. *
* Для более точного определения нажмите
здесь
Пример:
Круг не является графиком функции, как показано ниже.
Пример:
(Невертикальная) линия — это график функции.
Обозначение функции
Определение Пишем ф (Икс) означает функцию, вход которой Икс. |
Пример:
Если
f(x) = 2x — 3
затем
f(4) = 2(4) — 3 = 5
Мы можем думать о f как о функции, которая принимает входные данные, умножая их на 2 и вычитает 3.