Ошибка
Перейти к основному содержанию
Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)
Извините, не удалось найти запрашиваемый Вами файл
Подробнее об этой ошибке
Перейти на…
Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ).
Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления.
Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий.
Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа.
Формула Пуассона для редких событий. Теория вероятностей
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Пусть производится
независимых
испытаний, в каждом из которых вероятность появления события
равна
.
Для определения вероятности
появлений
события в этих испытаниях используют
формулу Бернулли. Если же
велико,
то пользуются локальной формулой Лапласа
или
интегральной формулой Лапласа. Однако эта формула непригодна,
если вероятность случайного события мала. В этих случаях (
велико,
мало)
прибегают к асимптотической формуле Пуассона.
Поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно раз. Сделаем важное допущение: произведение сохраняет постоянное значение, а именно . Это означает, что среднее число появления события в различных сериях испытаний, т.е. при различных значениях , остается неизменным.
Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:
Так как , то , следовательно:
Приняв во внимание, что имеет очень большое значение, вместо найдем
При этом будет найдено
лишь приближенное значение отыскиваемой вероятности:
хотя
и велико, но конечно, а при отыскании предела мы устремим
к
бесконечности.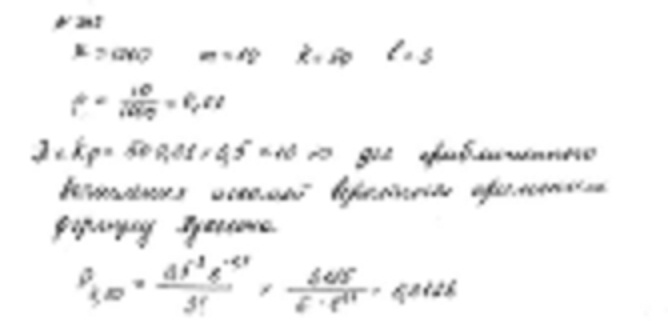
Затем, что поскольку произведение
сохраняет
постоянное значение, то при
вероятность
.
Таким образом:
Условие применимости формулы Пуассона
Если вероятность появления события в отдельном испытании достаточно близка к нулю, то даже при больших значениях количества испытаний вероятность, вычисляемая по локальной теореме Лапласа, оказывается недостаточно точной. В таких случаях используют формулу, выведенную Пуассоном.
Формула Пуассона
где
При подсчете пуассоновских вероятностей полезно пользоваться рекуррентной формулой:
Смежные темы решебника:
- Формула Бернулли
- Локальная теорема Муавра-Лапласа
- Интегральная теорема Муавра-Лапласа
- Следствия интегральной теоремы Муавра-Лапласа
Примеры решения задач
Пример 1
На базе
получено 10000 электроламп.
Вероятность того, что в пути лампа разобьется,
равна 0,0003. Найдите вероятность того, что среди полученных ламп будет пять
ламп разбито.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пусть событие – 5 ламп будет разбито
Воспользуемся формулой Пуассона:
В нашем случае:
Ответ: p=0.1008
Пример 2
Из 100
изделий, среди которых имеется 3 нестандартных, выбраны случайным образом 9
изделий для проверки их качества.
Определить вероятность того, что среди
выбранных 9 изделий окажется ровно 1 нестандартное изделие, используя
классическое определение вероятностей, формулу Бернулли, формулу Пуассона и
локальную теорему Лапласа.
Решение
Воспользуемся классическим определением вероятности:
-общее число возможных исходов испытания
-число испытаний, благоприятствующих интересующему нас событию
Искомая вероятность:
Воспользуемся формулой Бернулли:
В нашем случае:
Воспользуемся формулой Пуассона:
Искомая вероятность:
Воспользуемся локальной теоремой Лапласа:
В нашем случае:
Пример 3
Вероятность
«сбоя» в работе телефонной станции при каждом вызове равна 0.
05. Поступило 100
вызовов. Определить вероятность того, что произойдет не более 3 сбоев.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Воспользуемся формулой Пуассона:
В нашем случае:
Не более 3-х сбоев – это значит 0,1, 2 или 3 сбоя
Искомая вероятность:
Ответ:
Пример 4
Вероятность
потери банковской карты 0,03. Найти
вероятность того, что из 200 карт будут потеряны: а) 4 карты; б) хотя бы одна
карта; в) более 2 карт.
Решение
Число велико, вероятность мала, и рассматриваемые события независимы, поэтому имеет место формула Пуассона:
Найдем
а) Пусть событие — потеряно ровно 4 карты:
б) Пусть событие — потеряна хотя бы одна карта:
Противоположное событие — не потеряно ни одной карты
в) Пусть событие — потеряно более 2-х карт. Тогда противоположное событие — потеряно 0,1 или 2 карты.
Ответ: а) ; б) ; в) .
Задачи контрольных и самостоятельных работ
Задача 1
Книга в 500 страниц содержит 500 опечаток. Найти вероятность того, что на определенной странице будет не менее трех опечаток.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач.
Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Вероятность сбоя в работе банкомата при каждом запросе равна 0,0016. Банкомат обслуживает 2000 клиентов в неделю. Определить вероятность того, что при этом число сбоев не превзойдет 3.
Задача 3
Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель ровно 100 раз, если было произведено 2000 выстрелов.
Задача 4
Прядильщица обслуживает 800 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты 0,003. Найти вероятность того, что в течение одной минуты обрыв произойдет на трех веретенах.
Задача 5
Станок-автомат
штампует детали.
Вероятность того, что изготовленная деталь окажется
бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется
ровно четыре бракованных.
Задача 6
Владельцы кредитных карточек ценят их и теряют весьма редко. Пусть вероятность потерять в течение недели кредитную карточку для произвольного владельца равна 0,001. Всего банк выдал карточки 2000 клиентам. Найти вероятность того, что в предстоящую неделю будет потеряна: а) хотя бы одна; б) ровно одна кредитная карточка. Найти наивероятнейшее число карточек, теряемых за неделю.
Задача 7
Найти среднее число l бракованных изделий в партии изделий, если вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0,92. Предполагается, что число бракованных изделий в рассматриваемой партии распределено по закону Пуассона.
Задача 8
Телефонный
кабель состоит из 400 жил. С какой вероятностью этим кабелем можно подключить к
телефонной сети не менее 395 абонентов, если для подключения каждого из них
нужна одна жила, а вероятность того, что она повреждена – 0,0125.
Задача 9
Среди семян пшеницы 0,6% семян сорняков. Какова вероятность при случайном отборе 1000 семян обнаружить не менее трех семян сорняков?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 10
Учебник по теории вероятностей издан тиражом 10000 экз. Вероятность бракованного экземпляра . Найти вероятность того, что в тираже будет ровно 2 бракованных книги.
Задача 11
Среди семян риса 0,2% семян сорняков, т.е. число сорняков в рисе распределено по закону Пуассона. Найти вероятность того, что при случайном отборе 10000 семян будет обнаружено
1) не менее 2 семян — сорняков;
2) хотя
бы 1 семя -сорняк.
Задача 12
Вероятность того, что изделие не выдержит испытания равна 0.0004. Найдите вероятность того, что из 1000 наудачу взятых изделий не выдержит испытаний не менее двух изделий.
Задача 13
Станок состоит из 2000 независимо работающих узлов. Вероятность отказа одного узла в течение года равна 0,0005. Найти вероятность отказа в течение года: а) двух узлов; б) не более 5 узлов.
Задача 14
В среднем левши составляют 1%. Какова вероятность того, что среди 200 студентов найдется: а) ровно 4 левши; б) не менее чем 4 левши.
Задача 15
Среди 100 изготавливаемых микросхем в среднем одна бракованная. Найти вероятность того, что в партии из 1000 микросхем не более двух бракованных.
Задача 16
Телефонная станция обслуживает 600 абонентов. Вероятность звонка абонента в течение часа равна 0,05. Какова вероятность того, что в течение часа поступят звонки не более чем от трех абонентов?
Задача 17
Сборник
содержит 400 задач с ответами.
В каждом ответе вероятность ошибки 0,01. Какова
вероятность того, что в сборнике не более двух задач с ошибочными ответами?
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Из партии из 100$ изделий, из которых 20$ бракованных, выбирают ровно два изделия, по одному, без замены. Вычислите вероятность того, что второй выбранный элемент неисправен. (a) $\dfrac{2}{5}$ (b) $\dfrac{19}{100}$ (c) $\dfrac{1}{5}$ (d) Ничего из этого
Ответ
Подтверждено
247,5 тыс.+ просмотров
Подсказка: Событие выбора второго элемента как дефектного состоит из двух подсобытий. Один — когда первый выбранный товар хороший, а другой — когда первый выбранный товар неисправен. Используя правило умножения вероятности, мы можем определить вероятности этих двух событий. И итоговая вероятность будет равна сумме вероятностей двух событий.
Полное пошаговое решение:
Общее количество изделий в партии равно $100$, из которых $20$ бракованные. Это означает, что количество хороших предметов равно $80$.
По заданному вопросу ровно два товара выбраны без замены, причем второй товар бракованный. Термин «без замены» означает, что первый товар не возвращается в партию до выбора второго товара. Поскольку в партии есть два вида изделий, один бракованный, а другой исправный, будет два случая выбора двух изделий без замены из партии. Рассмотрим эти два случая по отдельности.
Случай I: первый товар исправен, а второй дефектен.
Вероятность выбора хорошего изделия из 80$ бракованных изделий из партии, содержащей всего 100$ изделий, равна $\dfrac{80}{100}$.
Теперь, когда был выбран один предмет, у нас осталось предметов на 99$. Но так как был выбран хороший товар, количество бракованных изделий остается прежним, то есть $20$. Таким образом, вероятность выбора второго изделия как бракованного равна $\dfrac{20}{99}$.
По правилу умножения вероятности вероятность возникновения этого случая равна
$\Rightarrow {{p}_{1}}=\dfrac{80}{100}\times \dfrac{20}{99}……..(i)$
Случай II: Оба элемента являются дефектными.
Вероятность выбора бракованного изделия из $20$ бракованных изделий из партии, состоящей всего из $100$ изделий, равна $\dfrac{20}{100}$.
Теперь, как и в предыдущем случае, общее количество предметов в партии становится $99$. Но так как дефектный товар уже выбран, то теперь у нас осталось дефектных товаров на 19$. Таким образом, вероятность выбора второго изделия как бракованного равна $\dfrac{19{99}$. Следовательно, по теореме умножения вероятность появления этого случая равна
$\Rightarrow {{p}_{2}}=\dfrac{20}{100}\times \dfrac{19}{99}.. ……(ii)$
Таким образом, общая вероятность выбора второго элемента как дефектного определяется как
$\begin{align}
& \Rightarrow p={{p}_{1}}+{ {p}_{2}} \\
& \Rightarrow p=\dfrac{80}{100}\times \dfrac{20}{99}+\dfrac{20}{100}\times \dfrac{19} {99} \\
& \Rightarrow p=\dfrac{20}{100\times 99}\left( 80+19 \right) \\
& \Rightarrow p=\dfrac{20}{100\times 99}\left( 99 \right) \\
& \Rightarrow p=\dfrac{20} {100} \\
& \Rightarrow p=\dfrac{1}{5} \\
\end{align}$
Следовательно, правильный ответ — вариант (c).
Примечание: Не думайте, что выбор второго товара как бракованного означает, что первый товар должен быть исправен. Первый выбор полностью независим, поэтому может произойти любое событие. Также, поскольку в этом случае предметы выбираются без замены, общее количество предметов не будет фиксированным.
Дата последнего обновления: 21 апреля 2023
•
Всего просмотров: 247,5 тыс.
•
Просмотров сегодня: 3,16 тыс.
6.2 Использование нормального распределения 9000 1
Введение Расчеты вероятностей
Введение
Заштрихованная область на следующем графике обозначает область слева от x . Эта область может представлять процент учащихся, набравших меньше определенного балла на выпускном экзамене. Эта область представлена вероятностью Р ( х х).
Обычные таблицы, компьютеры и калькуляторы используются для получения или вычисления вероятности P ( X x).
Рисунок 6.4
Площадь справа равна P ( X > x ) = 1 – P ( X x). Помните, P ( X x) = Площадь слева от вертикальной линии, проходящей через x . Р ( Х х) = 1 – Р ( X x) = Площадь справа от вертикальной линии через x . P ( X x) совпадает с P ( X ≤ x ) и P ( X > x ) то же, что и P ( X ≥ x ) для непрерывных раздач.
Предположим, что приведенный выше график представляет процент учащихся, набравших менее 75 баллов на выпускном экзамене, с вероятностью, равной 0,39.. Это также указывало бы на то, что процент учащихся, набравших более 75 баллов, был равен 1 минус 0,39 или 0,61.
Расчеты вероятностей
Вероятности рассчитываются с помощью технологии. Приведены необходимые инструкции для калькуляторов ТИ-83+ и ТИ-84.
ПРИМЕЧАНИЕ
Для расчета вероятности используйте таблицы вероятностей, представленные на рисунке G1, без использования технологии. Таблицы содержат инструкции по их использованию.
Вероятность представлена площадью под нормальной кривой. Чтобы найти вероятность, вычислите z -оценку и найдите z -оценку в таблице z в столбце z . Большинство таблиц z показывают площадь под нормальной кривой слева от z . Другие показывают среднее значение для области z .
Используемый метод будет указан в таблице.
Мы обсудим таблицу z , которая представляет площадь под кривой нормали слева от z . После того, как вы нашли счет z , найдите соответствующую область. Это будет область под нормальной кривой слева от z -значений. Эту площадь можно использовать для нахождения площади справа от z -оценки или путем вычитания из 1 или общей площади под нормальной кривой. Эти площади можно также использовать для определения площади между двумя z -значениями.
Пример 6.7
Если площадь слева равна 0,0228, то площадь справа равна 1 – 0,0228 = 0,9772.
Пример 6.8
Итоговые баллы за экзамен по статистике были нормально распределены со средним значением 63 и стандартным отклонением, равным пяти.
а. Найти вероятность того, что случайно выбранный студент наберет на экзамене более 65 баллов.
Раствор 6.8
а. Пусть X = балл на выпускном экзамене.
X ~ N (63, 5), где μ = 63 и σ = 5.
Нарисуйте график.
Вычислить z -значение:
z=x−μσ=65−635=25=.40z=x−μσ=65−635=25=.40
Таблица z показывает, что площадь слева от z равна 0,6554. Вычитание этой площади из 1 дает 0,3446.
Затем найдите P ( x > 65).
P(x > 65) = 0,3446P(x > 65) = 0,3446
Рис. 6.5
Вероятность того, что любой учащийся, выбранный случайным образом, наберет больше 65 баллов, равна 0,3446.
Историческая справка
Программа вероятностей TI вычисляет z -показателей, а затем вероятность на основе z -показателей. До появления технологий значение z искалось в стандартной таблице нормальных вероятностей, также известной как Z-таблица — математические расчеты, необходимые для определения вероятности, громоздки.
В этом примере использовалась стандартная нормальная таблица с областью слева от z -счетов. Вы вычисляете z -score и ищете область слева. Вероятность – это площадь справа.
б. Найти вероятность того, что случайно выбранный студент наберет меньше 85 баллов.
Решение 6.8
b. Нарисуйте график.
Затем найдите P ( x
Используя компьютер или калькулятор, найдите P ( x
normalcdf(0,85,63,5) = 1 (округляется до единицы)
Вероятность того, что один учащийся наберет меньше 85 баллов, приблизительно равна единице, или 100 процентам.
в. Найдите 90 -й процентиль, т. е. найти показатель k, у которого 90% баллов ниже k и 10% баллов больше k.
Раствор 6.8
c. Найдите 90 90 257 90 258 процентилей. Для каждой проблемы или части проблемы нарисуйте новый график. Нарисуйте ось x . Заштрихуйте область, соответствующую 90 90 257 90 258 процентилю. На этот раз мы ищем оценку, которая соответствует заданной области под кривой.
Пусть к = 90 -й -й процентиль. Переменная k расположена на оси x . P ( x k) это область слева от k . 90 й процентиль k разделяет экзаменационные баллы на те, которые равны или ниже k , и такие же или выше. Девяносто процентов результатов теста равны или ниже k , а 10 процентов равны или выше. Переменная k часто называют критическим значением.
Мы знаем среднее значение, стандартное отклонение и площадь под нормальной кривой. Нам нужно найти z -значение, которое соответствует площади 0,9, а затем заменить его средним значением и стандартным отклонением в нашу формулу z -значение. Таблица z показывает z-значение приблизительно 1,28 для площади под нормальной кривой слева от z (большая часть) приблизительно 0,9. Таким образом, мы можем написать следующее:
1,28=x−6351,28=x−63,5
Умножение каждой части уравнения на 5 дает
6,4=x−636,4=x−63
Добавление 63 к обеим частям уравнения дает
9000 2 69,4=х. 69,4=х.Таким образом, наш счет k равен 69,4.
к = 69,4 к = 69,4
Рисунок 6.6
90 90 257 й 90 258 процентиль равен 69,4. Это означает, что 90 процентов результатов тестов находятся на уровне 69,4 или ниже, а 10 процентов — на уровне или выше. Чтобы получить этот ответ на калькуляторе, выполните следующий шаг.
д. Найдите 70 -й -й процентиль, то есть найдите число 90 059 k , такое, что 70 % баллов меньше 90 059 k , а 30% баллов больше 90 059 k .
Раствор 6.8
d. Найдите 70 -й -й процентиль.
Нарисуйте новый график и подпишите его соответствующим образом. k = 65,6
70 -й -й процентиль равен 65,6. Это означает, что 70 % результатов тестов находятся на уровне 65,5 или ниже, а 30 % — на уровне или выше.
инвНорма(0,70,63,5) = 65,6
Пример 6.9
Персональный компьютер используется для офисной работы дома, исследований, общения, личных финансов, образования, развлечений, общения в социальных сетях и множества других целей. Предположим, что среднее количество часов, в течение которых домашний персональный компьютер используется для развлечения, составляет два часа в день. Предположим, что время развлечений распределено нормально, а стандартное отклонение времени составляет полчаса.
а. Найти вероятность того, что домашний персональный компьютер используется для развлечения от 1,8 до 2,75 часов в день.
Раствор 6.9
а. Пусть X = количество времени в часах, в течение которого домашний персональный компьютер используется для развлечения. X ~ N (2, 0,5), где μ = 2 и σ = 0,5.
Найти P (1,8 x
Сначала подсчитайте z -баллов для каждого x -значение.
z=1,8−20,5=−0,20,5=−0,40z=2,75−20,5=0,750,5=1,5z=1,8−20,5=−0,20,5=−0,40z=2,75−20,5=0,750,5=1,5
Теперь используйте таблицу Z , чтобы найти площадь под кривой нормали слева от каждой из этих z -оценок.
Площадь слева от z -оценка -0,40 равна 0,3446. Площадь слева от z с показателем 1,5 равна 0,9332.
Площадь между этими показателями будет разницей между двумя областями, или 0,9332−0,34460,9.332−0,3446, что равно 0,5886.
Рисунок 6.7
normalcdf(1,8,2,75,2,0,5) = 0,5886
Вероятность того, что домашний персональный компьютер используется для развлечения от 1,8 до 2,75 часов в день, равна 0,5886.
б. Найдите максимальное количество часов в день, в течение которых нижний квартиль домохозяйств использует персональный компьютер для развлечения.
Раствор 6.9
б. Чтобы найти максимальное количество часов в день, в течение которых нижний квартиль домохозяйств использует персональный компьютер для развлечения, найти 25 й процентиль, k , где P ( x k) = 0,25.
Рисунок 6.8
invNorm(0.25,2,0.5) = 1,66
Мы используем invNorm, потому что ищем значение k .
Максимальное количество часов в день, в течение которых нижний квартиль домохозяйств использует персональный компьютер для развлечения, составляет 1,66 часа.
Пример 6.10
В США пользователи смартфонов в возрасте от 13 до 55+ примерно следуют нормальному распределению с приблизительным средним значением и стандартным отклонением 36,9.лет и 13,9 лет соответственно.
а. Определите вероятность того, что случайному пользователю смартфона в возрасте от 13 до 55+ лет будет от 23 до 64,7 лет.
Раствор 6.10
а. normalcdf(23,64,7,36,9,13,9) = 0,8186
z -оценки рассчитываются как
z=23−36,913,9=−13,913,9=−1z=64,7−36,913,9=27. 813,9 =2z=23−36,913,9=−13,913,9=−1z=64,7−36,913,9=27,813,9=2
Таблица Z показывает область слева от z — оценка с абсолютным значением 1 должна быть 0,1587. Он показывает, что площадь слева от z — оценка 2 равна 0,9772. Разница в двух областях составляет 0,8185.
Это немного отличается от площади, указанной калькулятором, из-за округления.
б. Определите вероятность того, что случайно выбранному пользователю смартфона в возрасте от 13 до 55+ лет будет не более 50,8 лет.
Раствор 6.10
б. normalcdf(–10 99 ,50,8,36,9,13,9) = 0,8413
в. Найдите 80 90 257-й 90 258 процентиль этого распределения и интерпретируйте его в виде полного предложения.
Раствор 6.10
c.
- инвНорма(0,80,36,9,13,9) = 48,6
- 80 -й -й процентиль равен 48,6 годам.
- 80 процентов пользователей смартфонов в возрасте от 13 до 55 лет старше 48,6 лет.
Пример 6.11
В США пользователи смартфонов в возрасте от 13 до 55+ примерно следуют нормальному распределению с приблизительным средним значением и стандартным отклонением 36,9.лет и 13,9 лет соответственно. Используя эту информацию, ответьте на следующие вопросы, округлив ответы до одного знака после запятой:
a. Рассчитайте межквартильный размах ( IQR ).
Раствор 6.11
а.
- IQR = Q 3 – Q 1
- Рассчитать Q 3 = 75 th процентиль и Q 1 = 25 th процентиль.
- Вспомните, что мы можем использовать invNorm, чтобы найти k -значение. Мы можем использовать это, чтобы найти значения квартилей.
- invNorm(0,75,36,9,13,9) = Q 3 = 46,2754
- invNorm(0,25,36,9,13,9) = Q 1 = 27,5246
- IQR = Q 3 – Q 1 = 18,8
б. 40% людей в возрасте от 13 до 55+ относятся к какому возрасту?
Решение 6.11
б.
- Найдите k , где P ( x ≥ k ) = 0,40. По крайней мере преобразуется в больше или равно .
- 0,40 = площадь справа
- Площадь слева = 1 – 0,40 = 0,60.
- Площадь слева от k = 0,60
- инвНорма(0,60,36,9,13,9) = 40,4215
- к = 40,4.
- Сорок процентов людей в возрасте от 13 до 55+ составляют по крайней мере 40,4 года.
Пример 6.12
Фермер, выращивающий цитрусовые, который выращивает мандарины, обнаружил, что диаметры мандаринов, собранных на его ферме, подчиняются нормальному распределению со средним диаметром 5,85 см и стандартным отклонением 0,24 см.
а. Найти вероятность того, что случайно выбранный мандарин с этой фермы будет иметь диаметр больше 6,0 см. Нарисуйте график. 999,5,85,0,24) = 0,2660
Рисунок 6.9
б. Средние 20 процентов мандаринов с этой фермы имеют диаметр от ______ до ______.
Раствор 6.12
б.
- 1 – 0,20 = 0,80. За пределами средних 20 процентов будет 80 процентов значений.
- Каждый хвост графика нормального распределения имеет площадь 0,40.
