|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Например: стол, компьютер, лук / корова, ручка, кастрюля / село, знамя, перо — это существительные, классифицированные по родам. Определите основания классификаций:
Отношения объектов
Материалы к урокам 7 класса
Главная | Информатика и информационно-коммуникационные
технологии | Планирование уроков и материалы к урокам | 7 классы | Планирование уроков на учебный год | Отношения объектов.
Разновидности объектов и их классификация
Практическая работа №2
«Работаем с объектами файловой системы»
Отношения объектов
Человек может рассказать не только о свойствах объекта, но и об отношениях, в которых этот объект находится с другими объектами.
Например:
• «Иван — сын Андрея»;
• «Эверест выше Эльбруса»;
• «Винни Пух дружит с Пятачком»;
• «21 кратно 3»;
• «Кострома такой же старинный город, как и Москва»;
• «Текстовый процессор входит в состав программного обеспечения компьютера».
В каждом из приведенных предложений выделено имя отношения, которое обозначает характер связи между двумя объектами.
Отношения могут существовать не только между двумя объектами, но и между объектом и множеством объектов, например:
• «Дискета является носителем информации»;
• «Камчатка — это полуостров (является полуостровом)».
В каждом из этих предложений описано отношение «является элементом множества».
Отношение может связывать два множества объектов, например:
• «Колеса входят в состав автомобилей»;
Попарно связаны одним и тем же отношением могут быть несколько объектов. Соответствующее словесное описание может оказаться очень длинным, и тогда в нем трудно разобраться.
Пусть про населенные пункты А, Б, В, Г, Д и Е известно, что некоторые из них соединены железной дорогой: населенный пункт А соединен железной дорогой с населенными пунктами В, Г и Е, населенный пункт Е — с населенными пунктами В, Г и Д.
Для большей наглядности имеющиеся связи («соединен железной дорогой») можно изобразить линиями на схеме отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т.
д. (рис. 1.2).
Имена некоторых отношений изменяются, когда меняются местами имена объектов, например: «выше» — «ниже», «приходится отцом» — «приходится сыном». В этом случае направление отношения обозначают стрелкой на схеме отношений.
Так, на рис. 1.3 каждая стрелка направлена от отца к его сыну и поэтому отражает отношение «приходится отцом», а не «приходится сыном». Например: «Андрей приходится отцом Ивану».
Стрелки можно не использовать, если удается сформулировать и соблюсти правило взаимного расположения объектов на схеме. Например, если на рис. 1.3 имена детей всегда располагать ниже имени их отца, то можно обойтись без стрелок.
Такие отношения, как «приходится сыном», «соединен железной дорогой», «покупает», «лечит» и т. д., могут связывать только объекты некоторых видов. А в отношениях «входит в состав» и «является разновидностью»
Коротко о главном
В сообщении об объекте могут быть приведены не только свойства данного объекта, но и отношения, которые связывают его с другими объектами. Имя отношения обозначает характер этой связи. Отношения могут связывать не только два объекта, но и объект с множеством объектов или два множества.
Любые отношения между объектами можно наглядно описать с помощью схемы отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т. д. Связи между объектами могут быть изображены линиями или стрелками.
Вопросы и задания
1. Назовите имя отношения в каждом приведенном предложении. Какое имя можно будет дать отношению, если имена объектов в предложении поменять местами? В каких парах имя отношения при этом не изменится?
а) Колобок поет песню Лисе.
б) Конек-Горбунок помогает Ивану.
в) В Москве есть Манежная площадь.
г) Пилюлькин лечит Сиропчика.
д) Страшила путешествует вместе с Элл и.
2. Для каждой пары объектов укажите соответствующее отношение.
3. Какую связь отражает каждая схема отношений на рис. 1.4-1.8? Выберите правильный ответ из следующих вариантов:
• «является разновидностью»;
• «входит в состав»;
• «является условием (причиной)»;
• «предшествует».
Разновидности объектов и их классификация
Из двух множеств, связанных отношением «является разновидностью», одно является подмножеством другого. Например, множество попугаев является подмножеством множества птиц, множество натуральных чисел является подмножеством множества целых чисел.
Схему отношения «является разновидностью» мы будем называть схемой разновидностей (рис.
1.9). Такие схемы используются в учебниках, каталогах и энциклопедиях для описания самых разных объектов, например растений, животных, сложных предложений, транспортных средств и т. д.
На схеме разновидностей имя подмножества всегда располагается ниже имени включающего его множества.
Объекты подмножества обязательно обладают всеми признаками объектов множества (наследуют признаки множества) и кроме них имеют еще свой, дополнительный признак (или несколько признаков). Этим дополнительным признаком может быть свойство или действие. Например, любое домашнее животное нужно кормить, собаки, кроме того, лают и кусаются, а ездовые собаки, кроме того, еще и бегают в упряжке.
Важно понимать, что сами по себе объекты не делятся ни на какие множества и подмножества. Например, арбузу совершенно «безразлично», относят его к семейству тыквенных растений, к подмножеству полосатых или шарообразных объектов.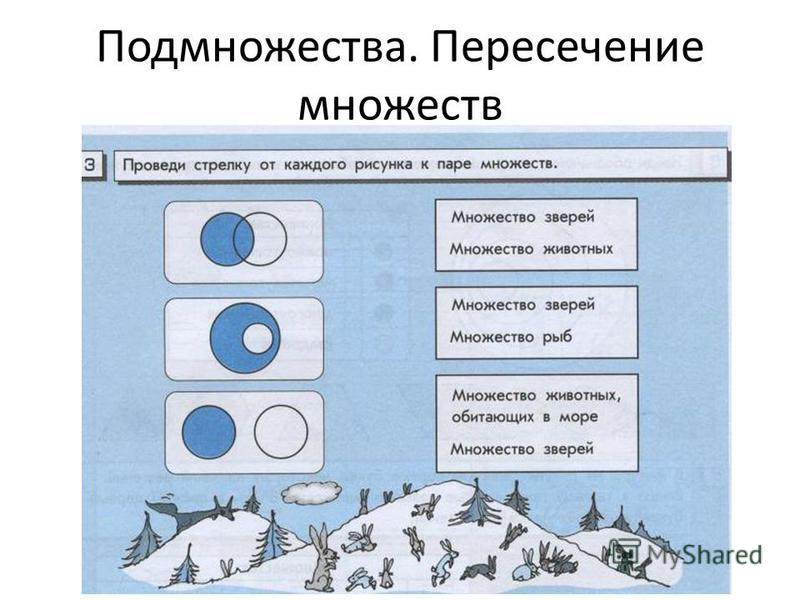
Подмножества объектов выделяет и обозначает человек, потому что ему так удобнее усваивать и передавать информацию. Дело в том, что человек одновременно может концентрировать свое внимание лишь на 5-9 объектах. Для упрощения работы с множеством объектов его делят на несколько частей; каждую из этих частей опять делят на части; те, в свою очередь, еще раз и т. д. Деление большого множества на подмножества происходит не стихийно, а по некоторым признакам его объектов.
Подмножество объектов, имеющих общие признаки, называется классом. Деление множества объектов на классы называется классификацией. Признаки, по которым один класс отличается от другого, называются основанием классификации.
Классификация называется естественной, если в качестве ее основания взяты существенные признаки объектов. Примером естественной классификации является классификация живых существ, предложенная Карлом Линнеем (1735 г.). В настоящее время ученые разделяют множество всех живых существ на пять основных царств: растения, грибы, животные, простейшие и прокариоты.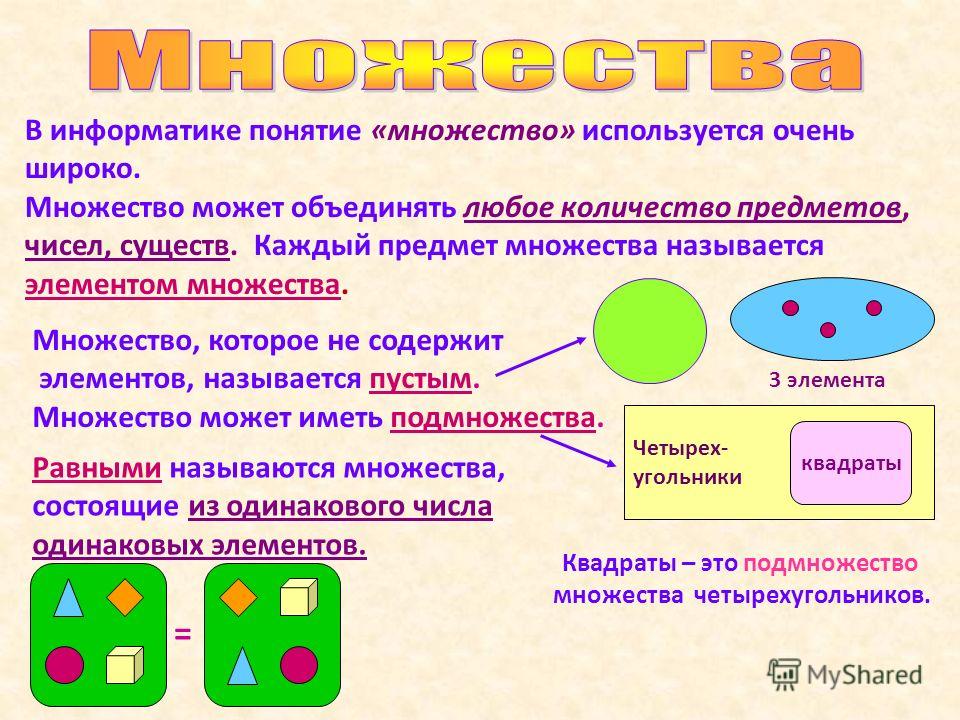
Каждое царство разделено на уровни — систематические единицы. Высший уровень называется типом. Каждый тип делится на классы, классы — на отряды, отряды — на семейства, семейства — на роды, а роды — на виды.
Классификация называется искусственной, если в качестве ее основания взяты несущественные признаки объектов. К искусственным классификациям относятся вспомогательные классификации (алфавитно-предметные указатели, именные каталоги в библиотеках). Пример искусственной классификации — деление множества звезд на небе на созвездия, проводившееся по признакам, которые к самим звездам не имели никакого отношения.
Можно предложить следующую классификацию объектов, с которыми взаимодействует пользователь в операционной системе Windows (рис. 1.10).
Коротко о главном
Схема разновидностей — это схема отношений «является разновидностью» между множествами и подмножествами объектов.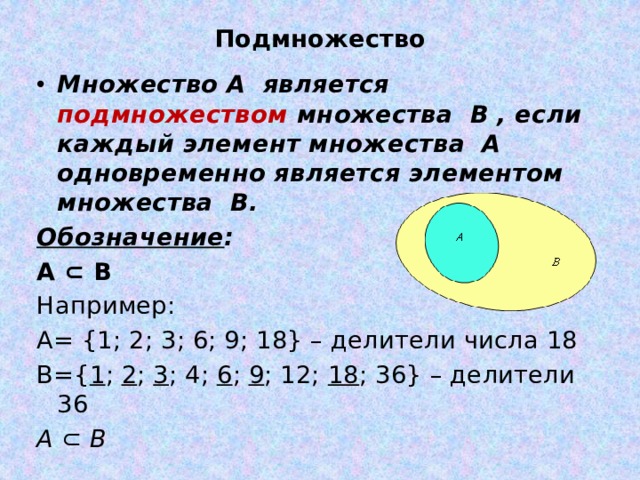
У объектов подмножества есть дополнительные признаки, кроме тех, которые есть у объектов множества, включающего данное подмножество.
Подмножество объектов, имеющих общие признаки, называется классом. Деление множества объектов на классы называется классификацией. Признаки, по которым один класс отличается от другого, называются осно¬ванием классификации.
Вопросы и задания
1. Для каждого из указанных подмножеств назовите множество, с которым оно связано отношением «является разновидностью» (назовите общее имя, отвечающее на вопрос «Что это такое?»):
а) местоимение;
б) запятая;
в) джойстик;
г) параллелограмм;
д) ратуша;
е) басня;
ж) капилляр.
2. Найдите в списке шесть пар множеств, между которыми существуют отношения «является разновидностью». Определите в каждой такой паре имя подмножества. Назовите для него хотя бы одно дополнительное свойство:
• книга;
• бензин;
• врач;
• молоко;
• строитель;
• учебник;
• жидкость;
• справочник;
• человек.
3. Выберите из списка имена девяти множеств, связанных отношениями «является разновидностью». Составьте схему разновидностей:
• яблоня;
• хвойное дерево;
• сосна;
• пихта;
• дерево;
• лиственное дерево;
• яблоко;
• ствол;
• фруктовое дерево;
• береза;
• дуб;
• лиственница;
• корень;
• желудь.
4. Используя предложенную классификацию паралле-лограммов, опишите свойства квадрата, наследующего их сразу у двух предков — прямоугольника и ромба. Какими дополнительными свойствами обладает квадрат:
а) по отношению к прямоугольнику;
б) по отношению к ромбу?
5. В каждом пункте перечислены объекты, сгруппированные по классам. Например: стол, компьютер, лук / корова, ручка, кастрюля / село, знамя, перо — это существительные, классифицированные по родам. Определите основания классификаций:
а) ель, сосна, кедр, пихта / береза, осина, липа, тополь;
б) картофель, лук, огурцы, помидоры / яблоки, апельсины, груши, мандарины;
в) рожь, тишь, ложь, рысь / пшеница, тишина, истина, кошка;
г) рубашка, пиджак, платье, сарафан / пальто, шуба, плащ, штормовка;
д) волк, медведь, лиса, лось / корова, собака, кошка, лошадь.
6. Предложите свою классификацию компьютерных объектов «файл» и «документ».
Практическая работа №2
«Работаем с объектами файловой системы»
1. Откройте окно Мой компьютер. Просмотрите файлы и папки, расположенные на диске С:.
2. Воспользуйтесь кнопками Вперед и Назад на панели инструментов Обычные кнопки для перемещения между ранее просмотренными объектами.
3. Выберите в меню Вид команды: Эскизы страниц, Плитка, Значки, Таблица. Проследите за изменениями в отображении папок и файлов. Найдите на панели инструментов Обычные кнопки кнопку, обеспечивающую быстрое изменение вида содержимого папок.
4. С помощью кнопки Папки отобразите в левой части окна панель Обозревателя Папки.
С ее помощью еще раз просмотрите файлы и папки, расположенные на диске С:. Проследите за изменениями, происходящими в правой части окна.
5. С помощью кнопки Поиск найдите собственную папку — папку, в которой хранятся ваши работы. Для этого в окне Помощника по поиску щелкните на ссылке Файлы и папки. В соответствующих полях укажите имя папки и область поиска.
6. Откройте собственную папку. В ней должны быть вложенные папки Документы, Заготовки_6, Заготовки_7, Презентации и Рисунки. Просмотрите содержимое этих папок.
7. Папка Заготовки_6 содержит файлы, которыми вы пользовались при выполнении работ компьютерного практикума в пошлом году. Так как эта папка вам больше не нужна, удалите ее (например, командой контекстного меню).
8. Папки Документы, Презентации и Рисунки содержат ваши прошлогодние работы. Их хотелось бы сохранить.
Создайте в собственной папке папку Архив. Для этого переведите указатель мыши в чистую область окна собственной папки и щелкните правой кнопкой мыши (вызов контекстного меню). Выполните команду [Создать-Папку].
Поочередно переместите папки Документы, Презентации и Рисунки в папку Архив. Для этого:
1) выделите папку Документы и, удерживая нажатой левую кнопку мыши, перетащите папку Документы в нанку Архив;
2) откройте контекстное меню панки Презентации, выполните команду Вырезать. Откройте папку Архив и с помощью контекстного меню вставьте в нее папку Презентации;
3) вырежьте папку Рисунки и вставьте ее в папку Архив с помощью команд строки меню.
9. С помощью контекстного меню переименуйте папку Заготовки_7 в Заготовки.
10. Убедитесь, что ваша папка имеет структуру, аналогичную приведенной ниже:
11.
Откройте файл Описание.doc из папки Заготовки.
Внесите в соответствующие ячейки таблицы информацию о свойствах трех своих файлов — текстового документа, рисунка и презентации.
12. Сохраните файл в собственной папке под именем Описание1. Вспомните как можно больше способов завершения работы с программой. Завершите работу с программой.
Теперь мы умеем
- выполнять операции с объектами файловой системы — папками и файлами; - определять свойства объектов файловой системы.
Принцип Pigeonhole (подмножества)
Покажите, что если выбрано более половины подмножеств множества из n элементов, то некоторые два из выбранных подмножеств обладают тем свойством, что одно является подмножеством другого.
Раствор
|Контакты| |Главная страница| |Содержание| |Вверх|
Copyright © 1996-2018 Александр Богомольный
Покажите, что если выбрано более половины подмножеств n-элементного множества, то некоторые два из выбранных подмножеств обладают тем свойством, что одно является подмножеством другого.
Я приведу два доказательства этого факта.
(В дальнейшем |X| обозначает количество элементов в конечном множестве X, а 2 X обозначает множество всех подмножеств множества X.)
Выбор произвольного элемента x из множества A с n элементами ( n-множество ) и рассмотрим два семейства подмножеств. Семейство N состоит из всех подмножеств A , не содержащих x; семейство Y включает оставшиеся подмножества (каждое из них содержит x). Имеется ровно 2 n-1 подмножества как в N , так и в Y .
Начнем с семейства B , которое содержит более половины всех подмножеств A . По принципу Pigeonhole одно из семейств N или Y содержит не менее половины подмножеств из B . Если это N , мы можем продолжить прямо. Если это Y , мы сначала отметим, что все задействованные подмножества содержат выбранное число x. Если мы отбросим его из всех подмножеств, мы придем к точно такой же ситуации, как и в первом случае.
Подведем итоги.
Нам задано множество A new (это прежнее A с удаленным элементом x), для которого множество N (или Y с удаленным x) служит множеством всех подмножеств . Теперь мы знаем, что | Б | > |2 А |/2 = | A новый |. Но | Б | = | Н ∩ В | + | Y B |. Следовательно, либо | Н В | > | A новый |/2 или | Y B | > | A новый |/2.
В зависимости от того, какое из неравенств выполняется, пусть B new обозначает либо N ∩ B , либо Y B с удаленным x. В любом случае | B новый | > |2 A новый |/2. Это в точности наша исходная задача, за исключением того, что набор A теперь содержит на 1 элемент меньше, чем раньше.
Теперь мы можем перейти либо к по индукции (все, что нужно, это проверить некоторый минимальный набор из нескольких элементов), либо просто регрессировать назад к набору с небольшим числом элементов, что составляет одно и то же.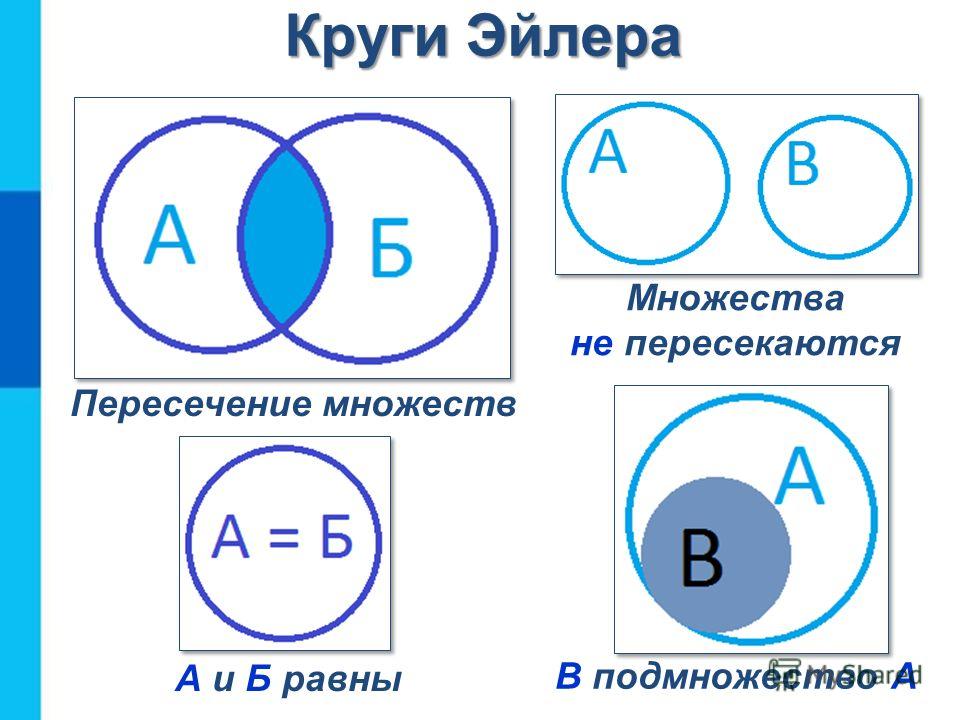
Итак, рассмотрим множество с небольшим количеством элементов. Сколько мы должны взять? Возьмем n = 1. Множество всех подмножеств {1} состоит из двух множеств — пустого множества {} и {1}. Чтобы содержать более половины всех подмножеств , B обязательно будет содержать их оба. В этом случае он явно содержит два набора, из которых один {} является подмножеством другого {1}.
Следующее доказательство принадлежит Уильяму А. Маквортеру-младшему. п=0). Для каждого из 2 n-1 подмножеств A из A , не содержащих x, сформируйте пара {A, A∪{x}}. Эти пары образуют раздел подмножеств А . Теперь, учитывая более половины его подмножеств, некоторые два должны принадлежать одной и той же паре, и поэтому обладают свойством, что одно является подмножеством другого.
Примечание
Результат, полученный с помощью принципа Pigeonhole, можно значительно усилить: для обеспечения
что среди выбранных подмножеств одно содержит другое, не нужно выбирать более половины подмножеств.
Меньше будет
достаточно.
Существует очень связанная проблема:
| Покажите, что если более половины подмножеств множества из n элементов
выбрано, существует пара из них, такая что не является подмножеством другого при условии
ни один из выбранных наборов не пуст. Объединить все подмножества в пары {X,X c } множества и его дополнения X c = A — X. Число 2 n-1 таких пар составляет ровно половину числа 2 n всех подмножеств. Следовательно, если выбрано более половины подмножеств, есть два, которые попадают в одну пару {X,X c }. Поскольку ни одно из выбранных множеств не пусто, ни X, ни X c не пусты. Следовательно, ни одно не содержит другого. Пример Нельзя снять запрет на выбор пустого множества. Действительно, 2-множество A = {1,2} имеет четыре
подмножества: Ø, {1}, {2}, {1,2}. Можно выбрать, для
например, три подмножества Ø, {1}, {1,2} такие, что они образуют
включение цепи : Ø⊂{1}⊂{1,2}. ПримечаниеВ качестве альтернативы можно запретить выбор самого A . |Контакты| |Главная страница| |Содержание| |Вверх| Copyright © 1996-2018 Александр Богомольный70532987 |
Трансфинитные числа и теория множеств
Трансфинитные числа и теория множествПонимание математики к Питер Альфельд, кафедра математики, Университет Юты
Трансфинитные числа и теория множеств
Примечание: Гораздо более подробное и точное обсуждение
Темы, проиллюстрированные здесь, — это статья Теория множеств. в Macropedia Британской энциклопедии (1992 г.
версия).
Основные понятия и обозначения
Как можно обобщить понятие натуральное число за бесконечностью? Оказывается, есть естественный способ что приводит к неожиданным открытиям.
Он основан на концепции набора . В соответствии с Джордж Кантор (1845-1918), основатель множества теория),
Отдельными объектами множества являются его элементов. Набор может не иметь элементов, и в этом случае он называется . пустой набор и обозначается
Есть только один пустой набор. Множества могут быть определены словами,
или перечислив элементы между фигурными скобками, разделенными
запятыми или между фигурными скобками, содержащими некоторые другие
определяющие символы.
Множество конечно , если оно пусто или содержит конечное число элементов. Это бесконечное в противном случае.
Набор S является подмножеством набора T , обозначаемого
если каждый член S также является членом T . Пустое множество является подмножеством каждого множества, и каждое множество подмножество самого себя.
Мы будем использовать следующие наборы на основе числа и простые числа.
Очевидно, что эти множества связаны. Например:
Два конечных множества эквивалентны , если они содержат
одинаковое количество элементов.
Затем мы делаем ключевой шаг: определяем эквивалентность в таком таким образом, что это также работает для бесконечных множеств. Подумайте о двух конечные эквивалентные множества S и T как заказал. Таким образом, у каждого из них есть первое, второе, третье и т. на элемент. Ясно, что мы можем пар первого элемента S с первым элементом T , и так до тех пор, пока каждый элемент S и T не станет член уникальной пары. Ясно также, что два конечных множества эквивалентны, если мы можем соединить их таким образом. Эта идея может быть обобщены на бесконечные множества. Два комплекта С и T эквивалентны, обозначаются
если мы можем соединить их элементы так, чтобы каждый элемент S и T встречаются ровно в одной паре.
Вы можете
хотеть
более техническое определение
.
Мы говорим, что набор S на больше , чем набор T. , если T эквивалентен подмножеству S , но S не эквивалентен ни одному подмножеству T .
Для конечных множеств S обозначим количество элементов из S по
Силовые наборы
Силовой набор набора S представляет собой набор всех подмножества S , обозначается
.
Это определение можно пояснить несколькими примерами:.
Основные результаты
Теперь мы можем понять следующие утверждения, которые были
впервые доказано Кантором.
Чтобы увидеть доказательство, нажмите на
соответствующее заявление.
- Пусть S — конечное множество. Затем
.
Другими словами, любой конечный набор N элементов имеет 2 в степени N подмножеств.
- Мощность набора любого набора S больше чем С . Этот результат известен как Теорема Кантора . Его очевидно для конечных множеств (см. предыдущее утверждение), но не так очевидно для бесконечных множеств.
Другими словами, рациональных чисел столько же, как есть натуральные числа, или простые числа, или четные числа, или нечетные числа, или целые числа.
Это
удивительный! Все натуральные числа являются рациональными числами,
но интуитивно большинство рациональных чисел не
натуральные числа. Так как же может быть столько
натуральные числа как бывают рациональные числа? Помещать
иначе: как любое множество может быть эквивалентно
«намного меньшее» подмножество?- Набор действительных чисел больше, чем набор натуральные числа. Это опять-таки неудивительно, но, возможно, после предыдущее утверждение, мы должны чувствовать, что бесконечность есть бесконечность есть бесконечность, и поэтому, может быть, мы должны быть удивлен!
Это
удивительный! Все натуральные числа являются рациональными числами,
но интуитивно большинство рациональных чисел не
натуральные числа. Так как же может быть столько
натуральные числа как бывают рациональные числа? Помещать
иначе: как любое множество может быть эквивалентно
«намного меньшее» подмножество?Трансфинитные числа
Для любого бесконечного множества S мы можем рассмотреть свойство
что оно имеет общее со всеми эквивалентными множествами.
Это
называется кардиналом из S . Для конечных
множеств, кардинал — это просто количество элементов. Для
бесконечные множества, которые определить сложнее. Однако,
кажется, ясно, что мы имеем в виду. Мы можем думать о кардинале
как некоторая мера размера набора.
Кардиналу некоторых наборов были даны имена. кардинал множеств натуральных чисел обозначается
где символ справа от уравнений произносится алеф-нуль . Точно так же кардинал множества действительные числа обозначаются
Кардиналы также называются трансфинитными числами . Ясно, что можно получить иерархию, многократно формируя powerset набора мощности следующим образом:
Гипотеза континуума
Естественно спросить, существует ли множество, большее, чем
набор натуральных чисел и меньше, чем набор действительных
числа.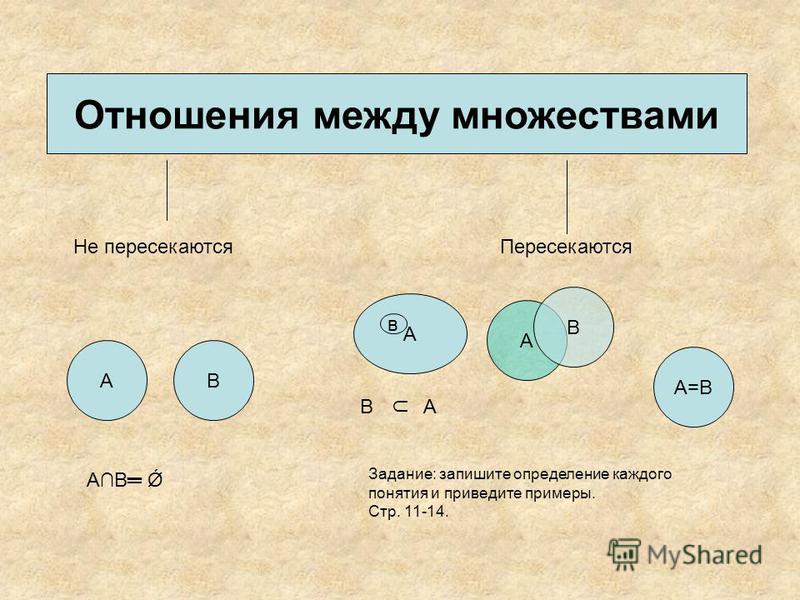
гипотеза континуума утверждает, что такие
это не так. Правда это или ложь, не
известно, но неизвестно в более тонком смысле, чем то, что мы
просто не могу понять!
Оказывается, наивное применение понятия множеств
приводит к противоречиям. Самый простой пример выглядит так
следующим образом: рассмотрим множество всех множеств. Так как это набор
содержит себя как элемент. Поэтому имеет смысл определить
набор , который является набором всех наборов, которые не
содержат себя как элемент. Теперь, если A является
элемент A , то по определению A является
не является элементом A . С другой стороны, если А не является элементом А, то по определению А является элементом A . В любом случае у нас есть
противоречие.
Аксиоматическая теория множеств
Чтобы избежать противоречий, нужно построить систему Аксиом.
которые непротиворечивы и допускают все соответствующие заявления
быть выведенным. Итак, разумно выглядящие системы аксиом
могут быть построены, содержащие континуум-гипотезу в качестве
аксиому и другие разумно выглядящие системы можно построить
которые содержат свою противоположность. Так что в каком-то смысле
гипотеза континуума верна или нет, зависит от вкуса
математик. Есть математики, которые счастливы
с таким положением дел. С другой стороны, глядя на
проблема наивно, кажется очевидным, что это либо правда
или ложь, что существует подмножество действительных чисел,
меньше множества действительных чисел и больше множества
натуральных чисел. Другими словами, кажется, что есть
должна быть метаматематическая концепция множеств, которая делает
гипотеза континуума либо верна, либо ложна.