Тригонометрические неравенства и методы их решения – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.
Методы решений неравенств:
- Решение тригонометрических неравенств с помощью единичной окружности.
- Графическое решение тригонометрических неравенств.
- Решение неравенств методом интервалов.
При решении более сложных тригонометрических неравенств пользуются двумя основными приемами:
I. Данное неравенство с помощью равносильных преобразований сводится к простейшим тригонометрическим неравенствам. При выполнении преобразований пользуются теми же приемами, что и при решении тригонометрических уравнений.
II. Применяется метод интервалов для определения числовых промежутков, в которых содержатся решения неравенства. Предварительно решается соответствующее тригонометрическое уравнение и устанавливаются интервалы знакопостоянства с учетом области определения неравенства.
Неравенство \(sinx>a\)
- При \(|a|≥1\) неравенство \(sinx>a\) не имеет решений: \(x\in \varnothing\).
- При \(a<−1\) решением неравенства \(sinx>a\) является любое действительное число: \(x\in \mathbb R\).
- При \(−1≤a<1\) решение неравенства \(sinx>a\) выражается в виде \(arcsin a + 2\pi n < x < \pi -arcsin a + 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(sinx≥a\)
- При \(|a|>1\) неравенство \(sinx\ge a\) не имеет решений: \(x\in \varnothing\).
- При \(a\le−1\) решением неравенства \(sinx\ge a\) является любое действительное число: \(x\in \mathbb R\).
- При \(-1<a<1\) решение неравенства \(sinx\ge a\) выражается в виде \(arcsin a + 2\pi n \le x \le \pi — arcsin a + 2\pi n,\;n \in \mathbb{Z}\).
- Случай \(a=1 \): \(x = \frac{\pi}2 +2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(sinx<a\)
- При \(a>1\) решением неравенства \(sinx<a\) является любое действительное число: \(x\in \mathbb R\).
 \)
\) - При \(a≤−1\) у неравенства \(sinx<a\) решений нет: \(x\in \varnothing\).\)
- При \(-1<a\leq1\) решение неравенства \(sinx<a\) лежит в интервале \(-\pi — arcsin a + 2\pi n < x < arcsin a + 2\pi n,\;n \in \mathbb{Z}\).\)≤1\)
Неравенство \(sinx≤a\)
- При \(a≥1\) решением неравенства \(sinx≤a\) является любое действительное число: \(x\in \mathbb R\).
- При \(a<−1\) неравенство \(sinx≤a\) решений не имеет: \(x \in \varnothing\).
- При \(-1<a<1\) решение нестрогого неравенства \(sinx≤a\) находится в интервале \(-\pi — arcsin a + 2\pi n \le x \le arcsin a + 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(cosx>a\)
- При \(a≥1\) неравенство \(cosx>a\) не имеет решений: \(x\in \varnothing\).
- При \(a<−1\) решением неравенства \(cosx>a\) является любое действительное число: \(x\in \mathbb R\).

- При \(−1≤a<1\) решение неравенства \(cosx>a\) имеет вид \(-arccos a + 2\pi n < x < arccos a + 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(cosx≥a\)
- При \(a>1\) неравенство \(cosx≥a\) не имеет решений: \(x\in \varnothing\).
- При \( a≤−1\) решением неравенства \(cosx≥a\) является любое действительное число: \(x\in \mathbb R\).
- При \(-1<a<1\) решение неравенства \(cosx≥a\) имеет вид \(-arccos a + 2\pi n \le x \le arccos a + 2\pi n,\;n \in \mathbb{Z}\).
- Случай \(a=1\): \(x = 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(cosx<a\)\)
- При \(a>1\) неравенство \(cosx<a\) справедливо при любом действительном значении x: \(x\in \mathbb R\).\)
- При \(a≤−1\) неравенство \(cosx<a\) не имеет решений: \(x\in \varnothing\).\)
- При \(-1<a\leq1\) решение неравенства \(cosx<a\) записывается в виде \(arccos a + 2\pi n < x < 2\pi — arccos a + 2\pi n,\;n \in \mathbb{Z}\).
 \)≤1\)
\)≤1\)
Неравенство \(cosx≤a\)
- При \(a≥1\) решением неравенства \(cosx≤a\) является любое действительное число: \(x\in \mathbb R\).
- При \(a<−1\) неравенство \(cosx≤a\) не имеет решений: \(x\in \varnothing\).
- При \(-1<a<1\) решение нестрогого неравенства \(cosx≤a\) записывается как \(arccos a + 2\pi n \le x \le 2\pi — arccos a + 2\pi n,\;n \in \mathbb{Z}\).
- Случай \(a=−1\): \(x = \pi + 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(tgx>a\)
При любом действительном значении \(a\) решение строгого неравенства \(tgx>a\) имеет вид \(arctg a + \pi n < x < \frac{\pi}2 + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(tgx≥a\)
Для любого значения \(a\) решение неравенства \(tgx≥a\) выражается в виде \(arctg a + \pi n \le x < \frac{\pi}2 + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(tgx<a\)\)
Для любого значения \(a\) решение неравенства \(tgx<a\) записывается в виде \(-\frac{\pi}2 + \pi n < x < arctg a + \pi n,\;n \in \mathbb{Z}\).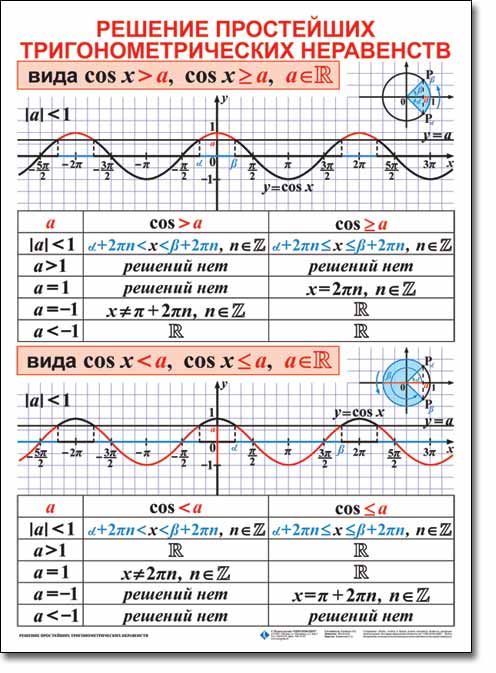 \)
\)
Неравенство \(tgx≤a\)
При любом \(a\) неравенство \(tgx≤a\) имеет следующее решение: \(-\frac{\pi}2 + \pi n < x \le arctg a + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(ctgx>a\)
При любом \(a\) решение неравенства \(ctgx>a\) имеет вид \(\pi n < x < arcctg a + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(ctgx≥a \)
Нестрогое неравенство \(ctgx≥a\) имеет аналогичное решение \(\pi n < x \le arcctg a + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(ctgx<a\)\)
Для любого значения \(a\) решение неравенства \(ctgx<a\) лежит в открытом интервале \(arcctg a + \pi n < x < \pi + \pi n,\;n \in \mathbb{Z}\).\)
Неравенство \(ctgx≤a\)
При любом \(a\) решение нестрогого неравенства \(ctgx≤a\) находится в полуоткрытом интервале \(arcctg a + \pi n \le x < \pi + \pi n,\;n \in \mathbb{Z}\).
Пример. Решите неравенство: \(cosx>\frac12\).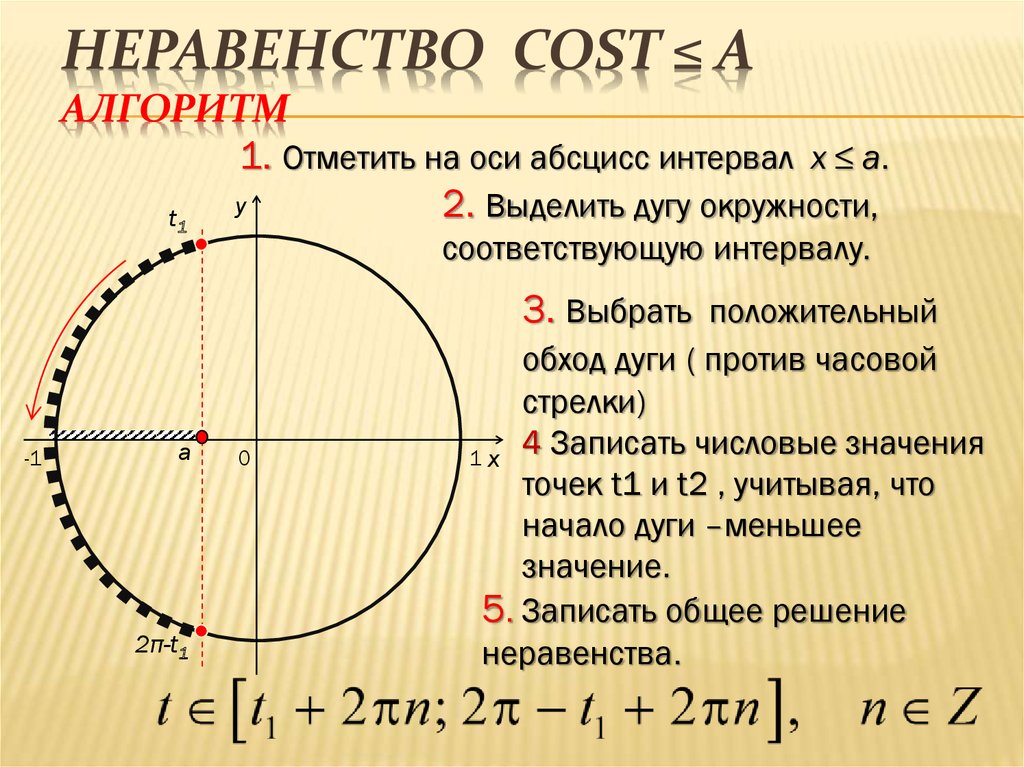
Решение: Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.
Первый способ. Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть \(y=cosx \ и \ y=\frac12\). Выделим промежутки, на которых график функции косинус \(y=cosx\) расположен выше графика прямой \(y=\frac12\).
Найдем абсциссы точек \(x_1\ и \ x_2\) – точек пересечения графиков функций \(y=cosx\ и\ y=\frac12\), которые являются концами одного из промежутков, на котором выполняется указанное неравенство: \(x_1=-arccos\frac12=-\frac{\pi}3; x_2=arccos\frac12=\frac{\pi}3\).
Учитывая, что косинус – функция периодическая, с периодом \(2\pi\), ответом будут значения x из промежутков \((-\frac{\pi}3+2\pi k;\frac{\pi}3+2\pi k), \ k\in Z\).
Второй способ.
Построим единичную окружность и прямую \(x=\frac12\) (так как на единичной окружности косинусам отвечает ось абсцисс).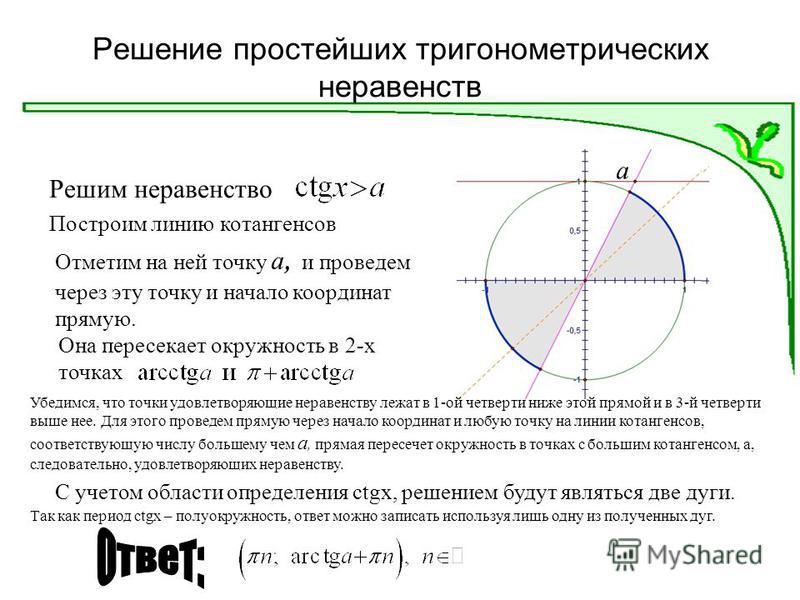 Обозначим \(P_{x_1}\ и \ P_{x_2}\) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше \(\frac12\). Найдем значение \(x_1 \ и \ x_2\), совершая обход против часовой стрелки так, чтобы \(x_1<x_2\): \)
Обозначим \(P_{x_1}\ и \ P_{x_2}\) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше \(\frac12\). Найдем значение \(x_1 \ и \ x_2\), совершая обход против часовой стрелки так, чтобы \(x_1<x_2\): \)\(x_1=-arccos\frac12=-\frac{\pi}3; x_2=arccos\frac12=\frac{\pi}3\).
Учитывая периодичность косинуса, окончательно получим интервалы \((-\frac{\pi}3+2\pi k;\frac{\pi}3+2\pi k), \ k\in Z\).
10.2.1. Решение тригонометрических неравенств. Часть 1.
Главная » 10 класс. Алгебра. » 10.2.1. Решение тригонометрических неравенств. Часть 1
На этом и последующих занятиях мы будем решать графическим способом тригонометрические неравенства одного какого-то вида. Сегодня мы решим три тригонометрических неравенства вида sint . Вот они:
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=sint и y=a.
3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается ниже прямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду.
Решим первое неравенство
Для построения графика функции y=sinx выберем единичный отрезок, равный двум клеткам. Тогда по горизонтальной оси Ох значение π (≈3,14) составит шесть клеток. Рассчитываем остальные значения аргументов (в клетках).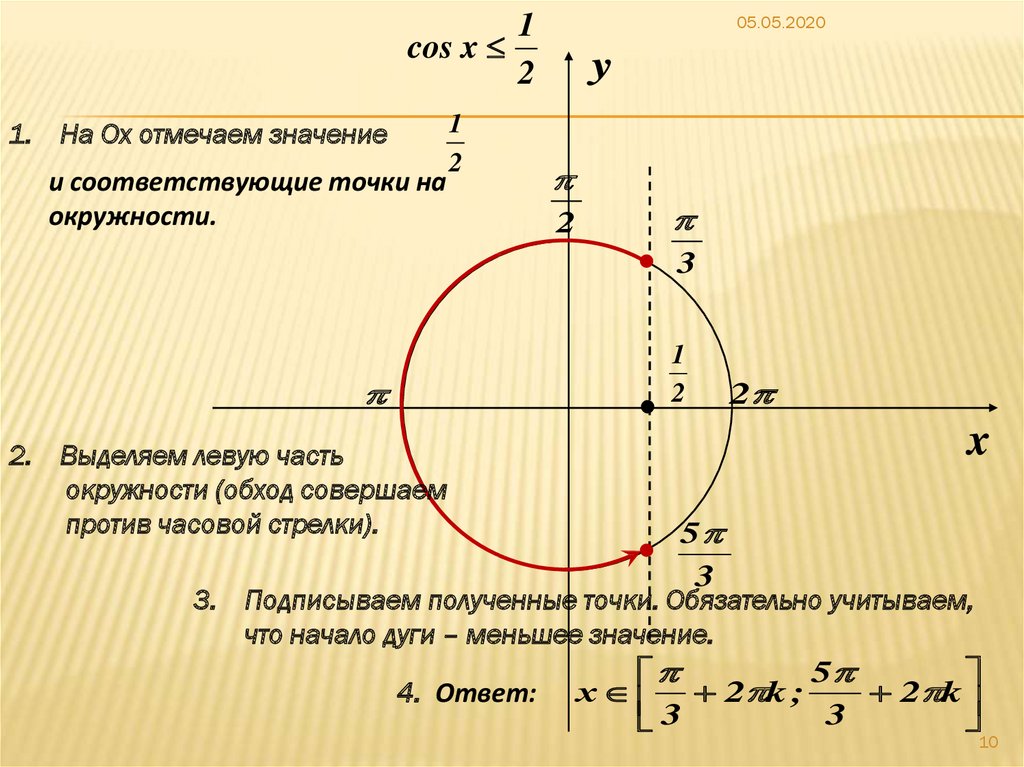
Вот как будет выглядеть координатная плоскость.
Эти точки мы взяли из таблицы значений синуса. Также используем свойство нечетности функции y=sinx (sin (-x)=-sinx), периодичность синуса (наименьший период Т=2π) и известное равенство: sin (π-x)=sinx. Проводим синусоиду
. Проводим прямую.
Теперь нам предстоит определить такие две точки пересечения синусоиды и прямой, между которыми синусоида располагается ниже, чем прямая. Крайняя точка справа определена, абсцисса ближайшей искомой отстоит от начала отсчета влево на 8 клеток. Построим ее и определим.
Между этими (выделенными) значениями аргумента и находится та часть синусоиды, которая лежит ниже данной прямой, а значит, промежуток между этими выделенными точками удовлетворяет данному неравенству. Учтем период синуса, запишем результат в виде двойного неравенства, а ответ в виде числового промежутка.
Решим второе неравенство
Синусоиду строим так же, а прямая будет параллельна оси Оt и отстоять от нее на 1 клетку вниз.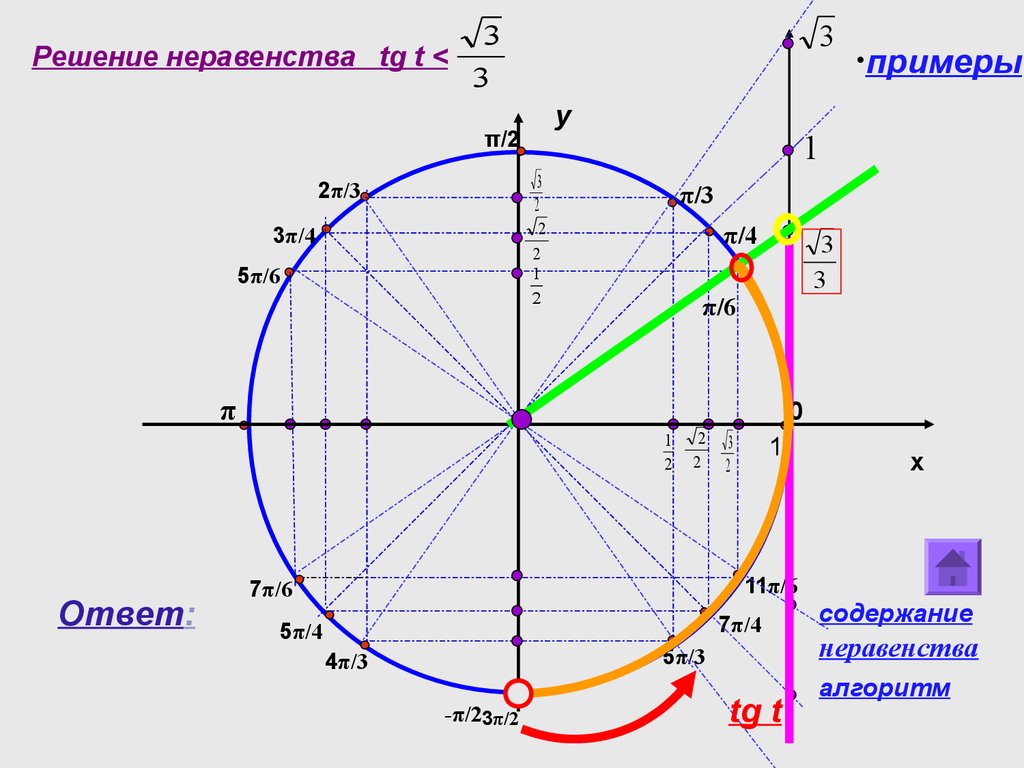
Определяем промежуток, внутри которого точки синусоиды лежат ниже прямой.
Записываем промежуток значений введенной переменной t. Возвращаемся к первоначальному значению аргумента (2х). Все части двойного неравенства делим на 2 и определяем промежуток значений х. Записываем ответ в виде числового промежутка.
Аналогично решаем и третье неравенство
В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения t. Затем вместо t подставим первоначальный аргумент синуса и будем выражать х из полученного двойного неравенства.
Ответ запишем в виде числового промежутка.
Смотрите видео: 10.2.1. Решение тригонометрических неравенств вида: sinx
И, напоследок: знаете ли вы, что математика — это определения, правила и ФОРМУЛЫ?!
Конечно, знаете! И самые любознательные, изучив эту статью и просмотрев видео, воскликнули: «Как долго и сложно! А нет ли формулы, позволяющей решать такие неравенства безо всяких графиков и окружностей?» Да, разумеется, есть!
ДЛЯ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА: sint (-1≤а≤1) справедлива формула:
— π — arcsin a + 2πn
Примените ее к рассмотренным примерам и вы получите ответ гораздо быстрее!
Вывод: УЧИТЕ ФОРМУЛЫ, ДРУЗЬЯ!
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА – ТРИГОНОМЕТРИЯ
Мы можем решить тригонометрические неравенства, глядя на графики основных тригонометрических функций на единичной окружности.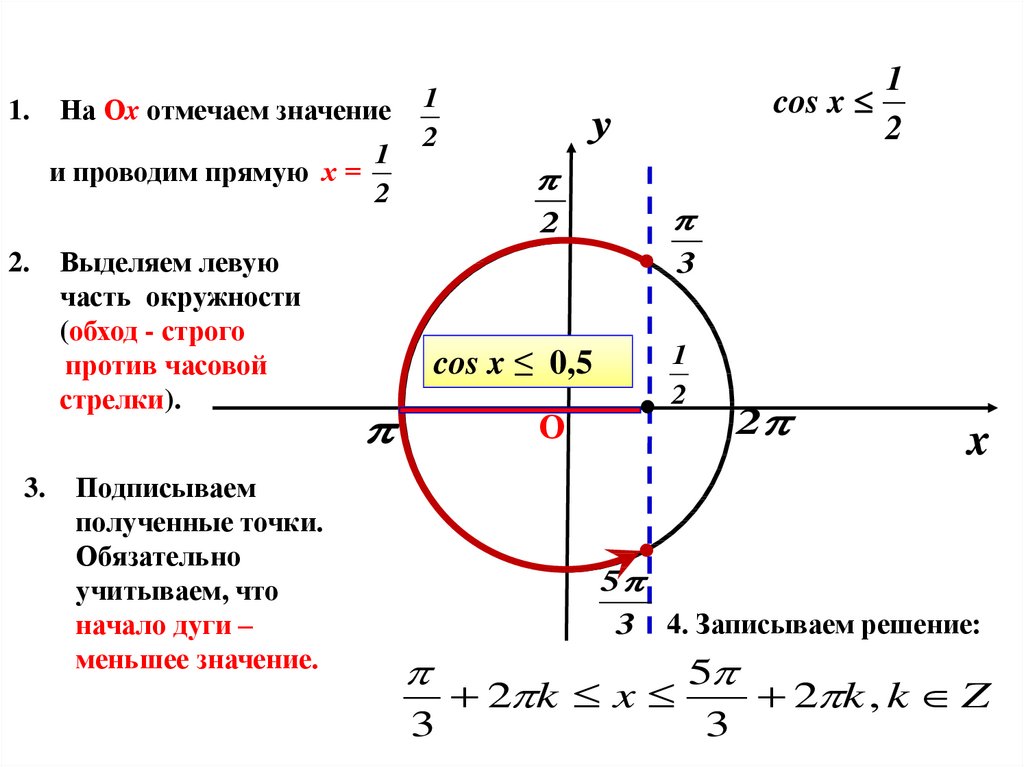 Используя следующие шаги, мы можем найти решение любого простого тригонометрического неравенства:
Используя следующие шаги, мы можем найти решение любого простого тригонометрического неравенства:
- Найдите область, которая удовлетворяет данному неравенству на единичной окружности.
- Записать границы выделенной области. Мы выделяем границы, двигаясь против часовой стрелки. Помните, что меньшая граница (например, отрицательная граница) всегда должна быть первой границей.
- К sin x и cos x добавьте 2kπ, а к tan x и cot x добавьте kπ.
Рассмотрим неравенство sin x > a . Если a > 1 , решения нет (поскольку -1 ≤ sin x ≤ 1 ). Если
a < -1 , ответом будут все действительные числа, то есть (-∞, ∞). Если -1 ≤ a ≤ 1 , ответ будет
(arcsin a + 2kπ) < x < (π – arcsin a + 2kπ), k ∈ Z. Мы можем записать это как:
x ∈ (arcsin a + 2kπ, π – arcsin a + 2kπ), k ∈ Z.
Теперь рассмотрим неравенство sin x < a.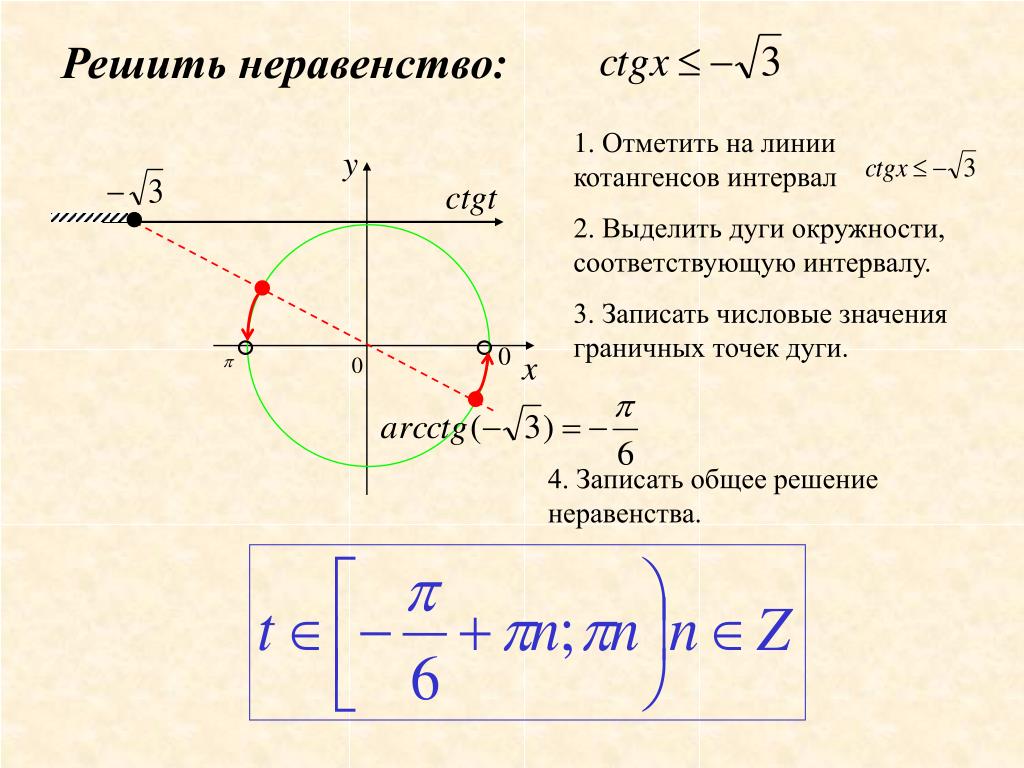
Если a < -1 , решения нет.
Если a > 1 , ответом будут все действительные числа, то есть (-∞, ∞).
Если -1 ≤ a ≤ 1 , ответ будет
(-π – arcsin a + 2kπ) < x < (arcsin a + 2kπ), k ∈ Z.
Рассмотрим неравенство cos х > а.
Если a > 1 решения нет.
Если a < -1 , ответом будут все действительные числа, то есть (-∞, ∞).
Если -1 ≤ a ≤ 1 , решение будет следующим:
(-arccos a + 2kπ) < x < (arccos a + 2kπ), k ∈ Z.
Теперь рассмотрим неравенство cos x < a.
Если a > -1 решения нет.
Если a < 1 , ответом будут все действительные числа, то есть (-∞, ∞).
Если -1 ≤ a ≤ 1 ответ:
arccos a + 2kπ < x < 2π – arccos a + 2kπ, k ∈ Z.
Рассмотрим неравенство tan x > a.
Как видно из рисунка, решения неравенства симметричны относительно начала координат. Поэтому мы напишем только один ответ и добавим kπ вместо 2kπ , чтобы получить окончательное решение. Итак, решение:
arctan a + kπ < x < π/2 + kπ, k ∈ Z.
Теперь рассмотрим неравенство tan x < a.
Из рисунка можно получить решение:
-π/2 + kπ < x < (arctan a + kπ), k ∈ Z.
036
Если неравенство дано с ≥ или ≤, ответ будет включать арктангенс а, но исключать ±π/2, потому что тангенс (±π/2) не определен.неравенства в кроватке x
Рассмотрим неравенство cot x > a и посмотрим на рисунок. Мы видим, что неравенство имеет решение:
kπ < x < (arccot a + kπ), k ∈ Z.
Теперь рассмотрим cot x < a.
Из рисунка можно получить решение:
(arccot a + kπ) < x < (π + kπ), k ∈ Z.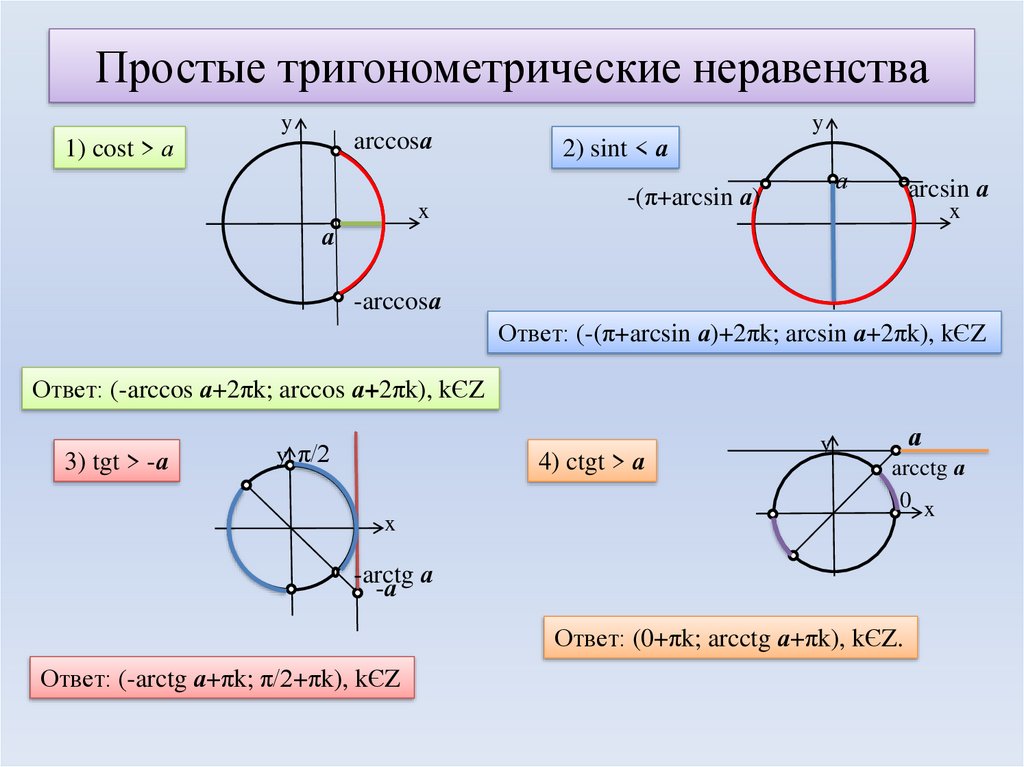
36
Если неравенство задано с ≥ или ≤, ответ будет включать arccot a, но исключать 0 и π, поскольку cot 0 и cot π не определены.
Подробности и примеры смотрите в видео ниже:
Нравится:
Нравится Загрузка…
Тригонометрические неравенства: задачи с решениями
Решите тригонометрическое неравенство: $8\left\vert \tan x\right\vert -1
$-\arctan \left( 8\right) +k\pi
$-\arctan \left( \frac{1}{8}\right) +k\pi
$-\arctan \left( \frac{1}{4}\right) +k\pi
$-8\arctan \left( 1\right) +k\pi
Задача 6
Если $x\in (0,2\pi ]$ , решить $\frac{\cos x}{1-\sin 2x}
$\left( 0,\pi \right) -\frac{\pi }{2}$
$\left( \frac{\pi }{2},\frac{3\pi }{2} \right) $
$\left( \frac{\pi }{3},\frac{3\pi }{4}\right) -\frac{\pi }{4}$
$\left( \frac{\pi }{2},\frac{3\pi }{2}\right) -\frac{5\pi }{4}$
Задача 7
Решить $\sin \left( x- \frac{\pi }{3}\right) >\sin x$, если $0\leq x\leq 2\pi $
$x\in \left( \frac{\pi }{3},\frac{ 2\пи }{3}\справа) $
$x\in \left( \frac{2\pi }{3},\frac{5\pi }{3}\right) $
$x\in \left( \frac{\pi }{ 4}, \frac{5\pi }{4}\right) $
$x\in \left( \pi ,2\pi \right) $
Задача 8
Учитывая неравенство $p\sin x-q \cos x>\frac{r}{2}$ с решением $x\in
\left( \frac{\pi }{3},\pi \right) $.
Если $\left( p,q\right) $ — точка, принадлежащая окружности с радиус $r$ и центр $\left( 0,0\right) $,
определить $\frac{p}{q}$
$\frac{p}{q}=1$
$\frac{p}{q}=\frac{1}{2}$
$\frac{p}{q}=2$
$\frac{p}{q}=\sqrt{3}$
Задача 9
Решить: $\sin x\geq \frac{1}{2}$; задано $n\in \mathbb{Z}$
$\left[ \frac{\pi} {6}+2n\pi ;\frac{5\pi} {6}+2n\pi \right]$
$\left[ \frac{\pi }{6}+2n\pi ;\left( 2n+1\right) \pi \right] $
$\left[ 2n\pi ;\frac{\pi } {6}+2n\pi \right]$
$\left[ \frac{\pi }{2};\pi \right] \cup \left[ \frac{\pi }{6};\pi \ справа] $
Задача 10
Решить: $\cos x\geq \frac{\sqrt{2}}{2}$; $0\leq x\leq 2\pi $
$\left[ \frac{\pi }{4};\frac{\pi }{2}\right]$
$\left[0; \frac{\pi }{4} \right]$
$\left[ \frac{7\pi }{4};2\pi \right]$
$\left[ 0;\frac{\pi }{4}\right] \cup \left[ \frac{7\pi }{4};2\pi \right]$
Задача 11
Определить все значения $x$ такие, что:
$\ sin (2x)>6\cos x$, учитывая $n\in \mathbb{Z}$
$x\in \left( n\pi +\frac{\pi }{3};n\pi +\ frac{2\pi }{3}\right)$
$x\in \left( 2n\pi +\frac{\pi }{2};2n\pi +\frac{3\pi }{2} \right)$
$x\in \left( 2n\pi +\frac{\pi }{3};2n\pi +\frac{2\pi }{3}\right) $
$x\in \left( n\pi +\frac{\pi }{2};n\pi +\frac{2\pi }{3}\right) $
Задача 12
Решите неравенство: $\tan x\geq 1$
$\left[ \frac{ \pi }{4}+n\pi ;\frac{\pi }{2}+n\pi \right]$
$\left[ \frac{3\pi }{4}+n\pi ;\ frac{\pi }{2}+n\pi \right] $
$\left[ \frac{3\pi }{4}+n\pi ;\frac{5\pi }{2}+n\ пи \справа] $
$\left[ \frac{\pi }{4}+n\pi ;\frac{5\pi }{2}+n\pi \right] $
Задача 13
Для каких значений $x $, ($0\leq x\leq 2\pi $) равно $\sin x>\cos x$?
$0
$0
$\frac{\pi }{4}
$0
Задача 14
Найдите все значения $x$, если $x\in (0;2\pi)$ удовлетворяют следующее тригонометрическое неравенство.

 \)
\)
 \)≤1\)
\)≤1\)