python — Как эффективней вычислить определитель матрицы?
Код ниже считает определитель матрицы 20х20 методом миноров и записывает время, которое ему понадобилось для расчета. Но такую большую матрицу он считает очень долго, несколько часов…
import time, random
from random import randint
Ic = [0 for i in range(10)]
def minor(array):
return array[0][0] * array[1][1] - array[1][0] * array[0][1]
def division(array):
if len(array[0]) > 2:
result = 0
for i in range(len(array[0])):
new_arr = []
for j in range(len(array[0])):
if j != i:
new_arr.append([array[j][k] for k in range(1, len(array[0]))])
result += division(new_arr) * array[i][0] * (-1 + 2 * ((i + 1) % 2))
return result
else:
return minor(array)
N = 20
result = 0
print(f"\nN:\t{N}\n")
timer = time.time()
matrix = [[randint(0, 9) for row in range(N)] for row in range(N)]
print(f"result:\t{division(matrix)}")
for i in range(N):
print(matrix[i])
print(f"Time:\t{time.
time() - timer}")
Как это можно оптимизировать?
- python
- алгоритм
- оптимизация
- матрицы
- линейная-алгебра
Как это можно оптимизировать?
воспользоваться модулем numpy:
In [32]: import numpy as np # pip install numpy In [33]: a = np.random.rand(20, 20) In [34]: res = np.linalg.det(a) In [35]: res Out[35]: 0.09252260373277807
время работы для матрицы 20×20:
In [36]: %timeit np.linalg.det(a) 27.6 µs ± 37 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
7
Вычисление определителя через миноры имеет факториальную сложность и непригодно для n>10.
Вместо этого стоит реализовать LU разложение матрицы (кубическая сложность) и затем вычислить определитель как произведение диагональных элементов L и U матриц.
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
что называют детерминантом, как вычислить произведение и сумму
Матрица в математике — это таблица упорядоченных взаимосвязанных элементов, состоящая из m-строк и n-столбцов.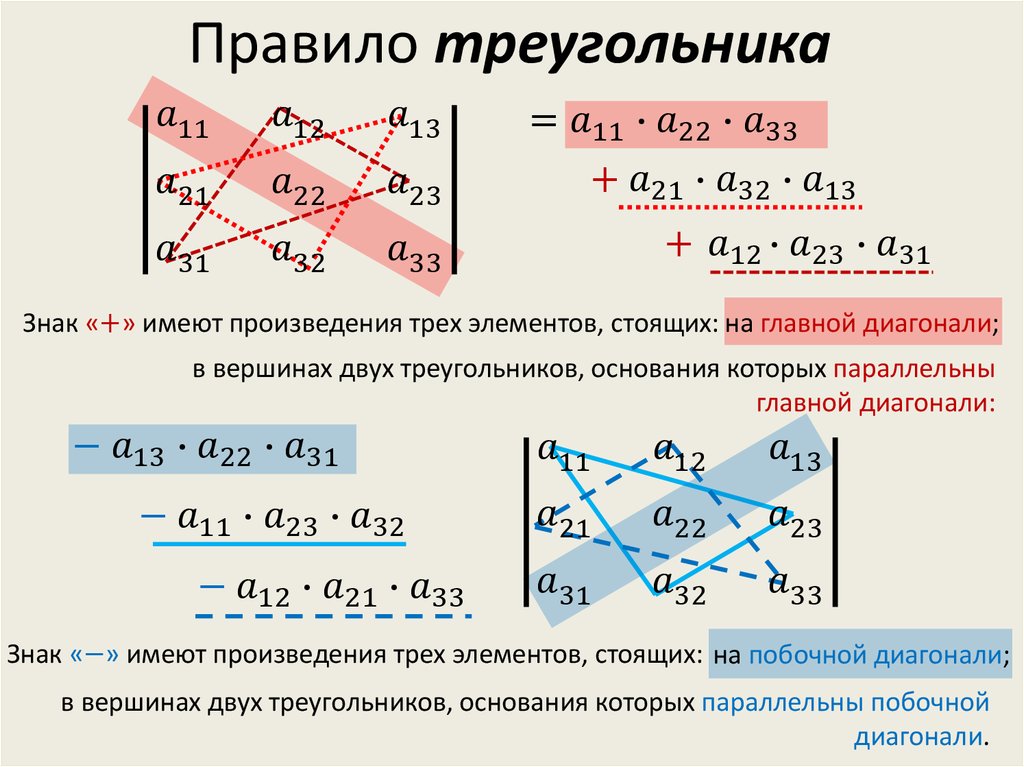 В квадратной матрице m=n, то есть A = (n×n). Одной из основных ее характеристик, применяемых в решении большинства задач, является определитель.
В квадратной матрице m=n, то есть A = (n×n). Одной из основных ее характеристик, применяемых в решении большинства задач, является определитель.
Определитель матрицы — что это такое, его свойства
Точного определения этого термина не существует, однако для понимания:
Определитель — это некоторая скалярная величина, с которой можно сопоставить любую квадратную матрицу.
Три альтернативных обозначения: |А|, Δ, det A. Методы вычисления варьируется в зависимости от порядка матрицы (количества строк или столбцов).
Что называют детерминантом
При изучении матричного определителя часто мелькает латинское слово «детерминант». На самом деле, разницы нет — это одно и то же понятие. Однако детерминант имеет множество значений в других областях науки, поэтому в математике чаще всего используют его русский перевод.
youtube.com/embed/YgGTT4bRgxE»>Расстановка индексов в матрице
Индексы — это координаты элемента в системе. У каждого элемента их два: первый указывает на строку, второй — на столбец.
Поскольку порядок — это количество строк или столбцов в квадратной матрице, то его можно определить по m-индексу нижней строки или n-индексу крайнего правого столбца. Такой способ применяется в том случае, если таблица очень большая и считать строки (столбцы) неудобно.
Алгебраическое определение
Алгебраический смысл таков:
Определитель матрицы А = (n×n) — это алгебраическая сумма n слагаемых.
Формула:
Каждое слагаемое — это произведение n-элементов, взятых по одному из каждой строки и каждого столбца, умноженное на (-1) в степени Np (количество инверсий).
Геометрическое определение
Геометрический смысл таков:
Определитель — это объем параллелепипеда, который получается, если рассмотреть строки в качестве векторов, образующих ребра.
Еще раз: количество строк (столбцов) равно количеству векторов. Таким образом, если нам дана матрица А = (2×2), то она является двухмерным параллелограммом, а детерминант — площадью данной фигуры. Если А = (3×3), то это трехмерный параллелепипед, а определитель — его объем.
Общая схема вычисления определителей
Для матрицы 1-го порядка определитель равен его единственному элементу:
\(|a_{11}| = a_{11}\)
Для 2-го порядка — произведение элементов главной диагонали минус произведение побочной.
\(|а_{11} а_{12}|\)
\(|а_{21} а_{22}| = а_{11} * а_{22} — а_{12} * а_{21}\)
Для нахождения А = (3×3) есть два способа:
- правило треугольника;
- правило Саррюса.
Правило треугольника выглядит следующим образом:
Если показывать графически, то:
По правилу Саррюса нужно:
- Дописать слева от определителя два первых столбца.

- Перемножить элементы главной диагонали и параллельных диагоналей, взяв произведения со знаком «+».
- Перемножить элементы побочных диагоналей и параллельных им, взяв произведения со знаком «–».
Матрицы от 4-го порядка считают разложением строк или столбцов, но такой метод применяется редко и требует знаний об алгебраическом дополнении и миноре.
Вычисление определителя матрицы, примеры с решением
Задача №1: вычислить детерминант матрицы A = (n×n), равной
| 11 -3 |
| 15 -2 |.
Решение:
\(|а_{11} а_{12}|\)
\(|а_{21} а_{22}| = а_{11} * а_{22} — а_{12} * а_{21}\), следовательно
det A = 11 * (-2) – (-15) * (-3) = (-22) – 45 = (-67)
Ответ: det A = (-67)
Задача №2: определить det A матрицы, равной
| 1 3 4 |
| 0 2 1 |
| 1 5 -1 |
Решение: если методом треугольника, то:
Следовательно:
det A = (1 * 2 * (-1) + 3 * 1 * 1 + 0 * 5 * 4) — (4 * 2 * 1 + 3 * 0 * (-1) + 1 * 5 * 1) =
((-2) + 3 + 0) — (8 + 0 + 5) = 1 — 13 = (-12)
Ответ: det A = (-12)
Сложно? Феникс. Хелп может помочь в решении домашних, самостоятельных и контрольных работ.
Хелп может помочь в решении домашних, самостоятельных и контрольных работ.
Найти определитель матрицы
математикаВик Паручури
• 3 мин чтения
Вычисление определителя является ключом ко многим аспектам линейной алгебры и, соответственно, к машинному обучению. Определитель матрицы 2×2 легко вычислить:
{%math%} \begin{align} A = \begin{bmatrix} a & b
c & d \end{bmatrix}
det A = \begin{ vmatrix} a & b
c & d \end{vmatrix}
det A = ad — bc \end{align} {%endmath%}
Вычисление определителя для матрицы большего размера, как мы увидим, немного сложнее . Весь код для этого доступен в репозитории алгоритмов.
Весь код для этого доступен в репозитории алгоритмов.
Разложение Лапласа
Определители для больших матриц могут быть рекурсивно получены с помощью разложения Лапласа. Это вычисляет определитель матрицы, делая его равным сумме масштабированных миноров матрицы. Минор — это определитель матрицы после удаления одной строки и одного столбца (таким образом, матрица 3×3 превратится в матрицу 2×2).
Итак, начнем с этой матрицы:
{%math%} A = \begin{bmatrix} 1 & 1 & 2
2 & 3 & 4
3 & 4 & 5 \end{bmatrix} {%endmath% } 9{1+j}{%em%} — это гарантирует, что чередующиеся элементы будут добавляться и вычитаться
Итак, мы берем сумму от j=1 до n от -1 в степени (1+j), умноженную на элемент a с индексом (1,j) в исходной матрице, умноженный на минор матрицы после удаления 1-я строка и j-й столбец.
Давайте расширим это для нашей матрицы:
{%math%} \begin{align} 1 * 1 * \begin{vmatrix} 3 и 4
4 и 5 \end{vmatrix} + -1 * 1 * \begin{vmatrix} 2 и 4
3 & 5 \end{vmatrix} + 1 * 2 * \begin{vmatrix} 2 и 3
3 и 4 \end{vmatrix}
(3 5 — 4 4) -(2 5 — 4 3) + 2 * (2 4 — 3 3)
-1 +2 -2
-1 \end{align} {%endmath%}
Итак, наш окончательный определитель этой матрицы равен -1.
Реализация
Теперь, когда мы знаем формулу, мы можем формализовать ее в псевдокоде:
Предположим, что у нас есть матрица A размера nxn с числом столбцов j.
если количество столбцов равно 2, вычислить определитель с помощью ad-bc и вернуть.
Перебрать все столбцы.
Рассчитайте множитель, взяв -1 в степени (1+j), умноженной на элемент в A[1][j].
Удалите строку 1 и столбец j из A и создайте новую матрицу X.
Найдите определитель X с помощью рекурсии (начните снова сверху с A = X).
Умножьте определитель на множитель. Суммируйте все значения и верните.
Суммируйте все значения и верните.
Это будет работать путем рекурсии по нашей матрице, чтобы в конечном итоге уменьшить ее до серии матриц 2×2, где можно вычислить второстепенные.
Чтобы реализовать это, мы будем использовать уже разработанный нами класс Matrix с одним дополнением:
def del_column(self, key):
"""
Удалить указанный столбец
"""
для я в xrange (0, self.rows):
del self.X[i][key]
Затем мы можем реализовать функцию, которая принимает матричный объект и вычисляет его определитель:
по определению рекурсивный_детерминант (X):
"""
Найдите определитель рекурсивным способом. Очень неэффективно
X - матричный объект
"""
#Должна быть квадратной матрицей
утверждать X.rows == X.cols
# Должно быть не менее 2x2
утверждать X.rows > 1
список_терминов = []
#Если строк больше 2, уменьшите и решите кусочно
если X.cols>2:
для j в xrange(0,X.cols):
#Удалить столбцы i и j
new_x = глубокая копия (X)
дель new_x[0]
new_x. del_column(j)
#Найти множитель
множитель = X[0][j] * math.pow(-1,(2+j))
# Рекурсия для нахождения определителя
det = рекурсивный_детерминант (новый_x)
term_list.append(множитель*det)
возвращаемая сумма (term_list)
еще:
возврат(Х[0][0]*Х[1][1] - Х[0][1]*Х[1][0])
del_column(j)
#Найти множитель
множитель = X[0][j] * math.pow(-1,(2+j))
# Рекурсия для нахождения определителя
det = рекурсивный_детерминант (новый_x)
term_list.append(множитель*det)
возвращаемая сумма (term_list)
еще:
возврат(Х[0][0]*Х[1][1] - Х[0][1]*Х[1][0])
Мы можем проверить, работает ли это, проверив матрицу, которую мы использовали выше:
X = Matrix([[1,1,2],[2,3,4],[3,4,5]]) рекурсивный_детерминант (X)
-1,0
Приложения
Теперь мы можем проверить матрицы на линейную зависимость их столбцов:
X = Matrix([[1,1,2],[2,2,4],[4,4,8]] ) рекурсивный_детерминант (X)
0,0
Ноль указывает, что столбцы зависят друг от друга.
Это также скажет нам, можно ли инвертировать матрицу.
X = Матрица([[1,1,2],[2,2,4],[4,4,8]]) X. инвертировать ()
Вышеприведенное должно вызвать ошибку.
Повышение производительности
Конечно, есть и другие, более эффективные решения для поиска определителя матрицы, такие как разложение LU, но мне нравится это, потому что оно позволяет легко понять, что происходит под капотом.
Возможными улучшениями производительности этого алгоритма могут быть:
- Создание глобального «второстепенного кэша», чтобы избежать многократного повторного вычисления одних и тех же второстепенных элементов для больших матриц.
- Используйте формулу 3×3 вместо формулы 2×2, что позволит избежать некоторых шагов рекурсии.
Brilliant Math & Science Wiki
Содержание
- Формальное определение и мотивация
- Свойства определителя
- Определитель по перестановкам
- Особые случаи
- Правило Сарруса
- Смотрите также
Формально определитель представляет собой функцию det\text{det}det от множества квадратных матриц к множеству действительных чисел, которая удовлетворяет 3 важным свойствам:
- det(I)=1\text{det}(I) = 1det(I)=1.
- det\text{det}det линейно по строкам матрицы.
- Если две строки матрицы МММ равны, det(M)=0\det(M)=0det(M)=0.
Второе условие является наиболее важным. Это означает, что любая из строк матрицы записывается как линейная комбинация двух других векторов, и определитель можно вычислить, «разбивая» эту строку. Например, в приведенном ниже примере вторая строка (0,2,3)(0,2,3)(0,2,3) может быть записана как 2⋅(0,1,0)+3⋅(0 ,0,1)2 \cdot (0,1,0) + 3 \cdot (0,0,1)2⋅(0,1,0)+3⋅(0,0,1), поэтому
det(100023001)=2⋅det(100010001)+3⋅det(100001001)=2.\text{det}\begin{pmatrix}1&0&0\\0&2&3\\0&0&1\end{pmatrix} = 2 \cdot \ text{det}\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}+3 \cdot \text{det}\begin{pmatrix}1&0&0\\0&0&1\\0&0&1\end{pmatrix}=2. det⎝⎛100020031⎠⎞=2⋅det⎝⎛100010001⎠⎞+3⋅det⎝⎛100000011⎠⎞=2.
Ключевая теорема показывает, что
существует ровно одна функция, удовлетворяющая трем указанным выше соотношениям.
К сожалению, с этим очень трудно работать для всех матриц, кроме самых простых, поэтому лучше использовать альтернативное определение. Есть два основных варианта: определитель по минорам и определитель по перестановкам .
Определитель является очень важной функцией, поскольку он удовлетворяет ряду дополнительных свойств, которые могут быть получены из трех условий, указанных выше. Они следующие:
- Мультипликативность: det(AB)=det(A)det(B)\text{det}(AB)=\text{det}(A)\text{det}(B)det( АВ)=det(A)det(B) 92 &=& ? \end{case} } ⎩⎪⎪⎪⎨⎪⎪⎪⎧a2−b2c2+d2(ac)2−(bd)2(ad)2−(bc)2====574341?
Учитывая приведенные выше ограничения, каково значение последнего уравнения?
Метод определителя по младшим вычисляет определитель с помощью рекурсии. Базовый случай прост: определитель матрицы 1 × 11 × 11 × 1 с элементом aaa равен просто aaa. Обратите внимание, что это согласуется с приведенными выше условиями, поскольку
det(a)=a⋅det(1)=a\text{det}\begin{pmatrix}a\end{pmatrix} = a \cdot \text{det} \begin{pmatrix}1\end{pmatrix}=adet(a)=a⋅det(1)=a 9{i+1}a_{1,i}\text{det}(A_{1i}) = a_{1,1}\text{det}A_{11}-a_{1,2}\text{det} A_{12}+\cdots.
 det(A)=i=1∑n(−1)i+1a1,idet(A1i)=a1,1detA11−a1,2detA12+⋯ .
det(A)=i=1∑n(−1)i+1a1,idet(A1i)=a1,1detA11−a1,2detA12+⋯ .Например,
Какой определитель (abcd)?\begin{pmatrix}a&b\\c&d\end{pmatrix}?(acbd)?
Пишем
det(abcd)=a det(d)−b det(c)=ad−bc. □\text{det}\begin{pmatrix}a&b\\c&d\end{pmatrix} = a ~\text{det}\begin{pmatrix}d\end{pmatrix} — b ~\text{det}\begin{ pmatrix}c\end{pmatrix} = ad-bc.\ _\squaredet(acbd)=a det(d)−b det(c)=ad-bc. □ 92?a2+b2?
К сожалению, эти вычисления могут оказаться довольно утомительными; уже для матриц 3 × 33 \× 33 × 3 формула слишком длинная, чтобы ее можно было запомнить на практике.
Альтернативный метод, определитель с помощью перестановок , вычисляет определитель с использованием перестановок элементов матрицы. Пусть σ\sigmaσ — перестановка {1,2,3,…,n}\{1, 2, 3, \ldots, n\}{1,2,3,…,n}, а SSS — множество те перестановки.
Тогда определитель матрицы AAA размера n×nn \times nn×n равен 9{n}a_{i,\sigma(i)}\right).
 σ∈S∑(sign(σ)i=1∏nai,σ(i)).
σ∈S∑(sign(σ)i=1∏nai,σ(i)).Это может выглядеть более пугающе, чем предыдущая формула, но на самом деле она более интуитивно понятна. По сути, это говорит следующее:
Выберите nnn элементов AAA так, чтобы никакие два не находились в одной строке и не два в одном столбце, и умножьте их, возможно, также на -1-1-1, если перестановка имеет нечетный знак. Определитель — это сумма всех вариантов выбора этих nnn элементов.
Это определение особенно полезно, когда матрица содержит много нулей, так как тогда большинство произведений исчезает.
Найдите определитель матрицы
(10−19110−6−19110013−8013000970000−5).\left(\begin{array}{cc}1&0&-1&9&11\\0&-6&-1&9&11\\0&0&\frac {1}{3}&-80&\frac{1}{3}\\0&0&0&9&7\\0&0&0&0&-5 \end{массив}\right).⎝⎜⎜⎜⎜⎛100000−6000−1− 1310099−80901111317−5⎠⎟⎟⎟⎟⎞.
Вот пример:
Какой определитель (abcd)?\begin{pmatrix}a&b\\c&d\end{pmatrix}?(acbd)? 9{n}a_{i,\sigma(i)}\right) = 1 \cdot a_{1,1}a_{2,2} + (-1) \cdot a_{1,2}a_{2,1 } = ad-bc.
 det(A)=σ∈S∑(sign(σ)i=1∏nai,σ(i))=1⋅a1,1a2,2+(−1 )⋅a1,2a2,1=ad−bc.
det(A)=σ∈S∑(sign(σ)i=1∏nai,σ(i))=1⋅a1,1a2,2+(−1 )⋅a1,2a2,1=ad−bc.Неудивительно, что это тот же результат, что и выше. □_\квадрат□
Вычислить det(264−315937).\det\left(\begin{array}{cc}2&6&4\\-3&1&5\\9&3&7 \end{array}\right).det⎝⎛2−39 613457⎠⎞.
Простейшими случаями для вычисления определителя являются верхнетреугольные (и нижнетреугольные ) матрицы, используя описанный выше метод перестановки:
Треугольный определитель
- Верхний треугольный определитель (элементы, расположенные ниже главной диагонали, равны нулю ):
X=det∣abcd0fgh00kl000p∣=a×f×k×p.X=\text{det}\begin{vmatrix} a & b & c & d \\ 0 & f & g & h \\ 0 & 0 & k & l \\ 0 & 0 & 0 & p \end{vmatrix}=a\times f\times k\times p.X=det∣∣∣ ∣∣∣∣∣a000bf00cgk0dhlp∣∣∣∣∣∣∣∣=a×f×k×p. - Нижний треугольный определитель (элементы выше главной диагонали равны нулю ):
X=det∣a000ef00ijk0mnop∣=a×f×k×p.
 X=\text{det}\begin{vmatrix} a & 0 & 0 & 0 \\ e & f & 0 & 0 \\ i & j & k & 0 \\ m & n & o & p \end{vmatrix}=a\times f\times k\times p.X=det∣∣∣∣∣∣∣∣aeim0fjn00ko000p∣∣∣∣∣∣ ∣∣=a×f×k×p.
X=\text{det}\begin{vmatrix} a & 0 & 0 & 0 \\ e & f & 0 & 0 \\ i & j & k & 0 \\ m & n & o & p \end{vmatrix}=a\times f\times k\times p.X=det∣∣∣∣∣∣∣∣aeim0fjn00ko000p∣∣∣∣∣∣ ∣∣=a×f×k×p.
- Верхний треугольный определитель (элементы, расположенные ниже главной диагонали, равны нулю ):
Определитель диагонали (элементы, находящиеся под и над главной диагональю, равны нулю ): X=det∣a0000f0000k0000p∣=a×f×k×p.X=\text{det}\begin{vmatrix} a & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & k & 0 \\ 0 & 0 & 0 & p \end{vmatrix}=a\times f\times k\times p.X=det∣∣∣∣∣∣∣∣a0000f0000k0000p∣∣∣∣∣∣ ∣∣=a×f×k×p.
Это полезно, потому что матрицы могут быть преобразованы в эту форму с помощью операций над строками, которые не влияют на определитель:
Найдите значение определителя
X=∣122112422752−14−63∣.X=\begin{vmatrix} 1 & 2 & 2 & 1 \\ 1 & 2 & 4 & 2 \\ 2 & 7 & 5 & 2 \\ -1 & 4 & -6 & 3 \end{vmatrix}.X=∣∣∣∣∣∣∣∣112−12274245−61223∣∣∣∣∣∣∣∣.
У нас есть
[X]=[122112422752−14−63]строка1→строка1строка2−2строка1→строка2строка3−2строка1→строка3строка4−3строка1→строка4⇒[1221−1−2000310−4−2−120]строка1→строка1строка2→строка2строка3→строка3строка4+12строка3 →строка4⇒[1221−1−2000310−43400]строка1→строка1строка2→строка2строка3→строка3строка4+17строка2→строка4⇒[1221−1−2000310−21000]строка4→строка1строка2→строка2строка3→строка3строка1→строка4⇒−[−21000−1− 20003101221].
 \begin{выровнено}
[X]=&\begin{bmatrix} 1 & 2 & 2 & 1 \\ 1 & 2 & 4 & 2 \\ 2&7&5&2 \\ -1&4&-6&3 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 — 2\text{row}_1 \rightarrow \text{row}_2 \\ \text{row} _3 — 2\text{row}_1 \rightarrow \text{row}_3 \\ \text{row}_4 — 3\text{row}_1 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\ begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -4&-2&-12&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_4 +12\text{row}_3 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -4&34&0&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_4 +17\text{row}_2 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -21&0&0&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_4 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_1 \rightarrow \text{row}_4 \end {matrix} \Rightarrow — &\begin{bmatrix} -21&0&0&0\\ -1&-2&0&0\\ 0&3&1&0\\ 1&2&2&1 \end{bmatrix} .
\begin{выровнено}
[X]=&\begin{bmatrix} 1 & 2 & 2 & 1 \\ 1 & 2 & 4 & 2 \\ 2&7&5&2 \\ -1&4&-6&3 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 — 2\text{row}_1 \rightarrow \text{row}_2 \\ \text{row} _3 — 2\text{row}_1 \rightarrow \text{row}_3 \\ \text{row}_4 — 3\text{row}_1 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\ begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -4&-2&-12&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_4 +12\text{row}_3 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -4&34&0&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_4 +17\text{row}_2 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -21&0&0&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_4 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_1 \rightarrow \text{row}_4 \end {matrix} \Rightarrow — &\begin{bmatrix} -21&0&0&0\\ -1&-2&0&0\\ 0&3&1&0\\ 1&2&2&1 \end{bmatrix} . \end{выровнено}[X]=строка1→строка1строка2−2строка1→строка2строка3−2строка1→строка3строка4−3строка1→строка4⇒строка1→строка1строка2→строка2 ряд3→ряд3строка4+12ряд3→строка4⇒ряд1→строка1строка2→строка2строка3→строка3строка4+17ряд2→строка4⇒строка4→строка1строка2→строка2 ряд3→строка3ряд1→строка4⇒−⎣⎢⎢⎡112−12274245−61223⎦⎥⎥⎤⎣⎢⎢⎡1−10−42−23 −2201−121000⎦⎥⎥⎤⎣⎢⎢⎡1−10−42−233420101000⎦⎥⎥⎤⎣⎢⎢⎡1−10−212 −23020101000⎦⎥⎥⎤⎣⎢⎢⎡−21−1010−23200120001⎦⎥⎥⎤.
\end{выровнено}[X]=строка1→строка1строка2−2строка1→строка2строка3−2строка1→строка3строка4−3строка1→строка4⇒строка1→строка1строка2→строка2 ряд3→ряд3строка4+12ряд3→строка4⇒ряд1→строка1строка2→строка2строка3→строка3строка4+17ряд2→строка4⇒строка4→строка1строка2→строка2 ряд3→строка3ряд1→строка4⇒−⎣⎢⎢⎡112−12274245−61223⎦⎥⎥⎤⎣⎢⎢⎡1−10−42−23 −2201−121000⎦⎥⎥⎤⎣⎢⎢⎡1−10−42−233420101000⎦⎥⎥⎤⎣⎢⎢⎡1−10−212 −23020101000⎦⎥⎥⎤⎣⎢⎢⎡−21−1010−23200120001⎦⎥⎥⎤.Следовательно, det[X]=X=−(−21)(−2)(1)(1)=−42. □\det {[X]} = X = -(-21)(-2)(1)(1) = -42.\ _\squaredet[X]=X=-(-21)(-2)( 1)(1)=-42. □
Правило Сарруса — это сокращенный способ вычисления определителя матрицы 3×33 × 33×3.
Перепишите первые две строки, занимая гипотетические четвертую и пятую строки соответственно: ∣123456789∣⇒∣123456789∣ 123456\левый| \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right| \Стрелка вправо\влево| \begin{матрица} 1 и 2 и 3 \\ 4 и 5 и 6 \\ 7 и 8 и 9\end{матрица} \right| \\ \quad \quad \quad \quad \quad \quad \ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}∣∣∣∣∣∣147258369 ∣∣∣∣∣∣⇒∣∣∣∣∣∣147258369∣∣∣∣∣∣ 142536
Перемножить диагональные элементы: ∣123456789∣123456=1⋅5⋅9+4⋅8⋅3+7⋅2⋅6−3⋅5⋅7−6⋅8⋅1−9⋅2⋅4=0.
 \begin{matrix} \left | \begin {matrix}1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{matrix}\right| \\ \begin{matrix} 1 & 2 & 3 \\ 4& 5 & 6 \end{matrix}\end{matrix}= 1 \cdot 5 \cdot 9+4 \cdot 8\cdot 3+7\cdot 2 \cdot 6 -3\cdot 5 \cdot 7 -6 \cdot 8 \cdot 1 — 9 \cdot 2 \cdot 4 = 0.∣∣∣∣∣∣ 147258369∣∣∣∣∣∣142536=1⋅5⋅9+4⋅8⋅3+7⋅2⋅6−3⋅5⋅7−6⋅8⋅1 −9⋅2⋅4=0.
\begin{matrix} \left | \begin {matrix}1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{matrix}\right| \\ \begin{matrix} 1 & 2 & 3 \\ 4& 5 & 6 \end{matrix}\end{matrix}= 1 \cdot 5 \cdot 9+4 \cdot 8\cdot 3+7\cdot 2 \cdot 6 -3\cdot 5 \cdot 7 -6 \cdot 8 \cdot 1 — 9 \cdot 2 \cdot 4 = 0.∣∣∣∣∣∣ 147258369∣∣∣∣∣∣142536=1⋅5⋅9+4⋅8⋅3+7⋅2⋅6−3⋅5⋅7−6⋅8⋅1 −9⋅2⋅4=0.Диагональ по убыванию слева направо имеет знак +++ , а диагональ по убыванию справа налево имеет знак —\text{}−.
Оценить
∣012355575∣.\левый| \begin{matrix} 0 & 1 & 2 \\ 3 & 5 & 5 \\ 5 & 7 & 5 \end{matrix} \right|. ∣∣∣∣∣∣035157255∣∣∣∣∣∣.
У нас есть
∣012355575∣⇒∣012355575∣012355\левый| \begin{matrix} 0 & 1 & 2 \\ 3 & 5 & 5 \\ 5 & 7 & 5 \end{matrix} \right| \Стрелка вправо\влево| \begin{matrix} 0 & 1 & 2 \\ 3 & 5 & 5 \\ 5 & 7 & 5 \end{matrix} \right| \\\quad \quad \quad\quad \quad \quad \begin{matrix} 0 & 1 & 2 \\ 3 & 5 & 5 \end{matrix}∣∣∣∣∣∣035157255∣ ∣∣∣∣∣⇒∣∣∣∣∣∣035157255∣∣∣∣∣∣031525
Это дает
(0×5×5)+(3×7×2)+(5×1×5)−(2×5×5)−(5×7×0)−(5×1×3)=2 .




 Суммируйте все значения и верните.
Суммируйте все значения и верните.
 del_column(j)
#Найти множитель
множитель = X[0][j] * math.pow(-1,(2+j))
# Рекурсия для нахождения определителя
det = рекурсивный_детерминант (новый_x)
term_list.append(множитель*det)
возвращаемая сумма (term_list)
еще:
возврат(Х[0][0]*Х[1][1] - Х[0][1]*Х[1][0])
del_column(j)
#Найти множитель
множитель = X[0][j] * math.pow(-1,(2+j))
# Рекурсия для нахождения определителя
det = рекурсивный_детерминант (новый_x)
term_list.append(множитель*det)
возвращаемая сумма (term_list)
еще:
возврат(Х[0][0]*Х[1][1] - Х[0][1]*Х[1][0])


 det(A)=i=1∑n(−1)i+1a1,idet(A1i)=a1,1detA11−a1,2detA12+⋯ .
det(A)=i=1∑n(−1)i+1a1,idet(A1i)=a1,1detA11−a1,2detA12+⋯ . σ∈S∑(sign(σ)i=1∏nai,σ(i)).
σ∈S∑(sign(σ)i=1∏nai,σ(i)).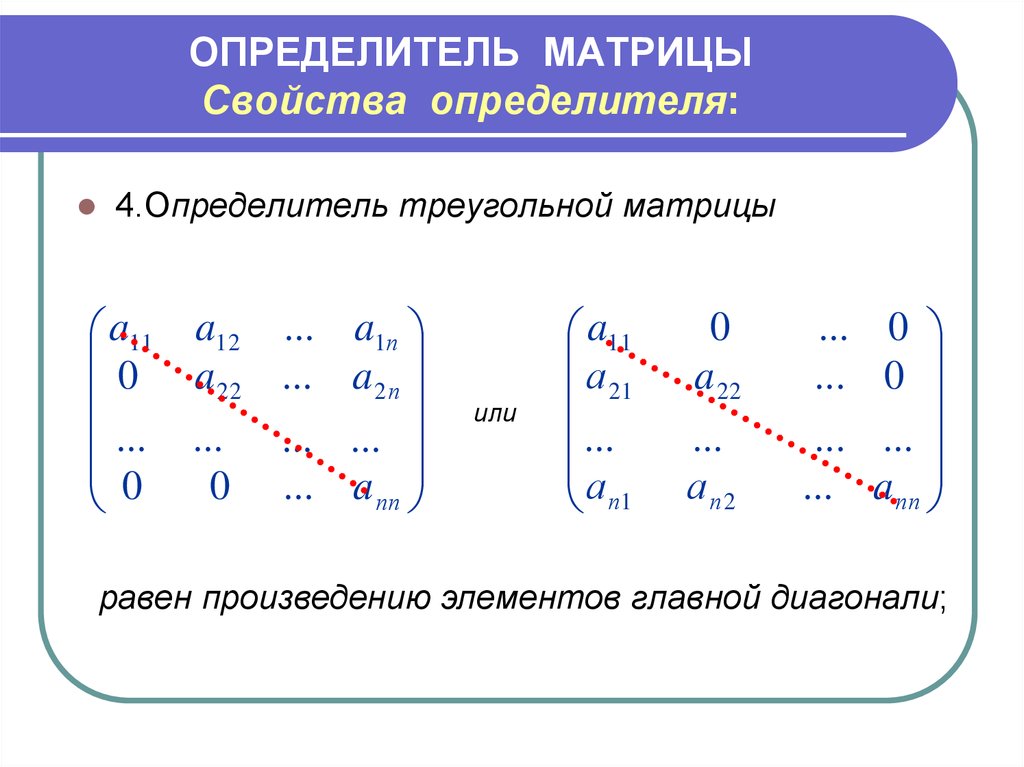 det(A)=σ∈S∑(sign(σ)i=1∏nai,σ(i))=1⋅a1,1a2,2+(−1 )⋅a1,2a2,1=ad−bc.
det(A)=σ∈S∑(sign(σ)i=1∏nai,σ(i))=1⋅a1,1a2,2+(−1 )⋅a1,2a2,1=ad−bc. X=\text{det}\begin{vmatrix} a & 0 & 0 & 0 \\ e & f & 0 & 0 \\ i & j & k & 0 \\ m & n & o & p \end{vmatrix}=a\times f\times k\times p.X=det∣∣∣∣∣∣∣∣aeim0fjn00ko000p∣∣∣∣∣∣ ∣∣=a×f×k×p.
X=\text{det}\begin{vmatrix} a & 0 & 0 & 0 \\ e & f & 0 & 0 \\ i & j & k & 0 \\ m & n & o & p \end{vmatrix}=a\times f\times k\times p.X=det∣∣∣∣∣∣∣∣aeim0fjn00ko000p∣∣∣∣∣∣ ∣∣=a×f×k×p. \begin{выровнено}
[X]=&\begin{bmatrix} 1 & 2 & 2 & 1 \\ 1 & 2 & 4 & 2 \\ 2&7&5&2 \\ -1&4&-6&3 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 — 2\text{row}_1 \rightarrow \text{row}_2 \\ \text{row} _3 — 2\text{row}_1 \rightarrow \text{row}_3 \\ \text{row}_4 — 3\text{row}_1 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\ begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -4&-2&-12&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_4 +12\text{row}_3 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -4&34&0&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_4 +17\text{row}_2 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -21&0&0&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_4 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_1 \rightarrow \text{row}_4 \end {matrix} \Rightarrow — &\begin{bmatrix} -21&0&0&0\\ -1&-2&0&0\\ 0&3&1&0\\ 1&2&2&1 \end{bmatrix} .
\begin{выровнено}
[X]=&\begin{bmatrix} 1 & 2 & 2 & 1 \\ 1 & 2 & 4 & 2 \\ 2&7&5&2 \\ -1&4&-6&3 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 — 2\text{row}_1 \rightarrow \text{row}_2 \\ \text{row} _3 — 2\text{row}_1 \rightarrow \text{row}_3 \\ \text{row}_4 — 3\text{row}_1 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\ begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -4&-2&-12&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_4 +12\text{row}_3 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -4&34&0&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_1 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_4 +17\text{row}_2 \rightarrow \text{row}_4 \end {matrix} \Rightarrow &\begin{bmatrix} 1&2&2&1\\ -1&-2&0&0\\ 0&3&1&0\\ -21&0&0&0 \end{bmatrix} \\\\\\
\begin{matrix} \text{row}_4 \rightarrow \text{row}_1 \\ \text{row}_2 \rightarrow \text{row}_2 \\ \text{row}_3 \rightarrow \text{row} _3 \\ \text{row}_1 \rightarrow \text{row}_4 \end {matrix} \Rightarrow — &\begin{bmatrix} -21&0&0&0\\ -1&-2&0&0\\ 0&3&1&0\\ 1&2&2&1 \end{bmatrix} .