«Основное тригонометрическое тождество. Тригонометрические тождества»
Цель: сформировать определения понятия основного тригонометрического тождества; научиться доказывать тригонометрические тождества
Теоретические сведения к практическому занятию:
Т.к. , уравнение единичной окружности имеет вид , то .
Это равенство, выполняемое при любых значениях α называется основным тригонометрическим тождеством.
Доказательство:
Равенство, справедливое при всех допустимых значениях, входящих в него букв, называют тождеством.
Способы доказательства тождеств:
— преобразование левой части к виду правой;
— преобразование правой части к виду левой;
— установление того, что разность между левой и правой частями равна нулю;
— преобразование левой и правой частей к одному и тому же выражению.
Пример. Вычислить
Вычислить
Решение.
Пример: Найти
Решение:
39
Пример. Доказать тождество:
Доказательство:
Самостоятельная работа:
1.Вычислить:
2. Доказать тождества:
Содержание практического занятия:
А. Ответить на вопросы:
1) Назовите основное тригонометрическое тождество. Приведите примеры.
2) Используя основное тригонометрическое тождество, выразите функции синуса и косинуса.
3) Назовите тригонометрическое тождество для функций тангенса и котангенса.
4) Дайте определение тождества. Приведите примеры.
5) Назовите способы доказательства тождеств.
Б. Выполнить задания:
1.Вычислить:
Тема: «Формулы сложения»
Цель: сформировать умение применять формулы сложения для нахождения значений тригонометрических выражений
Теоретические сведения к практическому занятию:
Формулами сложения называются формулы, выражающие через синусы и косинусы углов α и β.
1)
2)
3)
4)
5)
6)
Пример: Вычислить:
Решение:
Самостоятельная работа:
1) Вычислить:
Содержание практического занятия:
А. Ответить на вопросы:
1) Назовите формулы алгебраического сложения для функции синуса. Приведите доказательство одной из формул.
2) Назовите формулы алгебраического сложения для функции косинуса. Приведите доказательство одной из формул.
3) Назовите формулы алгебраического сложения для функции тангенса. Приведите доказательство одной из формул.
4) Приведите примеры применения формул сложения.
Б. Выполнить задания:
1) Вычислить:
Тема: «Формулы удвоения»
Цель: сформировать умение применять формулы удвоения для нахождения значений тригонометрических выражений
Теоретические сведения к практическому занятию:
1)
2)
3)
Пример: Вычислить
Решение:
Пример: Упростить
Решение:
Содержание практического занятия:
А. Ответить на вопросы:
Ответить на вопросы:
1) Назовите формулу двойного угла для функции синуса. Приведите доказательство этой формулы.
2) Назовите формулу двойного угла для функции косинуса. Приведите доказательство этой формулы.
3) Назовите формулу двойного угла для функции тангенса. Приведите доказательство этой формулы.
Б. Выполнить задания:
1)
Тема: «Формулы приведения»
Цель: сформировать умение применять формулы приведения для нахождения значений тригонометрических выражений
Теоретические сведения к практическому занятию:
Формулы приведения
| рад | ||||||||
| град | ||||||||
 Вычислить
ВычислитьРешение:
Самостоятельная работа:
1) Сформулируйте правила для запоминания формул приведения
2)
Содержание практического занятия:
А. Ответить на вопросы:
1) Назовите формулы приведения для тригонометрических функций.
2) Приведите примеры использования формул приведения.
Б. Выполнить задания:
43
Тема: «Преобразования тригонометрических выражений»
Цель: сформировать умение применять различные формулы тригонометрии для преобразования и нахождения значений тригонометрических выражений
Теоретические сведения к практическому занятию:
Формулы тригонометрии
Самостоятельная работа:
Тема: «Простейшие тригонометрические уравнения вида sinx = a »
Цель: сформировать умение решать простейшие тригонометрические уравнения
Теоретические сведения к практическому занятию:
Содержание практического занятия:
А. Ответить на вопросы:
Ответить на вопросы:
1) Назовите основные формулы для решения уравнений, содержащих функцию y=sin x. Приведите примеры.
2) Когда уравнение sinx=a не имеет решений? Приведите примеры.
Б. Выполнить задания:
1) Решить уравнения:
2) Решить уравнения:
Тема: «Простейшие тригонометрические уравнения cosx = a »
Цель: сформировать умение решать простейшие тригонометрические уравнения
Теоретические сведения к практическому занятию:
Содержание практического занятия:
А. Ответить на вопросы:
1) Назовите основные формулы для решения уравнений, содержащих функцию y=cos x. Приведите примеры.
2) Когда уравнение cosx=a не имеет решений? Приведите примеры.
Б. Выполнить задания:
1) Решить уравнения:
2) Решить уравнения:
Тема: «Простейшие тригонометрические уравнения вида tgx = a , ctgx = a »
Цель: сформировать умение решать простейшие тригонометрические уравнения
Теоретические сведения к практическому занятию:
Содержание практического занятия:
А. Ответить на вопросы:
Ответить на вопросы:
1) Назовите основные формулы для решения уравнений, содержащих функцию y=tg x. Приведите примеры.
2) Назовите основные формулы для решения уравнений, содержащих функцию y=ctg x. Приведите примеры.
Б. Выполнить задания:
1) Решить уравнения:
2) Решить уравнения:
их формулировки и вывод, связь косинуса и тангенса, как из синуса получить косинус
В статье подробно рассказывается об основных тригонометрических тождествах. Эти равенства устанавливают связь между sin, cos, tg, ctg заданного угла. При известной одной функции можно через нее найти другую.
Тригонометрические тождества для рассмотрения в денной статье. Ниже покажем пример их выведения с объяснением.
sin2α+cos2α=1tg α=sin αcos α, ctg α=cos αsin αtg α·ctg α=1tg2α+1=1cos2α, 1+ctg2α=1sin2α
Связь между sin и cos одного угла
Поговорим о важном тригонометрическом тождестве, которое считается основой основ в тригонометрии.
sin2α+cos2α=1
Заданные равенства tg2α+1=1cos2α, 1+ctg2α=1sin2α выводят из основного путем деления обеих частей на sin2α и cos2α. После чего получаем tg α=sin αcos α, ctg α=cos αsin α и tg α·ctg α=1 — это следствие определений синуса, косинуса, тангенса и котангенса.
Равенство sin2α+cos2α=1 является основным тригонометрическим тождеством. Для его доказательства необходимо обратиться к теме с единичной окружностью .
Пусть даны координаты точки А(1,0), которая после поворота на угол αстановится в точку А1. По определению sin и cos точка А1 получит координаты (cos α, sin α). Так как А1 находится в пределах единичной окружности, значит, координаты должны удовлетворят условию x2+y2=1 этой окружности. Выражение cos2α+sin2α=1 должно быть справедливым. Для этого необходимо доказать основное тригонометрическое тождество для всех углов поворота α.
В тригонометрии выражение sin2α+cos2α=1 применяют как теорему Пифагора в тригонометрии. Для этого рассмотрим подробное доказательство.
Используя единичную окружность, поворачиваем точку А с координатами (1,0) вокруг центральной точки О на угол α. После поворота точка меняет координаты и становится равной А1(х,у). Опускаем перпендикулярную прямую А1Н на Ох из точки А1.
На рисунке отлично видно, что образовался прямоугольный треугольник ОА1Н. По модулю катеты ОА1Н и ОН равные, запись примет такой вид: |А1H|=|у|,|ОН|=|х|. Гипотенуза ОА1 имеет значение равное радиусу единичной окружности, |ОА1|=1. Используя данное выражение, можем записать равенство по теореме Пифагора: |А1Н|2 +|ОН|2 =|ОА1|2. Это равенство запишем как |y|2+|x|2=12, что означает y2+x2=1.
Используя определение sin α=y и cosα=x, подставим данные угла вместо координат точек и перейдем к неравенству sin2α+cos2α=1.
Основная связь между sin и cos угла возможна через данное тригонометрическое тождество. Таким образом, можно считать sin угла с известным cos и наоборот. Чтобы выполнить это, необходимо разрешать sin2α+cos2=1 относительно sin и cos, тогда получим выражения вида sin α=±1-cos2α и cos α=±1-sin2α соответственно. Величина угла αопределяет знак перед корнем выражения. Для подробного выяснения необходимо прочитать раздел вычисление синуса, косинуса, тангенса и котангенса с использованием тригонометрических формул.
Величина угла αопределяет знак перед корнем выражения. Для подробного выяснения необходимо прочитать раздел вычисление синуса, косинуса, тангенса и котангенса с использованием тригонометрических формул.
Чаще всего основную формулу применяют для преобразований или упрощений тригонометрических выражений. Имеется возможность заменять сумму квадратов синуса и косинуса на 1. Подстановка тождества может быть как в прямом, так и обратном порядке: единицу заменяют на выражение суммы квадратов синуса и косинуса.
Тангенс и котангенс через синус и косинус
Из определения косинуса и синуса, тангенса и котангенса видно, что они взаимосвязаны друг с другом, что позволяет отдельно преобразовывать необходимые величины.
tg α=sin αcos αctg α=cos αsin α
Из определения синус является ординатой у, а косинус – абсциссой x. Тангенс – это и есть отношения ординаты и абсциссы. Таким образом имеем:
tg α=yx=sin αcos α, а выражение котангенса имеет обратное значение, то есть
ctg α=xy=cos αsin α.
Отсюда следует, что полученные тождества tg α=sin αcos α и ctg α=cos αsin α задаются с помощью sin и cos углов. Тангенс считаются отношением синуса к косинусу угла между ними, а котангенс наоборот.
Отметим, что tg α=sin αcos α и ctg α=cos αsin α верны для любого значение угла α, значения которого входят в диапазон. Из формулы tg α=sin αcos α значение угла α отлично от π2+π·z, а ctg α=cos αsin α принимает значение угла α, отличные от π·z, z принимает значение любого целого числа.
Связь между тангенсом и котангенсом
Имеется формула, которая показывает связь между углами через тангенс и котангенс. Данное тригонометрическое тождество является важным в тригонометрии и обозначается как tg α·ctg α=1. Оно имеет смысл при α с любым значением, кроме π2·z, иначе функции будут не определены.
Формула tg α·ctg α=1 имеет свои особенности в доказательстве. Из определения мы имеем, что tg α=yx и ctg α=xy, отсюда получаем tg α·ctg α=yx·xy=1. Преобразовав выражение и подставив tg α=sin αcos α и ctg α=cos αsin α, получим tg α·ctg α=sin αcos α·cos αsin α=1.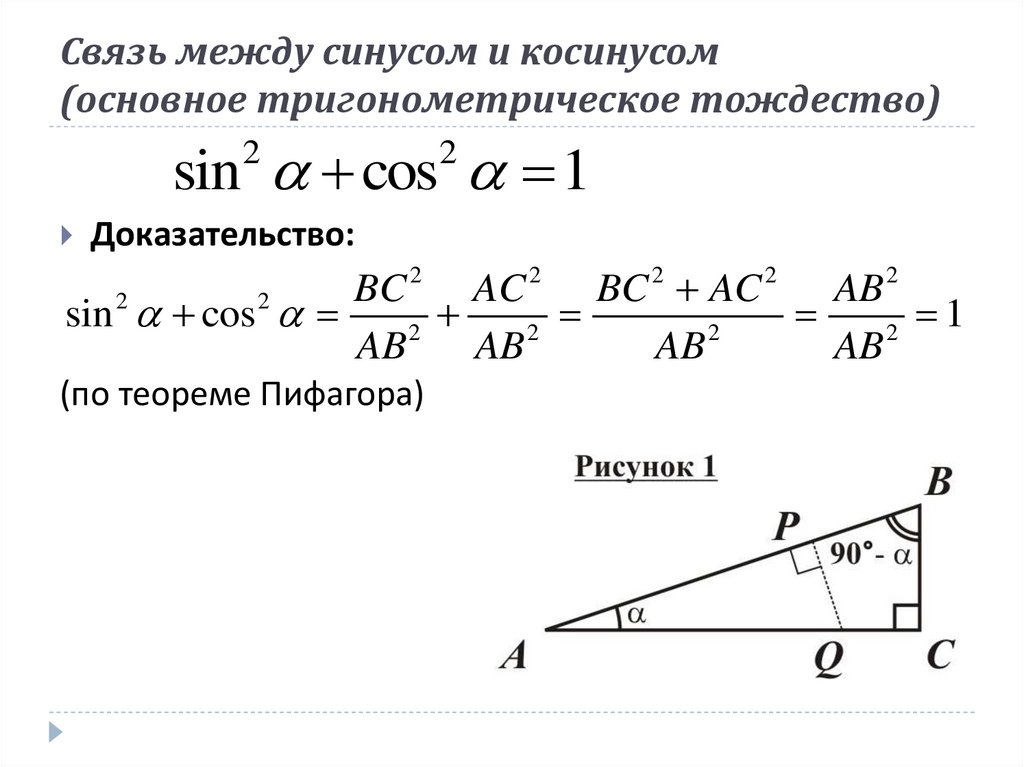
Тогда выражение тангенса и котангенса имеет смысл того, когда в итоге получаем взаимно обратные числа.
Тангенс и косинус, котангенс и синусПреобразовав основные тождества, приходим к выводу, что тангенс связан через косинус, а котангенс через синус. Это видно по формулам tg2α+1=1cos2α, 1+ctg2α=1sin2α.
Определение звучит так: сумма квадрата тангенса угла и 1 приравнивается к дроби , где в числителе имеем 1, а в знаменателе квадрат косинуса данного угла, а сумма квадрата котангенса угла наоборот. Благодаря тригонометрическому тождеству sin2α+cos2α=1, можно разделить соответствующие стороны на cos2α и получить tg2α+1=1cos2α, где значение cos2α не должно равняться нулю. При делении на sin2α получим тождество 1+ctg2α=1sin2α, где значение sin2α не должно равняться нулю.
Из приведенных выражений получили, что тождество tg2α+1=1cos2α верно при всех значениях угла α, не принадлежащих π2+π·z, а 1+ctg2α=1sin2α при значениях α, не принадлежащих промежутку π·z.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ СТУДЕНТОВ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОГО ЗАНЯТИЯ «Основные тригонометрические тождества» | Учебно-методический материал по математике на тему:
комитет образования и науки Волгоградской области
государственное бюджетное профессиональное образовательное учреждение
«Волжский политехнический техникум»
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ДЛЯ СТУДЕНТОВ
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОГО ЗАНЯТИЯ
«Основные тригонометрические тождества»
Учебная дисциплина: Математика: алгебра и начала математического анализа, геометрия.
Специальности: 23.02.03, 13.02.11, 15.02.07
Курс: 1
Автор: Курлович Елена Павловна, преподаватель первой квалификационной категории;
2016-2017 г.
Введение
Методические указания для выполнения практического занятия «Основные тригонометрические тождества», по дисциплине: Математика: алгебра и начала математического анализа, геометрия, созданы в помощь студентам, для успешной работы на занятие и подготовки к данному практическому занятию.
Приступая к выполнению практического задания, студенты должны внимательно прочитать цели занятия, ознакомиться с общими сведения и примерами выполнения заданий, с критериями оценивания работы, ответить на контрольные вопросы для закрепления теоретического материала.
Наличие положительной оценки по практическому занятию необходимо для получения допуска к экзамену, поэтому в случае отсутствия на уроке по любой причине или получения неудовлетворительной оценки за практическое занятие, студенты должны найти время для его выполнения или пересдачи.
Если в процессе подготовки к практическому занятию или при решении задач у студентов возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения дополнительных занятий.
Время проведения дополнительных занятий можно узнать у преподавателя или посмотреть на двери 122 кабинета.
Практическое занятие 7
Основные тригонометрические тождества.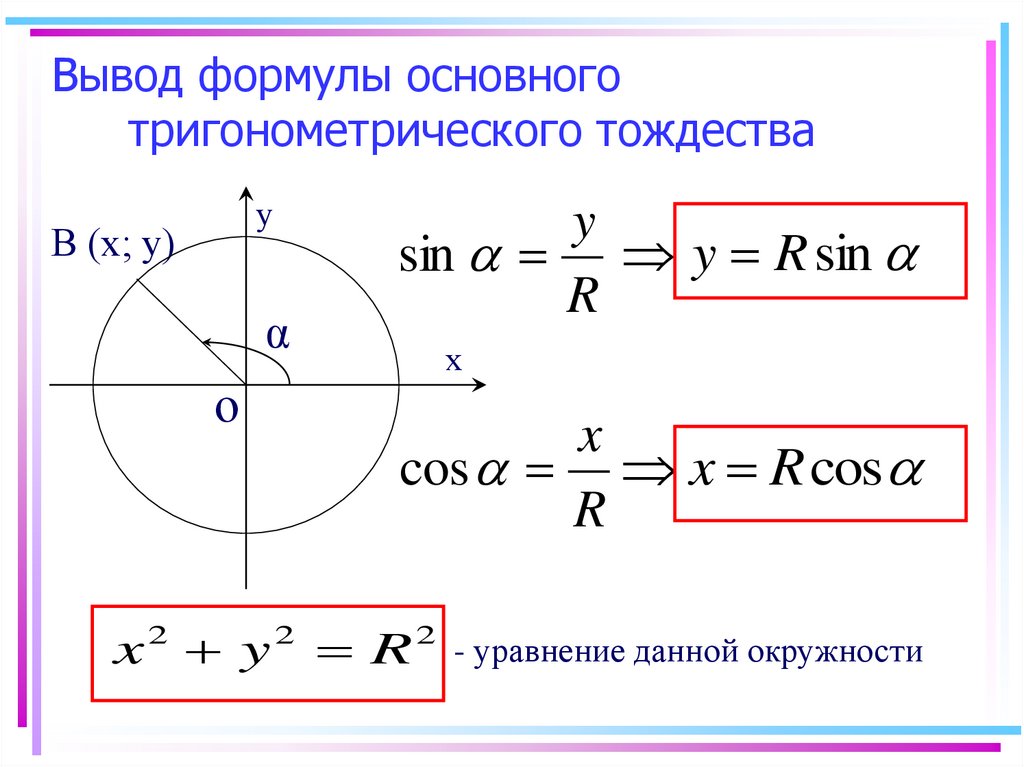
Продолжительность занятия: 2 часа
Общие сведения и примеры выполнения заданий:
При выполнении заданий по данной теме нужно помнить:
Основные тригонометрические тождества 1) 2) 3) 4) 5) 6) | Четность, нечетность тригонометри- ческих функций |
Знаки тригонометрических функций по четвертям
Таблица значений тригонометрических функций, некоторых углов.
Рассмотрим примеры выполнения заданий.
1. Упростите | Применяемые правила |
Найти неизвестные из тригонометрических функций: , если
Дано: Найти: . | Решение: Из формулы :, выразим учитывая, что четверти, , , Формуле (2): , Т.
Ответ: ,, . |
2.Дано . Какое значение имеют остальные тригонометрические функции этого угла. В ответе дроби не сокращайте.
Дано: Найти: . | Решение: Из формулы : , выразим учитывая, что четверти, , решим пропорцию , По формуле (1): , выразим учитывая, что четверти, Т.к. то Ответ: ,, . |
3. Доказательство тригонометрических тождеств
При доказательстве любых тождеств, и в частности тригонометрических, обычно используют следующие способы:
1) выражение, стоящее и одной части равенства, с помощью тождественных преобразований приводят к выражению, стоящему в другой части равенства;
2) выражения, стоящие в левой и правой частях тождества, с помощью тождественных преобразований приводят к одному и тому же виду;
3) доказывают, что разность между левой и правой частями данного тождества равна нулю.
Рассмотрим пример:
Доказать тождество: .
Используя формулу для разности квадратов двух чисел, получаем:
= () ().
Ho . Поэтому
, что и требовалось доказать.
Критерии оценивания работы:
На «3»:
1)
функций:.
На «4»:
2) Упростите выражение.
На «5»:
3) Докажите, что равенство, является тождеством.
Контрольные вопросы:
1. Значения тригонометрических функций основных углов.
2. Знаки тригонометрических функций по четвертям.
3. Свойства тригонометрических функций.
4. Перечислите свойства, основные тригонометрические тождества.
5. Формулы сокращенного умножения.
Задания для самостоятельной подготовки к практическому занятию:
Задание 1
;
Найти неизвестные из тригонометрических функций:
1 вариант | Если |
2 вариант | Если |
Задание 2
Дан тангенс (котангенс) угла. Какое значение имеют остальные тригонометрические функции этого угла. В ответе дроби не сокращайте.
Какое значение имеют остальные тригонометрические функции этого угла. В ответе дроби не сокращайте.
1 вариант | |
2 вариант |
Задание 3
Докажите, что равенство, является тождеством
1 вариант | |
2 вариант |
1. http://fizmat.by/math/trigonometry/trigon_formuly
2. http://oldskola1.narod.ru/trigF16.htm
3. В.С. Крамор: Повторяем и систематизируем школьный курс алгебры и начал анализа- М.:ООО «Издательство Оникс»: ООО «Издательство «Мир и образование», 2008
Основное тригонометрическое тождество. Формулы приведения
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами .
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т. д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Это последний и самый главный урок, необходимый для решения задач B11. Мы уже знаем, как переводить углы из радианной меры в градусную (см. урок «Радианная и градусная мера угла »), а также умеем определять знак тригонометрической функции, ориентируясь по координатным четвертям (см. урок «Знаки тригонометрических функций »).
Дело осталось за малым: вычислить значение самой функции — то самое число, которое записывается в ответ. Здесь на помощь приходит основное тригонометрическое тождество.
Основное тригонометрическое тождество. Для любого угла α верно утверждение:
sin 2 α + cos 2 α = 1.
Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Достаточно извлечь квадратный корень:
Обратите внимание на знак «±» перед корнями. Дело в том, что из основного тригонометрического тождества непонятно, каким был исходный синус и косинус: положительным или отрицательным. Ведь возведение в квадрат — четная функция, которая «сжигает» все минусы (если они были).
Именно поэтому во всех задачах B11, которые встречаются в ЕГЭ по математике, обязательно есть дополнительные условия, которые помогают избавиться от неопределенности со знаками. Обычно это указание на координатную четверть, по которой можно определить знак.
Внимательный читатель наверняка спросит: «А как быть с тангенсом и котангенсом?» Напрямую вычислить эти функции из приведенных выше формул нельзя. Однако существуют важные следствия из основного тригонометрического тождества, которые уже содержат тангенсы и котангенсы. А именно:
Важное следствие: для любого угла α можно переписать основное тригонометрическое тождество следующим образом:
Эти уравнения легко выводятся из основного тождества — достаточно разделить обе стороны на cos 2 α
(для получения тангенса) или на sin 2 α
(для котангенса).
Рассмотрим все это на конкретных примерах. Ниже приведены настоящие задачи B11, которые взяты из пробных вариантов ЕГЭ по математике 2012.
Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:
sin 2 α + cos 2 α = 1 ⇒ sin 2 α + 99/100 = 1 ⇒ sin 2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.
Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π /2; π ), то в градусной мере это записывается так: α ∈ (90°; 180°).
Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1.
Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:
sin 2 α + cos 2 α = 1 ⇒ 3/4 + cos 2 α = 1 ⇒ cos 2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α
принадлежит промежутку (π
3π
/2). Переведем углы из радианной меры в градусную — получим: α
∈ (180°; 270°).
Что выбрать: плюс или минус? По условию, угол α
принадлежит промежутку (π
3π
/2). Переведем углы из радианной меры в градусную — получим: α
∈ (180°; 270°).
Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.
Задача. Найдите tg α , если известно следующее:
Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:
Получаем: tg α = ±3. Знак тангенса определяем по углу α . Известно, что α ∈ (3π /2; 2π ). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.
Задача. Найдите cos α , если известно следующее:
Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 ⇒ 0,64 + cos 2 α = 1 ⇒ cos 2 α = 0,36 ⇒ cos α = ±0,6.
Знак определяем по углу. Имеем: α
∈ (3π
/2; 2π
). Переведем углы из градусной меры в радианную: α
∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α
= 0,6.
Имеем: α
∈ (3π
/2; 2π
). Переведем углы из градусной меры в радианную: α
∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α
= 0,6.
Задача. Найдите sin α , если известно следующее:
Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:
Отсюда получаем, что sin 2 α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π /2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.
Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2.
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье.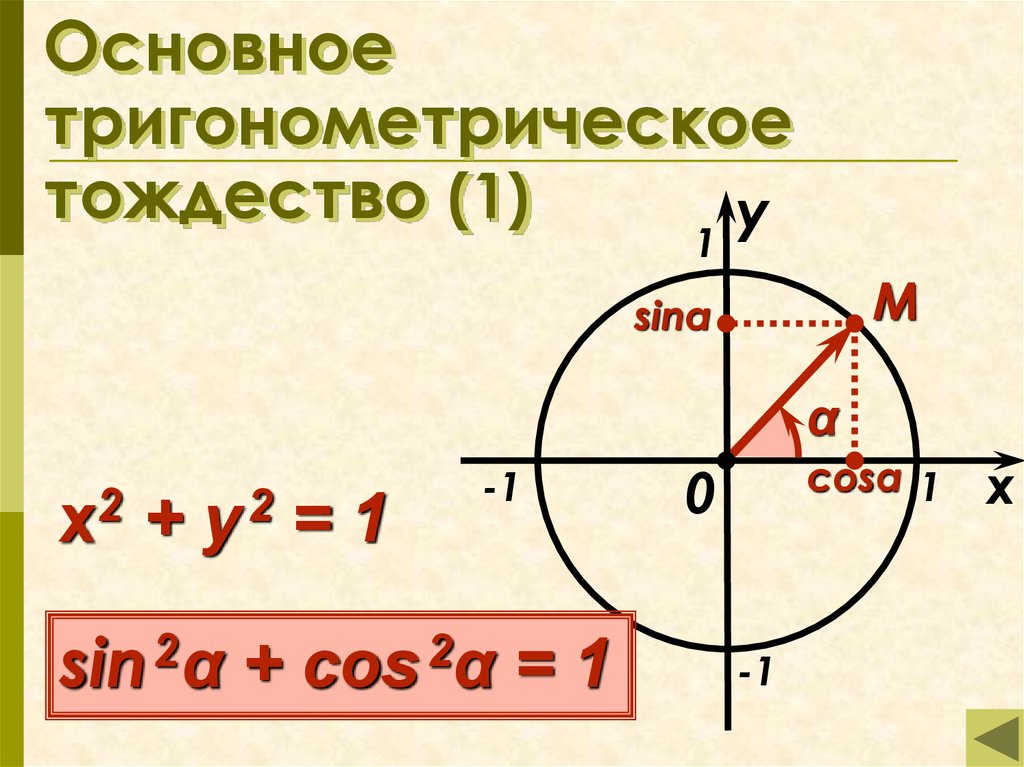 Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента . С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Формулы приведения:
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет
2. Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Пример:
Вычислить
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен «+». Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
Формулы приведения — это соотношения, которые позволяют перейти от синус, косинус, тангенс и котангенс с углами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно.
Всех вместе формул приведения есть 32 штуки. Они несомненно пригодятся на ЕГЭ, экзаменах, зачетах. Но сразу предупредим, что заучивать наизусть их нет необходимости! Нужно потратить немного времени и понять алгоритм их применения, тогда для вас не составит труда в нужный момент вывести необходимое равенство. \circ \pm \alpha`):
\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:
Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.
И вторая, аналогичная таблица, где углы записаны в градусах:
Мнемоническое правило формул приведения или как их запомнить
Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности. Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.
Само привило содержит 3 этапа:
- Аргумент функции должен быть представлен в виде `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, причем `\alpha` — обязательно острый угол (от 0 до 90 градусов).
- Для аргументов `\frac {\pi}2 \pm \alpha`, `\frac {3\pi}2 \pm \alpha` тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов `\pi \pm \alpha`, `2\pi \pm \alpha` функция не меняется.
- Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:
1. \circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac{\pi}2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac{\pi}2-\alpha)= — cos (\frac{\pi}2-\alpha)= — sin \alpha`.
Ответ: `cos(\frac {7\pi}2 — \alpha)=- sin \alpha`.
Лошадиное правило
Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?
Итак, мы имеем функции с аргументами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac {\pi}2`, `\pi`, `\frac {3\pi}2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac {\pi}2` и `\frac {3\pi}2` на вертикальной оси ординат.
Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.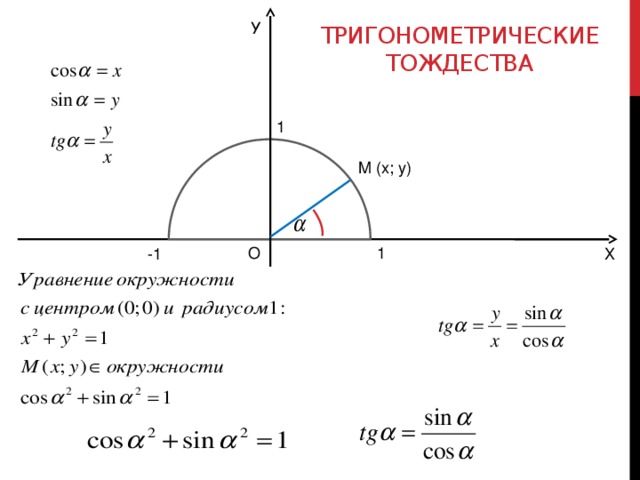 \circ=-\frac{\sqrt 3}2`.
\circ=-\frac{\sqrt 3}2`.
Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac {9\pi}8` и `cos \frac {9\pi}8`; 2) `sin \frac {\pi}8` и `cos \frac {3\pi}10`.
Решение: 1)`sin \frac {9\pi}8=sin (\pi+\frac {\pi}8)=-sin \frac {\pi}8`
`cos \frac {9\pi}8=cos (\pi+\frac {\pi}8)=-cos \frac {\pi}8=-sin \frac {3\pi}8`
`-sin \frac {\pi}8> -sin \frac {3\pi}8`
`sin \frac {9\pi}8>cos \frac {9\pi}8`.
2) `cos \frac {3\pi}10=cos (\frac {\pi}2-\frac {\pi}5)=sin \frac {\pi}5`
`sin \frac {\pi}8
`sin \frac {\pi}8
Докажем сначала две формулы для синуса и косинуса аргумента `\frac {\pi}2 + \alpha`: ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha` и` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.
Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac {\pi}2 + \alpha` в точку `А_2(-у,х)`. Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
Выходя из определения тангенса и котангенса, получим ` tg(\frac {\pi}2 + \alpha)=\frac {sin(\frac {\pi}2 + \alpha)}{cos(\frac {\pi}2 + \alpha)}=\frac {cos \alpha}{-sin \alpha}=-ctg \alpha` и ` сtg(\frac {\pi}2 + \alpha)=\frac {cos(\frac {\pi}2 + \alpha)}{sin(\frac {\pi}2 + \alpha)}=\frac {-sin \alpha}{cos \alpha}=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac {\pi}2 + \alpha`.
Чтобы доказать формулы с аргументом `\frac {\pi}2 — \alpha`, достаточно представить его, как `\frac {\pi}2 + (-\alpha)` и проделать тот же путь, что и выше. Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac {\pi}2 +(\frac {\pi}2+\alpha)` и `\frac {\pi}2 +(\frac {\pi}2-\alpha)` соответственно.
А `\frac {3\pi}2 + \alpha` и `\frac {3\pi}2 — \alpha` как `\pi +(\frac {\pi}2+\alpha)` и `\pi +(\frac {\pi}2-\alpha)`.
Уход за кожейОсновные тригонометрические тождества. Конспект урока по математике «тригонометрические формулы»
- sin(a) = ±√(1-(cos(a)) 2) = — √(1 – 9/25) = — 4/5.
Соотношение между тангенсом и котангенсом одного и того же угла
Теперь, попробуем найти зависимость, между тангенсом и котангенсов.
По определению tg(a) = sin(a)/cos(a), ctg(a) = cos(a)/sin(a).
Перемножим эти равенства, получим tg(a)*ctg(a) =1.
Из этого равенства можно выразить одну функцию через другую. Получим:
- tg(a) = 1/ctg(a),
- ctg(a) = 1/tg(a).
Следует понимать, что эти равенства справедливы лишь тогда, когда tg и ctg существуют, то есть для любых а, кроме а=k*pi/2, при любом целом k.
Теперь попробуем используя основное тригонометрическое тождество найти зависимости между тангенсом и косинусом.
Поделим основное тригонометрическое тождество, на (cos(a)) 2 . (cos(a) не равен нулю, иначе бы тангенс не существовал бы.
Получим следующее равенство ((sin(a)) 2 + (cos(a)) 2)/ (cos(a)) 2 =1/(cos(a)) 2 .
Разделив почленно получаем:
- 1+(tg(a)) 2 = 1/(cos(a)) 2 .
Как уже отмечалось выше, эта формула верна если cos(a) не равен нулю, то есть для всех углов а, кроме а=pi/2 +pi*k, при любом целом k.
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
«Теорема синусов и косинусов» — 1) Запишите теорему синусов для данного треугольника: Найдите угол В. Запишите формулу для вычисления: Теорема синусов: Найдите длину стороны ВС. Теоремы синусов и косинусов. Стороны треугольника пропорциональны синусам противолежащих углов. 2) Запишите теорему косинусов для вычисления стороны МК: Самостоятельная работа:
«Решение тригонометрических неравенств» — Все значения y на промежутке MN. 1. Строим графики функций: Остальные промежутки. Прямая y=-1/2 пересекает синусоиду в бесконечном числе точек, а тригонометрический круг — в точке А. бесконечного множества промежутков. А на синусоиде, ближайший к началу координат промежуток значений x, при которых sinx>-1/2,
1. Строим графики функций: Остальные промежутки. Прямая y=-1/2 пересекает синусоиду в бесконечном числе точек, а тригонометрический круг — в точке А. бесконечного множества промежутков. А на синусоиде, ближайший к началу координат промежуток значений x, при которых sinx>-1/2,
«Тригонометрические формулы» — Формулы преобразования суммы тригонометрических функций в произведение. Формулы преобразования произведения тригонометрических функций в сумму. Формулы сложения. По тригонометрическим функциям угла?. Формулы двойных углов. Сложив почленно равенства (3) и (4), получим: Выведем вспомогательные формулы, позволяющие находить.
«Решение простейших тригонометрических неравенств» — cos x. Методы решения тригонометрических неравенств. sin x. Тригонометрическими неравенствами называются неравенства, содержащие переменную в аргументе тригонометрической функции. Решение простейших тригонометрических неравенств.
«Sin и cos» — Верно ли,что косинус 6,5 больше нуля? Синус 60° равен?? Верно ли что соs? х — siп? х = 1? Раздел математики, изучающий свойства синуса, косинуса… Урок по алгебре и началам анализа в 10 классе. Решение тригонометрических уравнений и неравенств. Абсцисса точки на единичной окружности. Отношение косинуса к синусу…
Решение тригонометрических уравнений и неравенств. Абсцисса точки на единичной окружности. Отношение косинуса к синусу…
«Теорема косинусов для треугольника» — Устная работа. Неизвестные элементы. Треугольник. Квадрат стороны треугольника. Сформулируйте теорему косинусов. Теорема. Теорема косинусов. Решение задач на клеточной бумаге. Углы и стороны. Сформулировать теорему косинусов. Задачи по готовым чертежам. Данные, указанные на рисунке.
Всего в теме 21 презентация
Как решать тригонометрические тождества. Основные тригонометрические формулы
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.
tg \alpha = \frac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
tg \alpha \cdot ctg \alpha = 1
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y является синус, а абсциссой x — косинус. Тогда тангенс будет равен отношению \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha} , а отношение \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha} — будет являться котангенсом.
Добавим, что только для таких углов \alpha , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , ctg \alpha=\frac{\cos \alpha}{\sin \alpha} .
Например: tg \alpha = \frac{\sin \alpha}{\cos \alpha}
является справедливой для углов \alpha
, которые отличны от \frac{\pi}{2}+\pi z
, а ctg \alpha=\frac{\cos \alpha}{\sin \alpha}
— для угла \alpha
, отличного от \pi z
, z
— является целым числом. {2} \alpha = 1
. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14
.
{2} \alpha = 1
. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14
.
По условию \frac{\pi}{2}
Для того, чтобы найти ctg \alpha , воспользуемся формулой ctg \alpha = \frac{\cos \alpha}{\sin \alpha} . Соответствующие величины нам известны.
ctg \alpha = -\frac12: \frac{\sqrt3}{2} = -\frac{1}{\sqrt 3} .
Это последний и самый главный урок, необходимый для решения задач B11. Мы уже знаем, как переводить углы из радианной меры в градусную (см. урок «Радианная и градусная мера угла »), а также умеем определять знак тригонометрической функции, ориентируясь по координатным четвертям (см. урок «Знаки тригонометрических функций »).
Дело осталось за малым: вычислить значение самой функции — то самое число, которое записывается в ответ. Здесь на помощь приходит основное тригонометрическое тождество.
Основное тригонометрическое тождество. Для любого угла α верно утверждение:
sin 2 α + cos 2 α = 1.
Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Обратите внимание на знак «±» перед корнями. Дело в том, что из основного тригонометрического тождества непонятно, каким был исходный синус и косинус: положительным или отрицательным. Ведь возведение в квадрат — четная функция, которая «сжигает» все минусы (если они были).
Именно поэтому во всех задачах B11, которые встречаются в ЕГЭ по математике, обязательно есть дополнительные условия, которые помогают избавиться от неопределенности со знаками. Обычно это указание на координатную четверть, по которой можно определить знак.
Внимательный читатель наверняка спросит: «А как быть с тангенсом и котангенсом?» Напрямую вычислить эти функции из приведенных выше формул нельзя. Однако существуют важные следствия из основного тригонометрического тождества, которые уже содержат тангенсы и котангенсы. А именно:
Важное следствие: для любого угла α можно переписать основное тригонометрическое тождество следующим образом:
Эти уравнения легко выводятся из основного тождества — достаточно разделить обе стороны на cos 2 α
(для получения тангенса) или на sin 2 α
(для котангенса).
Рассмотрим все это на конкретных примерах. Ниже приведены настоящие задачи B11, которые взяты из пробных вариантов ЕГЭ по математике 2012.
Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:
sin 2 α + cos 2 α = 1 ⇒ sin 2 α + 99/100 = 1 ⇒ sin 2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.
Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π /2; π ), то в градусной мере это записывается так: α ∈ (90°; 180°).
Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1.
Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:
sin 2 α + cos 2 α = 1 ⇒ 3/4 + cos 2 α = 1 ⇒ cos 2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α
принадлежит промежутку (π
3π
/2). Переведем углы из радианной меры в градусную — получим: α
∈ (180°; 270°).
Что выбрать: плюс или минус? По условию, угол α
принадлежит промежутку (π
3π
/2). Переведем углы из радианной меры в градусную — получим: α
∈ (180°; 270°).
Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.
Задача. Найдите tg α , если известно следующее:
Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:
Получаем: tg α = ±3. Знак тангенса определяем по углу α . Известно, что α ∈ (3π /2; 2π ). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.
Задача. Найдите cos α , если известно следующее:
Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 ⇒ 0,64 + cos 2 α = 1 ⇒ cos 2 α = 0,36 ⇒ cos α = ±0,6.
Знак определяем по углу. Имеем: α
∈ (3π
/2; 2π
). Переведем углы из градусной меры в радианную: α
∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α
= 0,6.
Имеем: α
∈ (3π
/2; 2π
). Переведем углы из градусной меры в радианную: α
∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α
= 0,6.
Задача. Найдите sin α , если известно следующее:
Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:
Отсюда получаем, что sin 2 α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π /2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.
Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2.
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
3.1: Основные тригонометрические тождества — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3285
- Майкл Коррал
- Schoolcraft College
- \(\csc\;\theta ~=~ \dfrac{1}{\sin\;\theta} \qquad \) когда \(\sin\;\theta \ne 0\)
- \(\sec\;\theta ~=~ \dfrac{1}{\cos\;\theta} \qquad \) когда \(\cos\;\theta \ne 0\)
- \(\cot\;\theta ~=~ \dfrac{1}{\tan\;\theta} \qquad \), когда определено \(\tan\;\theta \), а не \(0\)
- \(\sin\;\theta ~=~ \dfrac{1}{\csc\;\theta} \qquad \), когда определено \(\csc\;\theta \), а не \(0\)
- \(\cos\;\theta ~=~ \dfrac{1}{\sec\;\theta} \qquad \), когда определено \(\sec\;\theta \), а не \(0\)
- \(\tan\;\theta ~=~ \dfrac{1}{\cot\;\theta} \qquad \), когда определено \(\cot\;\theta \), а не \(0\)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Майкл Коррал
- Лицензия
- ГНУ ФДЛ
- Версия лицензии
- 1,3
- Показать страницу TOC
- нет
- Теги
- источник@http://www.
 mecmath.net/trig/index.html
mecmath.net/trig/index.html
- источник@http://www.
- Смежное всегда очень близко к Тета θ или Угол
- И Противоположный всегда находится напротив Тета θ или Угол
- Гипотенуза
- Смежный
- Напротив
- Синус
- Косинус
- Касательная
- SIN 2 θ , , затем возвести результат в квадрат и
- sin θ 2 означает возведение в квадрат θ, , затем выполняет функцию синуса
- sin(32°) = 0,5299…
- cos(32°) = 0,8480…
-
Уравнение 18 - Хорошо выучите приведенные выше формулы (или, по крайней мере, научитесь их быстро находить). Чем лучше вы знаете основные тождества, тем легче будет распознать, что происходит в задачах.
- Работайте над самой сложной стороной и упростите ее так, чтобы она имела такую же форму, как и самая простая сторона.
- Не принимайте идентичность 1496 доказывают личность. Это означает, что не работайте по обе стороны от стороны равных, а старайтесь встретиться посередине. Начните с одной стороны и сделайте ее похожей на другую сторону.
- Многие из них получаются довольно легко, если выразить все на самой сложной стороне только через синус и косинус .
- В большинстве примеров, где вы видите степень 2 (то есть 2 ), будет использоваться тождество sin 2 θ + cos 2 θ = 1 (или одна из двух других формул, которые мы вывели выше).

- Доказательство тригонометрических тождеств — основы
- Доказательство тригонометрических тождеств — средний уровень
- Доказательство тригонометрических тождеств — продвинутый уровень
- Доказательство тригонометрических тождеств
- Основной подход
- Использование формул суммы и произведения
92 \тета = 1.
 sin2θ+cos2θ=1.
sin2θ+cos2θ=1.Чтобы доказать тригонометрические тождества, мы обычно используем другие известные тождества, такие как тождества Пифагора.
Докажите, что (1−sinx)(1+cscx)=cosxcotx.(1 — \sin x) (1 +\csc x) =\cos x \cot x.(1−sinx) (1+cscx)=cosxcotx.
У нас есть
(1−sinx)(1+cscx)=(1−sinx)(1+1sinx).(1 — \sinx) (1 +\cscx)=(1-\ sin x)\left(1 + \frac{1}{\sin x} \right).(1−sinx)(1+cscx)=(1−sinx)(1+sinx1).
Раскрывая скобки, получаем 92 х) + \sin x \cos x — \sin x \cos x \\\\ &= 2.\ _ \квадрат \end{align}cosx+sinxcos3x+sin3x+cosx-sinxcos3x-sin3x=cosx+sinx(cosx+sinx)(cos2x+sin2x-sinxcosx)+cosx-sinx(cosx-sinx)(cos2x+sin2x+ sinxcosx)=2(sin2x+cos2x)+sinxcosx−sinxcosx=2. □
Под доказательством тригонометрического тождества подразумевается демонстрация того, что тождество всегда истинно, независимо от того, какое значение x x x или θ \ theta θ используется.
Поскольку это должно выполняться для всех значений xxx, мы не можем просто подставить несколько значений xxx, чтобы «показать», что они равны.
 Возможно, что обе стороны равны при нескольких значениях (а именно, когда мы решаем уравнение), и мы можем ошибочно думать, что имеем истинное тождество.
Возможно, что обе стороны равны при нескольких значениях (а именно, когда мы решаем уравнение), и мы можем ошибочно думать, что имеем истинное тождество.Вместо этого мы должны использовать логические шаги, чтобы показать, что одна часть уравнения может быть преобразована в другую часть уравнения. Иногда мы будем работать отдельно с каждой стороны, пока они не сойдутся посередине.
Вы должны быть знакомы с различными тригонометрическими тождествами, такими как обратные тригонометрические функции и тождества Пифагора.
Существует множество различных способов подтверждения личности. Вот несколько советов на случай, если вы застряли:
1) Работайте на той стороне, которая сложнее. Попробуйте и упростите.
2) Замените все тригонометрические функции только на sinθ \sin \theta sinθ и cosθ \cos \theta cosθ, где это возможно.
3) Определите алгебраические операции, такие как разложение на множители, разложение, распределительное свойство, сложение и умножение дробей. Это позволяет еще больше упростить выражение.
Это позволяет еще больше упростить выражение.
4) Используйте различные тригонометрические тождества. В частности, следите за пифагорейской идентичностью.
5) Работа с обеих сторон.
6) Следите за другой стороной и двигайтесь к ней.
7) Рассмотрим «тригонометрическое сопряжение».Подтвердите личность
раскладушкаθcscθ=cosθ. \frac { \cot \theta } { \csc \theta } = \cos \theta. cscθcotθ=cosθ.
(Руководство 1)
Начнем с более сложного LHS. Обратите внимание, что если бы мы начали с правой стороны, неясно, как мы могли бы двигаться дальше.(Рекомендация 2)
Мы заменяем cotθ \cot \theta cotθ на cosθsinθ \frac{ \cos \theta} { \sin \theta } sinθcosθ и cscθ \csc \theta cscθ на 1sin θ \frac{ 1 } {\sin \theta } sinθ1, чтобы получить 92 x } = \frac{1} { \sin x } = \csc x = RHS.\ _\square LHS=sinx×sin2x1=sinx1=cscx=RHS. □Подтвердите личность
sinθ1−cosθ+1−cosθsinθ=2cscθ.
 \frac{ \sin \theta} { 1 — \cos \theta} + \frac{ 1 — \cos \theta} { \sin \theta } = 2 \csc \theta .1−cosθsinθ+sinθ1−cosθ= 2cscθ.
\frac{ \sin \theta} { 1 — \cos \theta} + \frac{ 1 — \cos \theta} { \sin \theta } = 2 \csc \theta .1−cosθsinθ+sinθ1−cosθ= 2cscθ.(рекомендация 2, 5) Поскольку левая часть уже выражена в терминах sinθ \sin\theta sinθ и cosθ \cos \theta cosθ, мы упрощаем правую часть до
.RHS=2sinθ. RHS = \ frac { 2 } { \ sin \ theta } . RHS=sinθ2. 92 \ тета = 1 — 2 \ соз \ тета + 1 = 2 — 2 \ соз \ тета . sin2θ+(1−cosθ)2=sin2θ+1−−2cosθ+cos2θ=1−2cosθ+1=2−2cosθ.
А-ха! Есть гораздо более простой способ записать числитель, и LHS станет равным
.LHS=2−2cosθsinθ(1−cosθ)=2sinθ=RHS. □ LHS = \frac{ 2 — 2 \cos \theta} { \sin \theta ( 1 — \cos \theta )} = \frac{ 2 } { \sin \theta } = RHS.\ _\square LHS=sinθ (1−cosθ)2−2cosθ=sinθ2=RHS. □
Вы можете попрактиковаться в доказательстве тригонометрических тождеств, участвуя в нашем обсуждении здесь:
- Докажите следующее — 1
- Докажи следующее — 2
Подтвердите личность
танθ+котθ=2sin2θ.
 2 \theta} { \sin \theta \cos \theta} = \frac{ 1} { \ грех \ тета \ соз \ тета }. LHS=cosθsinθ+sinθcosθ=sinθcosθsin2θ+cos2θ=sinθcosθ1.
2 \theta} { \sin \theta \cos \theta} = \frac{ 1} { \ грех \ тета \ соз \ тета }. LHS=cosθsinθ+sinθcosθ=sinθcosθsin2θ+cos2θ=sinθcosθ1.(Рекомендация 5) Теперь мы застряли, так как это очень просто. Смотрим на RHS. Заменив sin2θ \sin 2 \thetasin2θ на 2sinθcosθ 2 \sin \theta \cos \theta 2sinθcosθ, мы получим
RHS=2sin2θ=22sinθcosθ=1sinθcosθ. RHS = \ гидроразрыв {2} { \ грех 2 \ тета } = \ гидроразрыв { 2 } { 2 \ грех \ тета \ соз \ тета } = \ гидроразрыв { 1 } { \ грех \ тета \ соз \ тета } . RHS=sin2θ2=2sinθcosθ2=sinθcosθ1.
Таким образом имеем
ЛВС=1sinθcosθ=Правая. □ LHS = \frac{ 1}{ \sin \theta \cos \theta } =RHS.\ _\square LHS=sinθcosθ1=RHS. □
Подтвердите личность
sinx−cosxsinx+cosx=−cos2×1+sin2x. \frac{ \sin x — \cos x } { \sin x + \cos x } = — \frac{ \cos 2x} { 1 + \sin 2 x }. sinx+cosxsinx-cosx=−1+sin2xcos2x.
(рекомендация 6) Эту личность трудно атаковать напрямую.
 2x . cos2x=2cos2x-1=cos2x-sin2x=1-2sin2x. 92. 1+sin2x=1+2sinxcosx=sin2x+cos2x+2sinxcosx=(sinx+cosx)2.
2x . cos2x=2cos2x-1=cos2x-sin2x=1-2sin2x. 92. 1+sin2x=1+2sinxcosx=sin2x+cos2x+2sinxcosx=(sinx+cosx)2.Таким образом, это дает нам
RHS=-(cosx−sinx)(cosx+sinx)(sinx+cosx)(sinx+cosx)=sinx−cosxsinx +cosx=ЛВС. □ RHS = \frac{ — (\cos x — \sin x) (\cos x + \sin x)} { (\sin x + \cos x) (\sin x + \cos x)} = \frac{ \sin x — \cos x } { \sin x + \cos x } = LHS.\ _\square RHS=(sinx+cosx)(sinx+cosx)−(cosx−sinx)(cosx+sinx)=sinx +cosxsinx-cosx=LHS. □
Подтвердите личность
sin(A+B)+sin(A−B)sin(A+B)−sin(A−B)=tanAtanB. \frac{ \sin (A + B) + \sin (A — B)} { \sin (A + B) — \sin (A — B)} = \frac{ \tan A} { \tan B}. sin(A+B)−sin(A−B)sin(A+B)+sin(A−B)=tanBtanA.
Используя формулы суммы и разности, получаем
LHS=(sinAcosB+cosAsinB)+(sinAcosB−cosAsinB)(sinAcosB+cosAsinB)−(sinAcosB −cosAsinB)=2sinAcosB2cosAsinB=sinAcosBcosAsinB.\begin{выровнено} ЛХС &= \frac{ (\sin A \cos B + \cos A \sin B) + (\sin A \cos B — \cos A \sin B)} { (\sin A \cos B + \cos A \ sin B) — (\sin A \cos B — \cos A \sin B) } \\\\ &= \frac { 2 \sin A \cos B } { 2 \cos A \sin B } = \frac{ \sin A \cos B } { \cos A \sin B } .
 3\theta+3\sin\theta.sin3θ=−4sin3θ+3sinθ. 93\тета+3\sin\тета=RHS.\ _\квадрат
\end{выровнено}4sinθcos2θ−sinθ=4sinθ(1−sin2θ)−sinθ=−4sin3θ+3sinθ=RHS. □
3\theta+3\sin\theta.sin3θ=−4sin3θ+3sinθ. 93\тета+3\sin\тета=RHS.\ _\квадрат
\end{выровнено}4sinθcos2θ−sinθ=4sinθ(1−sin2θ)−sinθ=−4sin3θ+3sinθ=RHS. □Подтвердите личность
раскладушкаθ−cot2θ=1sin2θ.\cot\theta-\cot2\theta=\frac{1}{\sin2\theta}.cotθ−cot2θ=sin2θ1.
Так как cotθ=cosθsinθ\cot\theta=\frac{\cos\theta}{\sin\theta}cotθ=sinθcosθ, мы имеем
раскладушкаθ−cot2θ=cosθsinθ−cos2θsin2θ.\cot\theta-\cot2\theta=\frac{\cos\theta}{\sin\theta}-\frac{\ cos2\theta}{\sin2\theta}.cotθ−cot2θ=sinθcosθ−sin2θcos2θ. 92(А+В)}\\\\ &=\frac{\sin(AB)}{\sin(A+B)}. \end{выравнивание}2sin2(A+B)cos2B−cos2A=2sin2(A+B)−2sin(B+A)sin(B−A)=sin2(A+B)sin(A+B) sin(A−B)=sin(A+B)sin(A−B).
Следующим шагом является простое применение формулы суммы углов к числителю и знаменателю. Тогда у нас есть
sin(A−B)sin(A+B)=sinAcosB−cosAsinBsinAcosB+cosAsinB.\frac{\sin(AB)}{\sin (A+B)}=\frac{\sin A\cos B-\cos A\sin B}{\sin A\cos B+\cos A\sin B}.
 sin(A+B)sin(A-B )=sinAcosB+cosAsinBsinAcosB−cosAsinB.
sin(A+B)sin(A-B )=sinAcosB+cosAsinBsinAcosB−cosAsinB.Теперь разделим числитель и знаменатель на cosAcosB\cos A\cos BcosAcosB, чтобы получить тангенсы следующим образом:
sinAcosB−cosAsinBsinAcosB+cosAsinB=sinAcosA−sinBcosBsinAcosA+sinBcosB=tanA−tan БтанА+танБ. □\frac{\sin A\cos B-\cos A\sin B}{\sin A\cos B+\cos A\sin B}=\frac{\hspace{3mm} \frac{\sin A}{\ cos A} — \ frac {\ sin B} {\ cos B} \ hspace {3mm}} {\ frac {\ sin A} {\ cos A} + \ frac {\ sin B} {\ cos B}} = \frac{\tan A-\tan B}{\tan A+\tan B}.\ _\squaresinAcosB+cosAsinBsinAcosB-cosAsinB=cosAsinA+cosBsinBcosAsinA-cosBsinB=tanA+tanBtanA-tanB. □
[Другое решение]
Приведенное выше решение может показаться довольно сложным. Если вы застряли, пытаясь организовать LHS, переключение и решение RHS может сработать. Просто попробуйте преобразовать тангенсы в синусы и косинусы, используя формулу tan=sinθcosθ\tan=\frac{\sin\theta}{\cos\theta}tan=cosθsinθ, и решите задачу в обратном порядке.
 2(A+B)}\\\\
&=ЛВС.\ _\квадрат
\end{aligned}tanA+tanBtanA-tanB=cosAsinA+cosBsinBcosAsinA-cosBsinB=cosAcosBsinAcosB-cosAsinBcosAcosBsinAcosB-cosAsinB=sin(A+B)sin(A-B)=sin2 (A+B)sin(A−B)sin(A+B)=−21⋅sin2(A+B)cos2A−cos2B=−21⋅sin2(A+B)1−2sin2A−(1 −2sin2B)=sin2(A+B)sin2A−sin2B=LHS. □
2(A+B)}\\\\
&=ЛВС.\ _\квадрат
\end{aligned}tanA+tanBtanA-tanB=cosAsinA+cosBsinBcosAsinA-cosBsinB=cosAcosBsinAcosB-cosAsinBcosAcosBsinAcosB-cosAsinB=sin(A+B)sin(A-B)=sin2 (A+B)sin(A−B)sin(A+B)=−21⋅sin2(A+B)cos2A−cos2B=−21⋅sin2(A+B)1−2sin2A−(1 −2sin2B)=sin2(A+B)sin2A−sin2B=LHS. □Докажите, что если α+β+γ=π \alpha + \beta + \gamma = \pi α+β+γ=π, то
tanα+tanβ+tanγ=tanα×tanβ×tanγ. \тангенс \альфа + \тангенс \бета + \тангенс \гамма = \тангенс \альфа \раз \тангенс \бета \раз \тангенс \гамма. tanα+tanβ+tanγ=tanα×tanβ×tanγ.
Так как α=π−β−γ \alpha = \pi — \beta — \gammaα=π−β−γ, мы имеем
tanα=tan(π−β−γ)=−tan(β+γ)=−tanβ+tanγ1−tanβtanγ=tanβ+tanγtanβtanγ −1. \begin{выровнено} \загар \альфа & = \tan ( \pi — \beta — \gamma) \\\\ &= — \тангенс (\бета + \гамма) \\\\ & = — \frac{ \tan \beta + \tan \gamma } { 1 — \tan \beta \tan \gamma} \\\\ &= \frac{ \tan \beta + \tan \gamma } { \tan \beta \tan \gamma — 1 }.
 \end{выровнено} tanα=tan(π−β−γ)=−tan(β+γ)=−1−tanβtanγtanβ+tanγ=tanβtanγ−1tanβ+tanγ. 9{(n-1)/2}\\
&=\sin\left(\frac{\pi n}{2}\right).\ _\квадрат
\end{align} 2n−1k=1∏n−1cos(nkπ)=(−1)(n−1)/2=sin(2πn). □
\end{выровнено} tanα=tan(π−β−γ)=−tan(β+γ)=−1−tanβtanγtanβ+tanγ=tanβtanγ−1tanβ+tanγ. 9{(n-1)/2}\\
&=\sin\left(\frac{\pi n}{2}\right).\ _\квадрат
\end{align} 2n−1k=1∏n−1cos(nkπ)=(−1)(n−1)/2=sin(2πn). □Процитировать как: Доказательство тригонометрических тождеств. Brilliant.org . Извлекаются из https://brilliant.org/wiki/proving-trigonometric-identities/
Тригонометрические тождества — Доказательства | Список тригонометрических тождеств
Тригонометрические тождества — это равенства, включающие тригонометрические функции, которые выполняются для всех значений задействованных переменных, так что обе стороны равенства определены. В этом мини-уроке мы рассмотрим тригонометрические тождества. Есть три основных тригонометрических отношения sin, cos и tan. Три других тригонометрических отношения sec, cosec и cot в тригонометрии являются обратными значениями sin, cos и tan соответственно.
 Как эти тригонометрические отношения (sin, cos, tan, sec, cosec и cot) связаны друг с другом? Они связаны через тригонометрические тождества (или сокращенно тригонометрические тождества). Давайте подробно разберемся с тригонометрическими тождествами в следующих разделах.
Как эти тригонометрические отношения (sin, cos, tan, sec, cosec и cot) связаны друг с другом? Они связаны через тригонометрические тождества (или сокращенно тригонометрические тождества). Давайте подробно разберемся с тригонометрическими тождествами в следующих разделах.1. Что такое тригонометрические тождества? 2. Дополнительные и дополнительные тригонометрические тождества 3. Тригонометрические тождества суммы и разности 4. Двойные и полуугловые тригонометрические тождества 5. Правило синуса и косинуса 6. Часто задаваемые вопросы о тригонометрических тождествах Что такое тригонометрические тождества?
Тригонометрические тождества — это уравнения, относящиеся к различным тригонометрическим функциям и истинные для любого значения переменной, присутствующей в области.
 По сути, тождество — это уравнение, которое верно для всех значений переменных, присутствующих в нем.
По сути, тождество — это уравнение, которое верно для всех значений переменных, присутствующих в нем.Например, некоторые из алгебраических тождеств:
(а + б) 2 = а 2 + 2аб + б 2
(а — б) 2 = а 2 — 2аб+ б 2
(a + b)(a-b)= a 2 — b 2Алгебраические тождества связывают только переменные, тогда как тригонометрические тождества связывают 6 тригонометрических функций: синус, косинус, тангенс, косеканс, секанс и котангенс. Давайте узнаем о каждом типе тригонометрических тождеств подробно.
Взаимные тригонометрические тождестваМы уже знаем, что обратные величины синуса, косинуса и тангенса равны косекансу, секансу и котангенсу соответственно.
Таким образом, взаимные тождества задаются как
- sin θ = 1/cosecθ (ИЛИ) cosec θ = 1/sinθ
- cos θ = 1/с θ (ИЛИ) с θ = 1/cos θ
- tan θ = 1/cotθ (ИЛИ) cot θ = 1/tanθ
Тригонометрические тождества Пифагора в тригонометрии выводятся из теоремы Пифагора.
 Применяя теорему Пифагора к прямоугольному треугольнику ниже, мы получаем:
Применяя теорему Пифагора к прямоугольному треугольнику ниже, мы получаем:Opposite 2 + Adjacent 2 = Hypotenuse 2
Dividing both sides by Hypotenuse 2
Opposite 2 /Hypotenuse 2 + Adjacent 2 /Hypotenuse 2 = Hypotenuse 2 / Гипотенуза 2
- sin 2 θ + cos 2 θ = 1
Это одно из пифагорейских тождеств. Таким же образом мы можем вывести два других пифагорейских тригонометрических тождества.
- 1 + тангенс 2 θ = сек 2 θ
- 1 + детская кроватка 2 θ = cosec 2 θ
Дополнительные и дополнительные тригонометрические тождества
Дополнительные углы — это пара двух углов, сумма которых равна 90°. Дополнение угла θ равно (90 — θ). Тригонометрические отношения дополнительных углов:
- sin (90°- θ) = cos θ
- потому что (90°- θ) = sin θ
- косек (90°-θ) = сек θ
- сек (90°-θ) = cosec θ
- загар (90°- θ) = кроватка θ
- раскладушка (90°- θ) = загар θ
Дополнительные углы представляют собой пару двух углов, сумма которых равна 180°.
 Дополнение угла θ равно (180 — θ). Тригонометрические отношения дополнительных углов:
Дополнение угла θ равно (180 — θ). Тригонометрические отношения дополнительных углов:- sin (180°-θ) = sinθ
- cos (180°- θ) = -cos θ
- косек (180°-θ) = косек θ
- сек (180°-θ)= -сек θ
- тангенс (180°- θ) = -тангенс θ
- детская кроватка (180°- θ) = -кроватка θ
Тригонометрические тождества суммы и разности
Тождества суммы и разности включают формулы sin(A+B), cos(A-B), cot(A+B) и т. д.
- sin (A+B) = sin A cos B + cos A sin Б
- sin (A-B) = sin A cos B — cos A sin B
- cos (A+B) = cos A cos B — sin A sin B
- cos (A-B) = cos A cos B + sin A sin B
- тангенс (A+B) = (тангенс A + тангенс B)/(1 — тангенс A тангенс B)
- тангенс (A-B) = (тангенс A — тангенс B)/(1 + тангенс A тангенс B)
Двойные и полуугловые тригонометрические тождества
Формулы двойного угла: Тригонометрические тождества двойного угла можно получить, используя формулы суммы и разности.

Например, из приведенных выше формул:
sin (A+B) = sin A cos B + cos A sin B
Подставляем здесь A = B = θ с обеих сторон, получаем:
sin (θ + θ) = sinθ cosθ + cosθ sinθ
sin 2θ = 2 sinθ cosθТаким же образом мы можем вывести другие тождества двойного угла.
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos2θ — sin 2θ
= 2 cos2θ — 1
= 1 — sin 2 θ - тангенс 2θ = (2тангенс θ)/(1 – тангенс 2θ)
Используя одну из приведенных выше формул двойного угла,
cos 2θ = 1 — 2 sin 2 θ
2 sin 2 θ = 1- cos 2θ
sin 2 θ = (1 — cos2θ)/(2)
sin θ = ±√[(1 — cos 2θ)/2]Замена θ на θ/2 с обеих сторон,
sin (θ/2) = ±√[(1 — cos θ)/2]
Это формула половинного угла греха.
Таким же образом можно вывести и другие формулы половинного угла.
sin (θ/2) = ±√[(1 — cosθ)/2]
cos (θ/2) = ±√(1 + cosθ)/2
тангенс (θ/2) = ±√[ (1 — cosθ)(1 + cosθ)]
Тригонометрические тождества, которые мы изучили, выводятся с помощью прямоугольных треугольников.
 Есть несколько других тождеств, которые мы используем в случае непрямоугольных треугольников.
Есть несколько других тождеств, которые мы используем в случае непрямоугольных треугольников.Тригонометрические тождества по правилам синусов и косинусов
Правило синусов дает соотношение между углами и соответствующими сторонами треугольника. Для непрямоугольных треугольников нам придется использовать правило синусов и правило косинусов. Для треугольника со сторонами «a», «b» и «c» и соответствующими противоположными углами, равными A, B и C, правило синусов может быть задано как
- а/sinA = b/sinB = c/sinC
- sinA/a = sinB/b = sinC/c
- а/б = sinA/sinB; а/с = sinA/sinC; б/с = sinB/sinC
Правило косинусов дает соотношение между углами и сторонами треугольника и обычно используется, когда даны две стороны и угол между ними. Правило косинуса для треугольника со сторонами «a», «b» и «c» и соответствующими противоположными углами A, B и C, правило синуса может быть указано как,
- а 2 = b 2 + с 2 — 2bc·cosA
- b 2 = c 2 + a 2 — 2ca·cosB
- с 2 = а 2 + b 2 — 2ab·cosC
Статьи по теме Тригонометрические тождества:
- Тригонометрическая формула
- Тригонометрия
- Обратные тригонометрические формулы
- Калькулятор суммы и разности тождеств
Важные замечания о тригонометрических тождествах
- Чтобы записать тригонометрические отношения дополнительных углов, мы рассматриваем следующие пары как (sin, cos), (cosec, sec) и (tan, cot).

- При записи тригонометрических отношений дополнительных углов тригонометрическое соотношение не изменится. Знак можно определить, используя тот факт, что только sin и cosec положительны во втором квадранте, где угол имеет вид (180-θ).
- Есть 3 формулы для формулы cos 2x. Среди них можно вспомнить только первый, потому что два других можно получить из тождества Пифагора sin 2 x + cos 2 x = 1.
- Формула половинного угла для tan получается путем применения тождества tan = sin/cos и последующего использования формул половинного угла для sin и cos.
Примеры тригонометрических тождеств
Пример 1: Докажите следующее тождество, используя тригонометрические тождества:
[(sin 3θ + cos 3θ)/(sin θ + cos θ)] + sin θ cos θ = 1
Решение:
Воспользуемся следующим тождество:
a 3 +b 3 = (a+b)(a 2 -ab+b 2 )
Мы используем тождества Пифагора, чтобы доказать это тождество.

Л.Х.С. = [(sin 3θ + cos 3θ)(sin θ + cos θ)] + sin θ cos θ
= [(sin θ + cos θ)(sin 2 θ — sin θ cos θ + cos 2 θ)(sin θ + cos θ) + sin θ cos θ
= (sin 2 θ — sin θ cos θ + cos 2 θ) + sin θ cos θ
= sin 2 θ + cos 2 θ = 1 = R.H.S.Пример 2: Докажите следующее тождество, используя тригонометрические тождества:
(sin θ + cosec θ) 2 + (cos θ + sec θ) 2 = 7 + cottan 2 θ θ
Решение:
Мы используем взаимные тождества и тождества Пифагора, чтобы доказать это тождество.
L H S = (sin 2 θ + cosec 2 θ + 2 sin θ cosec θ) + (cos 2 θ + sec 2 θ + 2 cos θ sec θ)
= sin 2 θ + cos 2 θ + cosec 2 θ + sec 2 θ + 2 + 2
= 1 + (1 + кроватка 2 θ) + (1 + загар 2 θ) + 2 + 2
= 7 + коричневый 2 θ + детская кроватка 2 θ = R. H.S.
H.S.Пример 3: Найдите точное значение sin 75°, используя тригонометрические тождества.
Решение:
Мы знаем, что 75° = 30° + 45°
Применим тригонометрическое тождество суммы sin, чтобы найти значение sin 75°.
sin (A+B) = sin A cos B + cos A sin B
Замените здесь A = 30° и B = 45° с обеих сторон:
sin (30° + 45°) = sin 30° cos 45°+ cos 30° + sin 45°
sin 75° = (1/2)⋅(√2/2) + (√3/2)⋅(√2/2)
sin 75° = (√2 + √6)/4 = (√3 + 1)2√2Здесь значения sin 30°, cos 45°, cos 30° и sin 45° могут быть получены как с помощью тригонометрической таблицы.
Ответ: Sin 75°= (√3 + 1)/2√2
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок
Практические вопросы по тригонометрическим тождествам
перейти на слайдперейти на слайд
Часто задаваемые вопросы о тригонометрических тождествах
Что такое тригонометрические тождества в тригонометрии?
Тригонометрические тождества — это равенства, включающие тригонометрические функции, и они верны для каждого значения задействованных переменных таким образом, что обе части равенства определены. Некоторые важные тригонометрические тождества даны как,
- sin θ = 1/косек θ
- cos θ = 1/сек θ
- загар θ = 1/кот θ
- sin 2 θ + cos 2 θ = 1
- 1 + тангенс 2 θ = сек 2 θ
- 1 + детская кроватка 2 θ = cosec 2 θ
Что такое 3 тригонометрических тождества?
Три тригонометрических тождества задаются как
- sin 2 θ + cos 2 θ = 1
- 1 + тангенс 2 θ = сек 2 θ
- 1 + детская кроватка 2 θ = cosec 2 θ
Для чего используются тригонометрические тождества?
Тригонометрические тождества используются для решения различных геометрических, тригонометрических и других математических задач.
 Это уравнения, которые всегда верны.
Это уравнения, которые всегда верны.Как доказать тригонометрические тождества?
Тригонометрические тождества можно доказать, используя другие известные пифагорейские и тригонометрические тождества. Мы также можем использовать некоторые тригонометрические соотношения и формулы для доказательства тригонометрических тождеств.
Как вы решаете уравнения с тригонометрическими тождествами?
Различные математические задачи можно решать с помощью тригонометрических тождеств. Мы можем преобразовать уравнения в параметрические уравнения, а затем применить тригонометрические тождества для их решения.
Какие тригонометрические тождества мы должны знать?
При решении задач используются все триггерные тождества. Основными тригонометрическими тождествами являются тождества Пифагора, тождества взаимности, тождества суммы и разности, тождества двойного угла и тождества половинного угла. Для непрямоугольных треугольников нам придется использовать правило синусов и правило косинусов.

Пока мы знаем несколько соотношений между тригонометрическими функциями. Например, мы знаем взаимные отношения:
Например, мы знаем взаимные отношения:
Обратите внимание, что каждое из этих уравнений верно для всех углов \(\theta \), для которых определены обе части уравнения. Такие уравнения называются тождествами , и в этом разделе мы обсудим несколько тригонометрических тождеств , то есть тождества с тригонометрическими функциями. Эти тождества часто используются для упрощения сложных выражений или уравнений. Например, одним из наиболее полезных тригонометрических тождеств является следующее:
Эти тождества часто используются для упрощения сложных выражений или уравнений. Например, одним из наиболее полезных тригонометрических тождеств является следующее:
\[ \tan\;\theta ~=~ \frac{\sin\;\theta}{\cos\;\theta} \qquad \text{когда} \cos\;\theta \ne 0 \label{3.1 } \]
Чтобы доказать это тождество, выберите точку \((x,y) \) на конечной стороне \(\theta \) на расстоянии \(r >0 \) от начала координат и предположим, что \(\cos\ ;\тета\ne 0 \). Тогда \(x \ne 0 \) (поскольку \(\cos\;\theta = \frac{x}{r}\)), поэтому по определению
\[ \frac{\sin\;\theta}{\cos\;\theta} ~=~ \dfrac{~\dfrac{y}{r}~}{~\dfrac{x}{r}~} ~=~ \frac{y}{x} ~=~
\tan\;\theta ~.
\номер\]
Обратите внимание, как мы доказывали тождество, расширяя одну из его сторон (\(\frac{\sin\;\theta}{\cos\;\theta}\)) до тех пор, пока не получили выражение, равное другой стороне ( \(\загар\;\тета\)). Это, пожалуй, самый распространенный метод подтверждения личности. Взятие обратных значений в приведенном выше тождестве дает:
\[ \cot\;\theta ~=~ \frac{\cos\;\theta}{\sin\;\theta} \qquad \text{когда} \sin\;\theta \ne 0 \label{3. 2 \;\theta \) дает 92 \;\theta ~+~ 4
2 \;\theta \) дает 92 \;\theta ~+~ 4
\end{align*} \nonumber \]
Пример 3.3
Докажите, что \(\;\tan \;\theta ~+~ \cot \;\theta ~=~ \sec \;\theta ~ \csc \;\theta\; \).
Решение
Разложим левую часть и покажем, что она равна правой:
\[\nonumber \begin{alignat*}{3}
\tan \;\theta + \cot \;\theta ~ &= ~ \frac{\sin\;\theta}{\cos\;\theta} ~+~
\frac{\cos\;\theta}{\sin\;\theta} &{} \qquad &\ text{(по \ref{3.1} и
\ref{3.2})}\\ \nonumber 92 \;\theta}{\cos\;\theta ~ \sin\;\theta} &{} \qquad
&\text{(после получения общего знаменателя)}\\ \nonumber
&= ~ \frac{ 1}{\cos\;\theta ~ \sin\;\theta} &{} \qquad &\text{(by \ref{3.3})}\\ \nonumber
&= ~ \frac{1}{\ cos\;\theta} ~\cdot~ \frac{1}{\sin\;\theta}\\ \nonumber
&= ~ \sec \;\theta ~ \csc \;\theta
\end{alignat* } \nonumber \]
Как в приведенном выше примере мы узнали, что нужно расширять левую сторону вместо правой? В целом, хотя этот метод не всегда работает, более сложную сторону идентичности, вероятно, будет легче расширить. Причина в том, что из-за его сложности с этим выражением можно будет делать больше вещей. Например, если вас попросили доказать, что 92 \;\theta}{\sec\;\theta}
Причина в том, что из-за его сложности с этим выражением можно будет делать больше вещей. Например, если вас попросили доказать, что 92 \;\theta}{\sec\;\theta}
&{} \qquad &\text{(by \ref{3.11})}\\ \nonumber
&= ~ \dfrac{\csc\;\theta ~\cdot~ \dfrac{1}{\sin\;\theta}}{\dfrac{1}{\cos\;\theta}} &{}
&{}\\[2mm]\nonumber
&= ~ \csc\;\theta ~\cdot~ \frac{\cos\;\theta}{\sin\;\theta} &{} &{}\\ \nonumber
&= ~ \csc \;\theta ~ \cot \;\theta &{} \qquad &\text{(by \ref{3.2})}
\end{alignat*} \nonumber \]
При попытке доказать идентичность, где хотя бы одна сторона является соотношение выражений, перекрестное умножение может быть эффективной техникой:
\[ \frac{a}{b} ~=~ \frac{c}{d} \quad\text{если и только если}\quad ad ~=~ bc
\nonumber \]
Пример 3.6
Докажите, что \(\;\dfrac{1 ~+~ \sin\;\theta}{\cos\;\theta} ~=~ \dfrac{\cos\;\theta}{1 ~- ~ \sin\;\тета}\;\).
Решение
Перемножить и уменьшить обе стороны, пока не станет ясно, что они равны:
\[\nonumber \begin{align*}
( 1 ~+~ \sin\;\theta ) ( 1 ~- ~ \sin\;\theta ) ~ &= ~ \cos\;\theta ~\cdot~ \cos\;\theta\\ \nonumber 92 \;\тета = 1 \). Это распространенный метод исключения тригонометрических функций из систем уравнений.
Это распространенный метод исключения тригонометрических функций из систем уравнений.
Эта страница под названием 3.1: Основные тригонометрические идентификаторы распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Основные тригонометрические тождества — Список тригонометрических тождеств
основных тригонометрических тождеств или фундаментальных тригонометрических тождеств s на самом деле являются теми тригонометрическими функциями, которые верны каждый раз для переменных. Таким образом, эти тригонометрические тождества отображают определенные функции хотя бы одного угла (углов может быть больше). Он отождествляется с единичным кругом, где связь между прямыми и углами в декартовой плоскости. Сегодня в этой статье мы предоставим вам таблицу, состоящую из лота из основные тригонометрические тождества , которые можно использовать из основных тригонометрических функций.
Прямоугольный треугольник
Тригонометрические тождества или тригонометрические тождества — это уравнения, которые верны для прямоугольных треугольников. (Если это не прямоугольный треугольник, перейдите на страницу Тождества треугольников .)
(Если это не прямоугольный треугольник, перейдите на страницу Тождества треугольников .)
У каждой стороны прямоугольного треугольника есть имя
Всего у треугольника 6 основных элементов, т.е. 3 стороны и 3 угла. Вот названия 3-х сторон треугольника! Узнайте больше о тригонометрии.
Основные триггерные функции Синус, косинус и тангенс
Три основные функции в тригонометрии:
Вы можете легко получить вышеупомянутые тригонометрические функции, просто разделив длины одной стороны на другую
Для прямоугольного треугольника с углом
 = Напротив/ Смежно = tan(θ)
= Напротив/ Смежно = tan(θ)Таким образом, мы можем сказать:
тангенс (θ) = sin(θ)/ cos(θ)
Это наша первая тригонометрическая идентичность .
Косеканс, секанс и котангенс| Косеканс Функция: | csc( θ ) = гипотенуза / напротив |
| Секущая Функция: | сек( θ ) = Гипотенуза / Смежное |
| Функция котангенса: | детская кроватка( θ ) = Смежный / Напротив |
sin(θ) = 2/4 и csc(θ) = 4/2
Из-за всего, что мы можем сказать:
sin(θ) = 1/csc(θ)
cos(θ) = 1/сек(θ)
тангенс(θ) = 1/кот(θ)
И наоборот:
csc(θ) = 1/sin(θ)
сек(θ) = 1/cos(θ)
кроватка(θ) = 1/загар(θ)
А еще у нас есть:
раскладушка(θ) = cos(θ)/sin(θ)
Определение теоремы Пифагора
Теорема Пифагора
«Для любого прямоугольного треугольника квадрат гипотенузы равен сумме квадратов двух других сторон».

а2 + b2 = с2
Ключевое пифагорейское тригонометрическое тождество:
син 2 ( т ) + cos 2 ( т ) = 1
желтовато-коричневый 2 ( t ) + 1 = сек.
1 + детская кроватка 2 ( t ) = csc 2 ( t
2 3 49)
Итак, из этого рецепта мы можем дополнительно вывести уравнения для разных мощностей: Подробнее о Триггер Пифагора.
Dividing through by c 2 gives
a 2/ c 2 + b 2/ c 2 = c 2/ C 2
Это может быть упрощено до:
( A/ C ). c равно противоположность / гипотенуза , которая составляет SIN (θ)
c равно противоположность / гипотенуза , которая составляет SIN (θ)
и B / C — прилегающий / гипотенус , который составляет COS (θ)
SO (A / C) 2 + (A / C) 2 + (A / C) 2 B/C) 2 = 1 также можно записать:
SIN 2 θ + COS 2 θ = 1
ПРИМЕЧАНИЕ:
Решить Пифагора Пример: 32°
Используя Только 4 знака после запятой :
Теперь давайте рассчитаем SIN 2 θ + COS 2 θ :
0,5299 2 + 0,8480 2
= 0,2808… + 0,8480 2
= 0,2808… + 0,8480. 0493
0493
SIN 2 θ = 1 — COS 2 θ
COS 2 θ = 1 — SIN 2 θ
TAN 2 θ + 1 = Sec 2 θ θ θ θ θ θ θ θ θ θ 2 2 θ 2
2 2 θ 2
2 2 2 2 2 2 2 θ. 2 θ — 1
кроватка 2 θ + 1 = csc 2 θ
кроватка 2 θ = csc 2 θ — 1
Краткое изложение базовых идентификаторов триггеров
Базовые идентификаторы триггеров | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| желтовато-коричневый x = sin x /cos x | Уравнение 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| детская кроватка x = cos x /sin x | Уравнение 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| с x = 1/cos x | Уравнение 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| csc x = 1/sin x | Уравнение 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| кроватка x = 1/тан x | Уравнение 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 2 x + cos 2 x = 1 | Уравнение 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| желтовато-коричневый 2 x + 1 = сек 2 x | Уравнение 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 + детская кроватка 2 x = csc 2 x | Уравнение 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos ( x +- y ) = cos x cos y -+ sin x sin г | Уравнение 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
sin ( x +- y ) = sin x cos y +- cos x sin | Уравнение 10 | cos (- x ) = cos x | Уравнение 11 | cos ( пи /2 – x ) = sin x | Уравнение 12 | cos (2 x ) = cos 2 x – sin 2 x = 2 cos 2 x – 1 = 1 – 2 sin 2 |
Уравнение 13 | cos ( x /2) = +-[(1/2) (1 + cos x )] 1/2 | Уравнение 14 | sin (- x ) = -sin x | Уравнение 15 | sin ( пи /2 – x ) = cos x | Уравнение 16 | sin (2 x ) = 2 sin x cos x | Уравнение 17 | тангенс ( x +- y ) = (tan x +- тангенс y )/(1 — + тангенс x 903 | тангенс (- x ) = -тангенс x | Уравнение 19 | тангенс (2 x ) = 2 тангенс x /(1 – желтовато-коричневый 2 x ) | Уравнение 20 | tan ( x / 2) = sin x / (1 + cos x ) | Уравнение 21 | cos ( pi +- x ) = -cos x | Уравнение 22 | sin ( pi +- x ) = -+sin x | Уравнение 23 | загар ( pi +- x ) = +-тангенс x | Уравнение 24 | Производные. | 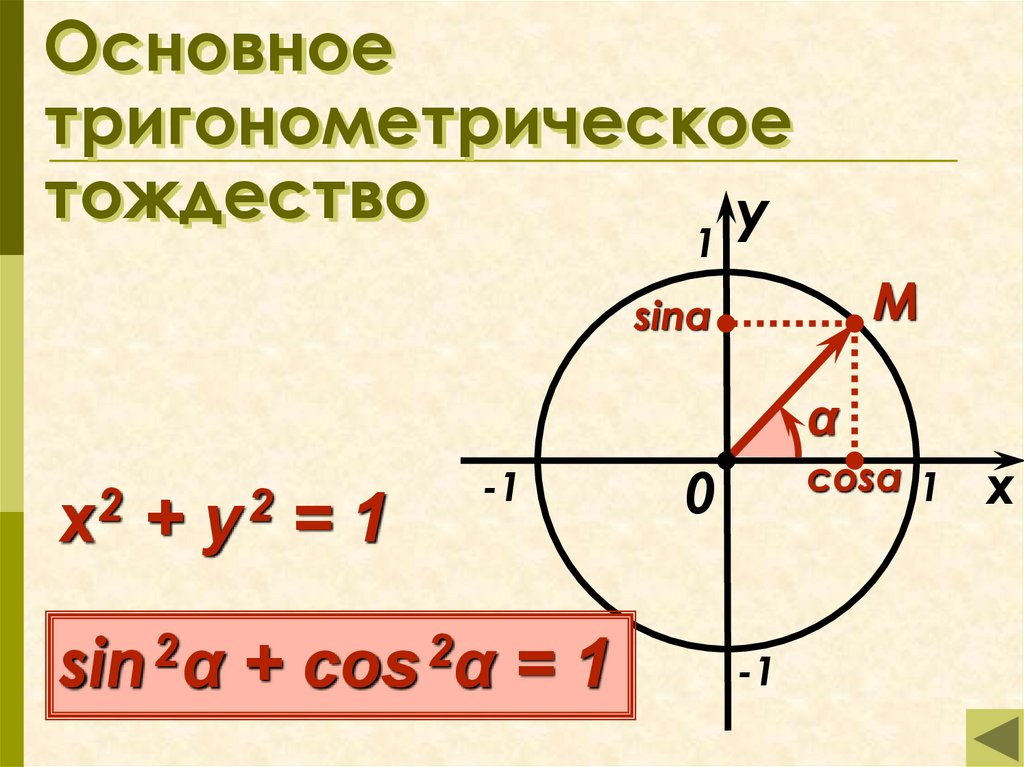 (d/d x ) sin x = cos x | Уравнение 25 | (d/d x ) cos x = -sin x | Уравнение 26 | (d/d x ) тангенс x = сек 2 x | Уравнение 27 | (д/д x ) детская кроватка x = -csc 2 x | Уравнение 28 | (d/d x ) сек x = сек x tan x | Уравнение 29 | (d/d x ) csc x = -csc x кроватка x | Уравнение 30 | Интегралы. | int sin x dx = -cos x + С | Уравнение 31 | int cos x dx = sin x + C | Уравнение 32 | int tan x dx = -ln |cos x | + С | Уравнение 33 | int кроватка x dx = ln |sin x | + С | Уравнение 34 | int sec x dx = ln |sec x + tan х | + С | Уравнение 35 | int csc x dx = -ln |csc x + кроватка x | + С | Уравнение 36 | |
Основные тригонометрические тождества
Горячая математика Тригонометрические тождества — это уравнения, содержащие
тригонометрические функции
которые верны для каждого значения вовлеченных переменных.
Некоторые из наиболее часто используемых тригонометрических тождеств получены из Теорема Пифагора , как показано ниже:
грех 2 ( Икс ) + потому что 2 ( Икс ) знак равно 1 1 + загар 2 ( Икс ) знак равно сек 2 ( Икс ) 1 + детская кроватка 2 ( Икс ) знак равно csc 2 ( Икс )
Пример 1:
Упростите выражение, используя тригонометрические тождества.
1 − грех 2 ( θ ) загар 2 ( θ )
Переписать загар в качестве грех / потому что .
знак равно 1 − грех 2 ( θ ) ( грех 2 ( θ ) потому что 2 ( θ ) ) знак равно 1 − грех 2 ( θ ) ⋅ потому что 2 ( θ ) грех 2 ( θ ) знак равно 1 − потому что 2 ( θ )
Используя фундаментальное тождество Пифагора, мы получаем
знак равно грех 2 ( θ )
Взаимные тождества
грех ( Икс ) знак равно 1 csc ( Икс ) потому что ( Икс ) знак равно 1 сек ( Икс ) загар ( Икс ) знак равно 1 детская кроватка ( Икс ) csc ( Икс ) знак равно 1 грех ( Икс ) сек ( Икс ) знак равно 1 потому что ( Икс ) детская кроватка ( Икс ) знак равно 1 загар ( Икс )
Пример 2:
Покажи это
сек
2
(
θ
)
+
csc
2
(
θ
)
знак равно
сек
2
(
θ
)
⋅
csc
2
(
θ
)
.
сек 2 ( θ ) + csc 2 ( θ ) знак равно 1 потому что 2 ( θ ) + 1 грех 2 ( θ ) ( Взаимная личность ) знак равно грех 2 ( θ ) + потому что 2 ( θ ) потому что 2 ( θ ) грех 2 ( θ ) знак равно 1 потому что 2 ( θ ) грех 2 ( θ ) ( Пифагорейская идентичность ) знак равно 1 потому что 2 ( θ ) ⋅ 1 грех 2 ( θ ) знак равно сек 2 ( θ ) ⋅ csc 2 ( θ ) ( Взаимная личность )
Частные тождества
загар ( ты ) знак равно грех ( ты ) потому что ( ты ) детская кроватка ( ты ) знак равно потому что ( ты ) грех ( ты )
Пример 3:
Подтвердить личность, потому что ( θ ) + грех ( θ ) загар ( θ ) знак равно сек ( θ )
Рассмотрим выражение в левой части уравнения.
потому что ( θ ) + грех ( θ ) загар ( θ ) знак равно потому что ( θ ) ( потому что ( θ ) потому что ( θ ) ) + грех ( θ ) ( грех ( θ ) потому что ( θ ) ) ( Частная идентичность ) знак равно потому что 2 ( θ ) + грех 2 ( θ ) потому что ( θ ) знак равно 1 потому что ( θ ) ( Пифагорейская идентичность ) знак равно сек ( θ )
1.
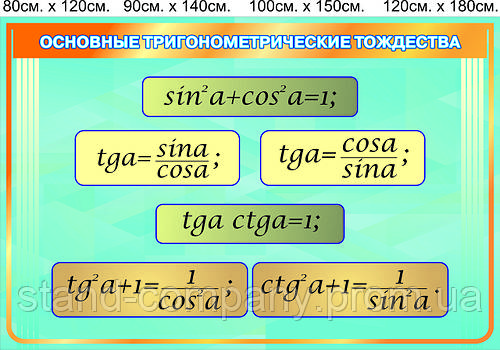 Тригонометрические тождества
Тригонометрические тождестваМ. Борна
Доказательство фундаментальных тригонометрических тождеств и изучение способов их использования для решения задач.
Далее на этой странице:
После повторения фундаментальных тождеств мы узнаем о:
Доказательстве тригонометрических тождеств
Но прежде чем мы начнем доказывать тригонометрические тождества, давайте посмотрим, откуда берутся основные тождества.
Вызов обратных тригонометрических функций, csc θ , sec θ и кроватка θ из главы тригонометрических функций:
`csc тета=1/(sin тета)`
`сек тета=1/(cos тета)`
`кот тета=1/(тан тета)`
Теперь рассмотрим следующую диаграмму, где точка ( x , y ) определяет угол θ в начале координат, а расстояние от начала координат до точки равно r единиц:
Из диаграммы видно, что коэффициенты sin θ и cos θ определяются как:
`sin theta=y/r`
и
`cos theta=x/r`
Теперь мы используем эти результаты, чтобы найти важное определение для tan θ :
`(sin theta)/(cos theta)=(y/r)/(x/r)=y/rxxr/x=y/x`
Теперь также `tan theta=y/x`, так что мы можем заключить:
`tan theta=(sin theta)/(cos theta)`
Соотношения, основанные на теореме Пифагора 92 тета`
Доказательство тригонометрических тождеств
Предложения. ..
..
Используя эти предложения, вы можете упростить и доказать выражения, включающие тригонометрические тождества.
Пример 1
Докажите, что
`(tan y)/(sin y)=sec y`
Ответить
Мы выражаем все через `sin y` и `cos y`, а затем упрощаем.
(«LHS» означает «левая часть» уравнения, а «RHS» означает «правая часть».) 92x)/(cos x\ sin x)`
`=1/(cos x\ sin x)`
`=1/(cos x)xx1/(sin x)`
`=sec\ x\ csc\ x`
`=»RHS»`
2. Докажите, что
`(1+cos x)/(sin x)=(sin x)/(1-cos x)`
Ответить
В этой задаче проще начать с правой стороны. Нам нужно выполнить трюк.
Умножаем числитель и знаменатель дроби на сопряженное знаменателя. (Мы видели эту идею в разделах «Рационализация знаменателя» (в сурдах) и при делении комплексных чисел.) 92 x)`
`=(1 + cos x)/(sin x)`
`=»LHS»`
Доказательство тригонометрических тождеств | Brilliant Math & Science Wiki
Чанг Кевин, Адитья Вирани, Рам Мохит, а также
способствовал

 к. то
к. то 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`. mecmath.net/trig/index.html
mecmath.net/trig/index.html

 sin2θ+cos2θ=1.
sin2θ+cos2θ=1. Возможно, что обе стороны равны при нескольких значениях (а именно, когда мы решаем уравнение), и мы можем ошибочно думать, что имеем истинное тождество.
Возможно, что обе стороны равны при нескольких значениях (а именно, когда мы решаем уравнение), и мы можем ошибочно думать, что имеем истинное тождество. Это позволяет еще больше упростить выражение.
Это позволяет еще больше упростить выражение.  \frac{ \sin \theta} { 1 — \cos \theta} + \frac{ 1 — \cos \theta} { \sin \theta } = 2 \csc \theta .1−cosθsinθ+sinθ1−cosθ= 2cscθ.
\frac{ \sin \theta} { 1 — \cos \theta} + \frac{ 1 — \cos \theta} { \sin \theta } = 2 \csc \theta .1−cosθsinθ+sinθ1−cosθ= 2cscθ. 2 \theta} { \sin \theta \cos \theta} = \frac{ 1} { \ грех \ тета \ соз \ тета }. LHS=cosθsinθ+sinθcosθ=sinθcosθsin2θ+cos2θ=sinθcosθ1.
2 \theta} { \sin \theta \cos \theta} = \frac{ 1} { \ грех \ тета \ соз \ тета }. LHS=cosθsinθ+sinθcosθ=sinθcosθsin2θ+cos2θ=sinθcosθ1. 2x . cos2x=2cos2x-1=cos2x-sin2x=1-2sin2x. 92. 1+sin2x=1+2sinxcosx=sin2x+cos2x+2sinxcosx=(sinx+cosx)2.
2x . cos2x=2cos2x-1=cos2x-sin2x=1-2sin2x. 92. 1+sin2x=1+2sinxcosx=sin2x+cos2x+2sinxcosx=(sinx+cosx)2.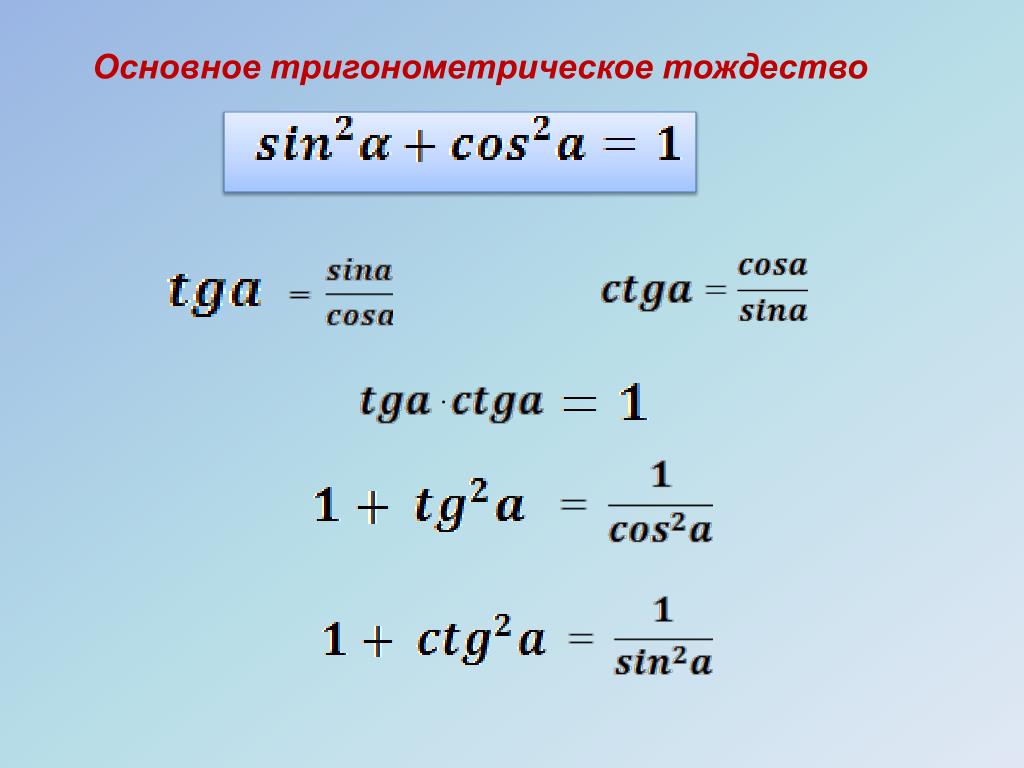 3\theta+3\sin\theta.sin3θ=−4sin3θ+3sinθ. 93\тета+3\sin\тета=RHS.\ _\квадрат
\end{выровнено}4sinθcos2θ−sinθ=4sinθ(1−sin2θ)−sinθ=−4sin3θ+3sinθ=RHS. □
3\theta+3\sin\theta.sin3θ=−4sin3θ+3sinθ. 93\тета+3\sin\тета=RHS.\ _\квадрат
\end{выровнено}4sinθcos2θ−sinθ=4sinθ(1−sin2θ)−sinθ=−4sin3θ+3sinθ=RHS. □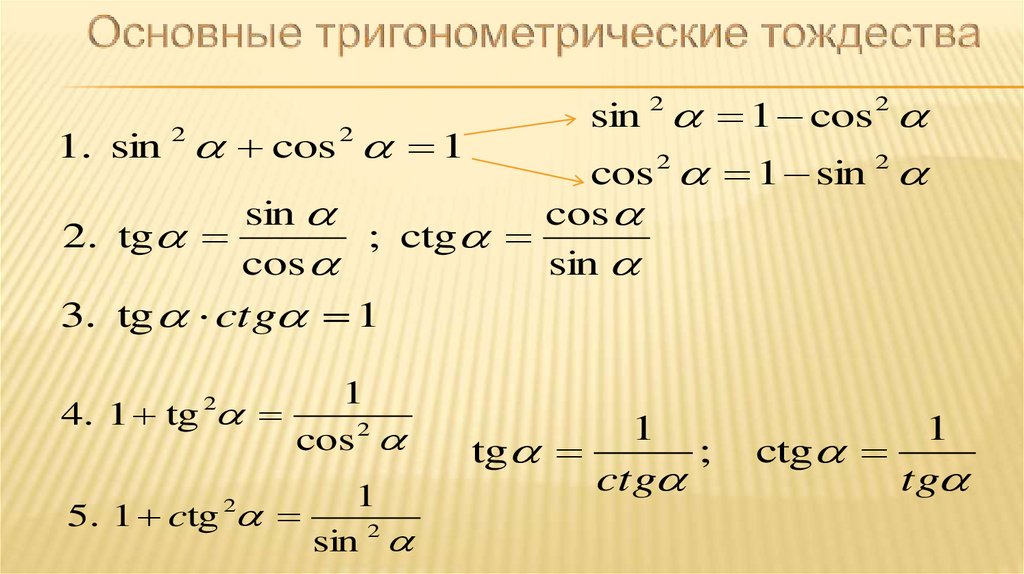 sin(A+B)sin(A-B )=sinAcosB+cosAsinBsinAcosB−cosAsinB.
sin(A+B)sin(A-B )=sinAcosB+cosAsinBsinAcosB−cosAsinB.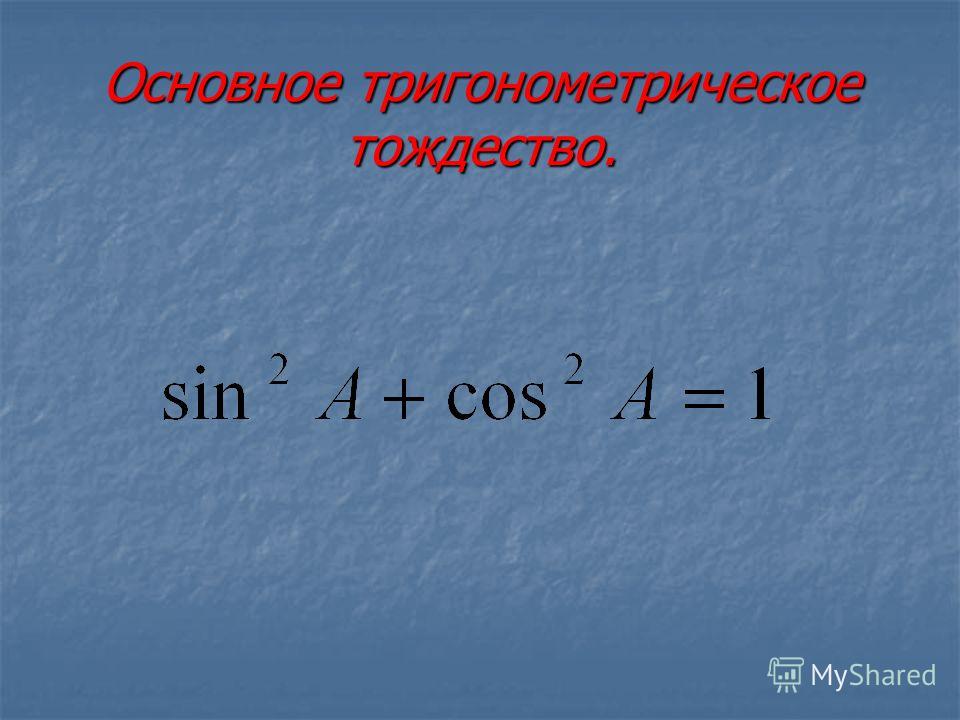 2(A+B)}\\\\
&=ЛВС.\ _\квадрат
\end{aligned}tanA+tanBtanA-tanB=cosAsinA+cosBsinBcosAsinA-cosBsinB=cosAcosBsinAcosB-cosAsinBcosAcosBsinAcosB-cosAsinB=sin(A+B)sin(A-B)=sin2 (A+B)sin(A−B)sin(A+B)=−21⋅sin2(A+B)cos2A−cos2B=−21⋅sin2(A+B)1−2sin2A−(1 −2sin2B)=sin2(A+B)sin2A−sin2B=LHS. □
2(A+B)}\\\\
&=ЛВС.\ _\квадрат
\end{aligned}tanA+tanBtanA-tanB=cosAsinA+cosBsinBcosAsinA-cosBsinB=cosAcosBsinAcosB-cosAsinBcosAcosBsinAcosB-cosAsinB=sin(A+B)sin(A-B)=sin2 (A+B)sin(A−B)sin(A+B)=−21⋅sin2(A+B)cos2A−cos2B=−21⋅sin2(A+B)1−2sin2A−(1 −2sin2B)=sin2(A+B)sin2A−sin2B=LHS. □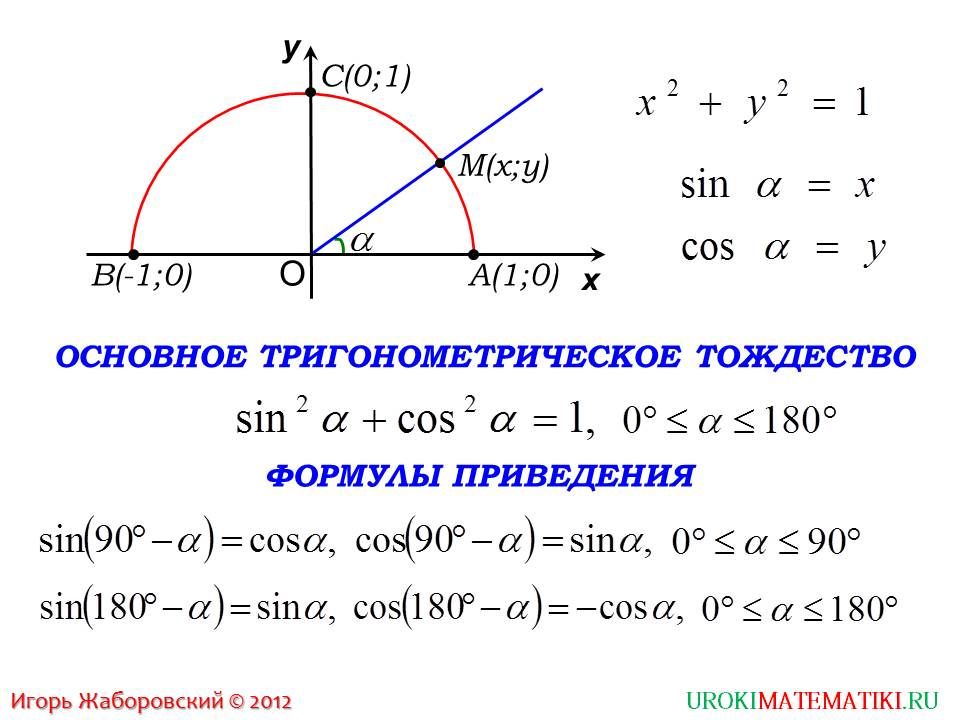 \end{выровнено} tanα=tan(π−β−γ)=−tan(β+γ)=−1−tanβtanγtanβ+tanγ=tanβtanγ−1tanβ+tanγ. 9{(n-1)/2}\\
&=\sin\left(\frac{\pi n}{2}\right).\ _\квадрат
\end{align} 2n−1k=1∏n−1cos(nkπ)=(−1)(n−1)/2=sin(2πn). □
\end{выровнено} tanα=tan(π−β−γ)=−tan(β+γ)=−1−tanβtanγtanβ+tanγ=tanβtanγ−1tanβ+tanγ. 9{(n-1)/2}\\
&=\sin\left(\frac{\pi n}{2}\right).\ _\квадрат
\end{align} 2n−1k=1∏n−1cos(nkπ)=(−1)(n−1)/2=sin(2πn). □ Как эти тригонометрические отношения (sin, cos, tan, sec, cosec и cot) связаны друг с другом? Они связаны через тригонометрические тождества (или сокращенно тригонометрические тождества). Давайте подробно разберемся с тригонометрическими тождествами в следующих разделах.
Как эти тригонометрические отношения (sin, cos, tan, sec, cosec и cot) связаны друг с другом? Они связаны через тригонометрические тождества (или сокращенно тригонометрические тождества). Давайте подробно разберемся с тригонометрическими тождествами в следующих разделах.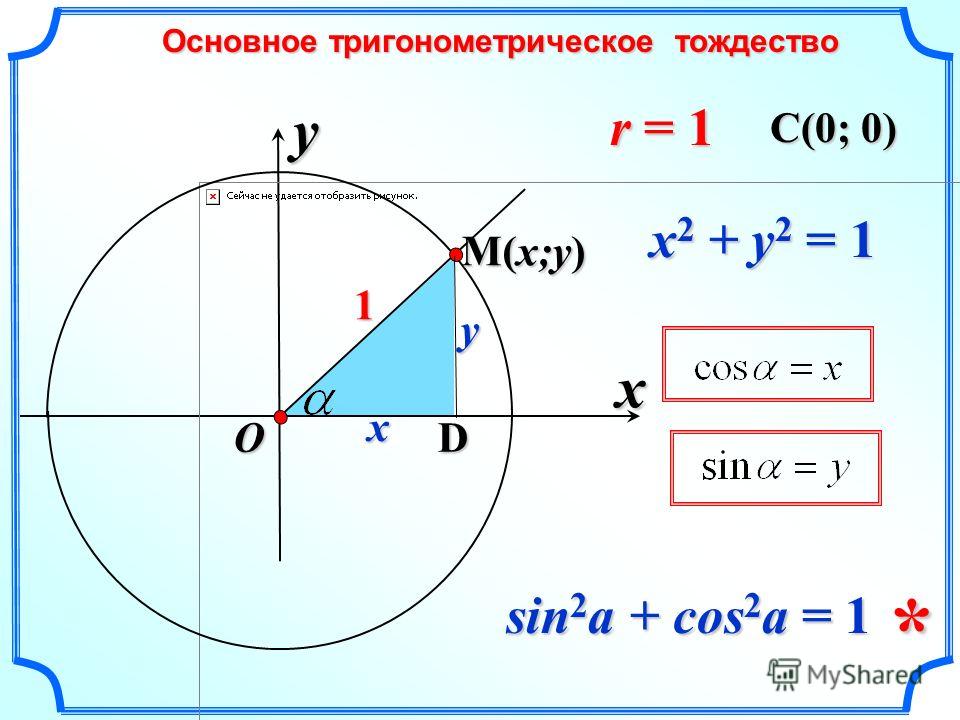 По сути, тождество — это уравнение, которое верно для всех значений переменных, присутствующих в нем.
По сути, тождество — это уравнение, которое верно для всех значений переменных, присутствующих в нем. Применяя теорему Пифагора к прямоугольному треугольнику ниже, мы получаем:
Применяя теорему Пифагора к прямоугольному треугольнику ниже, мы получаем: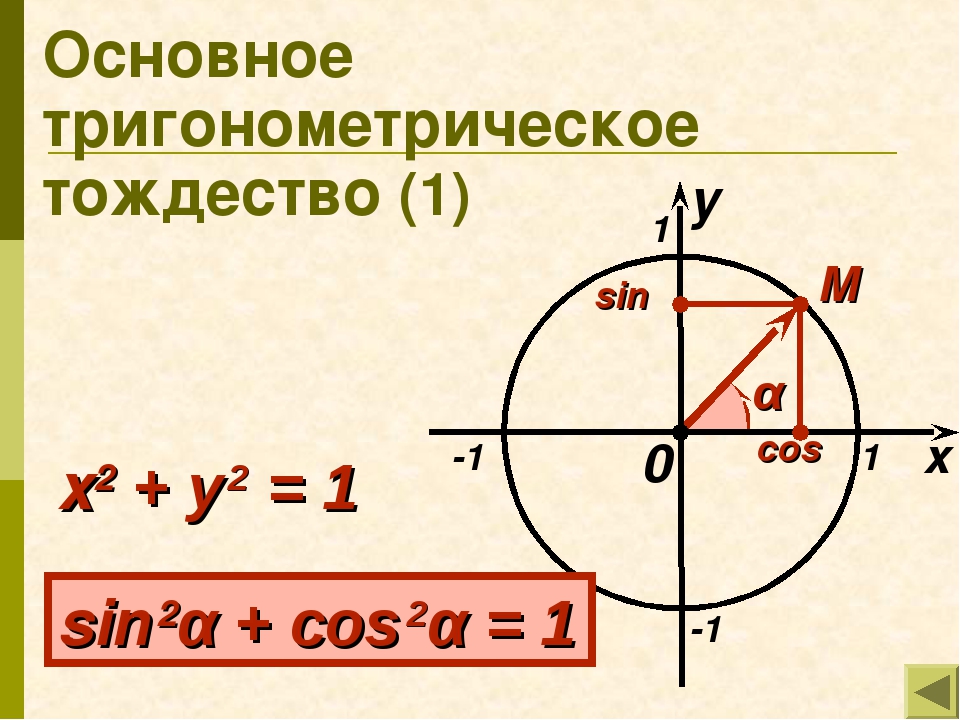 Дополнение угла θ равно (180 — θ). Тригонометрические отношения дополнительных углов:
Дополнение угла θ равно (180 — θ). Тригонометрические отношения дополнительных углов:
 Есть несколько других тождеств, которые мы используем в случае непрямоугольных треугольников.
Есть несколько других тождеств, которые мы используем в случае непрямоугольных треугольников.

 H.S.
H.S.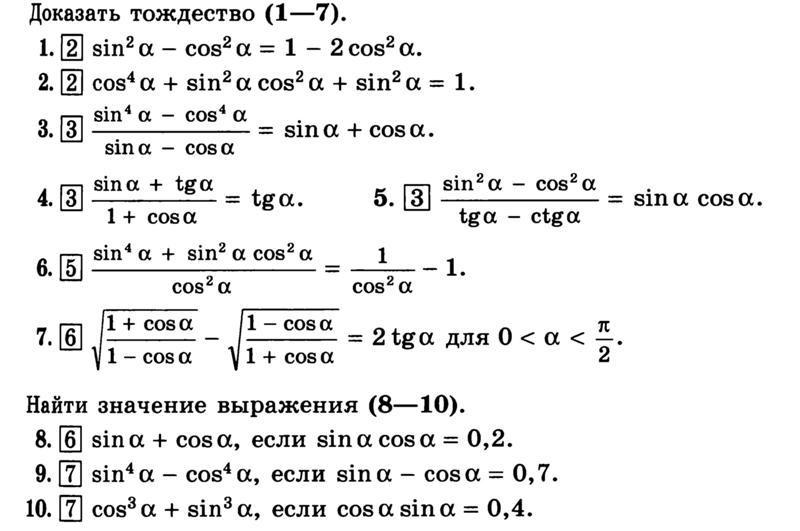
 Это уравнения, которые всегда верны.
Это уравнения, которые всегда верны.