Решение неопределенный интеграл онлайн: Калькулятор Интегралов • По шагам! — ЭкоДом: Дом своими руками
Содержание
Неопределенный интеграл. Онлайн калькулятор с примерами
Неопределенный интеграл онлайн
В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!
Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?
Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!
Вводная к интегралам
В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.
Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
В этом заключается один из физических смыслов интеграла.
Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.
Решение интегралов
Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.
Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.
Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
Калькулятор решения интегралов
Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.
И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.
Интеграл
Решение интегралов
Наш калькулятор интегралов онлайн с подробным решением поможет
вычислить интегралы и
первообразные функции онлайн
— бесплатно! Пользоваться калькулятором просто. Чтобы ввести определенный интеграл или
Чтобы ввести определенный интеграл или
неопределенный интеграл, нажмите «+условие» и введите интеграл
Например:
Нажав кнопку Решить вы получите подробное решение интеграла онлайн.
Калькулятором интегралов поддерживается вычисление определенных и неопределенных интегралов
(первообразных
функций), включая интегрирование функций с несколькими переменными.
Как решить интеграл онлайн с решением?
Введите неопределенный интеграл, нажав на кнопку ∫. Затем введите подинтегральное выражение, после чего
нажмите на кнопку d и введите переменную, по которой нужно провести интегрирование. Оставьте
незаполненными серые квадратики.
Введите определенный интеграл, нажав на кнопку ∫. Затем введите подинтегральное выражение, после чего
нажмите на кнопку d. Это можно сделать как на своей клавиатуре, так и на клавиатуре сайта. Введите
переменную, по которой нужно провести интегрирование. Далее кликните на нижний серый квадратик и введите
нижний предел, кликните на верхний серый квадратик и введите верхний предел.
На серые квадратики можно перейти либо кликнув на них, либо используя кнопки влево, вправо.
В определённых интегральных уравнениях применяется такое понятие как “предел”. Предел обозначает отрезок
функции, в которой происходит вычисление интеграла и результатом такого действия будет число. Физический
смысл такого числа — это размер площади под графиком соответствующей функции интеграла, эта операция
часто применяется в науке, в частности в физике.
Операция интегрирования является своего рода обратной операции вычисления производной. Если мы будем
с
.
Таблица интегралов
Чтобы найти интеграл, нужно знать таблицу ниже:
Мы живем в удивительное время. Сегодня вы можете получить онлайн решение интегралов с подробным
решением.
Подробное решение интегралов онлайн стало доступным благодаря современным разработкам в области
искусственного интеллекта.
Где можно решить онлайн интеграл? Интеграл калькулятор онлайн Pocket Teacher!
Онлайн интегралы — это просто!
Решить онлайн интегралы вы можете на нашем сайте. Бесплатный
онлайн
решатель
позволит решить интегралы любой сложности за считанные секунды. Вы получите
решение интеграла онлайн с подробными шагами. Все, что вам
необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть
видео
инструкцию
и узнать, как получить решение интегралов онлайн с решением на нашем сайте. А если у вас остались
вопросы, то вы можете задать их в
нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Так же читайте нашу статью «Решить
систему
уравнений методом сложения онлайн решателем»
Оператор | Описание |
Простейшие математические операции | |
+ — * / () | Сложение, вычитание, умножение, деление и группирующие символы: + — * / () . Знак умножения * — необязателен: выражение 2sin(3x) эквивалентно 2*sin(3*x). Cкобки используются для группирования выражений. |
0.5 | Десятичные дроби записываются через точку:
|
Тригонометрические функции | |
sin(x) | Синус от x: sin(x) |
cos(x) | Косинус от x: cos(x) |
tg(x) | Тангенс от x: tan(x) |
ctg(x) | Котангенс от x: 1/tan(x) |
arcsin(x) | Арксинус от x: arcsin(x) |
arccos(x) | Арккосинус от x: arccos(x) |
arctan(x) | Арктангенс от x: arctan(x) |
arcctg(x) | Арккотангенс от x: \pi/2 — arctan(x) |
Некоторые константы | |
e | Число Эйлера e: \e |
π | Число π: \pi |
Калькулятор Интегралов — определенный & неопределенный
Онлайн-калькулятор интегралов поможет вам вычислить интегралы функций по отношению к задействованной переменной и покажет вам полные пошаговые вычисления. Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-интеграл калькулятор:
Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-интеграл калькулятор:
- Определенные интегралы
- Неопределенные интегралы (первообразная)
Интегральный расчет довольно сложно решить вручную, так как он включает в себя различные сложные формулы интегрирования. Итак, рассмотрим интерактивный интегральный решатель, который решает простые и сложные функции решение интегралов онлайн и показывает вам пошаговые вычисления.
Итак, сейчас самое время понять формулы интегрирования, как интегрировать функцию шаг за шагом, с помощью калькулятора интегрирования и многое другое. Во-первых, давайте начнем с основ:
Читать дальше!
Что такое интеграл?
В математике интеграл функций описывает площадь, смещение, объем и другие понятия, которые возникают, когда мы объединяем бесконечные данные. В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.
В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.
Вы также можете использовать бесплатную версию онлайн-калькулятора факторов, чтобы найти факторы, а также пары факторов для положительных или отрицательных целых чисел.
- Процесс нахождения интегралов, называемый интегрированием
- Интегрируемая функция называется подынтегральной функцией.
- В интегральных обозначениях ∫3xdx, ∫ – символ интеграла, 3x – интегрируемая функция, а dx – дифференциал переменной x.
Где f (x) – функция, а A – площадь под кривой. Наш бесплатный калькулятор интегралов легко вычисляет интегралы и определяет площадь под заданной функцией. Что ж, теперь поговорим о типах интегралов:
Типы интегралов:
По сути, есть два типа интегралов:
- Неопределенные интегралы
- Определенные интегралы
Неопределенные интегралы:
определенный интеграл онлайн функции принимает первообразную другой функции. Взять первообразную функции – это самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.
Взять первообразную функции – это самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.
Определенные интегралы:
Определенный интеграл функции имеет начальное и конечное значения. Просто существует интервал [a, b], который называется пределами, границами или границами. Этот тип можно определить как предел интегральных сумм, когда диаметр разбиения стремится к нулю. Наш интеграл онлайн калькулятор определенных интегралов с оценками вычисляет интегралы, учитывая верхний и нижний предел функции. Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме:
Основные формулы для интеграции:
Существуют разные формулы для интеграции, но здесь мы перечислили некоторые общие:
- ∫1 dx = x + c
- ∫xn dx = xn + 1 / n + 1 + c
- ∫a dx = ax + c
- ∫ (1 / х) dx = lnx + c
- ∫ ax dx = ax / lna + c
- ∫ ex dx = ex + c
- ∫ sinx dx = -cosx + c
- ∫ cosx dx = sinx + c
- ∫ tanx dx = – ln | cos x | + c
- ∫ cosec2x dx = – детская кроватка x + c
- ∫ sec2x dx = tan x + c
- ∫ cotx dx = ln | sinx | + c
- ∫ (secx) (tanx) dx = secx + c
- ∫ (cosecx) (cotx) dx = -cosecx + c
Помимо этих уравнений интегрирования, есть еще несколько важных формул интегрирования, которые упомянуты ниже:
- ∫ 1 / (1-x2) 1/2 dx = sin-1x + c
- ∫ 1 / (1 + x2) 1/2 dx = cos-1x + c
- ∫ 1 / (1 + x2) dx = tan-1x + c
- ∫ 1 / | x | (x2 – 1) 1/2 dx = cos-1x + c
Запоминание всех этих формул интегрирования и выполнение вычислений вручную – очень сложная задача.
Как решать интегралы вручную (шаг за шагом):
Большинство людей раздражается начинать с вычислений интегральной функции. Но здесь мы собираемся решать интегральные примеры шаг за шагом, что поможет вам разобраться, как легко интегрировать функции! Итак, это точки, которым нужно следовать для вычисления решение интегралов онлайн:
- Определить функцию f (x)
- Возьмите первообразную функции
- Вычислить верхний и нижний предел функции
- Определите разницу между обоими пределами
Если вас интересует вычисление первообразной (неопределенного интеграла), тогда возьмите онлайн-калькулятор первообразной, который быстро решит первообразную данной функции.
Смотрит на примеры:
Пример 1:
Решить интегралы от ∫ x3 + 5x + 6 dx?
Решение:
Применяя правило функциональной мощности для интегрирования:
∫xn dx = xn + 1 / n + 1 + c
∫ x3 + 5x + 6 dx = x3 + 1/3 + 1 + 5 x1 + 1/1 + 1 + 6x + c
Шаг 2:
∫ x3 + 5x + 6 dx = x4 / 4 + 5 x2 / 2 + 6x + c
Шаг 3:
∫ x3 + 5x + 6 dx = x4 + 10×2 + 24x / 4 + c
Этот калькулятор неопределенного интеграла помогает интегрировать интеграл калькулятор функции шаг за шагом, используя формулу интегрирования. 1_5 x * lnx dx = –14
1_5 x * lnx dx = –14
Поскольку это очень сложно для решения интегралов, когда две функции умножаются друг на друга. Для удобства просто введите функции в онлайн-калькулятор интегралов по частям, который помогает выполнять вычисления двух функций (по частям), которые точно умножаются друг на друга.
Пример 3 (Интеграл от тригонометрической функции):
Вычислить определенный интеграл для ∫sinx dx с интервалом [0, π / 2]?
Решение:
Шаг 1:
Используйте формулу для тригонометрической функции:
∫ sinx dx = -cosx + c
Шаг 2:
Вычислите верхний и нижний предел для функций f (a) и f (b) соответственно:
Поскольку a = 0 и b = π / 2
Итак, f (a) = f (0) = cos (0) = 1
f (b) = f (π / 2) = cos (π / 2) = 0
Шаг 3:
Рассчитайте разницу между верхним и нижним пределами:
f (а) – f (b) = 1 – 0
f (а) – f (b) = 1
Теперь вы можете использовать бесплатный калькулятор частичных интегралов для проверки всех этих примеров и просто добавлять значения в поля назначения для мгновенного вычисления интегралов.
Как найти первообразную и вычислить интегралы с помощью калькулятора интегралов:
Вы можете легко вычислить интеграл от определенных и неопределенных функций с помощью лучшего интегратора. Вам просто нужно следовать указанным пунктам, чтобы получить точные результаты:
Проведите по!
Входы:
- Во-первых, введите уравнение, которое вы хотите интегрировать.
- Затем выберите зависимую переменную, входящую в уравнение
- Выберите на вкладке определенный или определенный интеграл онлайн
- Если вы выбрали конкретный вариант, то вам следует ввести нижнюю и верхнюю границу или предел в предназначенное для этого поле.
- После этого пора нажать на кнопку расчета.
Выходы:
Интегральный оценщик показывает:
- Определенный интеграл
- неопределенный интеграл онлайн
- Выполните пошаговые расчеты
Часто задаваемые вопросы (FAQ):
Какое целое значение?
В математике интеграл – это числовое значение, равное площади под графиком некоторой функции на некотором интервале.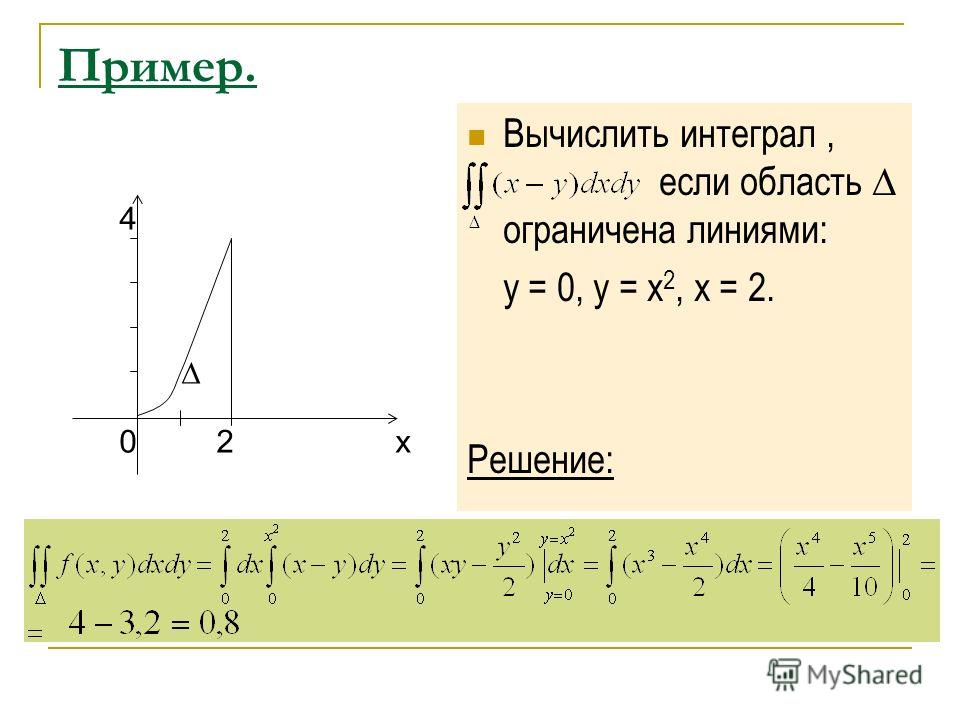 Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.
Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.
Как вы оцениваете интеграл, используя основную теорему исчисления?
Прежде всего, мы должны найти первообразную функции, чтобы решить интеграл, используя фундаментальную теорему. Затем используйте основную теорему исчисления для вычисления решение интегралов онлайн. Или просто введите значения в предназначенное для этого поле этого калькулятора интеграции и мгновенно получите результаты.
Что такое двойной интеграл?
Двойные интегралы – это способ интегрирования по двумерной области. Двойные интегралы позволяют вычислить объем поверхности под кривой. Они имеют две переменные и рассматривают функцию f (x, y) в трехмерном пространстве.
Заключительные слова:
Интегралы широко используются для улучшения архитектуры зданий, а также для мостов. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом.
В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом.
Other Languages: Integral Calculator, Integral Hesaplama, Kalkulator Integral, Kalkulator Integralny, Integralrechner, 積分計算, 적분계산기, Integrály Kalkulačka, Calculadora De Integral, Calcul Intégrale En Ligne, Calculadora De Integrales, Calcolatore Integrali, حساب متكامل, Integraatio Laskin, Integreret Lommeregner, Integral Kalkulator, Integralni Kalkulator, เครื่องคำนวณอินทิกรัล, Integrale Rekenmachine.
Решение интегралов онлайн калькулятор
Интегрирование или решение интегралов — операция, обратная дифференцированию. Геометрический смысл интеграла для функции у = f (х) — это площадь криволинейной трапеции.
Решение определенного интеграла предполагает поиск значения функции в заданных пределах.
Если интеграл неопределенный (нет границ интегрирования), решение предполагает нахождение первообразной:
ʃ – значок интеграла;
dх — значок дифференциала;
f (х) — подынтегральная функция;
f (х) dх — подынтегральное выражение;
F (х) — первообразная функция;
С — константа, которая плюсуется к ответу в любом неопределенном интеграле.
Решение интеграла означает нахождение определенной функции F (х) + C.
Если продифференцировать первообразную, мы должны получить исходное подынтегральное выражение.
Чтобы решить неопределенный интеграл, нужно превратить его в определенную функцию F (х) + C, используя таблицу.
Если интеграл табличного вида, значит он уже решен. В противном случае, интеграл нужно привести к одному из табличных интегралов, применяя основные свойства, правила и приемы решения.
Свойства интегралов:
Существуют функции, интеграл от которых нельзя выразить через элементарные функции. Решаются интегралы от таких функций с помощью таких приемов, как
- — замена подынтегральной функции близкой к ней функцией, интеграл от которой можно выразить через элементарные функции;
- — интегрирование по частям по формуле:
Для решения интегралов от дробно-рациональных функций, дробь раскладывают на простейшие, выделяют полный квадрат, после чего в числителе создают дифференциал знаменателя.
Чтобы решить интеграл от дробно-иррациональных функций, необходимо в подкоренном выражении выделить полный квадрат, после чего в числителе создать дифференциал подкоренного выражения.
Калькулятор решения интегралов поможет вам справиться с любыми задачами. Вам нужно:
- ввести в ячейку калькулятора подынтегральное выражение;
- ввести верхний предел для интеграла;
- ввести нижний предел для интеграла.
| При вводе функции используйте следующие обозначения: | ||||||||||
| + | — сложение; | Math.log (x) | — натуральный логарифм; | |||||||
| — | — вычитание; | Math.cos (x) | — косинус; | |||||||
| * | — умножение; | Math.sin (x) | — синус; | |||||||
| / | — деление; | Math.exp (x) | — экспонента; | |||||||
| Math.sqrt (x) | — квадратный корень; | Math. 2+x+1) соответствует Math.pow (x,4)*Math.cos (Math.pow (x,2)+x+1) 2+x+1) соответствует Math.pow (x,4)*Math.cos (Math.pow (x,2)+x+1)Решение неопределённых интегралов. Неопределенный интеграл Решение 3 интегралов онлайнНеопределенный интеграл онлайн В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно! Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен? Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех! Вводная к интегралам В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее. Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. В этом заключается один из физических смыслов интеграла. Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела. Решение интегралов Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов. Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов. Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. Калькулятор решения интегралов Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс. И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь. Введите функцию, для которой надо найти интегралПосле вычисления неопределённого интеграла, вы сможете получить Найдем решение неопределенного интеграла от функции f(x) (первообразную функции). Другие функции: Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла Решить неопределенный интегралОнлайн сервис на сайт Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Решение высшей математики онлайн‹— Назад Рассмотрим функцию и такой промежуток , на котором имеет несколько особенностей. Будем считать, что особенности имеются в тех точках промежутка, при приближении к которым функция имеет неинтегрируемые разрывы11, а также в и , если они являются концами рассматриваемого промежутка . Итак, пусть имеет особенности в , где, возможно, и , а все оставшиеся — точки оси . Точки разбивают промежуток на части — интервалы , где внутри интервалов функция уже не имеет особенностей, то есть интегрируема по любому отрезку . Если промежуток — это отрезок и в точках и функция не имеет особенностей, то к интервалам добавляются ещё полуинтервалы и с особенностями только в точках и . Выберем в каждом из интервалов по точке . Тогда на полуинтервалах и функция имеет ровно по одной особенности — в точке или соответственно. Присоединим, если нужно, к этим полуинтервалам ещё и и , то есть будем считать в этом случае и . Заметим, что мы уже давали аналогичное определение в случае, когда и этот интервал разбивается точкой деления на две части, то есть особенности имеются только в и ( определение 4.3). Вслед за тем мы проверили, что величина интеграла при определении 4.3 не зависит от выбора точки деления . Аналогичный результат верен и для общего определения 4.9. Доказывается он точно так же, на основе свойства аддитивности определённого интеграла, поэтому мы опускаем доказательство. Пример 4.16 Рассмотрим интеграл На промежутке интегрирования функция имеет особенность в точке , поскольку при . Точка разбивает на две части: и , причём у каждого из этих полуинтервалов лишь один конец (а именно, 0) соответствует особенности функции. Согласно определению, нужно положить причём нужно проверить сходимость интегралов в правой части. Имеем: (см. выше, пример 4.9). Поскольку этот интеграл расходится, то расходится и данный интеграл , и проверять сходимость слагаемого уже нет нужды (на самом деле он тоже расходится). Заметим, что было бы абсолютно неверно «не заметить» особенность функции в точке 0 и необоснованно применить формулу Ньютона — Лейбница, которая верна только для непрерывных подынтегральных функций: Рис.4.10. Мало того, что получился абсурдный результат: интеграл от положительной функции оказался отрицательным, так ещё при таком «способе» счёта мы упустили, что на самом деле площадь под графиком бесконечна. Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции Wolfram | Примеры альфа: интегралыНеопределенные интегралы Найдите первообразные математических выражений. Вычислить неопределенный интеграл: Вычислите неопределенный интеграл, который нельзя выразить элементарными терминами: Сгенерируйте таблицу интегралов, содержащих заданную функцию: Другие примеры Определенные интегралы Найдите интегралы с нижним и верхним пределами, также известные как интегралы Римана. Вычислить определенный интеграл: Вычислить неправильный интеграл: Составьте таблицу определенных интегральных формул: Другие примеры Кратные интегралы Вычисляет определенные вложенные интегралы от нескольких переменных. Вычислить кратный интеграл: Вычислить интеграл по неограниченной области: Другие примеры Другие примеры Численное интегрирование Интегрируйте выражения, используя численное приближение. Численно интегрируйте функции, которые не могут быть объединены символически: Приближаем интеграл с помощью указанного численного метода: Другие примеры Интегральные представления Исследуйте интегральные представления различных математических функций. Найдите интегральные представления для функции: Другие примеры Интегралы, относящиеся к специальным функциям Найдите определенные или неопределенные интегралы, связанные с определенной специальной функцией. | a b | exp | 4 | 5 | 6 | × | удалить | |
| ( | ) | | a | | лн | 7 | 8 | 9 | — | ↑ | ↓ | |
| √ | 3 √ | C | журнал a | 0 | . | ↵ | + | ← | → | |
| TRIG: | sin | cos | tan | детская кроватка | csc | sec | Назад | |||
| ОБРАТНЫЙ: | arcsin | arccos | arctan | acot | acsc | asec | удалить | |||
| HYPERB: | sinh | cosh | tanh | coth | x | π | ↑ | ↓ | ||
| ДРУГОЕ: | ‘ | , | y | = | > | ← | → | |||
Этот калькулятор для решения неопределенных интегралов взят от Wolfram Alpha LLC. Все права принадлежат собственнику!
Все права принадлежат собственнику!
Неопределенный интеграл
Нахождение неопределенного интеграла — очень распространенная задача в математике и других технических науках. На самом деле решение простейших физических задач редко обходится без нескольких вычислений простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов , даются многочисленные таблицы интегралов простых функций. Но со временем все благополучно забывается, или у нас нет времени на вычисления, или нам нужно найти неопределенный интеграл от очень сложной функции.Наш сервис идеально подойдет для решения этих проблем. Это позволяет точно находить неопределенные интегралы онлайн.
Решить неопределенный интеграл
Онлайн-сервис OnSolver.com позволяет быстро, бесплатно и эффективно решить комплексную онлайн-задачу. Вы можете заменить наш сервис на поиск нужного интеграла в таблицах. Здесь вы получите решение неопределенного интеграла в табличной форме, просто набрав нужную функцию. Не все математические сайты могут быстро и эффективно вычислять неопределенные интегралы функций в режиме онлайн, особенно если вы хотите найти неопределенный интеграл от сложных функций или функций, которые не включены в общий курс высшей математики.Сайт OnSolver.com поможет решить комплексную онлайн-задачу и хорошо справится с вашей работой. Онлайн-решение интегрального на сайте OnSolver.com всегда даст вам точный ответ.
Не все математические сайты могут быстро и эффективно вычислять неопределенные интегралы функций в режиме онлайн, особенно если вы хотите найти неопределенный интеграл от сложных функций или функций, которые не включены в общий курс высшей математики.Сайт OnSolver.com поможет решить комплексную онлайн-задачу и хорошо справится с вашей работой. Онлайн-решение интегрального на сайте OnSolver.com всегда даст вам точный ответ.
С помощью нашего сервиса вам будет легко проверить свой ответ, или найти внесенную ошибку, или оплошность, или просто убедиться, что вы выполнили свою работу безупречно, даже если вы хотите вычислить интеграл самостоятельно. Если вы решаете задачу и вам нужно решить неопределенный интеграл в качестве вспомогательной операции, зачем тратить время на то, что вы, возможно, уже делали тысячу раз? Более того, ненужные вычисления интеграла могут быть причиной канцелярских или других мелких ошибок, которые впоследствии приведут к неправильному ответу.Просто воспользуйтесь нашими услугами и без труда найдите неопределенный интеграл онлайн. Этот сервер очень полезен для практических задач нахождения интеграла функции онлайн. Вы должны ввести заданную функцию, получить неопределенное интегральное онлайн-решение и сравнить решение с вашим ответом.
Этот сервер очень полезен для практических задач нахождения интеграла функции онлайн. Вы должны ввести заданную функцию, получить неопределенное интегральное онлайн-решение и сравнить решение с вашим ответом.
Интегральный (первообразный) калькулятор с шагами
Этот онлайн-калькулятор найдет неопределенный интеграл (первообразную) заданной функции с указанием шагов (если возможно).
Введите функцию:
Интегрировать относительно: autoxtuvwyzabcdfghklmnopqrs
Пожалуйста, пишите без каких-либо различий, таких как «dx», «dy» и т. Д.
Определенный интеграл см. В калькуляторе определенного интеграла.
Некоторые интегралы могут занять много времени. Потерпи!
Если интеграл не рассчитывался или потребовалось слишком много времени, напишите об этом в комментариях. {2} \ right)}} {2} + C $$$
Интегральный калькулятор
| Лучший калькулятор интеграции
Определение интегрального калькулятора
Калькулятор интегралов — это математический инструмент, который упрощает вычисление интегралов. Онлайн-калькулятор интеграла обеспечивает быстрый и надежный способ решения различных интегральных запросов. онлайн-калькулятор интеграции и его процесс отличается
Онлайн-калькулятор интеграла обеспечивает быстрый и надежный способ решения различных интегральных запросов. онлайн-калькулятор интеграции и его процесс отличается
от обратного
производный калькулятор, поскольку эти два являются основными концепциями исчисления.
Ковариация, помимо математического интеграла, определяется таким же образом. Ознакомьтесь с примерами ковариационного уравнения и расчета.
Что такое интеграция?
Интеграция находит дифференциал
уравнение математических интегралов.Интегральная функция дифференцирует и вычисляет площадь под кривой графика.
Определение интеграла помогает найти площадь, центральную точку, объем и т. Д. Онлайн-калькулятор интеграции определяет интеграл, чтобы найти площадь под кривой следующим образом:
Где,
F (x) — функция, а
А — площадь под кривой.
Связанные: Что такое
дисперсия и как ее рассчитать.
Что такое интеграция в калькуляторе интеграции?
Интегральная функция — это интеграл
уравнение или формула интегрирования, она обозначается как функция f (x). В калькуляторе интеграции вам нужно будет ввести значение, чтобы оно работало правильно.
В калькуляторе интеграции вам нужно будет ввести значение, чтобы оно работало правильно.
Связанный: Узнайте, как вычислить логарифм и как найти антилогарифм числа?
Как калькулятор интегралов работает с интегральной записью?
Для интегрального уравнения
∫ 2x dx
∫ — это интегральный символ, а 2x — это функция, которую мы хотим интегрировать.
В этом интегральном уравнении dx — это дифференциал переменной x. Он подчеркивает, что переменная интеграции — x.Dx показывает направление по оси x, а dy показывает направление по оси y.
Интегральный символ и интегральные правила используются калькулятором интегралов для быстрого получения результатов. Узнайте больше о научных обозначениях и их расчетах здесь.
Как рассчитать интеграл?
Мы можем вычислить функцию, выполнив несколько простых шагов. Сначала разделите область на кусочки и сложите ширину этих кусочков Δx. Тогда ответ будет неточным.(см. рисунок 1)
Если мы сделаем Δx намного меньшей шириной и сложим все эти маленькие кусочки, то точность ответа станет лучше. (см. рисунок 2)
(см. рисунок 2)
Если ширина срезов приближается к нулю, то ответ приближается к истинному или фактическому результату. Итак,
Теперь мы говорим, что dx означает, что срезы Δx приближаются к нулю по ширине.
Обратите внимание, что интеграл является обратной производной
Узнайте, как найти и вычислить значение уклона, прежде чем решать интегральное уравнение.
Вычисляет ли калькулятор интегралов определенный интеграл и неопределенный интеграл?
Этот онлайн-калькулятор интегрирования позволит вам вычислять определенные интегралы и неопределенные интегралы. Вам просто нужно указать значения с помощью в поле ввода. Определенный интеграл имеет как начальное, так и конечное значение. Вычислительные интегралы функции f (x) представляют площадь под кривой от x = a до x = b.
Неопределенный интеграл не имеет верхнего и нижнего пределов функции f (x).Неопределенный интеграл также известен как первообразная.
Узнайте, как найти предел функции здесь.
Попробуйте калькулятор квадратной формулы и калькулятор формулы расстояния, чтобы узнать о различных математических формулах, используемых для решения различных математических уравнений.
Как вычислить двойные интегралы?
Одна из трудностей при вычислении двойных интегралов состоит в том, чтобы определить пределы интегрирования. Пределы интегрирования как порядок dxdydxdy требуются для определения пределов интегрирования для эквивалентного интегрального порядка dydxdydx.
Сложность вычисления двойных интегралов заключается в определении пределов интегрирования. Пределы интегрирования как порядок dxdydxdy определяют пределы интегрирования для интегрального порядка dydxdydx.
Узнайте разницу между средним и средним значением. Также узнайте, как рассчитать, используя среднее значение
калькулятор и калькулятор средней точки.
Есть ли в интегральном калькуляторе шаги?
Наш калькулятор интегрального исчисления предоставляет вам пошаговые инструкции, чтобы вы могли увидеть, как рассчитывается ваш запрос. Вы можете расширить свои знания и понимание, глядя на пошаговый ответ.
Вы можете расширить свои знания и понимание, глядя на пошаговый ответ.
Этот интегральный решатель очень эффективен для сложных задач интеграции, поскольку он обеспечивает быстрый ответ на сложные проблемы интеграции и решения.
Используйте калькулятор площади трапеции и калькулятор площади прямоугольника, чтобы еще больше укрепить свои математические концепции, связанные с площадью и поверхностью.
Как найти лучший интегральный калькулятор?
Calculatored имеет лучший калькулятор частичных интегралов с точки зрения точности, скорости и результатов.Методы калькулятора для интегрального исчисления могут быть разными, но методы и концепции остаются теми же. Вы можете выполнить поиск по калькулятору или найти наш онлайн-калькулятор интеграла в Google.
Как использовать калькулятор интегралов с шагом?
Для простых примеров интеграции и решений очень эффективен калькулятор линейного интеграла. Калькулятор интеграции по частям прост и удобен в использовании. Все, что вам нужно сделать, это выполнить следующие шаги:
Все, что вам нужно сделать, это выполнить следующие шаги:
Шаг №1: Заполните интегральное уравнение, которое вы хотите решить.
Шаг № 2: Выберите переменную как X или Y.
Шаг № 3: Введите значение верхней границы.
Шаг №4: Введите значение нижней границы.
Шаг № 5: Нажмите кнопку «РАССЧИТАТЬ».
После того, как вы выполните вышеуказанные шаги и нажмете кнопку «Рассчитать», онлайн-калькулятор интеграции с шагами немедленно решит интеграл по частям. Вы увидите результаты Antiderivative, Integral Steps, Parsing Tree и график результата.
Вы также можете заполнить примеры интегральных примеров для решения интегралов на практике.Мы надеемся, что вы найдете полезную информацию об интегралах и их вычислениях.
Вы также можете использовать наши другие бесплатные калькуляторы, такие как Standard
Калькулятор отклонений и калькулятор перекрестных произведений бесплатно.
Пожалуйста, поделитесь своими ценными отзывами ниже. Удачи в обучении и расчетах. Ваше здоровье!
Ваше здоровье!
Исчисление I — неопределенные интегралы
Показать уведомление для мобильных устройств
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 5-1: Неопределенные интегралы
В последних двух главах нам была задана функция \ (f \ left (x \ right) \), и мы спросили, какова производная этой функции.2} — 9x + c, \, \, \ hspace {0.25in} c {\ mbox {является константой}} \]
даст \ (f \ left (x \ right) \) при дифференцировании.
В последнем примере было два момента. Первым делом нужно было заставить вас задуматься о том, как решать эти задачи. Сначала важно помнить, что мы просто спрашиваем, что мы дифференцировали, чтобы получить данную функцию.
Сначала важно помнить, что мы просто спрашиваем, что мы дифференцировали, чтобы получить данную функцию.
Другой момент — признать, что на самом деле существует бесконечное количество функций, которые мы могли бы использовать, и все они будут отличаться константой.
Теперь, когда мы разобрались с примером, давайте избавимся от некоторых определений и терминологии.
Определения
Для данной функции \ (f \ left (x \ right) \), антипроизводная от \ (f \ left (x \ right) \) является любой функцией \ (F \ left (x \ right) \) такой, что
\ [F ‘\ left (x \ right) = f \ left (x \ right) \]
Если \ (F \ left (x \ right) \) — любая антипроизводная от \ (f \ left (x \ right) \), то самая общая антипроизводная от \ (f \ left (x \ right) \) называется неопределенным интегралом и обозначается
\ [\ int {{е \ влево (х \ вправо) \, dx}} = F \ влево (х \ вправо) + с, \ hspace {0.25in} \, \, \, \, c {\ mbox {любая константа}} \]
В этом определении \ (\ int {{}} \) называется интегральным символом , \ (f \ left (x \ right) \) называется подынтегральным выражением , \ (x \) называется Переменная интегрирования и «\ (c \)» называются константой интегрирования . 4} + 3x — 9 \, dx}} \]
4} + 3x — 9 \, dx}} \]
Показать решение
Поскольку здесь действительно требуется самая общая антипроизводная, нам просто нужно повторно использовать окончательный ответ из первого примера.2} — 9x + c \]
Теперь сделаем пару предупреждений. Одна из наиболее частых ошибок, которые студенты делают с интегралами (как неопределенными, так и определенными), — это опускать dx в конце интеграла. Это обязательно! Думайте о знаке интеграла и dx как о скобках. Вы уже знаете и, вероятно, вполне довольны мыслью о том, что каждый раз, когда вы открываете скобку, вы должны закрывать ее. При использовании интегралов воспринимайте знак интеграла как «открытую скобку», а dx — как «закрывающую скобку».5} + c + 3x — 9 \ end {align *} \]
Вы интегрируете только то, что находится между знаком интеграла и dx . Каждый из приведенных выше интегралов заканчивается в разных местах, поэтому мы получаем разные ответы, потому что каждый раз мы интегрируем разное количество членов. Во втором интеграле «-9» находится за пределами интеграла, поэтому остается отдельно и не интегрируется. Точно так же в третьем интеграле «\ (3x — 9 \)» находится вне интеграла и поэтому остается в покое.
Во втором интеграле «-9» находится за пределами интеграла, поэтому остается отдельно и не интегрируется. Точно так же в третьем интеграле «\ (3x — 9 \)» находится вне интеграла и поэтому остается в покое.
Знание, какие члены нужно интегрировать, — не единственная причина для записи \ (dx \) вниз.В разделе «Правило замены» мы фактически будем работать с \ (dx \) в задаче, и если у нас нет привычки записывать его, о нем будет легко забыть, и тогда мы получим неправильный ответ на этот этап.
Мораль заключается в том, чтобы убедиться и вставить \ (dx \)! На данном этапе это может показаться глупым поступком, но это просто необходимо, хотя бы по той причине, что знать, где заканчивается интеграл.
Кстати, обозначение \ (dx \) должно показаться вам немного знакомым.Мы видели подобные вещи пару разделов назад. Мы назвали \ (dx \) дифференциалом в этом разделе, и да, это именно то, что он есть. \ (Dx \), завершающий интеграл, — не что иное, как дифференциал. 2} — 9w + c \ end {align *} \]
Изменение переменной интегрирования в интеграле просто изменяет переменную в ответе. Однако важно отметить, что при изменении переменной интегрирования в интеграле мы также изменили дифференциал (\ (dx \), \ (dt \) или \ (dw \)), чтобы он соответствовал новой переменной. Это более важно, чем мы могли бы сейчас представить.
Однако важно отметить, что при изменении переменной интегрирования в интеграле мы также изменили дифференциал (\ (dx \), \ (dt \) или \ (dw \)), чтобы он соответствовал новой переменной. Это более важно, чем мы могли бы сейчас представить.
Еще одно использование дифференциала в конце интеграла — сообщить нам, по какой переменной мы интегрируем. На данном этапе это может показаться несущественным, поскольку большинство интегралов, с которыми мы собираемся здесь работать, будут включать только одну переменную.Однако, если вы находитесь на пути к получению степени, который приведет вас к исчислению с несколькими переменными, это будет очень важно на этом этапе, поскольку в задаче будет более одной переменной. Вам нужно выработать привычку записывать правильный дифференциал в конце интеграла, чтобы, когда это станет важным в этих классах, вы уже будете иметь привычку записывать его.
Чтобы понять, почему это важно, взгляните на следующие два интеграла.
\ [\ int {{2x \, dx}} \ hspace {1. 2} + c \]
2} + c \]
Второй интеграл также довольно прост, но нам нужно быть осторожными. dx сообщает нам, что мы интегрируем \ (x \) ’s. Это означает, что мы интегрируем только \ (x \), которые находятся в подынтегральном выражении, а все другие переменные в подынтегральном выражении считаются константами. Тогда второй интеграл равен
.
\ [\ int {{2t \, dx}} = 2tx + c \]
Таким образом, может показаться глупым всегда использовать dx , но это жизненно важная нотация, которая может привести к получению неправильного ответа, если мы не введем его.
Теперь есть несколько важных свойств интегралов, на которые мы должны обратить внимание.
Свойства неопределенного интеграла
- \ (\ displaystyle \ int {{k \, f \ left (x \ right) \, dx}} = k \ int {{f \ left (x \ right) \, dx}} \) где \ ( k \) — любое число. Итак, мы можем выделить мультипликативные константы из неопределенных интегралов.
См. Раздел «Доказательство различных интегральных формул» в главе «Дополнительно», чтобы увидеть доказательство этого свойства.

- \ (\ displaystyle \ int {{- f \ left (x \ right) \, dx}} = — \ int {{f \ left (x \ right) \, dx}} \). Это действительно первое свойство с \ (k = — 1 \), поэтому доказательства этого свойства не приводятся.
- \ (\ Displaystyle \ int {{е \ влево (х \ вправо) \ пм г \ влево (х \ вправо) \, dx}} = \ int {{е \ влево (х \ вправо) \, dx}} \ pm \ int {{g \ left (x \ right) \, dx}} \). Другими словами, интеграл от суммы или разности функций — это сумма или разность отдельных интегралов.Это правило можно распространить на любое количество функций.
См. Раздел «Доказательство различных интегральных формул» в главе «Дополнительно», чтобы увидеть доказательство этого свойства.
Обратите внимание, что когда мы работали с первым примером выше, мы использовали первое и третье свойство в обсуждении. Мы интегрировали каждый термин индивидуально, вернули все константы, а затем снова собрали все вместе с соответствующим знаком.
В приведенных выше свойствах не указаны интегралы от произведений и частных. Причина этого проста. Как и в случае с производными финансовыми инструментами, каждое из следующих действий НЕ будет работать.
Причина этого проста. Как и в случае с производными финансовыми инструментами, каждое из следующих действий НЕ будет работать.
\ [\ int {{f \ left (x \ right) g \ left (x \ right) \, dx}} \ ne \ int {{f \ left (x \ right) dx}} \ int {{g \ left (x \ right) \, dx}} \ hspace {0.75in} \ int {{\ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}} \, dx }} \ ne \ frac {{\ int {{f \ left (x \ right) \, dx}}}} {{\ int {{g \ left (x \ right) \, dx}}}} \]
Для деривативов у нас было правило продукта и правило частного, чтобы иметь дело с этими случаями. Однако с интегралами таких правил нет.Когда мы сталкиваемся с произведением и частным в интеграле, у нас будет множество способов справиться с этим в зависимости от того, что такое подынтегральное выражение. 4} + 3x — 9 \), что было \ (f \ left (x \ right) \)?
Показать решение
К этому моменту в этом разделе это простой вопрос.2} — 9x + c \]
В этом разделе мы продолжали вычислять один и тот же неопределенный интеграл во всех наших примерах. Целью этого раздела было не делать неопределенные интегралы, а вместо этого познакомить нас с обозначениями и некоторыми основными идеями и свойствами неопределенных интегралов. Следующая пара разделов посвящена фактическому вычислению неопределенных интегралов.
Целью этого раздела было не делать неопределенные интегралы, а вместо этого познакомить нас с обозначениями и некоторыми основными идеями и свойствами неопределенных интегралов. Следующая пара разделов посвящена фактическому вычислению неопределенных интегралов.
Решите неопределенный интеграл — WebMath
Быстрый! Мне нужна помощь с:
Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DividingFractions, MultiplyingFractions, SubplicationFractions are, SubplicationFractions , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов многочленов, разложение на множители трехчленов, многочленов, разложение на множители с GCF, многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Упрощение, Методы Правые треугольники, ветер, рисунок
.
Решение интеграла онлайн. Неопределенный интеграл Калькулятор решения интегралов
Неопределенный интеграл онлайн
В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!
Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?
Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!
Вводная к интегралам
В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.
Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
В этом заключается один из физических смыслов интеграла.
Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.
Решение интегралов
Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.
Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.
Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека. 3 — возведение в степень x + 7 — сложение x — 6 — вычитание
3 — возведение в степень x + 7 — сложение x — 6 — вычитание
Другие функции: floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция — округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция — Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа
Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн .
Решить неопределенный интеграл
Онлайн сервис на сайт позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте. Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт сайт поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте сайт, вы всегда получите точный ответ.
Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн без каких-либо усилий. Для практических задач по нахождению интеграла функции онлайн этот сервер очень полезен. Необходимо ввести заданную функцию, получить онлайн решение неопределенного интеграла и сравнить ответ с вашим решением.
Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн без каких-либо усилий. Для практических задач по нахождению интеграла функции онлайн этот сервер очень полезен. Необходимо ввести заданную функцию, получить онлайн решение неопределенного интеграла и сравнить ответ с вашим решением.
Калькулятор первообразных с шагами — Интегральный калькулятор
Калькулятор первообразных с шагами
Калькулятор первообразной находит первообразную функции шаг за шагом по переменной, т. е. x, y или z. Этот онлайн-калькулятор интеграции также поддерживает верхнюю и нижнюю границы, если вы работаете с минимальным или максимальным значением интервалов.
С помощью этого интегрального калькулятора вы можете получить пошаговые расчеты:
- Определенный интеграл
- Неопределенный интеграл
Он может найти интегралы логарифмических, а также тригонометрических функций. Этот инструмент оценивает входную функцию и соответственно использует интегральные правила для вычисления интегралов для площади, объема и т. д.
Как работает антипроизводный калькулятор?
Этот инструмент использует синтаксический анализатор, который анализирует заданную функцию и преобразует ее в дерево. Компьютер интерпретирует дерево для правильной оценки порядка операций и соответствующим образом реализует правила интеграции.
Вы можете найти первообразную (интеграл) любой функции, выполнив следующие действия.
- Выберите определенный или неопределенный вариант.
- Введите функцию в данное поле ввода.
- Нажмите кнопку «Загрузить пример», если вы хотите использовать образец примера.
- Укажите переменную.
 По умолчанию он установлен как x.
По умолчанию он установлен как x. - Введите верхнюю и нижнюю границы, если вы выбрали определенный интеграл выше.
- Нажмите кнопку «Рассчитать». Вы получите результат с пошаговыми расчетами.
Вы можете скачать решение, нажав на иконку.
Что такое интеграл?
Интеграл можно определить как
«Integral присваивает числа функциям таким образом, который описывает объем, площадь, перемещение и другие идеи, возникающие при объединении бесконечно малых данных».
Процесс нахождения интегралов называется интегрированием. Интеграл также называют первообразной, потому что это обратная операция вывода.
Наряду с дифференцированием интегрирование является важной операцией исчисления и служит инструментом для решения задач в математике и физике, связанных с длиной кривой, объемом твердого тела и площадью произвольной формы среди других.
Интеграл функции f(x) по действительной переменной x на интервале [a, b] записывается как:
\(\int _a^bf\left(x\right)dx\:\)
Как найти первообразную (интеграл)?
См. 2+C\)
2+C\)
Часто задаваемые вопросы
Чему равен интеграл от 1/x?
Интеграл от 1/x представляет собой абсолютное значение: ln (|x|) + C. Это стандартное значение интегрирования.
Чем отличается определенный интеграл от неопределенного?
Определенный интеграл обозначает число, когда верхняя и нижняя границы являются постоянными. С другой стороны, неопределенный интеграл – это семейство функций, производная которых равна f. Разница между двумя функциями является константой.
Что такое первообразная tan(x) dx?
Первообразная tan(x) dx равна,
тангенс x = — ln |cos x| + С
Math Cracks — крутой подход к интеграции по частям
Статьи Исчисление
Вступление
Идея интеграции по частям звучит довольно пугающе для многих студентов, изучающих математику, и я думаю, что для этого есть веская причина. Прежде всего, интеграция по частям — это метод, который включает в себя два (или более) шага вместо одного шага, как хотелось бы большинству студентов. Студенты захотят ПРИМЕНИТЬ какую-нибудь формулу и сразу же получить ответ, но в Calculus часто ответы приходят после последовательности (иногда длинной) шагов.
Прежде всего, интеграция по частям — это метод, который включает в себя два (или более) шага вместо одного шага, как хотелось бы большинству студентов. Студенты захотят ПРИМЕНИТЬ какую-нибудь формулу и сразу же получить ответ, но в Calculus часто ответы приходят после последовательности (иногда длинной) шагов.
Помимо метод замещения , метод интегрирования по частям является наиболее важным методом решения неэлементарных интегралов.
Во-первых, одна из причин, по которой интегральное исчисление обычно затруднительно для студентов, — это довольно неудачная система обозначений, используемая для интеграции. Фактически, при вычислении неопределенного интеграла функции \(f\left( x \right)\) мы сталкиваемся со следующими обозначениями
\[\int{f\left( x \right)dx}\] What many students do not understand is what is really meant by the «\(dx\)» in the expression above. Clearly, there are historical reasons why the «\(dx\)» appears in the notation stated above. But, actually there is no reason to include \(dx\) or even to add \(f\left( x \right)\). When we want to compute the indefinite integral of a function \(f\), we should be able to simply write
\[\int{f}\]
and that way we are stating the indefinite integral of the function \(f\).
Clearly, there are historical reasons why the «\(dx\)» appears in the notation stated above. But, actually there is no reason to include \(dx\) or even to add \(f\left( x \right)\). When we want to compute the indefinite integral of a function \(f\), we should be able to simply write
\[\int{f}\]
and that way we are stating the indefinite integral of the function \(f\).
Это такие же?
\[\int{f\left( x \right)dx}=\int{f\left( u \right)du}\]Абсолютно! Вот почему вы иногда видите переменную интеграции (x или u соответственно), которую называют «фиктивной» переменной, потому что она на самом деле не играет никакой роли в процессе интеграции.
Интеграция по частям как правило обратного произведения
После краткого введения мы переходим к делу. Типичная формула интегрирования по частям, показанная в учебниках, выглядит так:
Типичная формула интегрирования по частям, показанная в учебниках, выглядит так:
Затем вы говорите: «А? Что это?» Очевидно, что, не придавая значения приведенным выше \(u\) и \(dv\), трудно понять, что это такое. У вас может возникнуть один вопрос: почему формула интеграции по частям включает в себя dv и du, если они даже не играют роли в процессе интеграции, как показано во введении?
Ответ прост: в контексте приведенной выше формулы интегрирования по частям \(du\) и \(dv\) не являются «фиктивными переменными», а вместо этого являются функцией. Мнемонически это хорошо для решения задачи интеграции по частям, но бесполезно понимать, почему это действительно так или почему это работает.
Введите правило продукта:
Правило продукта гласит:
\[\frac{d}{dx}\left( fg \right)=\frac{df}{dx}g+f\frac{dg}{dx} \,\,\,\,\,(2)\]Для краткости я предпочитаю писать
\[\left( fg \right)’=f’g+fg’ \,\,\,\,\,(3)\]
Но ждать! Разве мы не интегрируемся в этой статье? Почему я использую правило дифференциации ?? Хм, разве не было бы здорово иметь правило произведения для интегралов? Было бы здорово, если бы \(\int{f’g’}=f\,g + C\) ?? К сожалению, это не так, НО все еще существует правило произведения интегралов, только оно немного сложнее.
Перепишем уравнение (3), получим:
\[fg’=\left( fg \right)’-f’g \,\,\,\,\,(4)\]Итак, если мы проинтегрируем обе части равенства выше, мы получим
\[\int{fg’}=\int{\left( \left( fg \right)’-f’g \right)}\]что по линейности интегрирования приводит к
\[\int{f\,g’}=f\,g-\int{f’g} \,\,\,\,\,(5)\]И здесь, друзья мои, у вас есть интеграция по частям. Интеграцию по частям следует рассматривать как отличный инструмент интеграции, который позволяет мне интегрировать продукт двух функций. Но это немного более ограничительно, потому что это произведение двух функций, НО одна из функций должна быть производной НЕКОТОРОЙ функции.
Итак, чтобы успешно применить правило интеграции по частям, мне нужно, чтобы произошло три вещи:
- Я пытаюсь интегрировать продукт ДВУХ функций.
-
Одна из этих функций является производной от чего-то (поэтому она имеет форму \(g’\)).
 {2}}}}dx}\), что на самом деле сложнее.
{2}}}}dx}\), что на самом деле сложнее.
Мораль этой истории заключается в том, что интеграция по частям — это своего рода правило произведения для интегралов, и вы ищете конкретную структуру: это интеграл произведения двух функций, и одну из этих функций вам нужно знать, как вычислить его первообразную. Если это так, значит, вы занимаетесь бизнесом и можете применить правило интеграции по частям.
НО, как видно из предыдущего примера, тот факт, что вы МОЖЕТЕ использовать интеграцию по частям, НЕ означает, что она будет полезна каждый раз.
Заключительные слова:
Как связать воедино формулу интеграции по частям?
\[\int{f\,g’}=f\,g-\int{f’g}\]«правила произведения интегралов» с
\[\int{udv}=uv-\int{vdu}\]Установив
\[\begin{aligned} & u=f\left( x \right) \\ & dv=g’\left( x \right)dx \\ \end{aligned}\]мы получаем \(v = g\left( x \right)\) и \(du = f’\left( x \right)dx\), что делает оба уравнения равными.

Учебники по алгебре Исчисление Учебники по исчислению Интеграция по частям Математические трещины
Геометрический калькулятор в Компас-3D
Комплекс операций инженерного калькулятора
Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
- с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
- с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами
Математические калькуляторы с решением
Математические онлайн-калькуляторы — это программы, с помощью которых можно получить решения математических задач.
https://calc-x.ru/
Математический калькулятор на этом сайте выполняет автоматическое и мгновенное решение как простых, так и сложных задач математики, в том числе операции над матрицами, геометрические расчеты, работа с дробями, логарифмами, уравнениями, процентами и т.д.
 Вы сможете произвести перевод чисел в другую систему счисления и перевод физических величин. Для теоретической помощи существует раздел «Полезное для решения математических задач», в котором можно найти различную табличную и другую информацию. Вычисления доступны 24 часа в сутки с телефона, планшета или компьютера подключенного к Internet.
Вы сможете произвести перевод чисел в другую систему счисления и перевод физических величин. Для теоретической помощи существует раздел «Полезное для решения математических задач», в котором можно найти различную табличную и другую информацию. Вычисления доступны 24 часа в сутки с телефона, планшета или компьютера подключенного к Internet.https://matematikam.ru/calculate-online/
В разделе «Онлайн сервисы» вам предоставлена возможность решать онлайн интегралы, брать производные, пределы, считать ряды практически для любых функций. Решение задач производится автоматически программой и является быстрым и абсолютно бесплатным. Все калькуляторы выдают ответ с подробным решением. Считайте легко, быстро и надежно вместе с нами.
https://www.kontrolnaya-rabota.ru/s/
На сайте представлены следующие сервисы:
- Решение интегралов
- Решение уравнений
- Производная функции
- Система уравнений
- Решение пределов
- Решение неравенств
- Построение графиков
- Комплексные числа
- Ряды
- Матрицы
- Вектора
- Теория вероятности
- Обычный и инженерный калькулятор
- Другие онлайн калькуляторы
Задачи в данных сервисах решаются в несколько шагов, после чего решение автоматически отправляется к Вам на ящик.
 Отправка на почтовый ящик позволяет решить проблему сохранности решения, а также позволяет напечатать решение на принтере.
Отправка на почтовый ящик позволяет решить проблему сохранности решения, а также позволяет напечатать решение на принтере.https://o-math.com/math/assistance/
Особенностью онлайн-калькуляторов по математике есть то, что они не только выдают ответ, но и детально расписывают ход решения задачи. Данные калькуляторы пригодятся и людям, которым просто нужно найти ответ, не вникая в ход решения, и людям, желающим выучить математику.
Высшая математика
- Решение пределов онлайн.
- Решение производных онлайн.
- Решение интегралов онлайн.
- Решение определенных интегралов онлайн.
Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты
- Онлайн калькулятор. Длина отрезка. Расстояние между точками.
- Онлайн калькулятор. Середина отрезка.
- Онлайн калькулятор. Уравнение прямой проходящей через две точки
- Онлайн калькулятор. Уравнение плоскости.
- Онлайн калькулятор. Расстояние от точки до плоскости.

- Онлайн калькулятор. Расстояние между плоскосями.
- Онлайн калькулятор. Расстояние от точки до прямой на плоскости.
- Онлайн калькулятор. Расстояние от точки до прямой в пространстве.
- Онлайн калькулятор. Угол между плоскостями.
- Онлайн калькулятор. Угол между прямой и плоскостью.
https://www.matburo.ru/
С помощью сайта-сервиса WolframAlpha
Вы можете выполнить самые разные математические вычисления on-line: построение графиков функции, работа с матрицами, решение алгебраических и дифференциальных уравнений, действия с числами и переменными, вычисление процентов и котировок акций, вычисление производных, интегралов, нулей функции, максимумов и минимумов… Кстати, возможны решения задач онлайн из разных областей наук: физика, химия, география, компьютеры, единицы измерения и др. Перейти к решению задач по математике онлайн (
с инструкциями и примерами
)- https://programmi-dlya-android.ru/category/ofis/kalkulyatory — представлены калькуляторы на Андроид
- https://www.
 matem96.ru/kalkulator.shtml
matem96.ru/kalkulator.shtml - https://www.mathforyou.net/SolutionsList.html
- https://www.calc.ru/kalkulyatory-po-matematike.html
- https://www.matcabi.net/
- https://www.math20.com/ru/
- https://math34.biz/
- https://mathserfer.com/
- https://mathonline.um-razum.ru/
- https://www.mathsolution.ru/
Этот список можно продолжать….
Инструкция по функциям инженерного калькулятора
Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн. Принцип работы с научным калькулятором такой: вводится число, с которым будет производиться вычисление, затем нажимается кнопка функции или операции, потом, если требуется, то еще цифра, например, степень, в конце — знак равенства.
- [Inv] – обратная функция для sin, cos, tan, переключает интерфейс на другие функции
- [Ln] – натуральный логарифм по основанию «e»
- [ ( ] и [ ) ] — вводит скобки
- [Int] – отображает целую часть десятичного числа
- [Sinh] — гиперболический синус
- [Sin] – синус заданного угла
- [X2] – возведение в квадрат (формула x^2)
- [n!] — вычисляет факториал введенного значения — произведение n последовательных чисел, начиная с единицы до самого введенного числа, например 4!=1*2*3*4, то есть 24
- [Dms] – переводит из десятичного вида в формат в градусы, минуты, секунды.
 x] – Возведение числа Эйлера в степень
x] – Возведение числа Эйлера в степень - [Frac] – отсекает целую часть, оставляет дробную
- [sinh-1] – обратный гиперболический синус
- [sin-1] – арксинус или обратный синус, arcsin или 1/sin
- [deg] – перевод угла в градусах, минутах и секундах в десятичные доли градуса, подробнее
- [cosh-1] — обратный гиперболический косинус
- [cos-1] – аркосинус или обрат. косинус arccos или 1/cos
- [2*Pi] – рассчитывает число Пи, помноженное на два
- [tanh-1] – обрат. гиперболический тангенс
- [tan-1] – арктангенс или обратный тангенс, arctg
Как пользоваться MR MC M+ M- MS
Все формулы по геометрии. Площади фигур
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
 3 вводите в следующей последовательности:
3 вводите в следующей последовательности:12 [xy] 3 [=]
12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]
Ответ: 1728
Как найти корень кубический
Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:
729 [3√x] [=]
729, [3√x] «кубический корень из икс», равенства [=]
Как найти корень на калькуляторе
Задача: Найти квадратный корень 36.
Решение: всё просто, нажимаем так:
36 [y√x] 2 [=]
36, [y√x] «корень из икса, в степени игрик», нужную нам степень 2, равно [=]
Ответ: 6
При помощи этой функции вы можете найти корень в любой степени, не только квадратный.
Как возвести в квадрат
Для возведения в квадрат онлайн вычислительная программа содержит две функции:
[xy] «икс в степени игрик», [X2] «икс в квадрате»
Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».

Например: 45 [xy] 6 [=]
Ответ: сорок пять в шестой степ. равно 8303765625
Тригонометрический калькулятор онлайн — примеры
Как произвести онлайн расчет синусов и косинусов, тангенсов
Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:
где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90 [sin] [=]
Ответ: единица
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60 [cos] [=]
Решение: 0,5
Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.

Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе
[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 [Deg] [=] 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453
Десятичный логарифм онлайн
Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1 [log] [=]
Получается 0 в итоге. Для подсчета lg100 нажмем так:
100 [log] [=]
Решение: два.
 Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.Так же вычисляется натуральный логарифм, но кнопкой [ln].
Интеграция по частям + онлайн-решатель с бесплатными шагами
Интеграция по частям — это онлайн-инструмент, который предлагает первообразную или представляет площадь под кривой. Этот метод приводит интегралы к стандартным формам, из которых можно определить интегралы.
Этот калькулятор Интеграция по частям использует все возможные способы интеграции и предлагает решения с этапами для каждого. Учитывая, что пользователи могут вводить различные математические операции с помощью клавиатуры, ее удобство использования превосходно.
Калькулятор интегрирования по частям способен интегрировать функции с многочисленными переменными, а также определенные и неопределенные интегралы (первообразные).
Что такое калькулятор интеграции по частям?
Калькулятор интегрирования по частям — это калькулятор, использующий математический подход для определения интеграла функционирующего продукта через интегралы его производной и первообразной.
По сути, формула интегрирования по частям изменяет первообразную функций в другую форму, чтобы было проще обнаружить упрощение/решение, если у вас есть уравнение с первообразной двух функций, умноженных вместе, и вы не знаете как вычислить первообразную. 9{}(v)dx]dx\]
Первообразная произведения двух функций, с которой вы начинаете, преобразуется в правую часть уравнения.
Если вам нужно определить первообразную сложной функции, которую сложно решить, не разбивая ее на две функции, умноженные вместе, вы можете использовать интегрирование по частям.
Как использовать калькулятор интегрирования по частям?Вы можете использовать калькулятор интеграции по частям 9{}v dx$
Шаг 4Чтобы выполнить интегрирование по частям, введите эти значения.
Шаг 5
Нажмите кнопку «ОТПРАВИТЬ» , чтобы получить интегральное решение, а также полное пошаговое решение для Интеграция по частям .
Наконец, в новом окне будет отображен график площади под кривой.
Как работает калькулятор интеграции по частям?Калькулятор интегрирования по частям работает путем удаления произведения из уравнения, чтобы можно было легко вычислить интеграл, и заменяет сложный интеграл на тот, который легче вычислить.
Нахождение интеграла произведения двух различных типов функций, таких как логарифмическая, обратная тригонометрическая, алгебраическая, тригонометрическая и экспоненциальная функции, выполняется с использованием формулы интегрирования по частям.
Интеграл продукта можно рассчитать по формуле интегрирования по частям u . v , U(x) и V(x) можно выбирать в любом порядке при применении правила дифференциации продукта для дифференциации продукта.

Однако, используя формулу интегрирования по частям, мы должны сначала определить, какая из следующих функций появляется первой в следующем порядке, прежде чем считать, что это первая функция, u(x) .
- Логарифмический (L)
- Обратное тригонометрическое (I)
- Алгебраическое (A)
- Тригонометрическое (T)
- Экспоненциальное (E)
Правило ILATE используется, чтобы помнить об этом. Например, если нам нужно определить значение x ln x dx (x — некоторая алгебраическая функция , а ln — логарифмическая функция ), мы поместим ln x как u(x), поскольку в LIATE сначала идет логарифмическая функция. Существует два определения формулы интегрирования по частям. Любая из них может использоваться для интегрирования результата двух функций.
Что такое интеграция?Интегрирование — это метод решения дифференциального уравнения интегралов по траекториям.
Подынтегральная функция в калькуляторе интегрирования Площадь под кривой графика рассчитывается дифференцированием интегральной функции.
Площадь под кривой графика рассчитывается дифференцированием интегральной функции.Подынтегральная функция представлена функцией f, которая представляет собой интегральное уравнение или формулу интегрирования (x). Вы должны ввести значение в калькулятор интегрирования, чтобы он работал правильно. 9{}$ — это интегральный символ, а 2x — это функция, которую мы хотим интегрировать.
Дифференциал переменной x в этом интегральном уравнении обозначается через dx. Это указывает на то, что переменная в интеграции равна x. Символы dx и dy указывают ориентацию по осям x и y соответственно.
Калькулятор интегралов использует знак интеграла и интегральные правила для быстрого получения результатов.
Интегрирование по формуле частейФормула для производной произведения двух функций может быть использована для доказательства интегрирования по частям.
 Производная произведения двух функций f(x) и g(x) равна произведению производных первой функции, умноженной на вторую функцию, и ее производной, умноженной на первую функцию для двух функций f(x ) и g(x).
Производная произведения двух функций f(x) и g(x) равна произведению производных первой функции, умноженной на вторую функцию, и ее производной, умноженной на первую функцию для двух функций f(x ) и g(x).Воспользуемся правилом дифференцирования произведения, чтобы вывести уравнение интегрирования по частям. Возьмем u и v, две функции. Пусть y т. е. y = u . v — их выход. Используя принцип дифференциации продукта, получаем: 9{}v du\]
Таким образом, выведена формула интегрирования по частям.
Функции и интегралы можно вычислить с помощью калькулятора интегралов по частям. Инструмент помогает нам сэкономить время, которое в противном случае было бы потрачено на выполнение вычислений вручную.
Кроме того, это помогает бесплатно предоставить результат интеграции. Он работает быстро и дает немедленные, точные результаты.
Этот онлайн-калькулятор предлагает четкие и пошаговые результаты. Этот онлайн-калькулятор можно использовать для решения уравнений или функций, содержащих определенные или неопределенные интегралы.
Преимущества использования Калькулятора интегрирования по частям 92)}| +C \]
92)}| +C \]Преимущества использования Калькулятора интегрирования по частям:
- Калькулятор интеграла по частям как определенные, так и неопределенные интегралы.
- Калькулятор устраняет необходимость в ручных вычислениях или длительных процессах благодаря быстрому решению интегральных уравнений или функций.
- Онлайн-инструмент экономит время и дает решение многих уравнений за короткий промежуток времени.
- Этот калькулятор позволит вам попрактиковаться в объединении принципов интегрирования по частям и шаг за шагом покажет вам результаты.
- Вы получите график и возможные промежуточные шаги интегрирования по частям из этого калькулятора .
- Результаты этого онлайн-калькулятора будут включать действительную составляющую, мнимую часть и альтернативную форму интегралов. 93}{9}+C\] Список математических калькуляторов.
 Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь!
Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь!1
2
3
4
5
6
7
8
2 9
A
B
C
D
F
G
M
N
U
V
W
X
Y
Z
.
(◻)
+
—
×
◻/◻
/
÷
◻ 2
◻ ◻
√◻
√
◻ √ ◻
◻ √
∞
E
π
LN
log
log ◻
LIM
D/DX
D □ x
□ x□ 0 x
92929292929292 0
2929292929292 0 xθ
=
>
<
>=
<=
sin
cos
tan
cot
sec
csc
asin
acos
atan
acot
asec
acsc
sinh
cosh
tanh
coth
sech
csch
asinh
acosh
atanh
acoth
asech
acsch
Пример
Решенные проблемы
Сложные задачи
1
Решенный пример тригонометрических интегралов 92dx$
Промежуточные шаги
Интеграл от константы равен произведению константы на переменную интеграла
$\frac{1}{4}x$
6
Интеграл $\frac{1}{4}\int1dx$ дает: $\frac{1}{4}x$
$\frac{1}{4}x$
Промежуточные шаги
Интеграл функции, умноженный на константу ($-2$), равен произведению константы на интеграл функции
$-\frac{1}{2}\int\cos\left(2x\right)dx$
Применить формулу: $\int\cos\left(ax\right)dx$$=\frac{1}{a}\sin\left(ax\right)$, где $a=2$
$ -\frac{1}{4}\sin\left(2x\right)$
7
Интеграл $\frac{1}{4}\int-2\cos\left(2x\right)dx$ дает: $-\frac{1}{4}\sin\left(2x\right) $
$-\frac{1}{4}\sin\left(2x\right)$
8
Умножить один член $\frac{1}{8}$ на каждый член многочлена $\left(x+\frac{1}{4}\sin\left(4x\right)\right)$ 92dx$, применяя интегрирование методом подстановки (также называемым U-подстановкой).
 Во-первых, мы должны идентифицировать секцию внутри интеграла с новой переменной (назовем ее $u$), замена которой упрощает вычисление интеграла. Мы видим, что $2x$ — хороший кандидат на замену. Определим переменную $u$ и назначим ее выбранной части
Во-первых, мы должны идентифицировать секцию внутри интеграла с новой переменной (назовем ее $u$), замена которой упрощает вычисление интеграла. Мы видим, что $2x$ — хороший кандидат на замену. Определим переменную $u$ и назначим ее выбранной части$u=2x$
Теперь, чтобы переписать $dx$ через $du$, нам нужно найти производную от $u$. Нам нужно рассчитать $du$, мы можем сделать это, выведя уравнение выше 9Результат 2dx$: $\frac{1}{8}x+\frac{1}{32}\sin\left(4x\right)$
$\frac{1}{8}x+\frac{1} {32}\sin\left(4x\right)$
10
Собрать результаты всех интегралов
$\frac{1}{4}x-\frac{1}{4}\sin\left(2x\right)+\frac{1}{32}\sin\ влево(4x\вправо)+\frac{1}{8}x$
11
Объединение одинаковых терминов $\frac{1}{4}x$ и $\frac{1}{8}x$
$\frac{3}{8}x-\frac{1}{4}\ sin\left(2x\right)+\frac{1}{32}\sin\left(4x\right)$
12
Поскольку интеграл, который мы решаем, является неопределенным интегралом, по окончании интегрирования мы должны добавить постоянную интегрирования $C$
$\frac{3}{8}x-\frac{1}{4}\ sin\left(2x\right)+\frac{1}{32}\sin\left(4x\right)+C_0$
Окончательный ответ
$\frac{3}{8}x-\frac{1}{4}\sin\left(2x\right)+\frac{1}{32}\sin\left(4x\right)+C_0$
Проблемы с математикой?
Доступ к подробным пошаговым решениям тысяч проблем, число которых растет с каждым днем!
Калькулятор интегралов: поиск первообразной, определенной, неопределенной
Онлайн-калькулятор интегралов поможет вам вычислить интегралы функций по отношению к задействованной переменной и покажет полные пошаговые расчеты.
 Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет решать неопределенные интегралы в кратчайшие сроки. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-калькулятора интегрирования:
Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет решать неопределенные интегралы в кратчайшие сроки. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-калькулятора интегрирования:- Определенные интегралы
- Неопределенные интегралы (первообразная)
Интегральный расчет довольно сложно решить вручную, так как он включает в себя различные сложные формулы интегрирования. Итак, рассмотрим онлайн-решатель интегралов, который решает простые и сложные интегральные функции и показывает пошаговые вычисления.
Итак, самое время разобраться в формулах интегрирования, как интегрировать функцию пошагово и с помощью калькулятора интегрирования и многое другое. Во-первых, давайте начнем с некоторых основ:
Читайте дальше!
Что такое интеграл?В математике интеграл функций описывает площадь, перемещение, объем и другие понятия, возникающие при объединении бесконечных данных.
 В исчислении дифференцирование и интегрирование являются фундаментальными операциями и служат наилучшей операцией для решения задач в физике и математике произвольной формы.
В исчислении дифференцирование и интегрирование являются фундаментальными операциями и служат наилучшей операцией для решения задач в физике и математике произвольной формы.Вы также можете использовать бесплатную версию онлайн-калькулятора коэффициентов, чтобы найти коэффициенты, а также пары коэффициентов для положительных или отрицательных целых чисел.
- Процесс нахождения интегралов, называемый интегрированием
- Интегрируемая функция называется подынтегральной функцией
- В интегральной записи ∫3xdx, ∫ — символ интеграла, 3x — интегрируемая функция, а dx — дифференциал переменной x
Где f(x) — функция, а A — площадь под кривой. Наш бесплатный калькулятор интегралов легко решает интегралы и определяет площадь под заданной функцией. Ну а теперь поговорим о типах интегралов:
Типы интегралов:В основном есть два типа интегралов:
- Неопределенные интегралы
- Определенные интегралы
Неопределенный интеграл функции является первообразной другой функции.
Определенные интегралы: Взятие первообразной функции — это самый простой способ символизировать неопределенные интегралы. Когда дело доходит до расчета неопределенных интегралов, калькулятор неопределенных интегралов поможет вам выполнять расчеты неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет ни верхнего, ни нижнего предела.
Взятие первообразной функции — это самый простой способ символизировать неопределенные интегралы. Когда дело доходит до расчета неопределенных интегралов, калькулятор неопределенных интегралов поможет вам выполнять расчеты неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет ни верхнего, ни нижнего предела.Определенный интеграл функции имеет начальное и конечное значения. Просто существует интервал [a,b], называемый пределами, границами или границами. Этот тип можно определить как предел интегральных сумм, когда диаметр разбиения стремится к нулю. Наш онлайн-калькулятор определенных интегралов с оценками вычисляет интегралы, учитывая верхний и нижний пределы функции. Разницу между определенным и неопределенным интегралом можно понять по следующей диаграмме:
Основные формулы для интегрирования:Существуют разные формулы для интегрирования, но здесь мы перечислили некоторые общие:
- ∫1 dx = x + c
- ∫x n dx = x n+1 / n+1 + c
- ∫a dx = ах + с
- ∫ (1/x) dx = lnx + c
- ∫ a x dx = a x / lna + c
- ∫ е х dx = е х + с
- ∫ sinxdx = -cosx + с
- ∫ cosx dx = sinx + c
- ∫ tanx dx = – ln|cos x| +с
- ∫ cosec 2 x dx = -cot x + c
- ∫ сек 2 х dx = тангенс х + с
- ∫ cotxdx = ln|sinx| +с
- ∫ (secx)(tanx) dx = secx + c
- ∫ (cosecx)(cotx) dx = -cosecx + c
Помимо этих уравнений интегрирования, есть еще несколько важных формул интегрирования, упомянутых ниже:
- ∫ 1/(1-x 2 ) 1/2 dx = sin -1 х + с
- ∫ 1/(1+x 2 ) 1/2 dx = cos -1 x + c
- ∫ 1/(1+x 2 ) dx = тангенс -1 x + c
- ∫ 1/|x|(x 2 – 1) 1/2 dx = cos -1 x + c
Запомнить все эти формулы интегрирования и произвести расчеты вручную — очень сложная задача.
Как решать интегралы вручную (шаг за шагом): Просто введите функцию в специальное поле онлайн-калькулятора интегралов, который использует эти стандартизированные формулы для точных расчетов.
Просто введите функцию в специальное поле онлайн-калькулятора интегралов, который использует эти стандартизированные формулы для точных расчетов.Большинство людей считают раздражающим начинать с вычислений интегральных функций. Но здесь мы собираемся шаг за шагом решать интегральные примеры, которые помогут вам легко разобраться с тем, как легко интегрировать функции! Итак, вот пункты, которые вам нужно выполнить для вычисления интегралов:
- Определить функцию f(x)
- Возьмем первообразную функции
- Вычислить верхний и нижний предел функции
- Определить разницу между обоими пределами
Если вас интересует вычисление первообразной (неопределенного интеграла), то воспользуйтесь онлайн-калькулятором первообразной, который быстро найдет первообразную заданной функции.
Посмотрите примеры:
Пример 1:
Решите интегралы от ∫ x 3 + 5x + 6 dx?
Решение:
Шаг 1:
Применяя правило степени функции для интегрирования:
∫x n dx = x n+1 / n+1 + c
∫ x 3 + 5x + 6 dx = x 3+1 / 3+1 + 5 x 904 1 /1+1 + 6x + c
Шаг 2:
∫ x 3 + 5x + 6 dx = x 4 / 4 + 5 x 2 + 905×2 c Шаг 3:
∫ x 3 + 5x + 6 dx = x 4 + 10x 2 + 24x / 4 + c
Этот пошаговый интегральный калькулятор помогает интегрировать интегральные функции с помощью используя формулу интегрирования.
 91_5 x*lnx dx = –14
91_5 x*lnx dx = –14Так как очень сложно решать интегралы, когда две функции перемножаются друг с другом. Для простоты просто введите функции в онлайн-калькулятор интеграции по частям, который помогает выполнять расчеты двух функций (по частям), которые точно перемножаются.
Пример 3 (Интеграл от тригонометрической функции):
Вычислить определенный интеграл для ∫sinx dx с интервалом [0,π/2]?
Решение:
Шаг 1:
Используйте формулу тригонометрической функции:
∫ sinx dx = -cosx + c
Шаг 2:
Расчет функции (b) соответственно:
As a = 0 & b = π/2
Итак, f (a) = f (0) = cos (0) = 1
f (b) = f (π/2) = cos (π/2) = 0
Шаг 3:
Рассчитайте разницу между верхним и нижним пределами:
f (a) – f (b) = 1 – 0
f (a) – f (b) = 1
Теперь вы можете использовать бесплатный калькулятор частных интегралов, чтобы проверить все эти примеры и просто добавить значения в обозначают поля для мгновенного вычисления интегралов.
Как найти первообразную и вычисление интегралов с помощью калькулятора интегралов:
Вы можете легко вычислить интеграл от определенных и неопределенных функций с помощью лучшего калькулятора интегрирования. Вам просто нужно следовать указанным пунктам, чтобы получить точные результаты:
Проведите пальцем по экрану!
Входные данные:
- Во-первых, введите уравнение, которое вы хотите проинтегрировать
- Затем выберите зависимую переменную, участвующую в уравнении
- Выберите определенный или неопределенный интеграл на вкладке
- Если вы выбрали определенный вариант, то вы должны ввести нижнюю и верхнюю границу или предел в специальном поле
- Когда закончите, пора нажать на кнопку расчета
Выходы:
Интегральный анализатор показывает:
- Определенный интеграл
- Неопределенный интеграл
- Завершение пошаговых расчетов
Интеграл в математике представляет собой числовое значение, равное площади под графиком некоторой функции на некотором интервале.
Как вычислить интеграл, используя основную теорему математического анализа? Это может быть график новой функции, производной которой является исходная функция (неопределенный интеграл). Таким образом, для мгновенных и быстрых расчетов вы можете использовать бесплатный онлайн-калькулятор первообразных, который позволяет решать неопределенные интегральные функции.
Это может быть график новой функции, производной которой является исходная функция (неопределенный интеграл). Таким образом, для мгновенных и быстрых расчетов вы можете использовать бесплатный онлайн-калькулятор первообразных, который позволяет решать неопределенные интегральные функции.Прежде всего, мы должны найти первообразную функции, чтобы решить интеграл, используя фундаментальную теорему. Затем используйте фундаментальную теорему исчисления для вычисления интегралов. Или просто введите значения в специальное поле этого калькулятора интеграции и получите мгновенные результаты.
Что такое двойной интеграл?Двойные интегралы — это способ интегрирования по двумерной области. Двойные интегралы позволяют вычислить объем поверхности под кривой. Они имеют две переменные и рассматривают функцию f(x,y) в трехмерном пространстве.
Final-Words:Интегралы широко используются для улучшения архитектуры зданий, а также для мостов.
Ссылки: В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся далеко друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для обучения K-12, поскольку он легко вычисляет интеграл любой заданной функции шаг за шагом.
В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся далеко друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для обучения K-12, поскольку он легко вычисляет интеграл любой заданной функции шаг за шагом.Из официального источника Википедии: Общее представление об интегралах и их типах
С сайта mathisfun: График интегрирования и подынтегральных выражений, целочисленное представление calculus
Other Languages: Integral Hesaplama, Kalkulator Integral, Kalkulator Integralny, Integralrechner, 積分計算, 적분계산기, Integrály Kalkulačka, Calculadora De Integral, Calcul Intégrale En Ligne, Calculadora De Integrales, Calcolatore Integrali, Калькулятор Интегралов, حساب متكامل, Integraatio Laskin , Integreret Lommeregner, Integral Kalkulator, Integralni Kalkulator, เครื่องคำนวณอินทิกรัล, Integrale Rekenmachine.
▷Step by Step Приложения для TI-Nspire CX и CX CAS Скачать бесплатно.
 Пройдите курсы по математике, естественным наукам и бизнесу
Пройдите курсы по математике, естественным наукам и бизнесу
Для подготовки к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.
— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—
95% купили больше ПРИЛОЖЕНИЙ. 97% сообщили об улучшении результатов. Рейтинг: 4,89из 5 звезд. Доступно 46 ПРИЛОЖЕНИЙ. КОВИД СПЕЦИАЛЬНЫЙ
Купите 3 приложения Made Easy по цене 2 приложений.
Выберите 3 приложения. EasyBusiness Stats Made EasyCalculus with Physics Apps Calculo de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht Gemacht DiscreteMDisateM de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenie ur Mathematik Leicht GemachtFinance Made EasyКонечная математика Made EasyGeometry Made EasyGeometrie Leicht GmachtGeometria de Manera FacilLand Survey Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GmachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyЧисленный анализ Made EasyPhysik Leicht EasyPhysik Research Made EasyPhysik Research Made Easy GemachtFisica de Manera FacilPortfolio & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathSignals and Systems Made EasyStatistics and Probability Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatic and Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation Solver Ecuaciones de Manera FacilПошаговый конвертер единиц измеренияThermodynamics Made EasyThermodynamik Leicht GemachtTrigonometry Made EasyTrigonometria de Manera FacilTr igonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics with de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysics Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtTrigonometric Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtВекторный расчет us Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics with de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysics Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtTrigonometric Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtВекторный расчет us Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Введите последние 8 цифр вашего 27-значного идентификатора продукта TI-Nspire.

Находится в разделе 5:Настройки → 4:Статус → О программе
ID может выглядеть так: 1008000007206E210B0 BD92F455 . ПОМОГИТЕ НАЙТИ ID.
Если бы это был ваш ID, вы бы набрали только BD92F455.или на международном уровне:
В конце оплаты через PayPal вам будет отправлено электронное письмо с вашим ключом и программным обеспечением.
Хотите купить TI-калькулятор?
Получите самые низкие цены на TI-Calculators
(со сравнением цен)СРАВНИТЕ лучшие цены на Amazon, Ebay, Target, Walmart, Office Max, Best Buy.
Сравните лучшие цены на Amazon, Walmart, Ebay, Target, Best Buy и т. д.
Изучите историю цен калькуляторов за последние несколько месяцев.
Установите оповещение по электронной почте при снижении цен, чтобы получать уведомления.
Сравните различные модели, чтобы найти калькулятор, который лучше всего соответствует вашим потребностям.
Найдите новые, обновленные, восстановленные, подержанные калькуляторы.
Смотрите обучающие видео и читайте руководства по калькуляторам.
Читайте последние новости о калькуляторах в Интернете.БЕСПЛАТНАЯ загрузка:
Решение квадратных уравнений (шаг за шагом)Загрузите пошаговый решатель квадратных уравнений
. Этот решатель является частью приложения Algebra Made Easy.
— Загрузите бесплатные пробные версии здесь.
— Срок действия пробных и платных приложений неограничен.
— Будущие обновления бесплатны — навсегда!
Онлайн-репетиторство по математике
Получите онлайн-репетиторство.
Репетиторы с отличными оценками по математике будут рады помочь вам.
Получите индивидуальную помощь по математике.
Мы используем Zoom для обучения онлайн, мы шаг за шагом объясняем, как решать математические задачи.

Репетиторы в настоящее время преподают алгебру, алгебру 2, предварительное исчисление, AP исчисление AB и BC, AP статистику, тригонометрию, дискретную математику.
Репетиторы более 10 лет работали в качестве читателей AP Calculus (те люди, которые оценивают экзамены AP Calculus).
Репетиторы также обучают навыкам сдачи тестов, которые так же важны, как и само содержание.
Наши преподаватели имеют более 20 лет опыта преподавания.
1. урок стоит 50$, после этого 100$ в час.
оптом: 540 долларов за 6 часов, 1000 долларов за 12 часов.Забронируйте сеанс репетиторства по электронной почте: [email protected]
Для вопросов, заказов и т. д.: НАПИШИТЕ С НАМИ.
Первый урок (50 долларов США) Один урок (100 долларов США) Несколько уроков Определенный интеграл функции Калькулятор
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:
Просмотрите полный список инструментов dCodeОпределенный интеграл
Инструмент для вычисления интеграла функции.
 Вычисление определенного интеграла по интервалу состоит в измерении площади под кривой интегрируемой функции.
Вычисление определенного интеграла по интервалу состоит в измерении площади под кривой интегрируемой функции.Результаты
Определенный интеграл — dCode
Теги: Функции, Символьные вычисления
Поделиться
dCode и многое другое решать каждый день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !Калькулятор примитивов
⮞ Перейти к: Функции примитивов
Калькулятор определенных интегралов
Функция (f(x)=)
По отношению кНижняя граница
Нижнее значение
$ -\infty $ (-Бесконечность -∞)
Верхняя граница
Верхнее значение
$ +\infty $ (+Бесконечность +∞)
Формат результата Автоматический выбор
Точное значение (если возможно)
Приблизительное числовое значение
Научное обозначениеСм. также: Функции примитивов — среднее значение функции
Калькулятор кратных интегралов
⮞ Перейти к: Двойной интеграл — тройной интеграл
Ответы на вопросы (FAQ)
Что такое интервал? (Определение)
Интеграл является оператором вычисления интегрирования в математике.

Интегрирование обычно представляет собой метод вычисления площади под кривой функции, но его также можно применять для расчета поверхностей и объемов твердых тел.
Интегральное исчисление обычно устанавливается на интервал и использует функциональные примитивы.
Некоторые говорят о неопределенных интегралах для описания примитивных функций (первообразных). Определенные интегралы — это интегралы по интервалу.
Как вычислить определенный интеграл по интервалу?
Чтобы выполнить вычисление интеграла (интегрирование ), сначала вычислите соответствующую примитивную функцию. 91_0 f(x) \mathrm{ dx} = F(1)-F(0) = \frac{1}{2} $$
Введите функцию, ее нижнюю и верхнюю границы и переменную для интегрирования, dCode сделать расчет автоматически.
Каков список общих примитивов?
Полный список общих примитивов доступен на странице примитивов функций.

В чем разница между интегралом и примитивом?
Интеграция включает примитивы функций для выполнения вычислений. Примитивы — это инструмент для вычисления интегралов.
В чем разница между интегралом и производной?
Интеграл является оператором вычисления интегрирования , производная является результатом вычисления дифференциала . Интегральное исчисление и дифференциальное исчисление — это две области исчисления бесконечно малых.
Что такое функции E, F, I0, K0?
При вычислении некоторых форм интегралов используются специальные функции, такие как $E$ и $F$, которые являются эллиптическими интегралами, или $I_0, I_n, J_0, J_n, K_0, K_n$, которые являются функциями Бесселя.
Исходный код
dCode сохраняет за собой право собственности на исходный код «Definite Integral». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Определенный интеграл», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Определенного интеграла» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.
 д.) и загрузка всех данных, скрипт, или API-доступ для «Definite Integral» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android! 907:35 Напоминание: dCode можно использовать бесплатно.
д.) и загрузка всех данных, скрипт, или API-доступ для «Definite Integral» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android! 907:35 Напоминание: dCode можно использовать бесплатно.Cite dCode
Копирование и вставка страницы «Определенный интеграл» или любых его результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Definite Integral на dCode.fr [онлайн-сайт], получено 01 октября 2022 г., https://www.dcode.fr/definite-integralСводка
- Калькулятор примитивов
- Калькулятор определенных интегралов
- Калькулятор множественных интегралов
- Что такое интервал? (Определение)
- Как вычислить определенный интеграл по интервалу?
- Каков список общих примитивов?
- В чем разница между интегралом и примитивом?
- В чем разница между интегралом и производной?
- Что такое функции E, F, I0, K0?
Похожие страницы
- Примитивы Функции
- Тройной интеграл
- Двойной интеграл
- Mean of a Function
- Square Root
- Differential Equation Solver
- Cube Root
- DCODE’S TOOLS LIST
Support
- Paypal
- Patreon
- More
Forum/Help
Keywords
интеграл, функция, интегрирование, интегрирование, исчисление, производная, первообразная, примитив
Ссылки
▲
Четыре лучших интегральных калькулятора для математических заданий — UniCreds
25 октября 2021 г.

Большинство людей наверняка осознают важность калькуляторы и особенно в образовательном секторе.
Можно сказать, что некоторые математические задачи, необходимые для решать только калькуляторами.
И некоторые студенты не так эффективны в математике, поэтому им нужны калькуляторы, но можем ли мы использовать калькуляторы для каждой математической задачи?
Ответ очень прост: да, мы можем использовать калькуляторы. для решения любой математической задачи. Либо это простая, как основная операция, или она связана с некоторые сложные проблемы, такие как интеграция.

Всегда есть два варианта, когда вы собираетесь сделать любую задачу, а когда дело доходит до решения математических проблемы, у нас также есть два варианта.
Один из них — решать свои математические задачи самостоятельно. или вы можете использовать калькулятор, и мы рекомендуем вам перейти для онлайн-калькулятора.
Мы живем в эпоху, когда у нас есть много онлайн калькуляторы, которые, безусловно, бесплатны и легко доступный.
Основным примером является интегральный калькулятор, и мы собираюсь обсудить некоторые интегральные онлайн-калькуляторы и после прочтения этого руководства вы должны четко понимать значение калькуляторов.
Онлайн-калькуляторы VS. Общепринятый калькуляторы
Неправильно недооценивать любой из них, общепринятый калькуляторы очень полезны, а онлайн-калькуляторы тоже очень полезно.
Но когда дело доходит до расширенных или современных функций, онлайн-калькуляторы являются лучшими, и мы собираемся упомяните, почему лучше всего использовать онлайн-калькуляторы вариант.
Мы говорим конкретно о важности интегральные калькуляторы при подготовке математических задания.

Совершенно очевидно, что вам просто нужно решить вопрос интеграции и запишите правильные шаги участвует в расчете.
И это невозможно, когда вы используете обычный калькулятор, как этот калькулятор разработан чтобы показать вам окончательный ответ на проблему.
Но когда вы собираетесь использовать онлайн-калькулятор, вы можете получить все шаги, связанные с расчетом и второе самое главное, онлайн калькуляторы в основном бесплатны.
И именно поэтому мы выбрали четыре лучших встроенные калькуляторы, которые могут делать задания очень легко сделать.
Лучшие интегральные калькуляторы в Интернете
Когда дело доходит до Интернета, есть несколько калькуляторы доступны в Интернете, и вы можете выбрать любой из них.
Но держать в фокусе точность и эффективность очень важно, и не все онлайн-калькуляторы предоставляют вы с этими двумя вещами.
Итак, мы собираемся поделиться подробностями о четырех лучших онлайн-калькуляторы, которые могут решить вашу интеграцию проблема за пару секунд.
- Meracalculator.
 com
com
Прежде всего, говоря об основном понятии интеграция очень важна, поэтому интеграл — это обратная производная, и ее можно решить с помощью или без калькулятора.
Но использование калькулятора может удлинить расчет прост и экономичен по времени, поэтому мы собираемся поделиться информацией об этом калькуляторе.
Когда дело доходит до MeraCalculator, интерфейс этого инструмент очень прост, вам не нужно ничего техническая информация или любое понятие интеграла.
Некоторые поля обязательны для заполнения и после заполнив эти поля, вы можете легко получить отвечать.

Но на этом еще не все, с помощью этого калькулятор, вы можете получить все шаги, связанные с расчет, и вы можете добавить эти шаги, как в ваше задание по математике.
И именно поэтому мы предпочитаем онлайн-калькуляторы, потому что если вы используете обычный, несмотря ни на что, вы будете получить свои результаты с точностью, но вы не получите этапы расчета.
В конце концов, этот калькулятор должен заслужить хотя бы один попробуй, и тогда уж точно решишь, так ли это намеревался использовать или просто игнорировать его.
- Antiderivativecalculator.
 net
net
Пусть вас не смущает название, интеграл и первообразные — это тот же термин, и, как мы уже упоминали, выше этого интеграла является обратным выводом и то же самое касается термина первообразная.
Самое первое, на что следует обратить внимание, это интерфейс этого инструмента. Либо этот инструмент имеет удобный интерфейс или сложный интерфейс?
Не будет ошибкой сказать, что этот инструмент довольно прост. и ясно, как только вы войдете в инструмент, все обязательные поля видны.
Все, что вам нужно, это заполнить эти поля с релевантные данные, такие как поля функций, верхние граница, нижняя граница и поле переменной относительно вы решаете проблему.

Указав все данные во всех этих полях, вы можете обязательно получите ответ, и это займет всего несколько секунд только из-за эффективности, которую мы заметили.
- Maplesoft.com
Если вы хотите получить калькулятор, который может быть считается универсальным, тогда вы можете пойти на это калькулятор.
Имея личный опыт, мы можем сказать, что используя этот инструмент или калькулятор, мы можем легко решить графики тоже.
Но здесь речь идет именно о проблемы с интеграцией, и этого калькулятора достаточно, чтобы решить эти проблемы.

И хорошо, что этот калькулятор легко доступны в Интернете, все, что вам нужно, это ввести бренд, и вы получите свой калькулятор прямо в спереди тебя.
- Cuemath.com
Есть два типа интегралов; один определен и второй бессрочный. Мы можем сказать, что это калькулятор специально разработан для решения определенных интегралы.
Не будет ошибкой сказать, что работа всех интегральные калькуляторы почти одинаковы и когда это подходит к этому калькулятору, в нем тоже есть такие же поля которые мы обсуждали в предыдущем инструменте.

Вы можете быть ограничены при использовании этого калькулятора потому что он специально разработан для решения определенных интегралы.
Если вы хотите решать неопределенные интегралы, то вы должны переключиться на какой-нибудь другой калькулятор, который может решать оба или хотя бы неопределенные интегралы.
Заключение
Калькуляторы очень важны, особенно в мир сегодня, потому что у нас много работы и мы не тратим много времени на одну задачу.
Как уже упоминалось выше, существует два основных типа калькуляторы, но здесь мы обсуждали онлайн калькуляторы, которые более эффективны, экономят время и экономически эффективным.

Ищете студенческие кредиты на образование?
Имя
Электронная почта
Номер телефона (с кодом страны)
Предпочтительная страна назначения выберите странуСШАКанадаВеликобританияАвстралияБельгияКанадаФинляндияФранцияГрузияГерманияИрландияИндияИталияЯпонияКыргызстанЛатвияМалайзияМальтаНидерландыНовая ЗеландияСингапурИспанияШвецияШвейцарияПольшаПортугалия Российская Федерация Соединенное Королевство Украина Объединенные Арабские Эмираты Соединенные Штаты Не уверен“Другое
Сумма кредита
Время присоединиться к университету
Статус приема Не применяется Применяемый Подтвержденный
Ваш запрос был успешно полученный.
 Мы свяжемся с вами
в течение 24 часов по электронной почте/телефону.
Мы свяжемся с вами
в течение 24 часов по электронной почте/телефону.Не позволяйте вашим друзьям пропустить все веселье! Просто порекомендуй своего друга взять кредит и получить Rs. 5000.
продолжить чтениеОшибка! Пожалуйста, проверьте все значения и Попробуйте еще раз
Виттен Шефали Кто-то где-то сказал вещь.


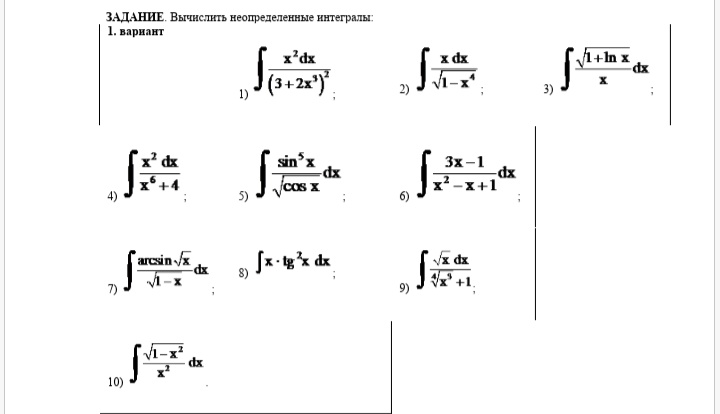 Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека. 3
3 Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн .
Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн . Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн
Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн



 2-3 \ right) dx $, применив интегрирование методом подстановки (также называемое U-подстановкой).»> a b
2-3 \ right) dx $, применив интегрирование методом подстановки (также называемое U-подстановкой).»> a b 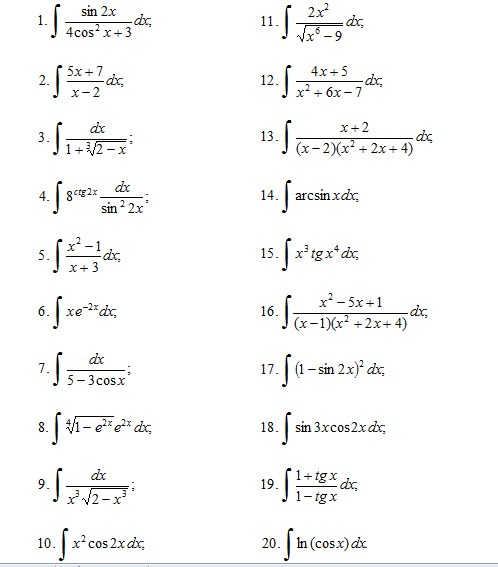
 По умолчанию он установлен как x.
По умолчанию он установлен как x. {2}}}}dx}\), что на самом деле сложнее.
{2}}}}dx}\), что на самом деле сложнее.


 Вы сможете произвести перевод чисел в другую систему счисления и перевод физических величин. Для теоретической помощи существует раздел «Полезное для решения математических задач», в котором можно найти различную табличную и другую информацию. Вычисления доступны 24 часа в сутки с телефона, планшета или компьютера подключенного к Internet.
Вы сможете произвести перевод чисел в другую систему счисления и перевод физических величин. Для теоретической помощи существует раздел «Полезное для решения математических задач», в котором можно найти различную табличную и другую информацию. Вычисления доступны 24 часа в сутки с телефона, планшета или компьютера подключенного к Internet. Отправка на почтовый ящик позволяет решить проблему сохранности решения, а также позволяет напечатать решение на принтере.
Отправка на почтовый ящик позволяет решить проблему сохранности решения, а также позволяет напечатать решение на принтере.
 matem96.ru/kalkulator.shtml
matem96.ru/kalkulator.shtml x] – Возведение числа Эйлера в степень
x] – Возведение числа Эйлера в степень

 3 вводите в следующей последовательности:
3 вводите в следующей последовательности:

 Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.


 Площадь под кривой графика рассчитывается дифференцированием интегральной функции.
Площадь под кривой графика рассчитывается дифференцированием интегральной функции. Производная произведения двух функций f(x) и g(x) равна произведению производных первой функции, умноженной на вторую функцию, и ее производной, умноженной на первую функцию для двух функций f(x ) и g(x).
Производная произведения двух функций f(x) и g(x) равна произведению производных первой функции, умноженной на вторую функцию, и ее производной, умноженной на первую функцию для двух функций f(x ) и g(x). 92)}| +C \]
92)}| +C \] Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь!
Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь! Во-первых, мы должны идентифицировать секцию внутри интеграла с новой переменной (назовем ее $u$), замена которой упрощает вычисление интеграла. Мы видим, что $2x$ — хороший кандидат на замену. Определим переменную $u$ и назначим ее выбранной части
Во-первых, мы должны идентифицировать секцию внутри интеграла с новой переменной (назовем ее $u$), замена которой упрощает вычисление интеграла. Мы видим, что $2x$ — хороший кандидат на замену. Определим переменную $u$ и назначим ее выбранной части Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет решать неопределенные интегралы в кратчайшие сроки. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-калькулятора интегрирования:
Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет решать неопределенные интегралы в кратчайшие сроки. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-калькулятора интегрирования: В исчислении дифференцирование и интегрирование являются фундаментальными операциями и служат наилучшей операцией для решения задач в физике и математике произвольной формы.
В исчислении дифференцирование и интегрирование являются фундаментальными операциями и служат наилучшей операцией для решения задач в физике и математике произвольной формы. Взятие первообразной функции — это самый простой способ символизировать неопределенные интегралы. Когда дело доходит до расчета неопределенных интегралов, калькулятор неопределенных интегралов поможет вам выполнять расчеты неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет ни верхнего, ни нижнего предела.
Взятие первообразной функции — это самый простой способ символизировать неопределенные интегралы. Когда дело доходит до расчета неопределенных интегралов, калькулятор неопределенных интегралов поможет вам выполнять расчеты неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет ни верхнего, ни нижнего предела. Просто введите функцию в специальное поле онлайн-калькулятора интегралов, который использует эти стандартизированные формулы для точных расчетов.
Просто введите функцию в специальное поле онлайн-калькулятора интегралов, который использует эти стандартизированные формулы для точных расчетов. 91_5 x*lnx dx = –14
91_5 x*lnx dx = –14
 Это может быть график новой функции, производной которой является исходная функция (неопределенный интеграл). Таким образом, для мгновенных и быстрых расчетов вы можете использовать бесплатный онлайн-калькулятор первообразных, который позволяет решать неопределенные интегральные функции.
Это может быть график новой функции, производной которой является исходная функция (неопределенный интеграл). Таким образом, для мгновенных и быстрых расчетов вы можете использовать бесплатный онлайн-калькулятор первообразных, который позволяет решать неопределенные интегральные функции. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся далеко друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для обучения K-12, поскольку он легко вычисляет интеграл любой заданной функции шаг за шагом.
В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся далеко друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для обучения K-12, поскольку он легко вычисляет интеграл любой заданной функции шаг за шагом.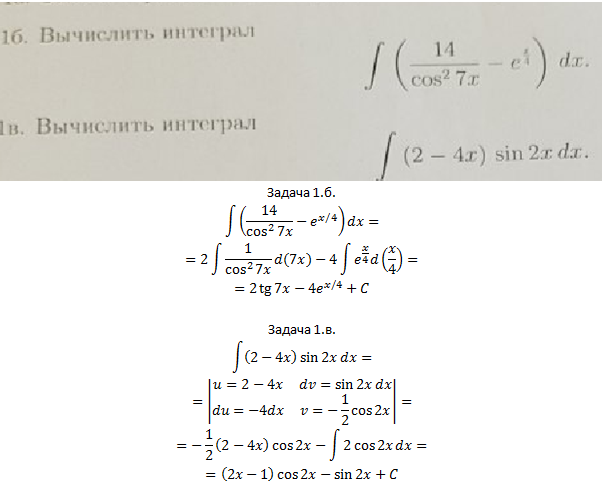 Пройдите курсы по математике, естественным наукам и бизнесу
Пройдите курсы по математике, естественным наукам и бизнесу


 Вычисление определенного интеграла по интервалу состоит в измерении площади под кривой интегрируемой функции.
Вычисление определенного интеграла по интервалу состоит в измерении площади под кривой интегрируемой функции.

 д.) и загрузка всех данных, скрипт, или API-доступ для «Definite Integral» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android! 907:35 Напоминание: dCode можно использовать бесплатно.
д.) и загрузка всех данных, скрипт, или API-доступ для «Definite Integral» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android! 907:35 Напоминание: dCode можно использовать бесплатно.
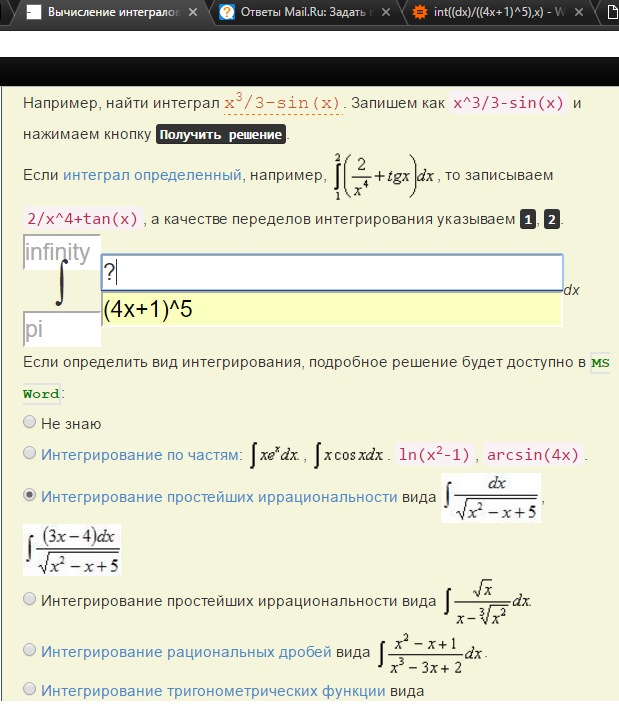



 com
com 
 net
net 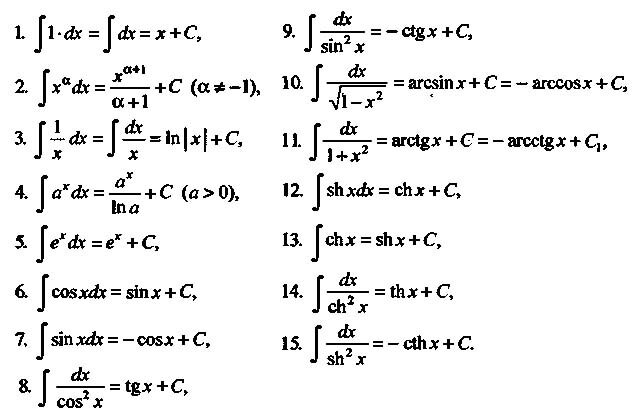



 Мы свяжемся с вами
в течение 24 часов по электронной почте/телефону.
Мы свяжемся с вами
в течение 24 часов по электронной почте/телефону.