Остаточная дисперсия: Остаточная дисперсия | База знаний OpenHealth

Содержание

Что такое остаточная дисперсия? (Определение и пример)

Остаточная дисперсия (иногда называемая «необъяснимой дисперсией») относится к дисперсии в модели, которая не может быть объяснена переменными в модели.

Чем выше остаточная дисперсия модели, тем меньше модель способна объяснить изменение данных.

Остаточная дисперсия появляется на выходе двух разных статистических моделей:

1. Дисперсионный анализ: используется для сравнения средних значений трех или более независимых групп.

2. Регрессия: используется для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .

В следующих примерах показано, как интерпретировать остаточную дисперсию в каждом из этих методов.

Остаточная дисперсия в моделях ANOVA

Всякий раз, когда мы подбираем модель ANOVA («дисперсионный анализ»), мы получаем таблицу ANOVA, которая выглядит следующим образом:

Значение остаточной дисперсии модели ANOVA можно найти в столбце SS («сумма квадратов») для варианта внутри групп .

Это значение также называется «сумма квадратов ошибок» и рассчитывается по следующей формуле:

Σ( Xij – Xj ) 2

куда:

Σ : греческий символ, означающий «сумма».
X ij : i -е наблюдение в группе j
X j : среднее значение группы j

В приведенной выше модели ANOVA мы видим, что остаточная дисперсия составляет 1100,6.

Чтобы определить, является ли эта остаточная дисперсия «высокой», мы можем рассчитать среднюю сумму квадратов для внутри групп и среднюю сумму квадратов для между группами и найти соотношение между ними, что приводит к общему F-значению в таблице ANOVA.

F = MS между / MS внутри
F = 96,1/40,76296
F = 2,357

Значение F в приведенной выше таблице ANOVA равно 2,357, а соответствующее значение p равно 0,113848. Поскольку это p-значение не меньше α = 0,05, у нас нет достаточных доказательств, чтобы отклонить нулевую гипотезу.

Это означает, что у нас нет достаточных доказательств, чтобы сказать, что средняя разница между группами, которые мы сравниваем, значительно отличается.

Это говорит нам о том, что остаточная дисперсия в модели ANOVA высока по сравнению с вариацией, которую модель фактически может объяснить.

Остаточная дисперсия в регрессионных моделях

В регрессионной модели остаточная дисперсия определяется как сумма квадратов разностей между прогнозируемыми точками данных и наблюдаемыми точками данных.

Он рассчитывается как:

Σ(ŷ i – y i ) 2

куда:

Σ : греческий символ, означающий «сумма».
ŷ i : прогнозируемые точки данных
y i : наблюдаемые точки данных

Когда мы подбираем регрессионную модель, мы обычно получаем результат, который выглядит следующим образом:

Значение остаточной дисперсии модели ANOVA можно найти в столбце SS («сумма квадратов») для остаточной вариации.

Отношение остаточной вариации к общей вариации в модели говорит нам о проценте вариации переменной отклика, которая не может быть объяснена предикторными переменными в модели.

Например, в приведенной выше таблице мы рассчитали бы этот процент как:

Необъяснимая вариация = SS Residual / SS Total
Необъяснимая вариация = 5,9024 / 174,5
Необъяснимая вариация = 0,0338

Мы также можем рассчитать это значение, используя следующую формулу:

Необъяснимая вариация = 1 – R 2
Необъяснимая вариация = 1 – 0,96617
Необъяснимая вариация = 0,0338

Значение R-квадрата для модели говорит нам о процентной вариации переменной отклика, которая может быть объяснена переменной-предиктором.

Таким образом, чем ниже необъяснимая вариация, тем лучше модель способна использовать переменные-предикторы для объяснения вариации переменной отклика.

Дополнительные ресурсы

Что такое хорошее значение R-квадрата?
Как рассчитать R-квадрат в Excel
Как рассчитать R-квадрат в R

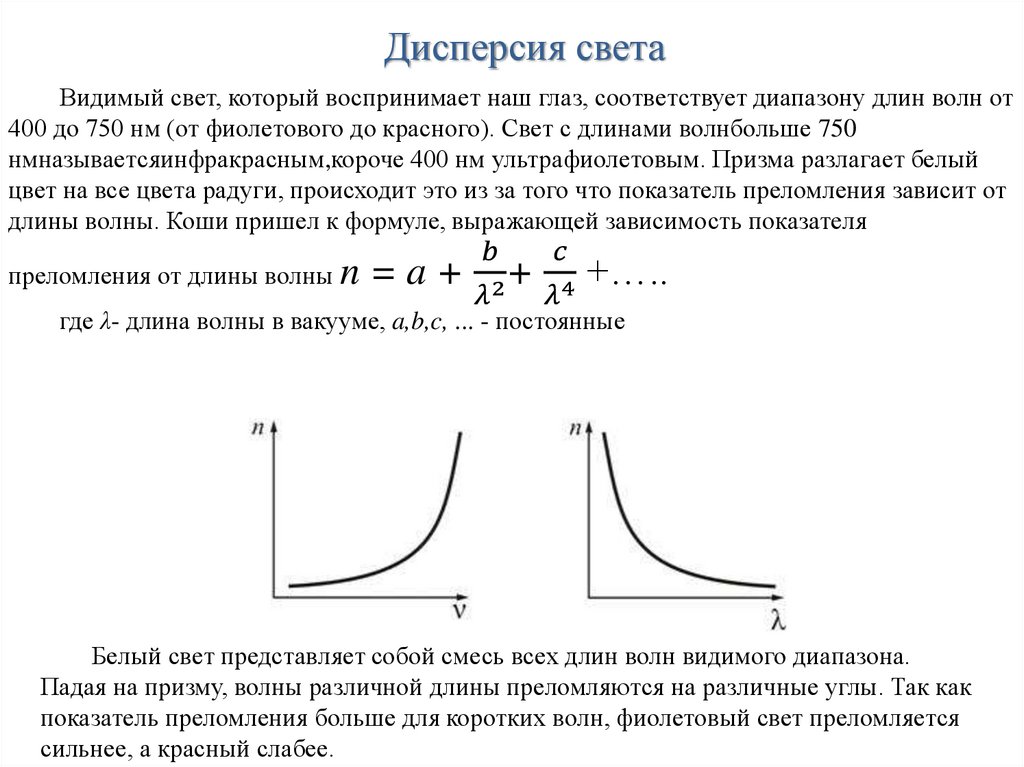
Остаточной дисперсией называется величина

(11)

В знаменателе остаточной дисперсии стоит число степеней свободы равное (n – 2), а не n, так как две степени свободы теряются при определении двух параметров (a, b).

Далее вычислим значения математических ожиданий и дисперсий для коэффициентов а и b. Для коэффициента a мы имеем:

(12)

Для коэффициента b получаем:

(13)

Подставив в выражения теоретических дисперсий параметров a и b вместо σ² ее оценку S², получим оценки дисперсий этих параметров:

, (14)

. (15)

Для проверки значимости коэффициентов a и b вычислим статистики:

, , (16)

здесь S_a, S_b— стандартные ошибки коэффициентов регрессии т. е.

; .

Статистики t_a и t_bподчиняются распределению Стьюдента с числом степени свободы v = n – 2. Выдвинем гипотезу Н₀: a = 0 и для заданного уровня значимости α (обычно α

= 0,05) и числа степеней свободы v = n – 2 найдем из таблицы распределения критерия Стьюдента критическое значение t_кр= t(α,v).

Если t_a > t_кр гипотезу Н₀ отвергаем и считаем коэффициент а значимо отличным от нуля.

Если t_a> t_кр у нас нет оснований отвергать гипотезу Н₀ т. е. в этом случае считаем, что коэффициент а не значимо отличается от нуля.

Аналогично производится проверка на значимость и коэффициента b.

Выборочный коэффициент парной корреляции между переменными x и

y определяемый по выборке из n наблюдений вычисляется по формуле: (17)

Более удобным для практических расчетов значений r_xy является формула: (18)

Выборочный коэффициент парной корреляции дает количественную оценку тесноты линейной связи между переменными x и y. Он является безразмерной величиной и изменяется в диапазоне —1 ≤ r_xy ≤ 1. Если r_xy = 1, это означает, что между переменными x и y существует прямо пропорциональная линейная функциональная зависимость, если r_xy = -1 это означает, что между переменными x и y существует обратно пропорциональная линейная функциональная зависимость. Если

r_xy = 0, то это означает, что между переменными x и y линейной зависимости нет (хотя нелинейная зависимость может существовать), в этом случае говорят, что переменные x и y некоррелированы. В случае, когда -1 < r_xy < 1, говорят что переменные x и y стохастически (вероятностно) линейно связаны. Значимость этой зависимости проверяется следующим образом: вычисляется статистика:

(19)

Статистика t_rподчиняется распределению Стьюдента с числом степени свободы v = n – 2. Выдвигается нулевая гипотеза Н₀: ρ_xy = 0. Далее для заданного уровня значимости α и числа степени свободы v = n – 2 по таблице распределения критерия Стьюдента находим

t_кр = t(α, v).

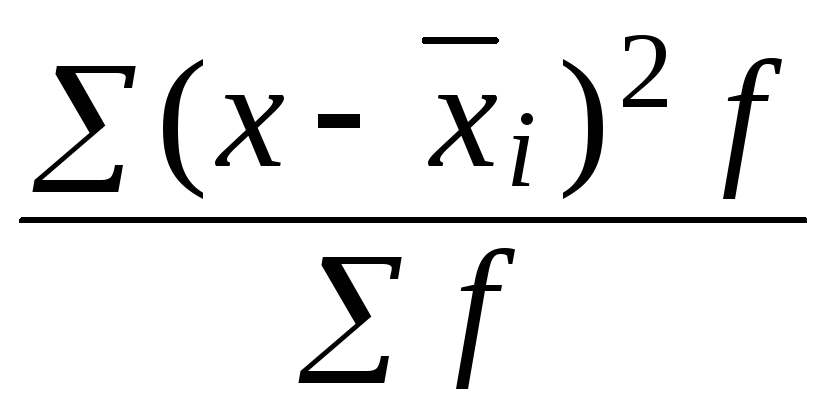
Если |t_r| > t_кр, то нулевая гипотеза об отсутствии линейной зависимости между переменными x и y отвергается, в этом случае переменные x и y считаются коррелированными.

Если |t_r| < t_кр, то у нас нет оснований для того, чтобы отвергнуть нулевую гипотезу, в этом случае мы должны признать, что между переменными x и y не существует значимой линейной зависимости т. е. они не коррелированы.

Теперь покажем, что проверка на значимость выборочного коэффициента парной корреляции r_xy и коэффициента детерминации R²

эквивалентны. С одной стороны:

(20)

с другой стороны

(21)

Из формул (20) и (21) следует, что

(22)

Из формулы (22) следует, что t_r= из чего делаем вывод о том, что проверка на значимость выборочного коэффициента парной корреляции r_xy и коэффициента детерминации R²эквивалентны.

Наблюдаемые значения объясняемой переменной y_i () отличаются от прогнозируемых значений , рассчитанных по уравнению регрессии. Чем меньше эти отличия, тем ближе прогнозируемые значения подходят к наблюдаемым значениям y

i, и тем лучше качество построенной модели. Величина отклонения наблюдаемого и прогнозируемого значения объясняемой переменной по каждому наблюдению представляет собой ошибку аппроксимации. Так как может быть как величиной положительной, так и отрицательной, то ошибку аппроксимации для каждого наблюдения принято определять в процентах и по модулю.

Выражение можно рассматривать как абсолютную ошибку аппроксимации, а выражение:

как относительную ошибку аппроксимации для i-го наблюдения.

Чтобы иметь показатель, характеризующий качество модели в целом, определяют среднюю ошибку аппроксимации по всем наблюдениям в выборке по формуле:

Считается [2, 3], что построенное уравнение регрессии достаточно хорошо прогнозирует наблюдаемые значения объясняемой переменной, если .

В прогнозных расчетах по построенному уравнению регрессии (2) определяется предсказываемое значение, как точечный прогноз при x = x_p, т. е. путем подстановки в уравнение регрессии (2) соответствующего значения объясняющей переменной x. Однако надо признать, что точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки т.е. и соответственно интервальной оценкой наблюдаемых значений.

Ошибка предсказания равна разности между предсказанным и действительным значениями:

Ошибка предсказания имеет нулевое математическое значение:

Вычислим дисперсию прогноза, поскольку

то для дисперсии прогноза имеем

Из этой формулы следует, что чем больше x_p отклоняется от выборочного среднего , тем больше дисперсия ошибки предсказания, и чем больше объем выборки n, тем меньше дисперсия.

Заменяя в дисперсии прогноза на ее оценку S² и извлекая квадратный корень, получим стандартную ошибку предсказания

Доверительный интервал для действительного значения y_p определяется выражением:

где t_кр – критическое значение t – статистики при заданном уровне значимости и соответствующем объему выборки числе степеней свободы.

На Рис. 1 отрезок отмеченный стрелками определяет доверительный интервал истинного значения объясняемой переменной

y_p относительно предсказанного по уравнению регрессии значения .

Рис. 1

Теперь рассмотрим на конкретном примере, как применяется на практике изложенная выше теория парного линейного регрессионного анализа.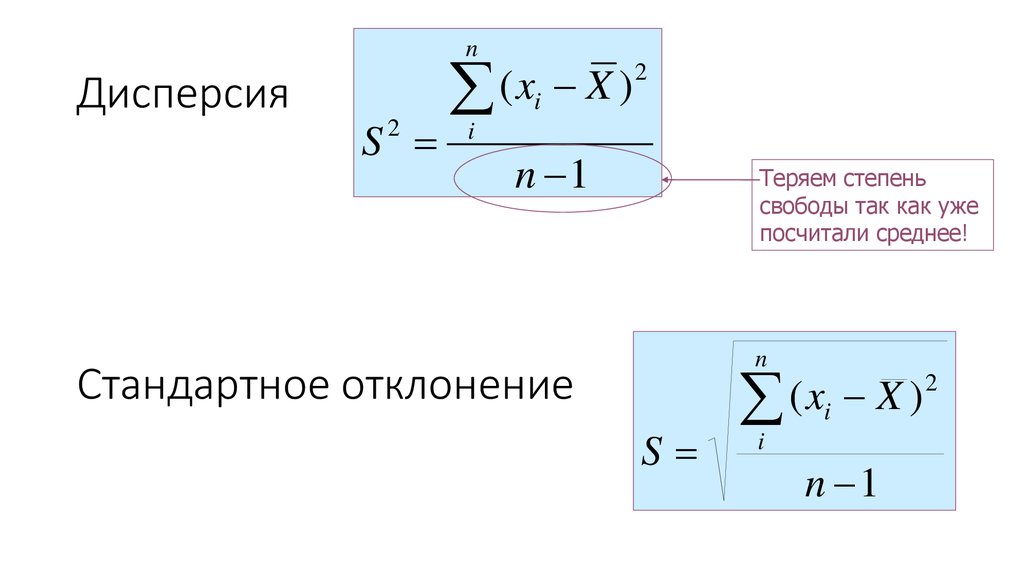

В качестве примера рассмотрим зависимость между сменной добычей торфа на одного рабочего y(т) и мощностью пласта x(м) по следующим (условным) данным, характеризующим процесс добычи торфа в n = 10 карьерах.

Таблица 1

I	1	2	3	4	5	6	7	8	9	10
x_i	4	11	14	9	8	8	15	9	8	12
y_i	2	8	10	6	4	5	12	4	5	9

Для определения вида зависимости между x и y построим корреляционное поле ( смотрите Рис. 2 ):

Рис. 2

По расположению точек на корреляционном поле полагаем, что зависимость между x и y линейная: y = a + bּx.

По формулам, приведенным ранее, находим:

;

Для повышения наглядности вычислений по МНК построим таблицу 2:

Таблица 2

№	x_i	y_i	x²_i	x_iּy_i	y²_i					А_i
1	4	2	16	8	4	1. 100	20.250	29.155	0.809	44.950
2	11	8	121	88	64	7.617	2.250	1.248	0.147	4.775
3	14	10	196	140	100	10.410	12.250	15.288	0.168	4.110
4	9	6	81	54	36	5. 755	0.250	0.555	0.066	4.667
5	8	4	64	32	16	4.824	6.25	2.808	0.679	20.625
6	8	5	64	40	25	4.824	2.25	2.808	0.031	3.500
7	15	12	225	180	144	11. 341	30.25	23.435	0.424	5.483
8	9	4	81	36	16	5.755	6.25	0.555	3.081	43.900
9	8	5	64	40	25	4.824	2.25	2.808	0.031	3.500
10	12	9	144	108	81	8. 548	6.25	4.195	0.204	5.011
∑	98	65	1056	726	511	65	88.50	82.856	5.044	139.92
среднее	9.8	6.5	105.6	72.6	51.1	6.5	8.85	8.286	0.564	13.992

Теперь определим значимость параметров a = -2.623 и b = 0,931, входящих в построенное уравнение регрессии. Для этого зададимся уровнем значимости α = 0,05; вычислим число степеней свободы v = n – 2 = 10 – 2 = 8. И далее по таблице распределения критерия Стьюдента определим t_кр= t(α,v₁) = t(0,05; 8) = 2,301. Так как t_a= 2,972 > t_кр = 2,301 и t_b = 10.837 > t_кр = 2,301 оба параметра значимо отличаются от нуля и должны быть оставлены в модели. Значит, построенное уравнение регрессии будет иметь вид:

(23)

Теперь определим, насколько хорошо построенное уравнение регрессии описывает наблюдаемые значения y. Для этого снова зададимся уровнем значимости α = 0,05; найдем по формулам: k₁ = 1, k₂ = n – 2 = 10 – 2 = 8 числа степеней свободы; далее по таблице распределения критерия Фишера — Снедекора найдем F_кр = F(α, k_1,k₂) = F(0,05;1;8) = 5,320. Так как F = 117,000 > F_кр = 5,320; то делаем вывод, что построенное уравнение регрессии адекватно описывает наблюдаемые значения переменной y и им можно пользоваться для прогнозирования значений y при соответствующих значениях x.

Для построенной модели значение коэффициента детерминации R² = 0,936; что свидетельствует о том, что 93,6% вариации значений переменной y объясняется изменчивостью переменной x, и только 6,4% вариации значений y объясняется воздействием случайного фактора.

Для построенной модели значение выборочного коэффициента корреляции есть r_xy = 0,968. По формуле (19) вычислим значение . (24)

Выдвинем гипотезу Н₀: ρ_xy = 0. Зададимся уровнем значимости α = 0,05, вычислим v = n – 2= 10 – 2 = 8 и по таблице распределения критерия Стьюдента найдем t_кр = 2,310.

Для t_кри t_r выполняется неравенство t_r = 10.823 > t_кр = 2,301 из которого мы делаем вывод, что нулевая гипотеза должна быть отвергнутаи мы должны признать, что между переменными x и y существует значимая линейная зависимость. Это является еще одним подтверждением адекватности построенного уравнения регрессии (23).

Уровень вариации остаточной дисперсии и мощность тестов дифференциальной экспрессии для данных RNA-Seq

. 7 апреля 2015 г .; 10 (4): e0120117.

doi: 10.1371/journal.pone.0120117. Электронная коллекция 2015.

Гу Ми ¹ , Яньмин Ди ²

Принадлежности

¹ Департамент статистики Орегонского государственного университета, Корваллис, Орегон, Соединенные Штаты Америки.
² Статистический факультет Орегонского государственного университета, Корваллис, Орегон, Соединенные Штаты Америки; Программа молекулярной и клеточной биологии, Университет штата Орегон, Корваллис, штат Орегон, Соединенные Штаты Америки.

PMID: 25849826
PMCID: PMC4388866
DOI: 10.1371/journal.pone.0120117

Бесплатная статья ЧВК

Гу Ми и др. ПЛОС Один. 2015 .

Бесплатная статья ЧВК

. 7 апреля 2015 г .; 10 (4): e0120117.

doi: 10.1371/journal.pone.0120117. Электронная коллекция 2015.

Авторы

Гу Ми ¹ , Яньмин Ди ²

Принадлежности

¹ Департамент статистики Орегонского государственного университета, Корваллис, Орегон, Соединенные Штаты Америки.
² Статистический факультет Орегонского государственного университета, Корваллис, Орегон, Соединенные Штаты Америки; Программа молекулярной и клеточной биологии, Университет штата Орегон, Корваллис, штат Орегон, Соединенные Штаты Америки.

PMID: 25849826
PMCID: PMC4388866
DOI: 10. 1371/journal.pone.0120117

Абстрактный

Секвенирование РНК (RNA-Seq) получило широкое распространение для количественной оценки изменений экспрессии генов при сравнительном анализе транскриптома. Для обнаружения дифференциально экспрессируемых генов были предложены различные статистические методы, основанные на отрицательном биномиальном (NB) распределении. Эти методы различаются тем, как они обрабатывают мешающие параметры NB (т. е. параметры дисперсии, связанные с каждым геном) для экономии энергии, например, используя модель дисперсии для использования очевидной взаимосвязи между параметром дисперсии и средним значением NB. Предположительно, дисперсионные модели с меньшим количеством параметров приведут к большей мощности, если модели верны, но в противном случае приведут к вводящим в заблуждение выводам. В этой статье исследуется этот компромисс мощности и надежности путем оценки скорости определения истинного дифференциального выражения с использованием различных методов при реалистичных предположениях о параметрах дисперсии NB. Наши результаты показывают, что относительные характеристики различных методов тесно связаны с уровнем вариации дисперсии, не объясняемой моделью дисперсии. Мы предлагаем простую статистику для количественной оценки уровня вариации остаточной дисперсии из подобранной модели дисперсии и показываем, что величина этой статистики дает подсказки о том, можем ли мы и в какой степени мы можем получить статистическую мощность с помощью подхода моделирования дисперсии.

Заявление о конфликте интересов

Конкурирующие интересы: Авторы заявили об отсутствии конкурирующих интересов.

Цифры

Рис. 1. Графики средней дисперсии для человека…

Рис. 1. Графики средней дисперсии для набора данных RNA-Seq человека.

Левая панель предназначена для… 9MOM) по оси y и оценочной относительной средней частоте по оси x . Подобранные кривые для пяти моделей дисперсии наложены на график рассеяния.

Рис. 2. Истинный положительный показатель (TPR) по сравнению с…

Рис. 2. Графики истинного положительного результата (TPR) и ложного обнаружения (FDR) для шести…

Рис. 2. Графики «Истинно положительные результаты» (TPR) и «Ложные результаты обнаружения» (FDR) для шести методов тестирования DE, выполненных на наборах данных RNA-Seq, смоделированных для имитации реальных наборов данных.

По реальным данным оценены кратности изменения генов ДЭ. Столбцы соответствуют следующим наборам данных (слева направо), используемым в качестве шаблонов при моделировании: человек, мышь, данио, арабидопсис и плодовая муха. Уровень вариации остаточной дисперсии, σ , определяется как расчетное значение (σ˜) на панелях, помеченных буквой A (первая строка), и половина расчетного значения (0,5σ˜) на панелях, помеченных буквой B (вторая строка). . В каждом сюжете 9Ось 0105 x — это TPR (то же самое, что полнота и чувствительность), а ось y — это FDR (то же самое, что один минус точность). Процент действительно генов DE указан на уровне 20% во всех наборах данных. Значения FDR сильно варьируются, когда TPR близок к 0, поскольку знаменатель TP + FP близок к 0,

Рис. 3. Истинный положительный показатель (TPR) по сравнению с…

Рис.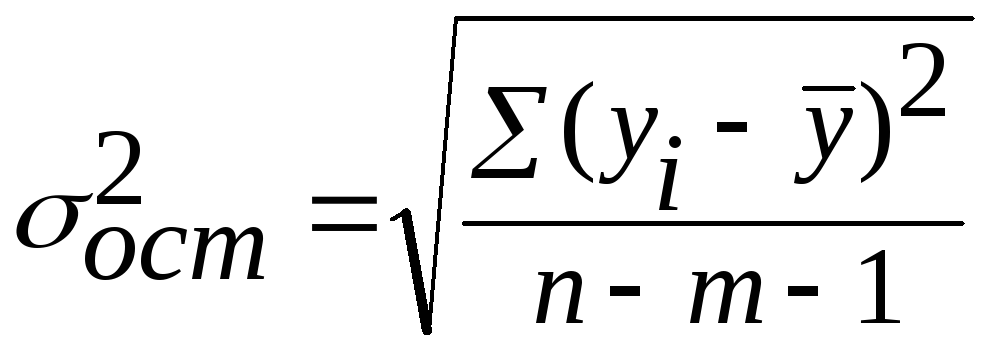 3. Графики истинного положительного результата (TPR) и показателя ложного обнаружения (FDR) для шести…

Рис. 3. Графики «Истинно положительные результаты» (TPR) и «Ложные результаты обнаружения» (FDR) для шести методов тестирования DE, выполненных на наборах данных RNA-Seq, смоделированных для имитации реальных наборов данных.

Кратность изменения генов DE зафиксирована на уровне 1,2 (половина генов DE сверхэкспрессирована, а другая половина недостаточно экспрессирована). Остальные настройки моделирования идентичны описанным в легенде к рис. 2.

Рис. 4. Истинный положительный показатель (TPR) по сравнению с…

Рис. 4. Графики истинных положительных результатов (TPR) и частоты ложных открытий (FDR) для шести…

Рис. 4. Графики «Истинно положительные результаты» (TPR) и «Ложные результаты обнаружения» (FDR) для шести методов тестирования DE, выполненных на наборах данных RNA-Seq, смоделированных для имитации реальных наборов данных.

Кратность изменения генов DE зафиксирована на уровне 1,5 (половина генов DE сверхэкспрессирована, а другая половина — недостаточно экспрессирована). Остальные настройки моделирования идентичны описанным в легенде к рис. 2.

Рис. 5. Истинный положительный показатель (TPR) по сравнению с…

Рис. 5. Графики истинного положительного результата (TPR) и ложного обнаружения (FDR) для шести…

Рис. 5. Графики «истинно положительные результаты» (TPR) и «частота ложных открытий» (FDR) для шести методов тестирования DE, выполненных на наборе данных RNA-Seq, смоделированном для имитации набора данных человека.

На каждой кривой мы отметили положение, соответствующее сообщаемому FDR 10%, крестиком. Кратность изменения генов DE зафиксирована на уровне 1,2 (половина генов DE сверхэкспрессирована, а другая половина — недостаточно экспрессирована). Остальные настройки моделирования идентичны настройкам для верхней строки рис. 2.

Рис. 6. Гистограммы p -значений для…

Рис. 6. Гистограммы p -значений для не-DE генов из шести тестов DE…

Рис. 6. Гистограммы значений p для генов, не являющихся DE, по шести методам тестирования DE.

Набор данных моделирования основан на наборе данных человека с σ указано как оценочное значение σ=σ˜. Из 5000 генов 80% не являются DE.

Рис. 7. Гистограммы p -значений для…

Рис. 7. Гистограммы p -значений для не-DE генов из шести тестов DE…

Рис. 7. Гистограммы значений p для генов, не являющихся DE, по шести методам тестирования DE.

Набор данных моделирования основан на наборе данных человека с σ , указанным как половина оценочного значения σ=0,5σ˜. Из 5000 генов 80% не являются DE.

Рис. 8. Графики MA для edgeR:trending,…

Рис. 8. Графики MA для методов edgeR:trended, NBPSeq:genewise, edgeR:tagwise-trend и QuasiSeq:QLSpline, выполненных на…

Рис. 8. Графики MA для методов edgeR:trending, NBPSeq:genewise, edgeR:tagwise-trend и QuasiSeq:QLSpline, выполненных на наборе данных мыши.

Прогнозируемые изменения логарифмической кратности (апостериорные байесовские оценки истинных логарифмических изменений кратности, значения «М») показаны на оси y . Средние значения количества журналов на миллион (CPM) показаны на оси x (значения «A»). Значения M и A рассчитываются с использованием edgeR. Выделенные точки соответствуют первым 200 генам DE, идентифицированным каждым из методов тестирования DE. 9ценности.

Рис. 10. Калибровочный график для оценки…

Рис. 10. Калибровочный график для оценки вариации остаточной дисперсии σ для набора данных мыши.

Рис. 10. Калибровочный график для оценки вариации остаточной дисперсии σ для набора данных мыши. 9оценивается по набору данных мыши.
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Тесты согласия и диагностика моделей для отрицательной биномиальной регрессии данных секвенирования РНК.
Ми Г, Ди Ю, Шафер Д.В. Ми Г и др. ПЛОС Один. 2015 18 марта; 10 (3): e0119254. doi: 10.1371/journal.pone.0119254. Электронная коллекция 2015. ПЛОС Один. 2015. PMID: 25787144 Бесплатная статья ЧВК.
Анализ мощности и оценка размера выборки для дифференциальной экспрессии RNA-Seq.
Чинг Т., Хуан С., Гармир Л.С. Чинг Т. и др. РНК. 2014 ноябрь;20(11):1684-96. doi: 10.1261/РНК.046011.114. Epub 2014 22 сентября. РНК. 2014. PMID: 25246651 Бесплатная статья ЧВК.
Обнаружение высокой изменчивости в экспрессии генов с помощью профилирования одноклеточной РНК-seq.
Чен ХИ, Джин И, Хуан Ю, Чен Ю. Чен Х.И. и др. Геномика BMC. 2016 авг. 22; 17 Приложение 7 (Приложение 7): 508. doi: 10.1186/s12864-016-2897-6. Геномика BMC. 2016. PMID: 27556924 Бесплатная статья ЧВК.
Статистическое обнаружение дифференциально экспрессируемых генов на основе РНК-секвенирования: от биологических до филогенетических повторов.
Гу Х. Гу Х. Кратко Биоинформ. 2016 март; 17 (2): 243-8. дои: 10. 1093/биб/bbv035. Epub 2015 24 июня. Кратко Биоинформ. 2016. PMID: 26108230 Обзор.
Сила и перспективы секвенирования РНК в экологии и эволюции.
Тодд Э.В., Блэк Массачусетс, Геммелл, Нью-Джерси. Тодд Э.В. и соавт. Мол Экол. 2016 март; 25(6):1224-41. doi: 10.1111/mec.13526. Epub 2016 1 марта. Мол Экол. 2016. PMID: 26756714 Обзор.
Посмотреть все похожие статьи
Цитируется
Тесты согласия и диагностика моделей для отрицательной биномиальной регрессии данных секвенирования РНК.
Ми Г, Ди Ю, Шафер Д.В. Ми Г и др. ПЛОС Один. 2015 18 марта; 10 (3): e0119254. doi: 10.1371/journal.pone.0119254. Электронная коллекция 2015. ПЛОС Один. 2015. PMID: 25787144 Бесплатная статья ЧВК.
Рекомендации
Ван З., Герштейн М., Снайдер М. RNA-Seq: революционный инструмент для транскриптомики. Природа Обзоры Генетика. 2009;10(1):57–63. 10.1038/nrg2484 — DOI — ЧВК — пабмед
Робинсон, доктор медицины, Маккарти ди-джей, Смит Г. К. edgeR: пакет Bioconductor для анализа дифференциальной экспрессии цифровых данных экспрессии генов. Биоинформатика. 2010;26(1):139–140. 10.1093/биоинформатика/btp616 — DOI — ЧВК — пабмед
Андерс С., Хубер В. Дифференциальный анализ экспрессии для данных подсчета последовательностей. Геномная биология. 2010;11(10):R106 10.1186/gb-2010-11-10-r106 — DOI — ЧВК — пабмед
Ди Ю, Шафер Д. В., Камби Дж.С., Чанг Дж.Х. Отрицательная биномиальная модель NBP для оценки дифференциальной экспрессии генов из RNA-Seq. Статистические приложения в генетике и молекулярной биологии. 2011;10(1):1–28. 10.2202/1544-6115.1637 — DOI
Marioni JC, Mason CE, Mane SM, Stephens M, Gilad Y. RNA-seq: оценка технической воспроизводимости и сравнение с массивами экспрессии генов. Геномные исследования. 2008;18(9):1509–1517. 10.1101/гр.079558.108 — DOI — ЧВК — пабмед
Типы публикаций
термины MeSH
Грантовая поддержка
R01 GM104977/GM/NIGMS NIH HHS/США
R01GM104977/GM/NIGMS NIH HHS/США
Измерение остаточной дисперсии — новый метод анализа поверхностных волн | Бюллетень сейсмологического общества Америки
Пропустить пункт назначения навигации
Исследовательская статья| 01 февраля 1972 г.
А. Дзевонски;
Дж. Миллс;
С. Блох
Информация об авторе и статье
Издательство: Сейсмологическое общество Америки.
Полученный: 08 июн 1971
Первый онлайн: 03 мар 2017
Онлайновый ISSN: 1943-3573
Печатный ISSN: 0037-1106
Copyright © 1972, Американское сейсмологическое общество
Бюллетень Американского сейсмологического общества (1972) 62 (1): 129– 139.
https://doi.org/10.1785/BSSA0620010129
История статьи
Получено:
08 июня 1971 г.
Первый онлайн:
03 марта 2017 г.
Цитирование
А. Дзиевонски, Дж. Миллс, С. Блох; Измерение остаточной дисперсии — новый метод анализа поверхностных волн. Бюллетень сейсмологического общества Америки 1972; 62 (1): 129–139. doi: https://doi.org/10.1785/BSSA0620010129
Скачать файл цитаты:
Ris (Zotero)
Реф-менеджер
EasyBib
Подставки для книг
Менделей
Бумаги
Конечная примечание
РефВоркс
Бибтекс
панель инструментов поиска
Расширенный поиск
Измерения групповых скоростей с помощью полосовой фильтрации приводят к систематическим ошибкам, когда групповая скорость быстро изменяется с частотой. Новый метод, именуемый далее «измерение остаточной дисперсии», позволяет избежать этой трудности за счет преобразования сигнала перед фильтрацией. Наблюдаемая сейсмограмма взаимно коррелируется с теоретической сейсмограммой, в которой дисперсия приближается к наблюдаемой дисперсии с точностью до нескольких процентов. Дисперсия результирующего импульса может быть измерена с гораздо большей точностью, так как du/dω уменьшен как минимум на порядок. Кроме того, метод можно использовать многократно для получения большей точности измерения.
Дисперсия мантийных волн Рэлея измерена по сумме 48 автокоррелограмм записей аляскинского землетрясения 28 марта 1964 г. Групповая и фазовая скорости получены для порядковых номеров между ₀ S ₉ и ₀ S ₄₇ . Подсчитано, что абсолютная погрешность измерения групповой скорости не превышает 0,015 км/сек.
Анализ суммы 13 автокоррелограмм сейсмограмм горизонтальной составляющей с преимущественно поперечным движением показывает, что данные волны Лява фундаментальной моды могут быть загрязнены более высокими торсионными модами. Сравнение нескольких наборов средних фазовых скоростей волн Лява показывает расхождение порядка 0,4% в диапазоне периодов от 350 до 170 сек.
No related posts.