Острый угол начертить: Острые и тупые углы — урок. Математика, 2 класс.

что это такое, признаки и свойства, примеры решения задач

Содержание:

• Что такое острый угол
• Признаки и свойства острых углов
• Примеры решения задач

Содержание

• Что такое острый угол
• Признаки и свойства острых углов
• Примеры решения задач

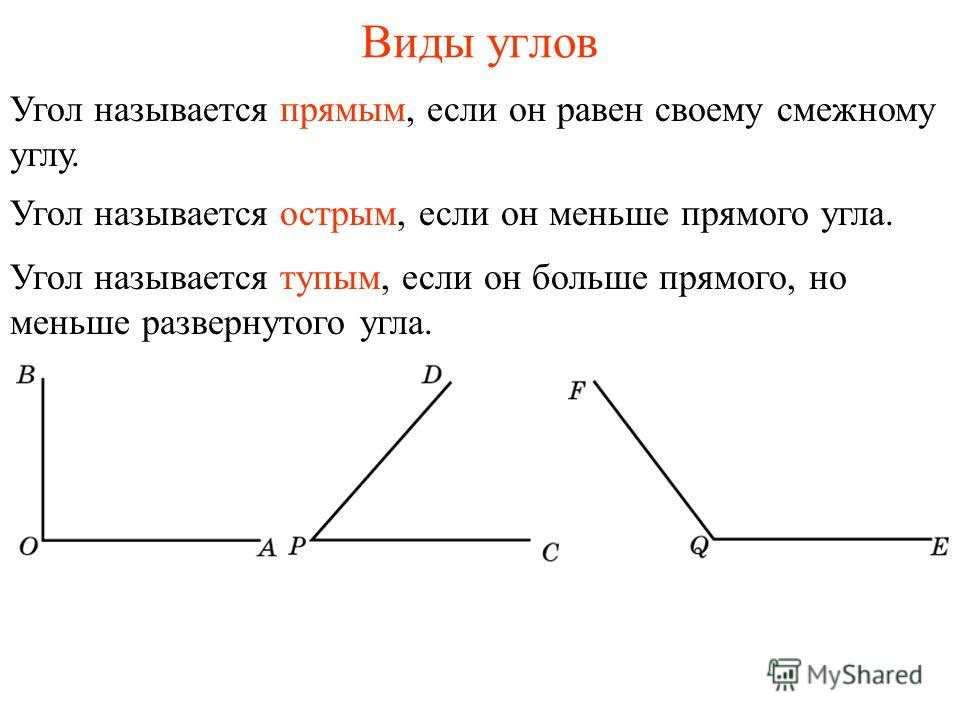
Что такое острый угол

Острым углом принято обозначать такой угол, который меньше по сравнению с прямым, то есть имеет градусную меру больше, чем ноль, но меньше, чем 90°.

Изобразим на рисунке, как выглядит острый угол, исходя из рассмотренного определения:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Источник: www.treugolniki.ru

На уроках геометрии и математике при решении различных задач школьники пользуются специальными измерительными и чертежными инструментами. Одним из таких полезных приспособлений является транспортир. С его помощью можно достаточно быстро и просто выполнить построение острого угла какой-либо градусной меры.

Порядок действий при построении острого угла с применением транспортира:

1. Отметить некую точку на листе бумаги, которая будет играть роль вершины заданного угла.
2. Используя полученную точку, построить луч, вершина которого совпадает с ней. Данный луч является одной из сторон искомого угла.
3. С помощью транспортира совместим вершину угла с отверстием, расположенным по центру инструмента, таким образом, чтобы отмеченный на нем ноль градусов совпал с определенной ранее стороной угла.
4. Предположим, что необходимо рассмотренным способом начертить угол в 72°. На шкале транспортира в данном случае потребуется найти отметку в соответствии с заданной градусной мерой и нарисовать точку.
5. Далее следует соединить полученную точку с вершиной угла с помощью луча, который является второй стороной искомого угла.

Перенесем рассмотренную схему изображения острого угла в 72°. Заметим, что отчет градусной меры допустимо начинать с нижней или верхней шкалы, отмеченной на транспортире:

Источник: www.treugolniki.ru

Признаки и свойства острых углов

Перечислим свойства, которые характерны для любого острого угла:

1. При рассмотрении пары смежных углов, один из которых меньше по сравнению с прямым, то есть определяется как острый, можно сделать вывод, что второй из смежных углов является тупым.
2. Какой-либо произвольный треугольник обладает как минимум одним острым углом.
3. Треугольники, которые образованы тремя острыми углами, носят название остроугольных.

Признаком любого острого угла является его градусная мера, которая в любом случае будет меньше, чем 90°. В геометрии часто встречаются задачи, когда необходимо идентифицировать тот или иной угол по его признаку. Тогда целесообразно воспользоваться еще одним полезным инструментом под названием угольник.

В качестве примера воспользуемся угольником и соединим его вершину с вершиной искомого угла, который необходимо идентифицировать. При этом расположим угольник так, чтобы его грань проходила по какой-нибудь одной стороне рассматриваемого угла. В результате другая сторона измерительного инструмента перекроет вторую сторону угла. Изобразим схематично принцип выполнения этой процедуры:

Источник: www.treugolniki.ru

Примеры решения задач

Задача 1

На рисунке изображено несколько углов.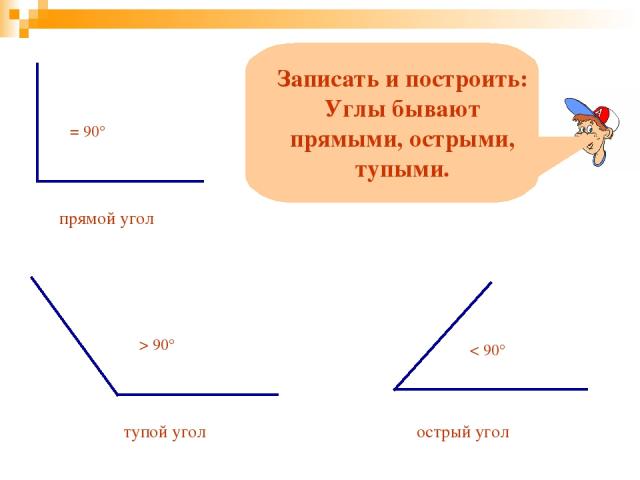 Требуется выяснить, какой из представленных углов является острым. 

Решение

Воспользуемся определением острого угла и вспомним, что его градусная мера меньше, чем 90°.

Рассмотрим изображение угла на рисунке (а). Заметим, что в данном случае одна сторона угла играет роль перпендикуляра по отношению ко второй. Тогда угол, который расположен между ними, составляет 90°. Сделаем вывод, что такой угол является прямым.

Далее обратимся к рисунку (б). Построим к одной из сторон угла перпендикуляр. Изобразим это действие наглядно, дополнив начальное изображение:

 

Заметим, что угол меньше по сравнению с прямым. Это утверждение полностью соответствует понятию острого угла. Сделаем вывод о том, что угол, изображенный на рисунке (б), является острым.

Перейдем к третьему варианту. Аналогично предыдущему примеру, построим перпендикулярную прямую к углу, изображенному на рисунке (в), которая проходит через его вершину:

 

Заметим, что искомый угол больше по сравнению с прямым, то есть имеет такую градусную меру, которая превышает 90°.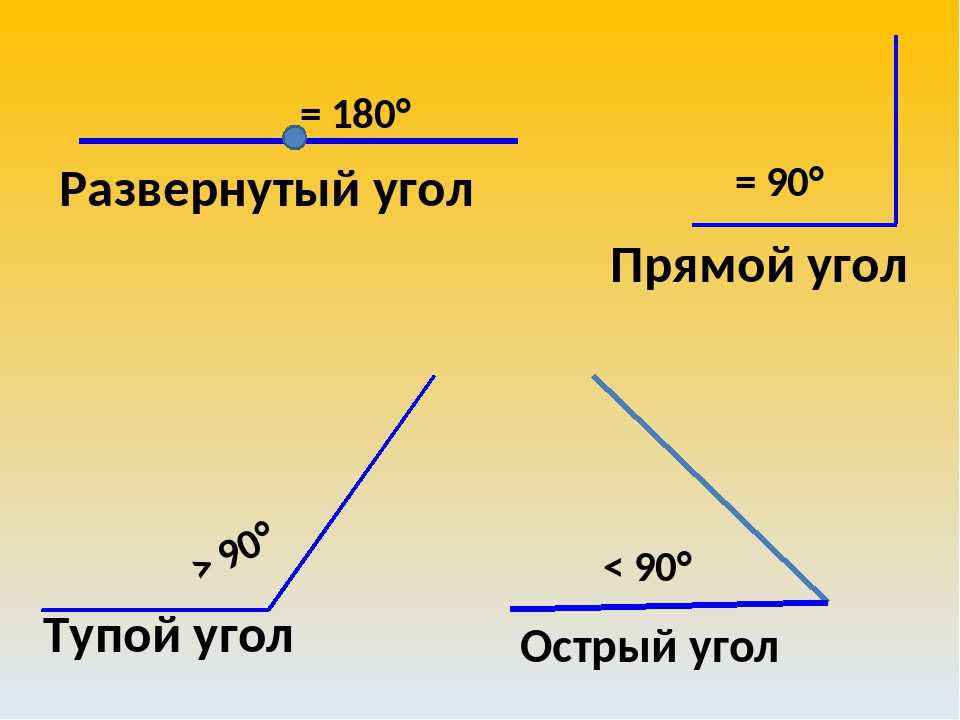  Данный угол можно идентифицировать как тупой. Он не является острым.

Ответ: острым является угол, изображенный на рисунке (б).

Задача 2

Имеется пара смежных углов. Один из них имеет градусную меру, которая на 30° меньше, чем у второго. Необходимо определить, чему равен острый угол.

Решение

Введем обозначение х для неизвестного острого угла. В таком случае угол, градусная мера которого больше, можно записать в виде следующего выражения:

х + 30

Вспомним, что острый угол обладает полезным свойством. При рассмотрении пары смежных углов, один из которых меньше по сравнению с прямым, то есть определяется как острый, можно сделать вывод, что второй из смежных углов является тупым. В сумме смежные углы составляют 180°. Запишем справедливое равенство:

х + (х+30) = 180

2х = 150

х = 75

Угол, который ранее был обозначен за х, составляет 75°. Заметим, что такая градусная мера меньше, чем 90°.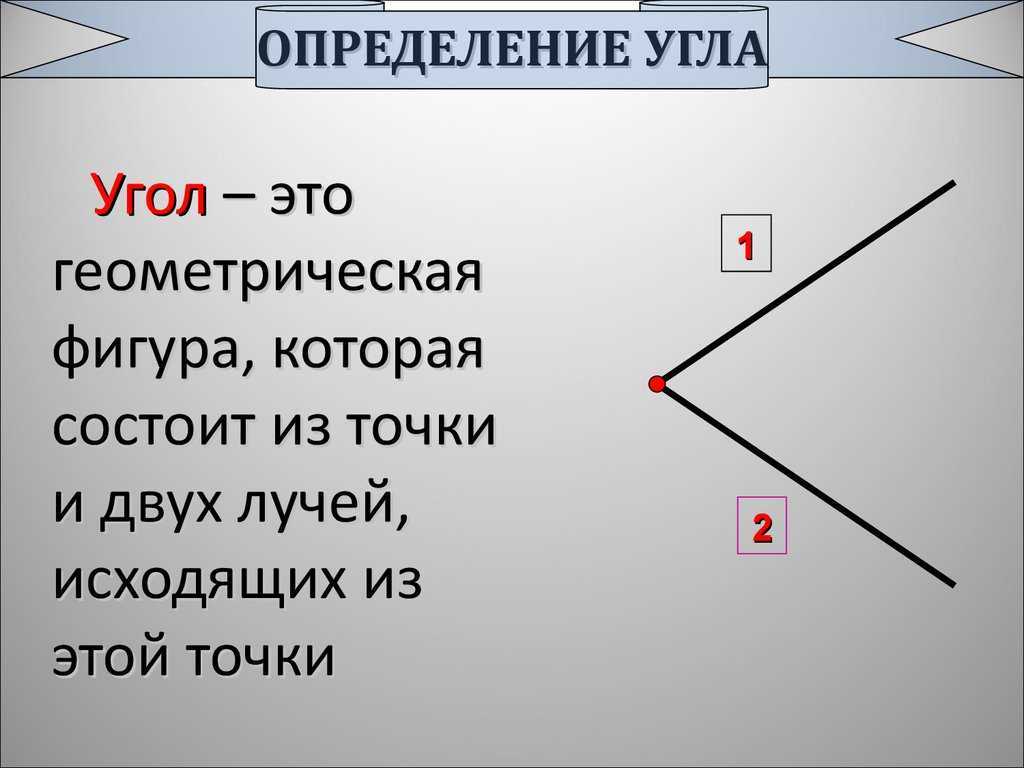 На основании этого факта острый угол равен 75°.

Ответ: 75°.

Задача 3

На рисунке изображена окружность с центром в точке О. К окружности построена касательная СА, которая играет роль одной из сторон угла с вершиной в точке С. Вторая сторона угла пересекает точку О. Градусная мера полученной дуги АD составляет 100°. Необходимо вычислить, чему равен угол АСО.

 

Решение

Построим в заданной окружности радиус, который обозначим как ОА. Перенесем действия на рисунок:

 

Заметим, что полученный треугольник АОС имеет прямой угол, то есть по определению является прямоугольным:

АОС  = 90°

Вспомним, что в сумме все углы в треугольнике составляют 180°. На основании этого соотношения вычислим градусную меру угла СОА:

СОА = 180 – АОD = 180 – 100 = 80

В результате угол АОС составит:

АОС  = 90 – 80 = 10

Ответ: 10°

Задача 4

На рисунке изображены два смежных угла.

Необходимо вычислить, чему равен угол АОЕ при условии, что ОЕ является биссектрисой угла АОС. Аналогично, ОD играет роль биссектрисы угла СОВ. Градусная мера угла ВОD составляет 25°. Необходимо вычислить угол АОЕ.

 

Решение

Исходя из того, что биссектриса делит угол на две равные части, вычислим градусную меру угла СОВ:

СОВ  = \(25 \cdot 2\) = 50

Развернутый угол АОВ составляет 180° по определению. Тогда можно найти величину угла АОС:

АОС = 180 – 50 = 130

Зная, что биссектриса ОЕ делит угол АОС на два равных угла, получим, что искомый угол АОЕ равен:

АОЕ = \(130 \div 2\) = 65

Ответ: 65°.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Узнаем, как начертить угол, какие могут быть углы, научимся строить углы

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Узнаем, как начертить угол, какие
могут быть углы, научимся строить
углы и выделять их в различных
фигурах.
Устный счёт. В тетрадь записывай только ответы.
Назовите сколько десятков и единиц
в числе 87.
87 36
25 8 дес. 7 ед.

46 65
99
46
60
Какое число предшествует числу 100?
87 36
25 8 дес. 7 ед.
46 65
99
46
60
Уменьшите число 66 на 20.
87 36
25 8 дес. 7 ед.
46 65
99
46
60
Увеличьте 30 на 35.
87 36
25 8 дес. 7 ед.
46 65
99
46
60
Найдите сумму чисел 20 и 67.
87 36
25 8 дес. 7 ед.
46 65
99
46
60
Найдите разность чисел 100 и 40.
87 36
25 8 дес. 7 ед.
46 65
99
46
60
Первое слагаемое 40, второе
слагаемое 6, найдите сумму.
87 36
25 8 дес. 7 ед.
46 65
99
46
60
Уменьшаемое 80, вычитаемое 55.
Чему равна разность?
87 36
25 8 дес. 7 ед.
46 65
99
46
60
Все получившиеся цепочки запиши в тетрадь. От
Устного счёта отступи 2 клетки вниз.
6
5
1
Из разных цифр мы нарисовали бусы,
А в тех кружках, где чисел нет,
Расставьте минусы и плюсы,
Чтоб данный получить ответ.
10
=
20
3
15
7
2
Из разных цифр мы нарисовали бусы,
А в тех кружках, где чисел нет,
Расставьте минусы и плюсы,
Чтоб данный получить ответ.
13
=
10
4
6
10
26
Из разных цифр мы нарисовали бусы,
А в тех кружках, где чисел нет,
Расставьте минусы и плюсы,
Чтоб данный получить ответ.
1
=
45
Угол имеет стороны и вершины.
Лучи — это стороны угла.
Точка, из которой проведены лучи —
это вершина угла.
Возьмите
лист
бумаги.
Потом
Согните
ещёего
разпополам.
пополам.
Линии сгиба
Стороны
Вершина
образовали
прямого
прямого
4 прямых
угла.
угла. угла.
Разверните
лист.
Угол — это геометрическая
фигура, которая состоит из
точки-вершины и двух сторон,
которые выходят из этой
точки.
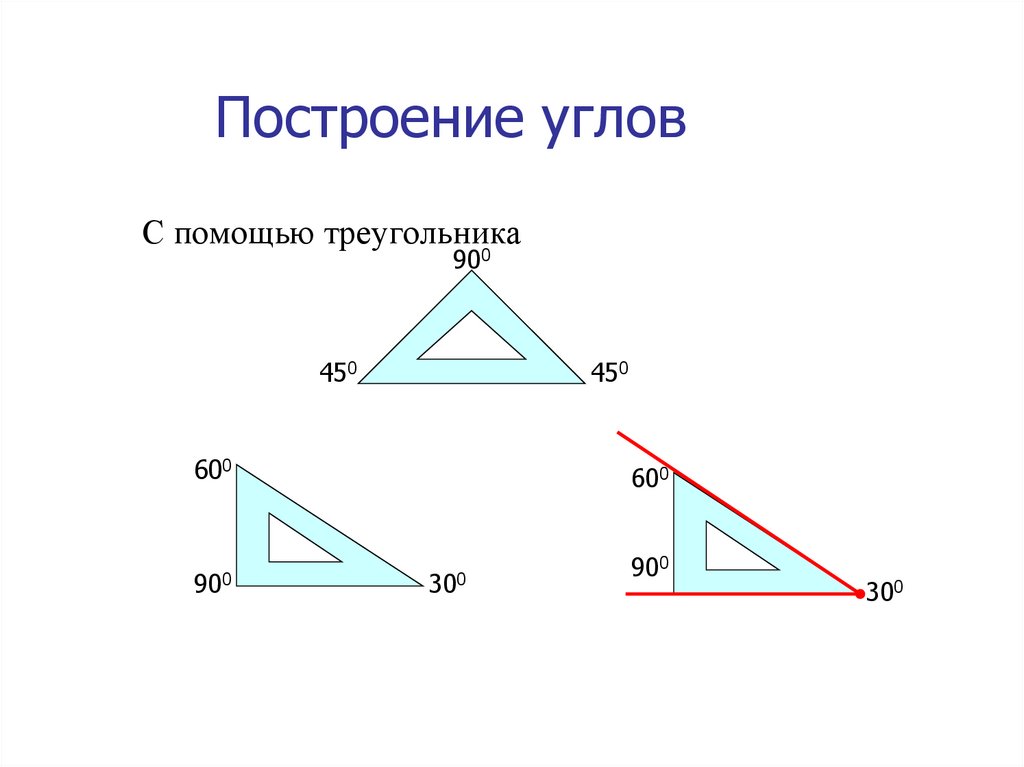
Чтобы определить, какой угол начерчен, на него прикладывают
какую-нибудь модель прямого угла. Обычно в качестве модели
прямого угла используют прямой угол чертежного треугольника.
Острый угол
Тупой угол
Прямой угол
Острым углом называется
угол, который меньше прямого
угла.
Тупым углом называется угол,
который больше прямого угла.
Назовите
фигуры:
Как можно
назвать
все фигуры?
Треугольник
Шестиугольник
Пятиугольник
Многоугольники
Четырёхугольник
Сколько углов
в каждом
многоугольнике?
Проверьте
себя:
Запишите номера тупых
углов, острых
углов, прямых углов.
5
2
6
7
4
1
3
Три угла.
9
8
11
10
12
16
17
13
14
Прямые
углы — 10,
12,
14.
Шесть
углов.
Пять
углов.
15
18
Четыре угла.
Острые углы — 1, 2, 3, 15, 17.
Тупые углы — 4, 5, 6, 7, 8, 9, 11, 13, 16, 18.
Найдите значение выражения (запишите в
Проверьте себя:
тетрадь):
100 – (50 + 18) = 100 – 68 = 32
(30 + 25) – 25 = 55 – 25 = 30
70 – (60 – 36) = 70 – 24 = 46
40 – (30 – 8) = 40 – 22 = 18
(34 + 27) – 16 = 61 – 16 = 45
Сперва выполняются действия в
скобках, а потом в том порядке,
в котором они записаны.
Вершина угла — это…точка, из
которой проведены лучи.
Стороны — это …лучи, которые
проведены из вершины.
Острый угол — это …
угол, который
Проговорите
меньше прямого
угла.
угол, который
Тупой угол — этоправила
больше прямого угла.
проверки.

English     Русский Правила

Используя только линейку, начертите в тетради острый угол, прямой угол и тупой угол и назовите.

..

Перейти к

• Углы. Упражнение 11.1.
• Углы. Упражнение 11.2.

• Зная свои числа
• Игра с числами
• Целые числа
• Действия над целыми числами
• Отрицательное число и целые числа
• Фракции
• Десятичные
• Введение в алгебру
• Соотношение, пропорция и унитарный метод
• Основные геометрические понятия
• Углы
• Треугольники
• Круги
• Пара прямых и поперечная
• Понимание трехмерных форм
• Симметрия
• Основные геометрические инструменты
• Геометрические построения
• Измерение
• Обработка данных Представление данных
• Обработка данных – II
• Гистограммы обработки данных

Главная > РД Шарма Решения Класс 6 Математика > Глава 11 — Углы > Углы. Упражнение 11.2. > Вопрос 11

Вопрос 11 Углы Упражнение 11.2

Используя только линейку, начертите в тетради острый, прямой и тупой углы и назовите их. их.

Ответ:

Похожие вопросы

Приведите по два примера прямых, острых и тупых углов из вашей среды.

Угол образован двумя соседними пальцами. Под каким углом он появится?

Шиха гребет на лодке на северо-восток. В каком направлении она будет грести, если перевернет ее…

Какова мера угла в градусах между: (i) Севером и Западом? (ii) Севером и Югом? (iii) Нет…

Корабль, плывущий по реке Джелам, движется на восток. Если она поворачивает на север, под каким углом она…

Вы стоите в классе лицом на север. В каком направлении вы смотрите после того, как сделаете акварели?

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Углы Упражнения 11.1

Углы Упражнения 11,2

Главы

к алгебре

Отношение, пропорция и унитарный метод

Основные геометрические понятия

Углы

Треугольники

Круги

Пара линий и поперечных

Понимание трехмерных форм

Симметрия

Основные геометрические инструменты

Геометрические конструкции

Муженая Мужье

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

Нарисуйте острый угол ABC и тупой угол WXY.

a Постройте ∠FGH, конгруэнтную ∠WXY. b Постройте дополнение к ∠ABC. c Построить дополнение к ∠WXY. г Постройте угол, градусом которого является разность ∠WXY и ∠ABC. e Постройте угол, градусная мера которого в два раза больше угла ∠ABC.

Вопрос

Изобразите острый угол $A B C$ и тупой угол $W X Y$. a Постройте $\angle \mathrm{FGH}$, конгруэнтный $\angle \mathrm{WXY}$. b Построить дополнение к $\angle \mathrm{ABC}$. c Построить дополнение $\angle \mathrm{WXY}$. d Постройте угол, мера которого есть разность $\angle \mathrm{WXY}$ и $\angle \mathrm{ABC}$. e Постройте угол, мера которого в два раза больше, чем у $\angle \mathrm{ABC}$.

Пошаговый ответ:

Шаг 1/4
а) Нам нужно построить угол, равный $\углу WXY$. Мы можем использовать транспортир, чтобы измерить угол, а затем нарисовать его. Кроме того, мы можем использовать компас, чтобы скопировать угол.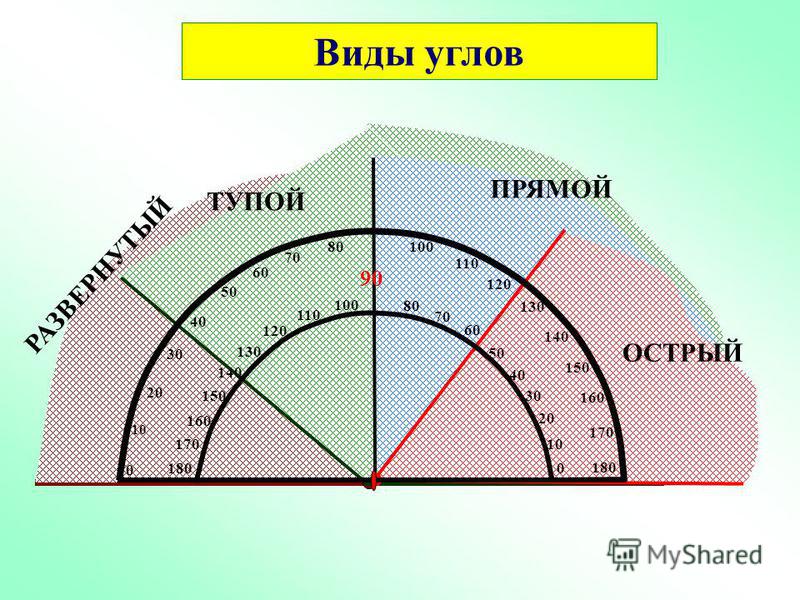 \circ$. Другими словами, это угол, образующий прямую с $\angle WXY$. Вот как его построить: — Нарисуйте луч $WX$. — Поместите компас в точку $W$ и начертите дугу, пересекающую $WX$. — Не меняя ширины компаса, поместите циркуль в точку $X$ и начертите дугу, пересекающую предыдущую дугу. — Нарисуйте луч $YZ$, проходящий через пересечение двух дуг. — $\angle WXY$ и $\angle XYZ$ являются дополнительными.

---

Рекомендация видео с лучшим совпадением:

Решено проверенным экспертом

У нас нет заданного вами вопроса, но вот рекомендуемое видео, которое может помочь.

Лучшее совпадение Вопрос

Пошаговый ответ

Нарисуйте острый угол $A B C$ и тупой угол $W X Y$. a Постройте $\angle \mathrm{FGH}$, конгруэнтный $\angle \mathrm{WXY}$. b Построить дополнение к $\angle \mathrm{ABC}$. c Построить дополнение $\angle \mathrm{WXY}$. d Постройте угол, мера которого есть разность $\angle \mathrm{WXY}$ и $\angle \mathrm{ABC}$. e Постройте угол, мера которого в два раза больше, чем у $\angle \mathrm{ABC}$.