Паралелограм це: Паралелограм — Вікіпедія

Содержание

Паралелограм — Вікіпедія

Паралелогра́м — чотирикутник, протилежні сторони якого попарно паралельні, тобто лежать на паралельних прямих.

Існує декілька окремих видів паралелограма:

Прямокутник — паралелограм, всі кути якого прямі;
Ромб — паралелограм, всі чотири сторони якого рівні між собою;
Квадрат — рівнобічний прямокутник або ромб з прямими кутами при вершинах.

Паралелограм є плоскою геометричною фігурою, його аналогом у тривимірному просторі є паралелепіпед.

Ромбоїд – чотирикутник, протилежні сторони якого паралельні, а прилеглі сторони не рівні, а його кути не є прямими кутами.
Прямокутник – паралелограм, чотири кути якого рівні (прямі).
Ромб – паралелограм, чотири сторони якого є рівними.
Квадрат – паралелограм, чотири сторони і чотири кути якого є рівними.

Простий (не перехрещений) чотирикутник є паралелограмом тоді й лише тоді якщо одне із наведених нижче тверджень є вірним:

[1]^[2]

В паралелограмі дві сторони рівні та паралельні.
В паралелограмі протилежні сторони попарно рівні.
В паралелограмі протилежні кути попарно рівні.
Точка перетину діагоналей є центром симетрії паралелограма.
Будь-яка пряма, яка проходить через центр паралелограма поділяє його площу навпіл.^[4]
Сума кутів при кожній стороні становить 180 ∘ {\displaystyle 180^{\circ }} .
В паралелограмі діагоналі перетинаються і точкою перетину діляться навпіл.
Діагоналі паралелограма поділяють його на чотири трикутника однакової площі.

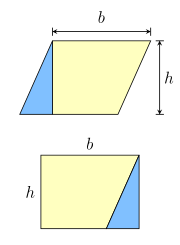Малюнок показує як паралелограм можна перебудувати у фігуру прямокутника

Паралелограм можна перебудувати у прямокутник з такою ж площею.

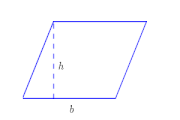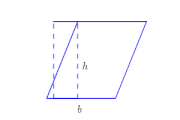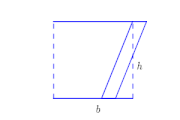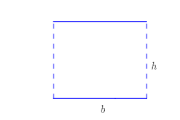Анімація для формули визначення площі S = b h {\displaystyle S=bh} .

Паралелограм із основою b і висотою h можна розділити на трапецію і прямокутний трикутник, і перебудувати у прямокутник, як показано на малюнку праворуч. Це означає, що площа паралелограма є такою ж як у прямокутника із такою ж основою і висотою:

S = b h . {\displaystyle S=bh.}

Іншими словами, площа паралелограма дорівнює добутку його сторони на висоту, яка перпендикулярна до цієї сторони:

S = D C ⋅ h D C = B C ⋅ h B C {\displaystyle S=DC\cdot h_{DC}=BC\cdot h_{BC}} .

$S=DC\cdot h_{DC}=BC\cdot h_{BC}$

Площа паралелограма, це площа внутрішньої області, що виділена синім і визначається як : S = B ⋅ C ⋅ sin ⁡ θ {\displaystyle S=B\cdot C\cdot \sin \theta \,} , де
B і C — сторони паралелограма.

Також площа паралелограма рівна добутку двох його непаралельних сторін та синуса кута між ними:

S = D C ⋅ A D ⋅ sin ⁡ ∠ D = D C ⋅ B C ⋅ sin ⁡ ∠ C . {\displaystyle S=DC\cdot AD\cdot \sin \angle D=DC\cdot BC\cdot \sin \angle C.}

Якщо розглядати паралелограм як геометричну фігуру, яка побудована на двох векторах D A → {\displaystyle {\vec {DA}}} та D C → {\displaystyle {\vec {DC}}} , то площа паралелограма буде дорівнювати модулю векторного добутку цих векторів: S = | D C → × D A → | = | D C | ⋅ | D A | ⋅ sin ⁡ ∠ A E D . {\displaystyle S=|{\vec {DC}}\times {\vec {DA}}|=|DC|\cdot |DA|\cdot \sin \angle AED.}

Площа паралелограма (як і будь-якого чотирикутника без самоперетинів) рівна півдобутку діагоналей, помноженому на синус кута між ними: S = d 1 d 2 sin ⁡ γ 2 {\displaystyle S={\frac {d_{1}d_{2}\sin \gamma }{2}}} .

Площа паралелограма із сторонами B і C (B ≠ C) і кутом γ {\displaystyle \gamma } утвореним перетином діагоналей дорівнює наступному^[5]

S = | tan ⁡ γ | 2 ⋅ | B 2 − C 2 | . {\displaystyle S={\frac {|{\tan \gamma }|}{2}}\cdot \left|B^{2}-C^{2}\right|.}

Якщо паралелограм заданий довжинами B і C двох прилеглих сторін і довжиною однієї з діагоналей D₁, тоді площу можна знайти за допомогою формули Герона. Що задається наступним чином

S = 2 K ( K − B ) ( K − C ) ( K − D 1 ) {\displaystyle S=2{\sqrt {K(K-B)(K-C)(K-D_{1})}}}

де K = ( B + C + D 1 ) / 2 {\displaystyle K=(B+C+D_{1})/2} і перший множник 2 додано оскільки, будь-яка обрана діагональ поділяє паралелограм на два конгруентні трикутники.

Площа паралелограма при відомих декартових координатах вершин[ред. | ред. код]

Нехай існують вектори a , b ∈ R 2 {\displaystyle \mathbf {a} ,\mathbf {b} \in \mathbb {R} ^{2}} і нехай V = [ a 1 a 2 b 1 b 2 ] ∈ R 2 × 2 {\displaystyle V={\begin{bmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{bmatrix}}\in \mathbb {R} ^{2\times 2}} позначає матрицю елементів a і b. Тоді площею паралелограма, що заданий за допомогою a і b буде | det ( V ) | = | a 1 b 2 − a 2 b 1 | {\displaystyle |\det(V)|=|a_{1}b_{2}-a_{2}b_{1}|\,} .

Нехай існують вектори a , b ∈ R n {\displaystyle \mathbf {a} ,\mathbf {b} \in \mathbb {R} ^{n}} і нехай V = [ a 1 a 2 … a n b 1 b 2 … b n ] ∈ R 2 × n {\displaystyle V={\begin{bmatrix}a_{1}&a_{2}&\dots &a_{n}\\b_{1}&b_{2}&\dots &b_{n}\end{bmatrix}}\in \mathbb {R} ^{2\times n}} . тоді площа паралелограма, що задана за допомогою a і b буде дорівнювати det ( V V T ) {\displaystyle {\sqrt {\det(VV^{\mathrm {T} })}}} .

Нехай існують точки a , b , c ∈ R 2 {\displaystyle a,b,c\in \mathbb {R} ^{2}} . Тоді площа паралелограма із вершинами в точках a, b і c є еквівалентною абсолютному значенню детермінанта матриці, що побудована так, що a, b і c є її рядками і остання колонка доповнена одиницями, як наведено нижче:

S = | det [ a 1 a 2 1 b 1 b 2 1 c 1 c 2 1 ] | . {\displaystyle S=\left|\det {\begin{bmatrix}a_{1}&a_{2}&1\\b_{1}&b_{2}&1\\c_{1}&c_{2}&1\end{bmatrix}}\right|.}

Доведення, що діагоналі паралелограма перетинаються і точкою перетину діляться навпіл[ред. | ред. код]

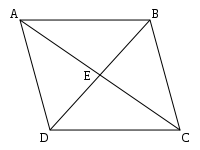
Аби довести, що діагоналі паралелограма перетинаються, використаємо конгруентні трикутники:

∠ A B E ≅ ∠ C D E {\displaystyle \angle ABE\cong \angle CDE} (внутрішні різносторонні кути рівні за розміром)

∠ B A E ≅ ∠ D C E {\displaystyle \angle BAE\cong \angle DCE} (внутрішні різносторонні кути рівні за розміром).

(оскільки це кути, що утворені перетином прямої із двома паралельними прямими AB і DC).

Також, сторона AB має таку ж саму довжину, що і сторона DC, оскільки протилежні сторони паралелограма є рівними.

Таким чином, трикутники ABE і CDE конгруентні (постулат Кут-Сторона-Кут (КСК), два відповідні кути і прилегла сторона).

Тому,

A E = C E {\displaystyle AE=CE}

B E = D E . {\displaystyle BE=DE.}

Оскільки діагоналі AC і BD поділяють одна одну на відрізки однакової довжини, діагоналі перетинають одна одну.

Відповідно, оскільки діагоналі AC і BD перетинають одна одну в точці E, точка E є серединою кожної діагоналі.

↑ Owen Byer, Felix Lazebnik and Deirdre Smeltzer, Methods for Euclidean Geometry, Mathematical Association of America, 2010, pp. 51-52.
↑ Zalman Usiskin and Jennifer Griffin, «The Classification of Quadrilaterals. A Study of Definition», Information Age Publishing, 2008, p. 22.
↑ Chen, Zhibo, and Liang, Tian. «The converse of Viviani’s theorem», The College Mathematics Journal 37(5), 2006, pp. 390–391.
↑ Dunn, J.A., and J.E. Pretty, «Halving a triangle», Mathematical Gazette 56, May 1972, p. 105.
↑ Mitchell, Douglas W., «The area of a quadrilateral», Mathematical Gazette, July 2009.

Eric W. Weisstein, Parallelogram at MathWorld.
Геометрія: Підруч. для 7— 9 кл. серед. шк./ Л. С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев та ін. — К.: Освіта, 1993. — 304 с.

Паралелограм та його властивості. Ознаки паралелограма

Паралелограм та його властивості. Ознаки паралелограма

Великий клас чотирикутників становлять паралелограми.

Чотирикутник, у якого протилежні сторони паралельні, називається

паралелограмом.

Висотою паралелограма називається відрізок, що є перпендикуляром до прямої, яка містить протилежну сторону.

У паралелограма з кожної його вершини можна провести по дві висоти. Висоти, проведені з вершин тупих кутів паралелограма, лежать у паралелограмі; висоти, проведені з гострих тупих кутів паралелограма, лежать зовні паралелограма.

Властивості паралелограма

У паралелограмі протилежні сторони рівні.

У паралелограмі протилежні кути рівні.

У паралелограмі сума кутів, прилеглих до однієї сторони, дорівнює 180°.

Діагоналі паралелограма перетинаються і точкою перетину діляться навпіл.

Діагоналі паралелограма ділять його на два рівні трикутники.

Ознаки паралелограма

Якщо діагоналі чотирикутника перетинаються й у точці перетину діляться навпіл, то цей чотирикутник паралелограм.

Якщо в чотирикутнику дві протилежні сторони паралельні і рівні, то цей чотирикутник паралелограм.

Якщо в чотирикутнику протилежні сторони попарно рівні, то цей чотирикутник паралелограм.

Якщо в чотирикутнику протилежні кути попарно рівні, то цей чотирикутник паралелограм.

Властивість діагоналей паралелограма:

Діагоналі паралелограма перетинаються й у точці перетину діляться навпіл.

Властивість протилежних сторін і кутів паралелограма:

У паралелограма протилежні сторони й кути рівні.

Це цікаво.

Якщо провести бісектриси двох протилежних кутів паралелограма, то вони будуть паралельні або співпадуть.

Якщо провести бісектриси двох кутів, прилеглих до однієї сторони паралелограма, то вони будуть перпендикулярні.

Параллелограмм. Свойства и признаки параллелограмма

Определение параллелограмма

Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Свойства параллелограмма

1. Противоположные стороны параллелограмма попарно равны

2. Противоположные углы параллелограмма попарно равны

3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов

4. Сумма всех углов равна 360°

5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

6. Точка пересечения диагоналей является центром симметрии параллелограмма

7. Диагонали $d_1,\;d_2$ параллелограмма и стороны
$a,\;b$

связаны следующим соотношением:

8. Биссектриса отсекает от параллелограмма равнобедренный треугольник

Признаки параллелограмма

Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:

1. Противоположные стороны попарно равны: $AB=CD,\;BC=AD$

2. Противоположные углы попарно равны: $\angle A=\angle C,\;\angle B=\angle D$

3. Диагонали пересекаются и в точке пересечения делятся пополам

4. Противоположные стороны равны и параллельны: $AB=CD,\;AB$

Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:

Формулы площади параллелограмма смотрите здесь.

Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.

Параллелограмм

Определение

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Теорема (первый признак параллелограмма)

Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

Доказательство

Пусть в четырехугольнике $ABCD$ стороны $AB$ и $CD$ параллельны и $AB = CD$.

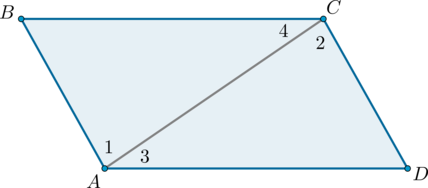
Проведём диагональ $AC$, разделяющую данный четырехугольник на два равных треугольника: $ABC$ и $CDA$. Эти треугольники равны по двум сторонам и углу между ними ($AC$ – общая сторона, $AB = CD$ по условию, $\angle 1 = \angle 2$ как накрест лежащие углы при пересечении параллельных прямых $AB$ и $CD$ секущей $AC$), поэтому $\angle 3 = \angle 4$. Но углы $3$ и $4$ накрест лежащие при пересечении прямых $AD$ и $BC$ секущей $AC$, следовательно, $AD\parallel BC$. Таким образом, в четырехугольнике $ABCD$ противоположные стороны попарно параллельны, и, значит, четырехугольник $ABCD$ – параллелограмм.

Теорема (второй признак параллелограмма)

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

Доказательство

Проведём диагональ $AC$ данного четырехугольника $ABCD$, разделяющую его на треугольники $ABC$ и $CDA$.

Эти треугольники равны по трем сторонам ($AC$ – общая, $AB = CD$ и $BC = DA$ по условию), поэтому $\angle 1 = \angle 2$ – накрест лежащие при $AB$ и $CD$ и секущей $AC$. Отсюда следует, что $AB\parallel CD$. Так как $AB = CD$ и $AB\parallel CD$, то по первому признаку параллелограмма четырёхугольник $ABCD$ – параллелограмм.

Теорема (третий признак параллелограмма)

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Доказательство

Рассмотрим четырехугольник $ABCD$, в котором диагонали $AC$ и $BD$ пересекаются в точке $O$ и делятся этой точкой пополам.

Треугольники $AOB$ и $COD$ равны по первому признаку равенства треугольников ($AO = OC$, $BO = OD$ по условию, $\angle AOB = \angle COD$ как вертикальные углы), поэтому $AB = CD$ и $\angle 1 = \angle 2$. Из равенства углов $1$ и $2$ (накрест лежащие при $AB$ и $CD$ и секущей $AC$) следует, что $AB\parallel CD$.

Итак, в четырехугольнике $ABCD$ стороны $AB$ и $CD$ равны и параллельны, значит, по первому признаку параллелограмма четырехугольник $ABCD$ – параллелограмм.

Свойства параллелограмма:

1. В параллелограмме противоположные стороны равны и противоположные углы равны.

2. Диагонали параллелограмма точкой пересечения делятся пополам.

Свойства биссектрисы параллелограмма:

1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.

2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.

3. Отрезки биссектрис противоположных углов равны и параллельны.

Доказательство

1) Пусть $ABCD$ – параллелограмм, $AE$ – биссектриса угла $BAD$.

Углы $1$ и $2$ равны как накрест лежащие при параллельных прямых $AD$ и $BC$ и секущей $AE$. Углы $1$ и $3$ равны, так как $AE$ – биссектриса. В итоге $\angle 3 = \angle 1 = \angle 2$, откуда следует, что треугольник $ABE$ – равнобедренный.

2) Пусть $ABCD$ – параллелограмм, $AN$ и $BM$– биссектрисы углов $BAD$ и $ABC$ соответственно.

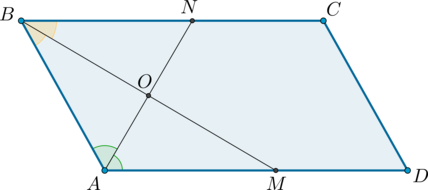
Так как сумма односторонних углов при параллельных прямых и секущей равна $180^{\circ}$, тогда $\angle DAB + \angle ABC = 180^{\circ}$.

Так как $AN$ и $BM$ – биссектрисы, то $\angle BAN + \angle ABM = 0,5(\angle DAB + \angle ABC) = 0,5\cdot 180^\circ = 90^{\circ}$, откуда $\angle AOB = 180^\circ — (\angle BAN + \angle ABM) = 90^\circ$.

3. Пусть $AN$ и $CM$ – биссектрисы углов параллелограмма $ABCD$.

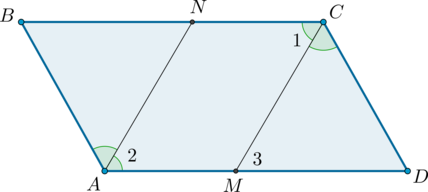
Так как в параллелограмме противоположные углы равны, то $\angle 2 = 0,5\cdot\angle BAD = 0,5\cdot\angle BCD = \angle 1$. Кроме того, углы $1$ и $3$ равны как накрест лежащие при параллельных прямых $AD$ и $BC$ и секущей $CM$, тогда $\angle 2 = \angle 3$, откуда следует, что $AN\parallel CM$. Кроме того, $AM\parallel CN$, тогда $ANCM$ – параллелограмм, следовательно, $AN = CM$.

Паралелограм та його властивості. Ознаки паралелограма

Великий клас чотирикутників становлять паралелограми.

Чотирикутник, у якого протилежні сторони паралельні, називається паралелограмом.

Властивості паралелограма

У паралелограмі протилежні сторони рівні.

У паралелограмі протилежні кути рівні.

У паралелограмі сума кутів, прилеглих до однієї сторони, дорівнює 180°.

Діагоналі паралелограма перетинаються і точкою перетину діляться навпіл.

Діагоналі паралелограма ділять його на два рівні трикутники.

Ознаки паралелограма

Якщо в чотирикутнику дві протилежні сторони паралельні і рівні, то цей чотирикутник паралелограм.

Якщо в чотирикутнику протилежні сторони попарно рівні, то цей чотирикутник паралелограм.

Якщо в чотирикутнику протилежні кути попарно рівні, то цей чотирикутник паралелограм.

Властивість діагоналей паралелограма:

Діагоналі паралелограма перетинаються й у точці перетину діляться навпіл.

Властивість протилежних сторін і кутів паралелограма:

У паралелограма протилежні сторони й кути рівні.

Це цікаво.

Якщо провести бісектриси двох протилежних кутів паралелограма, то вони будуть паралельні або співпадуть.

Параллелограмм — Википедия. Что такое Параллелограмм
Материал из Википедии — свободной энциклопедии Параллелограмм

Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам. Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

Противолежащие стороны параллелограмма равны.
Противолежащие углы параллелограмма равны.
Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:
| A O | = | O C | , | B O | = | O D | {\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|} .
Точка пересечения диагоналей является центром симметрии параллелограмма.
Параллелограмм диагональю делится на два равных треугольника.
Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d 1 {\displaystyle d_{1}} и d 2 {\displaystyle d_{2}} — длины диагоналей; тогда
d 1 2 + d 2 2 = 2 ( a 2 + b 2 ) . {\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}

Тождество параллелограмма есть простое следствие формулы Эйлера для произвольного четырехугольника: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумма квадратов его диагоналей. У параллелограмма противоположные стороны равны, а расстояние между серединами диагоналей равно нулю.

Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий (в этом случае выполняются и все остальные):

У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: A B = C D , A B ∥ C D {\displaystyle AB=CD,AB\parallel CD} .
Все противоположные углы попарно равны: ∠ A = ∠ C , ∠ B = ∠ D {\displaystyle \angle A=\angle C,\angle B=\angle D} .
У четырёхугольника без самопересечений все противоположные стороны попарно равны: A B = C D , B C = D A {\displaystyle AB=CD,BC=DA} .
Все противоположные стороны попарно параллельны: A B ∥ C D , B C ∥ D A {\displaystyle AB\parallel CD,BC\parallel DA} .
Диагонали делятся в точке их пересечения пополам: A O = O C , B O = O D {\displaystyle AO=OC,BO=OD} .
Сумма соседних углов равна 180 градусов: ∠ A + ∠ B = 180 ∘ , ∠ B + ∠ C = 180 ∘ , ∠ C + ∠ D = 180 ∘ , ∠ D + ∠ A = 180 ∘ {\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }} .
Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: A C 2 + B D 2 = A B 2 + B C 2 + C D 2 + D A 2 {\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}} .

Площадь параллелограмма

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для площади произвольных четырёхугольников.

Площадь параллелограмма равна произведению его основания на высоту:

S = a h {\displaystyle S=ah} , где a {\displaystyle a} — сторона, h {\displaystyle h} — высота, проведенная к этой стороне.

Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S = a b sin ⁡ α , {\displaystyle S=ab\sin \alpha ,}

где a {\displaystyle a} и b {\displaystyle b} — стороны, а α {\displaystyle \alpha } — угол между сторонами a {\displaystyle a} и b {\displaystyle b} .

Также площадь параллелограмма может быть выражена через стороны a , b {\displaystyle a,\ b} и длину любой из диагоналей d {\displaystyle d} по формуле Герона как сумма площадей двух равных примыкающих треугольников:

S = 2 p ( p − a ) ( p − b ) ( p − d ) {\displaystyle S=2{\sqrt {p(p-a)(p-b)(p-d)}}}

где p = ( a + b + d ) / 2. {\displaystyle p=(a+b+d)/2.}

См. также

Примечания

Параллелограмм — Википедия

Материал из Википедии — свободной энциклопедии

Параллелограмм

Свойства

Противолежащие стороны параллелограмма равны.
Противолежащие углы параллелограмма равны.
Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:
| A O | = | O C | , | B O | = | O D | {\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|} .
Точка пересечения диагоналей является центром симметрии параллелограмма.
Параллелограмм диагональю делится на два равных треугольника.
Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d 1 {\displaystyle d_{1}} и d 2 {\displaystyle d_{2}} — длины диагоналей; тогда
d 1 2 + d 2 2 = 2 ( a 2 + b 2 ) . {\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}

Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

Признаки параллелограмма

У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: A B = C D , A B ∥ C D {\displaystyle AB=CD,AB\parallel CD} .
Все противоположные углы попарно равны: ∠ A = ∠ C , ∠ B = ∠ D {\displaystyle \angle A=\angle C,\angle B=\angle D} .
У четырёхугольника без самопересечений все противоположные стороны попарно равны: A B = C D , B C = D A {\displaystyle AB=CD,BC=DA} .
Все противоположные стороны попарно параллельны: A B ∥ C D , B C ∥ D A {\displaystyle AB\parallel CD,BC\parallel DA} .
Диагонали делятся в точке их пересечения пополам: A O = O C , B O = O D {\displaystyle AO=OC,BO=OD} .
Сумма соседних углов равна 180 градусов: ∠ A + ∠ B = 180 ∘ , ∠ B + ∠ C = 180 ∘ , ∠ C + ∠ D = 180 ∘ , ∠ D + ∠ A = 180 ∘ {\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }} .
Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: A C 2 + B D 2 = A B 2 + B C 2 + C D 2 + D A 2 {\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}} .

Площадь параллелограмма

Площадь параллелограмма равна произведению его основания на высоту:

S = a h {\displaystyle S=ah} , где a {\displaystyle a} — сторона, h {\displaystyle h} — высота, проведенная к этой стороне.

Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S = a b sin ⁡ α , {\displaystyle S=ab\sin \alpha ,}

где a {\displaystyle a} и b {\displaystyle b} — стороны, а α {\displaystyle \alpha } — угол между сторонами a {\displaystyle a} и b {\displaystyle b} .

S = 2 p ( p − a ) ( p − b ) ( p − d ) {\displaystyle S=2{\sqrt {p(p-a)(p-b)(p-d)}}}

где p = ( a + b + d ) / 2. {\displaystyle p=(a+b+d)/2.}

См. также

Примечания

90000 Parallelogram 90001 90002 90003 (Jump to Area of a Parallelogram or Perimeter of a Parallelogram) 90004 90005 90002 A Parallelogram is a flat shape with opposite sides parallel and equal in length. 90005 90008 90003 90010 | and || show equal sides 90004 90005 90013 90014 90015 90016 90015 Opposite sides are parallel 90016 90019 90014 90015 90016 90015 90002 Opposite sides are equal in length 90005 90016 90019 90014 90015 90016 90015 Opposite angles are equal (angles «a» are the same, and angles «b» are the same) 90016 90019 90014 90015 90016 90015 Angles «a» and «b» add up to 180 °, so they are supplementary angles.90016 90019 90040 90002 Play with a Parallelogram: 90005 90008 NOTE: Squares, Rectangles and Rhombuses are all Parallelograms! 90005 90045 Example: 90046 90002 90005 90002 A 90050 parallelogram 90051 where all angles are right angles is a 90050 rectangle 90051! 90005 90055 Area of a Parallelogram 90056 90057 90014 90015 90016 90015 90016 90015 90002 The Area is the 90050 base times the height 90051: 90005 90002 Area = b × h 90005 90002 (90050 h 90051 is at right angles to 90050 b 90051) 90005 90016 90019 90040 90045 Example: A parallelogram has a base of 6 m and is 3 m high, what is its Area? 90046 90002 Area = 6 m × 3 m = 90050 18 m 90083 2 90084 90051 90005 90055 Perimeter of a Parallelogram 90056 90002 The Perimeter is the distance around the edges.90005 90057 90014 90015 90016 90015 90016 90015 90002 The Perimeter is 90050 2 times the (base + side length) 90051: 90005 90002 Perimeter = 2 (b + s) 90005 90016 90019 90040 90045 Example: A parallelogram has a base of 12 cm and a side length of 6 cm, what is its Perimeter? 90046 90002 Perimeter = 2 × (12 cm + 6 cm) = 2 × 18 cm = 90050 36 cm 90051 90005 90055 Diagonals of a Parallelogram 90056 90002 90005 90002 The diagonals of a parallelogram bisect each other.90005 90002 In other words the diagonals intersect each other at the half-way point. 90005 90055 Inside Any Quadrilateral 90056 90002 And there is a parallelogram in any quadrilateral. 90005 90002 90005 90002 90005 .90000 Parallelogram — math word definition 90001 Parallelogram — math word definition — Math Open Reference Try this Drag the orange dots on each vertex to reshape the parallelogram. Notice how the opposite sides remain parallel. 90002 A parallelogram is a quadrilateral with opposite sides parallel. But there are various tests that can be applied to see if something is a parallelogram. 90003 90002 It is the «parent» of some other quadrilaterals, which are obtained by adding restrictions of various kinds: 90003 90006 90007 A rectangle is a parallelogram but with all four interior angles fixed at 90 ° 90008 90007 A rhombus is a parallelogram but with all four sides equal in length 90008 90007 A square is a parallelogram but with all sides equal in length and all interior angles 90 ° 90008 90013 90014 A quadrilateral is a parallelogram if: 90015 90016 90007 Both pairs of opposite sides are parallel.(By definition). Or: 90008 90007 Both pairs of opposite sides are congruent. If they are congruent, they must also be parallel. Or: 90008 90007 One pair of opposite sides are congruent 90022 and 90023 parallel. Then, the other pair must also be parallel. 90008 90025 90014 Properties of a parallelogram 90015 These facts and properties are true for parallelograms and the descendant shapes: square, rectangle and rhombus. 90028 90029 90030 Base 90031 90032 Any side can be considered a base.Choose any one you like. If used to calculate the area (see below) the corresponding altitude must be used. In the figure above, one of the four possible bases and its corresponding altitude has been chosen. 90031 90034 90029 90030 Altitude 90037 (height) 90031 90032 The altitude (or height) of a parallelogram is the perpendicular distance from the base to the opposite side (which may have to be extended). In the figure above, the altitude corresponding to the base CD is shown. 90031 90034 90029 90030 Area 90031 90032 The area of a parallelogram can be found by multiplying a base by the corresponding altitude.See also Area of a Parallelogram 90031 90034 90029 90030 Perimeter 90031 90032 The distance around the parallelogram. The sum of its sides. See also Perimeter of a Parallelogram 90031 90034 90029 90030 Opposite 90037 sides 90031 90032 Opposite sides are congruent (equal in length) and parallel. As you reshape the parallelogram at the top of the page, note how the opposite sides are always the same length. 90031 90034 90029 90030 Diagonals 90031 90032 Each diagonal cuts the other diagonal into two equal parts, as in the diagram below.90065 See Diagonals of a parallelogram for an interactive demonstration of this. 90031 90034 90029 90030 Interior 90037 angles 90031 90032 Opposite angles are equal as can be seen below. 90037 Consecutive angles are always supplementary (add to 180 °) 90074 90002 For more on both these properties, see Interior angles of a parallelogram. 90003 90031 90034 90079 90014 Parallelogram inscribed in any quadrilateral 90015 90002 90083 If you find the midpoints of each side of any quadrilateral, then link them sequentially with lines, the result is always a parallelogram.90003 90002 This may seem counter-intuitive at first, but see Parallelogram inscribed in any quadrilateral for an animated exploration of this fact. 90003 90014 Other polygon topics 90015 90089 General 90090 90089 Types of polygon 90090 90089 Area of various polygon types 90090 90089 Perimeter of various polygon types 90090 90089 Angles associated with polygons 90090 90089 Named polygons 90090 90002 (C) 2011 Copyright Math Open Reference.90037 All rights reserved 90003 .90000 meaning in the Cambridge English Dictionary 90001 PARALLELOGRAM | meaning in the Cambridge English Dictionary 90002 Thesaurus: synonyms and related words .90000 Definition of Parallelogram by Merriam-Webster 90001 90002 To save this word, you’ll need to log in. 90003 par · al · lel · o · gram | \ ˌPer-ə-le-lə-ˌgram, ˌpa-rə- \ 90004 Definition of 90005 parallelogram 90006 90007 90008: 90009 a quadrilateral with opposite sides parallel and equal 90004 Examples of 90005 parallelogram 90006 in a Sentence 90007 90002 Rectangles, squares, and rhombuses are all 90005 parallelograms 90006. 90003 Recent Examples on the Web His greatest mark on Boston is the Hancock building, an 800-foot-tall glass 90005 parallelogram 90006 that towers over Trinity Church, a beloved Romanesque edifice by the 19th-century architect Henry Hobson Richardson.- Fred A. Bernstein, 90005 New York Times 90006, «Henry Cobb, Courtly Architect of Boston’s Hancock Tower, Dies at 93,» 4 Mar. 2020 Until 2018 there was never a doubt that the boundaries, a jagged 90005 parallelogram 90006 over North Texas ‘two largest counties, would hold steady. — Nic Garcia, 90005 Dallas News 90006, «Why everyone is focused on this suburban Texas congressional race,» 1 Mar. 2020 The tower would gradually widen at the northeast and southwest corners, transitioning from an efficient rectangle at the base to an expansive 90005 parallelogram 90006 at the top.- Ryan Ori, 90005 chicagotribune.com 90006, «A Helmut Jahn-designed tower — the largest condo building launched in Chicago since the recession — breaks ground on South Michigan Avenue next week,» 16 Oct. 2019 About all there is to the constellation Lyra is the bright star Vega, which shines very high in the southeastern sky, with four dimmer stars forming a lopsided rectangle, or 90005 parallelogram 90006, just to the lower left of Vega. — Mike Lynch, 90005 Twin Cities 90006, «Sky Watch: Lyra the Lyre may be a small constellation, but it has a big story,» 18 Aug.2019 Vega and a small faint 90005 parallelogram 90006 below it are supposed to outline a celestial harp. — Mike Lynch, 90005 Twin Cities 90006, «Sky Watch: There are many delights to be found in August’s evening skies,» 4 Aug. 2019 Vega and a small 90005 parallelogram 90006 of fainter stars to the lower right is all there is to Lyra. — Mike Lynch, 90005 Twin Cities 90006, «Sky Watch: The great Summer Triangle will take you places,» 21 July 2019 The pattern of creases forms a tessellation of 90005 parallelograms 90006, and the whole structure collapses and unfolds in a single motion — providing an elegant way to fold a map.- 90005 Quanta Magazine 90006, «The Atomic Theory of Origami,» 31 Oct. 2017 Instead of the standard 90-degree angles found in many houses, the building uses the 90005 parallelogram 90006 shape and features a single right angle in its design. — Megan Barber, 90005 Curbed 90006, «Frank Lloyd Wright-inspired ‘parallelogram’ house asks $ 560K,» 3 Dec. 2018 90002 These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘parallelogram.’Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback. 90003 See More 90004 First Known Use of 90005 parallelogram 90006 90007 90056 1570, in the meaning defined above 90003 90004 History and Etymology for 90005 parallelogram 90006 90007 90002 Late Latin or Greek; Late Latin 90005 parallelogrammum 90006, from Greek 90005 parallēlogrammon 90006, from neuter of 90005 parallēlogrammos 90006 bounded by parallel lines, from 90005 parallēlos 90006 + 90005 grammē 90006 line, from 90005 graphein 90006 to write — more at carve 90003 90004 Learn More about 90005 parallelogram 90006 90007 90004 Statistics for 90005 parallelogram 90006 90007 90002 Cite this Entry 90003 90002 «Parallelogram.»90005 Merriam-Webster.com Dictionary 90006, Merriam-Webster, https://www.merriam-webster.com/dictionary/parallelogram. Accessed 12 Jul. 2020. 90003 MLA Chicago APA Merriam-Webster 90002 More Definitions for 90005 parallelogram 90006 90003 par · al · lel · o · gram | \ ˌPer-ə-le-lə-ˌgram \ 90004 Kids Definition of 90005 parallelogram 90006 90007 90002 90008: 90009 a plane figure with four sides whose opposite sides are parallel and equal 90003 90002 Comments on 90005 parallelogram 90006 90003 90002 What made you want to look up 90005 parallelogram 90006? Please tell us where you read or heard it (including the quote, if possible).90003.
No related posts.

Паралелограм — Вікіпедія

Площа паралелограма при відомих декартових координатах вершин[ред. | ред. код]

Доведення, що діагоналі паралелограма перетинаються і точкою перетину діляться навпіл[ред. | ред. код]

Определение параллелограмма

Свойства параллелограмма

Признаки параллелограмма

Параллелограмм

Свойства

Признаки параллелограмма

Площадь параллелограмма

См. также

Примечания

Параллелограмм — Википедия

Свойства

Признаки параллелограмма

Площадь параллелограмма

См. также

Примечания

Добавить комментарий Отменить ответ