3.2. Метод Гаусса.
Следует
отметить, что метод Крамера является
очень трудоемким по количеству вычислений
и требует порядка 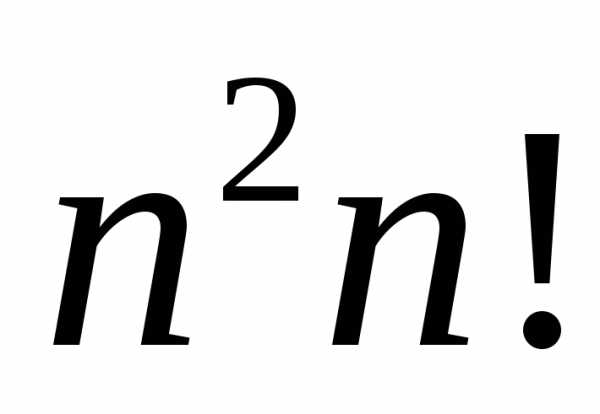 арифметических действий для нахождения
решения системы линейных уравнений.
При
арифметических действий для нахождения
решения системы линейных уравнений.
При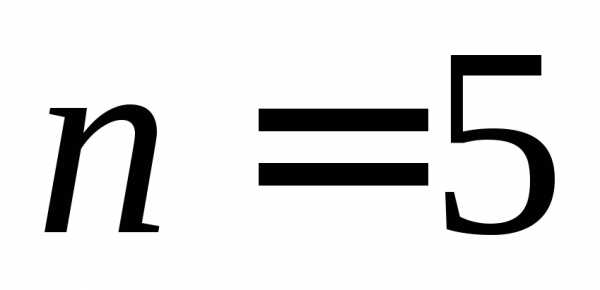 это составит около 3000 действий. При
решении серьезных задач приходится
иметь дело с системами уравнений порядка
это составит около 3000 действий. При
решении серьезных задач приходится
иметь дело с системами уравнений порядка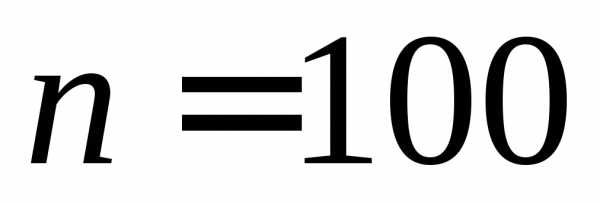 и более. При таких масштабах даже
суперкомпьютерам потребуется огромное
время для вычисления решения. Кроме
того, погрешности компьютерного
округления чисел приводят к значительным
ошибкам в расчетах численного решения
систем уравнений большего порядка.
Между тем существует более экономичный
способ решения систем линейных уравнений,
основанные на предварительном
преобразовании расширенной матрицы
системы к специальному виду. В частности,
одним из них является метод Гаусса.
и более. При таких масштабах даже
суперкомпьютерам потребуется огромное
время для вычисления решения. Кроме
того, погрешности компьютерного
округления чисел приводят к значительным
ошибкам в расчетах численного решения
систем уравнений большего порядка.
Между тем существует более экономичный
способ решения систем линейных уравнений,
основанные на предварительном
преобразовании расширенной матрицы
системы к специальному виду. В частности,
одним из них является метод Гаусса.
Рассмотрим
систему линейных уравнений общего вида
(1). Пусть для определенности 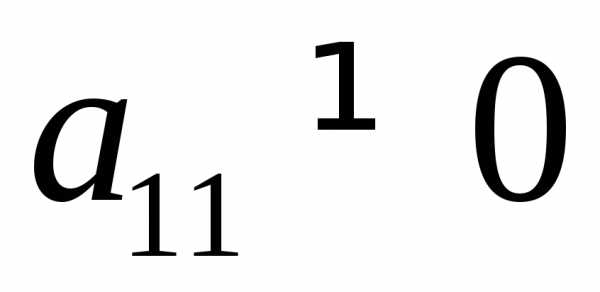 (если
(если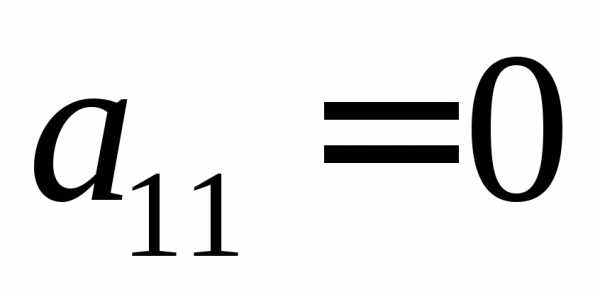 ,
то можно переставить на первое место
ненулевое слагаемое или начать с другого
уравнения). Умножим первое уравнение
системы (1) на число
,
то можно переставить на первое место
ненулевое слагаемое или начать с другого
уравнения). Умножим первое уравнение
системы (1) на число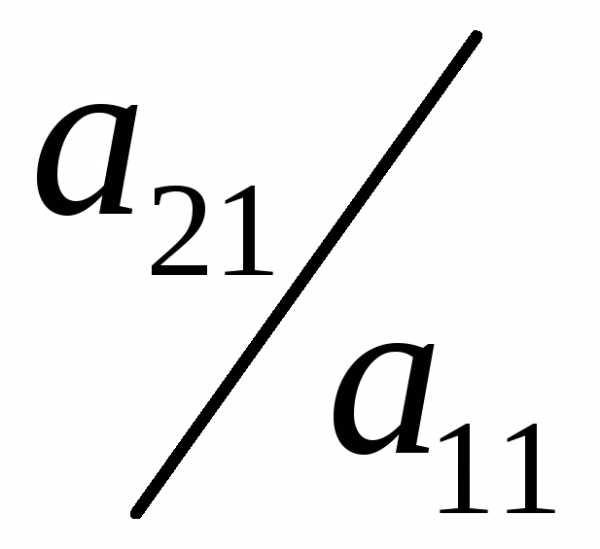 и
затем вычтем его из второго уравнения
этой системы. Умножим обе части первого
уравнения на число
и
затем вычтем его из второго уравнения
этой системы. Умножим обе части первого
уравнения на число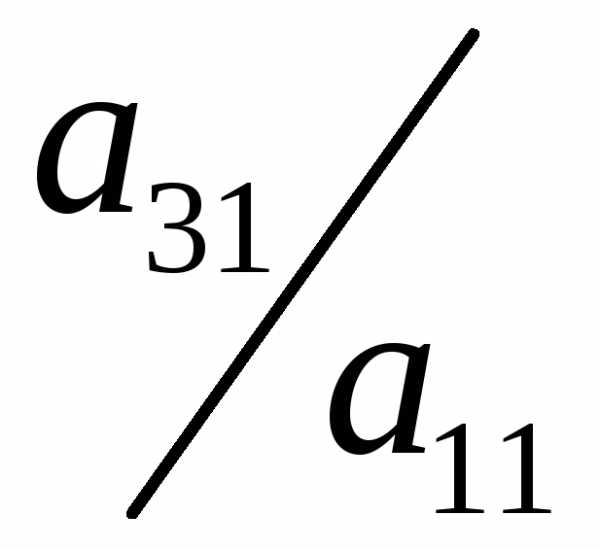 и затем вычтем его из третьего уравнения
и так далее, т.е. процесс заключается в
последовательном вычитании первого
уравнения, умножаемого на числа
и затем вычтем его из третьего уравнения
и так далее, т.е. процесс заключается в
последовательном вычитании первого
уравнения, умножаемого на числа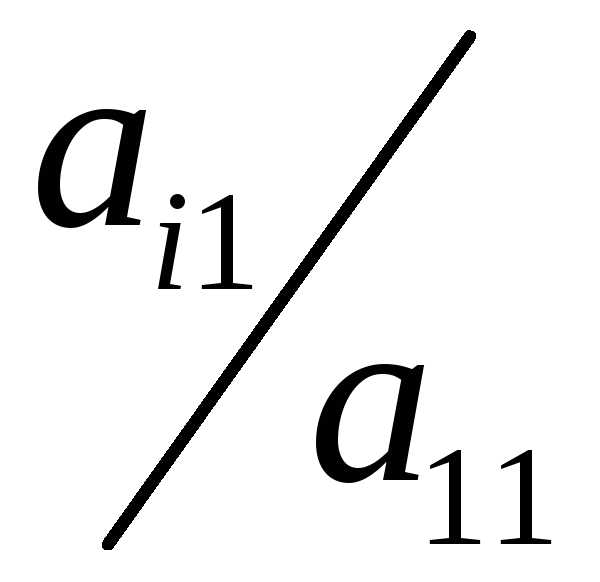 ,
из
,
из уравнения. Таким образом, в результате
элементарных преобразований мы получим
эквивалентную систему, в которой начиная
со второго уравнения отсутствуют
слагаемые, содержащие неизвестное
уравнения. Таким образом, в результате
элементарных преобразований мы получим
эквивалентную систему, в которой начиная
со второго уравнения отсутствуют
слагаемые, содержащие неизвестное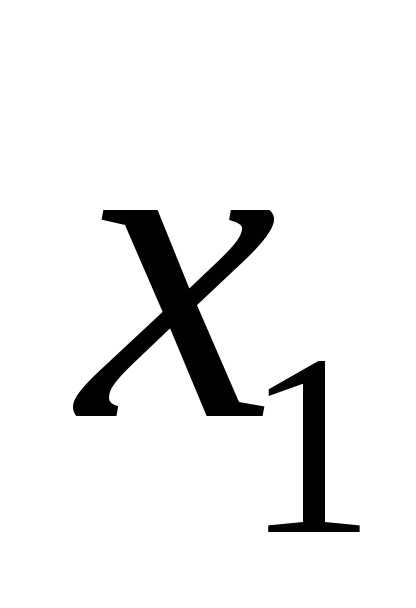
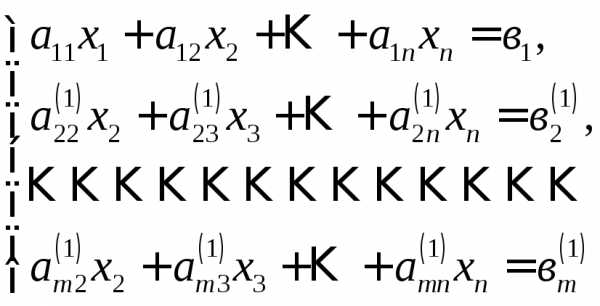

где
верхний индекс в скобках означает новые
коэффициенты, полученные после первого
шага. Для удобства записи будем оперировать
расширенной матрицей системы, отделяя
в ней вертикальной чертой столбец
свободных членов. Итак, после первого
шага, содержащего 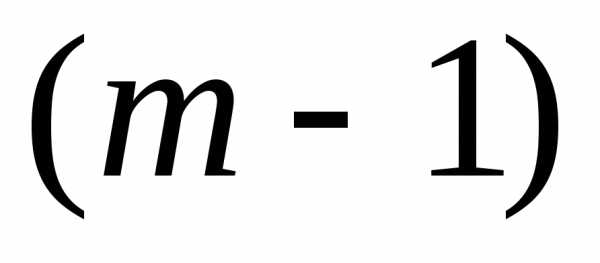 элементарных преобразований системы,
мы переходим от расширенной матрицы
(1.4) исходной системы к расширенной
матрице
элементарных преобразований системы,
мы переходим от расширенной матрицы
(1.4) исходной системы к расширенной
матрице
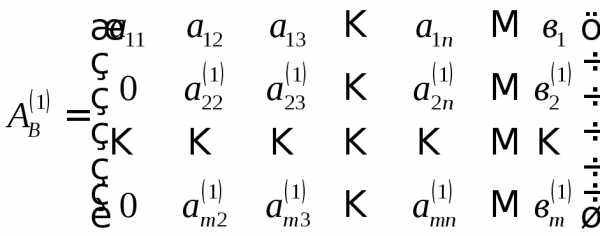 .
.
Второй
шаг заключается в том, что теперь второе
уравнение системы или вторая строка
матрицы используется для аналогичных
элементарных преобразований строк с
третьей по:
эта строка последовательно умножается
на число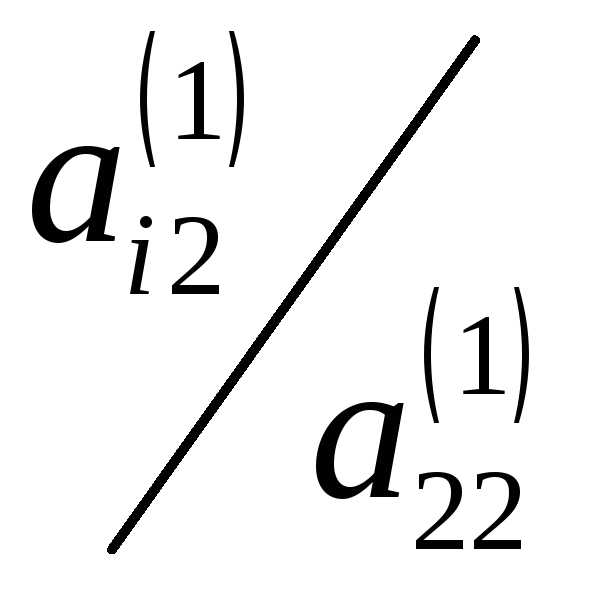
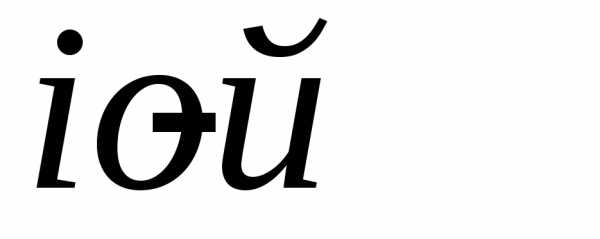 строки. В результате этих
строки. В результате этих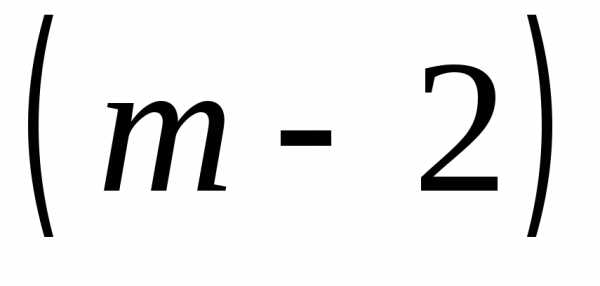 элементарных преобразований получаем
новую расширенную матрицу, соответствующую
новой эквивалентной системе уравнений.
Эта матрица имеет вид
элементарных преобразований получаем
новую расширенную матрицу, соответствующую
новой эквивалентной системе уравнений.
Эта матрица имеет вид,
где
верхний индекс означает новые коэффициенты.
В случае если элемент 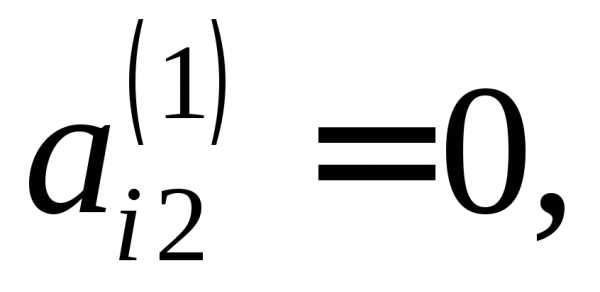 то второе уравнение можно поменять
местами с другим уравнением, у которого
элемент
то второе уравнение можно поменять
местами с другим уравнением, у которого
элемент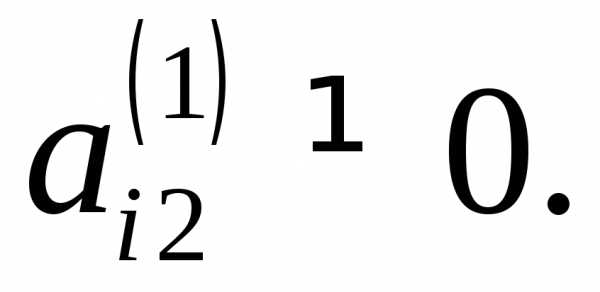
Продолжаем
этот процесс аналогичным образом до
тех пор, пока не дойдем до последней 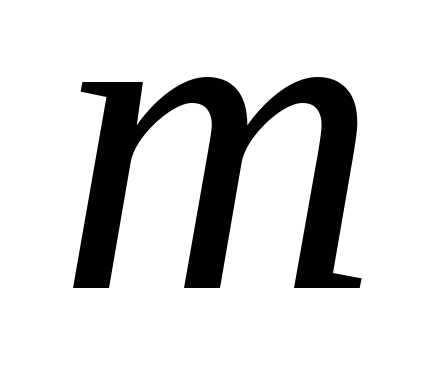
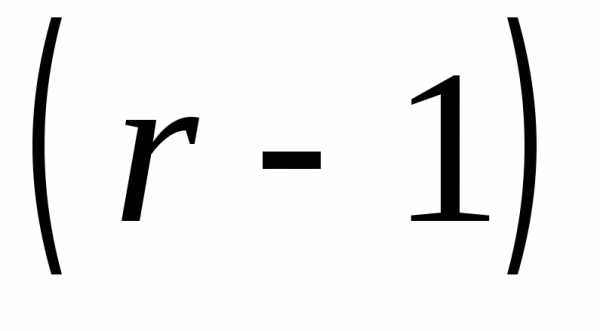 -го
шага процесса последовательного
исключения неизвестных мы получим
следующую расширенную матрицу:
-го
шага процесса последовательного
исключения неизвестных мы получим
следующую расширенную матрицу: 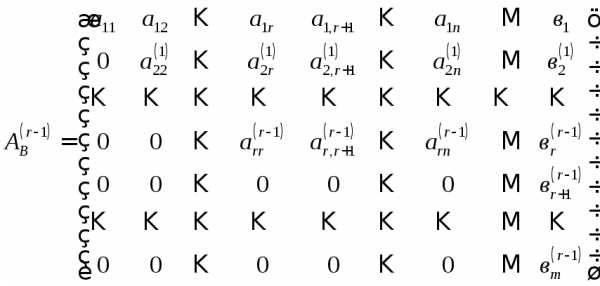 .
.
Последние  строк этой матрицы соответствуют
уравнениям эквивалентной системы
уравнений
строк этой матрицы соответствуют
уравнениям эквивалентной системы
уравнений
; 
Эти уравнения могут появляться, если соответствующие уравнения исходной системы (1) представляют собой линейные комбинации других уравнений этой системы. Таким образом метод Гаусса, позволяет на определенном шаге установить возможную несовместность исходной системы линейных уравнений или выявить и удалить уравнения, являющиеся линейными комбинациями других уравнений системы (1), если она совместна.
Пусть
система (1) совместна, тогда все правые
части уравнений (2) равны нулю, и после
удаления нулевых уравнений в эквивалентной
системе и нулевых строк в расширенной
матрице получаем матрицу специфического
ступенчатого вида, ранг которой равен
r. Все элементы этой
матрицы, стоящие слева или ниже элементов


Эта
расширенная матрица соответствует
системе уравнений ранга ,
которая имеет вид:
,
которая имеет вид:
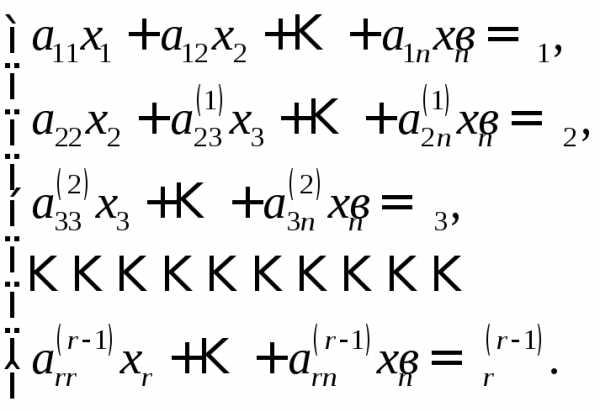

Система уравнений (4) уже полностью подготовлена к нахождению решения, процесс которого осуществляется снизу вверх, т.е. от последнего уравнения к первому. Переход от системы (1.1) к эквивалентной ей системе (4) называется прямым ходом, а нахождение неизвестных из системы (4) обратным ходом метода Гаусса. Далее последовательность действий аналогична изложенной выше.
Пример. Решить систему линейных уравнений методом Гаусса.
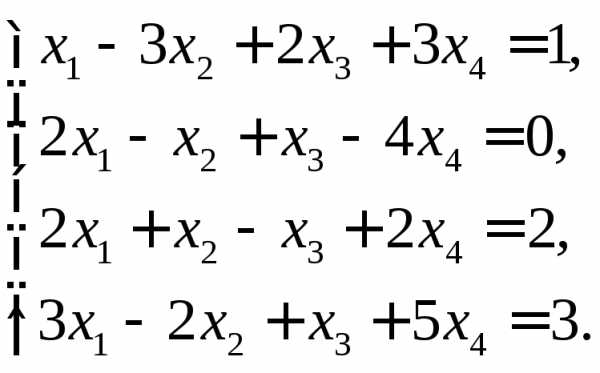
Решение. Составим расширенную матрицу этой системы, после чего выполним соответствующие преобразования методом Гаусса. Имеем
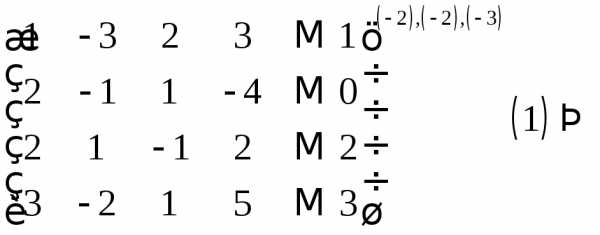
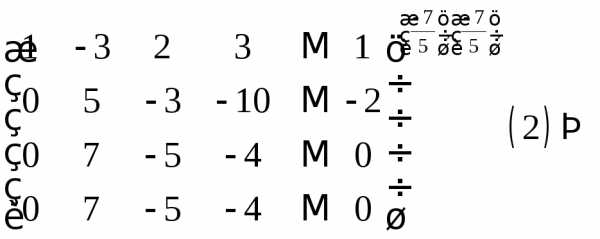


Последняя
нулевая строка в расширенной матрице,
полученной после 3-го шага, появилась
из-за того, что в исходной системе
четвертого уравнения является суммой
1-го и 3-го уравнений. Система совместна
, и после удаления нулевой строки
заключительный вид расширенной матрицы
соответствует системе трех уравнений
с четырьмя неизвестными (ранг системы
меньше числа неизвестных). Полагая 
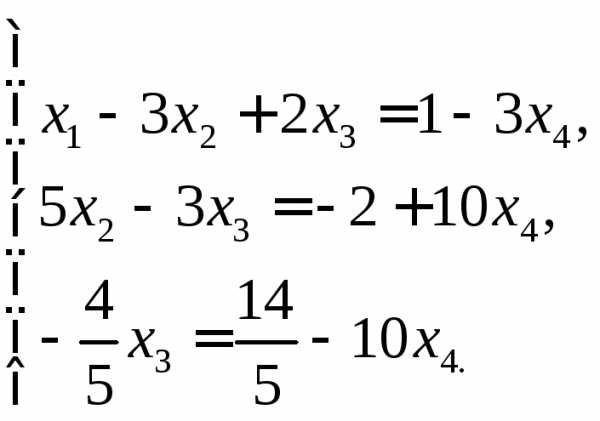
Из этой системы обратным ходом метода Гаусса находим
 ,
, 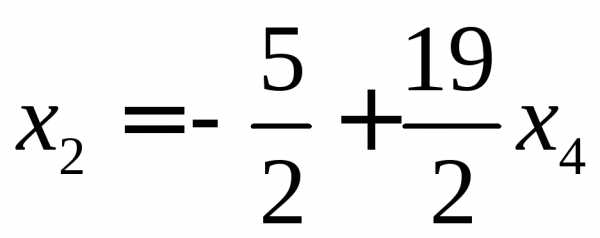 ,
,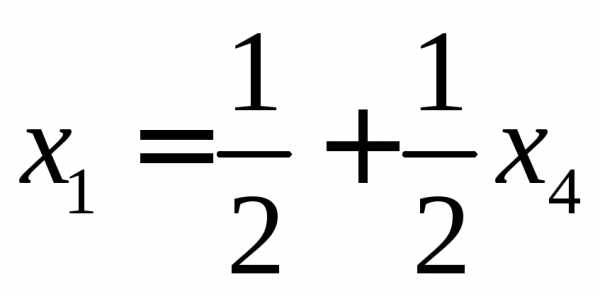 .
.
Данная
система уравнений имеет бесконечное
множество решений, поскольку  может принимать любые значения.
может принимать любые значения.
studfiles.net
Решение методом Гаусса СЛАУ 3-5-ого порядка
Метод Гаусса решения систем линейных алгебраических уравнений состоит в последовательном исключении неизвестных с помощью элементарных преобразований и сведении к верхней треугольной (ступенчатой или трапециевидной). После чего решают систему с конца к началу, подстановкой найденных решений.
Рассмотрим примеры решения систем линейных уравнений методом Гаусса, взяв за справочник сборник задач Дубовика В.П., Юрика И.И. «Высшая математика».
————-
Задача.
Решить систему линейных алгебраических уравнений.
1) (1. 189)
2) (4. 195)
3) (4. 198)
Решение.
1) Преобразуем исходную систему к ступенчатому виду. Для этого от второго уравнения вычтем первое, умноженное на 3, а от четвертого вычтем первое, умноженное на 4.
В результате с третьего уравнения имеем Полученное значение подставляем в исходное уравнение для нахождения
Полученные значения подставляем в первое уравнение
Решением системы трех линейных уравнений будут следующие значения переменных
2) Имеем систему трех уравнений с четырьмя неизвестными. В таких случаях одна переменная может быть свободна, а остальные будут выражаться через нее. Сведем систему к ступенчатому виду. Для этого от второго и третьего уравнения вычтем первое
Из последних двух уравнений получаем идентичные решения
.
После подстановки в первое уравнение получим
Данное уравнение связывает три переменные. Таким образом любая из переменных может быть выражена через две других
Итак получим следующее решение
3) Имеем разреженную систему линейных уравнений пятого порядка с пятью неизвестными. Сведем ее к ступенчатому виду. От второго уравнения вычтем первое и запишем в удобном для анализа виде
Из второго уравнения находим, что . Подставляем значения во все нижние уравнения и переносим за знак равенства. Также поменяем второе с третьим уравнения местами
Четвёртое и пятое уравнения эквивалентны. Выразим одну из переменных через другую
Полученное значение подставим во второе уравнение и найдем
Из первого уравнения определяем
Решение системы уравнений следующее
При вычислениях систем линейных алгебраических уравнений методом Гаусса нужно свезти систему линейных уравнений к ступенчатому виду. Для этого удобно записывать переменные под переменными, как в последнем примере, это ускорит решение. Остальное все зависит от матрицы, которую нужно решить и Ваших умений.
———————————————-
Посмотреть материалы:
yukhym.com
1.2.3. Метод Гаусса
Как было отмечено выше, метод Крамера и матричный метод имеют один существенный недостаток: они неприменимы, если определитель системы равен нулю. В связи с этим, рассмотрим еще один, наиболее универсальный метод решения систем линейных алгебраических уравнений – метод Гаусса.Пусть число уравнений системы совпадает с числом неизвестных1.
| (1.2) |
Расширенной матрицей системы (1.2) называется матрица системы, дополненная столбцом свободных членов:
| (1.3) |
Расширенная матрица системы называется верхнетреугольной, если в матрице системы все элементы ниже главной диагонали равны нулю:
| (1.4) |
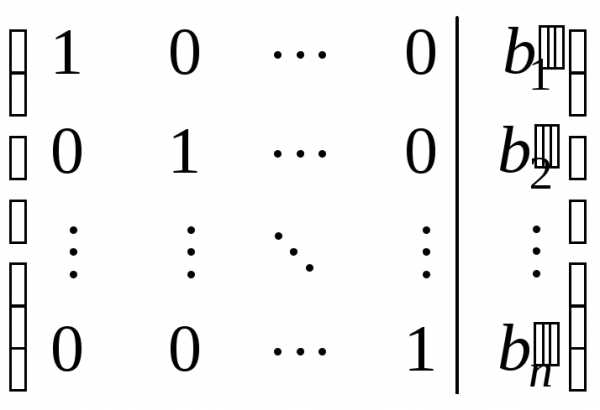
Расширенную матрицу системы мы будем называть диагональной, если матрица системы представляет собой единичную:
| (1.5) |
К элементарным преобразованиям расширенной матрицы системы относятся преобразования трех типов:
1) Перемена местами любых двух строк:
.
2) Умножение любой строки на любое число, отличное от нуля
.
3) Прибавление к любой строке любой другой, умноженной на произвольное число:
.
Известно, что элементарные преобразования расширенной матрицы системы приводят к эквивалентной матрице, т.е. система линейных алгебраических уравнений, соответствующая полученной матрице, имеет те же решения, что и исходная.
Идея метода Гаусса заключается в том, чтобы с помощью элементарных преобразований от расширенной матрицы системы вида (1.3) перейти вначале к верхнетреугольной матрице (1.4) (прямой ход метода Гаусса), а затем и к диагональной (1.5) (обратный ход метода Гаусса).
Если при переходе к верхнетреугольной матрице в матрице системы не возникло ни одной нулевой строки (это соответствует тому, что определитель исходной системы отличен от нуля), то система имеет единственное решение. Его легко найти, исходя из диагонального вида: .
Продемонстрируем на примерах технику использования элементарных преобразований.
Пример
8. Решить
систему уравнений 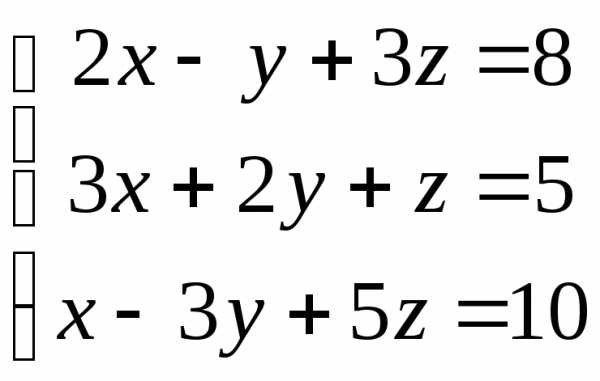 .
.
Решение. Запишем расширенную матрицу системы:
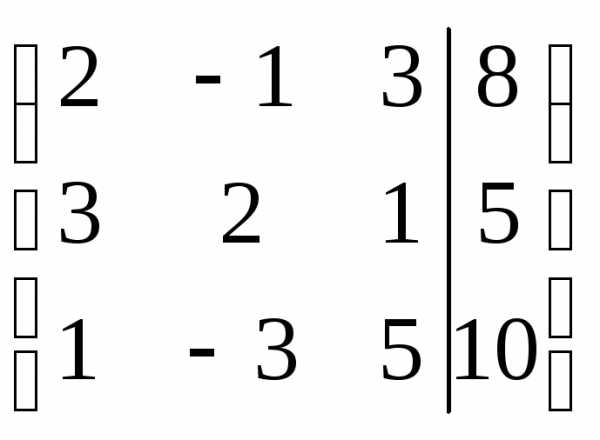 .
.
Выберем
в первом столбце ведущий элемент, т.е.
элемент, с помощью которого удобно будет
сделать нули под ним. Таким числом
является единица. Поменяем местами
первую и третью строки ( элементарное преобразование 1-го вида):
элементарное преобразование 1-го вида):
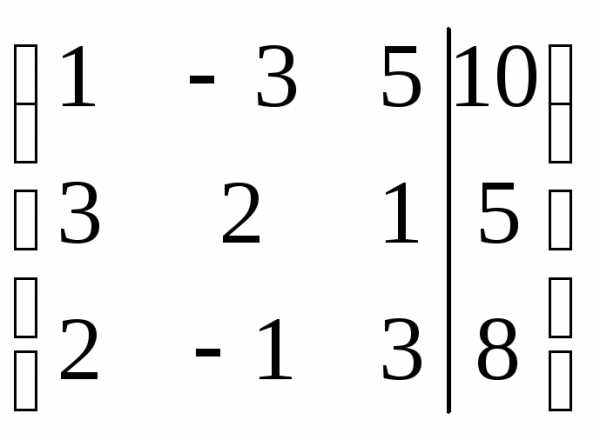
С помощью элементарных преобразований 3-го типа делаем нули под ведущим элементом ():
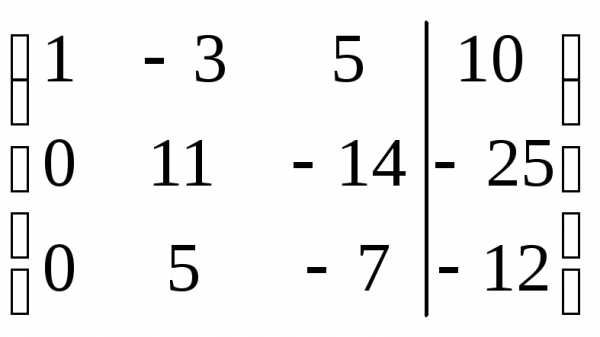 .
.
Теперь выбираем ведущий элемент во втором столбце. Поскольку пока единицы нет, то её желательно создать. Для этого из второй строки вычтем удвоенную третью ():
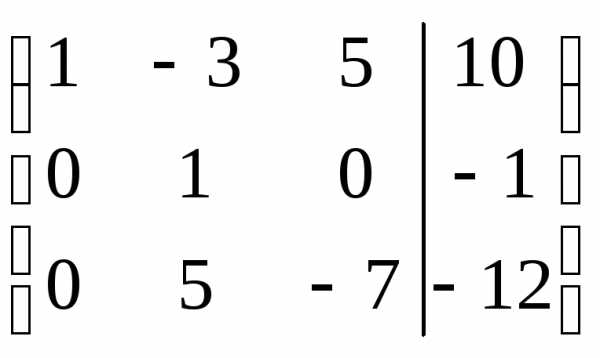 .
.
Делаем
нуль под ведущим элементом (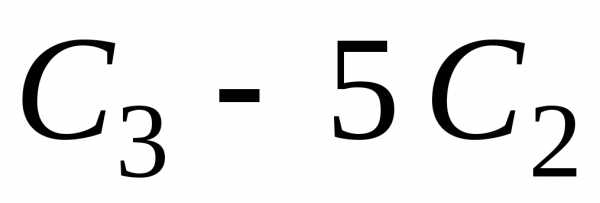 ):
):
 .
.
Умножим
третью строку на 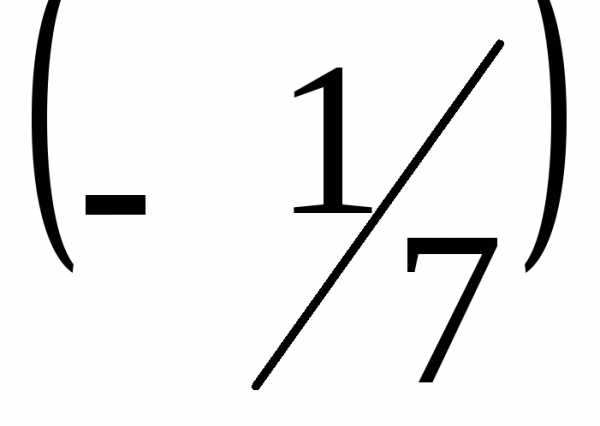 (
(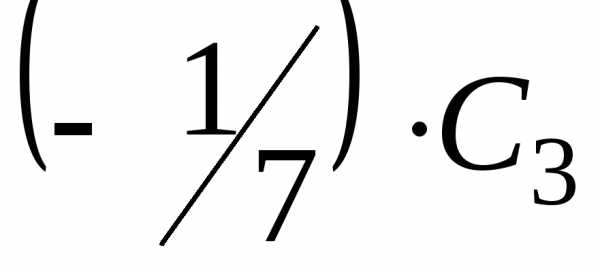 – элементарное преобразование 2-го
типа):
– элементарное преобразование 2-го
типа):
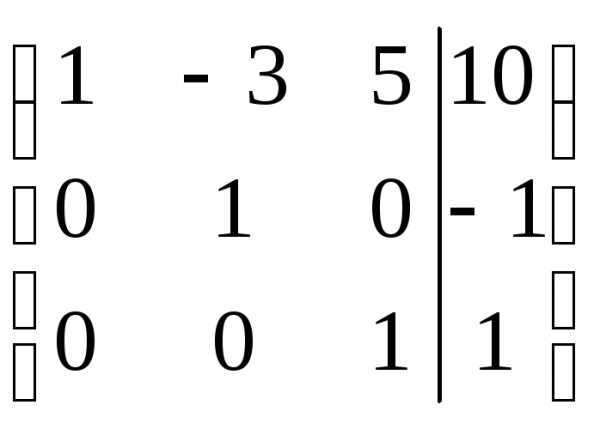 .
.
Мы получили
матрицу верхнетреугольного вида.
Переходим к обратному ходу метода
Гаусса. В качестве ведущего элемента
выбираем единицу, стоящую в третьем
столбце. Делаем нули над ней (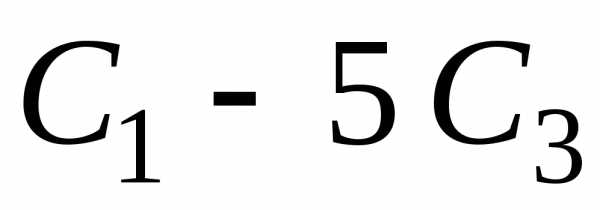 ):
):
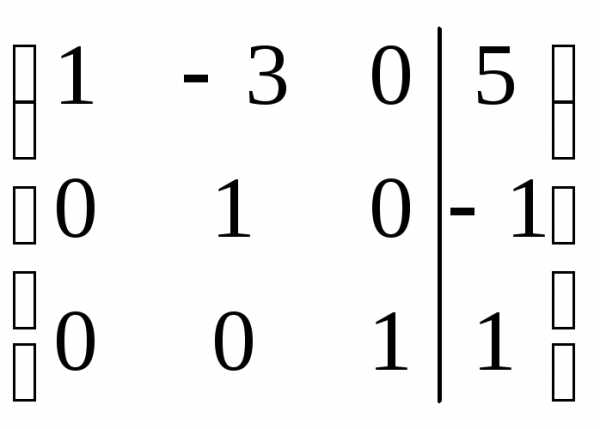 .
.
Последний
шаг. С помощью единицы во втором столбце
зануляем элемент над ней (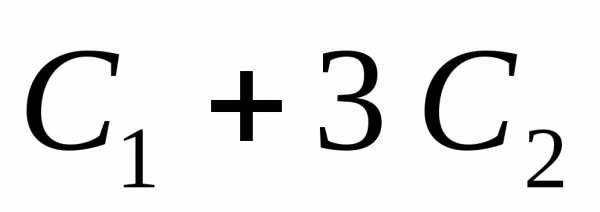 ):
):
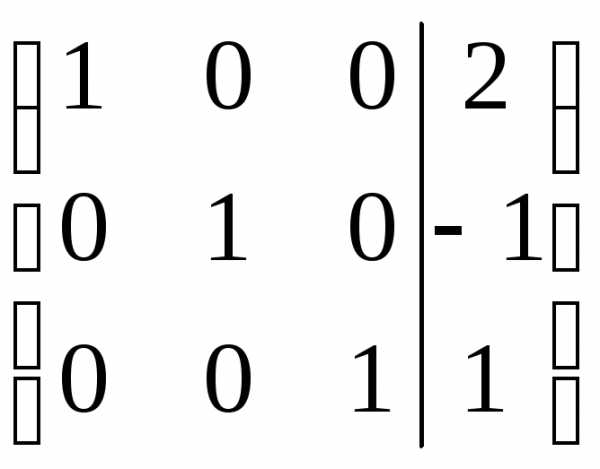 .
.
Получена матрица диагонального вида. Проверку полученного решения сделайте самостоятельно. Ответ: .n
Если при переходе к верхнетреугольной матрице в матрице системы возникает хотя бы одна нулевая строка (это означает, что определитель исходной системы равен нулю), то система либо не имеет решения вовсе, либо имеет бесчисленное множество решений.
Пример
9. Решить
систему уравнений 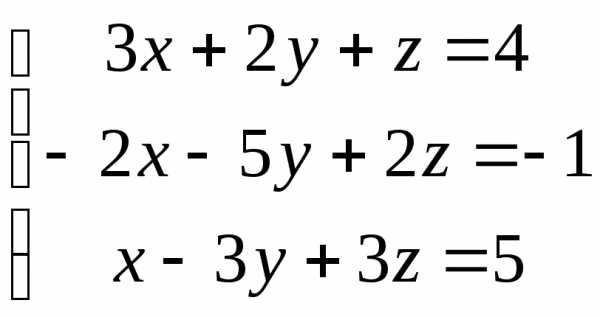
Решение.
Распишем последнюю строку полученной матрицы в виде уравнения:
Очевидно, что это уравнение, а значит и вся система, решений не имеет. n
Пример
10. Решить
систему уравнений 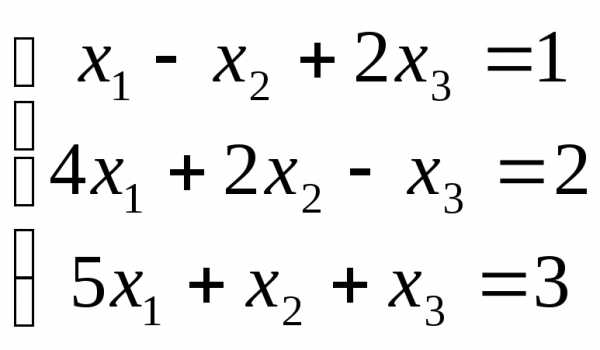 .
.
Решение.
.
Вотличие от предыдущего примера, последняя строка непротиворечива. Она указывает на то, что третье уравнение системы является следствием первых двух. Таким образом, мы, фактически, получили систему из двух уравнений с тремя неизвестными. Такая система имеет бесчисленное множество решений. Для того чтобы их найти, одну из переменных (её называют свободной) переносят в правую часть расширенной матрицы, а остальные переменные (их называют базисными или связными) выражают через эту свободную. Имеем
.
Таким образом, .
Это
общее решение системы. Присваивая
свободной переменной 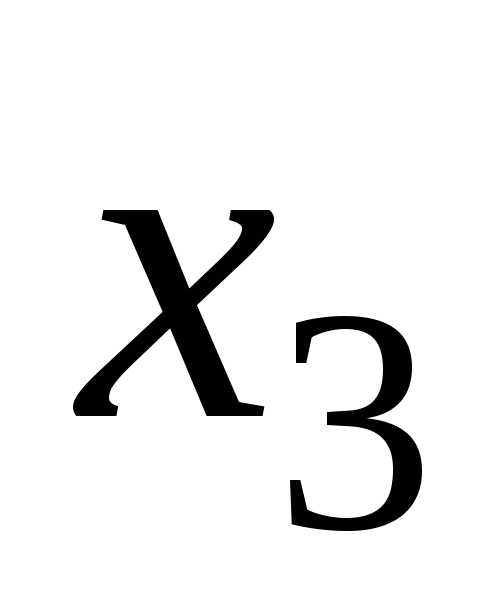 конкретные значения, можно получать
частные решения, например,
конкретные значения, можно получать
частные решения, например,
и т.д.
Ответ: .n
Отметим ещё одно достоинство метода Гаусса. Для систем линейных уравнений 4-го порядка и выше метод Гаусса оказывается эффективнее метода Крамера и матричного метода и приводит к решению гораздо быстрее.
Пример 11. Решить систему уравнений
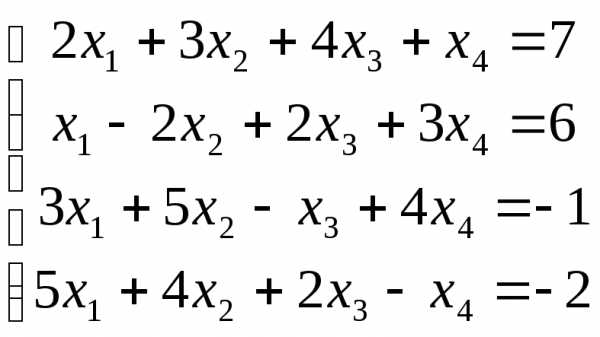 .
.
Решение.
Проверку сделайте самостоятельно.
Ответ: .n
studfiles.net
Тема 3 системы линейных уравнений. Правила крамера. Метод гаусса конспект 3
3.1 Правило крамера
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными, которые ждут вас в электротехнике на 2 курсе!
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Теорема
Система nуравнений сnнеизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов.
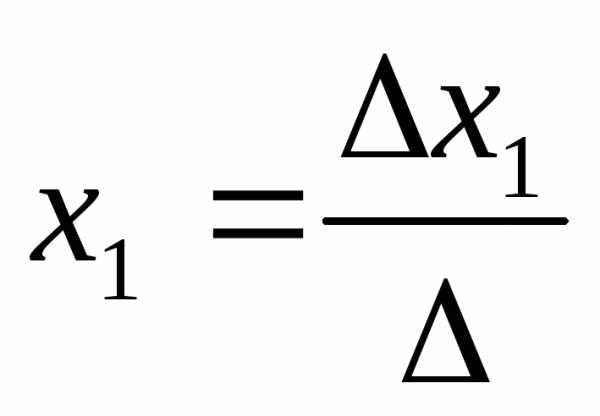
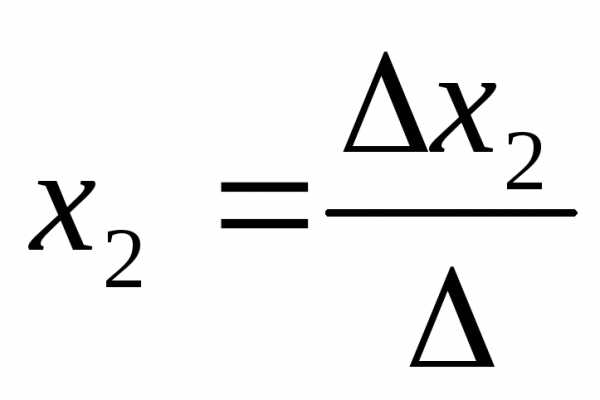 …
…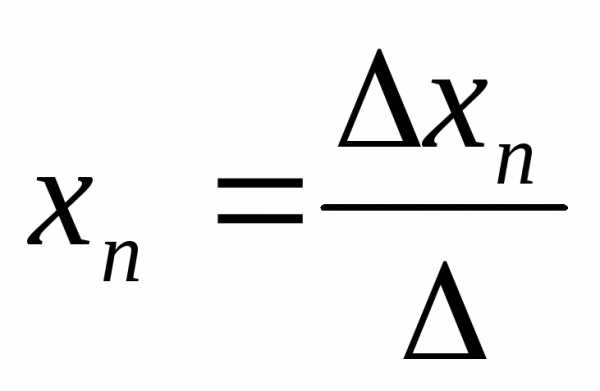

Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называютглавным определителем системы.
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам: ,
Пример 1
Решить систему уравнений: 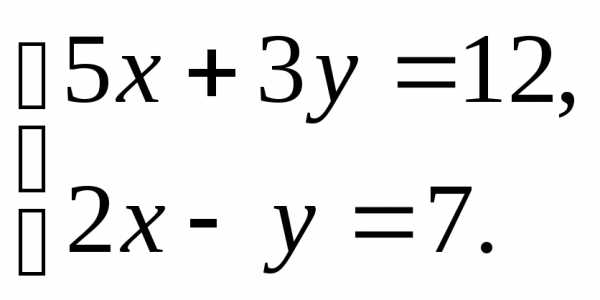
Решение
Составим и вычислим определитель
 :
: — система имеет одно решение, можно
применить теорему Крамера
— система имеет одно решение, можно
применить теорему Крамера
2) Составим и вычислим определитель 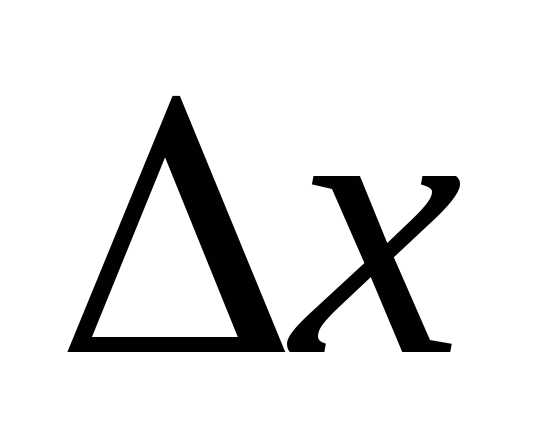 :
: 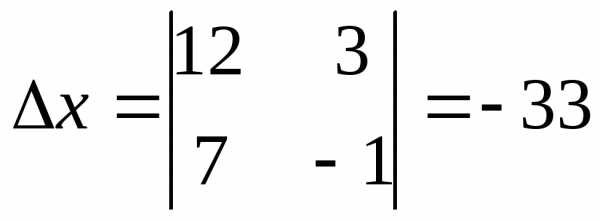
Составим и вычислим определитель
 :
:Найдем значения xиyпо формулам Крамера
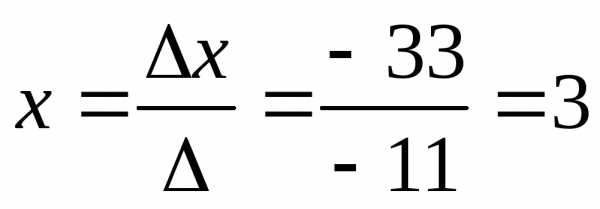
Ответ: (3; -1)
Пример 2
Решить систему линейных уравнений
Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему мы взяли из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
, значит, система имеет единственное решение.
;
;
Ответ: ,
3.2 МЕТОД ГАУССА
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной).
Вернемся к простейшей системе и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы:. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица система записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строкиматрицыможнопереставлятьместами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:
2) Строку матрицы можно умножить (разделить)на любое число,отличное от нуля. Рассмотрим, например, матрицу. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:. Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
3) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера:. Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2:, ико второй строке прибавляем первую строку умноженную на –2:. Теперь первую строку можно разделить «обратно» на –2:.
Как видите, строка, которую ПРИБАВЛЯЛИ–не изменилась.Всегдаменяется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
На практике так подробно, конечно, не расписывают, а пишут короче: Еще раз: ко второй строкеприбавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: »
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку:»
«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку:»
«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку:»
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ:рассмотренные манипуляциинельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических»действиях с матрицамичто-то переставлять внутри матриц ни в коем случае нельзя! Вернемся к нашей системе. Она уже почти решена.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
(1) Ко второй строке прибавили первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований –привести матрицу к ступенчатому виду:. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называетсятрапециевидный видилитреугольный вид.
В результате элементарных преобразований получена эквивалентнаяисходной система уравнений:
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.
В нижнем уравнении у нас уже готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:
Ответ:
Пример 1
Решить методом Гаусса систему уравнений:
Запишем расширенную матрицу системы:
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?
Сначала смотрим на левое верхнее число: Почти всегда здесь должна находитьсяединица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:
Теперь первая строка у нас останется неизменной до конца решения. Уже легче.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение,ко второй строке прибавляем первую строку, уже умноженную на –2:
Результат записываем во вторую строку: Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужнок третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). Ик третьей строке прибавляем первую строку, умноженную на –3:
Результат записываем в третью строку:
На практике эти действия обычно выполняются устно и записываются в один шаг:
Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатовпоследователени обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО:Далее нужно получить единицу на следующей «ступеньке»:
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:
Для этого к третьей строке прибавляем вторую строку, умноженную на –2:Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат:
Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:
И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:
Ответ:
ПРАКТИКУМ 3
ЗАДАНИЕ N 1
Систему решают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)2)3)x 4)y
Решение:Решение системы линейных уравнений по правилу Крамера находится по формулами, где. Здесь– главный определитель системы, в котором первый столбец состоит из коэффициентов приx, а второй столбец – из коэффициентов приy. В нашем случаеЕсли, то правило Крамера для решения системы уравнений не применяют.– это определитель, который получается из главного определителя системы путем замены столбца, состоящего из коэффициентов приxна столбец, состоящий из соответствующих свободных членов. Имеем, тогдаАналогично– это определитель, который получается из главного определителя системы путем замены столбца, состоящего из коэффициентов приy, на столбец, состоящий из соответствующих свободных членов. Получим, тогда
ЗАДАНИЕ N 2
Тема: Правило КрамераСистемурешают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)2)3)4)y
Решение:Решение системы линейных уравнений по правилу Крамера находится по формулами, где. Здесь– главный определитель системы, в котором первый столбец состоит из коэффициентов приx, а второй столбец – из коэффициентов приy. В нашем случаеЕсли, то правило Крамера для решения системы уравнений не применяют.– это определитель, который получается из главного определителя системы путем замены столбца, состоящего из коэффициентов приxна столбец, состоящий из соответствующих свободных членов. ИмеемАналогично– это определитель, который получается из главного определителя системы путем замены столбца, состоящего из коэффициентов приy, на столбец, состоящий из соответствующих свободных членов. Получим, тогда
ЗАДАНИЕ N 3Тема: Системы линейных уравненийСистема линейных уравнений
имеет решение …
Решение:Из третьего уравнения системы найдемИз второго уравнения легко получить, чтоЗная значенияyиz, из первого уравнения системы получим Решение данной системы:
ЗАДАНИЕ N 4
Тема: Системы линейных уравненийСистема линейных уравнений
имеет решение …
Решение:Из третьего уравнения системы найдем, чтоИз второго уравнения системы получимЗная значенияyиz, из первого уравнения системы найдем Решение данной системы:
ЗАДАНИЕ N 5
Тема: Системы линейных уравненийСистема линейных уравнений
имеет решение …
Решение:Найдем сумму первого и второго уравнений системы, получим, тогдаНайдемyиз первого или второго уравнений системы, получимИз третьего уравнения имеемРешение данной системы:
ЗАДАНИЕ 6
Тема: Системы линейных уравнений
Решить систему по формулам Крамера.
Решение:
Решим систему по формулам Крамера. , значит, система имеет единственное решение.
Ответ: .
ЗАДАНИЕ 7
Решить систему линейных уравнений методом Гаусса
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху –1, что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по накатанной колее:
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно,, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх: Да тут подарок получился:
Ответ: .
САМОСТОЯТЕЛЬНАЯ РАБОТА 3
ЗАДАНИЕ N 1
Тема: Правило КрамераСистемурешают по правилу Крамера. Вычислите: 1)2)3)4)x
ЗАДАНИЕ N 2
Тема: Правило Крамера Системурешают по правилу Крамера. Вычислите: 1)2)3)x 4)y
ЗАДАНИЕ N 3
Правило КрамераСистемурешают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)2)3)x 4)y
1 | 2 | 3 | 4 | 5 |
— 14 | 14 | — 2 | 2 | 1 |
ЗАДАНИЕ N 4
Правило КрамераСистемурешают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)2)3)4)x
ЗАДАНИЕ N 5Тема: Системы линейных уравненийСистема линейных уравнений
имеет решение …
ЗАДАНИЕ N 6Тема: Системы линейных уравнений Система линейных уравненийимеет решение …
ЗАДАНИЕ N 7
Тема: Системы линейных уравненийСистема линейных уравненийимеет решение …
ЗАДАНИЕ N 8Тема: Системы линейных уравненийСистема линейных уравненийимеет решение …
ЗАДАНИЕ N 9
Тема: Системы линейных уравненийСистема линейных уравненийимеет решение …
ЗАДАНИЕ N 10
Решить систему линейных уравнений методом Гаусса
studfiles.net
Решение СЛАУ 4-ого порядка методом Гаусса, пример № 4
СЛАУ 3-его порядка:
1 —
2 —
3 —
4 —
5 —
6 —
7 —
8 —
9 —
10 —
11 —
12
СЛАУ 4-ого порядка:
1 —
2 —
3 —
4 —
5 —
6 —
7 —
8 —
9 —
10 —
11 —
12
Условие
|
Решение системы линейных алгебраических уравнений методом Гаусс
Для проверки ответов можете воспользоваться нашим онлайн сервисом — Решение системы линейных уравнений методом Гаусса. Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются элементарными преобразованиями матрицы. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по математике и другим предметам!
Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 4 × 5, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.
Проведём следующие действия:
- Поменяем местами строку № 1 и строку № 4
Получим:
Проведём следующие действия:
- Из строки № 2 вычтем строку № 1 умноженную на 2 (Строка 2 — 2 × строка 1)
- Из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 — 2 × строка 1)
- Из строки № 4 вычтем строку № 1 умноженную на 3 (Строка 4 — 3 × строка 1)
Получим:
Проведём следующие действия:
- Строку № 3 умножим на -1 (Строка 3 = строка 3 * -1)
- Поменяем местами строку № 2 и строку № 3
Получим:
Проведём следующие действия:
- К строке № 3 прибавим строку № 2 умноженную на 3 (Строка 3 + 3 × строка 2)
- К строке № 4 прибавим строку № 2 умноженную на 2 (Строка 4 + 2 × строка 2)
Получим:
Проведём следующие действия:
- Строку № 4 поделим на -3 (Строка 4 = строка 4 / -3)
- Поменяем местами строку № 3 и строку № 4
Получим:
Проведём следующие действия:
- К строке № 4 прибавим строку № 3 умноженную на 7 (Строка 4 + 7 × строка 3)
Получим:
Проведём следующие действия:
- Строку № 4 поделим на 55 (Строка 4 = строка 4 / 55)
- Из строки № 3 вычтем строку № 4 умноженную на 6 (Строка 3 — 6 × строка 4)
- Из строки № 2 вычтем строку № 4 умноженную на 5 (Строка 2 — 5 × строка 4)
- Из строки № 1 вычтем строку № 4 умноженную на 2 (Строка 1 — 2 × строка 4)
Получим:
Проведём следующие действия:
- К строке № 2 прибавим строку № 3 умноженную на 5 (Строка 2 + 5 × строка 3)
- К строке № 1 прибавим строку № 3 умноженную на 3 (Строка 1 + 3 × строка 3)
Получим:
Проведём следующие действия:
- Из строки № 1 вычтем строку № 2 (Строка 1 — строка 2)
Получим:
В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:
х1 = 0
х2 = 0
х3 = 1
х4 = 0
Вы поняли, как решать? Нет?
Помощь с решением
www.webmath.ru
Метод Гаусса.
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находят все остальные переменные.
Предположим, что
в системе уравнений коэффициент при
переменной  в первом уравнении
в первом уравнении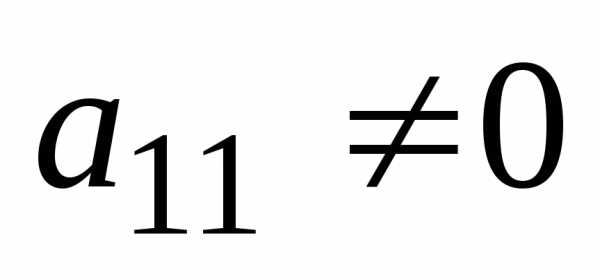 (Если это не так, то перестановкой местами
уравнений добьемся того, что
(Если это не так, то перестановкой местами
уравнений добьемся того, что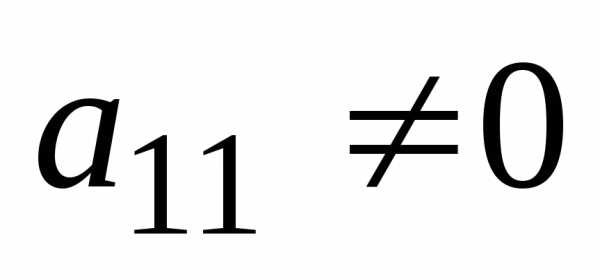 ).
).
Шаг 1.
Умножая первое уравнение на подходящие
числа (а именно на 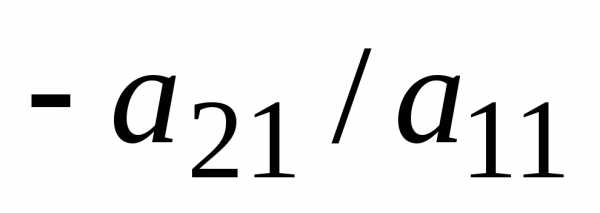 ,
,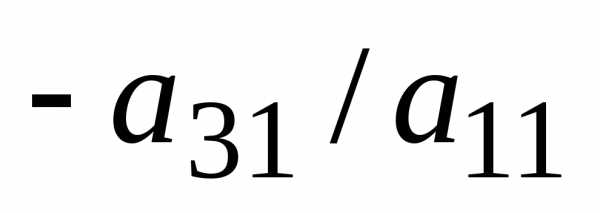 ,
…,
,
…, )
и прибавляя полученные уравнения
соответственно ко второму, третьему
,…,
)
и прибавляя полученные уравнения
соответственно ко второму, третьему
,…,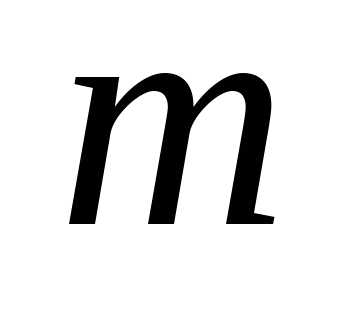 -тому
уравнению системы, исключим переменную
-тому
уравнению системы, исключим переменную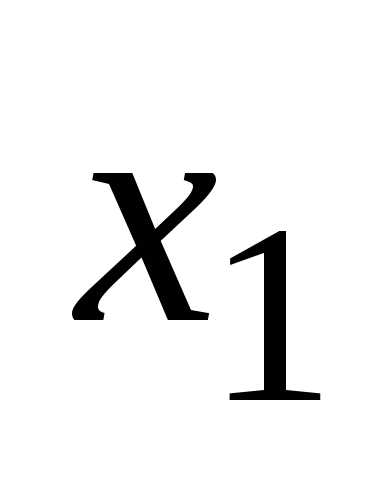 из всех последующих уравнений, начиная
со второго. Получим
из всех последующих уравнений, начиная
со второго. Получим
,
где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага.
Шаг 2.
Предположим, что 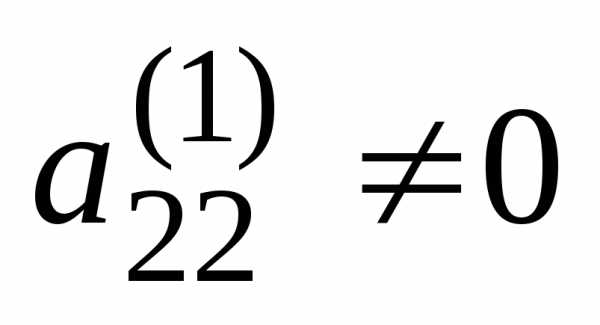 (если это не так, то соответствующей
перестановкой уравнений или переменных
с изменением их номеров добьемся того,
чтобы
(если это не так, то соответствующей
перестановкой уравнений или переменных
с изменением их номеров добьемся того,
чтобы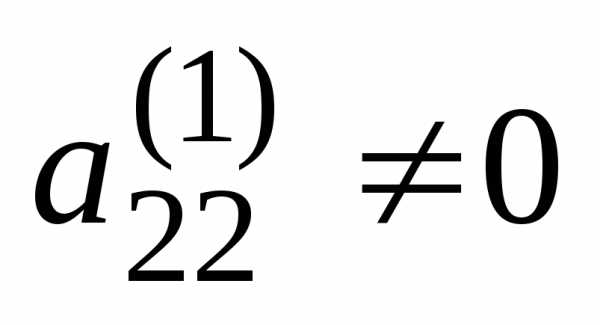 ).
).
Умножая второе
уравнение на подходящие числа (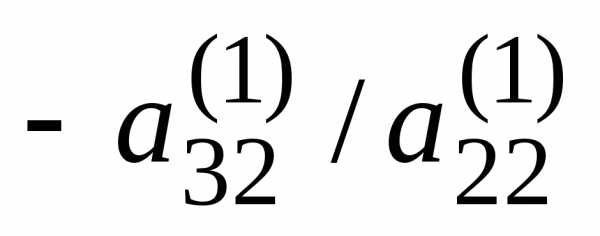 ,
,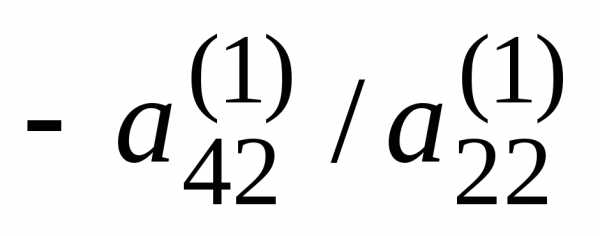 ,
…,
,
…,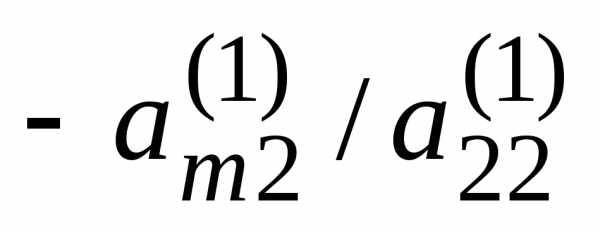 )
и прибавляя полученные уравнения
)
и прибавляя полученные уравнения соответственно
к третьему, четвертому,…,
соответственно
к третьему, четвертому,…,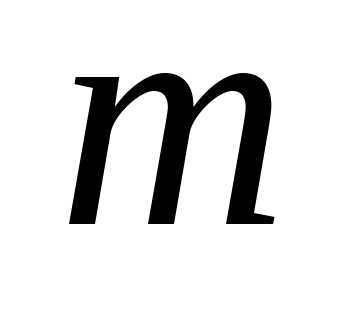 -тому
уравнению системы, исключим переменную
-тому
уравнению системы, исключим переменную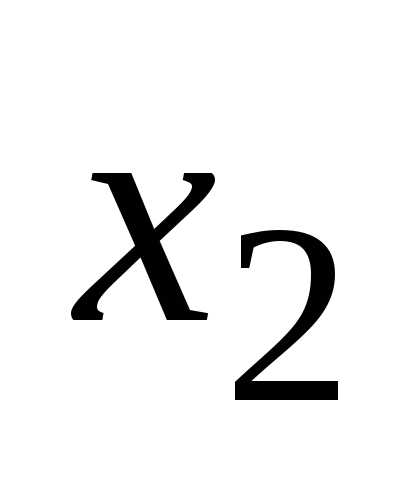 из всех последующих уравнений, начиная
с третьего.
из всех последующих уравнений, начиная
с третьего.
Продолжая процесс
последовательного исключения переменных,
после (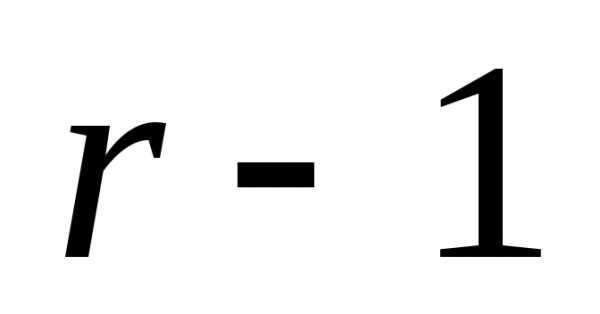 )-го
шага получим систему
)-го
шага получим систему
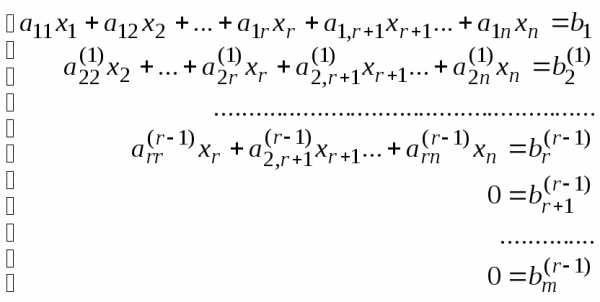 (2)
(2)
Число нуль в
последних 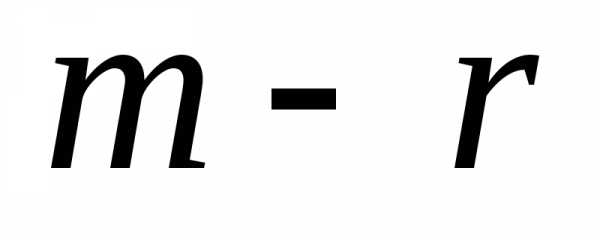 уравнениях означает, что их левые части
имеют вид.Если хотя бы
одно из чисел
уравнениях означает, что их левые части
имеют вид.Если хотя бы
одно из чисел 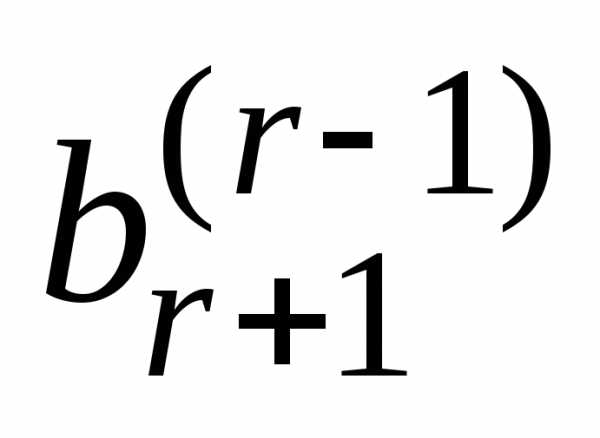 ,…,
,…, не равно нулю, то соответствующее
равенство противоречиво, и система(1) несовместна.
не равно нулю, то соответствующее
равенство противоречиво, и система(1) несовместна.
Таким образом, для
любой совместной системы числа  ,…,
,…,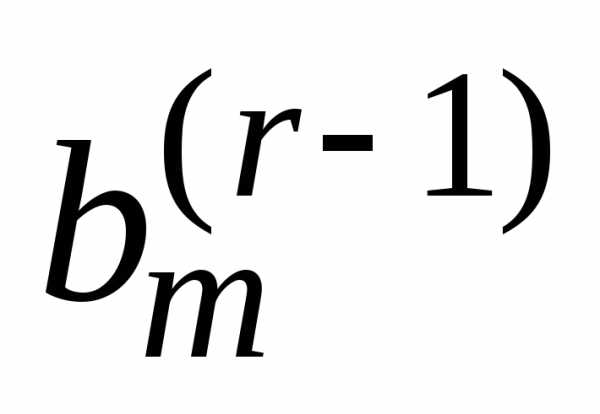 в системе
(2) равны нулю. В этом случае последние
в системе
(2) равны нулю. В этом случае последние  уравнений в системе являются тождествами
и их можно не принимать во внимание при
решении системы (1). Переход от системы
(1) к равносильной ей системе (2) называетсяпрямым ходом
метода Гаусса,
а нахождение переменных из системы (2)
– обратным
ходом.
уравнений в системе являются тождествами
и их можно не принимать во внимание при
решении системы (1). Переход от системы
(1) к равносильной ей системе (2) называетсяпрямым ходом
метода Гаусса,
а нахождение переменных из системы (2)
– обратным
ходом.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу
называемую расширенной
матрицей системы (1), т.к. в нее, кроме матрицы системы  ,
дополнительно включен столбец свободных
членов.
,
дополнительно включен столбец свободных
членов.
Пример. Решить систему уравнений:
.
Решение. Расширенная матрица системы имеет вид:
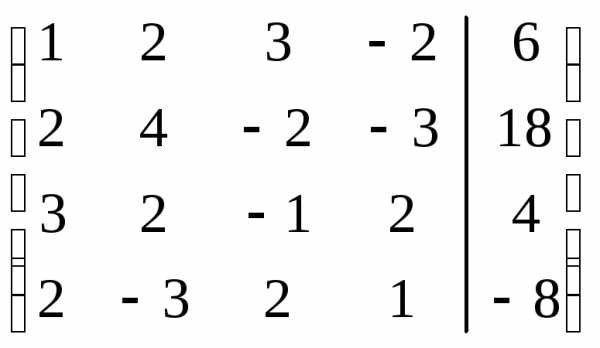 .
.
Шаг
1.
Так как 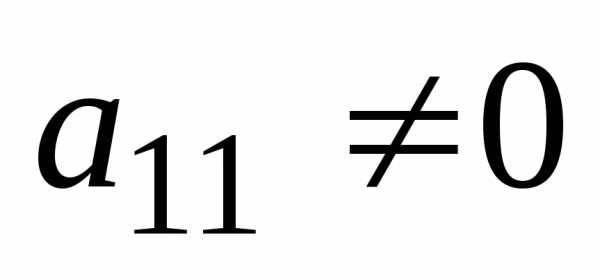 ,
то умножая на вторую, третью и четвертую
строки матрицы на числа (-2), (-3), (-2) и
прибавляя полученные строки соответственно
ко второй, третьей, четвертой строкам,
исключим переменную
,
то умножая на вторую, третью и четвертую
строки матрицы на числа (-2), (-3), (-2) и
прибавляя полученные строки соответственно
ко второй, третьей, четвертой строкам,
исключим переменную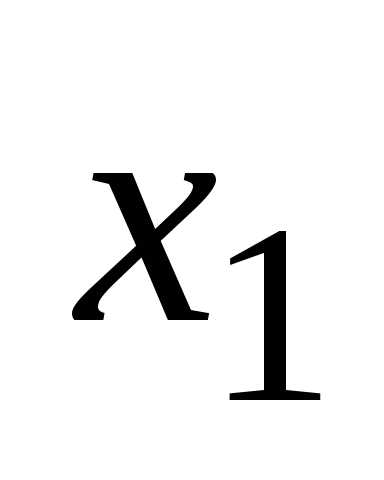 из всех строк, начиная со второй. Заметив,
что в новой матрице
из всех строк, начиная со второй. Заметив,
что в новой матрице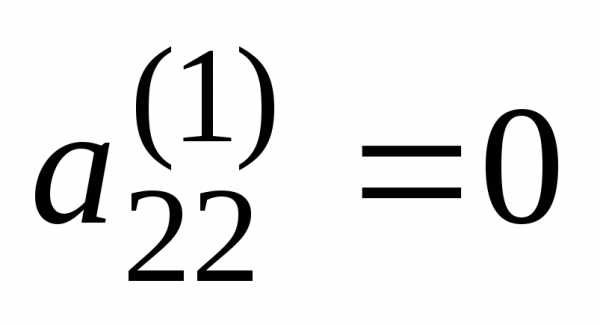 ,
поменяем местами вторую и третью строки:
,
поменяем местами вторую и третью строки:
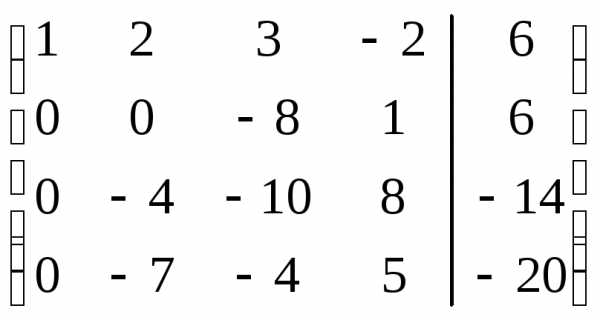

 .
.
Шаг
2.
Так как теперь 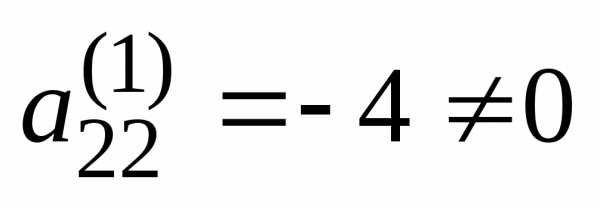 ,
то умножая вторую строку на (-7/4) и
прибавляя полученную строку к четвертой,
исключим переменную
,
то умножая вторую строку на (-7/4) и
прибавляя полученную строку к четвертой,
исключим переменную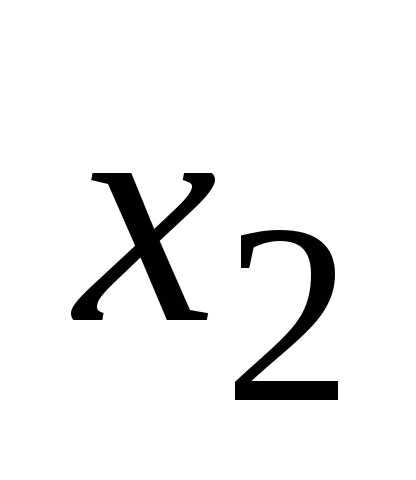 из всех строк, начиная с третьей:
из всех строк, начиная с третьей:


 .
.
Шаг 3.
Учитывая, что
,умножаем
третью строку на 13,5/8=27/16, и прибавляя
полученную строку к четвертой, исключим
из нее переменную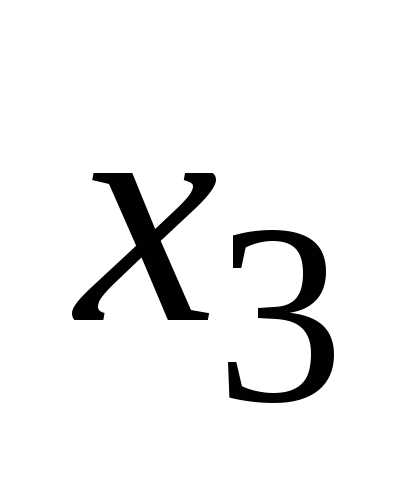 .
Получим (см. последнюю матрицу) систему
уравнений:
.
Получим (см. последнюю матрицу) систему
уравнений:
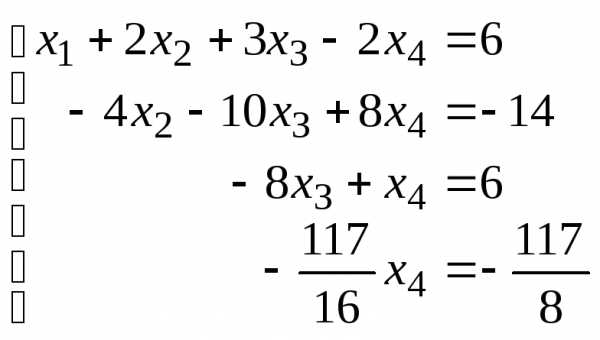 ,
,
откуда,
используя обратгный ход метода Гаусса,
найдем из четвертого уравнения 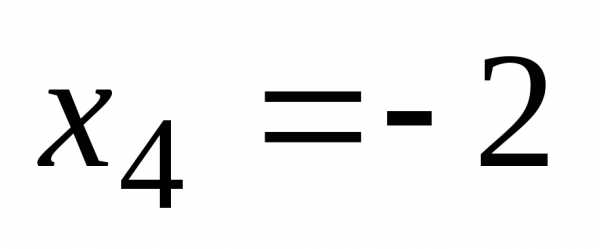 ;
из третьего;
из второгои из первого уравнения,
то есть решение системы (1;2;-1;-2).
;
из третьего;
из второгои из первого уравнения,
то есть решение системы (1;2;-1;-2).
studfiles.net
Вычисление определителя методом Гаусса
Вычислим определитель методом Гаусса.
Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.
Идея метода состоит в следующем: пусть дан определитель третьего порядка
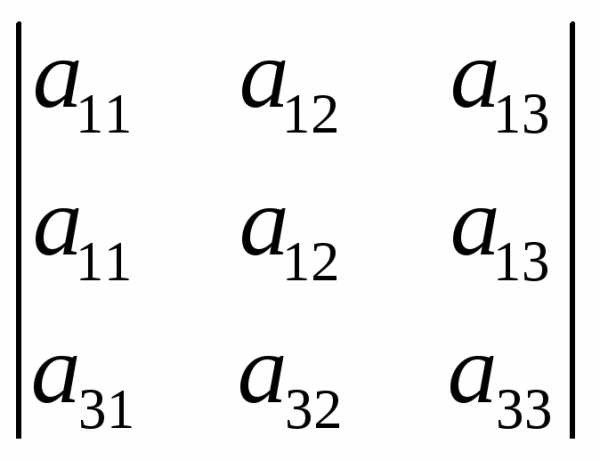 (1)
(1)
элемент должен быть равен
должен быть равен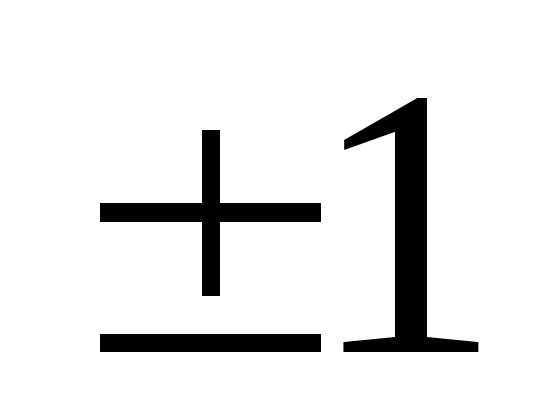 ,
для этого первую строку разделим на
,
для этого первую строку разделим на .
.
Получим определитель вида  (2)
(2)
Обнулим элементы, стоящие в первом
столбце, кроме первого. Для этого из
второй строки вычтем первую, умноженную
на 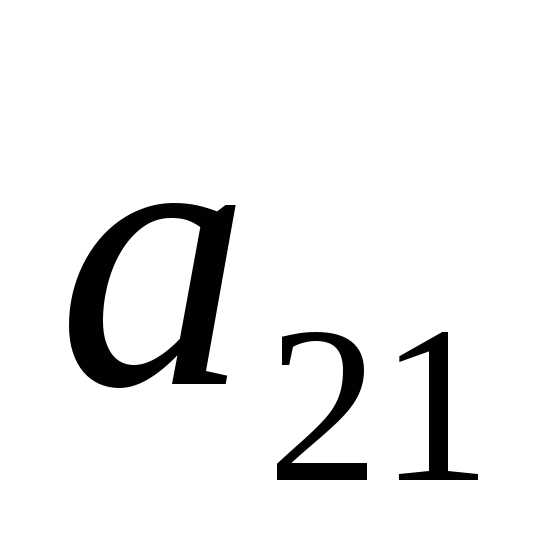 ,
далее из третьей строки вычтем первую,
умноженную на
,
далее из третьей строки вычтем первую,
умноженную на .
Получим определитель вида
.
Получим определитель вида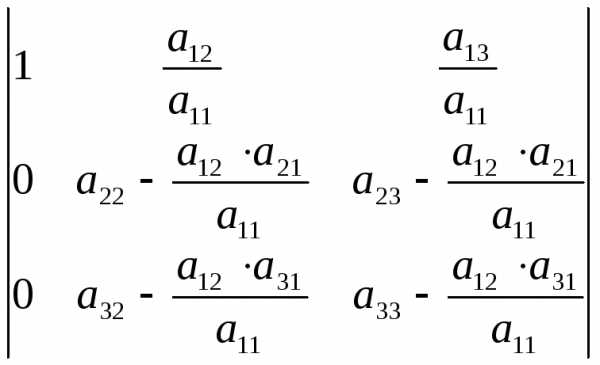 .
.
Обозначим его элементы буквой с, тогда
 (3)
(3)
Теперь надо обнулить элемент  .
Элемент
.
Элемент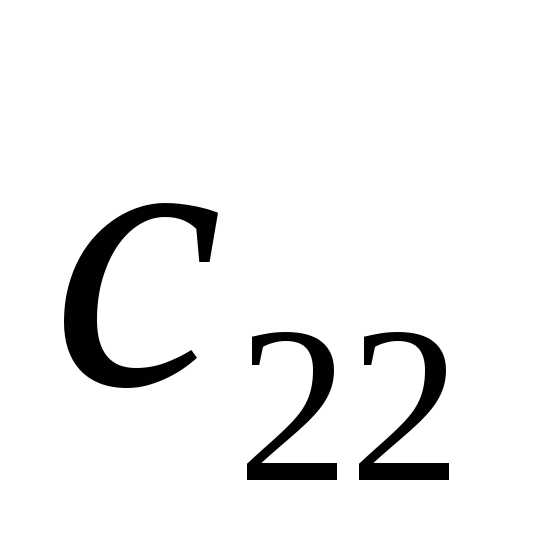 должен быть равен
должен быть равен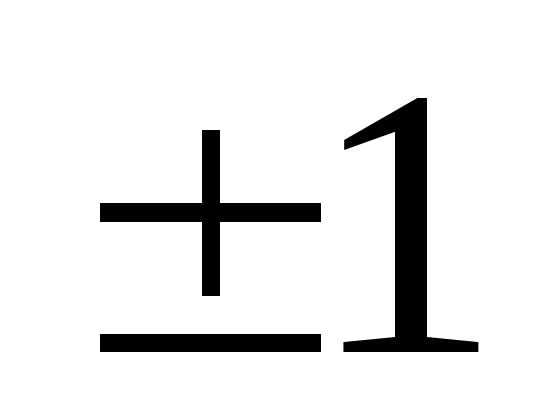 ,
для этого вторую строку разделим на
,
для этого вторую строку разделим на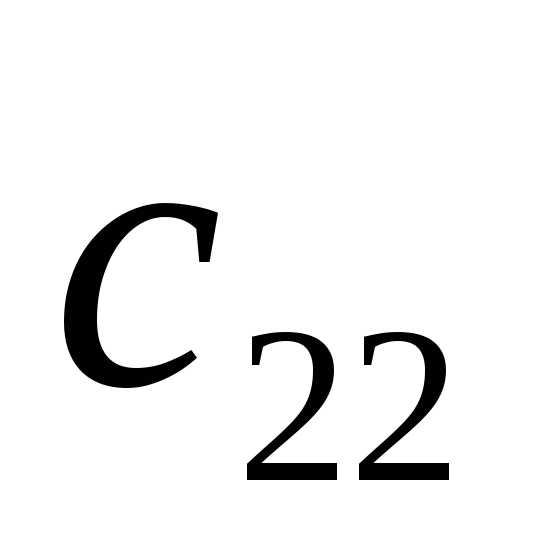 .
Получим определитель вида
.
Получим определитель вида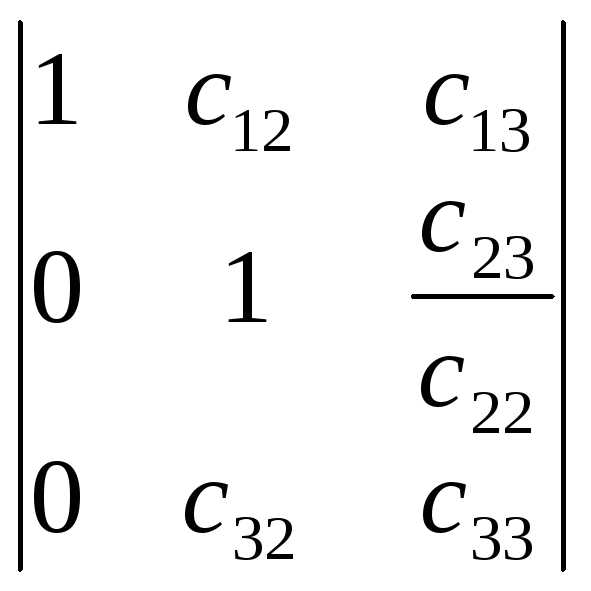 .
.
Далее из третьей строки вычтем вторую,
умноженную на  .
.
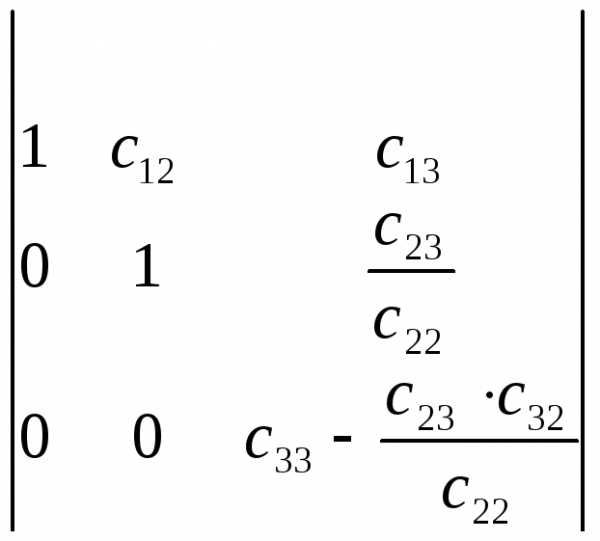 .
.
Обозначим его элементы буквой t, тогда
 (4)
(4)
Вот мы привели определитель к треугольному виду, теперь он равен .
Разберем теперь это на конкретном примере.
Пример 4:Вычислить определитель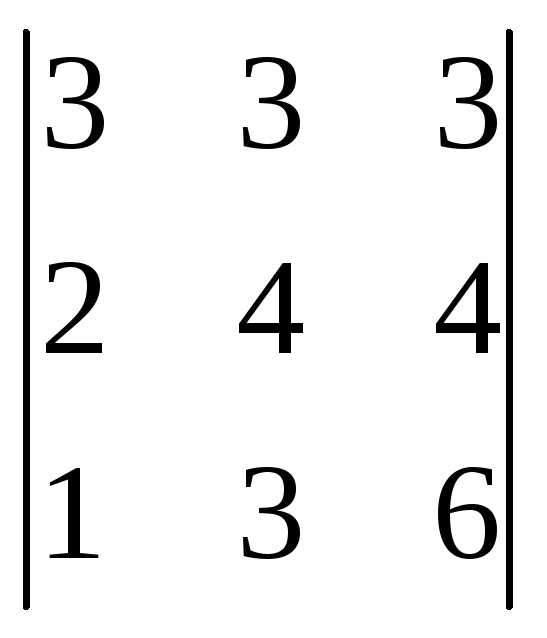 методом Гаусса.
методом Гаусса.
Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).
Получили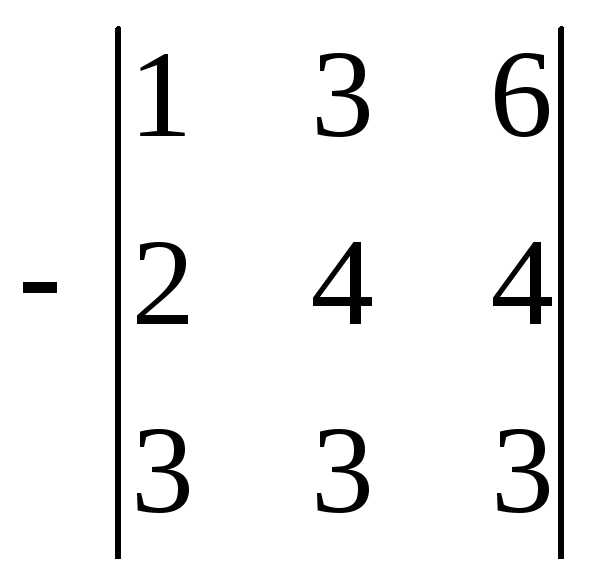
Из второй строки вычтем первую, умноженную
на 2, далее из третьей строки вычтем
первую, умноженную на 3. Получили 
Далее из третьей строки вычтем вторую, умноженную на 3.
Получили — 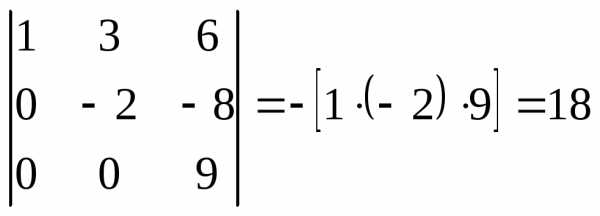
§2.Матрицы Виды матриц
Определение 7: Если в матрицеmстрок иnстолбцов, то она
называетсяразмерностьюm nи пишут
nи пишут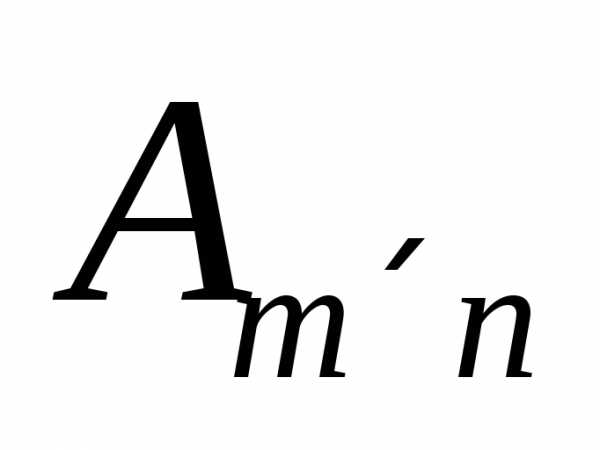 .
.
Определение 8: Если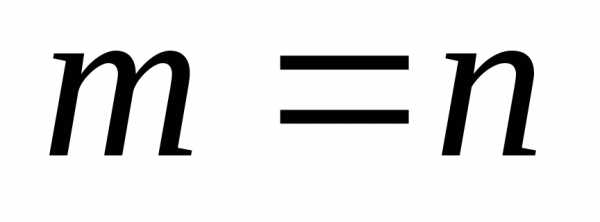 ,
то матрица называется квадратной.
,
то матрица называется квадратной.
Определение 9:Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).
Определение 10:Матрица, состоящая из нулей, называется нулевой матрицей.
Определение 11:Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.
Определение 12:Единичной матрицей называется диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице.
Определение 13:Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.
Действиянад матрицами.
Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.
Пример 5:
Матрицы А и В равны, т.е. 
Определение 15: Суммой (разностью) матриц А и В называется такая матрица С, у которой каждый элемент равен.
Пример 6: Найти матрицу, если
Решение:
Cвойства сложения
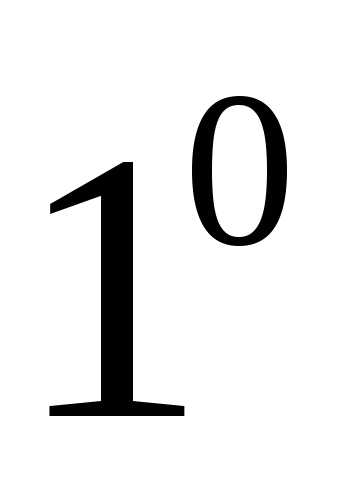 А+В=В+А(переместительное)
А+В=В+А(переместительное)
20А+О=А, где О-нулевая матрица
30 А+(В+С)=(А+В)+С (дистрибутивное)
40А+(-А)=О, где – А противоположная матрица
(т.е. элементы имеют противоположные знаки)
Определение 16: Произведением матрицы
А на число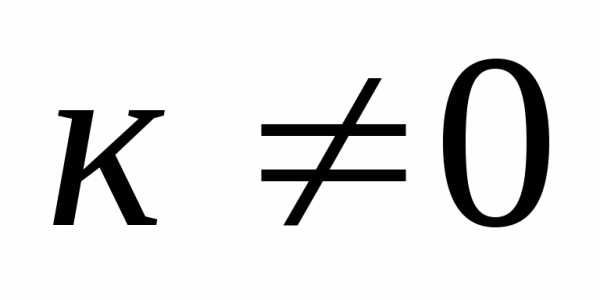 называется матрица, полученная из
данной умножением всех ее элементов на
число
называется матрица, полученная из
данной умножением всех ее элементов на
число .
.
Пример 7:
Умножение матиц
Это действие распространяется на так называемые согласованные матрицы.
Определение 17: Матрица А называется согласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.
Пример 8: и
и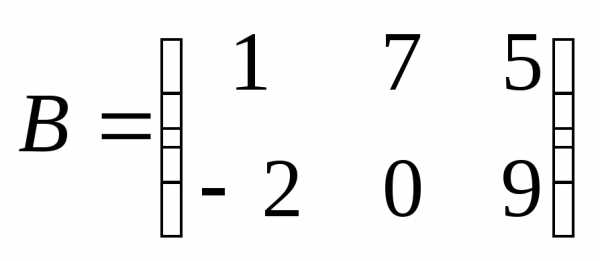 — согласованные
— согласованные
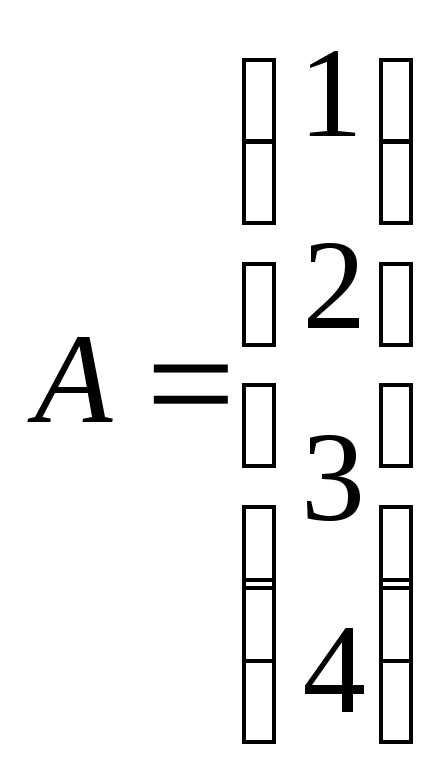 и- несогласованные
и- несогласованные
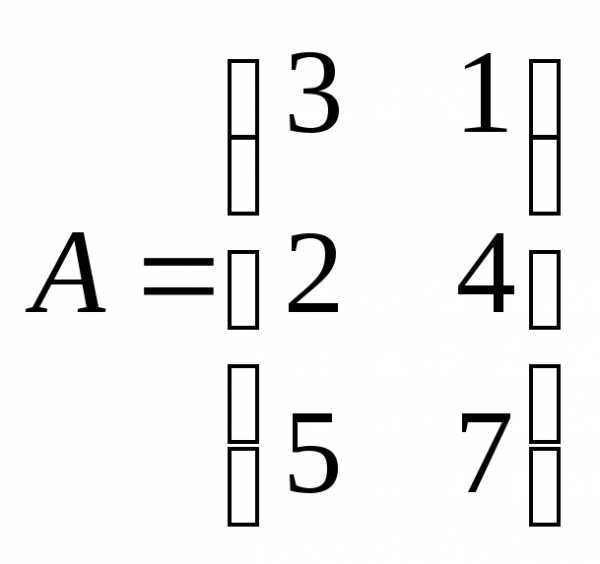 и
и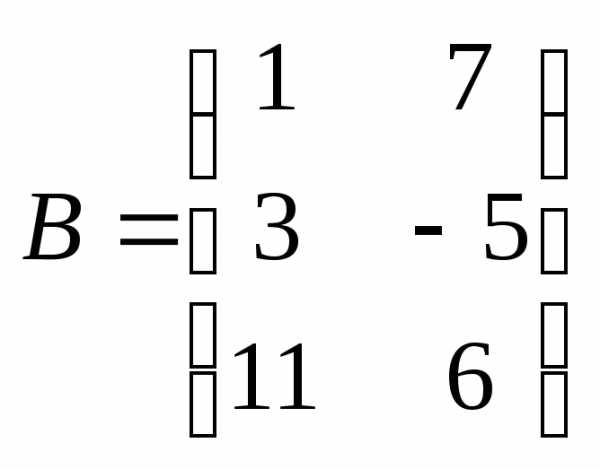 несогласованные
несогласованные
Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.
Если матрица А имеет размерность 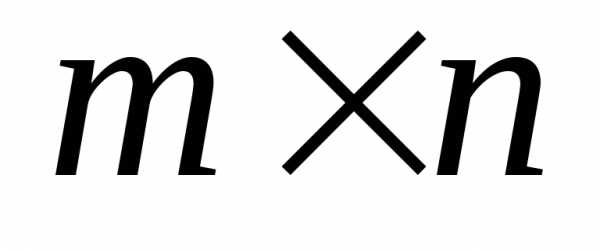 ,
а матрица В
,
а матрица В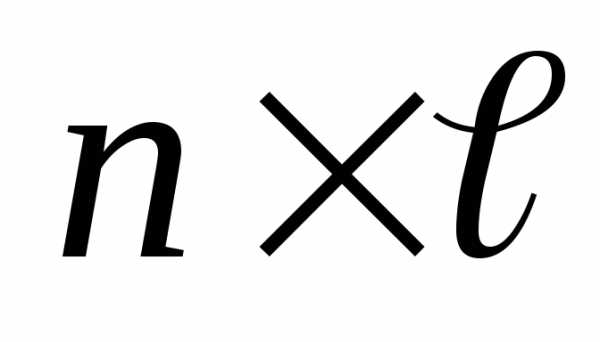 ,
то.
,
то.
Пример 9: Умножить матрицы

studfiles.net

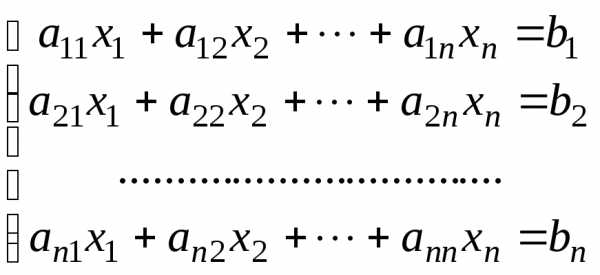
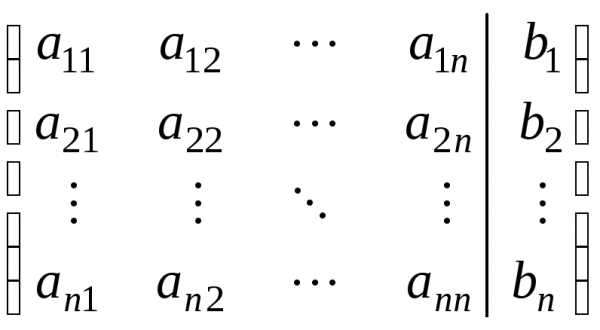
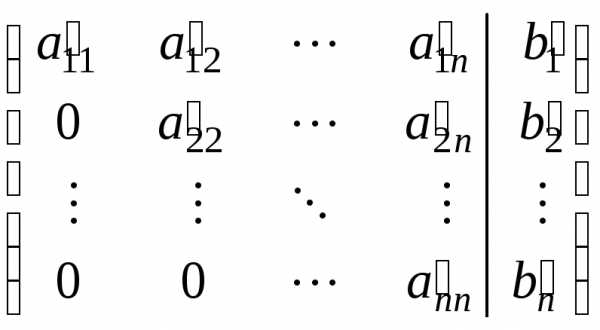
 :
: — система имеет одно решение, можно
применить теорему Крамера
— система имеет одно решение, можно
применить теорему Крамера :
: