Параллельность прямых как определить: Ошибка 403 — доступ запрещён

Параллельные прямые: что это, признаки, доказательство

Содержание:

• Что такое параллельные прямые в пространстве
  • Обозначение параллельных прямых
• Теорема о параллельных прямых, формулировка
• Типы углов при параллельных прямых
  • Односторонние
  • Соответственные
  • Накрест лежащие
• Условия параллельности
  • Накрест лежащие углы равны
  • Соответственные углы равны
  • Сумма односторонних углов равна 180 градусов
  • Если обе прямые параллельны третьей
  • В трехмерном пространстве прямые, параллельные третьей, параллельны друг с другом
  • Две прямые, перпендикулярные третьей, параллельны
• Доказательство параллельности прямых
• Уравнение параллельной прямой

Содержание

• Что такое параллельные прямые в пространстве
  • Обозначение параллельных прямых
• Теорема о параллельных прямых, формулировка
• Типы углов при параллельных прямых
  • Односторонние
  • Соответственные
  • Накрест лежащие
• Условия параллельности
  • Накрест лежащие углы равны
  • Соответственные углы равны
  • Сумма односторонних углов равна 180 градусов
  • Если обе прямые параллельны третьей
  • В трехмерном пространстве прямые, параллельные третьей, параллельны друг с другом
  • Две прямые, перпендикулярные третьей, параллельны
• Доказательство параллельности прямых
• Уравнение параллельной прямой

Что такое параллельные прямые в пространстве

Прямые в пространстве могут быть параллельны, пересекаться или скрещиваться. Мы рассмотрим первое свойство.

Впервые теорию о параллельности научно обосновал греческий ученый Евклид в своей работе под названием  «Начала».

Определение

Параллельные прямые в пространстве — прямые, лежащие в одной плоскости и не имеющие пересечений друг с другом.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

 

Обозначение параллельных прямых

Сами прямые обозначаются латинскими буквами. Например, l и k. Параллельность обозначается символом: ||

Теорема о параллельных прямых, формулировка

Теорема

Если любая точка в пространстве не расположена на рассматриваемой прямой, то через нее проводима лишь одна прямая, которая будет параллельна рассматриваемой.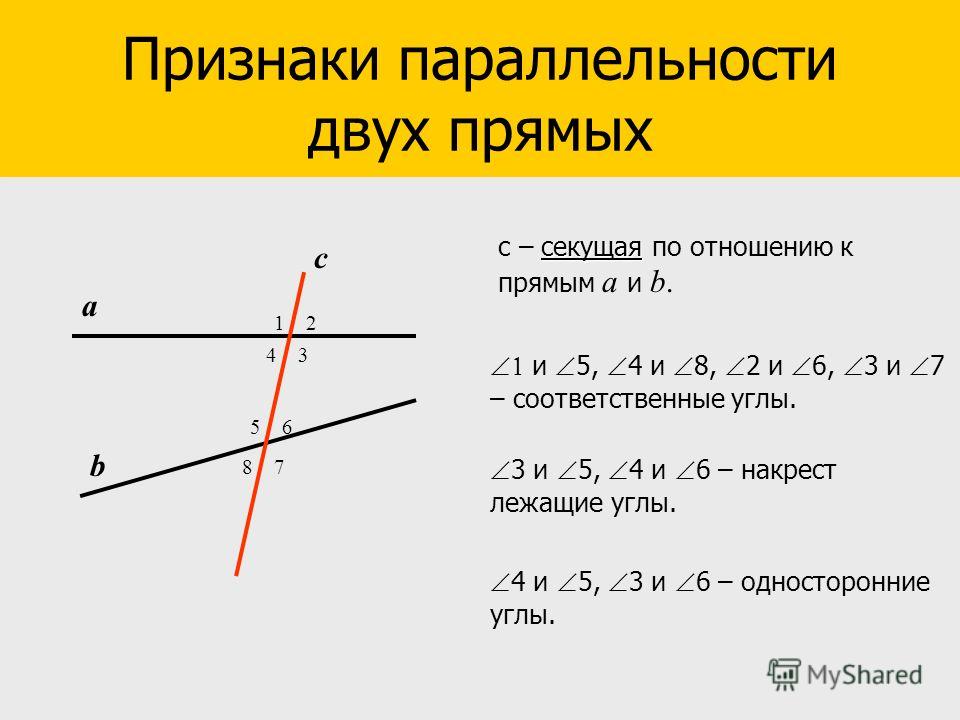

Доказательства закона представим в заключительном разделе статьи.

 

Типы углов при параллельных прямых

Когда прямая пересекает две другие параллельные друг другу прямые, образуется восемь углов. В геометрии они имеют свои названия и свойства. Для дальнейшего разбора темы этой статьи достаточно разобраться в трех видах. Далее при рассмотрении каждого вида в отдельности ориентируйтесь на рисунок ниже:

 

Односторонние

 На рисунке выше это ∠1 и ∠6, а также ∠4 и ∠7. Они расположены с одной стороны относительно прямых.

Соответственные

Углы 2 и 6, 3 и 7, 1 и 5, 4 и 8. Их расположения отличается тем, что они как бы разделены между собой одной из прямых.

Накрест лежащие

На данном рисунке это ∠3 и ∠5, ∠2 и ∠8, ∠1 и ∠7, ∠4 и ∠6. Их расположение легко запомнить, так как они размещаются по принципу «крест-накрест».

Условия параллельности

Чтобы доказать параллельность прямых, нужно знать признаки, по которым она определяется. Достаточно соблюдения хотя бы одного из нижеследующих условий.

Накрест лежащие углы равны

 

Дано:  \(a\;\vert\vert b\), AB является секущей, углы 1 и 2 — накрест лежащими.

Доказать: равенство ∠1 и ∠2.

Доказательство: допустим, что ∠1 и ∠2 не равные. Тогда проведем угол PAB, причем он будет накрестлежащим с ∠2.

 

Накрест лежащие углы равны. Из этого следует, что AP \(\vert\vert\) b. Но это невозможно, потому что через точку a может проходить только одна прямая, согласно аксиоме, а у нас получилось две — b и A. Поэтому наше предположение неправильное и ∠1=∠2. Ч.т.д.

Соответственные углы равны

 

∠1 и ∠2 являются соответственными.

Задача

 

MN \(\vert\vert\) AD. Доказать, что\( \angle NMC=\angle BAD\).

Решение: \(\angle NMC=\angle DAC\) (как соотв.), а \(\angle DAC=\angle BAD\) (AD — биссектриса). Следовательно, \(\angle NMC=\angle BAD\).

Сумма односторонних углов равна 180 градусов

 

Сумма ∠1 и ∠2 равна 180º

Доказательство:

a \(\vert\vert\) b, поэтому ∠1=∠3 (соотв. ). ∠2+∠3=180º (смеж.). Поэтому при сложении получаем 180º.

Если обе прямые параллельны третьей

 

Этот признак называют также теоремой о трех параллельных прямых на плоскости. Если a \(\vert\vert\) b и c \(\vert\vert\) b, то a \(\vert\vert\) c.

Доказательство

Есть a \(\vert\vert\) b. Допустим, что существует еще c \(\vert\vert\) a. Согласно условию, a не пересекает b и наоборот.

В трехмерном пространстве прямые, параллельные третьей, параллельны друг с другом

Здесь то же самое, что в предыдущем пункте: в случае, когда a и c ||, а b и c также ||, то a и b тоже ||.

Две прямые, перпендикулярные третьей, параллельны

 

Обозначение перпендикулярных прямых: ⊥

На картинке видно, что a \(\perp\) c и b \(\perp\) c. Отсюда, согласно этому признаку-теореме, следует, что a \(\vert\vert\) b.

Доказательство

Допустим, что a \(\perp\) c и b \(\perp\) c, но a не \(\vert\vert\;\)b.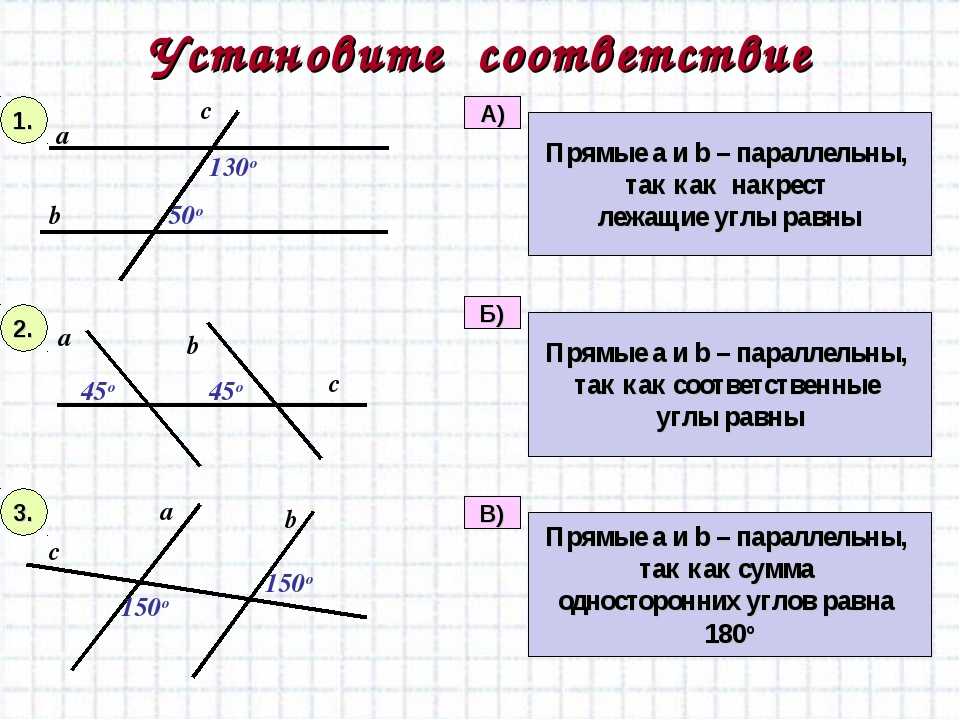 Тогда a и b пересекаются в какой-то точке. Рассмотрим треугольник ABC. Сумма его углов будет равна 180º+∠C. Но так быть не может. Значит, наше предположение неверно, и a \(\vert\vert\) b.

Доказательство параллельности прямых

Ниже представлено доказательство теоремы из первого раздела статьи.

 

1. Есть a (прямая) и М (точка, далее — т.). Она не принадлежит a. Через них проходит плоскость альфа (\(\alpha\)). Известно, она единственная.Прямая b проходит через т.М и \(\vert\vert\;\) а. Она существует, что доказывает аксиома о \(\;\vert\vert.\)
2. Предположим, что существует прямая с, которая тоже проходит через т.М, причем c \(\vert\vert\) a. В этом случае потребуется другая плоскость \(\beta\), такая, чтобы прошла через т.М. Такое невозможно, потому что есть теорема, которая говорит, что плоскость только одна. Значит это одна и та же плоскость (\(\alpha\) совпала с \(\beta\)) и одна и та же прямая (b совпал с c). Единственность прямой доказана.

Теорема доказана.

Уравнение параллельной прямой

Если известно, что прямая проходит через какую-то точку с координатами и параллельна другой прямой y=kx+a, то ее уравнение можно найти по формуле:

\(\gamma-\gamma_0=\kappa\left(\chi-\chi_0\right)\)

где k —  угловой коэффициент.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 3)

Выделите текст и нажмите одновременно клавиши

«Ctrl» и «Enter»

Поиск по содержимому

Прямая. Параллельные и перпендикулярные прямые.

Определение

Линия, которую изображают на плоскости при помощи линейки, причем, эта линия не должна быть ограничена точкой ни с одной стороны, называют прямой. Другими словами, прямая не имеет ни начала, ни конца.

Обозначения прямой

Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки).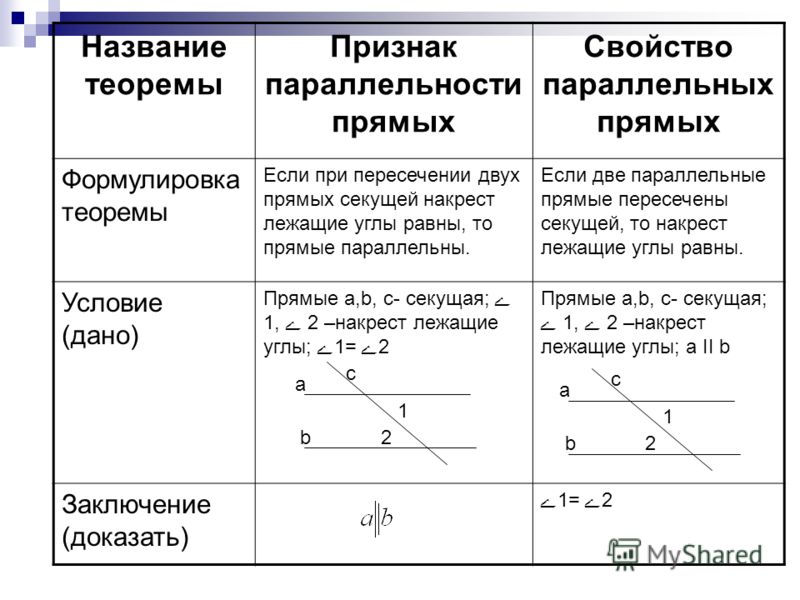 Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.

Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.

Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а∩b=А, где ∩ – это знак «пересечение».

Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | – знак параллельности.

Признаки параллельности прямых

Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют – секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.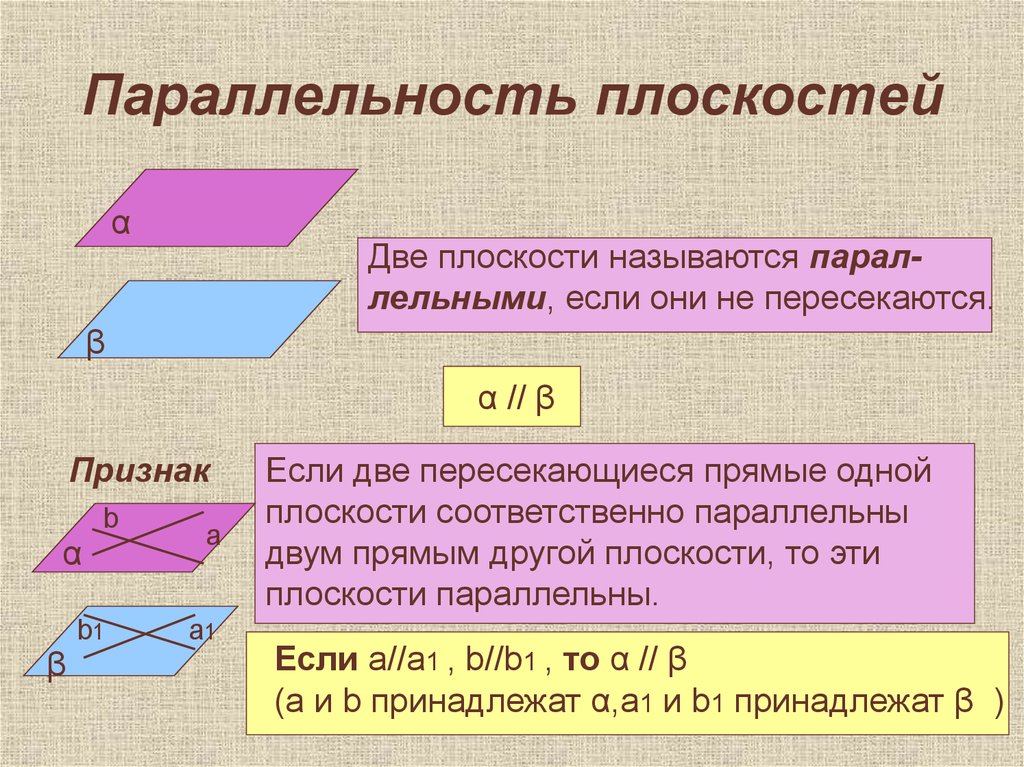

Необходимо запомнить названия следующих углов:

1. накрест лежащие углы: 4 и 5; 3 и 6;
2. односторонние углы: 4 и 6; 3 и 5;
3. соответственные углы: 1 и 5; 3 и 7; 2 и 6; 4 и 8.

С данными углами связаны следующие признаки параллельности прямых:

1. если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
2. если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
3. если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180⁰, то прямые параллельны.

Аксиома параллельных прямых

Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.

Аксиома №1

Через любые две точки на плоскости проходит прямая и притом только одна.

Аксиома №2Через точку, не лежащую на данной прямой, можно провести только одну прямую параллельную данной.

Следствия из аксиом параллельных прямых

• Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

На данном рисунке видно, что а и b параллельные прямые, с – секущая, она пересекает прямую а в точке А, значит и будет пересекать прямую b в некоторой точке С.

• Если две прямые параллельны третьей, то они параллельны.

По данному рисунку видно, что если прямая CD параллельна АВ и прямая MN параллельна АВ, то CD и MN тоже будут параллельны.

Перпендикулярные прямые

Определение

Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а⊥b, где «⊥» – знак перпендикулярности. Заметим, что две прямые, перпендикулярные к третьей, не пересекаются. На данном рисунке а⟂с, b⟂c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.

Даниил Романович | Просмотров: 3.4k

Как найти уравнение параллельной прямой

Все ресурсы по алгебре 1

10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

Алгебра 1 Помощь » Функции и линии » Уравнения прямых » Параллельные линии » Как найти уравнение параллельной прямой

Найти прямую, параллельную

Возможные ответы:

Правильный ответ:

Объяснение:

В этом случае параллельная линия будет иметь то же значение, что и исходная линия, но пересечет ее в другом месте.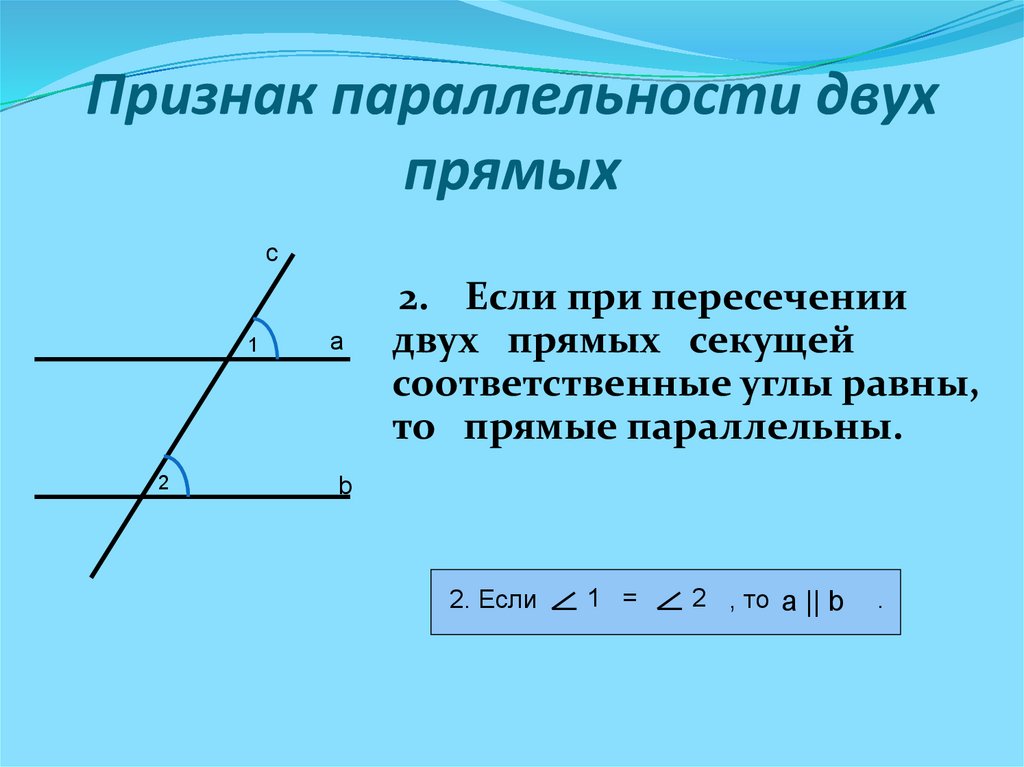

Сообщить об ошибке

Какие из следующих прямых параллельны прямой, определяемой уравнением:

Возможные ответы:

Правильный ответ:

Объяснение:

Параллельность означает одинаковый наклон:

Решите для:

Найдите линейное уравнение, где

.

 

Сообщить об ошибке

Каково уравнение прямой, параллельной  , которая проходит через (1,1)?

Возможные ответы:

Правильный ответ:

Объяснение:

Линия, параллельная , будет иметь такой же наклон.

Уравнение для нашей параллельной прямой будет таким:  .

Используя точку (1,1), мы можем найти точку пересечения с осью Y:

Сообщить об ошибке

Какая из этих прямых параллельна ?

Возможные ответы:

Правильный ответ:

Объяснение:

Параллельные линии имеют одинаковый наклон. Если вы преобразуете данное уравнение в форму , оно станет

Наклон этого уравнения равен , поэтому его параллельная линия также должна иметь наклон . Единственная другая линия с наклоном в размере

Отчет о ошибке

Какая из этих строк параллельна

Возможные ответы:

. правильный.

Правильный ответ:

Пояснение:

Параллельные прямые имеют одинаковый наклон. Чтобы определить наклон данной линии, преобразуйте ее в форму:

2y = 3x + 8

Эта линия имеет наклон .

Единственный вариант ответа с наклоном  – .

Сообщить об ошибке

Выберите, какое из четырех перечисленных уравнений параллельно данному уравнению.

Возможные ответы:

Правильный ответ:

Объяснение:

 является правильным ответом, потому что, когда каждый член делится на 2, чтобы увидеть уравнение с точки зрения y, наклон уравнения равен  , что совпадает с наклоном в данном уравнении.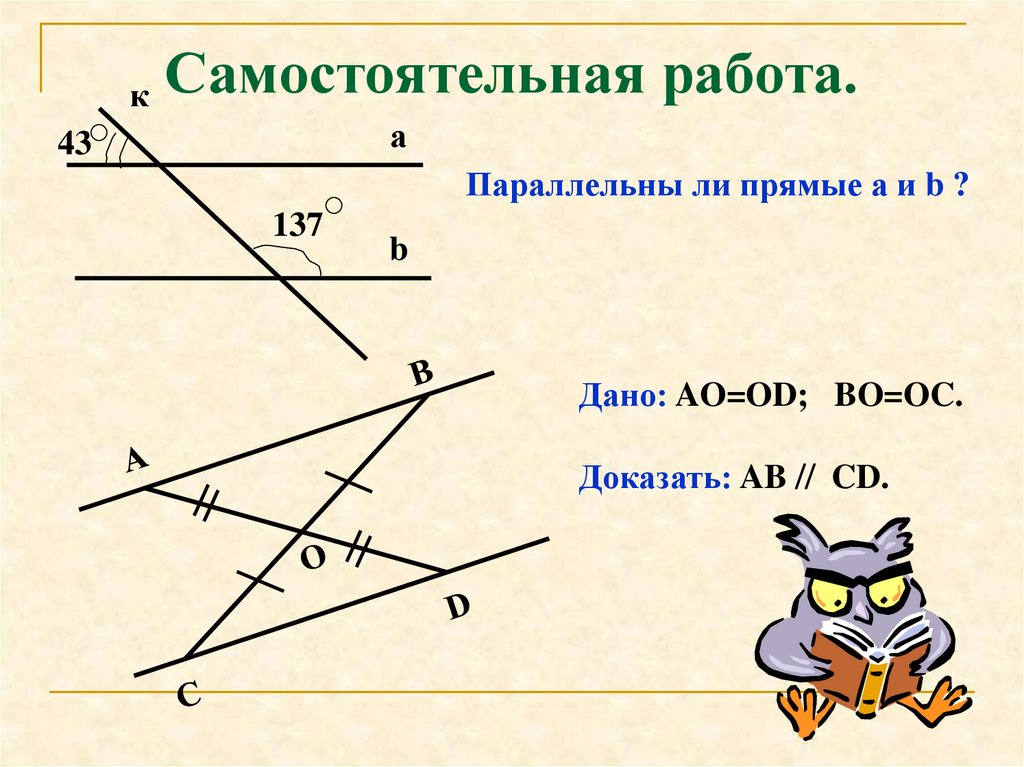 Параллельные прямые имеют одинаковый наклон.

Сообщить об ошибке

Напишите уравнение для прямой, параллельной  и пересекающей ось Y.

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение прямой может быть записано с использованием выражения, где                                               . Когда линии параллельны друг другу, это означает, что они имеют одинаковый наклон, поэтому . Y-пересечение задается в задаче как . Это означает, что уравнение будет .

Сообщить об ошибке

Напишите уравнение прямой, параллельной проходящей через точку.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы подойти к этой задаче, мы должны быть знакомы с уравнением пересечения наклона линии, где m — это наклон, а b — это пересечение с осью y. Линия, которой должна быть параллельна наша линия, это . Параллельные линии имеют одинаковый наклон m, поэтому наклон нашей новой линии равен . Поскольку мы еще не знаем точку пересечения по оси y, на данный момент мы запишем наше уравнение как просто:

. Мы можем найти b, используя точку, через которую, как мы знаем, проходит линия, . Мы можем подставить 4 вместо x и -2 вместо y, чтобы найти b:

сначала мы умножим, чтобы получить 1:

 теперь мы можем вычесть 1 с обеих сторон, чтобы найти b:

Теперь мы можем просто вернитесь к нашему уравнению и подставьте -3 для b:

Сообщить об ошибке

Найдите уравнение прямой, параллельной  и проходящей через точку .

Возможные ответы:

Прямая не может проходить через эту точку и быть параллельной исходной прямой.

Ни один из других ответов.

Правильный ответ:

Ни один из других ответов.

Объяснение:

Параллельные прямые имеют одинаковый наклон. Таким образом, наша линия должна иметь наклон 2x. Затем мы используем формулу наклона точки, чтобы найти уравнение прямой, которая проходит через  и параллельна .

Формула наклона точки:

 – это наклон линии, параллельной  которая проходит через .

Отчет о ошибке

Найдите уравнение линии, параллельной данным критериям: и проходит через точку

Возможные ответы:

Правильный ответ:

9005

Объяснение:

Параллельные линии имеют одинаковый наклон, поэтому наклон новой линии также будет иметь наклон

Используйте форму точка-наклон, чтобы найти уравнение новой линии.

Подставьте известные значения и решите.

Отчет о ошибке

← Предыдущий 1 2 3 Следующие →

Уведомление об авторских правах

All Algebra 1 Ресурсы

10 Тесты Диагностики. 557 практических тестов Вопрос дня Карточки Учитесь по концепции

Уравнения параллельных прямых (Видео с практическими вопросами)

Стенограмма практики

Здравствуйте! Сегодня мы рассмотрим, как найти уравнение прямой, которая проходит через заданную точку и параллельна другой прямой. Начнем с примера.

Найдите уравнение прямой, проходящей через точку \((2,-1)\) и параллельной прямой \(y=3x+4\).

Помните, параллельные линии имеют одинаковый наклон, поэтому нам нужно начать с определения наклона данной нам линии. Строка нам дана в наклон-пересечение формы , \(y=mx+b\), где \(m\) — наклон линии. Таким образом, наклон линии \(y=3x+4\) равен 3.

\(m=3\)

 

Теперь, когда мы знаем наклон линии и точку, через которую проходит линия \((2,-1)\), мы можем подставить эти значения либо в наше общее уравнение наклон-пересечение, либо в наше общее уравнение точка-наклон.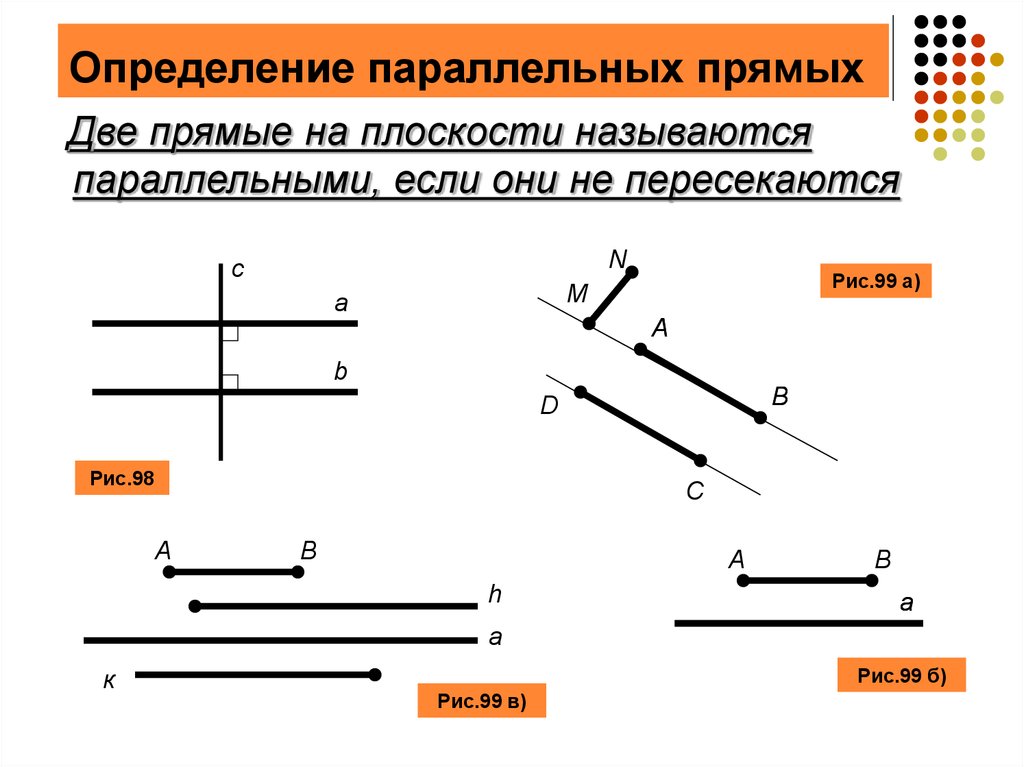 В этом примере мы будем использовать уравнение пересечения наклона.

\(y=mx+b\)

 

Мы знаем наше значение \(m\) и знаем значения \(x\) и \(y\), которые делают это уравнение верным (поскольку линия проходит через них), поэтому мы можем подставить эти три значения в и решить для \(b\).

\(-1=3(2)+b\)

 

Сначала умножьте.

\(-1=6+b\)

 

Затем вычтите 6 с обеих сторон.

\(-7=b\)

 

Теперь, когда мы знаем, что такое \(b\), мы можем использовать наши значения для \(m\) и \(b\), чтобы составить уравнение для наша линия. Наша линия в форме пересечения наклона:

\(y=3x+(-7)\)

 

Это упрощает до:

\(y=3x-7\)

 

900! Уравнение прямой, проходящей через точку \((2,-1)\) и параллельной прямой \(y=3x+4\), равно \(y=3x-7\).

Давайте попробуем другой пример.

Найдите уравнение прямой, проходящей через точку \((4,6)\) и параллельной прямой \(y=-2x-1\).

Сначала найдите наклон новой линии. Поскольку параллельные наклоны одинаковы, наклон нашей новой линии также равен \(-2\).

\(m=-2\)

 

В этом примере мы собираемся найти наше уравнение, подставив наш наклон и точку в уравнение точка-наклон.

\(y-y_{1}=m(x-x_{1})\)

 

Помните, поскольку эта форма создана, чтобы сообщить вам конкретную точку на линии, мы вставим точка \((4,6)\) для \((x_{1},y_{1})\) вместо \((x,y)\), как в последнем примере. Подставим известные нам значения.

\(y-6=-2(x-4)\)

 

Теперь, если мы хотим получить ответ в виде точек и наклонов, мы можем остановиться здесь. Если мы хотим, чтобы это было в форме пересечения наклона, нам просто нужно немного изменить порядок. Сначала распределите по правой стороне, а затем переместите \(-6\) на правую сторону.

\(y-6=-2x+8\)
 
\(y=-2x+14\)

 

Итак, наш ответ: \(y=-2x+14\). Это прямая, параллельная прямой \(y=-2x-1\) и проходящая через точку \((4,6)\).

Прежде чем идти, попробуем вместе еще один пример.

Найдите уравнение прямой, проходящей через точку \((-3,8)\) и параллельной прямой \(y=7x-16\).

Сначала определите наклон новой линии. Он будет таким же, как наклон данной линии, поэтому наклон равен 7.

\(m=7\)

 

Затем подставьте свой наклон либо в уравнение пересечения наклона, либо в точку -уравнение наклона. В этом примере мы рассмотрим оба способа, начиная с уравнения пересечения наклона. Во-первых, напишите уравнение пересечения наклона.

\(y=mx+b\)

 

Затем мы подставим наши значения для \(m\), \(x\) и \(y\).

\(8=7(-3)+b\)

 

Итак, чтобы решить, мы начнем с умножения 7 и \(-3\).

\(8=-21+b\)

 

Затем прибавляем 21 к обеим сторонам.

\(29=b\)

Теперь, когда мы знаем наше значение для \(b\), подставим его в уравнение пересечения наклона вместе со значением для \(m\). Итак, наше окончательное уравнение:

\(y=7x+29\)

 

Если бы мы вместо этого использовали уравнение точка-наклон, мы бы получили тот же ответ.

\(y-y_{1}=m(x-x_{1})\)

 

Подставьте значения для \(m\), \(x_{1}\) и \ (у_{1}\).

\(y-8=7(x-(-3))\)

 

Если упростить вычитание отрицательной части, то получим:

\(y-8=7(x+ 3)\)

 

Теперь мы можем распределить и изменить порядок, чтобы преобразовать наше уравнение в форму пересечения наклона.

\(y-8=7x+21\)
 
\(y=7x+29\)

 

Конечно, это то же самое уравнение, которое мы получили раньше, поэтому мы знаем, что наш ответ правильный любой способ, который мы выбираем для решения этой проблемы.

Я надеюсь, что это видео было полезным. Спасибо за просмотр и удачной учебы!

Вопрос №1:

 
Найдите уравнение прямой, содержащей точку \((3,-5)\) и параллельной прямой \(y=2x+1\).

\(y=-2x+1\)

\(y=2x-11\)

\(y=x-8\)

\(y=-x+1\)

Показать ответ

Ответ:

Прямые параллельны, если они имеют одинаковый наклон. Данная линия имеет вид \(y=mx+b\), где \(m\) — наклон, а \(b\) — \(y\)-отрезок. Для данной линии наклон равен \(m=2\), поэтому наклон параллельной линии также равен \(m=2\).

Мы можем подставить заданную точку и наклон в форму пересечения наклона линии, чтобы найти уравнение для линии, содержащей точку \((3,-5)\). Подставьте значения в форму пересечения наклона, затем найдите \(b\).

\(y=mx+b\)
\(-5=2(3)+b\)
\(-5=6+b\)
\(-5-6=6+b-6 \)
\(-11=b\)

Подставить \(b=-11\) и \(m=2\) в форму пересечения наклона линии, уравнение линии, содержащей точку \( (3,-5)\) равно:

\(y=mx+b\)
\(y=(2)x+(-11)\)
\(y=2x-11\)

Скрыть Ответ

Вопрос №2:

 
Найдите уравнение прямой, содержащей точку \((2,11)\) и параллельной прямой \(y=3x-10\).

\(y=-10x+33\)

\(y=10x-9\)

\(y=-3x+17\)

\(y=3x+5\)

Показать ответ

Ответ:

Прямые параллельны, если они имеют одинаковый наклон. Данная линия имеет вид \(y=mx+b\), где \(m\) — наклон, а \(b\) — \(y\)-отрезок. Для данной линии наклон равен \(m=3\), поэтому наклон параллельной линии также равен \(m=3\).

Мы можем подставить заданную точку и наклон в форму пересечения наклона линии, чтобы найти уравнение для линии, содержащей точку \((2,11)\). Подставьте значения в форму пересечения наклона, затем найдите \(b\).

\(y=mx+b\)
\(11=3(2)+b\)
\(11=6+b\)
\(11-6=6+b-6\)
\(5=b\)

Подставить \(b=5\) и \(m=3\) в форму пересечения наклона линии, уравнение линии, содержащей точку \((2,11) \) is:

\(y=mx+b\)
\(y=(3)x+(5)\)
\(y=3x+5\)

Скрыть ответ

Вопрос №3 :

 
Найдите уравнение прямой, содержащей точку \((7,-4)\) и параллельной прямой \(y=-3x+5\).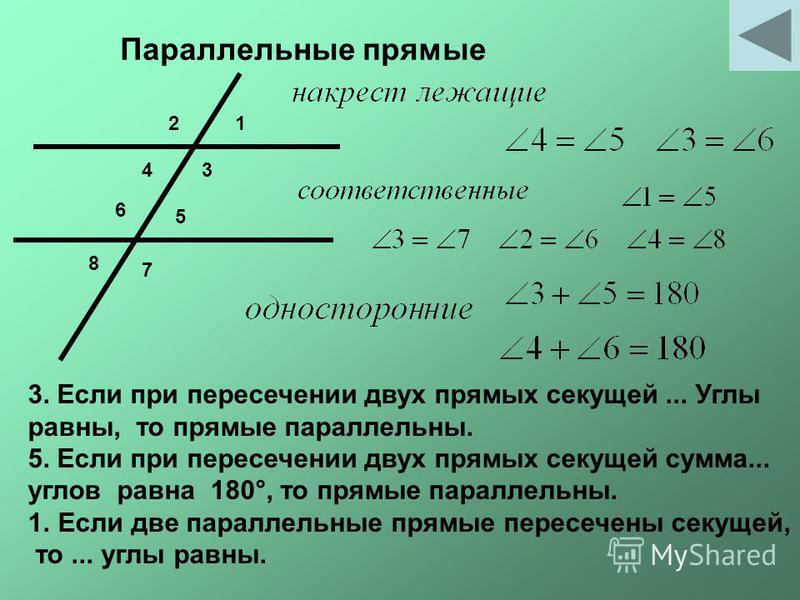

\(y=3x+17\)

\(y=-3x+17\)

\(y=3x-19\)

\(y=-3x-5\)

Показать ответ

Ответ:

Прямые параллельны, если они имеют одинаковый наклон. Данная линия имеет вид \(y=mx+b\), где \(m\) — наклон, а \(b\) — \(y\)-отрезок. Для данной линии наклон равен \(m=-3\), поэтому наклон параллельной линии также равен \(m=-3\).

Мы можем подставить данную точку и наклон в форму точки-наклона линии, чтобы найти уравнение для линии, содержащей точку \((7,-4)\). Форма точки-наклона линии:

\(y-y_1=m(x-x_1)\)

где \(m\) — наклон линии, а \((x_1,y_1)\) — точка, через которую проходит линия. Подставьте значения в форму точка-наклон и упростите.

\(y-(-4)=-3(x-7)\)
\(y+4=-3(x-7)\)

Чтобы преобразовать в форму пересечения наклона, найдите \ (у\).

\(y+4=-3(x)-3(-7)\)
\(y+4=-3x+21\)

Вычтите 4 из обеих частей уравнения.

\(у+4-4=-3х+21-4\)
\(у=-3х+17\)

В качестве альтернативы мы можем подставить \(m=-3\), \(x=7\) и \(y=-4\) в форму пересечения наклона, а затем найти \(b\).

\(y=mx+b\)
\(-4=-3(7)+b\)
\(-4=-21+b\)
\(-4+21=-21+ b+21\)
\(17=b\)

Подставьте \(b=17\) и \(m=-3\) в форму пересечения наклона прямой, и уравнение нашей прямой, содержащей точка \((7,-4)\) совпадает.

\(y=mx+b\)
\(y=-3x+17\)

Скрыть ответ

Вопрос №4:

 
Изготовление флешки стоит компании А 8 долларов. Фиксированная стоимость изготовления флешек составляет 100 долларов. Пусть \(x\) представляет количество флэш-накопителей, которые производит компания, а \(y\) представляет собой общую стоимость изготовления флэш-накопителей в долларах. Тогда общая стоимость производства флешек для компании А может быть представлена ​​линейным уравнением \(y=8x+100\). Кроме того, производство флеш-накопителей того же типа, что и компания А, обходится компании Б в 8 долларов. Если точка \((5,120)\) лежит на линии, представляющей общие затраты компании B, какое из следующих уравнений является уравнением общих затрат компании B?

\(y=8x-380\)

\(y=8x+380\)

\(y=8x+80\)

\(y=8x-80\)

Показать ответ

Ответ:

Поскольку изготовление флешки обходится компании Б в ту же цену, что и компании А, наклон уравнения прямой для общих затрат компании Б также равен \(m=8\) , делая две прямые параллельными.

Мы можем написать уравнение для общих затрат для компании B, используя форму наклона-пересечения \(y=mx+b\), где m — наклон, а \(b\) — \(y\)-отрезок . Используя точку \((5,120)\) и наклон \(m=8\), мы имеем:

\(y=mx+b\)
\(120=8(5)+b\)
\(120=40+b\)
\(120-40=40+b-40\)
\(80=b\)

Подставьте \(b=80\) и \(m=8\) в форму прямой с пересечением наклона, уравнение общих затрат для компании B:

\ (y=mx+b\)
\(y=(8)x+(80)\)
\(y=8x+80\)

Скрыть ответ

Вопрос №5:

 
Жидкий раствор нагревается со временем.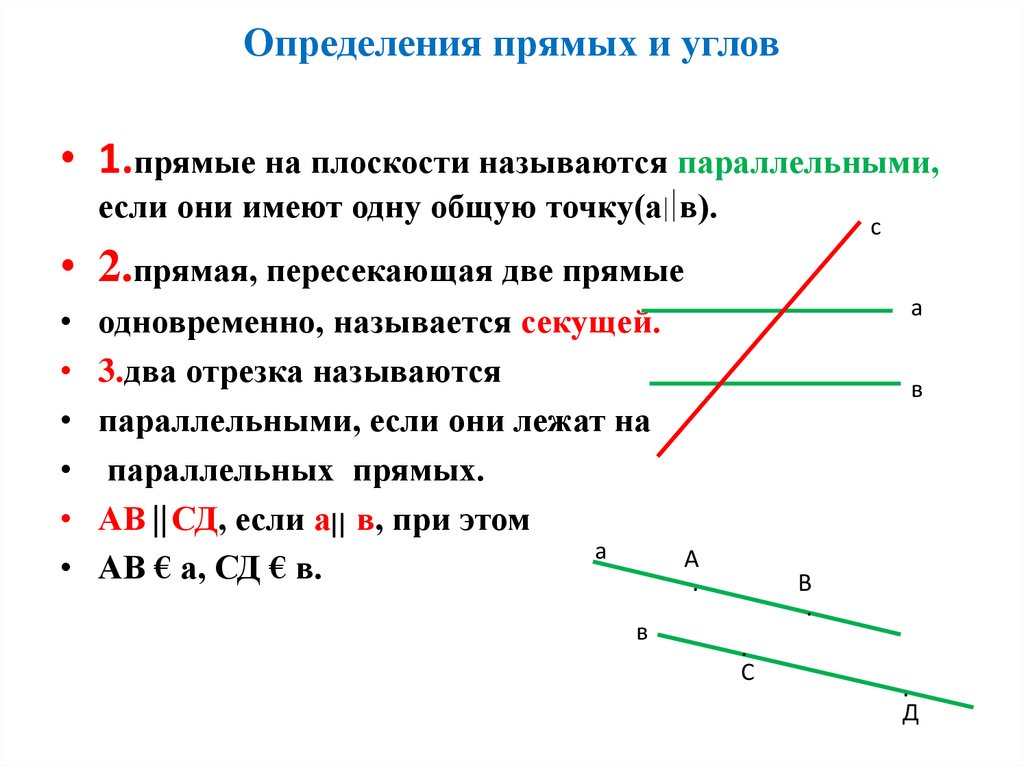 Температура раствора в градусах Цельсия при его нагревании может быть смоделирована линейным уравнением \(y=5x+20\), где \(x\) — время в минутах, а y — температура раствора. в момент времени \(х\). Линейное уравнение температуры второго жидкого раствора, нагреваемого во времени, параллельно линейному уравнению температуры первого жидкого раствора. Если через 6 минут температура составила 68 градусов, какое из следующих уравнений является уравнением линии, представляющей температуру второго раствора?

\(y=5x+38\)

\(y=-5x+38\)

\(y=5x+98\)

\(y=-5x+98\)

Показать ответ

Ответ:

Прямые параллельны, если они имеют одинаковый наклон. Данная линия имеет вид \(y=mx+b\), где m — наклон, а \(b\) — точка пересечения \(y\). Для уравнения линии, представляющей температуру первой жидкости, наклон равен \(m=5\), поэтому наклон уравнения для температуры второго жидкого раствора также равен \(m=5\).