Параллельные прямые пересекают стороны угла ahb: Уроки геометрии в задачах. 7-8 классы: [12+] [3-е изд. стер.] 9785443928180

СУНЦ УрФУ

Расписание

Электронный журнал

Поступающим

Олимпиады, турниры, конкурсы

Планы работы

Подготовительные курсы

Новости:

07.05.2023

Учимся и побеждаем!

Лицеисты заняли I и II места в Школе практического программирования.

06.05.2023

Поэзии чарующие звуки…

В СУНЦ стартует регистрация на поэтический вечер, который пройдёт 15 мая в 15:30 в актовом зале.

05.05.2023

Заключительный этап. Успех!

Наши лицеисты достойно выступили на заключительном этапе Всероссийской олимпиады школьников.

04.05.2023

Успехи на международном форуме в Кыргызстане

Лицеисты привезли из солнечного Кыргызстана золотую и бронзовую медали международного форума «Мы — интеллектуалы XXI века!».

04.05.2023

Зарядись «Энергией будущего»!

Лицеисты СУНЦ с успехом выступили на всероссийском конкурсе научно-исследовательских работ и проектов.

25.04.2023

Время зарабатывать!

Соцэки СУНЦ совершенствуют свои практические навыки.

Больше новостей

Видеогалерея:

Мужчины СУНЦ о 8 Марта (2023)

Концерт к 8 Марта (2023)

Поздравление с Днем защитника Отечества (2023)

Больше видео

О нас:

Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).

В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским  программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.

Иногородние обучающиеся проживают в уютном общежитии.

Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы.

Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону +7 343 367-82-22 и в разделе нашего сайта «Поступающим».

Как нас найти:

Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝

Проезд:

• автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
• автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
• троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
• троллейбусами № 4 до остановки «Сулимова», № 19, 32 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.

Математика. Основы геометрии: площади треугольника, параллелограмма, трапеции

<< Назад  |   Оглавление  |   Далее >>

Многоугольники

Пусть на плоскости задано n произвольных точек. И пусть они соединены отрезками таким образом, что эти отрезки образуют замкнутую цепочку.

 

Особенно нас интересует случай, когда цепочка не содержит точек самопересечений и ни одна из пар соседних отрезков не лежит на одной прямой.

 

Внутренняя часть плоскости, ограниченная такой цепочкой (включая саму цепочку), называется многоугольником, или, точнее,

n-угольником. Многоугольник обычно обозначают перечисляя его вершины. Например, многоугольник, изображенный на рисунке можно обозначить как ABCDE. Мы уже имели дело с одной разновидностью многоугольников, а именно — с параллелограммом [4.4] (и, в частности, с прямоугольником [4.8]). Поэтому нижеследующая терминология должна быть нам уже хорошо знакома.

Отрезки, служащие границей многоугольника называются его сторонами.

Концы сторон, где они соединяются друг с другом, называются вершинами многоугольника.

Внутренние углы между соседними сторонами (при вершинах) называются углами многоугольника.

Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями.

В ближайшем будущем мы будем рассматривать только такие n-угольники, у которых n равно трем или четырем. Они называются, соответственно,

треугольниками и четырехугольниками.

Площадь геометрической фигуры

Как ни странно, такое распространенное понятие, как геометрическая фигура, не имеет общепринятого четкого математического определения. Давайте договоримся, что под (плоской) фигурой мы будем понимать нечто такое, что можно начертить на листе бумаги и вырезать ножницами в виде единого куска. В частности, типичными геометрическими фигурами являются многоугольники. Всякая фигура характеризуется площадью S, которую мы определим таким образом, чтобы выполнялось соотношение

m = ρ∙S,

где m — это масса вырезанной фигуры, а ρ — поверхностная плотность бумаги. Разумеется, мы говорим о бумаге только ради определенности. С тем же успехом можно брать любой другой листовой материал. Поверхностную плотность 

ρ легко установить, если вырезать из того же материала прямоугольник со сторонами a₀ и b₀ и измерить его массу m₀. Тогда, как мы знаем,

ρ =	m0	.
	a0b0

В случае прямоугольника справедливость соотношения m₀ = ρ∙S₀, где площадь S₀ равна S₀ = a₀b₀, была уже установлена нами ранее.

Разрежем фигуру площадью S и массой m на две части.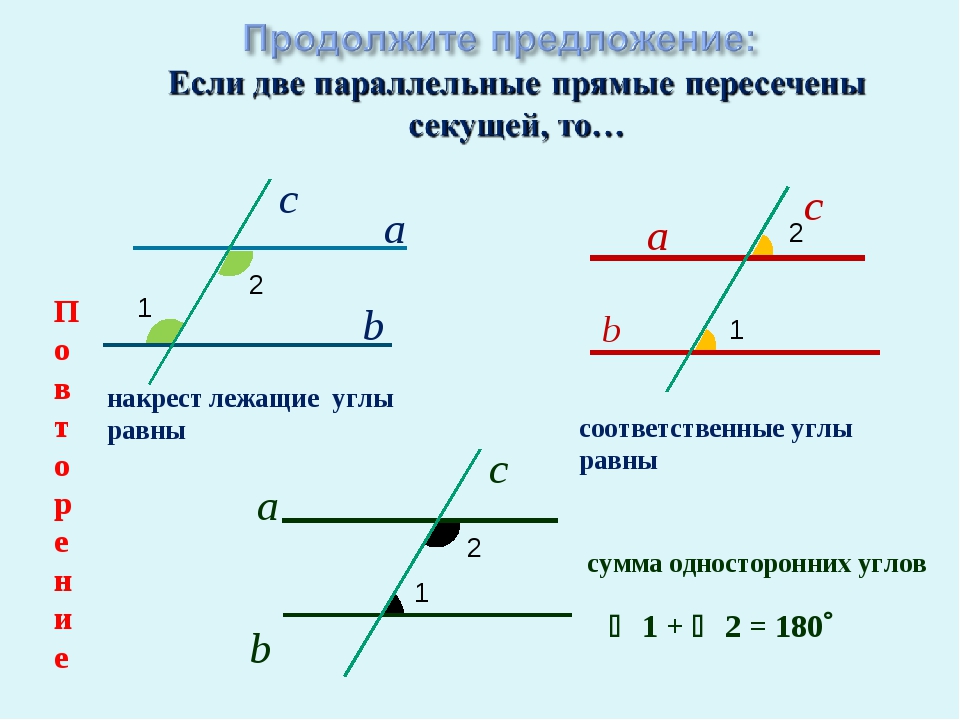

Тогда массы частей m₁ и m₂ составляют в сумме исходную массу m:

m₁ + m₂ = m.

Поделив обе части этого равенства на ρ, получаем, что площади отдельных частей S₁ и S₂ подчиняются подобному же соотношению:

S₁ + S₂ = S.

Это равенство послужит нам основой для вычисления площади треугольников, да и вообще любых других геометрических фигур.

Площадь прямоугольного треугольника

Треугольник, в котором один из углов — прямой (то есть равен 90°), называется прямоугольным. При этом стороны, примыкающие к прямому углу называются катетами, а сторона, лежащая напротив прямого угла, — гипотенузой. На чертежах прямой угол часто помечается небольшим квадратиком («носиком»), как показано на рисунке.

 

Пусть в треугольнике ABC угол при вершине C равен 90°. Проведем через вершины A и B прямые, параллельные противоположным катетам BC и AC. В результате образуется прямоугольник, выделенный на рисунке серым цветом.

 

Гипотенуза AB служит прямоугольнику диагональю, причем ее центр является центром симметрии прямоугольника [4.4]. Эта диагональ делит прямоугольник на два симметричных треугольника с одинаковыми площадями S. Взятые вместе, эти площади составляют площадь всего прямоугольника, которая, таким образом, равна 2S. Обозначим длины катетов исходного треугольника через a и b. В прямоугольнике эти катеты играют роль сторон. Следовательно, площадь прямоугольника можно найти как 2S = ab. Отсюда, площадь каждого из треугольников — в том числе, исходного треугольника 

ABC — равна

S = ½ ab.

Площадь прямоугольного треугольника равна половине произведения катетов.

Площадь произвольного треугольника

Рассмотрим произвольный треугольник АВС. Выберем одну из его сторон и назовем ее основанием. Пусть для определенности это будет сторона ВС. Обозначим ее длину через a, так что a = |BC|.

 

Из противоположной вершины A опустим перпендикуляр на прямую BC и обозначим точку его пересечения с этой прямой через H. Отрезок AH называется высотой треугольника АВС, проведенной к основанию BC. Обозначим длину этого отрезка через h: h = |AH|. Возможны два случая.

Случай 1. Точка 

H лежит на основании BC.

 

Ведем обозначения: a₁ = |BH| и a₂ = |HC|. Заметим, что a₁ + a₂ = a. Площадь S треугольника ABC найдем как сумму двух прямоугольных треугольников: темно-серого ABH и светло-серого AHC:

S = ½ a₁h + ½ a₂h = ½ (a₁ + a₂) h = ½ ah.

Случай 2. Точка H не принадлежит основанию BC. Пусть, для определенности, она лежит на прямой BC со стороны точки B.

 

Введем, как и раньше, обозначения a₁ = |BH| и a

₂ = |HC|. Длина основания на этот раз равна a = a₂ − a₁. Площадь светло-серого треугольника ABC находим как разность площадей большого «объединенного» треугольника AHC и темно-серого треугольника AHB:

S = ½ a₂h − ½ a₁h = ½ (a₂− a₁) h = ½ ah.

Таким образом, в обоих случаях мы получили для площади треугольника одну и ту же формулу:

S = ½ ah.

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.

Впрочем, оба случая можно объединить в один, если вспомнить, что мы умеем пользоваться отрицательными числами. Будем считать, что прямая, на которой лежит основание треугольника, представляет собой числовую ось 

x с нулем в точке H. Положение точек B и C на этой оси обозначим через x_B и x_C. Направление оси выберем так, чтобы выполнялось неравенство x_B < x_C. Далеко в отрицательной области отметим на оси некоторую точку H₁. Через точку A проведем прямую, параллельную оси x, а через точку H₁ — прямую, параллельную высоте AH треугольника ABC. Обозначим пересечение этих прямых через A₁.

 

Мы получили прямоугольник AA₁H₁H, площадь которого мы обозначим через S₀. При этом площадь четырехугольника AA₁H₁С равна, очевидно, S₀ + ½ x_Сh. Но нас на самом деле интересует не вся эта площадь целиком, а только ее отклонение от величины S₀. Это отклонение мы для краткости будем называть площадью треугольника AHC. Эта площадь, равная ½ x_Сh, может быть положительной или отрицательной в зависимости от знака числа x_С. Площадь S треугольника ABC может быть вычислена как разность площадей четырехугольников AA₁H₁С и AA₁H₁B:

S = (S₀ + ½ x_Сh) − (S₀ + ½ x_Bh),

или, говоря короче, как разность площадей треугольников AHС и AHB:

S = ½ x_Сh − ½ x_Bh = ½(x_С − x_B)h = ½ ah.

Как и следовало ожидать, результат получился таким же, как раньше.

Расстояние между параллельными прямыми

Рассмотрим две произвольные параллельные прямые m и n. Отметим на прямой m какую-либо точку M и опустим из нее перпендикуляр на прямую n. Обозначим точку пересечения перпендикуляра с прямой n через N.

 

Длина отрезка MN называется расстоянием между прямыми m и n. Это расстояние не зависит от положения точки M на прямой m. Действительно, возьмем на прямой m любую другую точку M₁, проведем через нее перпендикуляр к прямой n, и обозначим новую точку пересечения через N₁. У нас образовался прямоугольник NMM₁N₁, в котором отрезки MN и M₁N₁ являются противоположными сторонами, а потому их длины равны между собой.

Нетрудно также видеть, что точно такое же расстояние между прямыми мы получим, если будем измерять его не от прямой m к прямой n, а наоборот, от прямой n к прямой m.

Площадь трапеции

Трапеция — это четырехугольник, у которого какие-либо две противоположные стороны являются параллельными. Эти параллельные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Расстояние между прямыми, на которых лежат основания, носит название высоты трапеции.

 

Вычислим площадь S произвольной трапеции. Пусть a и b — длины ее оснований, а h — высота. Проведя в трапеции какую-либо диагональ, разобьем ее таким образом на два треугольника. Площади этих треугольников равны ½ ah и ½ bh, а значит площадь всей трапеции вычисляется как

S = ½ (a + b) h.

Площадь трапеции равна полусумме оснований, умноженной на высоту.

Площадь параллелограмма

Параллелограмм можно рассматривать как частный случай трапеции. Поскольку, однако, в параллелограмме имеется две пары параллельных сторон, то перед вычислением площади мы должны определиться с тем, чтó именно считать основаниями, а что — боковыми сторонами.

 

Также следует иметь в виду, что основания в параллелограмме имеют одинаковые длины, которые, таким образом, можно обозначить одной и той же буквой a. Высота h должна соответствовать выбранной паре оснований. С учетом этих оговорок, площадь S параллелограмма можно найти по формуле для площади трапеции, которая преобразуется в

S = ah.

Площадь параллелограмма равна произведению основания на высоту.

Конспект

1. Многоугольник, n-угольник: часть плоскости внутри ограниченной замкнутой несамопересекающейся цепочки из n отрезков, в которой соседние отрезки не лежат на одной прямой. Граница принадлежит многоугольнику.

2. Площадь S произвольной геометрической фигуры, которую можно вырезать из бумаги, определяется таким образом, чтобы масса m фигуры была равна m = ρ∙S, где ρ — поверхностная плотность бумаги.

3. Площадь прямоугольного треугольника равна половине произведения катетов.

4. Площадь произвольного треугольника равна половине произведения основания на высоту, проведенную к этому основанию.

5. Площадь трапеции равна полусумме оснований, умноженной на высоту.

6. Площадь параллелограмма равна произведению основания на высоту.

Искусство решения проблем

В любом треугольнике прямая Эйлера — это прямая, проходящая через ортоцентр, центр тяжести, центр описанной окружности, центр девяти точек и точку де Лоншана. Он назван в честь Леонарда Эйлера. Его существование — нетривиальный факт евклидовой геометрии. Между этими точками сохраняются определенные фиксированные порядки и отношения расстояний. В частности, и

линия Эйлера является центральной линией .

Учитывая ортогональный треугольник , линии Эйлера , и сходятся в , окружность с девятью точками .

Содержание

• 1 Доказательство, что центроид лежит на прямой Эйлера
• 2 Еще одно доказательство
• 3 Доказательство того, что центр из девяти точек лежит на прямой Эйлера
• 4 Аналитическое доказательство существования
• 5 Точки пересечения прямой Эйлера со сторонами треугольника
• 6 Углы между прямой Эйлера и сторонами треугольника
• 7 Расстояния по линии Эйлера
• 8 Положение центров Кимберлинга на линии Эйлера
• 9 Треугольники с углами или
• 10 Прямые Эйлера вписанного четырехугольника (теорема Виттаса)
• 11 Параллельные линии Эйлера и точки Ферма
• 12 Линия Эйлера треугольника Жергонна
• 13 Точка свода
• 14 точка Шиффлера
• 15 Линия Эйлера как радикальная ось
• 16 Де Лоншам-Пойнт X(20)
• 17 линия Де Лоншам
• 18 ЦЕНТР ОКРУЖНОСТИ КАСАТЕЛЬНОГО ТРЕУГОЛЬНИКА X(26)
• 19 ПЕРСПЕКТОР ОРТИЧНЫХ И КАСАТЕЛЬНЫХ ТРЕУГОЛЬНИКОВ X(25)
• 20 Эксетер пойнт Х(22)
• 21 Крайняя точка X(23)
• 22 симметричные линии
• 23 H–линия Заявление
• 24 См. также

Доказательство, что центроид лежит на прямой Эйлера

В этом доказательстве используется понятие спирального подобия, которое в данном случае представляет собой вращение с последующей гомотетией. Рассмотрим медиальный треугольник. Это похоже на . В частности, вращение вокруг средней точки с последующей гомотетией с масштабным коэффициентом в центре дает . Посмотрим, что еще будет делать это преобразование, которое мы обозначим .

Оказывается, это ортоцентр и центр тяжести . Таким образом, . Поскольку гомотетия сохраняет углы, отсюда следует, что . Наконец, как следует, что Таким образом, коллинеарны, и .

Другое доказательство

Пусть будет середина . Расширьте прошлое до такой точки, что . Мы покажем, что это ортоцентр. Рассмотрим треугольники и . Так как , и они оба имеют общий вертикальный угол, они подобны подобием SAS. Таким образом, , так лежит на высоте . Аналогично можно показать, что также лежит на высотах и ​​и ортоцентр.

Доказательство девятиточечного центра лежит на прямой Эйлера

Предполагая, что девятиточечный круг существует и это центр, обратите внимание, что гомотетия с центром в множителе переводит точки Эйлера на описанную окружность . Таким образом, он сводит девятиконечный круг к описанному кругу. Кроме того, должны быть отправлены в , таким образом и .

Аналитическое доказательство существования

Пусть центр описанной окружности представлен вектором , и пусть векторы соответствуют вершинам треугольника. Хорошо известно, что ортоцентр равен , а центр тяжести равен . Таким образом, коллинеарны и

Точки пересечения прямой Эйлера со сторонами треугольника

Остроугольный треугольник

Позвольте быть остроугольным треугольником, где Обозначим

. Пусть линия Эйлера пересекает прямые и в точках и соответственно.

Тогда точка лежит на отрезке

Точка лежит на отрезке

Точка лежит на луче

Доказательство

Обозначим

Используем формулы (см. Утверждение «Отрезки, пересекающиеся внутри треугольника» в «Точке Шиффлера» в «Линии Эйлера»).

Центроид лежит на медиане

Ортоцентр лежит на высоте Поэтому Воспользуемся подписанной версией теоремы Менелая и получим

Тупоугольный треугольник

Пусть будет тупоугольный треугольник где

Пусть линия Эйлера пересекает прямые и в точках и соответственно.

Аналогично получаем

луч

Прямоугольный треугольник

Позвольте быть прямоугольным треугольником, где Тогда линия Эйлера содержит медиану из вершины

Равнобедренный треугольник

Позвольте быть равнобедренным треугольником, где Тогда прямая Эйлера содержит медиану из вершины

Следствие: прямая Эйлера параллельна стороне

Прямая Эйлера параллельна стороне тогда и только тогда, когда

Доказательство

После упрощения в деле получаем

vladimir. [email protected], vvsss

Углы между прямой Эйлера и сторонами треугольника

Пусть линия Эйлера пересекает прямые и в точках и соответственно. Обозначим меньшие углы между прямой Эйлера и прямыми и как и соответственно.

Докажите, что

Доказательство

WLOG,

Пусть середина будет центром описанной окружности

Аналогично для других углов.

• Перспектор Госсарда

[email protected], vvsss

Расстояния по линии Эйлера

Пусть и будет ортоцентром, центром тяжести, центром описанной окружности и радиусом описанной окружности соответственно.

Докажите, что

Доказательство

WLOG, остроугольный треугольник,

[email protected], vvsss

Положение центров Кимберлинга на прямой Эйлера

Пусть дан треугольник ABC. Пусть и являются ортоцентром, центром описанной окружности, радиусом описанной окружности и внутренним радиусом соответственно.

Мы используем точку как начало координат и как единичный вектор.

Находим кимберлинговский центр X(I) на прямой Эйлера в виде Для многих центров Кимберлинга коэффициент является функцией только двух параметров и

Centroid Девятиточечный центр точка де Лоншам точка Шиффлера Эксетер Пойнт Дальняя точка Перспектор ABC и ортогональный треугольник Гомотетический центр орто- и тангенциального треугольников Центр окружности касательного треугольника

Середина X(3) и [email protected], vvsss

Треугольники с углами или

Пункт 1

Пусть в треугольнике будет Тогда прямая Эйлера параллельна биссектрисе

Доказательство

Пусть будет окружностью, описанной вокруг

Пусть будет центром описанной окружности

Пусть будет окружностью, симметричной относительно

Пусть будет точкой, симметричной относительно

Лежит на лежит на

радиус и вектор переноса до

Пусть — точка, симметричная относительно хорошо известной, лежащая на Следовательно, точка лежит на

Точка лежит на

Пусть биссектриса совпадает.

Прямая Эйлера параллельна биссектрисе желаемого.

Пункт 2

Пусть в треугольнике будет Тогда прямая Эйлера перпендикулярна биссектрисе

Доказательство

Пусть описанная окружность, центр описанной окружности, ортоцентр и центр вписанной точки совпадают.

Окружность с центром в середине малой дуги

является ромбом.

Следовательно, прямая Эйлера перпендикулярна желаемому.

Пункт 3

Позвольте быть четырехугольником, диагонали которого и пересекаются в и образуют угол Если треугольники PAB, PBC, PCD, PDA все неравносторонние, то их линии Эйлера попарно параллельны или совпадают.

Доказательство

Позвольте и быть внутренней и внешней биссектрисами угла .

Тогда прямые Эйлера и параллельны, а прямые Эйлера и перпендикулярны как угодно.

[email protected], ввсс

Прямые Эйлера вписанного четырехугольника (теорема Виттаса)

Утверждение 1

Позвольте быть вписанным четырехугольником с диагоналями, пересекающимися в. Прямые Эйлера треугольников совпадают.

Доказательство

Позвольте быть центром описанной окружности (ортоцентром) треугольников Пусть общая биссектриса и Следовательно, и — параллелограммы с параллельными сторонами.

делят эти углы пополам. Таким образом, точки коллинеарны и лежат на одной прямой, которая является стороной парных вертикальных углов, и Точно так же точки коллинеарны и лежат по другую сторону этих углов. Аналогично тупые, так что точки и лежат на одной стороне и лежат на одной стороне, а точки и лежат на одной стороне и лежат на другой стороне одних и тех же вертикальных углов.

Мы используем Утверждаем и получаем, что линии параллельны (или параллельны, если или ).

Утверждение 2 (Свойство вершины двух параллелограммов)

Пусть и параллелограммы, Пусть прямые и пересекаются в точке Тогда точки и коллинеарны, а прямые и параллельны.

Доказательство

Мы рассматриваем только случай, когда преобразование Shift позволяет обобщить полученные результаты.

Используем систему координат с началом в точке и осях

Используем и получаем точки и коллинеарны.

Вычисляем точку пересечения и и и и получаем тот же результат: по желанию (если при этом точка уходит в бесконечность и прямые параллельны, углы или

[email protected], vvsss ~ незначительная редакция Yiyj1

Совпадающие линии Эйлера и точки Ферма

Рассмотрим треугольник с точками Ферма–Торричелли и Линии Эйлера треугольников с вершинами, выбранными из и совпадающими в центроиде треугольника. и линии треугольников зеленый цвет для треугольников и синий цвет для треугольников

Кейс 1

Пусть — первая точка Ферма с максимальным углом меньше чем Тогда центр тяжести треугольника лежит на прямой Эйлера Парные углы между этими прямыми Эйлера равны

Доказательство

Пусть и будет центроидом, центром окружности и описанной окружностью соответственно.

Пусть будет внешним для равностороннего треугольника вписанным.

Точка является центром тяжести точек и коллинеарна, поэтому точка лежит на прямой Эйлера из

Случай 2

Пусть первая точка Ферма

Тогда центр тяжести треугольника лежит на Эйлеровых прямых треугольников и Попарные углы между этими Эйлеровыми прямыми равны

Доказательство

Пусть будет внешним для равностороннего треугольника, будет описанная окружность циклическая.

Точка является центроидом

Точки коллинеарны, поэтому точка лежит на линии Эйлера, как и требовалось.

Корпус 3

Пусть вторая точка Ферма Тогда центр тяжести треугольника лежит на линиях Эйлера треугольников и

Попарные углы между этими линиями Эйлера равны

Доказательство

Пусть будет внутренним для равностороннего треугольника, будет описанной окружностью

Пусть и будут центрами описанных окружностей треугольников и Точка является центром тяжести линии Эйлера параллели

— биссектриса — биссектриса — биссектриса — правильного треугольника.

— внутренний треугольник Наполеона центроида этого правильного треугольника.

точки и коллинеарны по желанию.

Точно так же точки и коллинеарны.

Чемодан 4

Позвольте и быть точками Ферма Тогда центроид точки лежит на линии Эйлера (центр окружности, центроид)

Доказательство Шаг 1 0087 Этап 2 Докажем, что прямая параллельна

Пусть внутренний треугольник Наполеона. Позвольте быть внешним треугольником Наполеона. Эти треугольники правильные с центрами в

точек и коллинеарны (они лежат на биссектрисе

Точки и коллинеарны (они лежат на биссектрисе

Точки и коллинеарны (они лежат на биссектрисе угла между и

Точки и концикличны Точки и конциклические

точки и конциклические

Следовательно и коллинеарны или точка лежит на прямой Эйлера

[email protected], vvsss

Прямая Эйлера треугольника Жергонна

Докажите, что прямая Эйлера треугольника Жергонна проходит через центр описанной окружности треугольника

Треугольник Жергонна также известен как контактный треугольник или треугольник касания. Если вписанный круг касается сторон в точках, а затем треугольник Жергонна .

Другая формулировка: Касательные к описанной окружности проведены в вершинах треугольника. Докажите, что центр описанной окружности треугольника, образованного этими тремя касательными, лежит на прямой Эйлера исходного треугольника.

Доказательство

Позвольте и быть ортоцентром и центром описанной окружности соответственно. Пусть будет ортическим треугольником

Тогда линия Эйлера является центром центра

Аналогично,

где является перспективой треугольников и

При гомотетии с центром P и коэффициентом центр карт в центр центра окружности карты в центр окружности коллинеарны по желанию.

[email protected], ввсс

Точка свода

Пусть и будут высотами где

а) Докажите, что линии Эйлера треугольников совпадают на девятиточечной окружности в точке T (точка Thebault )

б) Докажите, что если то еще

Доказательство

Случай 1 Остроугольный треугольник

а) Известно, что прямые Эйлера остроугольного треугольника пересекают АВ и ВС (самую короткую и длинную стороны) во внутренних точках.

Пусть будут центрами описанных окружностей

Пусть и будут центроидами

Обозначает круг (круг с девятью точками).

— середина, где находится ортоцентр

Аналогично

— средняя линия

Пусть пересекаются в точке, отличной от

спиральное подобие с центром в картах на

треугольников

Пусть эти линии пересеклись в точке Поэтому точки и концикличны

Точно так же, как нужно.

б) Точка лежит на медиане и делит ее в отношении 2 : 1.

Точка лежит на прямой Эйлера

Согласно Утверждению,

Аналогично

Случай 2 Тупоугольный треугольник

а) Известно, что прямая Эйлера тупого креста AC и BC (средняя и длинная стороны) во внутренних точках.

Пусть будут центрами описанных окружностей

Пусть и будут центроидами

Обозначим окружность (окружность с девятью точками).

— середина, где находится ортоцентр

Аналогично

— средняя линия

Перекрестимся в точке, отличной от

Спиральное подобие с центром в картах на

треугольников

Пусть эти линии пересеклись в точке Поэтому точки и концикличны

Точно так же, как нужно.

б)

Точка лежит на медиане и делится на

Точка лежит на прямой Эйлера По Претензия,

Аналогично

Претензия (Отрезок, пересекающий медиану)

Пусть будет середина стороны

Тогда

Доказательство

Пусть будет (Мы используем знак для обозначения площади

Обозначаем [email protected], vvsss

Точка Шиффлера

Пусть и будет центром вписанной окружности, центром окружности, центром тяжести, радиусом описанной окружности и внутренним радиусом соответственно. Тогда линии Эйлера четырех треугольников совпадают в точке Шиффлера.

Доказательство

Докажем, что прямая Эйлера пересекает прямую Эйлера в такой точке, что .

Позвольте и быть центром описанной окружности и центроидом соответственно.

Известно, что лежит на описанной окружности

Обозначим

Известно, что средняя точка лежит на срединных точках, принадлежащих биссектрисе

Легко найти, что ,

Мы используем знак [t] для площади t. Мы получаем

Использование Претензия получаем Следовательно, каждая линия Эйлера треугольников пересекает линию Эйлера в одной и той же точке, что и требовалось.

Претензия (Отрезки пересекаются внутри треугольника)

Дан треугольник GOY. Точка лежит на

Точка лежит на

Точка лежит на

Точка лежит на Тогда

Доказательство

Пусть будет (Используем знак для области [email protected], vvsss

Линия Эйлера как радикальная ось

Пусть даны высоты и .

Позвольте и быть описанной окружностью, описанной окружностью, ортоцентром и описанной окружностью соответственно.

Окружность с центром проходит через радиус AO и касается его. Аналогично определим окружности

и

. Тогда линия Эйлера является радикальной осью этих окружностей.

Если острая, то эти три окружности пересекаются в двух точках, расположенных на прямой Эйлера

Доказательство

Степень точки по отношению к

Степень точки по отношению к

Степень точки по отношению к

Степень точки по отношению к

Известно, что

Следовательно указывает и лежит на радикальной оси этих трех окружностей по желанию.

[email protected], ввсс

Пойнт де Лоншам X(20)

Определение 1

Точка треугольника Де Лоншана является радикальным центром кругов власти треугольника. Докажите, что точка де Лоншана лежит на прямой Эйлера.

Мы называем окружностью A-степени а окружность с центром в средней точке с радиусом. Две другие окружности определяются симметрично.

Доказательство

Пусть и будет ортоцентром, центром описанной окружности и точкой де Лоншана соответственно.

Обозначим круг силы через круг силы через WLOG,

Обозначим проекцию точки на

Докажем, что радикальные оси силовых и силовых циклов симметричны высоте относительно Далее, придем к выводу, что точка пересечения радикалов осей, симметричных высотам относительно О, симметрична точке пересечения высот относительно

Точка пересечения средней линии силового и силового кругов и находящейся там радикальной оси. Используем претензию и получаем:

и медианы, поэтому

Используем Claim несколько раз и получаем: радикальные оси силовых и силовых циклов симметричны высоте относительно

Аналогично радикальные оси силовых и силовых циклов симметричны высоте радикальные оси силовых и силовых циклов симметричны высоте относительно Поэтому точка пересечения радикальных осей, симметричная высотам относительно , ​​симметрична точке пересечения высот относительно , ​​лежит на прямой Эйлера

Претензия (Расстояние между выступами)

Определение 2

Мы называем кругом круг с центром в и радиусом. Два других круга определены симметрично. Точка де Лоншана треугольника — это радикальный центр окружности, окружности и окружности треугольника (Кейси — 1886). Докажите, что точка Де Лоншана по этому определению совпадает с точкой по определению 1 .

Доказательство

Позвольте и быть ортоцентром, центроидом и точкой де Лоншана соответственно. Пусть пересекаются в точках и Остальные точки определяются симметрично. Точно так же диаметр

Следовательно, антидополнительный треугольник является ортоцентром треугольника Итак, ортоцентр

по желанию.

[email protected], ввсс

Линия де Лоншана

Линия де Лоншана определяется как радикальные оси окружности де Лоншана и описанной окружности

Позвольте быть описанной окружностью (антидополнительного треугольника

Позвольте быть кругом с центром в (центроиде) с радиусом где

Докажите, что линия де Лоншана перпендикулярна линии Эйлера и является радикальными осями и

Доказательство

Центр , центр где находится линия Эйлера. Гомотетия с центром и соотношением отображается в Эта гомотетия отображается в и есть две инверсии, которые меняются местами и

Первая инверсия с центром в точке Пусть будет точка пересечения и

Радиус можно найти с помощью

Вторая инверсия с центром в точке Мы можем произвести те же расчеты и получить желаемое.

[email protected], ввсс

ЦЕНТР ОКРУЖНОСТИ КАСАТЕЛЬНОГО ТРЕУГОЛЬНИКА X(26)

Докажите, что центр описанной окружности касательного треугольника (точка Кимберлинга лежит на прямой Эйлера

Доказательство

Пусть и будут серединами и соответственно.

Пусть будет описанная окружность Это девятиконечная окружность

Пусть будет описанная окружность Пусть будет описанная окружность

и являются касательными к инверсии относительно своп и Аналогично, это инверсия своп и и Следовательно это инверсия своп и

центр и центр лежат на линии Эйлера, поэтому центр лежит на этой линии, что и требовалось.

После некоторых вычислений можно найти положение точки на линии Эйлера (см. точку Кимберлинга

[email protected], vvsss

ПЕРСПЕКТОР ОРТИЧНЫХ И КАСАТЕЛЬНЫХ ТРЕУГОЛЬНИКОВ X(25)

Пусть будет ортотреугольником Пусть будет центром описанной окружности Пусть будет касательным треугольником Пусть будет центром описанной окружности

Докажите, что прямые и параллельны в точке, лежит на прямой Эйлера

Доказательство

и антипараллельны ВС относительно

Аналогично,

Следовательно, гомотетичный центр и является точкой пересечения прямых и Обозначим эту точку как

Точки и являются соответствующими точками (центрами окружности) и поэтому точка лежит на line

Указывает и лежит на прямой Эйлера, поэтому лежит на прямой Эйлера

vladimir. [email protected], vvsss

Точка Эксетера X(22)

Точка Эксетера — это точка зрения окружного треугольника и касательного треугольника Другими словами, пусть будет опорным треугольником (кроме прямоугольного треугольника). Пусть медианы, проходящие через вершины, пересекают описанную окружность треугольника в точках и соответственно. Позвольте быть треугольником, образованным касательными в и к (Позвольте быть вершиной, противоположной стороне, образованной касательной в вершине A). Докажите, что прямые, проходящие через и, пересекаются, точка пересечения лежит на прямой Эйлера треугольника точка пересечения лежит на прямой Эйлера треугольника, где — центр описанной окружности, — ортоцентр, — радиус описанной окружности.

Доказательство

Сначала докажем, что прямые и параллельны. Это следует из того факта, что прямые и пересекаются в точке и Теорема отображения .

Позвольте и быть серединами и соответственно. Точки и лежат на одной прямой. Точно так же точки и коллинеарны.

Обозначим инверсию относительно Очевидно, что

Обозначим

Степень точки относительно

Точно так же степень точки относительно

лежит на радикальной оси и

Следовательно, вторая точка пересечения и точка лежит на прямой, которая является линией Эйлера Точка лежит на той же линии Эйлера, что и требовалось.

Последний мы найдем длину по желанию.

Теорема отображения

Пусть даны треугольник и вписанная окружность. Пусть точка на плоскости Пусть линии и пересечения второй раз в точках и соответственно.

Докажите, что прямые и пересекаются.

Доказательство

Используем Claim и получаем: Точно так же

Мы используем тригонометрическую форму теоремы Чевы для точки и треугольника и получаем Мы используем тригонометрическую форму теоремы Чевы для треугольника и заканчиваем доказательство того, что прямые и пересекаются.

Претензия (точка на окружности)

Пусть даны треугольник и вписанная окружность. Докажите, что

Доказательство

Аналогично

Умножаем и делим эти уравнения и получаем:

[email protected], ввсс

Дальняя точка X(23)

Пусть будет касательным треугольником

Пусть и будет центром тяжести, описанной окружностью, центром описанной окружности, радиусом описанной окружности и ортоцентром

Докажите, что вторая точка пересечения описанных окружностей и является точкой Точка лежит на Эйлер линия

Доказательство

Обозначим инверсию относительно середины

Очевидно, что

Инверсия окружностей — это линии, которые пересекаются в точке

Следовательно, точка лежит на прямой Эйлера как и требовалось.

[email protected], ввсс

Симметричные прямые

Пусть дан треугольник с описанной окружностью.