Теория вероятности определения и формулы: Теория вероятностей — урок. Основной государственный экзамен 9 класс, Математика.

формулы для решения типичных задач, объяснение теории

• Теория вероятностей о видах событий и вероятности их появления
• Задачи на классическую и статистическую вероятности. Формулы вероятностей: классической и статистической
• Свойства вероятностей

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

На этом уроке освоим формулы для решения типичных задач по теории вероятностей. Узнаем виды событий и научимся вычислять вероятности их появления. Немаловажно, как появилась теория вероятностей: математика занялась проблемами азартных игр, в частости, вероятностью выпадения выигрыша. Поэтому до сих пор в задачах, в том числе тех, которые мы будем рассматривать, часто описываются различные игровые ситуации.

Если говорить о теории вероятностей простыми словами, то это математическая наука о вычислении вероятностей случайных событий. Нередко приходится слышать, что вероятность такого-то события равна нулю, единице, 50 процентам или другому числовому значению. Но насколько достоверны те или иные утверждения, а точнее, в каких случаях они достоверны, а в каких — нет? Например, «блондинка из анекдота» утверждает, что вероятность случайно встретить на улице динозавра равна 1/2 или 50 процентам. Насколько это достоверно?

Нельзя утверждать, что «блондинка из анекдота» совершенно не права. Ее заключение основано на том, что динозавра на улице «можно встретить, а можно не встретить». Такое заключение может быть истолковано по классическому определению вероятности: из двух возможностей одна благоприятствует наступлению события, следовательно, вероятность наступления события равна 1/2. Но такие заключения, как говорят умудренные опытом люди, не представляют окончательной познавательной ценности.

Ценность с точки зрения теории вероятностей представляют лишь такие заключения, которые связывают наступление или ненаступление события с большим числом случайных и часто мало связанных друг с другом факторов или условий.

Данная статья — вводная во множество уроков по теории вероятностей, а также математической статистике. На них можно научиться находить скрытые закономерности в данных о различных событиях и явлениях.

Теперь наиболее точное определение теории вероятностей. Теория вероятностей — математическая наука, выясняющая закономерности, которые возникают при взаимодействии большого числа случайных факторов. Например, в случае анекдота про блондинку и динозавра требуется установить, сохранились ли где-либо на Земле динозавры, и если да, то где их больше и где на карте «динозавренности Земли» находится совершенно определенная улица. Если рассматривать более серьезные заключения, например, о том, что футбольный матч между командами

A и B закончится со счетом 3:1, то это субъективное заключение, если оно не учитывает историю матчей между этими командами, матчей этих команд с другими командами, текущего состава игроков команд и истории достижений этих игроков.

Обобщенно: о вероятности события A можно говорить с предположением, что выполнен некоторый комплекс условий S. Если этот комплекс условий изменился, то и вероятность наступнения собятия S должна измениться. Например, утверждение о том, что при бросании игральной кости каждая сторона выпадет с одной и той же вероятностью, равной 1/6, предполагает следующий комплекс условий: кость имеет одинаковую плотность, имеет точную форму куба и подбрасывается совершенно случайным образом.

Именно на примерах азартных игр, в том числе игре в кости, учеными были впервые обнаружены статистические закономерности, описывающие частоту наступления события. Это было сформулировано так: наличие у события A при условиях S определенной вероятности, равной p, проявляется в том, что в почти каждой достаточно длинной серии испытаний частота события приблизительно равна p. На этой основе и возникла теория вероятностей в середине XVII века, когда математики заинтересовались задачами, поставленными азартными игроками и стали изучать такие события, как появление выигрыша. Ученые того времени – Гюйгенс (1629-1695), Паскаль (1623-1662), Ферма (1601-1665) и Бернулли (1654-1705) были убеждены, что на базе массовых случайных событий могут возникать четкие закономерности. При этом для исследований было достаточно элементарных арифметических и комбинаторных действий.

Итак, теория вероятностей объясняет и исследует различные закономерности, которым подчинены случайные события и случайные величины. Событием является любой факт, который можно констатировать в результате наблюдения, испытания или опыта. Наблюдением, испытанием или опытом называют реализацию определенных условий, в которых событие может состояться.

Что нужно знать, чтобы решать задачи на определение вероятности появления события

Все события, за которыми люди наблюдают или сами создают их, делятся на:

• достоверные события;
• невозможные события;
• случайные события.

Достоверные события наступают всегда, когда создан определенный комплекс обстоятельств. Например, если работаем, то получаем за это вознаграждение, если сдали экзамены и выдержали конкурс, то достоверно можем рассчитывать на то, что включены в число студентов. Достоверные события можно наблюдать в физике и химии. В экономике достоверные события связаны с существующим общественным устройством и законодательством. Например, если мы вложили деньги в банк на депозит и выразили желание в определенный срок их получить, то деньги получим. На это можно рассчитывать как на достоверное событие.

Невозможные события определенно не наступают, если создался определенный комплекс условий. Например, вода не замерзает, если температура составляет плюс 15 градусов по Цельсию, производство не ведется без электроэнергии.

Случайные события при реализации определенного комплекса условий могут наступить и могут не наступить. Например, если мы один раз подбрасываем монету, герб может выпасть, а может не выпасть, по лотерейному билету можно выиграть, а можно не выиграть, произведенное изделие может быть годным, а может быть бракованным.

Появление бракованного изделия является случайным событием, более редким, чем производство годных изделий.

Ожидаемая частота появления случайных событий тесно связана с понятием вероятности. Закономерности наступления и ненаступления случайных событий исследует теория вероятностей.

Если комплекс нужных условий реализован лишь один раз, то получаем недостаточно информации о случайном событии, поскольку оно может наступить, а может не наступить. Если комплекс условий реализован много раз, то появляются известные закономерности. Например, никогда невозможно узнать, какой кофейный аппарат в магазине потребует очередной покупатель, но если известны марки наиболее востребованных в течение длительного времени кофейных аппаратов, то на основе этих данных возможно организовать производство или поставки, чтобы удовлетворить спрос.

Знание закономерностей, которым подчинены массовые случайные события, позволяет прогнозировать, когда эти события наступят. Например, как уже ранее отмечено, заранее нельзя предусмотреть результат бросания монеты, но если монета брошена много раз, то можно предусмотреть выпадение герба. Ошибка может быть небольшой.

Методы теории вероятностей широко используются для решения задач в различных отраслях естествознания, теоретической физике, геодезии, астрономии, теории автоматизированного управления, теории наблюдения ошибок, и во многих других теоретических и практических науках. Теория вероятностей широко используется в планировании и организации производства, анализе качества продукции, анализе технологических процессов, страховании, статистике населения, биологии, баллистике и других отраслях.

Случайные события обычно обозначают большими буквами латинского алфавита A, B, C и т.д.

Случайные события могут быть:

• несовместными;
• совместными.

События A, B, C … называют несовместными, если в результате одного испытания может наступить одно из этих событий, но невозможно наступление двух или более событий.

Если наступление одного случайного события не исключает наступление другого события, то такие события называют совместными. Например, если с ленты конвейера снимают очередную деталь и событие А означает «деталь соответствует стандарту», а событие B означает «деталь не соответствует стандарту», то A и B – несовместные события. Если событие C означает «взята деталь II сорта», то это событие совместно с событием A, но несовместно с событием B.

Если в каждом наблюдении (испытании) должно произойти одно и только одно из несовместных случайных событий, то эти события составляют полное множество (систему) событий.

Достоверным событием является наступление хотя бы одного события из полного множества событий.

Если события, образующие полное множество событий, попарно несовместны, то в результате наблюдения может наступить только одно из этих событий. Например, студент должен решить две задачи контрольной работы. Определенно произойдет одно и только одно из следующих событий:

• будет решена первая задача и не будет решена вторая задача;
• будет решена вторая задача и не будет решена первая задача;
• будут решены обе задачи;
• не будет решена ни одна из задач.

Эти события образуют полное множество несовместных событий.

Если полное множество событий состоит только из двух несовместных событий, то их называют взаимно противоположными или альтернативными событиями.

Событие, противоположное событию , обозначают . Например, в случае одного подбрасывания монеты может выпасть номинал () или герб ().

События называют равновозможными, если ни у одного из них нет объективных преимуществ. Такие события также составляют полное множество событий. Это значит, что в результате наблюдения или испытания определенно должно наступить по меньшей мере одно из равновозможных событий.

Например, полную группу событий образуют выпадение номинала и герба при одном подбрасывании монеты, наличие на одной печатной странице текста 0, 1, 2, 3 и более 3 ошибок.

Классическое определение вероятности. Возможностью или благоприятным случаем называют случай, когда при реализации определённого комплекса обстоятельств события А происходят. Классическое определение вероятности предполагает напрямую вычислить число благоприятных случаев или возможностей.

Вероятностью события А называют отношение числа благоприятных этому событию возможностей к числу всех равновозможных несовместных событий N, которые могут произойти в результате одного испытания или наблюдения. Формула вероятности события А:

                             (1)

Если совершенно понятно, о вероятности какого события идёт речь, то тогда вероятность обозначают маленькой буквой p, не указывая обозначения события.

Чтобы вычислить вероятность по классическому определению, необходимо найти число всех равновозможных несовместных событий и определить, сколько из них благоприятны определению события А. Перейдём к задачам.

---

Пример 1. Найти вероятность выпадения числа 5 в результате бросания игральной кости.

Решение. Известно, что у всех шести граней одинаковая возможность оказаться наверху. Число 5 отмечено только на одной грани. Число всех равновозможных несовместных событий насчитывается 6, из них только одна благоприятная возможность выпадения числа 5 (М = 1). Это означает, что искомая вероятность выпадения числа 5

Пример 2. В ящике находятся 3 красных и 12 белых одинаковых по размеру мячиков. Не глядя взят один мячик. Найти вероятность, что взят красный мячик.

Решение. Искомая вероятность

Найти вероятности самостоятельно, а затем посмотреть решение

Пример 3. Бросается игральная кость. Событие B — выпадение чётного числа. Вычислить вероятность этого события.

Посмотреть правильное решение и ответ.

Пример 4. Бросается игральная кость. Какова вероятность выпадения числа 7?

Посмотреть правильное решение и ответ.

Пример 5. В урне 5 белых и 7 чёрных шаров. Случайно вытаскивается 1 шар. Событие A — вытянут белый шар. Событие B — вытянут чёрный шар. Вычислить вероятности этих событий.

Посмотреть правильное решение и ответ.

---

Классическую вероятность называют также априорной вероятностью, так как её рассчитывают перед началом испытания или наблюдения. Из априорного характера классической вероятности вытекает её главный недостаток: только в редких случаях уже перед началом наблюдения можно вычислить все равновозможные несовместные события и в том числе благоприятные события. Такие возможности обычно возникают в ситуациях, родственных играм.

Сочетания. Если последовательность событий не важна, число возможных событий вычисляют как число сочетаний:

                    (2)

---

Пример 6. В группе 30 студентов. Трём студентам следует направиться на кафедру информатики, чтобы взять и принести компьютер и проектор. Вычислить вероятность того, что это сделают три определённых студента.

Решение. Число возможных событий рассчитываем, используя формулу (2):

Вероятность того, что на кафедру отправятся три определённых студента:

---

Пример 7. Продаются 10 мобильных телефонов. Их них у 3 есть дефекты. Покупатель выбрал 2 телефона. Вычислить вероятность того, что оба выбранных телефона будут с дефектами.

Решение. Число всех равновозможных событий находим по формуле (2):

По той же формуле находим число благоприятных событию возможностей:

Искомая вероятность того, что оба выбранных телефона будут с дефектами:

Найти вероятность самостоятельно, а затем посмотреть решение

Пример 8. В экзаменационных билетах 40 вопросов, которые не повторяются. Студент подготовил ответы на 30 из них. В каждом билете 2 вопроса. Какова вероятность того, что студент знает ответы на оба вопроса в билете?

Посмотреть правильное решение и ответ.

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Пройти тест по теме Теория вероятностей и математическая статистика

Свойство 1. Если можно вычислить возможности возникновения события А и их число совпадает общим числом равновозможных событий, то вероятность события А равна 1.

Например, при бросании игральной кости число возможностей выпадения чисел 1, 2, 3, 4, 5, 6 равно 6. Насчитывается также 6 равновозможных несовместимых событий. Таким образом, M = N  и

Свойство 2. Вероятность невозможного события равна 0. Если число возможностей события А равна 0, то и

Например, при бросании игральной кости не может выпасть число 9, потому что такого числа нет на гранях игральной кости.

Свойство 3. Вероятность случайного события всегда больше 0 и меньше 1:

или

Определение статистической вероятности. В определении статистической вероятности используется понятие относительно частоты события А. Относительной частотой события А называют отношение числа наблюдений, в которых наблюдается А, к числу всех наблюдений. Относительную частоту обычно обозначают буквой W. Если в n наблюдениях событие А наблюдается m раз, то относительная частота события А:

Например, баскетболист у штрафной линии готовится совершить бросок. Из собранной тренером статистической информации известно, что у этого баскетболиста из 100 штрафных бросков успешны 70. Вероятность того, что баскетболист реализует штрафной бросок:

Длительные наблюдения показали, что с увеличением числа наблюдений относительная частота события А становится всё более стабильной. Число, около которого при серии наблюдений колеблется относительная частота, называется статистической вероятностью события А. Формула статистической вероятности события А:

если .

Вычислить точную статистическую вероятность невозможно, так как невозможно выбрать бесконечно большое число наблюдений.

Преимущество статистического определения вероятности в том, что оно не требует априорных знаний об исследуемом объекте. Классическую вероятность можно вычислить до наблюдения или испытания, а статистическую – после наблюдения или испытания.

Назад

Листать

Вперёд>>>

Статистика — не Ваша специализация? Закажите статистическую обработку данных

К началу страницы

Действия над вероятностями

Различные задачи на сложение и умножение вероятностей

Формула полной вероятности

Формула Байеса

Независимые испытания и формула Бернулли

Пройти тест по теме Теория вероятностей и математическая статистика

Распределение вероятностей дискретной случайной величины

Распределение вероятностей непрерывной случайной величины

Математическое ожидание и дисперсия случайной величины

Биномиальное распределение дискретной случайной величины

Распределение Пуассона дискретной случайной величины

Равномерное распределение непрерывной случайной величины

Нормальное распределение непрерывной случайной величины

Теория вероятности: основные понятия и определения, основы, предмет, события, формулы и примеры простыми словами

С чего начать изучение теории вероятностей? 

Итак, теория вероятностей — это раздел математики, который изучает закономерности случайных событий, операции над ними.  

У теории вероятностей нет цели что-либо угадать и предсказать. Предположим, что мы подбрасываем монету — нам нет необходимости угадывать, какой стороной она упадёт. 

Однако если одну и ту же монету в одинаковых условиях подбрасывать сотни и тысячи раз, то будет прослеживаться чёткая закономерность, описываемая вполне жёсткими законами. 

Событие — это базовое понятие теории вероятности. События бывают достоверными, невозможными и случайными.

• Достоверным является событие, которое в результате испытания обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз.
• Невозможным является событие, которое заведомо не произойдёт в результате испытания. Например, камень при падении улетит вверх. Например, монета зависнет в воздухе или вообще полетит вверх. 
• Случайным называется событие, которое в результате испытания может произойти, а может не произойти. Например, уже знакомая монетка может упасть либо орлом вверх, либо решкой — это и есть случайное событие.

Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события.

В частности, при подбрасывании монеты возможно 2 исхода (случайных события): выпадет орёл или выпадет решка. Подразумевается, что опыт проводится в таких условиях, что монета не может встать на ребро или зависнуть в невесомости.

События (любые) обозначают большими латинскими буквами A, B, C… либо буквами с индексами, например: A1, A2, A3…. 

Исключение составляет буква P, которая используется для обозначения вероятности события. Например, вероятность события А обозначается Р(А).

Ещё события можно обозначать индексами в виде букв, например: АО — в результате броска монеты выпадет орёл.

Самая важная формула для решения самых простых задач выглядит так: 

P(A) = m/n, где n — общее число всех равновозможных, элементарных исходов данного испытания, а m — количество элементарных исходов, благоприятствующих событию A.

Другая важная характеристика событий — это их равновозможность. Два или большее количество событий называют равновозможными, если ни одно из них не является более возможным, чем другие. Например: выпадение орла или решки при броске монеты, выпадение 1, 2, 3, 4, 5 или 6 очков при броске игрального кубика (при условии, что монета и кубик имеют геометрически правильную форму), извлечение карты трефовой, пиковой, бубновой или червовой масти из колоды с учётом, что количество всех мастей одинаковое).

События могут быть не равновозможными. Например, если в колоде не хватает одной червовой карты — тогда вероятность выпадения этой масти будет меньше. Или если игральный кубик не является геометрически правильным кубиком.

 

 

 

 

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Теоретическая вероятность и экспериментальная вероятность

Вероятность определяется как вероятность наступления или возникновения события. Обычно возможность анализа возникновения какого-либо события по отношению к предыдущим данным называется вероятностью. Например, если подбросить правильную монету, какова вероятность того, что она упадет решкой? Ответы на вопросы такого типа даются под вероятностью. В этой статье мы подробно узнаем о теории вероятностей, ее формулах и многом другом.

Что такое теория вероятностей?

Теория вероятностей использует концепцию случайных величин и распределения вероятностей, чтобы найти исход любой ситуации. Теория вероятностей — это продвинутый раздел математики, который имеет дело с вероятностью и статистикой наступления события.

Как подбрасывание монеты связано с вероятностью?

Как только вы подбросите монету, результат будет случайным. Это может быть решек или орлов. и орел, и решка имеют одинаковую вероятность приземления, поэтому оба имеют шанс 50-50. Таким образом, мы можем сказать, что вероятность выпадения орла или решки равна 1/2.

Определение теории вероятностей

Теория вероятностей изучает случайные события и сообщает нам об их возникновении. Два основных подхода к изучению теории вероятностей таковы.

• Теоретическая вероятность
• Экспериментальная вероятность

Теоретическая и экспериментальная вероятности

На приведенном ниже рисунке показаны теоретическая и экспериментальная вероятности и их различия.

 

Теоретическая вероятность

Теоретическая вероятность имеет дело с предположениями, позволяющими избежать неосуществимого или дорогостоящего повторения экспериментов. Теоретическая вероятность события А может быть рассчитана следующим образом:    

P(A) = (количество исходов, благоприятных для события А) / (количество всех возможных исходов)

На приведенном ниже рисунке показана теоретическая формула вероятности.

 

Примечание: Здесь исходы события предполагаются равновероятными.

Теперь, когда мы изучим формулу, давайте поместим эту формулу в наш случай с подбрасыванием монеты. При подбрасывании монеты возможны два исхода: орёл или решка. Следовательно, вероятность выпадения решки при подбрасывании монеты равна

P(H) = 1/2

. Точно так же вероятность выпадения решки при подбрасывании монеты равна

P(T) = 1/2.

На следующем рисунке показана непредвзятая монета, которая имеет равную вероятность выпадения орла и решки

 

Экспериментальная вероятность

Экспериментальная вероятность определяется путем проведения серии экспериментов и наблюдения за их результатами. Эти случайные эксперименты также известны как испытания. Экспериментальная вероятность события A может быть рассчитана следующим образом:

P(E) = (количество раз, когда произошло событие A) / (общее количество испытаний)

На следующем рисунке показана экспериментальная формула вероятности,

 

Теперь, когда мы изучим формулу, давайте поместим ее в наш случай с подбрасыванием монеты. Если мы подбросили монету 10 раз и зарегистрировали решку 4 раза и решку 6 раз, то вероятность выпадения орла при подбрасывании монеты:

P(H) = 4/10

Аналогично, вероятность выпадения решки при подбрасывании монеты:

P(T) = 6/10

Пример теории вероятностей

Мы можем изучить понятие вероятности с с помощью примера, рассмотренного ниже,

Пример: Возьмем два случайных кубика и бросим их случайным образом, теперь вычисляется вероятность получения в сумме 10.

Решение:

Всего Возможные события, которые могут произойти (выборочное пространство) {(1,1), (1,2),…, (1,6),…, (6,6)}. Всего мест 36.

Теперь требуемые события {(4,6), (5,5), (6,4)} — это все, что в сумме дает 10.

Таким образом, вероятность получить в сумме 10 = 3/36 = 1/12

Основы теории вероятностей

Ниже обсуждаются различные термины, используемые в теории вероятностей,

Случайный эксперимент

называется случайным экспериментом. Подбрасывание монеты, бросание игральной кости и т. д. — это случайные эксперименты.

Пространство выборки

Множество всех возможных результатов любого случайного эксперимента называется пространством выборки. Например, при бросании игральной кости выпадает шесть результатов: 1, 2, 3, 4, 5 и 6. Таким образом, его выборочное пространство равно (1, 2, 3, 4, 5, 6)

Событие

Результат любого эксперимента называется событием. В теории вероятностей используются различные типы событий:

• Независимые события: События, на исходы которых не влияют исходы других будущих и/или прошлых событий, называются независимыми событиями. Например, , результат повторного подбрасывания монеты не зависит от предыдущего результата.
• Зависимые события: События, на исход которых влияет исход других событий, называются зависимыми событиями. Например, le, сбор апельсинов из мешка, в котором 100 апельсинов, без замены.
• Взаимоисключающие события: События, которые не могут произойти одновременно, называются взаимоисключающими. Например , получение орла или решки при подбрасывании монеты, потому что оба (орел и решка) не могут быть получены вместе.
• Равновероятные события: События, которые имеют равные шансы или вероятности произойти, называются равновероятными событиями. Например, , любая грань при бросании костей имеет равную вероятность 1/6.

Случайная переменная

Переменная, которая может принимать значения всех возможных исходов эксперимента, в теории вероятностей называется случайной величиной. Случайные величины в теории вероятностей бывают двух типов, которые обсуждаются ниже 9.0003

Дискретная случайная величина: Переменные, которые могут принимать исчисляемые значения, такие как 0, 1, 2,…, называются дискретными случайными величинами.

Непрерывная случайная переменная: Переменные, которые могут принимать бесконечное число значений в заданном диапазоне, называются непрерывными случайными величинами.

Формулы теории вероятностей

Существуют различные формулы, которые используются в теории вероятностей, и некоторые из них обсуждаются ниже,

• Теоретическая формула вероятности: (Число благоприятных исходов) / (Число всех исходов)
• Формула эмпирической вероятности: (Количество раз, когда произошло событие A) / (Общее число испытаний)
• Правило сложения вероятности: P(A ∪ B) = P(A) + P(B) – P(A∩B)
• Дополнительное правило вероятности: P(A’) = 1 – P(A)
• Независимые события: P(A ∩B) = P(A) ⋅ P(B)
• Условная вероятность: P(A | B) = P(A∩B) / P(B)
• Теорема Байеса. , он используется для поиска ответов на различные типы вопросов, например, будет ли завтра дождь? какова вероятность посадки на Луну? какова вероятность эволюции человека? и другие. Некоторые из важных применений теории вероятностей:
  • Теория вероятностей используется для прогнозирования поведения акций и облигаций.
  • Теория вероятностей используется в казино и азартных играх.
  • Теория вероятностей используется в прогнозировании погоды.
  • Теория вероятностей используется для снижения рисков.
  • Теория вероятностей используется в потребительской промышленности для снижения риска отказа продукта.

  Подробнее

  • Вероятность
  • Перестановки и комбинации
  • Биномиальная теорема

  Решенные примеры на Вероятность

  Пример 1. Рассмотрим банку с 7 красными, 3 зелеными и 4 синими шариками. Какова вероятность случайного выбора не синего шарика из банки?

  Решение:

  Дано,

  Количество красных шариков = 7, количество зеленых шариков = 3, количество синих шариков = 4

  Итак, общее количество возможных исходов в этом случае: 7 + 3 + 4 = 14

  Теперь количество несиних шариков: 7 + 3 = 10

  Согласно формуле теоретической вероятности мы можем найти, P(не синие) = 10/14 = 5/7

  Следовательно, теоретическая вероятность выбора не синего шарика равна 5/7.

  Пример 2. Рассмотрим двух игроков, Навину и Ишу, играющих в настольный теннис. Вероятность победы Навины в матче равна 0,76. Какова вероятность того, что Иша выиграет матч?

  Решение:

  Пусть N и M представляют события, когда Навина выигрывает матч, а Ашлеша выигрывает матч соответственно.

  Вероятность выигрыша Навины P(N) = 0,62 (задано)

  Вероятность выигрыша Иши P(I) = ?

  Победа в матче является взаимоисключающим событием, так как только один из них может выиграть матч.

  Следовательно,

  P(N) + P(I) =1

  P(I) = 1 – P(N)

  P(I) = 1 – 0,62 = 0,38

  Таким образом, вероятность Иша выигрыш в матче равен 0,38.

  Пример 3: Если кто-то вынет одну карту из колоды из 52 карт, какова вероятность того, что эта карта окажется червой? Какова вероятность получения карты с 7 номерами?

  Решение:

  Общее количество карт в колоде = 52

  Общее количество червовых карт в колоде = 13

  Таким образом, вероятность получения червы,

  P(heart) = 13 /52 = 1/4

  Общее количество 7-значных карт в колоде = 4

  Таким образом, вероятность получения 7-значной карты

  P(7-число) = 4/52 = 1/13

  Пример 4. Найдите вероятность выпадения четного числа при бросании игральной кости с числами от 1 до 6. Выразите вероятность в виде дроби, десятичной дроби, отношения или процента.

  Решение:

  Из чисел от 1 до 6 четные числа 2, 4 и 6.

  Таким образом, число благоприятных исходов = 3. 002 Вероятность получения четного числа P(Even)= 1/2 = 0,5 = 1 : 2 = 50%

  Часто задаваемые вопросы по теории вероятностей

  Q1: Что такое концепция теории вероятностей?

  Ответ:

  Раздел математики, изучающий вероятность наступления события, называется теорией вероятностей. Он сообщает нам о шансах возникновения события, а также обо всех возможных исходах любого события.

  Q2: Какие два типа вероятностей существуют в теории вероятностей?

  Ответ:

  В теории вероятностей есть два типа вероятностей: 009 Q3: Кто изобрел теорию вероятностей?

  Ответ:

  Заслуга в создании современной теории вероятностей принадлежит итальянскому математику Джероламо Кардано.

  Q4: Что такое случайная величина в теории вероятностей?

  Ответ:

  Переменная, которая описывает все возможные исходы любого случайного эксперимента, называется случайной величиной. Случайная величина может быть непрерывной или дискретной.

  Q5: Каковы формулы теории вероятностей?

  Ответ:

  Основные формулы, используемые в теории вероятностей:0022

  Экспериментальная вероятность: (количество раз, когда произошло событие А) / (общее количество испытаний)

Что это такое, формула и примеры

Что такое теорема Байеса?

Теорема Байеса, названная в честь британского математика XVIII века Томаса Байеса, представляет собой математическую формулу для определения условной вероятности. Условная вероятность — это вероятность возникновения исхода, основанная на предыдущем исходе, произошедшем в аналогичных обстоятельствах. Теорема Байеса дает возможность пересмотреть существующие прогнозы или теории (обновить вероятности) с учетом новых или дополнительных доказательств.

В финансах теорему Байеса можно использовать для оценки риска кредитования потенциальных заемщиков. Эта теорема также называется правилом Байеса или законом Байеса и является основой области байесовской статистики.

Ключевые выводы

• Теорема Байеса позволяет обновлять предсказанные вероятности события путем включения новой информации.
• Теорема Байеса была названа в честь математика 18-го века Томаса Байеса.
• Часто используется в финансах для расчета или обновления оценки риска.
• Теорема стала полезным элементом в реализации машинного обучения.
• Теорема не использовалась в течение двух столетий из-за большого объема вычислительных мощностей, необходимых для выполнения ее транзакций.

Понимание теоремы Байеса

Применение теоремы Байеса широко распространено и не ограничивается финансовой сферой. Например, теорему Байеса можно использовать для определения точности результатов медицинских анализов, принимая во внимание вероятность заболевания любого конкретного человека и общую точность теста. Теорема Байеса основана на включении априорных распределений вероятностей для получения апостериорных вероятностей.

Априорная вероятность в байесовском статистическом выводе — это вероятность того, что событие произойдет до того, как будут собраны новые данные. Другими словами, он представляет собой наилучшую рациональную оценку вероятности определенного результата, основанную на текущих знаниях до проведения эксперимента.

Апостериорная вероятность — это пересмотренная вероятность события, происходящего после учета новой информации. Апостериорная вероятность рассчитывается путем обновления априорной вероятности с использованием теоремы Байеса. В терминах статистики апостериорная вероятность — это вероятность наступления события А при условии, что произошло событие В.

Особые указания

Таким образом, теорема Байеса дает вероятность события на основе новой информации, которая связана или может быть связана с этим событием. Формулу также можно использовать для определения того, как гипотетическая новая информация может повлиять на вероятность события, если предположить, что новая информация окажется верной.

Например, вытяните одну карту из полной колоды из 52 карт.

Вероятность того, что карта является королем, равна четырем, разделенным на 52, что равно 1/13 или приблизительно 7,69.%. Помните, что в колоде четыре короля. Теперь предположим, что выяснилось, что выбранная карта является лицевой. Вероятность того, что выбранная карта является королем, если это фигурная карта, равна четырем, деленным на 12, или примерно 33,3%, поскольку в колоде 12 лицевых карт.

Формула теоремы Байеса

п ( А ∣ Б ) «=» п ( А ⋂ Б ) п ( Б ) «=» п ( А ) ⋅ п ( Б ∣ А ) п ( Б ) где: п ( А ) «=» Вероятность возникновения А п ( Б ) «=» Вероятность появления B п ( А ∣ Б ) «=» Вероятность A при B п ( Б ∣ А ) «=» Вероятность B при условии A п ( А ⋂ Б ) ) «=» Вероятность того, что произойдут события А и В. \begin{align} &P\left(A|B\right)=\frac{P\left(A\bigcap{B}\right)}{P\left(B\right)}=\frac{P\left (A\right)\cdot{P\left(B|A\right)}}{P\left(B\right)}\\ &\textbf{где:}\\ &P\left(A\right)= \text{ Вероятность появления A}\\ &P\left(B\right)=\text{ Вероятность появления B}\\ &P\left(A|B\right)=\text{Вероятность заданного A B}\\ &P\left(B|A\right)=\text{ Вероятность B при данном A}\\ &P\left(A\bigcap{B}\right))=\text{ Вероятность обоих A и B встречается}\\ \end{выровнено} ​P(A∣B)=P(B)P(A⋂B)​=P(B)P(A)⋅P(B∣A)​где: P(A) = вероятность наступления A P(B )= Вероятность В появления P(A∣B)= Вероятность A при заданном BP(B∣A)= Вероятность B при заданном AP(A⋂B))= Вероятность нахождения A и B 

Примеры теоремы Байеса

Ниже приведены два примера теоремы Байеса, в которых первый пример показывает, как формула может быть получена на примере инвестирования в акции с использованием Amazon.com Inc. (AMZN). Второй пример применяет теорему Байеса к тестированию фармацевтических препаратов.

Вывод формулы теоремы Байеса

Теорема Байеса следует просто из аксиом условной вероятности. Условная вероятность — это вероятность события при условии, что произошло другое событие. Например, простой вероятностный вопрос может звучать так: «Какова вероятность падения курса акций Amazon.com?» Условная вероятность поднимает этот вопрос еще на один шаг, спрашивая: «Какова вероятность того, что цена акций AMZN упадет 9?0434, учитывая, что промышленный индекс Доу-Джонса (DJIA) упал ранее?»

Условная вероятность A при условии, что B произошло, может быть выражена как:

Если A означает: «цена AMZN падает», то P(AMZN) — это вероятность того, что AMZN упадет; и B: «DJIA уже упал», а P(DJIA) — вероятность того, что DJIA упал; тогда выражение условной вероятности читается как «вероятность того, что AMZN упадет при снижении индекса DJIA, равна вероятности того, что цена AMZN упадет, а индекс DJIA упадет по сравнению с вероятностью снижения индекса DJIA».

P(AMZN|DJIA) = P(AMZN и DJIA) / P(DJIA)

P(AMZN и DJIA) – это вероятность того, что 90 434 произойдут как 90 435 A, так и B. Это также то же самое, что вероятность A, умноженная на вероятность B при условии, что A произойдет, выраженная как P(AMZN) x P(DJIA|AMZN). Тот факт, что эти два выражения равны, приводит к теореме Байеса, которая записывается как:

если P(AMZN и DJIA) = P(AMZN) x P(DJIA|AMZN) = P(DJIA) x P(AMZN|DJIA)

тогда P(AMZN|DJIA) = [P(AMZN) x P(DJIA|AMZN)] / P(DJIA).

Где P(AMZN) и P(DJIA) — вероятности падения Amazon и Dow Jones независимо друг от друга.

Формула объясняет взаимосвязь между вероятностью гипотезы до того, как будут получены доказательства P(AMZN), и вероятностью гипотезы после получения доказательств P(AMZN|DJIA), учитывая гипотезу для Amazon с учетом доказательств в индексе Доу.

Численный пример теоремы Байеса

В качестве числового примера представьте, что есть тест на наркотики, который составляет 9Точность 8% означает, что в 98% случаев он показывает действительно положительный результат для тех, кто употребляет наркотик, и в 98% случаев показывает истинно отрицательный результат для тех, кто не употребляет наркотик.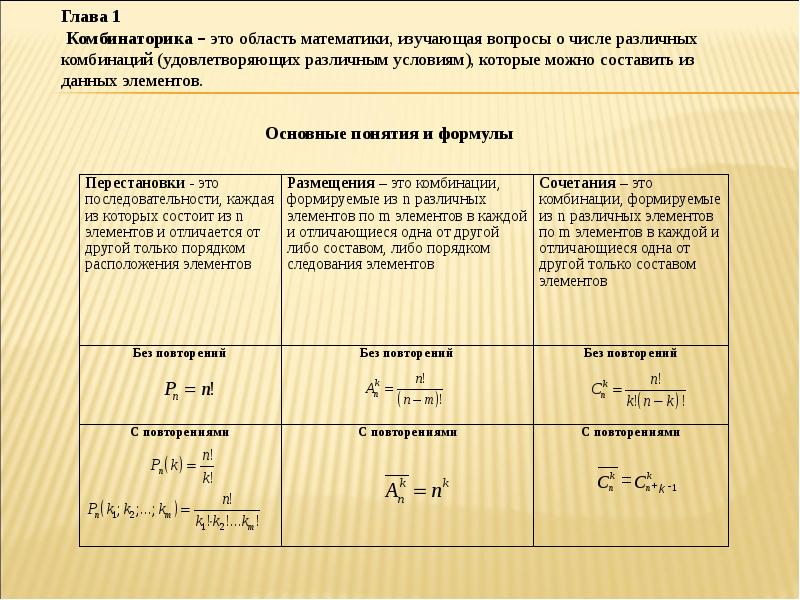

Далее предположим, что 0,5% людей употребляют наркотики. Если случайно выбранный человек дал положительный результат на наркотик, можно сделать следующий расчет, чтобы определить вероятность того, что человек действительно употребляет наркотик.

(0,98 х 0,005) / [(0,98 х 0,005) + ((1 — 0,98) х (1 — 0,005))] = 0,0049 / (0,0049+ 0,0199) = 19,76%

Теорема Байеса показывает, что даже если человек дал положительный результат в этом сценарии, вероятность того, что человек не примет наркотик, составляет примерно 80%.

Какова история теоремы Байеса?

Теорема была обнаружена среди бумаг английского пресвитерианского министра и математика Томаса Байеса и опубликована посмертно, будучи прочитанной в Королевском обществе в 1763 году. вычислительная мощность для выполнения сложных расчетов.

Эти достижения привели к увеличению числа приложений, использующих теорему Байеса. В настоящее время он применяется для самых разных вероятностных расчетов, включая финансовые расчеты, генетику, употребление наркотиков и борьбу с болезнями.

Что утверждает теорема Байеса?

Теорема Байеса утверждает, что условная вероятность события, основанная на появлении другого события, равна вероятности второго события при первом событии, умноженной на вероятность первого события.

Что вычисляется в теореме Байеса?

Теорема Байеса вычисляет условную вероятность события на основе значений конкретных связанных известных вероятностей.

Что такое калькулятор теоремы Байеса?

Калькулятор теоремы Байеса вычисляет вероятность события A в зависимости от другого события B, учитывая априорные вероятности A и B, и вероятность B в зависимости от A. Он вычисляет условные вероятности на основе известных вероятностей.

Как теорема Байеса используется в машинном обучении?

Теорема Байеса предлагает полезный метод для размышлений о взаимосвязи между набором данных и вероятностью. Другими словами, теорема гласит, что вероятность того, что данная гипотеза верна на основе конкретных наблюдаемых данных, может быть сформулирована как нахождение вероятности наблюдения данных с учетом гипотезы, умноженной на вероятность того, что гипотеза верна независимо от данных, разделенная вероятностью наблюдения данных независимо от гипотезы.