Гипербола: формулы, примеры решения задач
- Определение гиперболы, решаем задачи вместе
- Решить задачи на гиперболу самостоятельно, а затем посмотреть решение
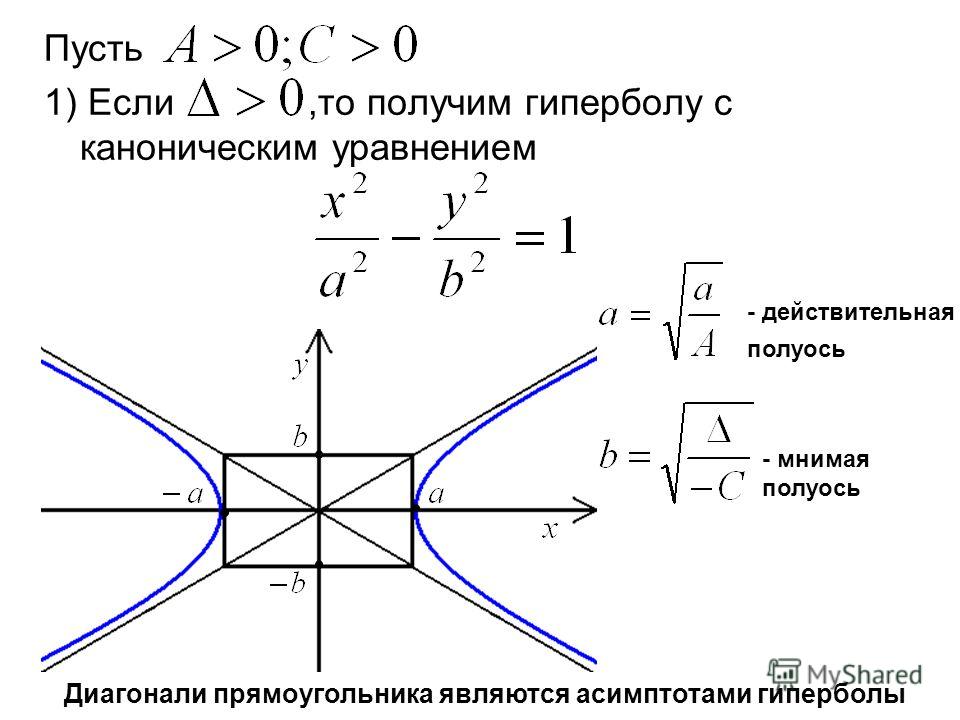
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:
,
где a и b — длины полуосей, действительной и мнимой.
На чертеже ниже фокусы обозначены как и .
На чертеже ветви гиперболы — бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы,
если его действительная полуось 
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:
.
Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки и , где
,
называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
Число
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Решение.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4,
е. полуось a = 4,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:
.
Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет .
Решение. Как следует из условия, действительная полуось a = 24. А эксцентриситет — это пропорция и
так как a = 24, то коэффициент пропорциональности
отношения
.
Результат — каноническое уравнение гиперболы:
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кривые второго порядка
Если — произвольная точка левой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Если — произвольная точка правой ветви гиперболы () и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы
,
где — расстояние от левого фокуса до точки любой ветви гиперболы, — расстояние от правого фокуса до точки любой ветви гиперболы и и — расстояния этой точки до директрис и .
Пример 4. Дана гипербола
.
Составить уравнение её директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. . Вычисляем:
.
Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями
.
На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:
, где .
В том случае, когда угол между асимптотами — прямой, гипербола называется
равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её
уравнение запишется в виде y = k/x,
то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы и координаты точки , лежащей на гиперболе. Составить уравнение гиперболы.
Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения . Для этого подставляем в формулу канонического уравнения гиперболы координаты точки M x и y и значения числителя и знаменателя из уравнения асимптоты, кроме того, умножаем каждую дробь в левой части на коэффициент пропорциональности k.
.
Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим
образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после
отражения движется так, как будто он исходит из другого фокуса.
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4, а один из фокусов в точке (5; 0)
посмотреть правильное решение и ответ,
2) действительная ось 6, расстояние между фокусами 8
посмотреть правильное решение и ответ,
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
посмотреть правильное решение и ответ.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кривые второго порядка
Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
Эллипс
Парабола
уравнений гиперболы | Колледж Алгебра
Результаты обучения
- Вывести уравнение для гиперболы с центром в начале координат
- Напишите уравнение для гиперболы с центром в начале координат
- Решить прикладную задачу с гиперболами
В аналитической геометрии гипербола представляет собой коническое сечение, образованное пересечением прямого кругового конуса с плоскостью под таким углом, что обе половины конуса пересекаются. Это пересечение дает две отдельные неограниченные кривые, которые являются зеркальным отображением друг друга.
Это пересечение дает две отдельные неограниченные кривые, которые являются зеркальным отображением друг друга.
Гипербола
Как и эллипс, гипербола также может быть определена как набор точек на координатной плоскости. Гипербола — это множество всех точек [латекс]\слева(х,у\справа)[/латекс] на плоскости, таких, что разность расстояний между [латекс]\слева(х,у\справа)[/латекс ], а фокусы — положительная постоянная.
Обратите внимание, что определение гиперболы очень похоже на определение эллипса. Отличие состоит в том, что гипербола определяется в терминах разности двух расстояний, тогда как эллипс определяется в терминах суммы двух расстояний.
Как и эллипс, каждая гипербола имеет две оси симметрии . Поперечная ось представляет собой отрезок, который проходит через центр гиперболы и имеет вершины в качестве своих концов. Фокусы лежат на линии, содержащей поперечную ось. Сопряженная ось перпендикулярна поперечной оси и имеет ко-вершины в качестве своих конечных точек.
Ключевые характеристики гиперболы
В этом разделе мы ограничим наше обсуждение гиперболами, расположенными вертикально или горизонтально в координатной плоскости; оси будут лежать или быть параллельными осям x и y . Мы рассмотрим два случая: те, которые сосредоточены в начале координат, и те, которые сосредоточены в точке, отличной от начала координат.
Стандартная форма уравнения гиперболы с центром в начале координат
Пусть [латекс]\влево(-c,0\вправо)[/латекс] и [латекс]\влево(с,0\вправо)[/латекс ] быть фокусов гиперболы с центром в начале координат.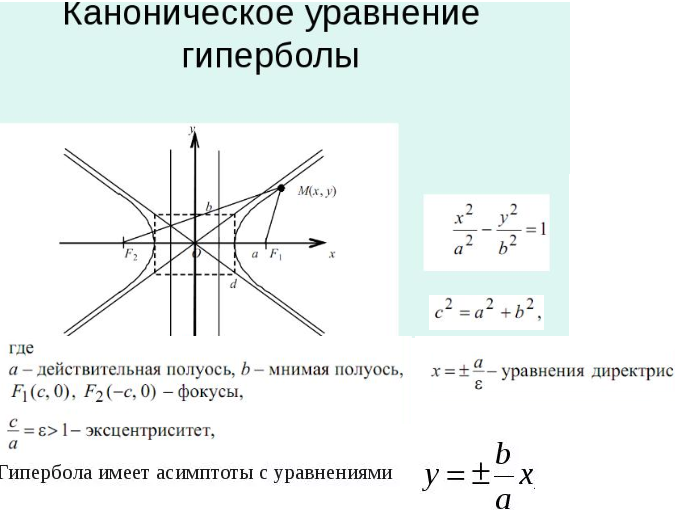 Гипербола — это множество всех точек [латекс]\слева(х,у\справа)[/латекс], таких что разность расстояний от [латекс]\слева(х,у\справа)[/латекс] до очаги постоянны.
Гипербола — это множество всех точек [латекс]\слева(х,у\справа)[/латекс], таких что разность расстояний от [латекс]\слева(х,у\справа)[/латекс] до очаги постоянны.
Если [латекс]\влево(а,0\вправо)[/латекс] является вершиной гиперболы, расстояние от [латекс]\влево(-c,0\вправо)[/латекс] до [латекс] \left(a,0\right)[/latex] равно [latex]a-\left(-c\right)=a+c[/latex]. Расстояние от [латекс]\слева(с,0\справа)[/латекс] до [латекс]\слева(а,0\справа)[/латекс] равно [латекс]с-а[/латекс]. Разность расстояний от фокусов до вершины равна
[латекс]\влево(а+с\вправо)-\влево(с-а\вправо)=2а[/латекс]
Если [латекс]\влево(х,у\вправо)[/латекс] является точкой на гиперболе мы можем определить следующие переменные:
[латекс]\begin{align}&{d}_{2}=\text{расстояние от }\left(-c,0\right)\text{ до }\left(x,y\right)\\ &{d}_{1}=\text{расстояние от }\left(c,0\right)\text{ до }\left(x,y\ right)\end{align}[/latex]
По определению гиперболы [latex]\lvert{d}_{2}-{d}_{1}\rvert[/latex] постоянна для любой точки [латекс]\влево(х,у\вправо)[/латекс] на гиперболе. {2}[/latex] всегда находится под переменной с положительным коэффициентом. Итак, если вы установите другую переменную равной нулю, вы можете легко найти точки пересечения. В случае, когда центр гиперболы находится в начале координат, точки пересечения совпадают с вершинами. 9{2}}{25}=1[/латекс].
{2}[/latex] всегда находится под переменной с положительным коэффициентом. Итак, если вы установите другую переменную равной нулю, вы можете легко найти точки пересечения. В случае, когда центр гиперболы находится в начале координат, точки пересечения совпадают с вершинами. 9{2}}{25}=1[/латекс].
Запись уравнений гиперболы в стандартной форме
Как и в случае с эллипсами, запись уравнения гиперболы в стандартной форме позволяет вычислить ключевые характеристики: ее центр, вершины, ко-вершины, фокусы, асимптоты, а также длины и положения поперечной и сопряженной осей. И наоборот, уравнение гиперболы можно найти, учитывая ее ключевые особенности. Начнем с нахождения стандартных уравнений для гипербол с центром в начале координат. Затем мы обратим наше внимание на поиск стандартных уравнений для гипербол с центром в какой-либо точке, отличной от начала координат. 9{2}[/латекс]. Это соотношение используется для записи уравнения гиперболы при заданных координатах ее фокусов и вершин.
Как сделать: Имея вершины и фокусы гиперболы с центром в точке [латекс]\влево(0,\текст{0}\вправо)[/латекс], запишите ее уравнение в стандартной форме.
- Определите, лежит ли поперечная ось на оси x или y .
- Если заданные координаты вершин и фокусов имеют вид [latex]\left(\pm a,0\right)[/latex] и [latex]\left(\pm c,0\right)[/latex ] соответственно, то поперечной осью является 9{2}[/latex] в стандартную форму уравнения, определенного на шаге 1.
Пример: нахождение уравнения гиперболы с центром в точке (0,0) при заданных фокусах и вершинах
Какова стандартная форма уравнения гиперболы с вершинами right)[/latex] и фокусы [latex]\left(\pm 2\sqrt{10},0\right)?[/latex]
Показать решениеПопробуйте
Уравнение стандартной формы гиперболы с вершинами [латекс]\влево(0,\pm 2\вправо)[/латекс] и фокусами [латекс]\влево(0,\pm 2\ sqrt{5}\справа)?[/latex]
Показать решениеГиперболы, не центрированные в начале координат
Как и графики для других уравнений, график гиперболы можно трансформировать.
 Если перевести гиперболу [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр гиперболы будет [latex]\left(h,k\right)[/ латекс]. Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [latex]x[/latex] на [latex]\left(x-h\right)[/latex] и [latex]y[/latex] на [латекс]\влево(у-к\вправо)[/латекс]. 9{2}[/латекс]
Если перевести гиперболу [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр гиперболы будет [latex]\left(h,k\right)[/ латекс]. Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [latex]x[/latex] на [latex]\left(x-h\right)[/latex] и [latex]y[/latex] на [латекс]\влево(у-к\вправо)[/латекс]. 9{2}[/латекс] - координаты фокусов: [латекс]\влево(ч\пм с,к\вправо)[/латекс]
- координаты фокусов: [латекс]\влево(ч,к\пм с\вправо)[/латекс]
Асимптоты гиперболы совпадают с диагоналями центрального прямоугольника. Длина прямоугольника равна [латекс]2а[/латекс], а ширина — [латекс]2b[/латекс]. Наклоны диагоналей равны [латекс]\pm \frac{b}{a}[/латекс], и каждая диагональ проходит через центр [латекс]\влево(ч,к\вправо)[/латекс]. Используя формулу точек-наклонов , легко показать, что уравнения асимптот таковы: [latex]y=\pm \frac{b}{a}\left(x-h\right)+k[/latex]. 9{2}[/латекс]
Используя вышеприведенные рассуждения, уравнения асимптот таковы: [латекс]y=\pm \frac{a}{b}\left(x-h\right)+k[/latex]. {2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти стандартное уравнение гиперболы, когда заданы вершины и фокусы. 9{2}[/latex] в стандартную форму уравнения, определенного на шаге 1.
{2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти стандартное уравнение гиперболы, когда заданы вершины и фокусы. 9{2}[/latex] в стандартную форму уравнения, определенного на шаге 1.
Пример: нахождение уравнения гиперболы с центром в точке (
h , k ) с учетом ее фокусов и вершин ,-2\вправо)[/латекс] и [латекс]\влево(6,-2\вправо)[/латекс] и фокусы в [латекс]\влево(-2,-2\вправо)[/латекс] и [латекс]\влево(8,-2\вправо)?[/латекс] Показать решениеПопробуйте
Уравнение стандартной формы гиперболы с вершинами [латекс]\влево(1,-2\вправо)[/латекс] и [латекс]\влево(1,\текст{8}\вправо) )[/latex] и фокусы [латекс]\левый(1,-10\правый)[/латекс] и [латекс]\левый(1,16\правый)?[/латекс]
Показать решениеРешение прикладных задач, связанных с гиперболами
Как мы обсуждали в начале этого раздела, гиперболы находят практическое применение во многих областях, таких как астрономия, физика, инженерия и архитектура. Эффективность конструкции гиперболических градирен особенно интересна. Градирни используются для передачи отработанного тепла в атмосферу и часто рекламируются за их способность эффективно генерировать энергию. Из-за своей гиперболической формы эти конструкции способны противостоять сильным ветрам, при этом требуя меньше материала, чем любые другие формы их размера и прочности. Например, 500-футовая башня может быть сделана из железобетонной оболочки шириной всего 6 или 8 дюймов!
Эффективность конструкции гиперболических градирен особенно интересна. Градирни используются для передачи отработанного тепла в атмосферу и часто рекламируются за их способность эффективно генерировать энергию. Из-за своей гиперболической формы эти конструкции способны противостоять сильным ветрам, при этом требуя меньше материала, чем любые другие формы их размера и прочности. Например, 500-футовая башня может быть сделана из железобетонной оболочки шириной всего 6 или 8 дюймов!
Градирни на электростанции Drax в Северном Йоркшире, Великобритания (фото: Les Haines, Flickr)
Первые гиперболические градирни были спроектированы в 1914 году и имели высоту 35 метров. Сегодня самые высокие градирни находятся во Франции, их высота составляет 170 метров. В Примере 6 мы будем использовать проектную схему градирни, чтобы найти гиперболическое уравнение, моделирующее ее стороны.
Пример: решение прикладных задач, связанных с гиперболой
Схема градирни показана ниже. Башня стоит 179.6 метров в высоту. Диаметр вершины 72 метра. Ближайшие стороны башни находятся на расстоянии 60 метров друг от друга.
Башня стоит 179.6 метров в высоту. Диаметр вершины 72 метра. Ближайшие стороны башни находятся на расстоянии 60 метров друг от друга.
Проект градирни с естественной тягой
Найдите уравнение гиперболы, моделирующей стороны градирни. Предположим, что центр гиперболы , обозначенный на рисунке пересечением пунктирных перпендикулярных линий, является началом координатной плоскости. Округлите окончательные значения до четырех знаков после запятой.
Показать решениеПопробуйте
Ниже показан проект градирни. Найдите уравнение гиперболы, моделирующей стороны градирни. Предположим, что центр гиперболы, обозначенный на рисунке пересечением пунктирных перпендикулярных линий, является началом координатной плоскости.
Показать решениеПоддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Конические сечения и стандартные формы уравнений
Горячая математика А коническое сечение является пересечением плоскости и двойной правой окружности
конус
. Изменяя угол и место пересечения, мы можем создавать различные типы коник. Существует четыре основных типа:
круги
,
эллипсы
,
гиперболы
и
параболы
. Ни одно из пересечений не будет проходить через вершины конуса.
Изменяя угол и место пересечения, мы можем создавать различные типы коник. Существует четыре основных типа:
круги
,
эллипсы
,
гиперболы
и
параболы
. Ни одно из пересечений не будет проходить через вершины конуса.
Если прямой круговой конус разрезается плоскостью, перпендикулярной оси конуса, пересечение представляет собой окружность. Если плоскость пересекает одну из частей конуса и его ось, но не перпендикулярна оси, то пересечение будет эллипсом. Чтобы образовалась парабола, пересекающая плоскость должна быть параллельна одной стороне конуса и должна пересекать одну часть двойного конуса. И, наконец, для создания гиперболы плоскость пересекает обе части конуса. Для этого наклон пересекающейся плоскости должен быть больше, чем у конуса.
Общее уравнение для любого конического сечения:
А
Икс
2
+
Б
Икс
у
+
С
у
2
+
Д
Икс
+
Е
у
+
Ф
«=»
0
где
А
,
Б
,
С
,
Д
,
Е
и
Ф
являются константами.
При изменении значений некоторых констант изменится и форма соответствующей коники. Важно знать различия в уравнениях, чтобы помочь быстро определить тип коники, представленной данным уравнением.
Если
Б
2
−
4
А
С
меньше нуля, то если коника существует, то это будет либо окружность, либо эллипс.
Если
Б
2
−
4
А
С
равна нулю, то если коника существует, то это будет парабола.
Если
Б
2
−
4
А
С
больше нуля, то если коника существует, то это будет гипербола.
СТАНДАРТНЫЕ ФОРМЫ УРАВНЕНИЙ КОНИЧЕСКИХ СЕЧЕНИЙ:
| Круг | ( Икс − час ) 2 + ( у − к ) 2 «=» р 2 | Центр
(
час
,
к
)
. Радиус р . |
| Эллипс с горизонтальной большой осью | ( Икс − час ) 2 а 2 + ( у − к ) 2 б 2 «=» 1 | Центр
(
час
,
к
)
. |
| Эллипс с вертикальной большой осью | ( Икс − час ) 2 б 2 + ( у − к ) 2 а 2 «=» 1 | Центр
(
час
,
к
)
. |
| Гипербола с горизонтальной поперечной осью | ( Икс − час ) 2 а 2 − ( у − к ) 2 б 2 «=» 1 | Центр
(
час
,
к
)
. |
| Гипербола с вертикальной поперечной осью | ( у − к ) 2 а 2 − ( Икс − час ) 2 б 2 «=» 1 | Центр
(
час
,
к
)
. |
| Парабола с горизонтальной осью | ( у − к ) 2 «=» 4 п ( Икс − час ) , п ≠ 0 | Вершина
(
час
,
к
)
. |
| Парабола с вертикальной осью | ( Икс − час ) 2 «=» 4 п ( у − к ) , п ≠ 0 | Вершина
(
час
,
к
)
. |
Решение систем уравнений
Вы должны быть знакомы с решение системы линейных уравнений . Геометрически это дает точку (точки) пересечения двух или более прямых линий. Точно так же решения системы квадратных уравнений давали бы точки пересечения двух или более коник.
Алгебраически система квадратных уравнений может быть решена с помощью устранение или замена как и в случае линейных систем.
Пример:
Решите систему уравнений.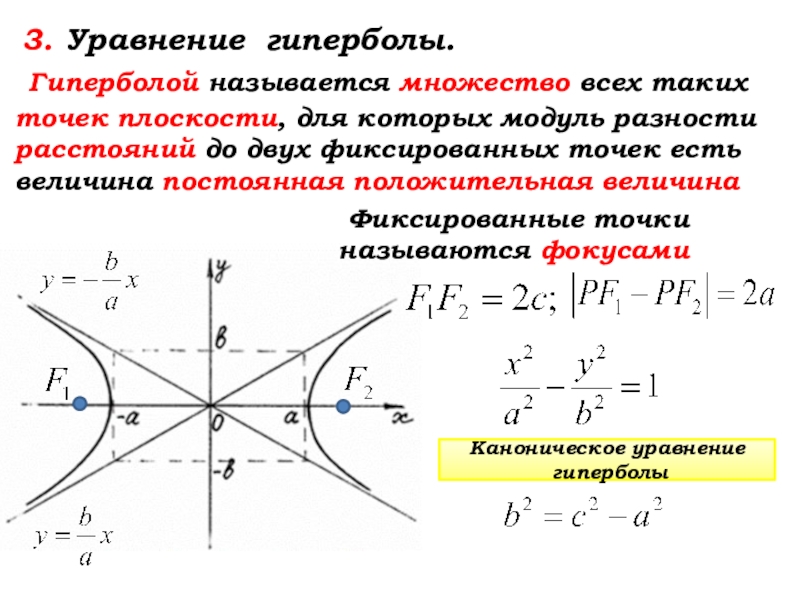
Икс 2 + 4 у 2 «=» 16 Икс 2 + у 2 «=» 9
Коэффициент Икс 2 одинаково для обоих уравнений. Итак, вычтем второе уравнение из первого, чтобы исключить переменную Икс . Вы получаете:
3 у 2 «=» 7
Решение для у :
3 у 2 3 «=» 7 3 у 2 «=» 7 3 у «=» ± 7 3
Используйте значение
у
оценить
Икс
.
Икс 2 + 7 3 «=» 9 Икс 2 «=» 9 − 7 3 «=» 20 3 Икс «=» ± 20 3
Следовательно, решения
(
+
20
3
,
+
7
3
)
,
(
+
20
3
,
−
7
3
)
,
(
−
20
3
,
+
7
3
)
и
(
−
20
3
,
−
7
3
)
.

 Если перевести гиперболу [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр гиперболы будет [latex]\left(h,k\right)[/ латекс]. Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [latex]x[/latex] на [latex]\left(x-h\right)[/latex] и [latex]y[/latex] на [латекс]\влево(у-к\вправо)[/латекс]. 9{2}[/латекс]
Если перевести гиперболу [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр гиперболы будет [latex]\left(h,k\right)[/ латекс]. Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [latex]x[/latex] на [latex]\left(x-h\right)[/latex] и [latex]y[/latex] на [латекс]\влево(у-к\вправо)[/латекс]. 9{2}[/латекс]