Смежные углы равны то прямые. Признаки параллельности двух прямых. Свойства параллельных прямых
Смежные углы равны то прямые. Признаки параллельности двух прямых. Свойства параллельных прямых
Признаки параллельности двух прямых
Теорема 1. Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Следствие 1 . Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны
Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное) тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
Затем проводим через точку М прямую b
перпендикулярно прямой р.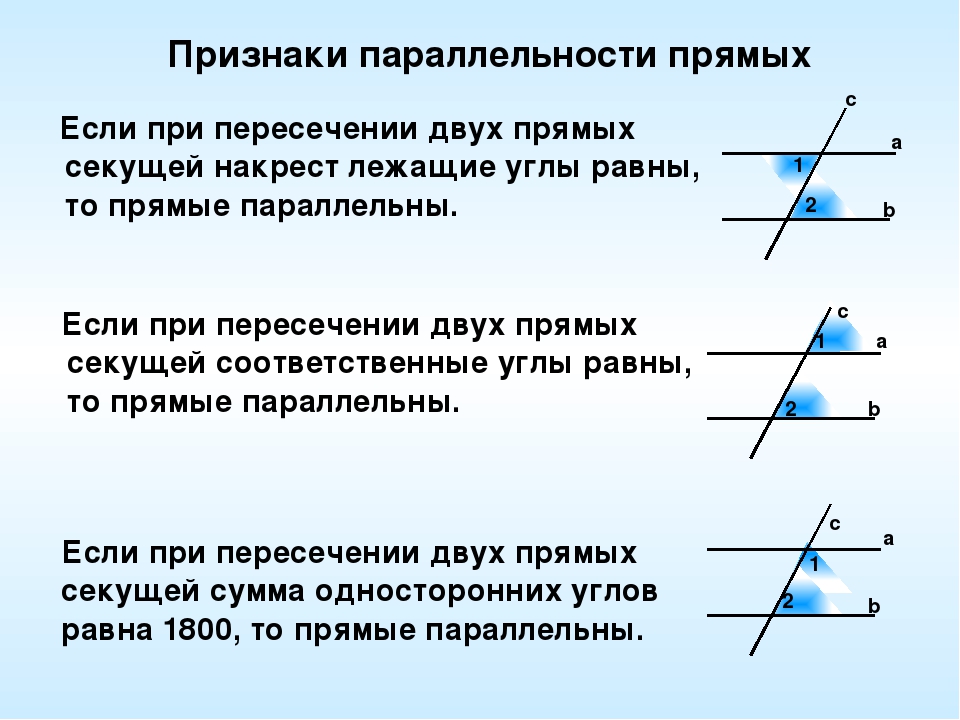
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной .
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;
соответственные углы равны;
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см.
рис.2).
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные.
У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.
Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d.
По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис. 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2).
Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.
Вопрос 8.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°.
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
Которые лежат в одной плоскости и либо совпадают, либо не пересекаются. В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается.
Свойства
- Параллельность — бинарное отношение эквивалентности , поэтому разбивает всё множество прямых на классы параллельных между собой прямых.
- Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии , в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две)
- 2 параллельные прямые в пространстве лежат в одной плоскости.
- При пересечении 2 параллельных прямых третьей, называемой секущей :
- Секущая обязательно пересекает обе прямые.
- При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Накрест лежащие углы равны.
- Соответственные углы равны.
- Односторонние углы в сумме составляют 180°.
- Накрест лежащие углы равны.
В геометрии Лобачевского
В геометрии Лобачевского в плоскости через точку C вне данной прямой A B проходит бесконечное множество прямых, не пересекающих A B . Из них параллельными к A B называются только две. Прямая C E называется равнобежной (параллельной) прямой A B в направлении от A к B , если:
- точки B и E лежат по одну сторону от прямой A C ;
- прямая C E не пересекает прямую A B , но всякий луч, проходящий внутри угла A C E , пересекает луч A B .
Аналогично определяется прямая, равнобежная A B в направлении от B к A .
Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися .
См. также
Wikimedia Foundation . 2010 .
Смотреть что такое «Накрест лежащие» в других словарях:
Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему. Теорема Фалеса одна из теорем планиметрии. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести… … Википедия
Русский орден Св. Анны, учрежден был владетельным герцогом Шлезвиг Гольштинским Карлом Фредериком в 1736 г. в честь супруги своей цесаревны Анны Петровны (дочери Петра Великого) и причислен к русским орденам императором Петром III. Орден Св. Анны …
Для испытания охотничьих ружейных стволов учреждены во всех западно европейских государствах. Наиболее известные из них находятся в Лондоне, Бирмингеме, Люттихе, Зуле и Сент Этьене. По новым, недавно введенным в Англии правилам каждый ствол… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Так называется один из способов количественного определения содержания веществ в растворах; методы К.
применимы к количественному определению всех тех веществ, которые дают окрашенные растворы, или могут быть, с помощью какой либо реакции,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Жалуемый за особые заслуги или отличие знак, установленной формы, носимый на ленте, цепи или иным образом. Имеются указания, что в восточной римской империи еще со времен Константина Великого императоры установляли кавалерские товарищества или… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Жалуемый за особые заслуги или отличие знак, установленной формы, носимый на ленте, цепи или иным образом. Имеются указания, что в вост. римской империи еще со времен Константина Вел., императоры установляли кавалерские товарищества или ордена,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Второе семейство этого отряда состоит из одного рода и вида моржа (Odobenus rosmarus)*, самого огромного из всех ластоногих. * Моржи имеют в анатомии черты сходства с ушастыми тюленями и также происходят от примитивного медведеобразного… … Жизнь животных
— (др.
греч. παραλληλόγραμμον от παράλληλος параллельный и γραμμή линия) это четырёхуго … Википедия
Пересечения прямых (анимация) Аксиома параллельности Евклида, или пятый постулат одна из аксиом, лежащ … Википедия
Пересечения прямых (анимация) Аксиома параллельности Евклида, или пятый постулат одна из аксиом, лежащих в основании классической планиметрии. Впервые приведена в «Началах» Евклида : И если прямая, падающая на две прямые, образует внутренние и … Википедия
Свойства параллельных прямых – основные определения
4.3
Средняя оценка: 4.3
Всего получено оценок: 300.
4.3
Средняя оценка: 4.3
Всего получено оценок: 300.
Свойства параллельных прямых крайне часто встречаются при решении задач и доказательств теорем. Произвольные прямые – редкость, но есть такие фигуры, как квадрат или параллелограмм, где параллельные прямые могут стать основой задачи, а без знания свойств параллельных прямых решить такие задачи невозможно.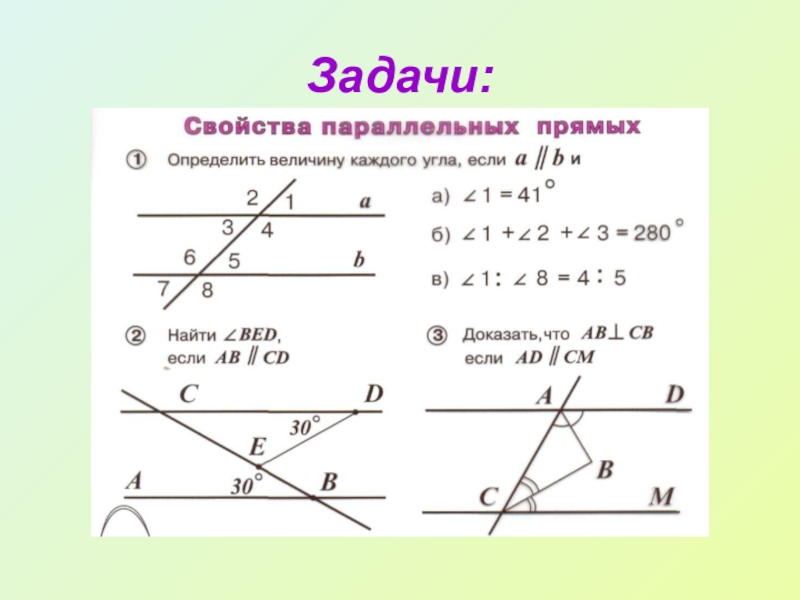
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Что такое свойства параллельных прямых
Для начала выделим определения, которые необходимо знать для изучения свойств параллельных прямых.
Параллельные прямые это прямые, которые не имеют общих точек, или прямые, которые не пересекаются и лежат в одной плоскости.
Пересечение означает, что у двух объектов есть общая точка или набор точек. Поэтому когда в геометрии говорят, что прямые имеют общую точку, имеется в виду, что они пересекаются.
При пересечении двух прямых секущей, образуются накрест лежащие, соответственные и односторонние углы.
Существует аксиома параллельных прямых, которая крайне важна при доказательстве некоторых свойств и является основным свойством параллельных прямых. Аксиома гласит, что через точку на плоскости можно провести только одну прямую, параллельную данной.
Две группы свойств параллельных прямых
Свойств у параллельных прямых всего 5, но они делятся на две большие группы: следствия из аксиомы параллельных прямых и следствия из признаков параллельности прямых.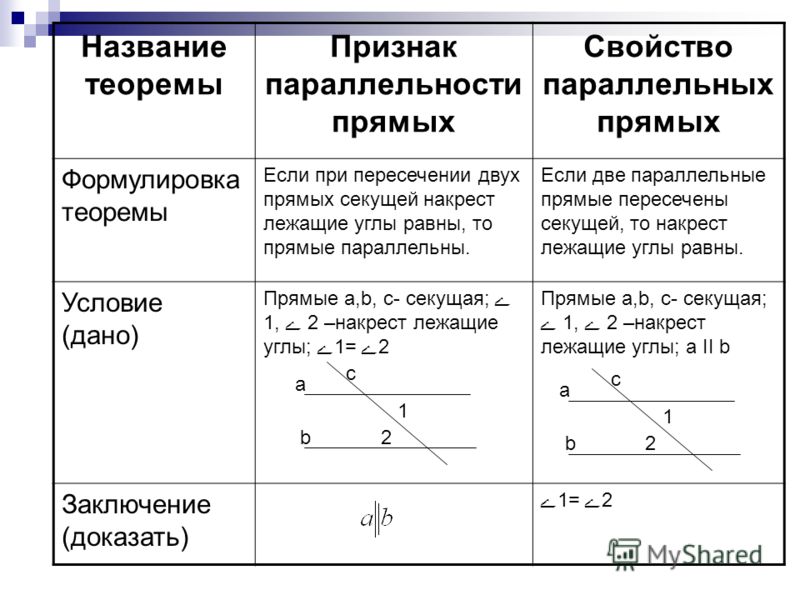
Начнем с первой группы.
Следствия из аксиомы параллельных прямых
Следствие 1
Если одна из двух параллельных прямых, параллельна третьей, то и другая прямая ей параллельна.
Кажется, что это логично и не требует доказательства. Но в геометрии количество утверждений, не требующих обоснования, крайне мало, и каждое из них носит название – аксиома.
Аксиомы были выведены еще на заре геометрии и с тех пор мало что изменилось. Большая часть современных теорем выведена на основании аксиом Древней Греции. Эти утверждения единственные, что в математике не требует доказательства.
Проведем две параллельные прямые а и b. Прямая с параллельна прямой а. Предположим, что при этом с не параллельна прямой b. Тогда у нее должна быть какая-то точка пересечения К. То есть через точку К проходит две прямые с и b. При этом каждая из этих прямых должна быть параллельна прямой а.
То есть, через одну точку на плоскости проведены две прямые, параллельные данной.
Это невозможно, потому что противоречит аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямые с и b параллельны.
Следствие 2
Следствие 2 очень важно, так как говорит о секущей двух параллельных прямых. Свойство гласит: если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.
Доказательство также ведется методом от противного. Проведем две прямые: а и b. Представим, что прямая с пересекает прямую а, но не пересекает прямую b. Тогда прямые c и b параллельны. При этом с пересекает а, то есть у этих прямых есть общая точка К.
Тогда через точку К проходит прямая а и прямая с, но каждая из них параллельна b. Значит, через одну точку проходит две прямых параллельных прямой b, а это невозможно по аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямая с пересекает каждую из прямых а и b, что и требовалось доказать.
Рис. 2. Рисунок к доказательству.Следствия из признаков параллельности
Эту группу запомнить проще всего.
Свойств параллельности прямых всего 3 и каждому из них соответствует свое следствие.
- Прямые параллельны, если накрест лежащие углы при секущей равны. Следствие вполне логично: Накрест лежащие углы при двух параллельных прямых и секущей равны.
- Прямые параллельны, если соответственные углы равны. Следствие: соответственные углы при параллельных прямых и секущей равны.
- Прямые параллельны, если сумма односторонних углов равна 180. Следствие: сумма односторонних углов при параллельных прямых и секущей равны 180
Что мы узнали?
Мы дали понятие параллельным прямым, выделили две большие группы свойств параллельных прямых и доказали два свойства. Разобрались с использованием аксиомы параллельных прямых при доказательстве теорем в геометрии.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Девлет Болтаев
5/5
Иван Маковецкий
5/5
Иришка Чипрягова
5/5
Елена Иванова
5/5
Константин Никитич
5/5
Манижа Гуломджонова
5/5
Екатерина Лобычева
4/5
Оценка статьи
4.
3
Средняя оценка: 4.3
Всего получено оценок: 300.
А какая ваша оценка?
Параллельные прямые — определение, свойства
Две или более прямых, лежащих в одной плоскости и никогда не пересекающихся друг с другом, называются параллельными прямыми . Они равноудалены друг от друга и имеют одинаковый наклон. Давайте узнаем больше о параллельных прямых, свойствах параллельных прямых и углах, которые образуются при пересечении параллельных прямых секущей.
| 1. | Что такое параллельные линии? |
| 2. | Параллельные линии и поперечные |
| 3. | Свойства параллельных линий |
| 4. | Часто задаваемые вопросы о параллельных линиях |
Что такое параллельные линии?
Параллельные линии — это прямые линии, которые никогда не пересекаются друг с другом, как бы мы их ни растягивали.
Обратите внимание на следующий рисунок, на котором показаны параллельные линии. Линия «а» параллельна линии «b», а линия «p» параллельна линии «q».
Параллельные линии и поперечные
При пересечении любых двух параллельных прямых другой прямой, называемой секущей, образуется множество пар углов. В то время как некоторые углы конгруэнтны (равны), другие являются дополнительными. Обратите внимание на следующий рисунок, чтобы увидеть параллельных прямых, пересекаемых поперечной . Параллельные прямые обозначены как L1 и L2, которые пересекаются секущей. Восемь отдельных углов были образованы двумя параллельными прямыми и секущей. Каждый угол был помечен с помощью алфавита.
Ниже приведены пары углов, образованных двумя параллельными прямыми L1 и L2.
- Соответствующие углы: Следует отметить, что пара соответствующих углов равна по размеру. На данном рисунке четыре пары соответствующих углов, то есть ∠a = ∠e, ∠b = ∠f, ∠c = ∠g и ∠d = ∠h
- Альтернативные внутренние углы: Альтернативные внутренние углы образуются внутри двух параллельных линий, которые пересекаются секущей. Они равны в меру. На этом рисунке ∠c = ∠e, ∠d = ∠f
- Альтернативные внешние углы: Альтернативные внешние углы образованы по обе стороны от поперечной, и они равны по размеру. На этом рисунке ∠a = ∠g, ∠b = ∠h
- Последовательные внутренние углы: Последовательные внутренние углы или ковнутренние углы образуются на внутренней стороне поперечной и являются дополнительными. Здесь ∠c + ∠f = 180°, а ∠d + ∠e = 180°
- Вертикально противоположные углы: Вертикально противоположные углы образуются, когда две прямые пересекают друг друга, и они равны по размеру. Здесь ∠a = ∠c, ∠b = ∠d, ∠e = ∠g, ∠f = ∠h
Они равны в меру. На этом рисунке ∠c = ∠e, ∠d = ∠fСвойства параллельных линий
Параллельные линии можно легко идентифицировать по основным свойствам, приведенным ниже.
- Параллельные линии — это прямые линии, которые всегда находятся на одинаковом расстоянии друг от друга.
- Параллельные линии никогда не пересекаются, независимо от того, насколько они вытянуты в любом направлении.
Как узнать, параллельны ли линии?
Помимо характеристик, приведенных выше, когда любые две параллельные прямые пересекаются секущей, их можно идентифицировать по следующим свойствам.
- Любые две прямые называются параллельными, если соответствующие углы, образованные таким образом, равны.
- Любые две прямые называются параллельными, если образованные таким образом альтернативные внутренние углы равны.
- Любые две прямые называются параллельными, если образованные таким образом альтернативные внешние углы равны.
- Любые две прямые называются параллельными, если смежные внутренние углы по одну сторону от секущей являются дополнительными.
Уравнение параллельных линий
Уравнение прямой линии, как правило, записывается в форме наклона и точки пересечения, представленной уравнением y = mx + b, где «m» — это наклон, а «b» — это точка пересечения с осью y. Значение «m» определяет наклон или градиент и сообщает нам, насколько крута линия.
Следует отметить, что наклон любых двух параллельных линий всегда одинаков. Например, если наклон линии с уравнением y = 4x + 3 равен 4. Следовательно, любая линия, параллельная y = 4x + 3, будет иметь одинаковый наклон, то есть 4. Параллельные прямые имеют разные y- пересекаются и не имеют общих точек.
Параллельные линии Символ
Параллельные линии — это линии, которые никогда не пересекаются, независимо от того, как долго мы их продлеваем. Для обозначения параллельных прямых используется символ || . Например, AB II PQ указывает, что линия AB параллельна линии PQ. Символ, обозначающий непараллельные прямые, равен ∦ .
Примеры параллельных линий в реальной жизни
Ниже приведены несколько примеров параллельных линий в реальной жизни:
- Железнодорожные пути
- Зебра-переход
- Лестница и перила
☛ Ссылки по теме
- Точки и линии
- Пересекающиеся линии
- Линейный сегмент
- Свойства параллельных линий
- Параллельные и перпендикулярные линии
- Уравнение прямой
Часто задаваемые вопросы о параллельных линиях
Что такое параллельные линии в математике?
Параллельные линии — это линии, которые всегда находятся на одном и том же расстоянии друг от друга и никогда не пересекаются.
Для обозначения параллельных прямых используется символ || . Например, AB || CD означает, что линия AB параллельна линии CD.
Что такое параллельные линии и перпендикулярные линии?
Параллельные линии — это линии, которые равноудалены друг от друга и никогда не пересекаются, независимо от того, насколько они могут быть продлены в любом направлении. Например, противоположные стороны прямоугольника представляют собой параллельные линии. С другой стороны, если любые две прямые пересекаются друг с другом в точке 90°, они называются перпендикулярными линиями. Например, смежные стороны прямоугольника являются перпендикулярными линиями, поскольку они пересекают друг друга под углом 90°.
Какие бывают типы углов в параллельных линиях?
Когда любые две параллельные прямые пересекаются секущей, они образуют множество пар углов, таких как соответствующие углы, чередующиеся внутренние углы, чередующиеся внешние углы и последовательные внутренние углы.
Что происходит, когда параллельные прямые пересекаются секущей?
При пересечении любых двух параллельных прямых секущей образуются следующие углы.
- Соответственные углы, равные по размеру.
- Чередующиеся внутренние углы, равные по размеру.
- Альтернативные внешние углы, равные по размеру.
- Последовательные внутренние углы, которые являются дополнительными.
Как выглядят параллельные линии?
Параллельные линии выглядят как железнодорожные пути, которые никогда не пересекаются и всегда равноудалены. Противоположные стороны прямоугольника также представляют собой параллельные линии, находящиеся на равном расстоянии друг от друга.
Каков наклон параллельных линий?
Если две линии параллельны, они имеют одинаковый наклон. Например, если уравнение прямой линии y = 1/2x + 17, ее наклон равен 1/2. Теперь, если линия имеет одинаковый наклон 1/2 в той же плоскости, она будет параллельна данной линии.
Каковы реальные примеры параллельных линий?
Реальные примеры параллельных линий включают железнодорожные пути, края тротуаров, перила лестницы, бесконечные рельсовые пути, противоположные стороны линейки, противоположные края ручки, ластика и т. д.
Каково правило параллельных линий?
Правило для параллельных линий состоит в том, что линии не должны пересекаться друг с другом. Другими словами, если две прямые в одной плоскости находятся на одинаковом расстоянии друг от друга и никогда не пересекаются, то такие прямые называются параллельными.
Что такое символ параллельных линий?
Для обозначения параллельных линий используется символ ||. Любые две параллельные прямые AB и CD изображаются как AB||CD.
Параллельные прямые пересекаются в бесконечности?
Нет, само определение предполагает, что параллельные линии никогда не пересекаются. Следовательно, параллельные прямые не пересекались бы даже на бесконечности.
Параллельные прямые имеют одно и то же уравнение?
Нет, параллельные прямые не имеют одинакового уравнения, но имеют одинаковый наклон.
Например, если уравнение линии представлено как y = 4x + 2, это означает, что наклон этой линии равен 4. Таким образом, другая прямая линия в той же плоскости с таким же наклоном 4 будет параллельна заданная линия.
Параллельные прямые равны по длине?
Нет, параллельные линии могут быть разной длины, но они должны находиться на одинаковом расстоянии друг от друга.
Есть ли в треугольнике параллельные линии?
Нет, в треугольнике нет параллельных прямых. Так как треугольник всегда имеет 3 пересекающиеся стороны; а мы знаем, что параллельные прямые никогда не пересекаются друг с другом, следовательно, в треугольнике не может быть параллельных прямых.
Сколько параллельных линий имеет шестиугольник?
Шестиугольник — это многоугольник с шестью сторонами. В правильном шестиугольнике три пары параллельных прямых.
Какие углы образуются при пересечении параллельных прямых секущей?
При пересечении двух параллельных прямых секущей образуются следующие углы:
- Соответствующие углы
- Альтернативные внутренние углы
- Альтернативные внешние углы
- Последовательные внутренние углы
- Вертикально противоположные углы
Параллельные прямые и пары углов
Параллельные прямые и пары угловПоказать рекламу
Скрыть рекламу
О рекламе
Параллельные линии
Линии параллельны, если они всегда находятся на одном и том же расстоянии друг от друга (называемом «эквидистантными») и никогда не пересекутся.
Просто помните:
Всегда на одинаковом расстоянии друг от друга и никогда не касаясь
.Красная линия параллельна синей линии в каждом из следующих примеров:
Пример 1 | Пример 2 |
Параллельные линии также указывают в одном направлении.
У параллельных линий так много общего. Жаль, что они никогда не встретятся!
Попробуйте сами:
Пары углов
Когда параллельные прямые пересекаются другой прямой (называемой секущей), вы видите, что многие углы совпадают, как в этом примере:
Эти углы можно составить из пар углов , которые имеют специальные названия.
Нажмите на каждое имя, чтобы выделить его:
Теперь поиграйте с ним здесь. Попробуйте перетаскивать точки и выбирать разные типы углов. Вы также можете включить или выключить «Параллельность»:
Проверка параллельных линий
Некоторые из этих специальных пар углов можно использовать для проверки параллельности прямых:
| |||||||||||||||||||||||
..Примеры
Эти прямые параллельны, потому что пара соответствующих углов равна. |