Уравнение перпендикулярной прямой: Уравнение перпендикулярной прямой онлайн

2

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения

Задана точка M₀(x₀, y₀, z₀) и прямая L:

Построить уравнение плоскости α, проходящей через точку M₀ и перпендинулярной прямой L.

Решение. Уравнение плоскости, проходящей через точку M₀ и имеющий нормальный вектор n={A, B, C} имеет следующий вид:

A(x−x0)+B(y−y0)+C(z−z0)=0.

(2)

Направляющий вектор прямой L имеет вид q={m, p, l}. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой

L. Получим следующее уравнение плоскости:

m(x−x0)+p(y−y0)+l(z−z0)=0.

(3)

Упростим уравнение (3):

mx+py+lz+D=0,

(4)

где D=−mx₀−px₀−lx₀.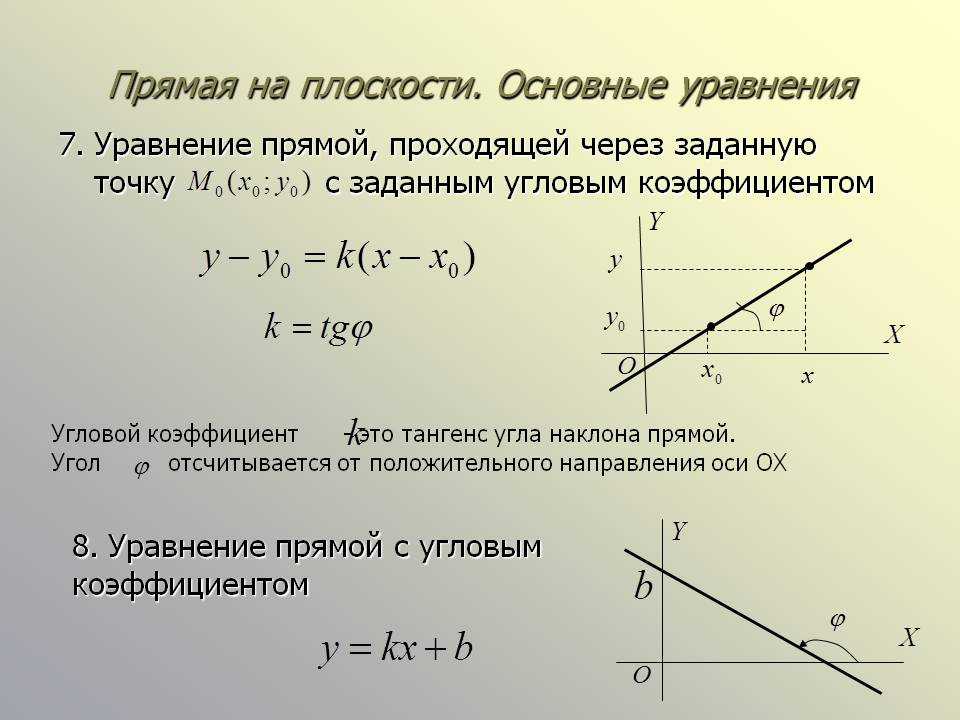

Таким образом уравнение (4) определяет плоскость, проходящей через точку M₀(x₀, y₀, z₀) и перпендикулярной прямой (1).

Ответ. Уравнение плоскости прпоходящей через точку

M₀(x₀, y₀, z₀) и перпендикулярной прямой (1) имеет вид (4).

Пример 1. Найти уравнение плоскости α, проходящую через точку M₀(3, −1, 2) и перпендикулярной прямой L:

Решение. Уравнение плоскости α, проходящей через точку M₀(x₀, y₀, z₀) и имеющий нормальный вектор n={A, B, C} представляется формулой (2).

Направляющий вектор прямой L имеет следующий вид: :

q={m, p, l}={2, 5, 4}

Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.

е. уравнение плоскости (2) примет следующий вид:

m(x−x0)+p(y−y0)+l(z−z0)=0.

(8)

Подставляя координаты точки M₀ и направляющего вектора q в (8), получим:

Упростим уравнение (9):

2x+5y+4z−9=0.

(10)

Ответ: Уравнение плоскости, проходящей через точку M₀(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).

Пример 2. Найти уравнение плоскости α, проходящую через точку M₀(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:

Решение. Приведем параметрическое уравнение (11) к каноническому виду:

Уравнение плоскости α, проходящей через точку M₀(x

₀, y₀, z₀) и имеющий нормальный вектор n={A, B, C} представляется формулой:

A(x−x0)+B(y−y0)+C(z−z0)=0.

(12)

Направляющий вектор прямой L имеет следующий вид:

q={m, p, l}={−5, 3, 11}

Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:

m(x−x0)+p(y−y0 )+l(z−z0)=0.

(13)

Подставляя координаты точки M₀ и направляющего вектора q в (13), получим:

Упростим уравнение (13):

−5x+3y+11z+77=0.

(14)

Ответ. Уравнение плоскости, проходящей через точку M₀(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).

Как найти уравнение перпендикулярной прямой

Все ресурсы по алгебре 1

10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

Алгебра 1 Помощь » Функции и линии » Уравнения прямых » Перпендикулярные линии » Как найти уравнение перпендикулярной прямой

Найдите уравнение перпендикулярной прямой в точке .

Возможные ответы:

Правильный ответ:

Объяснение:

Наклон должен быть обратным отрицательным, а линия должна проходить через точку (3,2). Таким образом, наклон становится , и он подключается к , чтобы найти -intercept.

Сообщить об ошибке

Какая линия перпендикулярна ?

Возможные ответы:

Правильный ответ:

Объяснение:

Перпендикулярные линии имеют отрицательные обратные наклоны друг к другу. Поскольку исходное уравнение имеет наклон , перпендикулярная линия должна иметь наклон . Единственным другим уравнением с наклоном  является .

Сообщить об ошибке

Какое уравнение дает прямую, перпендикулярную проходам через ?

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала преобразуйте данное уравнение в форму пересечения наклона.

 

В этом формате мы можем сказать, что наклон равен . Наклон перпендикулярной линии будет обратной отрицательной величиной, что составляет .

Затем подставьте наклон в форму пересечения наклона, чтобы получить точку пересечения, используя точку, указанную в вопросе.

Перпендикулярное уравнение становится . Это уравнение можно переписать в формате вариантов ответов.

или

Сообщить об ошибке

Какая из этих прямых перпендикулярна?

Возможные ответы:

Ни один из других ответов

Правильный ответ:

Объяснение:

Перпендикулярные линии имеют наклоны, которые являются отрицательными обратными величинами. Наклон данной линии равен 9, поэтому линия, перпендикулярная ей, должна иметь наклон, эквивалентный ее отрицательной обратной величине, которая равна .

Сообщить об ошибке

Какая из этих прямых перпендикулярна ?

Возможные ответы:

Правильный ответ:

Объяснение:

Перпендикулярные линии имеют наклоны, которые являются отрицательными обратными величинами. Данная линия имеет наклон . Отрицательная обратная величина равна , поэтому перпендикулярная линия должна иметь наклон . Единственная линия с наклоном .

Сообщить об ошибке

Найдите уравнение прямой, перпендикулярной  и содержащей точку (5,3).

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти уравнение прямой, нам нужно знать наклон и точку, проходящую через прямую. Зная это, мы можем использовать уравнение, где m — наклон линии, а — точка на линии. Для перпендикулярных линий наклоны являются отрицательными обратными величинами. Наклон равен 5, поэтому наклон перпендикулярной линии будет иметь наклон . Мы знаем, что перпендикулярная линия должна содержать точку (5,3), поэтому у нас есть вся необходимая информация. Теперь мы можем использовать уравнение  

Сообщить об ошибке

Линия проходит через следующие точки:

: (2,3)

: (4,7)

Найдите уравнение прямой , которая перпендикулярна прямой и проходит через точку .

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение прямой записывается в следующем формате: 

1) Итак, первый шаг – найти наклон .

 равно изменению  , деленному на изменение .

Итак,

2) Перпендикулярный наклон линии с наклоном 2 противоположен обратному значению 2, то есть .

3) Следующим шагом будет поиск . Нам не нужно находить уравнение исходной линии; все, что нам нужно от исходной линии, это наклон. Итак, все, что нам нужно, это перпендикулярная линия. Мы можем найти значения для и из одной точки перпендикулярной линии, подставить их и найти .

Наша точка равна (4,7)

Итак, 

Затем мы просто вводим наше значение для , и мы имеем  как функцию .

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Сообщить об ошибке

Напишите уравнение прямой, перпендикулярной с точкой пересечения .

Возможные ответы:

Правильный ответ:

Объяснение:

Эта задача сначала опирается на знание формы пересечения наклона линии, , где m — наклон, а b — пересечение оси y.

Чтобы линия была перпендикулярна другой линии, ее наклон должен быть обратной отрицательной величиной. В этом случае мы ищем прямую, перпендикулярную . Эта линия имеет наклон 2, она же . Это означает, что отрицательный обратный наклон будет . Нам говорят, что точка пересечения по оси Y этой новой строки равна 4,9.0005

Теперь мы можем ввести эти две новые части информации, чтобы получить уравнение

.

Сообщить об ошибке

Напишите уравнение прямой, проходящей через точку , перпендикулярную прямой.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить задачу такого типа, мы должны быть знакомы с формой линии, пересекающей наклон, где m — наклон, а b — точка пересечения с осью y. Линия, к которой наша линия перпендикулярна, имеет уравнение пересечения наклона, что означает, что наклон равен .

Наклон перпендикулярной линии был бы обратной отрицательной величиной, поэтому наш наклон равен .

Мы еще не знаем точку пересечения по оси y нашей линии, поэтому мы можем написать уравнение только так:

.

Мы знаем, что точка находится на этой линии, поэтому, чтобы найти b, мы можем подставить -2 вместо x и 3 вместо y:

Сначала мы можем умножить, чтобы получить .

Получается наше уравнение:

Либо вычитая 3 с обеих сторон, либо просто критически взглянув на это, мы можем увидеть, что b = 0,

Наш оригинал становится , или просто .

Сообщить об ошибке

← Назад 1 2 3 Далее →

Уведомление об авторских правах

Все ресурсы по алгебре 1

10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept

4.6: Параллельные и перпендикулярные линии

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

61388

Цели обучения

• Определение наклона параллельных и перпендикулярных линий.
• Найти уравнения параллельных и перпендикулярных линий

Определение параллели и перпендикуляра

Параллельные линии — это линии в одной плоскости, которые никогда не пересекаются. Две невертикальные линии в одной плоскости с наклонами \(m_{1}\) и \(m_{2}\) параллельны, если их наклоны одинаковы, \(m_{1}=m_{2}\) . Рассмотрим следующие две линии:

Рассмотрим соответствующие им графики:

Рисунок \(\PageIndex{1}\)

Обе линии имеют наклон \(m=\frac{3}{4} \) и, следовательно, параллельны.

Перпендикулярные прямые — это прямые, лежащие в одной плоскости и пересекающиеся под прямым углом (\(90\) градусов). Две невертикальные линии в одной плоскости с наклонами \(m_{1}\) и \(m_{2}\) перпендикулярны, если произведение их наклонов равно \(−1: m1⋅m2=−1\) . Мы можем найти \(m_{1}\) и получить \(m_{1}=\frac{−1}{m_{2}}\). В этой форме мы видим, что перпендикулярные линии имеют наклоны, которые являются отрицательными обратными величинами или противоположными обратными величинами. Например, если задан наклон

\(m=-\frac{5}{8}\)

, то наклон перпендикулярной линии обратно пропорционален:

\(m_{\perp}=\frac{8}{5}\)

Математическая запись \(m_{⊥}\) читается как «\(m\) перпендикулярно». Мы можем проверить, что два наклона образуют перпендикулярные линии, если их произведение равно \(−1\).

\(m\cdot m_{\perp}=-\frac{5}{8}\cdot\frac{8}{5}=-\frac{40}{40}=-1\quad\color{ Cerulean}{\checkmark}\)

Геометрически мы замечаем, что если линия имеет положительный наклон, то любая перпендикулярная линия будет иметь отрицательный наклон. Кроме того, подъем и разбег между двумя перпендикулярными линиями меняются местами.

Рисунок \(\PageIndex{2}\)

Наклоны перпендикулярных прямых противоположны обратным величинам, поэтому не забудьте найти обратную величину и изменить знак. Другими словами,

Если \(m=\frac{a}{b}\), то \(m_{\perp}=-\frac{b}{a}\)

Определение наклона перпендикуляра линию можно выполнить мысленно. Ниже приведены некоторые примеры

Таблица \(\PageIndex{1}\)

Данный уклон	Наклон перпендикулярной линии
\(m=\frac{1}{2}\)	\(м_{\перп}=-2\)
\(m=-\frac{3}{4}\)	\(m_{\perp}=\frac{4}{3}\)
\(м=3\)	\(m_{\perp}=-\frac{1}{3}\)
\(т=-4\)	\(m_{\perp}=\frac{1}{4}\)

Пример \(\PageIndex{1}\)

Определить наклон прямой, параллельной \(y=−5x+3\).

Решение :

Поскольку данная линия имеет форму пересечения наклона, мы можем видеть, что ее наклон равен \(m=−5\). Таким образом, наклон любой линии, параллельной данной линии, должен быть одинаковым, \(m_{∥}=−5\). Математическая запись \(m_{∥}\) читается как «\(m\) параллельно».

Ответ :

\(m_{∥}=−5\)

Пример \(\PageIndex{2}\)

Определить наклон линии, перпендикулярной \(3x−7y=21\) .

Решение :

Сначала найдите \(y\) и представите прямую в виде точки пересечения.

В этой форме мы можем видеть, что наклон данной линии равен \(m=\frac{3}{7}\), и, таким образом, \(m_{⊥}=−\frac{7}{3} \).

Ответ :

\(m_{⊥}=−\frac{7}{3}\)

Упражнение \(\PageIndex{1}\)

Найдите наклон линии, перпендикулярной \( 15х+5у=20\).

Ответить

\(m_{\perp}=\frac{1}{3}\)

Нахождение уравнений параллельных и перпендикулярных прямых

Мы видели, что график прямой полностью определяется двумя точками или одной точкой и ее наклоном. Часто вас будут просить найти уравнение линии с учетом некоторого геометрического соотношения, например, параллельна ли линия другой линии или перпендикулярна ей.

Пример \(\PageIndex{3}\)

Найдите уравнение прямой, проходящей через \((6, −1)\) и параллельной \(y=\frac{1}{2}x+2 \)

Решение

Здесь заданная линия имеет наклон \(m=\frac{1}{2}\), а наклон параллельной прямой равен \(m_{∥}=\frac{1}{2 }\). Поскольку вам дана точка и наклон, используйте форму точки-наклона линии, чтобы определить уравнение.

\(\begin{array}{cc}{\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(6,-1)}&{m_{\parallel} =\frac{1}{2}} \end{array}\)

Ответ :

\(y=\frac{1}{2}x-4\)

Важно иметь геометрическое понимание этого вопроса. Нас попросили найти уравнение прямой, параллельной другой прямой, проходящей через определенную точку.

Рисунок \(\PageIndex{3}\)

Через точку \((6, −1)\) мы нашли параллельную прямую, \(y=\frac{1}{2 }x−4\), показан пунктиром. Обратите внимание, что наклон такой же, как у данной линии, но точка пересечения \(y\) отличается. Если иметь в виду геометрическую интерпретацию, то будет легче запомнить процесс, необходимый для решения задачи.

Пример \(\PageIndex{4}\)

Найдите уравнение прямой, проходящей через \((−1, −5)\) и перпендикулярной \(y=−\frac{1}{4}x +2\).

Решение :

Данная линия имеет наклон \(m=−\frac{1}{4}\), поэтому \(m_{⊥}=+\frac{4}{1}=4\ ). Подставьте этот наклон и данную точку в форму точка-наклон.

\(\begin{array}{cc} {\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(-1,-5)}&{m_{\perp }=4}\end{array}\)

Ответ :

\(y=4x-1\)

Геометрически мы видим, что линия \(y=4x−1\), показанная пунктиром ниже , проходит через \((−1, −5)\) и перпендикулярен данной прямой.

Рисунок \(\PageIndex{4}\)

Не всегда данная линия имеет форму пересечения наклона. Часто приходится выполнять дополнительные действия для определения уклона. Общие шаги для нахождения уравнения линии изложены в следующем примере.

Пример \(\PageIndex{5}\)

Найдите уравнение прямой, проходящей через \((8, −2)\) и перпендикулярной \(6x+3y=1\).

Решение :

Шаг 1 : Найдите уклон \(м\). Сначала найдите наклон данной линии. Чтобы сделать это, найдите \(y\), чтобы изменить стандартную форму на форму пересечения наклона, \(y=mx+b\).

\(\begin{align} 6x+3y&=1 \\ 6x+3y\color{Cerulean}{-6x}&=1\color{Cerulean}{-6x} \\ 3y&=-6x+1 \\ \frac{3y}{\color{Cerulean}{3}}&=\frac{-6x+1}{\color{Cerulean}{3}} \\ y&=\frac{-6x}{3}+\ frac{1}{3}\\y&=-2x+\frac{1}{3} \end{aligned}\)

В этой форме вы можете видеть, что наклон равен \(m=−2=−\ frac{2}{1}\), и, таким образом, \(m_{⊥}=\frac{−1}{−2}=+\frac{1}{2}\).

Шаг 2 : Подставьте найденный вами наклон и заданную точку в форму уравнения точки-наклона для прямой. В этом случае наклон равен \(m_{⊥}=\frac{1}{2}\), а заданная точка равна \((8, −2)\).

\(\begin{выровнено} y-y_{1}&=m(x-x_{1}) \\ y-(-2)&=\frac{1}{2}(x-8) \ end{align}\)

Шаг 3 : Найдите \(y\).

Ответ :

\(y=\frac{1}{2}x−6\)

Пример \(\PageIndex{6}\)

Найдите уравнение прямой, проходящей через \(( \frac{7}{2}, 1)\) и параллельно \(2x+14y=7\).

Решение :

Найдите наклон \(m\), найдя \(y\).

\(\begin{align} 2x+14y&=7 \\ 2x+14y\color{Cerulean}{-2x}&=7\color{Cerulean}{-2x} \\ 14y&=-2x+7 \\ \frac{14y}{\color{Cerulean}{14}}&=\frac{-2x+7}{\color{Cerulean}{14}} \\ y&=\frac{-2x}{14}+\ frac{7}{14} \\ y&=-\frac{1}{7}x+\frac{1}{2} \end{aligned}\)

Данная линия имеет наклон \(m=−\ frac{1}{7}\), и поэтому \(m_{∥}=-\frac{1}{7}\). Мы используем это и точку \((\frac{7}{2}, 1)\) в форме точка-наклон.

\(\begin{align} y-y_{1}&=m(x-x_{1}) \\ y-1&=-\frac{1}{7}\left(x-\frac{7) {2} \right) \\ y-1&=-\frac{1}{7}x+\frac{1}{2} \\ y-1\color{Cerulean}{+1}&=-\frac {1}{7}x+\frac{1}{2}\color{Cerulean}{+1} \\ y&=-\frac{1}{7}x+\frac{1}{2}+\color{ Cerulean}{\frac{2}{2}} \\ y&=-\frac{1}{7}x+\frac{3}{2} \end{aligned}\)

Ответ :

\ (y=-\frac{1}{7}x+\frac{3}{2}\)

Упражнение \(\PageIndex{2}\)

Найдите уравнение прямой, перпендикулярной \(x−3y =9\) и проходящей через \((−\frac{1}{2}, 2)\).

Ответить

\(y=-3x+\frac{1}{2}\)

При нахождении уравнения прямой, перпендикулярной горизонтальной или вертикальной линии, лучше всего учитывать геометрическую интерпретацию.

Пример \(\PageIndex{7}\)

Найдите уравнение прямой, проходящей через \((−3, −2)\) и перпендикулярной \(y=4\).

Решение :

Мы знаем, что \(y=4\) является горизонтальной линией, и мы хотим найти перпендикулярную прямую, проходящую через \((−3, −2)\).

Рисунок \(\PageIndex{5}\)

Если провести линию перпендикулярно заданной горизонтальной линии, результатом будет вертикальная линия.

Рисунок \(\PageIndex{6}\)

Уравнения вертикальных прямых имеют вид \(x=k\). Поскольку он должен проходить через \((−3, −2)\), мы заключаем, что \(x=−3\) является уравнением. Все упорядоченные парные решения вертикальной линии должны иметь одну и ту же координату \(x\).

Ответ :

\(x=−3\)

Мы можем переписать уравнение любой горизонтальной линии \(y=k\) в форме пересечения наклона следующим образом:

\(y=0x +k\)

Записав в этой форме, мы видим, что наклон равен \(m=0=\frac{0}{1}\). Если мы попытаемся найти наклон перпендикулярной линии, найдя обратную обратную, мы столкнемся с проблемой: \(m_{⊥}=−\frac{1}{0}\), которая не определена. Вот почему мы позаботились о том, чтобы ограничить определение двумя невертикальными линиями. Помните, что горизонтальные линии перпендикулярны вертикальным линиям.

Ключевые выводы

• Параллельные линии имеют одинаковый наклон.
• Перпендикулярные линии имеют наклоны, противоположные обратным. Другими словами, если \(m=\frac{a}{b}\), то \(m_{⊥}=-\frac{b}{a}\).
• Чтобы найти уравнение прямой, сначала используйте данную информацию для определения наклона. Затем используйте наклон и точку на линии, чтобы найти уравнение, используя форму точка-наклон.
• Горизонтальные и вертикальные линии перпендикулярны друг другу.

Упражнение \(\PageIndex{3}\) Параллельные и перпендикулярные линии

Определение наклона параллельных и перпендикулярных линий.

1. \(y=−\frac{3}{4}x+8\)
2. \(y=\frac{1}{2}x−3\)
3. \(у=4х+4\)
4. \(у=-3x+7\)
5. \(y=−\frac{5}{8}x−12\)
6. \(y=\frac{7}{3}x+\frac{3}{2}\)
7. \(у=9x−25\)
8. \(у=-10x+15\)
9. \(у=5\)
10. \(х=-12\)
11. \(х-у=0\)
12. \(х+у=0\)
13. \(4x+3y=0\)
14. \(3x−5y=10\)
15. \(−2x+7y=14\)
16. \(−x−y=\frac{1}{5}\)
17. \(\frac{1}{2}x−\frac{1}{3}y=-1\)
18. \(−\frac{2}{3}x+\frac{4}{5}y=8\)
19. \(2x−\frac{1}{5}y=\frac{1}{10}\)
20. \(−\frac{4}{5}x−2y=7\)

Ответить

1. \(m_{∥}=−\frac{3}{4}\) и \(m_{⊥}=\frac{4}{3}\)

3. \(m_{∥}=4\) и \(m_{⊥}=−\frac{1}{4}\)

5. \(m_{∥}=−\frac{5}{8}\) и \(m_{⊥}=\frac{8}{5}\)

7. \(m_{∥}=9\) и \(m_{⊥}=−\frac{1}{9}\)

9. \(m_{∥}=0\) и \(m_{⊥}\) не определены

11. \(m_{∥}=1\) и \(m_{⊥}=−1\)

13. \(m_{∥}=−\frac{4}{3}\) и \(m_{⊥}=\frac{3}{4}\)

15. \(m_{∥}=\frac{2}{7}\) и \(m_{⊥}=−\frac{7}{2}\)

17. \(m_{∥}=\frac{3}{2}\) и \(m_{⊥}=-\frac{2}{3}\)

19. \(m_{∥}=10\) и \(m_{⊥}=−\frac{1}{10}\)

Упражнение \(\PageIndex{4}\) Параллельные и перпендикулярные линии

Определите, являются ли линии параллельными, перпендикулярными или ни тем, ни другим.

1. \(\left\{\begin{выровнено}y&=\frac{2}{3}x+3\\y&=\frac{2}{3}x−3\end{выровнено}\right. \)
2. \(\left\{\begin{выровнено}y&=\frac{3}{4}x−1\\y&=\frac{4}{3}x+3\end{выровнено}\right.\)
3. \(\left\{\begin{выровнено}y&=−2x+1\\ y&=\frac{1}{2}x+8\end{выровнено}\right.\)
4. \(\left\{\begin{выровнено}y&=3x−\frac{1}{2}\\ y&=3x+2\end{выровнено}\right. \)
5. \(\left\{\begin{выровнено}y&=5\\x&=-2\end{выровнено}\right.\)
6. \(\left\{\begin{выровнено}y&=7\\y&=-\frac{1}{7}\end{выровнено}\right.\)
7. \(\left\{\begin{выровнено}3x−5y&=15\\ 5x+3y&=9\end{выровнено}\right.\)
8. \(\left\{\begin{выровнено}x−y&=7\\3x+3y&=2\end{выровнено}\right.\)
9. \(\left\{\begin{выровнено}2x−6y&=4\\−x+3y&=-2 \end{выровнено}\right.\)
10. \(\left\{\begin{выровнено}−4x+2y&=3\\6x−3y&=-3 \end{выровнено}\right.\)
11. \(\left\{\begin{выровнено}x+3y&=9\\2x+3y&=6 \end{выровнено}\right.\)
12. \(\left\{\begin{выровнено}y−10&=0\\x−10&=0 \end{выровнено}\right.\)
13. \(\left\{\begin{выровнено}y+2&=0\\2y−10&=0 \end{выровнено}\right.\)
14. \(\left\{\begin{выровнено}3x+2y&=6\\2x+3y&=6 \end{выровнено}\right.\)
15. \(\left\{\begin{выровнено}−5x+4y&=20\\10x−8y&=16 \end{выровнено}\right.\)
16. \(\left\{\begin{align}\frac{1}{2}x−\frac{1}{3}y&=1\\\frac{1}{6}x+\frac{1}{ 4}y&=−2\end{выровнено}\вправо. \)

Ответить

1. Параллельный

3. Перпендикуляр

5. Перпендикуляр

7. Перпендикуляр

9. Параллельный

11. Ни

13. Параллельный

15. Параллельный

Упражнение \(\PageIndex{5}\) Уравнения в форме точка-наклон

Найдите уравнение прямой

1. , параллельной \(y=\frac{1}{2}x+2\) и проходящей через \((6, −1)\).
2. Параллельно \(y=−\frac{3}{4}x−3\) и проходит через \((−8, 2)\).
3. Перпендикулярно \(y=3x−1\) и проходит через \((−3, 2)\).
4. Перпендикулярно \(y=−\frac{1}{3}x+2\) и проходит через \((4, −3)\).
5. Перпендикулярно \(y=−2\) и проходит через \((−1, 5)\).
6. Перпендикулярно \(x=\frac{1}{5}\) и проходит через \((5, −3)\).
7. Параллельно \(y=3\) и проходит через \((2, 4)\).
8. Параллельно \(x=2\) и проходящей через (7, −3)\).
9. Перпендикулярно \(y=x\) и проходит через \((7, −13)\).
10. Перпендикулярно \(y=2x+9\) и проходит через \((3, −1)\).
11. Параллельно \(y=\frac{1}{4}x−5\) и проходит через \((−2, 1)\).
12. Параллельно \(y=−\frac{3}{4}x+1\) и проходит через \((4, \frac{1}{4})\).
13. Параллельно \(2x−3y=6\) и проходит через \((6, −2)\).
14. Параллельно \(−x+y=4\) и проходит через \((9, 7)\).
15. Перпендикулярно \(5x−3y=18\) и проходит через \((−9, 10)\).
16. Перпендикулярно \(x−y=11\) и проходит через \((6, −8)\).
17. Параллельно \(\frac{1}{5}x−\frac{1}{3}y=2\) и проходит через \((−15, 6)\).
18. Параллельно \(−10x−\frac{5}{7}y=12\) и проходит через \((−1, \frac{1}{2})\).
19. Перпендикулярно \(\frac{1}{2}x−\frac{1}{3}y=1\) и проходит через \((−10, 3)\).
20. Перпендикулярно \(−5x+y=−1\) и проходит через \((−4, 0)\).
21. Параллельно \(x+4y=8\) и проходит через \((−1, −2)\).
22. Параллельно \(7x−5y=35\) и проходит через \((2, −3)\).
23. Перпендикулярно \(6x+3y=1\) и проходит через \((8, −2)\).
24. Перпендикулярно \(−4x−5y=1\) и проходит через \((−1, −1)\).
25. Параллельно \(−5x−2y=4\) и проходит через \((\frac{1}{5}, −\frac{1}{4})\).
26. Параллельно \(6x−\frac{3}{2}y=9\) и проходит через \((\frac{1}{3}, \frac{2}{3})\).
27. Перпендикулярно \(y−3=0\) и проходит через \((−6, 12)\).
28. Перпендикулярно \(x+7=0\) и проходит через \((5, −10)\).

Ответить

1. \(y=\frac{1}{2}x−4\)

3. \(y=−\frac{1}{3}x+1\)

5. \(х=−1\)

7. \(у=4\)

9. \(у=-х-6\)

11. \(y=\frac{1}{4}x+\frac{3}{2}\)

13. \(y=\frac{2}{3}x−6\)

15. \(y=−\frac{3}{5}x+\frac{23}{5}\)

17. \(y=\frac{3}{5}x+15\)

19. \(y=-\frac{2}{3}x-\frac{11}{3}\)

21.

No related posts.